Conjunction of planets: procedures and examples from Indian astronomy texts

Abstract

The planetary conjunctions have always procured a very prominent place in astronomy texts from India. The calculations aim at the determination of exact instant of conjunction by method of iteration and prediction of the possibility of occultation, grazing or otherwise. We discuss details of the procedure from a text of 17th century and offer two examples from texts of 16th century devoted to worked examples based on different methods. One of them gives an angular separation of 1′, which would have been a challenge to observe. The possible sources of error in the estimates of longitude and speed are discussed. We also infer that the approximations in the estimation of angular diameter and node led to errors in the prediction of type of occultation.

1 Introduction

The starlit sky attracts attention of all when there are two bright objects almost touching each other. Almost all astronomy texts devote a chapter for calculations pertaining to conjunctions. The procedure is similar to the calculation of eclipses. The scheme of classification is based on the relative angular sizes. The general names are samāgama and yuddha, while the conjunctions with bright stars are defined as nakṣatragrahayuti. The stone inscriptions have recorded a good number of conjunctions (Shylaja & Geetha 2016, 2021; Tanikawa et al. 2019). The details of definitions and calculations are available in almost all astronomy texts. Here we present the basic definitions from Sūryasiddhānta (SS hereafter) in Section 2, a detailed commentary from a recently unearthed (Shylaja & Seetharama 2020, 2021) Kannaḍa text dated 1604 CE in Section 3. This text named Gaṇitagannaḍi (GG, hereafter) remained unnoticed for almost four centuries till the contents in a script called Nandināgari were deciphered. This is a commentary on a text called Vārśika Tantra written by a scholar named Viddaṇācārya; this commentary is written by Shankaranārāyaṇa Jōisaru. The section includes rationale for the procedure. A worked example from the text (Shubha 2020) Brahmatulya Udāharaṇam (BU hereafter) by Viśvanātha is described in Section 4. Another worked example by the same author based on Grahalāghavam of Ganeśa Daivajña from an unpublished manuscript is also included. In the latter case, the computational errors could be sorted out to get the time of conjunction. The possible sources of errors are discussed in Section 5.

2 Definition of conjunctions in texts

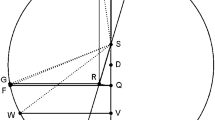
Sūryasiddhānta classifies the planetary conjunctions into five categories, depending on the minimum angle of approach (Shukla 1985), which can be understood with the help of Figure 1.

Figure 1

Definition of different types of conjunctions.

Let the separation between the two planets be d and the sum of the diameters be s. Here, 1° (double the angular size of moon) is taken as the reference.

Based on the values of s and d, five different possibilities are defined in the Sūryasiddhānta, which is explained in Figure 1 along with current terminologies.

• 1. Ullekha, when d = s, the discs are just touching each other. This is grazing occultation.

• 2. Bheda, when d < s, one disc is able to partially or wholly cover the other, this means one disc is piercing on to another occultation.

• 3. Apsavya, when d > s, but one of the planets is very small. The limit for d is taken as 1°. This may be called close conjunction.

• 4. Amṣu-vimarda, when d > s, and both the discs are quite large. This can happen only in the case of Jupiter and Venus.

• 5. Samāgama, when d ≫ 1°. This is the general word for conjunction.

This leads us to a basic question on how they estimated diameters of the planets. Venus, with the largest angular diameter is barely recognizable as a disc by naked eye. A logical deduction would be that they observed as many close conjunctions and occultations as possible and fixed a limit based on the resolution and duration of the event. It is unfortunate that the relevant discussions are not available in any text. The average values of the diameters called bimba are listed; the distance to the planet (from the Earth) is estimated and appropriate correction is applied.

We had an opportunity to verify the potential of naked eye observations of the conjunctions on 21 December 2020. There was a campaign to monitor the event of the conjunction of Jupiter and Saturn at 6.1′. The sky gazers were able to distinguish the two dots without much effort. Thus, we can declare that the naked eye can distinguish angles slightly less than about 6′ (for comparison, the separation between Alcor and Mizar is 12′). Thus, if there was a conjunction, say within 4′, it would assume great importance. If the planets involved are the brightest (Venus and Jupiter), this may increase to about 6′.

Different texts give the same values for the angular diameters as shown in Table 1. All the units in kalā and vikalā (arcminutes and arcseconds). It must also be remembered that the only tools they had to see the planets were the two eyes. It is not explicitly stated anywhere as to how these values were arrived at.

Table 1 Diameters of planets in some selected texts.

Gaṇitagannaḍi states that these diameters in yojanas (~ 5–8 km) have to be multiplied by 2 and radius, and divided by the sum of radius and hypotenuse to get the rectified diameters, which when divided by 15, will give the diameters in arcminutes.

Gaṇitagannaḍi states that the values listed are in units of arcminutes (kalā) multiplied by 10. We see that the procedure later requires a division by 10 and therefore, the provision is made already in the definition itself.

The word Bheda or Bhedayuti is used for occultations in many books: The most recent being the 19th century monograph on the transit of Venus by Raghoonathacharry (Shylaja 2012). The event occurred just before noon on 12 November 1874. Quite interestingly, although this is a day time event, the author explains how to locate the moon and Venus (in broad day light) and urges the readers to observe the occultation. The other book, which discusses the planetary conjunctions, is the Siddhānta Darpaṇa of Chandrasekhara Samanta (Upadhyaya 2013). Here, the technique of using the reflection to measure the angular separation is suggested. Many text books (in Kannaḍa) of modern astronomy utilize the word bheda yuti as well as āchhādane for occultation (Chikkanna 1914; Naraharaiah 1924).

3 Explanation in GG and rationale for procedure

The conjunctions of (star-like) planets namely, Mars and the others, are simple consequences of their motion, which may be direct or retrograde. Gaṇitagannaḍi (GG) defines the event in a much more detail in the seventh chapter as the conjunction of planets occur among themselves. The various possibilities are explained.

The procedure followed as prescribed in SS are:

• (a) Calculation of the instant of conjunction,

• (b) Calculation of the vikṣepa (north-south coordinates),

• (c) Compare the difference of vikṣepa with the sum of diameters to identify the type of conjunction.

3.1 Instant of conjunction

First step is to find the true positions of the planets and their gati (speed per day) for the given date. It commences with the day count ahargaṇa, getting the mean longitudes from the first equation, called mandaphala and subsequently, from the second equation called śīghraphala. The calculation is for Ujjain and corrections for other places have to be applied. In the example, in BU, the location of the observer is Vāranāsi. Depending on their relative position, one can infer if a conjunction is due or if it is just over.

The difference between their longitudes will have to be divided by the difference in their speed to get the date of conjunction to a first approximation. Then, the true longitudes are calculated again for that instant; the small difference in longitude is divided by the difference in instantaneous speed to get the revised instant of conjunction. Again, the longitudes are calculated for that instant and if they are unequal, the procedure is repeated to fine-tune the instant. This process of iteration called asakṛit is repeated till the longitudes become equal.

3.2 Difference in latitudes

At the instant of conjunction, the north–south coordinate called vikṣepa need to be calculated. The orbits of the planets are inclined to the ecliptic, though by a small angle, as shown in Figure 2. The orbit of the planet intersects the ecliptic at two points. Here, the ascending node is represented by N₁. The longitude calculated is for point P as the sum of $\gamma$A and $\gamma$N₁. By definition, the quantity measured along the hour circle is called vikṣepa (Venketeswara Pai & Shylaja 2016). However, since the angle is small (AP), marked along the latitude circle itself is called vikṣepa here.

Figure 2

(a) Orbit of planet and ecliptic and (b) vikṣepa of the planet is AP; i is the angle of inclination of the orbital plane to the ecliptic.

It may be seen that AP is given by:

$$ {\text{AP}} = i\,\,{\text{sin}}\,\,N_{{1}} P, $$

(1)

where i is the angle of inclination of the orbit and NP′ is the difference between the longitudes of the planet and node.

It can also be inferred that the maximum value that PP′ can take is $\iota$ itself. This is listed as parama vikṣepa in SS. Therefore, we have to find the position of node and difference in longitudes.

This is corrected further for the latitude of the observer just as in the case of solar eclipse to get the direction of approach of two planets in the sky.

We provide the procedure in GG (Shylaja & Seetharama Javagal 2021) for a comparison, described as follows:

“The pāta in bhāgas (multiplied by 10) for the five planets from Kuja are being told. Kuja 40, Budha 20, Brihaspati 80, Śukra 60, Śani 100; these are divided by 30 to get units of rāśi. The pāta of Budha and Śukra are subtracted from the planets corrected for mandaphala and śīghraphala.

The pātas have been obtained from Sūryasiddhānta as given in the verse starting with manudarāstu. The desired number of years are multiplied with these bhagaṇas for the kalpa and divided by the kalpābdya of 4,320,000,000. Then rāśyādi are calculated by dividing by 12 and other factors. As mentioned earlier, the pātas are subtracted from the graha and its Rsine values are taken. They are multiplied by the numbers 7$\mid$30 for Mangala, 10 for Budha, 5 for Guru, 10 for Śukra and 10 for Śani; then divided by calabāṇa to get respective vikśepa, with the appropriate sign for north or south. If the bhujaphala is Tulādi, it is dhana, to north. If the pāta is subtracted from it is Tulādi and vikṣepa is south. For Meśādi it is north. Now the yuddha and samāgama of the planets are being told. To start with one has to find if the time of samāgama and then check if it is samāgama or yudhha for planets like Mars. For the desired date the true positions of the two planets are found. If both are in direct motion and if the larger planet is ahead of the smaller, it should be understood that samāgama is yet to take place. Ahead means it [the longitude] is larger. If the faster planet is ahead, the samāgama has taken place already. One of them may be in retrograde motion; if the slow planet in direction motion is behind the faster planet in retrograde motion is ahead, it is to be understood that the samāgama is yet to take place. If the slow planet [in retrograde motion] is behind the fast planet [in direct motion] then the samāgama has taken place already. Both of them may be in retrograde motion; the slower one ahead of the faster one means samāgama is over; the slower one behind the faster one means samāgama implies that [yoga] is yet to take place.

Now we will find out how to make these [longitudes], which are continuously varying, equal in rāśi, bhāga, lipti [to get the time of samāgama].”

The first part defines the pāta, longitudes of the nodes. These are to be subtracted from the longitudes of the respective planets. The nodes are points of intersection of the orbit with the plane of the ecliptic. Generally, all calculations are based on Sūryasiddhānta, which gives the number of revolutions of the node pāta in a kalpa. For example, the node of Kuja would have made 204 revolutions in a kalpa. The computation is as per the rule of 3; for one revolution of pāta, 4320000000/204 bhagaṇas are needed; for the given year, how many bhagaṇas are calculated by rule of 3. The integers of the final number obtained are omitted because that represents the completion of 360°. The fraction is converted to rāśi, aṃśa, kala and vikala (zodiacal sign of 30°, degrees and subunits arcminutes and arcseconds).

Here, the values of the pāta (units are bhāga, degrees) are listed as:

Kuja (Mars) 4, Budha (Mercury) 2, Guru (Jupiter) 8, Śukra (Venus) 6 and Śani (Saturn) 10.

This idea is incorporated in Karaṇakutūhala (Balachandra Rao & Uma 2008) by providing the pāta for the epoch 1183 CE. The procedure is described in detail for the moon to get the vikṣepa (latitude), which require the angles of inclinations of the orbits with reference to the plane of ecliptic (in the case of moon, it was taken as 270′). It is a very small angle and so most of the texts do not discuss this procedure. Ideally one should use the declination, which will be the projection of PP′ on the hour circle. Thus, vikṣepa is added to the declination δ, of the point P, which is on the ecliptic given by:

$$ {\text{sin}}\,\beta = {\text{ sin}}\,\,\iota\,\,{\text{sin}\,\,}\lambda, $$

(2)

, where $\lambda$ is the longitude of P measured from the first point of Aries and $\iota$ is the angle of the plane of orbit with the ecliptic, which is a constant. In all texts, the value of $\iota$ is provided as parama vikṣepa, the maximum value of latitude. In GG the constants converted to the units required for calculation for each of the planets are provided: 7$\mid$30 for Mangala (same as Kuja, Mars), 10 for Budha (Mercury), 5 for Guru (Jupiter), 10 for Śukra (Venus) and 10 for Śani (Saturn).

It may be seen that these are related to the inclination angles of the plane of the orbits, so that

$$ R\,{\text{sin}}\,v \, = \,{\text{constant}}\,\times \,R\,{\text{sin}}(\lambda_{p} - \lambda_{g} ){/}calab\overline{a}na, $$

(3)

where v is the vikṣepa and the longitude difference of the node, pāta and the planet, graha is ($\lambda$_p − $\lambda$_g). The earth–planet distance, calabāṇa has been defined with reference to a constant 10 (in the chapter chāyādhikāra). Hence, here, the pāta is given as multiplied by 10. This procedure (Shylaja & Seetharama Javagal 2021), thus is equivalent of determining PP′ in Figure 2 in terms of NP ($=$ difference in longitudes of the planet and its node) and $\iota$, the angle of inclination of the orbit to the ecliptic.

The true positions of the two planets have to be corrected for the location of the observer. This is similar to the case of a solar eclipse where, to start with the longitudes of the Sun and moon that are obtained for the specific day. Two corrections called āyana and ākṣa dṛkkarma are applied based on the latitude and longitude of the observer using the values of ecliptic latitude, vikṣepa. This application of this correction is named dṛkkarma. The same procedure is to be followed for the two planets: The slower is treated as the Sun and the faster akin to the moon.

3.3 Type of conjunction

The next step is to get the diameters of the planets (called bimba) and compare their difference in vikṣepa with the sum of diameters. This is explained in a single sentence in GG as:

The bimba (diameter) of the planets are obtained from [these values]-Kuja 40, Budha 60, Jiva (Guru) 70, Śukra (80) and Śani (50). These are added to calabāṇa and divided by 10 to get [diameter] in liptā.

The angular diameters of the planets vary since their distance from the Earth continuously varies. The term calabāṇa defined earlier is a measure of the planet–Earth distance. The mean diameters (multiplied by 10) are provided as Kuja 40, Budha 60, Jiva (Guru) 70, Śukra (80) and Śani (50), in units of arcminutes, and corrected to get true diameters at that instant. These diameters are not realistic as explained in Section 2. We may also see the limitations of this method since they had no (telescope-like) device to measure the angular sizes <1′. The conjunctions predicted from longitudes are quite reliable and the sub-classification into any of the five categories may be in error.

Various possibilities of planetary movements leading to conjunctions are explained in very crisp sentences.

The possibilities are explained with the help of Figure 3, which shows two planets A and B. The angles of inclination of the orbits of planets are different and the nodes (points of intersection with ecliptic) also occur at different positions. Here, the node is shown to coincide with the first point of Aries for ease of explanation. On the given date, let A and B represent the positions; AM and BN are the vikṣepa and γM and γN are the dhruvā (longitudes). The text discusses the various possibilities of differences in their rate of motion and the type of motion: Direct or retrograde. These sentences are summarized in Table 2. Figure 2 corresponds to the longitude of B is greater than that of A; the other possibility namely B < A also is included in Table 2.

Figure 3

Two planets A and B are shown in their respective orbits, which are inclined to the ecliptic; the orbits are shown to intersect at the first point of Aries for illustration only.

Table 2 Conjunction for two planets A and B considering the positions on any given date, differences in their rate of motion and the type of motion: direct or retrograde.

From this and the difference in vikṣepa, one can deduce if the angular separation between the discs is less than a degree or more. That defines if it is a yuddha or samāgama.

The calculation for the conjunction of a star with a planet is relatively easy, since the movement of only the planet is involved. This is described as nakṣatragraha yoga. The difference in longitudes of the star and the planet is divided by the rate of motion of the planet to get the duration to the instant of conjunction—whether it is yet to occur or if it is already over. The true position corresponding to that instant is again calculated. After applying the ayanāṃśa (precession), we get the (precession corrected) sāyana longitude with which the declination can be calculated. Depending on the sign of the declination, krānti, it is added to or subtracted from its vikṣepa. This gives the angular separation of the planet from the star at the time of conjunction.

Thus, we see that the procedure for calculation of conjunctions is explained in this text with every detail. Other texts provide very brief descriptions and do not discuss the case when one of the planets (or both) is in retrograde motion.

4 Worked examples

4.1 Example from Brahmatulya Udāharaṇam

GG, which we discussed till now, is classified as a karaṇa text, a manual for calculations. There are some texts, which provide solved examples. Brahmatulya Udāharaṇam (BU) by Viśvanātha is one such text and here, we provide the solution explaining all the necessary steps.

The example chosen is for the date śaka 1531, Magha 30, which corresponds to 1610 CE, new moon, corresponding to 23rd February as we see below. The ahargaṇa count is 155951 and the precession correction (ayanāṃśa) is 18°$\mid$06′, which when added to the longitude renders it comparable to the longitudes from currently available software. This (corrected) value is used to get the declination.

• Step 1. Calculation of the mean and true positions of the Sun and planets from ahargaṇa (the day count). The corrections are carried out step by step for the longitude and latitude of the observer; the speed also is obtained based on the angular separation from apogee. The angles are written as rāśi$\mid$°$\mid$′$\mid$′′ (units are rāśi$\mid$deg$\mid$arcmin$\mid$arcsec). Rāsi corresponds to the number of zodiacal sign. However, for calculations, it can be considered as another unit equal to 30°. If rāśi is converted to degrees, it would be written as °$\mid$′$\mid$′′.

The instant of a new moon occurs when the longitude was 316°$\mid$46′$\mid$51′′. This corresponds to 14:12:45 UT on 23 February 1610 (it should be remembered that all the calculations are carried out without applying the precession correction).

The details of computations are given in step by step in Appendix A. The final values of longitudes are (units are rāśi$\mid$deg$\mid$arcmin$\mid$arcsec):

Venus $=$ 9$\mid$28$\mid$41$\mid$55 $=$ 298°41′15′′ and Saturn $=$ 9$\mid$26$\mid\mid$20$\mid$17 $=$ 296°20′17′′.

It should be noted that Venus is already ahead of Saturn (there is an error in the longitude of Venus as discussed in the next section).

The instantaneous speeds are also computed as:

$$ \frac{dm}{{dt}} = {\text{constant}} \times \frac{d}{dt}\left( {{\text{sin}}\,\,m} \right) \, = {\text{ constant}} \times {\text{cos}}\,m, $$

(4)

where m is the angle between the mean position and apogee. The constants are calculated separately for each planet. In the first step, the mean value mandakendra and in the second step, the final corrected value called śīghra kendra are used. This is crucial since the speed of the planet varies considerably (relative to the Earth) depending on the sun–earth–planet geometry.

In this case, the speeds are 75′11′′ and 7′11′′ per day for Venus and Saturn, respectively. The difference in speed is $=$ 68′. Generally, the speed is provided in units of arcminutes per day.

• Step 2. The difference in longitudes is divided by the difference in speed to get the instant of conjunction. The longitudes are recalculated for the instant of conjunction. If they are not equal, the procedure is repeated by several steps, till they become equal.

The difference in longitudes is 141°38′ (as given in the text; there is a typographical error: It should have been 131°38′). Dividing this by the difference, gati 68′, we get the time interval of the event from the date of calculation.

Therefore, the conjunction termed grahayuddham occurred for 2 days 4 h and 58 min before the instant of new moon. This date is given as the 12th day after full moon at 55$\mid$2 ghaṭikā corresponding to 11:32:49 UT on 21st February. This is in error, which we have discussed in the next section.

The longitude of Venus (and Saturn) at that time was 9$\mid$26$\mid$5$\mid$20.

• Step 3. The vikṣepa or śara (ecliptic latitude) of the planets are calculated at the time of conjunction. This is decided by the inclination of the orbit to the ecliptic and position of the nodes. Nodes, called pāta, and their slow movement is defined in Sūryasiddhānta, facilitating the fixing of its position on the same lines as the true longitude of the planet itself is calculated.

The śara are given in aṅgula (3′ $=$ 1 aṅgula), for Venus 7$\mid$36 S, for Saturn 16$\mid$13 S.

The difference is 8$\mid$27 aṅgula (corresponds to 1′).

• Step 4. The diameters are calculated based on the mean value and the actual distance of the planet from the Earth. Here, the assumption is that the diameter varies inversely with distance. The estimated diameters are 2$\mid$9 and 1$\mid$8 (in units of aṅgula) for Venus and Saturn, respectively.

• Step 5. The difference in latitudes is compared with half the sum of diameters to fix the type of conjunction.

The estimated diameters are 2$\mid$9 and 1$\mid$8 for Venus and Saturn, respectively. Half of their sum is 1$\mid$38. The śara is recalculated for the instant of conjunction. For Venus, it is 7$\mid$36, which is the same as that of Saturn. The difference works out to be 0$\mid$9 (the unit is here aṅgula$\mid$vyaṅgula), which is less than half the sum of diameters. The separation is very small, 9 vyaṅgula, which is about 1 arcmin. Therefore, this is called a grahayuddha, which is occultation.

Finally, the elongation, ascendant and hour angle at the time of conjunction is calculated just as in the case of solar eclipse (considering the faster planet to be equivalent of moon and the slower planet to be the Sun). A small correction will have to be made for the timing of the conjunction accordingly. The difference in declination is recalculated. This computation is included for the completion of procedure, ignoring the visibility criterion (when they were below the horizon). Even with an angular separation of about 3′, would have been a challenge to distinguish the two dots, owing to the dazzling brightness of Venus.

The conjunction occurred on 24th April at 20$\mid$20 UT as per Stellarium and Xavier Jubier (http://xjubier.free.fr/en/site_pages/astronomy/ephemerides.html). The errors and possible corrections are discussed in Section 5.

4.2 Example from Grahalāghava Ṭika

The other example of computation is from an unpublished manuscript called Grahalāghava Ṭīka (GT), which is also written by the same author Viśvanātha. Figure 4 shows the title page of the manuscript was procured from BORI, Pune.

Figure 4

Unpublished manuscript Grahalāghava Tīka by Viśvanātha.

Here, the computation is based on the Grahalāghava by Ganeśa Daivajña. The procedure and rationale are explained and compared with that of Karaṇakutūhala of Bhāskarācārya in Balachandra Rao & Uma (2008).

The example provided in the text corresponds to the conjunction of Mars and Saturn in śaka 1532 and the month Vaiśākha, which is just 3 months later than the conjunction discussed above (of Saturn and Venus). The day of calculation is the 10th day after new moon, which is 2nd May 1610 CE. The precession correction is given as 18°8′.

The procedure starts with the calculation of the day count ahargaṇa, which is used to get the mean longitudes of the Sun, Mars and Saturn for the given day. Here, the procedure utilizes a cycle called cakra to derive an intermediate epoch and the calculations are further refined from then onwards. This simplifies the computations. The two corrections to be applied subsequently, are provided as a function of the anomalies for every 15° and can be interpolated; this further reduces the computation time. Another additional improvement is the application of correction thrice. The first step applies half the value of the correction for conjunction (second equation, decided by the relative positions of the Sun, the Earth and the planet). The second step applies the correction for elliptical orbit (first equation, manda) and the third step derives a fresh correction for the second equation. The speeds of the planets by virtue of geometry of the location are calculated. The advantages of this method had been realized by many astronomers—as reflected by the immense popularity of the text all over India.

The mean values determined as the first step are listed as 0$\mid$23$\mid$55$\mid$38, 9$\mid$0$\mid$33$\mid$51 and 10$\mid$5$\mid$45$\mid$59 for the Sun, Mars and Saturn, respectively. The gati or speeds are 57$\mid$56, 42$\mid$50 and 3$\mid$3 arcmin per day. The details are provided in Appendix B. The difference in longitudes is 216$\mid$25 arcmin. The difference in speeds is 39$\mid$47. The division provides date of the conjunction, which occurred 5 days 26 ghați and 23 vighațis ago. That was on vaiśākha śukla 4 (4th day after new moon).

From the daily motion, gati, the movement of Mars and Saturn are calculated for that instant as 3$\mid$53$\mid$0 and 0$\mid$16$\mid$35, respectively. The longitude for both, at the instant of conjunction is 10$\mid$2$\mid$42$\mid$9. The positions of the nodes are 1$\mid$10 and 3$\mid$10, respectively. The difference in longitudes of planet and the respective nodes is multiplied by constants corresponding to the angle of inclination and divided by the planet–Earth distance. The corresponding śara (latitudes) are 16$\mid$11 S and 14$\mid$7 S in units of aṅgula. The difference is 2$\mid$04 aṅgula corresponding to 6′ (aṅgula $=$ 3′).

The diameters are calculated based on the distance, as 1$\mid$50 and 1$\mid$33, respectively; half of the sum called mānaikyakhanḍa, is 2$\mid$47 aṅgula (this should have been 1$\mid$47, error by the scribe). The difference in śara is 2$\mid$04. Therefore, there is no bhedayoga, occultation.

Thus, according to this example, the conjunction with separation of 6′ occurred on 28th April. According to Stellarium and Xavier Jubier, it occurred on 30th April at 02:32 UT. The error and possible correction values are discussed in the next section.

5 Discussion on procedure and possible sources of error

For both examples, the computations are verified with Stellarium and Xavier Jubier.

5.1 Conjunction of Mars and Saturn on 4th February

The reference instant chosen for calculation was the instant of a new moon, we were able to make use of the precise calculations from Prof. Mitsuru Soma of NAOJ (with ∆t $=$ 100 s) (Personal Communication), who provided the apparent longitudes, which are corrected for stellar aberration and the light path from the planets to the Earth. The other two sources do not specify if these corrections are incorporated.

As explained earlier, we are not discussing the type of conjunction (occultation or otherwise) since that depends on the angular diameters. The values of bimba provided in these texts are not realistic.

The computations of Stellarium and Xavier Jubier show that the conjunction occurred the day after new moon, 24th February at 20:20 UT, as against the result from sub-section 4.1 as 3 days before new moon. We verified all the computations step by step as given in BU, since there are two errors in the calculations.

• (a) There is an error of 3 days in the prediction of conjunction.

• (b) The angular separation at the instant of conjunction also appears to be in error.

The first step is fixing the instant of new moon. We compared the timings with the ephemeris provided by Stellarium and Xavier Jubier (with ∆t $=$ 89 s). The BU values are listed with precession correction in Table 3. As mentioned earlier, the precession correction has been added for ease of comparison.

Table 3 Longitudes of the Sun, Venus and Saturn at the instant of new moon.

It may be seen that the instant of new moon itself differs from the others. It may be recalled that all computations are done without the precession corrections. Here, for the sake of comparison, we have added the correction of 18$\mid$06 as stated in the text itself. We found that in Grahalāghava (Balachandra Rao & Uma 2006), there is another solved example of an eclipse for the same year 1610 CE with the precession correction as 18$\mid$09. This correction reduces the error for the position of the Sun; but not the discrepancy for the longitudes of planets.

Similarly, we verified the instant of conjunction, which seems to be completely off. The three computations give 20$\mid$40 UT on 24th (after the new moon), while BU gives it as 22nd before the new moon. The difference in the longitudes of Saturn and Venus is reflected in the latitude calculation too, resulting in a large difference in the angular separation. This calculation also involves the position of the node, which we could not verify for accuracy.

We investigated the possible source of error in the longitude calculations.

• (a) The derivation is done in 2 iterations and as a first step, we extended it to 4 iterations. This changed the time of conjunction and brought it within a few minutes after the new moon.

• (b) We had three manuscripts of BU for the study. One of them has some extra tables written on the margin in the context of getting true longitudes. One table is called Rāmabīja, the corrections provided by Rāmachandracārya. This correction was applied as a second alternative for correction. This altered the time of conjunction to the next day after new moon.

• (c) We used for a third alternative of using the second table, which is named Anyokta udārṇave also attributed to Rāmachandracārya. It specifically states that these corrections are necessary for use with the sighting tube (nalikāyantrayogyasca). Figure 5 shows the manuscript page with these tables added on the margins.

Figure 5

(a) Manuscript page referred in the text. The two tables named Rāmabīja and Anyokta udārṇave added on the left margin. (b) Close-up view of the tabular entries.

We applied the corrections from both the tables separately for the mean positions (as stated in the text) and recalculated the instant of conjunctions. The difference in declination as per the other sources ranges from 1.5 to 1.7′. The results are shown in Table 4. We found that the effect of corrections as Rāmabīja correction is too small and it leads to the conjunction happening on 24th, but 8 h earlier than the other predictions. Udārṇava correction is in excess; it takes it to 25th, 15 h later than the predictions by others. The reference to the latter on its application is yet to be understood.

Table 4 Comparison of differences in longitudes and the instant of conjunction (UT).

Thus, we found that the procedures given in the text give fairly accurate results for the time of conjunctions if the appropriate corrections are incorporated in the calculations of longitudes.

The error in the angular separation in latitude requires fixing the nodes accurately. With the Rāmabīja corrected values for longitudes, we get the separation as 3′.

The error in angular diameter can be corrected by incorporating the exact values from telescopic observations.

Table 4 shows that the corrections as per the second table in the manuscript are essential to match with observations. This leads to a possibility of correcting the positions of nodes, which will correct the declination also.

As discussed earlier, the angular diameters of the planets are erroneous and therefore, the type of conjunction (whether it is occultation or grazing occultation or a close passage) declared cannot be corrected.

Further, we noted from naked eye observations on 21 December 2020, the naked eye limit is about 2–3′. The angular separation of 1.6 or 2′ is a challenge to observe. An observational record of this event even before several hours of the conjunction (at sun rise) would have provided a limit on the resolving power of the human eye. Figure 6 depicts the probable view of the event; a measurement of this would have been very useful in verification of the calculations.

Figure 6

View at dawn of 25 February 1610 (from Stellarium). It would have been really a challenge to measure the angular separation although this was almost 5 h after the conjunction.

Thus, we can conclude that the procedure gives the following results:

• The instant of conjunction as 12:39 UT on 24th February (as against 20:20 UT).

• The angular separation is 3′ (as against 1.5′).

5.2 Conjunction of Venus and Saturn on 30th April

Now, we discuss the source of errors in the second example.

Fortunately, we were able to get this second example spaced apart from the earlier one by just a few months. Added to this advantage is the comparison with a different method to get the mean longitudes.

The manuscript that we had access appears to be a copy of the original, since we see many scribal errors as listed in Table B1 of Appendix B.

Comparison of timings with Stellarium or Xavier Jubier was difficult because the reference date was 10th day after new moon, unlike the new moon in the previous case. We used the precession corrected longitude of the Sun to fix the time as 14:10 UT on 2 May 1610. For this, the apparent coordinates corrected for the light path and stellar aberration were kindly provided by Prof. Mitsuru Soma.

2 May 1610 longitudes:

• Sun 41°$\mid$50′$\mid$41′′,

• Mars 324°$\mid$21′$\mid$47′′,

• Saturn 322°$\mid$43′$\mid$39′′.

The date of conjunction as per the calculation was off by 2 days as compared to Stellarium; hence, we verified the calculations step by step—the details are provided in Table B1 of Appendix B. The first major error was the use of mean longitude of the Sun. Although the listed value of 0$\mid$23$\mid$55$\mid$58 is correct, the one used in subsequent calculations was different (0$\mid$21$\mid$55$\mid$20). The final values give a difference of longitude as 2$\mid$20$\mid$14, which when divided by the difference in speed of 39$\mid$47, gives the duration (since the event has taken place) as 3.524 days. On the day of conjunction, the difference of 02$\mid$04 of the latitudes is larger than half the sum of bimba 1$\mid$47. Hence, there is no bheda yoga or occultation.

We recalculated all the values with the mean longitude of the Sun as 0$\mid$23$\mid$55$\mid$58 and the final result, now reads:

Longitude and speed of Mars on the date of calculation (2nd May at 14:10 UT): 10$\mid$5$\mid$48$\mid$11 and 42$\mid$50.

Longitude of Saturn:

• 10$\mid$03$\mid$48$\mid$11 and 3$\mid$3.

The instant of conjunction changes to: 30th April, 02:03 UT and the angular separation is 24′ as compared to those from Stellarium and Xavier Jubier as conjunction on 30th April, 02:32 UT and angular separation 33′ as depicted in Figure 7.

Figure 7

View on 30 April 1610 (from Stellarium).

We also noticed that the correction for precession is given as 18$\mid$9 in another example for the same year (for a lunar eclipse). A difference of 1̍ can alter the reference time, which gets reflected in the time of conjunction also.

Thus, we have verified the procedure of calculation in both examples. The deviation in the final result may be because of the scribe or human error, while computation occurs. The need for exact correction for precession and the position of the nodes also becomes apparent here.

6 Conjunctions of 2022 and 2023

As shown in the above section, the procedure provides quite precise timings for the conjunctions. However, the type of conjunction cannot be predicted since it requires knowledge of angular diameters. These are provided in almost all texts (Balachandra Rao et al. 2008), in the context of transits and occultations.

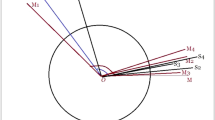
The planetary conjunction of Saturn and Jupiter in December 2020, has been discussed in great detail in another paper (Shubha & Shylaja 2023), using the tables of Mahādevī-Sāriṇī to get the longitudes for the whole year at intervals of 14 days. Venus and Jupiter provided an opportunity to verify the calculations of conjunctions during 2022–2023. We calculated the longitudes by extending the same method to reach the relevant tables and the result is shown in Figure 8.

Figure 8

Longitudes of Venus (brown) and Jupiter (blue) for the period of April 2022–March 2023. It may be seen that there were two conjunctions in April 2022 and March 2023.

These tables provide the true longitudes with the mean value of the Sun equals to zero as the starting point. We need to calculate the corresponding mean value of the planets and reach the relevant table. This procedure provided us the two conjunctions that happened between March 2022 and April 2023, as it is clearly depicted in the diagram.

On both occasions, we read out the longitudes at conjunctions as 357° and 345°. Using this value, we proceed to calculate the latitude (śara) for both of them. The results compared with the observed values show that they are within observational limits.

Date of conjunction	Longitude	śara of Guru	śara of Śukra	Difference in śara/angular separation	Observed angular separation
30-Apr-2022	345	84	101	17′	12′
01-Mar-2023	357	100	126	26′	31′

The last column of the table gives the angular separation derived from the collection of photographs taken by various amateur photographers all over the globe. Figure 9 gives the photograph taken in Bengaluru. It may be seen that a difference of 5′ is not observable with the naked eye.

Figure 9

Conjunction of Jupiter and Venus on 1 March 2023 at dusk (courtesy: Geetha G Kydala, Bengaluru).

7 Conclusion

We have presented the method of calculation from medieval astronomy texts of India, for prediction of conjunctions of planets. The details of the procedure as inferred from a recently discovered text in Kannada are presented. We have included two worked examples from unpublished manuscripts of 16th century. The verification establishes the procedure within observational limits. We discuss the possible sources of error in longitude estimates and in angular separation in the context of visibility criterion of occultation. We also report that the corrections as mentioned in one of the manuscripts of BU aims at rectification of the errors, which reduced the discrepancy to 6 h from 3 days. The second case agrees with the time given by Stellarium and Xavier Jubier within 30 min after the errors in the manuscript are rectified. Further, we have used this procedure for a contemporary conjunction; it yielded the angular separation accurate within observational limits.

Appendices

Appendix A: Computations as provided in Brahmatulya Udāharaṇam

The computations begin with the calculation of Ahargaṇa, from the knowledge of the śaka year, the month and tithi of the month. Let us represent A as Ahargaṇa.

From the epoch of 1183 CE to the current date the longitude is measured as

$$ \left\{ {{\text{A}} - {\text{A}}/903} \right\} = 155951\left| 0 \right|0{-}2245\left| 8 \right|30 = 153705^{^\circ } |51^{\prime } |30^{\prime \prime } . $$

This is equal to 426 complete revolutions and 11^R$\mid$15°$\mid$44′$\mid$48′′. The complete revolutions are not needed. As explained 11^R means the 11th zodiac sign corresponding to 330°:

$$ \begin{aligned} {\text{Mean}}\,{\text{Sun}}\, = & \,{\text{constant}}\,\,{\text{for}}\,{\text{the}}\,{\text{year}}\,{\text{1183}}\, \\ & \, + \{ {{\text{longitude}}\,{\text{from}}\,{\text{the}}\,{\text{epoch}}\,{\text{upto}}\,{\text{the}}\,{\text{present}}} \\ & \, + {{\text{day}}\,{\text{called}}\,K \acute{s} epaka} \} \\ & \, = \,\left\{ {{\text{1}}0\left| {{\text{29}}} \right|{\text{13}}|0} \right\}\, + \,\left\{ {{\text{11}}\left| {{\text{15}}} \right|{\text{44}}|{\text{48}}} \right\} \\ & \, = \,{\text{1}}0\left| {{\text{14}}} \right|{\text{57}}|{\text{48}}. \\ \end{aligned} $$

This value is used as the mean value for Venus (Śukra) also.

For Venus, the apogee (ucca) is calculated in the same way:

$$ \begin{aligned} & {\text{16}}A{\text{/7451}}\, + \,{\text{16}}A{\text{/1}}0\, + \,{\text{the}}\,{\text{constant}}\,K \acute{s} epaka, \\ & \quad = \,{\text{334}}\left| {{\text{53}}\, + \,{\text{249521}}} \right|{\text{36}}\, + \,{\text{8}}\left| {{\text{18}}} \right|{\text{5}}|{\text{55}}, \\ & \quad = \,{\text{25}}0{\text{114}}\,\left| {{\text{34}}} \right|{\text{55}}, \\ & \quad = \,{\text{694}}\,\,{\text{revolutions}}\,\,\,{\text{9}}\left| {\text{4}} \right|{\text{34}}|{\text{55}}. \\ \end{aligned} $$

For Saturn (Sani):

$$ A{\text{/3}}0\, + \,A{\text{/9367}}\, + \,{\text{123}}\left| {{\text{43}}} \right|{\text{17}}\, = \,{\text{5338}}\left| {{\text{44}}} \right|{\text{17}}\, = \,{\text{14}}\,\,{\text{revolutions}}\,\,{\text{and}}\,\,{\text{9}}\left| {{\text{28}}} \right|{\text{44}}|{\text{17}}. $$

Thus, the mean values of the Sun, apogee of Venus and Saturn are obtained.

The basis for these derivations is the number of revolutions in 43,200,000 days as defined in Sūryasiddhānta.

The first correction from the equation of center is defined by the angle between apogee and the mean position, called mandakendra.

The correction for the Sun is 47 arcsec, since the location of observer is Varanasi to the east of the reference location, Ujjain. The other correction udayāntara, due to the obliquity, is 19 arcsec. The apogee of the Sun is 2$\mid$18$\mid$0$\mid$0.

The angle mandakendra is the difference between apogee and the mean value equal to 4$\mid$3$\mid$2$\mid$27 $=$ 123$\mid$2$\mid$37.

The correction mandaphala is ($a/R$)R sin m, where $a/R$ is the ratio of the radii of the epicycle to 360. For the Sun, a is 13$\mid$40; mandaphala is 1$\mid$49$\mid$28.

Thus, the true value is: mean value – mandaphala $=$ 10$\mid$16$\mid$46$\mid$51.

(There is a typographical error in the value of arcseconds).

For Venus, the longitude of the apogee is corrected for the location of observer as 9$\mid$4$\mid$34$\mid$55.

The value of mean Sun is taken as the mean for Venus, mandocca is 2$\mid$21$\mid$0$\mid$0. Therefore, the angle mandakendra $=$ m $=$ 2$\mid$21$\mid$0$\mid$0 – 10$\mid$14$\mid$58$\mid$9 $=$ 4$\mid$6$\mid$1$\mid$57.

Venus has epicycle radius as 11°. The multiplying factor, a$/$R is 2$/$784. Mandaphala $=$ 1$\mid$14$\mid$3.

Thus, the longitude of Venus after the first correction is 10$\mid$16$\mid$12$\mid$12

The second correction requires the apogee called ucca 9$\mid$4$\mid$35$\mid$41; its difference with the just corrected value is called śighrakendra, which we will represent as s:

$$ s\, = \,{9}\left| {4} \right|{35}\left| {{41} - {1}0} \right|{16}\left| {{12}} \right|{12}\, = \,{1}0\left| {{18}} \right|{23}\left| {{58}\, = \,{318}} \right|{23}|{58}. $$

The correction in this case is decided by the radius of the epicycle and the angular separation from the Sun, and the distance from the Earth. As per the formula:

$$ R\sin \Delta \theta = \frac{{r\sin \theta_{ms} - \theta_{s} }}{{\left[ {\left[ {R + r\cos \left( {\theta_{ms} - \theta_{s} } \right)} \right]^{2} + \left[ {r\sin (\theta_{ms} - \theta_{s} )} \right]^{2} } \right]^{\frac{1}{2}} }} $$

and with the value of parākhya (r/R) as 87, we get the correction as 17$\mid$19$\mid$30. Thus, the true longitude is 9$\mid$28$\mid$52$\mid$42.

A second iteration is done using this as the mean value.

The second mandakendra m $=$ 4$\mid$22$\mid$7$\mid$18.

The second mandaphala is 0$\mid$56.

The second manda corrected value is 10$\mid$15$\mid$54$\mid$19.

Again, the second correction Śīghra is calculated with the apogee and the second epicycle as 17$\mid$22$\mid$24.

The final value is 9$\mid$28$\mid$31$\mid$55.

The procedure can be understood with the help of Figures A1 and A2, where the shaded portion represents the correction after second iteration.

Figure A1

Correction from S to S′ for the Sun is derived from the angle 123°, called mandakendra. The numbers 10$\mid$14 and 10$\mid$15 (Rasi$\mid$degrees) indicate the approximate uncorrected and corrected values.

Figure A2

There are three steps in the corrections for Saturn and Venus. The first one from m to m′ is from the angle shown with dashed marks; the second one (śighra) is derived from the angles 20° for Saturn, 120° for Mars; the third one uses the angles 324° and 318°.

The same procedure is followed for Saturn. Here, the mean value of the Sun is taken as the śīghrocca or the apogee for the second correction.

After two iterations, the value for true longitude of Saturn is 9$\mid$16$\mid$20$\mid$17.

After obtaining the true longitudes, the speeds, gati are computed as explained using by the cosine of the mandakendra taken to the nearest 10°. Then, the actual distance of the planet from the Earth as used in the second correction of longitude (Śīghrakarṇa) is used to get the second correction. For Venus, it is 75$\mid$11 and for Saturn, it is 7$\mid$11.

The mean diameters for the different planets are provided: For Venus, it is 9′, for Saturn, it is 5′. The diameters are corrected using the value of śīghrakarṇa (the hypotenuse in the planet–earth–apogee triangle). This is multiplied by the difference of 120 and śighrakendra, and divided by 3 and parākhya to get the correction at that instant.

In this example, for Venus, the difference of śīghrakarṇa and 120, is 73$\mid$59$\mid$41. This is multiplied by 9, to get mean diameter of 665$\mid$57$\mid$9 and divided by 261, which is the product of 87 and 3. The result is 2′33′′. This is subtracted from the mean value of 9 to get 6′27′′ as diameter, which, when divided by 3 becomes 2$\mid$9 aṅgulas. Similarly, the difference of śīghrakarṇa and 120 of Saturn is 12$\mid$16$\mid$32, multiplied by 5 (the mean diameter), to get 61$\mid$22$\mid$40. This is divided by product 3 and parākhya, 39 to get 1$\mid$34. This is subtracted from the mean diameter 5 to get 3$\mid$26 resulting in 1$\mid$8 aṅgulas.

The date of conjunction is arrived by taking the difference of longitudes (141$\mid$38) and dividing by the difference in gaṭi, the speed (68$\mid$0). This gives 2 days, 4 ghaṭi and 58 vighaṭi. Thus, the conjunction occurred on the 12th day after full moon at 55$\mid$02 ghaṭi.

The calculation of śara or the latitude requires the longitudes of the planets at the instant of conjunction. This is calculated by subtracting the motion of the planets during this interval. This works out as 9$\mid$26$\mid$5$\mid$20. For this instant, the nodes are also calculated as 10$\mid$0$\mid$56$\mid$10 and 8$\mid$15$\mid$1$\mid$10 and added to the longitudes as 7$\mid$05$\mid$31$\mid$50 (the typographical error puts the last value as 5 instead of 51) and 6$\mid$11$\mid$7$\mid$0. The maximum values are provided and that needs to be multiplied by the sine of the longitude difference with the node and divided by the hypotenuse (a measure of planet–Earth distance). These are called śīghrakarṇa.

The R sine of the difference in longitudes are (69$\mid$24$\mid$8 and 23$\mid$14$\mid$0); these are multiplied by the maximum values (136 for Venus and 130 for Saturn) and divided by the śīghrakarṇa calculated above (193$\mid$51$\mid$41 and 132$\mid$16$\mid$32), to get the śara for Venus as 48$\mid$39 and 22$\mid$49. These are divided by 3 to get units of aṅgula as 16$\mid$13 and 7$\mid$36 (both south).

The next step is to get the hour angle and altitude, at the instant of conjunction, which is considered equivalent to the instant of new moon in a solar eclipse calculation. The calculations are carried out analogous to solar eclipse with Saturn in the place of the Sun and Venus in the place of moon.

The instantaneous value for the sun is 10$\mid$14$\mid$41$\mid$42.

Ayanāṃśa is 18$\mid$6.

The ascendant is 9$\mid$8$\mid$38$\mid$36.

Declination of the point on the ecliptic 90° away from the ascendant i.e., at (6$\mid$8$\mid$38$\mid$36), is to the south.

The corresponding correction for the time is 51$\mid$59.

The longitude of the sun gets corrected to 10$\mid$14$\mid$38$\mid$38.

The difference in longitudes is corrected for this small angle 3$\mid$48 using the mean rate of motion of the planets.

The difference is śara corrected for this is 0$\mid$9 in units of hasta$\mid$aṅgula.

Appendix B: Computations as provided in Grahalāghava Tīkā

The example from Grahalāghava Tīkā by Visvanatha was examined for possible scribal errors and computational errors. The unpublished manuscript provided step by step calculations. Figure

Figure B1

Manuscript leaf giving the details of mean positions. The value for the Sun is underlined in red, i.e., 0$\mid$23$\mid$55$\mid$38, however, 0$\mid$21$\mid$55$\mid$20, is used for computations later resulting in an error.

B1 shows the original palm leaf copy.

Table B1 shows the calculations as given in the text and has been recalculated by us. The values in red fonts are erroneous.

Table B1 Longitudes—recalculated.

The deduction of mean longitudes from the day count, Ahargaṇa, is the first step. The values are given in units of Rāśi (the zodiacal sign number to be multiplied by 30 to get degrees) followed by degree, minutes and seconds. The correction is applied in three steps, the first one corresponds to the second equation of conjunction called śīghra. Only half of the correction is applied and the corrected value is used for getting the first equation correction, for apogee, called manda. Then, the second equation correction called śīghra is again applied. We have shown these steps in the table.

Apart from scribal errors shown in red font, there was a major error in the very first step. The mean longitude shows an error. Although it is given as 0$\mid$23$\mid$55$\mid$38, the value used is 0$\mid$21$\mid$55$\mid$20. Therefore, we had to recalculate all the corrections as shown. The final values give a difference of 2$\mid$20$\mid$14, which when divided by the difference in speed of 39$\mid$47, we get the duration since the event has taken place in 3.524 days. On the day of conjunction, the longitudes of the planets were 10$\mid$2$\mid$42$\mid$40. Then, the corresponding latitudes are calculated taking the difference with the respective nodes at 1$\mid$10$\mid$0$\mid$0 and 3$\mid$10$\mid$0$\mid$0 as 16$\mid$11 and 14$\mid$7 aṅgulas, both values to be marked towards southern direction. The difference of 02$\mid$04 of the latitudes is larger than half the sum of radii, (biṃba) 1$\mid$47. Hence, there is no bhedayoga or occultation.

The second major error was in the subtraction of the mean longitude from the mean value of śīghrocca or the Sun itself, the difference is one rāśi, equivalent to 30°.

The steps in between seem to have scribal errors, which can be traced working backwards. For example, although the steps for Mars seem to be free of errors (but for the value of mean longitude of the Sun), in the last step, 10$\mid$6$\mid$38$\mid$9 is written and it ought to have been 10$\mid$6$\mid$35$\mid$9.

In the last step of calculating the difference in longitudes, again there is a difference of 1° i.e., 3$\mid$36 instead of 2$\mid$26, which pushes back the date of conjunction by about 2 days.

The gaṭi or speed is free of error.