Tree Level Potential on Brane after Planck and BICEP2

Abstract

The recent detection of degree scale B-mode polarization in the Cosmic Microwave Background (CMB) by the BICEP2 experiment implies that the inflationary ratio of tensor-to-scalar fluctuations is $r=0.2_{-0.05}^{+0.07}$, which has opened a new window in the cosmological investigation. In this regard, we propose a study of the tree level potential inflation in the framework of the Randall–Sundrum type-2 braneworld model. We focus on three branches of the potential, where we evaluate some values of brane tension λ. We discuss how the various inflationary perturbation parameters can be compatible with recent Planck and BICEP2 observations.

1 Introduction

Inflation is an exponential expansion of the universe in a supercooled false vacuum state. False vacuum is a metastable state without any fields or particles, but with large energy density (Linde 2014). Inflation is also a successful scenario for production and evolution of the perturbation spectrum in primary stages of the universe evolution (Liddle & Lyth 2000). In the last few years, braneworld inflation became a central paradigm of cosmology (Brax et al. 2004). In this context, Randall–Sundrum II (RSII) model is one of the braneworld models suggested for solving the hierarchy problem, which arises from the large difference between the Planck scale and electroweak scale (Randall & Sundrum 1999). To describe early inflation and recent acceleration of the universe, various braneworld cosmological models have been proposed (Maartens et al. 2000) and deeply studied (Calcagni et al. 2014).

On the other hand, the single-field models as chaotic model, are the most probable to be a successful scenario of inflation (Antuscha & Noldea 2014; Kobayashi & Seto 2014; Nakayama et al. 2014). However, the polynomial or the monomial potential ϕ ⁿ inflation does not signify chaotic inflation, which must be related to initial conditions (Kallosh et al. 2014). In this context, the most of the monomial potentials have quadratic or quartic form, see, for example, in work (Yokokama 1998) a potential contains a quadratic and quartic field is used which is called simple double-well, to explain the formation of Primordial Black Holes. In addition, Rehman et al. 2008, have used the tree level potential which is known as Higgs potential to implement inflation in non-supersymmetric grand unified theories (GUT) in order to determine proton lifetime. In the same context, Rehman & Shafi (2010) and Okada et al. (2014) have studied the quantum smearing arising from the inflation couplings to other particles such as GUT scalars, to show that the Higgs potential one can be divided into three branches.

Recently, it has been shown that, in the framework of inflation with a scalar gauge singlet field driven by a tree level potential, the scalar-to-tensor ratio r is estimated to be larger than 0.036, provided the scalar spectral index n _s >0.96. Furthermore, these predictions were discussed by employing a Coleman–Weinberg (CW) potential for a scalar inflation field which must be a GUT singlet and it has been suggested that these corrections can provide r>0.02 for n _s >0.96 (Rehman & Shafi 2010).

Most recently, BICEP2 has made a dramatic discovery of inflationary gravitational waves (Ade & et al. 2014). If verified by Planck (Ade & et al. 2013), this would have far-reaching implications both for inflationary cosmology and particle physics. BICEP2 reported the first discovery of these gravity waves. The observed tensor-to-scalar ratio r, a canonical measure of gravity waves from inflation, is estimated by BICEP2 to be $r=0.2_{-0.05}^{+0.07}$, several types of models are motivated by these results (see, e.g., Gao & Gong 2014; Harigaya et al. 2014). Moreover, the combination of Planck + WP data, with the pivot scale chosen at $k_{0}=0.05~\text {Mpc}^{-1}$, gives n _s = 0.9603±0.0073 (68% CL) and $\frac {\mathrm {d}n_{s}}{\mathrm {d}\ln (k)}=-0.0134\pm 0.0090$ (68% CL).

In this work, we are interested in a Randall–Sundrum II (RSII) braneworld model, where inflation field is a scalar gauge singlet. Our setup is based on a tree level potential by adopting three branches of the potential, where we evaluate some values of brane tension λ. An outline of the remainder of this paper is as follows: in the next section, we discuss the braneworld inflation Randall–Sundrum type-II model and we present our results for a tree level potential, where we have applied the slow-roll approximation in high energy limit. The last section is devoted to a conclusion.

2 Randall–Sundrum braneworld model

2.1 Slow-roll approximation in braneworld inflation

The crucial moment is the creation of the hot big bang universe by the collision of the slowly moving bulk brane with our visible brane. Although the universe may exist for an indefinite period prior to the collision, cosmic time as normally defined begins at impact, this is known by ekpyrotic universe such that the idea that the hot big bang is the result of the violent collision between two infinite branes moving along a small extra dimension (Khoury et al. 2001).

Generally, in braneworld scenario, the observable universe can be considered as 3-brane, embedded in 4+d dimensional spacetime, the bulk in which, particles and fields trapped on the brane, while gravity is free to access the bulk. One of the brane inflation scenarios, where d = 1, is the Randall–Sundrum II (RS II) model, in which our four-dimensional universe is considered as a three-brane embedded in five-dimensional anti-de Sitter (AdS5) space–time (Randall & Sundrum 1999). This model is based on single brane which has positive brane tension. In this theory, the metric projected on the brane is a specially flat Friedmann–Robertson–Walker model. The Friedmann equation at high energy limit, ρ≫2λ, is then in a generalized form $H^{2}=\frac {4\pi }{3{m_{\mathrm {p}}^{2}}\lambda }\rho ^{2}$ (Maartens et al. 2000), where H is the Hubble parameter, ρ is the energy density and λ is the brane tension such that $\lambda =\frac {3}{4\pi } \frac {{m_{5}^{6}}}{{m_{\mathrm {p}}^{2}}}$, where m _p = 1.2 × 10¹⁹GeV is the Planck mass and m ₅ is the five-dimensional Planck mass. The first two parameters are given by $\epsilon =\frac {{m_{\mathrm {p}}^{2}}}{4\pi }\frac {\lambda V^{\prime 2}}{V^{3}},$ $\eta =\frac {{m_{\mathrm {p}}^{2}}}{4\pi }\frac {\lambda V^{\prime \prime }}{V^{2}}$ (Maartens et al. 2000). The scalar spectral index n _s , the ratio of tensor to scalar perturbations r and the running of pectral index $\frac {\mathrm {d}n_{s}}{\mathrm {d}\ln k}$ can be defined according to the slow-roll parameters as n _s ≃−6𝜖+2η+1, r≃24𝜖 and $\frac { \mathrm {d}n_{s}}{\mathrm {d}\ln k}\simeq \frac {m_{\mathrm {p}}^{2}}{2\pi }\frac {\lambda V^{\prime }}{ V^{2}}\left (3\frac {\partial \varepsilon }{\partial \sigma }-\frac {\partial \eta }{\partial \sigma }\right )$, respectively. The number of e-folds during braneworld inflation is given by

$$ N\simeq -\frac{4\pi }{{m_{\mathrm{p}}^{2}}\lambda }{\int}_{\phi_{\ast }}^{\phi_{\text{end}}} \frac{V^{2}}{V^{\prime }}\mathrm{d}\phi . $$

(1)

The small quantum fluctuations in the scalar field leads to fluctuations in the energy density. For this reason, we define the power spectrum of the curvature perturbations (Langlois 2000) by

$$ P_{R}\left( k\right) \simeq \frac{16\pi }{3{m_{\mathrm{p}}^{6}}}\frac{V^{6}}{V^{\prime^{2}}\lambda^{3}}. $$

(2)

2.2 Brane tension effect

The braneworld inflation models have been proposed to solve the problems that the standard model couldn’t solve. Among these models is Randal–Sundrum-II, which was suggested by some works, in order to explain and adopt the results of some models. In the RSII model, the value of the brane tension λ depends on the model and type of the problem addressed. The value λ may change significantly depending on the model. Hence, it is not a generic result and does not lead to a unique value for brane tension. In this context, we note that certain works suggest the brane tension value varies from 10⁵²GeV⁴ to 10⁶⁴GeV⁴. For instance, Panotopoulos (2007) discussed the validity of chaotic braneworld model from the power spectrum of the curvature perturbations P _R and the scalar spectral index n _s with values of m ₅ up to 2.4 × 10¹⁷ GeV implies λ∼10⁶⁴ GeV⁴. Moreover, Bento et al. (2006), have investigated the aspects of thermal leptogenesis in braneworld and found that the thermal equilibrium is expected at $m_{5}\prec 10^{16}~\text {GeV}$ for $\lambda \preceq 10^{58}~\text {GeV}^{4}$. In addition, according to the work of Safsafi et al. (2012), where it was shown that for some value of brane tension λ∼(10⁵⁷ GeV⁴), the fine tuning problem is eliminated and the value of FI-term ξ is reduced in order to solve the problem of cosmic strings. In the case of the F-term supergravity inflation, the η-problem is solved for some values of brane tension λ∼(1−10)10⁵⁷ GeV⁴ (Zarrouki et al. 2011). In the recent paper (Ferricha-Alami et al. 2014), to solve the problem related to the topological defects, caused by the instability of the magnetic monopoles with smooth hybrid inflation, the brane tension value was around ∼(1−10) × 10⁵² GeV⁴. Furthermore, different attempts have been made for some scenarios in which they have shown that their models depend on the brane tension value (see, for example Felipe 2005; Barenboim et al. 2014).

3 Perturbation spectrum for the tree level potential

In this section, we implement inflation by employing a tree level Higgs potential given by Rehman et al. (2008), Rehman & Shafi (2010), Kallosh & Linde (2007)

$$ V(\phi )=V_{0}\left[ 1-\left( \frac{\phi }{\mu }\right)^{2}\right]^{2}, $$

(3)

where V ₀ is the vacuum energy density at origin and μ is the vacuum expectation value of the inflation, denotes the VEV of ϕ at the minimum. Similar to Rehman et al. (2008) and Rehman & Shafi (2010) and motivated by the Planck and BICEP2 results, this potential will be discussed for three branches in the braneworld scenario, where ϕ ²≫μ ², the inflation field ϕ is above VEV (AV branch), ϕ∼μ, where the inflation ϕ is near to VEV and where ϕ ⁴≪μ ⁴ is below VEV (AV branch).

In what follows, we shall apply the Randall–Sundrum type-2 Braneworld formalism by using the potential eq. (3) for each case above.

3.1 AV branch: $\protect \phi ^{2}\gg \protect \mu ^{2}$

We consider the case of AV branch where the potential eq. (3) becomes

$$ V(\phi )=V_{0}\left( \frac{\phi }{\mu }\right)^{4}. $$

(4)

In this case, we evaluate some values of brane tension λ and the interval of μ in order to obtain the approximation $(\frac {\phi }{\mu } )^{2}\gg 1$.

The slow-roll parameters are given for this case by

$$ \epsilon =\frac{4}{3}\eta =\frac{4{m_{\mathrm{p}}^{2}}\lambda \mu^{4}}{\pi V_{0}\phi^{6}}. $$

(5)

On the other hand, equation (1) gives the integrated expansion from ϕ _∗ to ϕ _{e n d} as

$$ N\simeq -\frac{1}{6}\frac{\pi V_{0}}{{m_{\mathrm{p}}^{2}}\lambda \mu^{4}}\left( \phi_{\text{end}}^{6}-\phi_{\ast }^{6}\right) . $$

(6)

Thereafter, we calculate the value of the scalar field at the end of inflation in terms of μ, V ₀ and λ. For 𝜖 = 1, we find $\phi _{\text {end}}=\left (\frac {4{m_{\mathrm {p}}^{2}}\lambda \mu ^{4}}{\pi V_{0}}\right )^{1/6}$. Equation (6) can be solved to give $\phi _{\ast }\simeq \left (\frac {6{m_{\mathrm {p}}^{2}}\lambda \mu ^{4}N}{\pi V_{0}}\right )^{1/6}$, where ϕ _∗ is the value of the scalar field before the end of inflation. From this equation, we determine the interval of values of the three parameters ϕ _∗, μ and λ which verify the AV branch.

From the equations (2) and (4) and the expression of ϕ _∗, the power spectrum of the curvature perturbations is given by

$$ P_{R}(k)=\frac{8}{3}\frac{V_{0}(2+3N)^{3}}{\pi^{2} {\mu}^{4}}. $$

(7)

We remark that the power spectrum P _R (k) depends only on the energy VEV, since the e-folds does not affect due to its small value compared with μ. We fix $V_{0}\sim 10^{64}\,\text {GeV}^{4}$ and we take N = 60, where P _R (k) equals the experimental value ∼2.21 × 10⁻⁹ given by Planck (Ade & et al. 2013), the value of VEV is constant, μ≃2.6 × 10¹⁸ GeV. Therefore, we investigate the variation of brane tension λ and the inflation field ϕ _∗ in high energy limit.

Figure 1 shows the variation of ϕ _∗ with respect to λ for μ≃2.6 × 10¹⁸ GeV. We remark that ϕ _∗ is an increasing function with respect to brane tension. The condition ϕ ²≫μ ² is realised for$\ \lambda \precsim 10^{61}~\text {GeV}^{4}$.

Figure 1

Inflation field $\protect \phi _{\ast }$ versus the brane tension $\protect \lambda$.

As a numerical example, if we set λ = 10⁶⁰ GeV⁴, we get ϕ ²/μ ²≃1.5, if we take λ = 10⁶¹ GeV⁴, we get ϕ ²/μ ²≃15, and if we set λ = 5 × 10⁶¹ GeV⁴, we get ϕ ²/μ ²≃ 24. Consequently, to realize the condition ϕ ²≫μ ² in high energy limit the values of brane tension must be λ≻10⁶¹ GeV⁴.

Furthermore, to study the inflation driven by potential (4), we must choose the initial conditions on the brane tension λ and on the vacuum expectation VEV μ. The inflationary parameters depend only on e-folds number such as

$$ n_{s}\simeq 1-\frac{3}{N},\quad r\simeq \frac{16}{N}\quad\text{ and }\quad\frac{ \mathrm{d}n_{s}}{\mathrm{d}\ln k}\simeq -\frac{3}{N^{2}}. $$

(8)

For example, for N = 50 we find n _s = 0.94, r = 0.32 and $\frac {\mathrm {d}n_{s} }{\mathrm {d}\ln k}=-0.0012$ and for N = 60 we find n _s = 0.95, r = 0.26 and $\frac {\mathrm {d}n_{s}}{\mathrm {d}\ln k}=-0.0008$. To produce the central value of spectral index, the e-folds number must be near 75. The value of r increases when N is decreased and then r satisfies the bound from BICEP2 results when $60\lesssim N\lesssim 105$.

3.2 Near branch: $\protect \phi \sim \protect \mu$

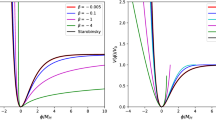
We will discuss the possible physical implications of the solutions in the case of ϕ∼μ, where the tree level potential becomes

$$ V(\phi )=V_{0}\left( 1-\left( \frac{\phi }{\mu }\right)^{2}\right)^{2}= \frac{V_{0}}{\mu^{4}}(\phi +\mu )^{2}(\mu -\phi )^{2}. $$

(9)

For simplicity, we consider the approximation: ϕ+μ≃2μ, where ϕ∼μ, whereas the potential (3) becomes

$$ V(\phi)\simeq \frac{4V_{0}}{\mu^{2}}(\mu -\phi )^{2}. $$

(10)

In this context, one can also consider the slow-roll parameters to study the perturbation spectrum on brane RSII, the first two parameters are given for this potential by

$$ \epsilon =2\eta =\frac{1}{4}\frac{{m_{\mathrm{p}}^{2}}T\mu^{2}}{V_{0}(\mu -\phi )^{4}\pi }. $$

(11)

We calculate the value of the scalar field at the end of inflation. Using this equation (11) for 𝜖 = 1, we get ϕ _end,

$$ \ \phi_{\text{end}}=\left( \frac{{m_{\mathrm{p}}^{2}}\lambda \mu^{2}}{4\pi V_{0}}\right)^{\frac{1}{4}}. $$

(12)

On the other hand, the number of e-folds gives the integrated expansion from ϕ _∗ to ϕ _end as

$$ \ N=-\frac{2\pi V_{0}}{{m_{\mathrm{p}}^{2}}\lambda \mu^{2}}(\phi_{\text{end}}^{4}-\phi_{\ast }^{4}) . $$

(13)

Equation (13) can be solved to give ϕ _∗, we find

$$ \phi_{\ast }\simeq \left( \frac{{m_{\mathrm{p}}^{2}}\lambda {\mu}^{2}N}{2\pi V_{0}}\right)^{\frac{1}{4}}. $$

(14)

From the expressions (10), (2) and (14), the power spectrum of the curvature perturbations is given by

$$ P_{R}\left( k\right) =\frac{128}{3}\left( \frac{2{V_{0}^{3}}N^{5}}{\pi^{3}\lambda \mu^{6}{m_{\mathrm{p}}^{2}}}\right)^{1/2}. $$

(15)

In high energy limit, V≫2λ, we fix the power spectrum $P_{R}\left (k\right )$ at the experimental value $P_{R}\left (k\right ) \simeq 2.21\times 10^{-9}$, given by Planck (Ade & et al. 2013), and we seek the interval of brane tension λ and μ energy VEV.

We plot the variations of ϕ _∗ as a function of VEV μ for various values of λ. Figure 2 shows the variations of ϕ _∗ according to the value of VEV μ for different values of brane tension λ. We show that, the field ϕ _∗, increases with respect to VEV μ and to satisfy the condition ϕ∼μ, brane tension must be in the range $10^{59}~\text {GeV}^{4}\lesssim \lambda \lesssim$ 10⁶¹ GeV⁴ and vacuum expectation value $\mu \succsim 10^{18}~\text {GeV}$.

Figure 2

$\protect \phi _{\ast }$ versus $\protect \mu$ for different values of $\protect \lambda$.

Furthermore, we vary bane tension value λ and the value of μ and we get the values of inflation mass $m_{\phi }=\frac {2\sqrt {2V_{0}}}{\mu }$ (Rehman & Shafi 2010) and the field ϕ _∗ which is summarised in Table 1.

Table 1 The values of some parameters with quadratic potential derived from the tree level potential.

On the other hand, the near branch is asymptotic to quadratic potential resulting in

$$ n_{s}\simeq 1-\frac{5}{2N},\quad r\simeq \frac{12}{N}\quad \text{and}\quad \frac{\mathrm{d}n_{s}}{ \mathrm{d}\ln k}\simeq -\frac{5}{2N^{2}}. $$

(16)

In the standard case, where the inflation field is near the vacuum expectation μ, the two inflationary parameters are: n _s = 1−2/N and r = 8/N (Rehman & Shafi 2010; Okada et al. 2014), therefore, to obtain the central value of spectral index n _s ≃0.96 the e-folds number must be N≃50.

In Randall–Sundrum-II branworld inflation, for some values of λ ∼ 10⁵⁹– 10⁶¹ GeV⁴, where the inflationary parameters are given in equation (16), for N = 50, gives n _s = 0.98, r = 0.24 and $\frac {\mathrm {d}n_{s}}{\mathrm {d}\ln k}\simeq -9.8\times 10^{-4}$, to obtain the central value of n _s ∼0.96, the e-folds number must be equal to 60, thus, one can conclude that the impact of brane tension is to increase the e-folds number.

To reconcile the Planck and BICEP2 results, where r is between 0.15 and 0.27 (Ade & et al. 2014), we need to have 55<N<78.

3.3 BV branch: $\protect \phi ^{4}\ll \protect \mu ^{4}$

In what follows, we will concentrate on inflationary potential, which can be expressed in BV branch as (Rehman & Shafi 2010)

$$ V(\phi )=V_{0}\left( 1-2\frac{\phi^{2}}{\mu^{2}}\right). $$

(17)

In this case, one can also consider the slow-roll parameters to study the spectrum of the perturbation in order to determine the relation between ϕ, μ and λ, and their values, in order to do the estimation $\left (\frac {\phi }{\mu }\right )^{4}\ll 1$. The two first parameters are given for this potential, by

$$ \epsilon =\frac{4{m_{\mathrm{p}}^{2}}\lambda \phi^{2}}{V_{0}\mu^{4}\pi (1-2\frac{\phi^{2}}{\mu^{2}})^{3}}\text{\ \ \quad and \quad \ }\eta =\frac{{m_{\mathrm{p}}^{2}}\lambda }{ V_{0}\mu^{2}\pi (1-2\frac{\phi^{2}}{\mu^{2}})^{2}}. $$

(18)

We calculate the value of the scalar field at the end of inflation. One can get ϕ _{e n d} by using 𝜖 = 1, we find

$$ \phi_{\text{end}}=\frac{1}{2}\frac{\sqrt{V_{0}\pi ({m_{\mathrm{p}}^{2}}\lambda -V_{0}\mu^{2}\pi )}}{V_{0}\pi }. $$

(19)

On the other hand, the number of e-folding N could be expressed as

$$ N=\frac{\pi V_{0}\mu^{2}}{{m_{\mathrm{p}}^{2}}\lambda }[\ln (\phi_{\text{end}})-\ln (\phi_{\ast })]. $$

(20)

The resolution of equation (20) implies the following expression of the scalar field during inflation ϕ _∗

$$ \phi_{\ast }=\frac{\sqrt{2}}{2}\frac{\sqrt{\frac{\mu (V_{0}\pi \mu +m_{\mathrm{p}} \sqrt{V_{0}\pi \lambda })}{V_{0}}}}{\sqrt{\pi }\exp \left( \frac{N{m_{\mathrm{p}}^{2}}\lambda }{V_{0}\pi \mu^{2}}\right)}. $$

(21)

From equations (2) and (17), the power spectrum of the curvature perturbations is given by

$$ P_{R}\left( k\right) \simeq \frac{1}{3}\frac{{V_{0}^{4}}\mu^{4}\pi (1-2\frac{ \phi_{\ast }^{2}}{\mu^{2}})^{6}}{{m_{\mathrm{p}}^{6}}\lambda^{3}\phi_{\ast }^{2}}. $$

(22)

According to the experimental value $P_{R}\!\left (k\right ) =2.21\times 10^{-9}$ given by Planck (Ade & et al. 2013) and in high energy limit V≫2λ, we determine from the expression of the power spectrum (22), the interval of λ and μ which gives the validity of this potential. In Table 2, we give the different values of λ,μ and ϕ _∗ obtained.

Table 2 The different values of the parameters λ, μ and ϕ _∗.

From Table 2, we have computed some values of VEV μ and ϕ _∗, which realize the conditions and ϕ ⁴/μ ⁴≪1. For λ = 10⁵⁹ GeV⁴ and $\mu \prec 8\times 10^{16}~\text {GeV}$ gives V(ϕ)≃constant, because ϕ ⁴/μ ⁴≪1 and ϕ ²/μ ²≪1, for μ≻9 × 10¹⁶ GeV, we can do the approximation ϕ ⁴≪μ ⁴, here the interval of μ where the last approximation is realised, which allows us to use the BV branch of the potential (3), is $9\times 10^{16}~\text {GeV}\prec \mu \prec 10^{19}~\text {GeV}$.

For λ = 10⁶⁰ GeV⁴ the range of VEV μ, which verifies the condition of BV branch in high energy limit, is ∼(4 × 10¹⁷−10¹⁹) GeV. In the same way, where λ = 10⁶¹ GeV⁴ we can also use the potential (17) when $4\times 10^{18}~\text {GeV}\prec \mu \prec 2\times 10^{19}~\text {GeV}$.

From the above analysis we will study, in what follows, the variations of these parameters according to the brane tension λ. Therefore, the value of spectral index n _s for different values of the brane tension λ for any values of μ, is below 0.93, which means that for a potential of the form (17), derived from tree level potential, the values of n _s lies outside the Planck data bounds.

On the other hand, from equations (18), (21) one can define the ratio r of tensor to scalar as

$$ r=\frac{48{m_{\mathrm{p}}^{2}}\lambda \phi_{\ast }^{2}}{V_{0}\mu^{4}\pi (1-2\frac{ \phi_{\ast }^{2}}{\mu^{2}})^{3}}. $$

(23)

We plot the variations of r, according to the values of the brane tension λ, for different values of μ (Figure 3). According to Figure 3, one could remark that, for each value of μ, the ratio r decreases as λ increases. It is also shown that, for large values of brane tension λ, one can cover an interval of r, which is in agreement with the Planck observations (r<0.11).

Figure 3

r versus $\protect \lambda$ for different values of $\protect \mu$.

Although the spectral index n _s is not favoured by the recent Planck data, the ratio r, corresponding to the potential (17), derived from the Higgs potential, is in agreement with the BICEP2 data for a range of brane tension λ∼10⁶⁰ GeV⁴ with an interval of VEV μ≃(5−10) × 10¹⁷ GeV.

In what follows, we give some numerical estimations in region given allowed by BICEP2 measurement, especially for the ratio which is $0.15\preceq r\preceq 0.27$.

If we take r = 0.15 and set μ≃5 × 10¹⁷ GeV we get brane tension and scalar field values λ≃7 × 10⁵⁹ GeV⁴, ϕ _∗≃9 × 10¹⁶ GeV. By taking the same value of the ratio as above and fixing the vacuum expectation value at μ≃7.5 × 10¹⁷ GeV, we get λ≃1.8 × 10⁶⁰ GeV⁴ and ϕ _∗≃2.7 × 10¹⁷ GeV.

Now, for r = 0.27, we get μ≃5 × 10¹⁷ GeV, λ = 6 × 10⁵⁹ GeV⁴ and ϕ _∗≃4.7 × 10¹⁷ GeV, by fixing μ≃10¹⁸ GeV we get λ≃2.8 × 10⁶⁰ GeV⁴ and ϕ _∗≃3 × 10¹⁸ GeV.

In the following, we plot the running of the scalar index $\frac {\mathrm {d}ns}{\mathrm {d}\ln (k)}$ versus brane tension value for different values of μ.

Figure 4 shows the variations of the running of the scalar index $\frac { \mathrm {d}n_{s}}{\mathrm {d}\ln k}$ according to the value of the brane tension λ for different values of μ. We remark that in the region below the magenta dash line, when the values of brane tension get smaller than 3.6 × 10⁶⁰ GeV⁴, such as the VEV μ energy, must be larger to give a $\frac { \mathrm {d}n_{s}}{\mathrm {d}\ln k}$ compatible with Planck data.

Figure 4

$\ \frac {\mathrm {d}n_{s}}{\mathrm {d}\ln k}$ versus $\protect \lambda$ for different values of $\protect \mu$.

4 Conclusion

In this work, we have studied the tree level potential model in the framework of the Randall–Sundrum type-2 braneworld model. We focussed on three branches of the potential, where we have applied the Slow–Roll approximation in the high energy limit. We have evaluated some values of brane tension λ, in order to derive analytical expressions for various perturbation spectrum (n _s , r, $\frac {\mathrm {d}n_{s}}{\mathrm {d}\ln (k)}$).

A confrontation with the recent Planck data shows that the best fit is achieved, in the AV branch, only for $N\geqslant 60$. In the near case, the values of the scalar spectral index n _s are in good agreement with observation, whereas the ratio r must satisfy the inequality N>60 in order to be consistent with Planck data, for $\left \vert \frac {\mathrm {d}n_{s}}{\mathrm {d}\ln k}\right \vert \sim O(10^{-3}$ to 10⁻⁴). In the BV branch, the tensor to scalar ratio r and the running $\frac {\mathrm {d}n_{s}}{\mathrm d\ln (k)}$ are consistent with Planck data for some values of μ and λ, whereas, the values of the scalar spectral index n _s remains lower than the central value.

However, to reconcile the BICEP2 data, in the AV branch, the ratio tensor-to-scalar r decreases with the number of e-folds such that the ratio r is consistent with BICEP2 data when N becomes larger. In the BV branch, the ratio r is a decreasing function with brane tension λ for different values of μ, which is in agreement with BICEP2 experiment.