Modelling Cross Talk in the Spatiotemporal System Dynamics of Calcium, IP₃ and Nitric Oxide in Neuron Cells

Abstract

The bioenergetic system of calcium ([Ca²⁺]), inositol 1, 4, 5-trisphophate (IP₃) and nitric oxide (NO) regulate the diverse mechanisms in neurons. The dysregulation in any or all of the calcium, IP₃ and nitric oxide dynamics may cause neurotoxicity and cell death. Few studies are noted in the literature on the interactions of two systems like [Ca²⁺] with IP₃ and [Ca²⁺] with nitric oxide in neuron cells, which gives limited insights into regulatory and dysregulatory processes in neuron cells. But, no study is available on the cross talk in dynamics of three systems [Ca²⁺], IP₃ and NO in neurons. Thus, the cross talk in the system dynamics of [Ca²⁺], IP₃ and NO regulation processes in neurons have been studied using mathematical model. The two-way feedback process between [Ca²⁺] and IP₃ and two-way feedback process between [Ca²⁺] and NO through cyclic guanosine monophosphate (cGMP) with plasmalemmal [Ca²⁺]-ATPase (PMCA) have been incorporated in the proposed model. This coupling handles the indirect two-way feedback process between IP₃ and nitric oxide in neuronal cells automatically. The numerical outcomes were acquired by employing the finite element method (FEM) with the Crank-Nicholson scheme (CNS). The present model incorporating the sodium-calcium exchanger (NCX) and voltage-gated calcium channel (VGCC) provides novel insights into the various regulatory and dysregulatory processes due to buffer, IP₃-receptor, ryanodine receptor, cGMP kinetics through PMCA channel, etc. and their impacts on the interactive spatiotemporal system dynamics of [Ca²⁺], IP₃ and NO in neurons. It is concluded that the behavior of different crucial mechanisms is quite different for interactions of two systems of [Ca²⁺] and NO and the interactions of three systems of [Ca²⁺], IP₃ and nitric oxide in neuronal cell due to mutual regulatory adjustments. The association of several neurological disorders with the alterations in calcium, IP₃ and NO has been explored in neurons.

Introduction

Various agents have emerged as indispensable signal carriers for the proper functioning of cellular life. Several crucial mechanisms including transport of different ions and molecules, buffer approximation, different inflow and outflow processes, etc. constitute the bioenergetic dynamical systems for several signaling ions and molecules like calcium, IP₃ and NO in neuronal cells. The interactions of calcium with other signaling molecules like IP₃ and nitric oxide regulate a variety of cellular mechanisms. The IP₃ mobilizes the intracellular calcium ions and controls numerous processes including metabolism, secretion, etc. in cells. The NO with several secondary messengers including [Ca²⁺], proteins, O₂, etc. influence the regulatory mechanisms in different cells. Nitric oxide is produced from L-arginine via NO enzymes synthase [1] and serves as a biological messenger, cytotoxic agent and regulator in a variety of central nervous system tissues.

The association of [Ca²⁺] buffer and the reduction in free calcium during transient calcium entry was reported in neuronal cells [2]. The different elementary [Ca²⁺] signaling events through several channels like IP₃-receptor (IP₃R), ryanodine receptor (RyR), etc. were explored for intracellular [Ca²⁺] signaling [3]. The IP₃-induced [Ca²⁺] fluctuations have been influenced by [Ca²⁺] buffering mechanisms [4], and this buffer approximation was validated close to the source location of calcium ions in cells [5]. Also, the behavior of [Ca²⁺]-induced calcium waves along with spatial dimension has been analyzed in excitable systems [6]. The higher concentration of slow buffer leads to fluctuations in calcium signaling [7], which is crucial to generate information of neuronal encoding and processing [8]. The alterations in neuronal calcium signaling contribute in different neurological disorders including Alzheimer’s [9]. Several research workers have investigated the [Ca²⁺] regulation in numerous cells including myocytes [10,11,12], fibroblast [13,14,15], astrocytes [16, 17], T-lymphocyte [18, 19], neurons [20,21,22,23,24,25,26], hepatocyte [27,28,29], acinar cells [30, 31], β-cell [32] and Oocytes [33, 34], etc. utilizing analytical and numerical methods in recent years. Incorporating biophysical components of [Ca²⁺] signaling like calcium channel, sodium channel, potassium channel, etc. the study on the behavior of [Ca²⁺] dynamics has been conducted in neurons [21], which was extended by utilizing the modified Bessel function for a one-dimensional cylindrical-shaped neurons [23]. The analytical work on the reaction-diffusion model of [Ca²⁺] dynamics was explored by employing Laplace and Fourier transformation with Atangana–Baleanu–Caputo derivatives in neuronal cells [35]. The neuronal calcium dynamics in association with NCX, endoplasmic reticulum (ER), buffer, VGCC, etc. were discussed concerning Alzheimer’s disorder [36].

The association of hydrolysis of PIP₂ and an elevation in intracellular [Ca²⁺] concentration has been noticed in human cells [37]. The different cellular processes like learning, memory, fertilization, cell development, etc. are regulated by the IP₃-induced calcium release through IP₃-receptor [38, 39]. The foundation for intricate calcium regulatory patterns is provided by the intracellular [Ca²⁺] release from ER via RyR and IP₃R in cells [40]. The messenger action ranges of calcium and IP₃ signaling mechanisms was examined by the measurements of their diffusion coefficients in cells [41]. To describe the calcium activation and inhibition of IP₃R in ER, the nine variables kinetic model has been constructed [42], which was minimized into two variables kinetic system [43]. The role of [Ca²⁺] signaling and IP₃ concentration in the chaotic oscillations was reported in bursting neuron cells [44]. The study on the association of the elevation in IP₃-induced calcium release and Alzheimer’s disorder was explored in neuronal cells [45]. The interdependent calcium and IP₃ dynamics has been studied in diverse cells including myocytes [11, 12], hepatocyte [46], etc. In neurons, Few studies are available on the interdependence of [Ca²⁺] and IP₃ signaling systems regulating the NO, β-amyloid and ATP formations [47,48,49].

The [Ca²⁺]-dependent and [Ca²⁺]-independent NO generation and their biological importance were discussed in neuronal cells [50]. The neuronal NO formation is simulated via [Ca²⁺] influx and induced by a glutamate receptor [51, 52]. The neuronal nitric oxide generation is regulated by different calcium channels including VGCC [53], R-type [Ca²⁺] channel [54], [Ca²⁺]-dependent K⁺ channel [55], etc. NO exhibits cytoprotective properties at low concentrations and cytotoxic effects at high concentration levels in neurons [56]. To maintain adequate nitric oxide concentration and prevent the neurons from toxicity, NO needs tight regulation by calcium signaling in cells [57]. The formation of potent vasodilators including NO controls the high concentration of calcium in neurons [58]. The elevated [Ca²⁺] concentration is reported during Ischemia [59], which may produce high amounts of nitric oxide in cells [60]. A computational model for synaptic activities associated with the variations in cerebral blood volume was explored in neuron cells [61]. The elevated NO levels cause an elevation in cGMP concentration, which further causes reduction in the cytosolic [Ca²⁺] levels through PMCA channel, and these reduced calcium levels lead to the decrease in the [Ca²⁺]-dependent NO generation in cells [62, 63]. The interaction of neuronal calcium signaling with nitric oxide dynamics was reported incorporating one-way feedback process between [Ca²⁺] and NO in neuronal cells with different neuronal illnesses like Parkinson’s, etc. [64]. The regulation of ATP via the mechanisms of the interdependent calcium and IP₃ systems has been reported in fibroblast cells [65].

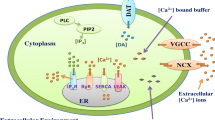
The neuron cell forms a complex media involving reaction-diffusion of bioenergetic dynamical systems of calcium, IP₃ and NO, etc. The study of independent dynamical systems of calcium, IP₃ and nitric oxide signaling offer very limited information about cellular functioning of neuronal cells. Few studies are reported on the cooperation of two system dynamics namely calcium dynamics with either IP₃ or nitric oxide in nerve cells that cast light on the mutual regulation and dysregulation of different cellular activities. The IP₃ concentration was taken as constant in the past to study mutual regulation of calcium and NO in neuronal cells [64]. But in fact the dynamics of IP₃ also influences the calcium signaling in neuronal cells and thus have consequent impacts on NO dynamics. No research is noted on the spatiotemporal cross talk of three systems namely [Ca²⁺], IP₃, and NO in neurons. Here, a new model of system dynamics of calcium, IP₃ and NO is proposed to explore the insights of their mutual spatiotemporal regulation in neuronal cells. Therefore, the study of interdependent dynamics of calcium, IP₃ and NO will give insights into the impacts of feedback control mechanics on their mutual regulation. The two-way feedback process between calcium and IP₃ systems, and two-way feedback between [Ca²⁺] and NO through NO/cGMP pathways and PMCA channel were incorporated in the proposed model. A FEM with the Crank-Nicholson technique is utilized to obtain the numerical findings of interactive systems dynamics of [Ca²⁺], IP₃ and NO in the presence of NCX and VGCC channels, and the effects of different parameters including buffer, IP₃-receptor, ryanodine channel, NO/cGMP kinetics with PMCA channel, etc. on the cross talk of [Ca²⁺], IP₃, and nitric oxide has been analyzed in neuron cells. The crucial information about the behavior of different mechanisms under the interactions of three dynamical systems of [Ca²⁺], IP₃ and NO has been explored in neuronal cells.

Mathematical Formulation

Incorporating buffer concentration, VGCC, NCX, RyR and PMCA channel in the Wagner et al. [66] model, the [Ca²⁺] regulation with IP₃ in neuron cells can be depicted as,

$$\begin{array}{c}\frac{\partial [{{\rm{Ca}}}^{2+}]}{\partial {\rm{t}}}={{\rm{D}}}_{{\rm{Ca}}}\frac{{\partial }^{2}[{{\rm{Ca}}}^{2+}]}{\partial {{\rm{x}}}^{2}}+(\frac{{{\rm{J}}}_{{\rm{IPR}}}-{{\rm{J}}}_{{\rm{SERCA}}}+{{\rm{J}}}_{{\rm{LEAK}}}+{{\rm{J}}}_{{\rm{RyR}}}}{{{\rm{F}}}_{{\rm{C}}}})-\\ {{\rm{K}}}^{+}{[{\rm{B}}]}_{\infty }([{{\rm{Ca}}}^{2+}]-{[{{\rm{Ca}}}^{2+}]}_{\infty })+{{\rm{J}}}_{{\rm{VGCC}}}-{{\rm{J}}}_{{\rm{PMCA}}}\end{array}$$

(1)

Here, [Ca²⁺]_∞ and [B]_∞ are respectively representing the steady state concentration levels of [Ca²⁺] and buffer. D_Ca and K⁺ are depicting the [Ca²⁺] diffusion coefficient and buffer association rate respectively. t and x respectively depict the time and distance parameters.

In Eq. (1), the expressions of the distinct inflow and outflow terms are shown as follows [66]:

$${{\rm{J}}}_{{\rm{IPR}}}={{\rm{V}}}_{{\rm{IPR}}}{{\rm{m}}}^{3}{{\rm{h}}}^{3}({[{{\rm{Ca}}}^{2+}]}_{{\rm{ER}}}-[{{\rm{Ca}}}^{2+}])$$

(2)

$${{\rm{J}}}_{{\rm{SERCA}}}={{\rm{V}}}_{{\rm{SERCA}}}(\frac{{[{{\rm{Ca}}}^{2+}]}^{2}}{{[{{\rm{Ca}}}^{2+}]}^{2}+{{\rm{K}}}_{{\rm{SERCA}}}^{2}})$$

(3)

$${{\rm{J}}}_{{\rm{LEAK}}}={{\rm{V}}}_{{\rm{LEAK}}}({[{{\rm{Ca}}}^{2+}]}_{{\rm{ER}}}-[{{\rm{Ca}}}^{2+}])$$

(4)

$${{\rm{J}}}_{{\rm{RyR}}}={{\rm{P}}}_{0}{{\rm{V}}}_{{\rm{RyR}}}({[{{\rm{Ca}}}^{2+}]}_{{\rm{ER}}}-[{{\rm{Ca}}}^{2+}])$$

(5)

Where, fluxes for IP₃R, RyR, SERCA Pump and Leak are denoted respectively by J_IPR, J_RyR, J_SERCA and J_LEAK. Also, V_RyR, V_LEAK and V_IPR are representing sequentially the flux rates for RyR, Leak and IP₃R. K_SERCA and V_SERCA represent the Michaelis constant and flux rate concerning SERCA pump.

The variable m and h from Eq. (2) are expressed as:

$${\rm{m}}=\left(\frac{[{\rm{IP}}_{3}]}{[{\rm{IP}}_{3}]+{{\rm{K}}}_{\rm{IP}{3}}}\right)\left(\frac{[{\rm{Ca}}^{2+}]}{[{{\rm{Ca}}}^{2+}]+{\rm{K}}_{\rm{Ac}}}\right)$$

(6)

$${\rm{h}}=\frac{{{\rm{K}}}_{{\rm{Inh}}}}{{{\rm{K}}}_{{\rm{Inh}}}+[{{\rm{Ca}}}^{2+}]}$$

(7)

Here, K_IP3, K_Ac and K_inh are denoting correspondingly the dissociation parameters of binding site of IP₃ and [Ca²⁺] activations and [Ca²⁺] inhibition.

J_VGCC represents the VGCC flux and framed by employing the following Goldmann-Hodgkin-Kartz (GHK) current equations [67],

$${{\rm{I}}}_{{\rm{Ca}}}={{\rm{P}}}_{{\rm{Ca}}}{{\rm{Z}}}_{{\rm{Ca}}}^{2}\frac{{{\rm{F}}}^{2}{{\rm{V}}}_{{\rm{m}}}}{{\rm{RT}}}\frac{{[{{\rm{Ca}}}^{2+}]}_{{\rm{i}}}-{[{{\rm{Ca}}}^{2+}]}_{0}\exp (-{{\rm{Z}}}_{{\rm{Ca}}}\frac{{{\rm{FV}}}_{{\rm{m}}}}{{\rm{RT}}})}{1-\exp (-{{\rm{Z}}}_{{\rm{Ca}}}\frac{{{\rm{FV}}}_{{\rm{m}}}}{{\rm{RT}}})}$$

(8)

Where, the intracellular and extracellular [Ca²⁺] levels are expressed sequentially by [Ca²⁺]_i and [Ca²⁺]₀. P_Ca and Z_Ca respectively demonstrate the permeability and valency of [Ca²⁺]. The Faradays constant and membrane potential are correspondingly represented by F and V_m. The absolute temperature and the real gas constant are sequentially depicted by T and R. The following equation converts Eq. (8) into molar/sec,

$${{\rm{J}}}_{{\rm{VGCC}}}=-\frac{{{\rm{I}}}_{{\rm{Ca}}}}{{{\rm{Z}}}_{{\rm{Ca}}}{{\rm{FV}}}_{{\rm{cytosol}}}}$$

(9)

The GHK equation for current yields the current density as a voltage function. The NCX involves the exchange of one [Ca²⁺] ion for three [Na⁺] ions and regulates the calcium concentrations as depicted below [68,69,70]:

$${\sigma }_{{\rm{NCX}}}={{\rm{Ca}}}_{0}{\left(\frac{{{\rm{Na}}}_{{\rm{i}}}}{{{\rm{Na}}}_{0}}\right)}^{3}\exp\left (\frac{{{\rm{FV}}}_{{\rm{m}}}}{{\rm{RT}}}\right)$$

(10)

Where, Na_i and Na₀ are correspondingly expressing the intracellular and extracellular Na⁺ levels.

The IP₃ dynamics with [Ca²⁺] proposed by Wagner et al. [66] is used and the IP₃ regulation with [Ca²⁺] can be depicted as,

$$\frac{\partial [{{\rm{IP}}}_{3}]}{\partial {\rm{t}}}={{\rm{D}}}_{{\rm{i}}}\frac{{\partial }^{2}[{{\rm{IP}}}_{3}]}{\partial {{\rm{x}}}^{2}}+\frac{{{\rm{J}}}_{{\rm{production}}}-\lambda ({{\rm{J}}}_{{\rm{kinase}}}+{{\rm{J}}}_{{\rm{phosphatase}}})}{{{\rm{F}}}_{{\rm{c}}}}$$

(11)

Here, D_i represents the IP₃ transport coefficient. The [Ca²⁺]-dependent IP₃ generation flux can be denoted as [66],

$${{\rm{J}}}_{{\rm{production}}}={{\rm{V}}}_{{\rm{production}}}\left(\frac{{[{{\rm{Ca}}}^{2+}]}^{2}}{{[{{\rm{Ca}}}^{2+}]}^{2}+{{\rm{K}}}_{{\rm{production}}}^{2}}\right)$$

(12)

Where, the IP₃ production flux is expressed by J_Production. The Michaelis constant for [Ca²⁺] activation and IP₃ formation rate are respectively K_Production and V_Production.

The IP₃ elimination fluxes by J_Kinase and J_phosphatase as depicted below [71],

$${{\rm{J}}}_{{\rm{kinase}}}=(1-\zeta ){{\rm{V}}}_{1}\left(\frac{[{{\rm{IP}}}_{3}]}{[{{\rm{IP}}}_{3}]+2.5}\right)+\zeta {{\rm{V}}}_{2}\left(\frac{[{{\rm{IP}}}_{3}]}{[{{\rm{IP}}}_{3}]+0.5}\right)$$

(13)

$${{\rm{J}}}_{{\rm{phosphatase}}}={{\rm{V}}}_{{\rm{ph}}}\left(\frac{[{{\rm{IP}}}_{3}]}{[{{\rm{IP}}}_{3}]+30}\right)$$

(14)

$$\zeta =\left(\frac{[{{\rm{Ca}}}^{2+}]}{[{{\rm{Ca}}}^{2+}]+0.39}\right)$$

(15)

Where, V₁ and V₂ are the rate constants concerning low and high [Ca²⁺] (3-kinase) and V_ph is a rate constant for phosphatase. λ is an controllable variable [66] used for the estimation of elimination rate. The expression for [Ca²⁺]_ER is depicted as follows,

$${{[{\rm{Ca}}}^{2+}]}_{{\rm{T}}}={{\rm{F}}}_{{\rm{E}}}{{[{\rm{Ca}}}^{2+}]}_{{\rm{ER}}}+{{\rm{F}}}_{{\rm{C}}}\,{{[{\rm{Ca}}}^{2+}]}_{{\rm{C}}}$$

(16)

The nitric oxide dynamics with [Ca²⁺] is reported by Gibson et al. [61] and expressed below as,

$$\frac{\partial [{\rm{NO}}]}{\partial {\rm{t}}}={{\rm{D}}}_{{\rm{NO}}}\frac{{\partial }^{2}[{\rm{NO}}]}{\partial {{\rm{x}}}^{2}}+({{\rm{J}}}_{{\rm{formation}}}-{{\rm{J}}}_{{\rm{degradation}}}),$$

(17)

Where, the nitric oxide diffusion coefficient is depicted by D_NO. The NO formation flux is given by as follows [61]:

$${{\rm{J}}}_{{\rm{production}}}={{\rm{V}}}_{{\rm{NO}}}\left(\frac{[{{\rm{Ca}}}^{2+}]}{[{{\rm{Ca}}}^{2+}]+{{\rm{K}}}_{{\rm{NO}}}}\right),$$

(18)

Where, V_NO and K_NO are the rate constants.

$${{\rm{J}}}_{{\rm{degradation}}}={{\rm{K}}}_{{\rm{\deg }}}[{\rm{NO}}],$$

(19)

Where, the NO degradation flux and NO degradation rate constant are respectively depicted by J_degradation and K_deg.

The NO/cGMP kinetics is expressed below as follows [72]:

$$\frac{\partial [{\rm{cGMP}}]}{\partial {\rm{t}}}={{\rm{V}}}_{{\rm{cGMP}}}\left(\frac{{{\rm{g}}}_{0}+{{\rm{g}}}_{1}[{\rm{NO}}]+{[{\rm{NO}}]}^{2}}{{{\rm{a}}}_{0}+{{\rm{a}}}_{1}[{\rm{NO}}]+{[{\rm{NO}}]}^{2}}\right)-{{\rm{X}}}_{{\rm{cGMP}}}\left(\frac{{[{\rm{cGMP}}]}^{2}}{{{\rm{K}}}_{{\rm{cGMP}}}+[{\rm{cGMP}}]}\right),$$

(20)

Where, the flux of cGMP generation is depicted as a function of NO distribution and g₀, g₁, a₀, a₁, V_cGMP, X_cGMP and K_cGMP are constant and their values are acquired in the model by fitting NO/cGMP pathways to experiment data [72].

The expression of plasmalemmal [Ca²⁺]-ATPase (PMCA) in the presence of cGMP can be represented as follows:

$${{\rm{J}}}_{{\rm{PMCA}}}={{\rm{V}}}_{{\rm{cGMP}}}^{{\rm{PMCA}}}\left(1+1.8\frac{2.[{\rm{cGMP}}]}{{{\rm{K}}}_{{\rm{cGMP}}}^{{\rm{PMCA}}}+[{\rm{cGMP}}]}\right)\left(\frac{[{{\rm{Ca}}}^{2+}]}{{{\rm{K}}}_{{\rm{PMCA}}}+[{{\rm{Ca}}}^{2+}]}\right),$$

(21)

Here, ${{\rm{V}}}_{{\rm{cGMP}}}^{{\rm{PMCA}}}\,{\rm{and}}\,{{\rm{K}}}_{{\rm{cGMP}}}^{{\rm{PMCA}}}$ are respectively the cGMP levels at half-activation of PMCA, maximum current in cGMP concentration’s absence.

Initial conditions

The reported initial conditions for [Ca²⁺] [73], IP₃ [74], and NO and cGMP [75] are sequentially depicted as follows:

$${[{{\rm{Ca}}}^{2+}]}_{{\rm{t}}=0}=0.1\,{\upmu}{\mathrm{M}}$$

(22)

$${[{{\rm{IP}}}_{3}]}_{{\rm{t}}=0}=0.16\,{\upmu}{\mathrm{M}}$$

(23)

$${[{\rm{NO}}]}_{{\rm{t}}=0}=0.0928\,{\upmu}{\mathrm{M}}$$

(24)

$${[{\rm{cGMP}}]}_{{\rm{t}}=0}=9.04\,{{\upmu }}{\mathrm{M}}$$

(25)

Boundary conditions

For [Ca²⁺], the reported boundary conditions as expressed below [73],

$$\mathop{\mathrm{lim}}\limits_{x\to 0}\left(-{{\rm{D}}}_{{\rm{c}}}\frac{\partial [{{\rm{Ca}}}^{2+}]}{\partial {\rm{x}}}\right)=\sigma -{\sigma }_{{\rm{NCX}}}$$

(26)

_{Where, σ is calcium source influx term.}

At opposite end from the source site, the [Ca²⁺] reaches concentration levels of 0.1 µm [73].

$$\mathop{\mathrm{lim}}\limits_{x\to 5}[{{\rm{Ca}}}^{2+}]={[{{\rm{Ca}}}^{2+}]}_{\infty }=0.1\,{\upmu} {\mathrm{M}}$$

(27)

The following are the derivations of the boundary concentrations for IP₃ regulation [74],

$$\mathop{\mathrm{lim}}\limits_{x\to 5}[{{\rm{IP}}}_{3}]=0.16\,{\upmu} {\mathrm{M}}$$

(28)

$$\mathop{\mathrm{lim}}\limits_{x\to 0}[{{\rm{IP}}}_{3}]=3{\upmu} {\mathrm{M}},\,{\rm{t}} > 0;$$

(29)

The deduced boundary conditions for NO regulation are depicted as follows [76]:

$$\mathop{\mathrm{lim}}\limits_{x\to 0}\left(\frac{\partial [{\rm{NO}}]}{\partial {\rm{x}}}\right)={\rm{0}}.$$

(30)

$$\mathop{\mathrm{lim}}\limits_{x\to 5}\left(\frac{\partial [{\rm{NO}}]}{\partial {\rm{x}}}\right)={\rm{0}}.$$

(31)

Appendix illustrates the description of the FEM with the Crank-Nicholson scheme, which is employed to get the solution of system of equations with initial boundary conditions.

Results and discussion

The numeric amounts and units for a variety of parameters are represented in Table 1.

Table 1 Numeric Data ([61] and [66])

To validate the proper functioning of the present model, the basic findings of the neuronal spatiotemporal calcium and IP₃ distribution at different times and locations in the presence of NCX and VGCC are exhibited in Fig. 1, that were also reported by previous researchers in the absence of NCX and VGCC for interactions between two systems of calcium and IP₃ in neuronal cells. It is noted that the [Ca²⁺] concentration falls spatially from the source to another side of neurons due to the removal of cytosolic [Ca²⁺] to ER by the SERCA pump, [Ca²⁺] binding by the buffer and transport of calcium from location of the source to another end of cells as illustrated in Fig. (1A). The [Ca²⁺] source inflow provides notable amounts of [Ca²⁺] ions, which causes the increase in the cytosolic [Ca²⁺] levels with time growth at different positions as depicted in Fig. (1B). The nonlinear behavior of spatial [Ca²⁺] distribution tends towards linearity with time because the [Ca²⁺] control mechanism balances different regulatory processes in neurons. Also, the spatial IP₃ levels decrease with locations from boundary x = 0 µm upto 5 µm due to the diffusion of IP₃ and different IP₃ degradation fluxes in neurons. The IP₃ control mechanism attempts to maintain a balance between disturbances induced by IP₃-elevating mechanisms and IP₃-reducing mechanisms with time thereby resulting the nonlinear behavior of IP₃ distribution tends towards linearity with increase in time as exhibited in Fig. (1 C & 1D). The temporal IP₃ levels rise over time growth and accomplish the steady state at several locations as depicted in Fig. (1D). Thus, the diffusion process, degradation fluxes and other mechanisms regulate the calcium and IP₃ distribution in neuronal cells.

Fig. 1

[Ca²⁺] and IP₃ distributions with NCX, VGCC and PMCA (A) [Ca2+] at t = 0.02, 0.05, 0.1, 1.0 sec (B) [Ca2+] at x = 0, 1.0, 2.0, 4.0 µm (C) IP3 at t = 0.01, 0.02, 0.03, 0.1 sec (D) IP3 at x = 0, 1.0, 2.0, 4.0 µm

Also, Fig. 2 depicts the basic outcomes of the spatial NO distribution in neuronal cells for t = 0.02, 0.05, 0.1 and 0.5 seconds in the presence of NCX and VGCC. With the distant site from the source (0 µm), the nitric oxide concentration decreases for different time instants due to the effects of NO diffusion and NO degradation in neuron cells. With passage of time, the nitric oxide concentration also increases as exhibited in Fig. 2. Thus, several NO-associated mechanisms affect the nitric oxide distribution in neuron cells.

Fig. 2

NO distribution with NCX, VGCC and PMCA (A) t = 0.02 sec (B) t = 0.05 sec (C) t = 0.1 sec (D) t = 0.5 sec

Figure 3 exhibits the novel findings regarding the impacts of higher buffer amounts on the [Ca²⁺] concentration and IP₃ and NO generation fluxes in the presence of NCX and VGCC are illustrated in Fig. 3 at x = 0 µm for the cooperation of three dynamical systems of [Ca²⁺], IP₃ and nitric oxide in neuronal cells. The higher amounts of buffer lead to a higher reduction in the cytosolic [Ca²⁺] levels by fixing additional [Ca²⁺] ions in cells, while other [Ca²⁺]-elevating mechanisms try to increase [Ca²⁺] levels in the cell. The mismatches among calcium-elevating mechanisms and buffering process cause disturbances in the form of fluctuations in neuron cells. However, the [Ca²⁺] control mechanism maintains equilibrium among these processes with time and the oscillations in the calcium concentration reduce and achieve a steady state in cells as exhibited in Fig. (3A). The effects of disturbances in calcium concentration also cause disturbances in the [Ca²⁺]-dependent IP₃ and NO formation fluxes in the form of oscillations and these fluxes achieve the steady state with time as depicted in Fig. (3B, C) in neurons. Thus, the dysregulation in the calcium-associated mechanism may be responsible for the disturbances in neuronal [Ca²⁺], IP₃ and NO levels.

Fig. 3

[Ca²⁺], IP₃ production flux, NO production flux with VGCC, NCX, buffer 250 µM, source inflow 15 pA at x = 0 µm (A) [Ca2+] concentration (B) IP3 production flux (C) NO production flux

The consequences of NO/cGMP pathways on the cytosolic calcium concentration through the plasmalemmal [Ca²⁺]-ATPase (PMCA) are illustrated as novel results in Fig. 4 at 2.0 sec and 0 µm in neuronal cells. When the PMCA channel is active, the spatiotemporal [Ca²⁺] levels are notable decreases in neuronal cells. Since, the NO-induced cGMP activation significantly lowers the cytosolic [Ca²⁺] concentration and elevating the [Ca²⁺] efflux into the extracellular environment by utilizing the PMCA channels in neuronal cells. Also, the decrease in the neuronal [Ca²⁺] concentration due to the presence of PMCA channel leads to the reduction in the spatiotemporal [Ca²⁺]-dependent IP₃ and NO productions in neuronal cells as exhibited in Fig. 5 at different times and positions. It is noted that the IP₃-induced calcium release via IP₃R elevates the cytosolic calcium concentration, resulting the NO production and NO concentration levels also elevates in neuronal cells. In the two-way feedback mechanism between calcium and nitric oxide exhibits that the enhancement in the NO concentration leads to the elevation in cGMP levels, which further lowers the cytosolic calcium concentration via PMCA channel, and these reduced calcium concentration causes decrease in the [Ca²⁺]-dependent NO production in neuron cells. Thus, one can conclude that the NO signaling may reduce the elevated NO levels by decreasing [Ca²⁺] concentration in neuronal cells by using cGMP and PMCA mechanisms.

Fig. 4

[Ca²⁺] concentration with NCX, VGCC, buffer 5 µM, source inflow 15 pA for distinct PMCA channel states (A) t = 2.0 sec (B) x = 0 µm

Fig. 5

IP₃ and NO generation fluxes with NCX, VGCC, buffer 5 µM, source inflow 15 pA for distinct PMCA channel states (A) IP3 production at t = 2.0 sec (B) IP3 production at x = 2.5 µm (C) NO production at t = 2.0 sec (D) NO production at x = 2.5 µm

Figure 6 shows the novel and interesting insights into the behavior of different cellular mechanisms like IP₃-receptor, which has been significantly differed for the cooperation of three dynamical systems of calcium, IP₃ and NO as compared to the cooperation of two dynamical systems of [Ca²⁺] and NO in neuronal cells. Figure 6A and C represent results for interactions of three systems of calcium, IP₃ and NO in neuronal cells. Figure 6B and D represent results for interactions of two systems of calcium and NO in neuronal cells as IP₃ is kept constant. The elevated spatiotemporal calcium levels are noted in the consideration of the IP₃R as it causes the IP₃-induced [Ca²⁺] release to the cytosol from the ER, resulting in the [Ca²⁺] levels elevation in neurons. In the absence of the IP₃R, the spatiotemporal [Ca²⁺] level decreases in the cell. The different IP₃R states cause higher changes in calcium levels near the center of cells. It is noted in Fig. 6 that when the interactions of three systems namely [Ca²⁺], IP₃ and NO are considered, the IP₃-receptor causes significant changes in calcium concentration levels. But, when the interactions of two systems namely [Ca²⁺] and NO are considered in neurons, the effect of the IP₃R decreases on [Ca²⁺] concentration since IP₃ dynamics is required for proper activation of the channel in neurons.

Fig. 6

[Ca²⁺] concentration with NCX, VGCC, buffer 5 µM, source inflow 15 pA for distinct IP₃R states (A) at t = 2.5 sec with dynamic IP3 (B) at t = 2.5 sec with constant IP3 (C) at x = 2.5 µm with dynamic IP3 (D) at x = 2.5 µm with constant IP3

For different IP₃R states, the cooperation of three systems of [Ca²⁺], IP₃ and NO bring significant changes in the IP₃ and NO formations as compared to the interactions of two systems of calcium and NO in neuronal cells. The novel outcomes about the influences of IP₃R on [Ca²⁺]-associated spatial IP₃ and NO formations in the presence of NCX and VGCC in neuron cells are depicted in Fig. 7 at 2.5 sec. Figure 7A and C represent results for interactions of three systems of calcium, IP₃ and NO in neurons. Figure 7B and D represent results for interactions of two systems of calcium and NO in neurons as IP₃ is kept constant. The [Ca²⁺] levels increase when IP₃R is in an active state as illustrated in Fig. 5, similarly the [Ca²⁺]-associated spatial IP₃ and NO formation fluxes also elevate in the presence of IP₃R and decrease in the absence of IP₃R in neuron cells as illustrated in Fig. 7. The variations in the spatial IP₃ and NO formation fluxes in Fig. 7 are higher near the center of the cell for active and inactive IP₃R states. The interaction of dynamic IP₃ with systems of calcium and NO activates the IP₃-receptor channel for regulating calcium and [Ca²⁺]-dependent activities like IP₃ and NO production at appropriate levels in neuron cells. When the IP₃ is not considered dynamic, the IP₃R effects on the calcium and [Ca²⁺]-dependent processes are not significant in the cell as exhibited in Fig. 7. Thus, the IP₃R regulates the IP₃ and NO formation through [Ca²⁺] signaling in neurons.

Fig. 7

IP₃ and NO production fluxes with NCX, VGCC, buffer 5 µM, source inflow 15 pA for distinct IP₃R states at t = 2.5 sec (A) IP3 production with dynamic IP3 (B) IP3 production with constant IP3 (C) NO production with dynamic IP3 (D) NO production with constant IP3

The neuronal IP₃ levels are regulated by different IP₃R states in neurons as depicted in Fig. 8 at various times and locations. For different IP₃R states, the spatial difference curves of IP₃ concentration initially increase to the center of the cell and then start decreasing to the other end of neurons concerning various time instants as illustrated in Fig. 8A. The temporal difference curves of IP₃ for different IP₃R states increase over time growth and accomplish equilibrium at distinct locations in neuron cells. Thus, the different IP₃-receptor states notably increase or decrease the IP₃ levels in neuron cells.

Fig. 8

Difference in IP₃ levels with NCX, VGCC and PMCA for different IP₃R states (A) at t = 0.04, 0.05, 0.07, and 0.2 sec (B) at x = 0.5, 1.5, 2.5, and 4.0 µm

The neuronal nitric oxide concentration depends on different IP₃R receptor states as depicted in Fig. 9 at t = 0.2 sec. It is noted in Fig. 9 that the NO concentration increases when the IP₃R is active and decreases when the IP₃R is in an inactive state in neurons. This relationship in Fig. 9 is due to the reason that the formation of NO is regulated by the [Ca²⁺]-associated IP₃R mechanism in the cell. Thus, the dysregulation in the IP₃-receptor may contribute to the neurotoxic levels of NO in neuronal cells.

Fig. 9

NO concentration with NCX, VGCC, buffer 5 µM, source inflow 15 pA at 0.2 sec for different IP₃R states (A) Without IP3-receptor (B) With IP3-receptor

Figure 10 displays the novel insights into the effects of different RyR states on the [Ca²⁺] distribution for the cases of the interactions of two dynamical systems of calcium and NO, and the interactions of the three dynamical systems of [Ca²⁺], IP₃ and nitric oxide in neuronal cells at 2.5 sec and 2.5 µm. When the entirely open RyR state (P₀ = 1.0) is considered, the elevated spatiotemporal calcium concentration is noted in neuron cells, since the RyR causes the calcium-induced [Ca²⁺] release to the cytosol from the ER and the [Ca²⁺] levels increase in neurons. When the completely closed (P₀ = 0) RyR state is considered, the lower neuronal spatiotemporal calcium levels are noted than those for the entirely open RyR state case. The higher impacts of different RyR states on the [Ca²⁺] concentration are noticed near the center of neuronal cells as depicted in Fig. 10 (A & B). The variations in the [Ca²⁺] concentration for the active and inactive RyR states are less when the dynamic interactions of the three systems namely calcium, IP₃ and NO are considered. But, when the interactions of calcium and NO are considered, there is a higher variation in the [Ca²⁺] concentration for distinct RyR states in neuron cells. This signifies that the interaction of IP₃ dynamics with calcium and NO increase the capabilities of cell control mechanisms to manage the dysregulatory effects of different processes in neuron cells. Thus, the RyR states regulate the [Ca²⁺] concentration in neurons and the disturbances in the RyR activities may lead to neurotoxicity by elevating neuronal calcium levels.

Fig. 10

[Ca²⁺] concentration with NCX, VGCC, buffer 5 µM, source inflow 15 pA for distinct RyR states (A) at t = 2.5 sec with dynamic IP3 (B) at t = 2.5 sec with constant IP3 (C) at x = 2.5 µm with dynamic IP3 (D) at x = 2.5 µm with constant IP3

The novel information about the effects of different ryanodine receptor states on the spatial IP₃ and NO production in neurons are shown in Fig. 11 at 2.5 sec with NCX and VGCC channels. In the presence of a completely open RyR state (P₀ = 1.0), the spatial IP₃ and NO formation fluxes are highly elevated in neurons as compared to the completely closed (P₀ = 0.0) RyR state in cells. The high influences of the different RyR states on the spatial IP₃ and NO formation fluxes are noticed near the center of neuronal cells as depicted in Fig. 11. When the IP₃ is not considered dynamic, the ryanodine receptor highly influences the generation of IP₃ and NO in neuron cells, while the interactions of the three systems namely calcium, IP₃ and NO reduce the effects of the ryanodine receptor on the production of IP₃ and NO in neuron cells. It is noted from Fig. 11B and D that the dominance of concentration-reducing mechanisms and concentration-elevating mechanisms is high in the case of the interactions of two systems of [Ca²⁺] and NO in neurons. Thus, the RyR mechanism affects the regulation of IP₃ and NO formation through neuronal calcium signaling.

Fig. 11

IP₃ and NO formation fluxes with NCX, VGCC, buffer 5 µM, source inflow 15 pA at t = 2.5 sec for different RyR states₃ (A) IP3 production with dynamic IP3 (B) IP3 production with constant IP3 (C) NO production with dynamic IP3 (D) NO production with constant IP3

The errors were calculated and exhibited in Tables 2–4 for the [Ca²⁺], IP₃ and nitric oxide respectively. E depicts the number of elements. For calcium, the present model’s accuracy is sequentially 99.52%, 99.71%, 99.938708% and 99.989417%, for IP₃ concentration, the accuracy is respectively 99.966925%, 99.965469%, 99.969886% and 99.977338% and for NO concentration, the accuracy is respectively 99.99967686%, 99.99963293%, 99.99960978% and 99.99960185% at time 0.1, 0.2, 0.5 and 1.0 sec. Therefore, for [Ca²⁺], IP₃ and NO distributions, the minimum accuracy and maximum error are correspondingly 99.52% and 0.48%. Thus, the solution is grid-independent due to its minimal grid sensitivity.

Table 2 Errors approximation for [Ca²⁺] concentration at position 0 μm

Table 3 Errors approximation for IP₃ concentration at position 0.125 μm

Table 4 Errors approximation for NO concentration at position 0.125 μm

If determined spectral radius (SR) concerning stability analysis is less or equal to unity then the system is deemed stable [77]. In our case, the SR is 0.9999. Therefore, the FEM used in the current circumstance is stable.

The presented data in Table 5 has been computed for interdependent [Ca²⁺], IP₃ and NO dynamics and compared to past studies [66] at 50 sec, and results are consistent as depicted in Table 5. Also, the calculated root mean square errors between earlier findings and present findings are 0.0000085539 and 0.00000000029159 respectively for [Ca²⁺] and IP₃, which are negligible. However, no experimental outcomes are observed under the circumstances of the current study, but the acquired outcomes are consistent with the biological facts.

Table 5 Comparison of [Ca²⁺] and IP₃ distribution with Wagner et al. [66] at 50 s

Conclusion

The FEM with the Crank-Nicholson method is very effective and flexible in generating information on the interactions of the three systems of [Ca²⁺], IP₃ and NO in neurons. Different regulatory and dysregulatory mechanisms like buffer, IP₃R, RyR, NCX, VGCC, NO/cGMP pathways with PMCA channel, etc. have been incorporated to explore the cross talk dynamics of calcium, IP₃ and nitric oxide in neuronal cells. Few studies on cooperation of calcium signaling with either nitric oxide or IP₃ are reported in the past, but in these studies, the researchers have incorporated one-way feedback between [Ca²⁺] and NO and two-way feedback between [Ca²⁺] and IP₃ in neuronal cells. Also, in these reported models, the research workers did not take into accounts the sodium-calcium exchanger (NCX), voltage-gated calcium channel (VGCC), and two-way feedback between [Ca²⁺] and nitric oxide through NO/cGMP pathways incorporating PMCA channel in neuronal cells. In the present work, few fundamental results of the calcium, IP₃ and NO dynamics have been included in the current work to illustrate the validation of the current model. The novel findings of the current study are the behavior and functioning of different crucial mechanisms, which significantly differs for interactions of two systems of [Ca²⁺] and NO and the cooperation of three systems of [Ca²⁺], IP₃ and nitric oxide in neuronal cell.

The following conclusions have been made on the basis of obtained findings.

• i. Calcium signaling regulates the concentration levels of IP₃ and NO in neurons. Any dysregulation in the calcium concentration may lead to dysregulation in IP₃ and nitric oxide production as well as in IP₃ and nitric oxide levels in neuron cells, which may further contribute to neurotoxic conditions and cell death.

• ii. The higher amounts of buffer concentration cause alterations in the [Ca²⁺] signaling in the form of fluctuations, which further causes disturbances in the IP₃ and NO generations in neuron cells. The [Ca²⁺] control mechanism regulates the equilibrium among different concentration-elevating and concentration-reducing mechanisms in the cell and provides stable dynamics. Any alterations either in the calcium control mechanism or buffering process may result in neurotoxic conditions in the form of multiple neuronal illnesses including Alzheimer’s.

• iii. In the two-way feedback mechanism between calcium and nitric oxide exhibits that the enhancement in the NO concentration leads to the elevation in cGMP levels, which further lowers the cytosolic calcium concentration via PMCA channel, and this reduced calcium concentration causes decrease in the [Ca²⁺]-dependent NO production in neuron cells. Thus, one can conclude that the NO signaling may reduce the elevated NO levels by decreasing [Ca²⁺] concentration in neuronal cells by using cGMP and PMCA mechanisms.

• iv. The IP₃-receptor regulates the [Ca²⁺], IP₃ and NO concentration levels in neurons. The IP₃ dynamics are responsible for the proper activation of the IP₃R channel in neurons. In the absence of IP₃ dynamics, the IP₃-receptor exhibits negligible effects on the [Ca²⁺], IP₃ and NO levels in neuron cells. Any disturbances in the IP₃R mechanism may be responsible for the alterations in the calcium, IP₃ and NO signaling and may be associated with different neuronal illnesses including Ischemia, Alzheimer’s etc.

• v. The ryanodine receptor is highly sensitive during disease-associated conditions. The dysregulatory effects of the ryanodine receptor decrease in the case of the cross-talk of three systems namely calcium, IP₃ and NO in neuron cells as compared to the case of the interactions among two systems namely calcium and NO in neurons. The interactive IP₃ dynamics with system dynamics of calcium and NO provide additional stability to the system to balance the dysregulatory effects of different processes like RyR in neuron cells and reduce the risk of the condition of disease-affected neurons like Ischemic neurons, Alzheimeric neurons etc.

Thus, one may conclude that the cross-talk of three systems calcium, IP₃ and nitric oxide regulates the concentration levels of each other in neurons. The loss of the interactions of [Ca²⁺] with other system dynamics like IP₃ or NO may be responsible for the disturbances in the [Ca²⁺], IP₃ and NO concentration levels due to the disturbances in different processes like buffer, IP₃-receptor, ryanodine receptor, NCX, NO/cGMP kinetics with PMCC, etc. in neurons and may lead to the conditions of multiple neurological illnesses including Ischemia, Alzheimer’s etc.

The finite element method is effective in generating novel insights into the regulatory as well as dysregulatory processes of interactive systems of [Ca²⁺], IP₃ and NO in neurons. The acquired information regarding the constitutive processes of the interactions of [Ca²⁺], IP₃ and NO in neuron cells can be utilized by biomedical scientists for advancement of the diagnostic and therapeutic procedures.

Appendix: Model Equations Description

The shape functions concerning each element of [Ca²⁺], IP₃ and NO concentration are exhibited as,

$${{\rm{u}}}^{({\rm{e}})}={{{\rm{p}}}_{1}}^{({\rm{e}})}+{{{\rm{p}}}_{2}}^{({\rm{e}})}{\rm{x}}$$

(32)

$${{\rm{v}}}^{({\rm{e}})}={{{\rm{q}}}_{1}}^{({\rm{e}})}+{{{\rm{q}}}_{2}}^{({\rm{e}})}\,{\rm{x}}$$

(33)

$${{\rm{w}}}^{({\rm{e}})}={{{\rm{r}}}_{1}}^{({\rm{e}})}{{+{\rm{r}}}_{2}}^{({\rm{e}})}\,{\rm{x}}$$

(34)

$${{\rm{u}}}^{({\rm{e}})}{={\rm{S}}}^{{\rm{T}}}{{\rm{p}}}^{({\rm{e}})}{,{\rm{v}}}^{({\rm{e}})}{={\rm{S}}}^{{\rm{T}}}{{\rm{q}}}^{({\rm{e}})},{{\rm{w}}}^{({\rm{e}})}{={\rm{S}}}^{{\rm{T}}}{{\rm{r}}}^{({\rm{e}})},$$

(35)

$${S}^{{\rm{T}}}=[\begin{array}{cc}1 & {\rm{x}}\end{array}],\,{{\rm{p}}}^{{({\rm{e}})}^{{\rm{T}}}}=[\begin{array}{cc}{{\rm{p}}}_{1}^{({\rm{e}})} & {{\rm{p}}}_{2}^{({\rm{e}})}\end{array}],\,{{\rm{q}}}^{{({\rm{e}})}^{{\rm{T}}}}=[\begin{array}{cc}{{\rm{q}}}_{1}^{({\rm{e}})} & {{\rm{q}}}_{2}^{({\rm{e}})}\end{array}],\,{{\rm{r}}}^{{({\rm{e}})}^{{\rm{T}}}}=[\begin{array}{cc}{{\rm{r}}}_{1}^{({\rm{e}})} & {{\rm{r}}}_{2}^{({\rm{e}})}\end{array}]$$

(36)

Utilizing the nodal conditions in Eq. (35),

$${\bar{{\rm{u}}}}^{({\rm{e}})}={{\rm{S}}}^{({\rm{e}})}{{\rm{p}}}^{({\rm{e}})},\,{\bar{{\rm{v}}}}^{({\rm{e}})}={{\rm{S}}}^{({\rm{e}})}{{\rm{q}}}^{({\rm{e}})},\,{\bar{{\rm{w}}}}^{({\rm{e}})}={{\rm{S}}}^{({\rm{e}})}{{\rm{r}}}^{({\rm{e}})},$$

(37)

Where,

$${\bar{{\rm{u}}}}^{({\rm{e}})}=\left[\begin{array}{c}{{\rm{u}}}_{{\rm{i}}}\\ {{\rm{u}}}_{{\rm{j}}}\end{array}\right],{\bar{{\rm{v}}}}^{({\rm{e}})}=\left[\begin{array}{c}{{\rm{v}}}_{{\rm{i}}}\\ {{\rm{v}}}_{{\rm{j}}}\end{array}\right],{\bar{{\rm{w}}}}^{({\rm{e}})}=\left[\begin{array}{c}{{\rm{w}}}_{{\rm{i}}}\\ {{\rm{w}}}_{{\rm{j}}}\end{array}\right]\,{\rm{and}}\,{S}^{({\rm{e}})}=\left[\begin{array}{cc}1 & {{\rm{x}}}_{{\rm{i}}}\\ 1 & {{\rm{x}}}_{{\rm{j}}}\end{array}\right]$$

(38)

By the Eq. (37), we get

$${{\rm{p}}}^{({\rm{e}})}={{\rm{R}}}^{({\rm{e}})}\,{\bar{{\rm{u}}}}^{({\rm{e}})},\,{{\rm{q}}}^{({\rm{e}})}={{\rm{R}}}^{({\rm{e}})}{\bar{{\rm{v}}}}^{({\rm{e}})},\,{{\rm{r}}}^{({\rm{e}})}={{\rm{R}}}^{({\rm{e}})}{\bar{{\rm{w}}}}^{({\rm{e}})}$$

(39)

And

$${{\rm{R}}}^{({\rm{e}})}={{\rm{S}}}^{{({\rm{e}})}^{-1}}$$

(40)

Putting ${{\rm{p}}}^{({\rm{e}})},\,{{\rm{q}}}^{({\rm{e}})}$ and ${{\rm{r}}}^{({\rm{e}})}$ from Eq. (39) in (35), we have

$${{\rm{u}}}^{({\rm{e}})}={{\rm{S}}}^{{\rm{T}}}\,{{\rm{R}}}^{({\rm{e}})}\,{\bar{{\rm{u}}}}^{({\rm{e}})},\,{{\rm{v}}}^{({\rm{e}})}={{\rm{S}}}^{{\rm{T}}}\,{{\rm{R}}}^{({\rm{e}})}\,{\bar{{\rm{v}}}}^{({\rm{e}})},\,{{\rm{w}}}^{({\rm{e}})}={{\rm{S}}}^{{\rm{T}}}\,{{\rm{R}}}^{({\rm{e}})}\,{\bar{{\rm{w}}}}^{({\rm{e}})}$$

(41)

Discretized form of Eq. (1, 11 & 17) are represented by the integral ${{\rm{I}}}_{1}^{({\rm{e}})},\,{{\rm{I}}}_{2}^{({\rm{e}})},\,{\rm{and}}\,{{\rm{I}}}_{3}^{({\rm{e}})}$ and represented in this formation as shown below,

$${{{\rm{I}}}_{1}}^{({\rm{e}})}\,=\,{{\rm{I}}}_{{\rm{a1}}}^{({\rm{e}})}-{{\rm{I}}}_{{\rm{b1}}}^{({\rm{e}})}{+{\rm{I}}}_{{\rm{c1}}}^{({\rm{e}})}-{{\rm{I}}}_{{\rm{d1}}}^{({\rm{e}})}{+{\rm{I}}}_{{\rm{e1}}}^{({\rm{e}})}{+{\rm{I}}}_{{\rm{f1}}}^{({\rm{e}})}-{{\rm{I}}}_{{\rm{g1}}}^{({\rm{e}})}{+{\rm{I}}}_{{\rm{h1}}}^{({\rm{e}})}-{{\rm{I}}}_{{\rm{i1}}}^{({\rm{e}})}$$

(42)

Where

$${{\rm{I}}}_{{\rm{a1}}}^{({\rm{e}})}={\int }_{{x}_{i}}^{{x}_{j}}\left\{{\left(\frac{\partial {{\rm{u}}}^{({\rm{e}})}}{\partial {\rm{x}}}\right)}^{2}\right\}{\rm{dx}}$$

(43)

$${{\rm{I}}}_{{\rm{b1}}}^{({\rm{e}})}=\frac{{\rm{d}}}{{\rm{dt}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}\left[\frac{({{\rm{u}}}^{({\rm{e}})})}{{{\rm{D}}}_{{\rm{Ca}}}}\right]{\rm{dx}}$$

(44)

$${{\rm{I}}}_{{\rm{c1}}}^{({\rm{e}})}=\frac{{{\rm{V}}}_{{\rm{IPR}}}}{{{\rm{D}}}_{{\rm{ca}}}{{\rm{F}}}_{{\rm{c}}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}[{{\rm{\alpha }}}_{1}{{\rm{u}}}^{({\rm{e}})}+{{\rm{\alpha }}}_{2}{{\rm{v}}}^{({\rm{e}})}+{{\rm{\alpha }}}_{3}]\,{\rm{dx}}$$

(45)

$${{\rm{I}}}_{{\rm{d1}}}^{({\rm{e}})}=\frac{{{\rm{V}}}_{{\rm{SERCA}}}}{{{\rm{D}}}_{{\rm{ca}}}{{\rm{F}}}_{{\rm{c}}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}[{{\rm{\kappa }}}_{1}{{\rm{u}}}^{({\rm{e}})}{+{\rm{\kappa }}}_{2}]\,{\rm{dx}}$$

(46)

$${{\rm{I}}}_{{\rm{e1}}}^{({\rm{e}})}=\frac{{{\rm{V}}}_{{\rm{LEAK}}}}{{{\rm{D}}}_{{\rm{ca}}}{{\rm{F}}}_{{\rm{c}}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}[{[{{\rm{Ca}}}^{2+}]}_{{\rm{ER}}}-{{\rm{u}}}^{({\rm{e}})}]\,{\rm{dx}}$$

(47)

$${{\rm{I}}}_{{\rm{f1}}}^{({\rm{e}})}=\frac{{{\rm{V}}}_{{\rm{RyR}}}{{\rm{P}}}_{0}}{{{\rm{D}}}_{{\rm{ca}}}{{\rm{F}}}_{{\rm{c}}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}[{[{{\rm{Ca}}}^{2+}]}_{{\rm{ER}}}-{{\rm{u}}}^{({\rm{e}})}]\,{\rm{dx}}$$

(48)

$${{\rm{I}}}_{{\rm{g1}}}^{({\rm{e}})}=\frac{{{\rm{K}}}^{+}}{{{\rm{D}}}_{{\rm{ca}}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}[{{\rm{u}}}^{({\rm{e}})}-{[{{\rm{Ca}}}^{2+}]}_{\infty }]\,{\rm{dx}}$$

(49)

$${{\rm{I}}}_{{\rm{h1}}}^{({\rm{e}})}=\frac{1}{{{\rm{D}}}_{{\rm{ca}}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}[{{\rm{\theta }}}_{1}{{\rm{u}}}^{({\rm{e}})}-{{\rm{\theta }}}_{2}]\,{\rm{dx}}$$

(50)

$${{\rm{I}}}_{{\rm{i1}}}^{({\rm{e}})}={{\rm{f}}}^{({\rm{e}})}{(\frac{\sigma }{{{\rm{D}}}_{{\rm{ca}}}}-\frac{{\sigma }_{{\rm{NCX}}}}{{{\rm{D}}}_{{\rm{ca}}}})}_{{\rm{x}}=0}$$

(51)

_Now,

$${{\rm{I}}}_{2}^{({\rm{e}})}={{\rm{I}}}_{{\rm{a2}}}^{({\rm{e}})}-{{\rm{I}}}_{{\rm{b2}}}^{({\rm{e}})}+{{{\rm{I}}}_{{\rm{c2}}}}^{({\rm{e}})}-{{\rm{I}}}_{{\rm{d2}}}^{({\rm{e}})}$$

(52)

$${{\rm{I}}}_{{\rm{a2}}}^{({\rm{e}})}={\int }_{{x}_{i}}^{{x}_{j}}\left\{{\left(\frac{\partial {{\rm{v}}}^{({\rm{e}})}}{\partial {\rm{x}}}\right)}^{2}\right\}\,{\rm{dx}}$$

(53)

$${{\rm{I}}}_{{\rm{b2}}}^{({\rm{e}})}=\frac{{\rm{d}}}{{\rm{dt}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}\left[\frac{{{\rm{v}}}^{({\rm{e}})}}{{{\rm{D}}}_{{\rm{i}}}}\right]\,{\rm{dx}}$$

(54)

$${{\rm{I}}}_{{\rm{c2}}}^{({\rm{e}})}=\frac{{{\rm{V}}}_{{\rm{PROD}}}}{{{\rm{D}}}_{{\rm{i}}}{{\rm{F}}}_{{\rm{c}}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}[{{\rm{\mu }}}_{1}{{\rm{u}}}^{({\rm{e}})}+{{\rm{\mu }}}_{2}]\,{\rm{dx}}$$

(55)

$${{\rm{I}}}_{{\rm{d2}}}^{({\rm{e}})}=\frac{\lambda }{{{\rm{F}}}_{{\rm{c}}}{{\rm{D}}}_{{\rm{i}}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}[{{\rm{\delta }}}_{1}{{\rm{u}}}^{({\rm{e}})}+{{\rm{\delta }}}_{2}{{\rm{v}}}^{({\rm{e}})}+{{\rm{\delta }}}_{3})]\,{\rm{dx}}$$

(56)

and

$${{\rm{I}}}_{3}^{({\rm{e}})}={{\rm{I}}}_{{\rm{a3}}}^{({\rm{e}})}-{{\rm{I}}}_{{\rm{b3}}}^{({\rm{e}})}+{{\rm{I}}}_{{\rm{c3}}}^{({\rm{e}})}-{{\rm{I}}}_{{\rm{d3}}}^{({\rm{e}})}$$

(57)

$${{\rm{I}}}_{{\rm{a3}}}^{({\rm{e}})}={\int }_{{x}_{i}}^{{x}_{j}}\left\{{\left(\frac{\partial {{\rm{w}}}^{({\rm{e}})}}{\partial {\rm{x}}}\right)}^{2}\right\}\,{\rm{dx}}$$

(58)

$${{\rm{I}}}_{{\rm{b3}}}^{({\rm{e}})}=\frac{{\rm{d}}}{{\rm{dt}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}\left[\frac{{{\rm{w}}}^{({\rm{e}})}}{{{\rm{D}}}_{{\rm{NO}}}}\right]\,{\rm{dx}}$$

(59)

$${{\rm{I}}}_{{\rm{c3}}}^{({\rm{e}})}=\frac{{{\rm{V}}}_{{\rm{NO}}}}{{{\rm{D}}}_{{\rm{NO}}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}[{{\rm{\tau }}}_{1}{{\rm{u}}}^{({\rm{e}})}+{{\rm{\tau }}}_{2}]\,{\rm{dx}}$$

(60)

$${{\rm{I}}}_{{\rm{d2}}}^{({\rm{e}})}=\frac{{{\rm{K}}}_{{\rm{\deg }}}}{{{\rm{D}}}_{{\rm{NO}}}}{\int }_{{{\rm{x}}}_{{\rm{i}}}}^{{{\rm{x}}}_{{\rm{j}}}}[{{\rm{w}}}^{({\rm{e}})}]\,{\rm{dx}}$$

(61)

Numerous parameters ${{\rm{\alpha }}}_{1},\,{{\rm{\alpha }}}_{2},\,{{\rm{\alpha }}}_{3},\,{{\rm{\kappa }}}_{1},\,{{\rm{\kappa }}}_{2},\,{{\rm{\beta }}}_{1},\,{{\rm{\beta }}}_{2},\,{{\rm{\mu }}}_{1},\,{{\rm{\mu }}}_{2},\,{{\rm{\delta }}}_{1},\,{{\rm{\delta }}}_{2},\,{{\rm{\delta }}}_{3},\,{{\rm{\theta }}}_{1},\,{{\rm{\theta }}}_{2},\,{{\rm{\tau }}}_{1},\,{\rm{and}}\,{{\rm{\tau }}}_{2}$ are obtained by linearization of nonlinear [Ca²⁺], IP₃ and NO terms. After analyzing and incorporating the boundary conditions, the following system of equations are acquired as depicted below,

$$\frac{{{\rm{dI}}}_{1}}{{{\rm{d}}\bar{{\rm{u}}}}^{({\rm{e}})}}=\mathop{\sum }\limits_{{\rm{e}}=1}^{{\rm{N}}}{\bar{{\rm{Q}}}}^{({\rm{e}})}\frac{{{\rm{dI}}}_{1}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{u}}}}^{({\rm{e}})}}{\bar{{\rm{Q}}}}^{{({\rm{e}})}^{{\rm{T}}}}=0$$

(62)

$$\frac{{{\rm{dI}}}_{2}}{{{\rm{d}}\bar{{\rm{v}}}}^{({\rm{e}})}}=\mathop{\sum }\limits_{{\rm{e}}=1}^{{\rm{N}}}{\bar{{\rm{Q}}}}^{({\rm{e}})}\frac{{{\rm{dI}}}_{2}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{v}}}}^{({\rm{e}})}}{\bar{{\rm{Q}}}}^{{({\rm{e}})}^{{\rm{T}}}}=0$$

(63)

$$\frac{{{\rm{dI}}}_{3}}{{{\rm{d}}\bar{{\rm{w}}}}^{({\rm{e}})}}=\mathop{\sum }\limits_{{\rm{e}}=1}^{{\rm{N}}}{\bar{{\rm{Q}}}}^{({\rm{e}})}\frac{{{\rm{dI}}}_{3}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{w}}}}^{({\rm{e}})}}{\bar{{\rm{Q}}}}^{{({\rm{e}})}^{{\rm{T}}}}=0$$

(64)

Where,

$${\bar{{\rm{Q}}}}^{({\rm{e}})}=\left[\begin{array}{cc}\begin{array}{c}0\\ \begin{array}{c}.\\ \begin{array}{c}0\\ 1\\ \begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ \begin{array}{c}.\\ 0\end{array}\end{array}\end{array}\end{array}\end{array} & \begin{array}{c}0\\ \begin{array}{c}.\\ \begin{array}{c}0\\ 0\\ \begin{array}{c}\begin{array}{c}1\\ 0\end{array}\\ \begin{array}{c}.\\ 0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]{\rm{and}}\,\bar{{\rm{u}}}=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{{\rm{u}}}_{1}\\ {{\rm{u}}}_{2}\end{array}\\ {{\rm{u}}}_{3}\end{array}\\ \begin{array}{c}.\\ \begin{array}{c}\begin{array}{c}\begin{array}{c}.\\ {{\rm{u}}}_{39}\end{array}\\ {{\rm{u}}}_{40}\end{array}\\ {{\rm{u}}}_{41}\end{array}\end{array}\end{array}\right],\,\bar{{\rm{v}}}=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{{\rm{v}}}_{1}\\ {{\rm{v}}}_{2}\end{array}\\ {{\rm{v}}}_{3}\end{array}\\ \begin{array}{c}.\\ \begin{array}{c}\begin{array}{c}\begin{array}{c}.\\ {{\rm{v}}}_{39}\end{array}\\ {{\rm{v}}}_{40}\end{array}\\ {{\rm{v}}}_{41}\end{array}\end{array}\end{array}\right],\,\bar{{\rm{w}}}=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{{\rm{w}}}_{1}\\ {{\rm{w}}}_{2}\end{array}\\ {{\rm{w}}}_{3}\end{array}\\ \begin{array}{c}.\\ \begin{array}{c}\begin{array}{c}\begin{array}{c}.\\ {{\rm{w}}}_{39}\end{array}\\ {{\rm{w}}}_{40}\end{array}\\ {{\rm{w}}}_{41}\end{array}\end{array}\end{array}\right]$$

(65)

$$\frac{{{\rm{dI}}}_{1}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{u}}}}^{({\rm{e}})}}=\frac{{{\rm{dI}}}_{{\rm{a1}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{u}}}}^{({\rm{e}})}}+\frac{{\rm{d}}}{{\rm{dt}}}\frac{{{\rm{dI}}}_{{\rm{b1}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{u}}}}^{({\rm{e}})}}+\frac{{{\rm{dI}}}_{{\rm{c1}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{u}}}}^{({\rm{e}})}}-\frac{{{\rm{dI}}}_{{\rm{d1}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{u}}}}^{({\rm{e}})}}+\frac{{{\rm{dI}}}_{{\rm{e1}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{u}}}}^{({\rm{e}})}}+\frac{{{\rm{dI}}}_{{\rm{f1}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{u}}}}^{({\rm{e}})}}-\frac{{{\rm{dI}}}_{{\rm{g1}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{u}}}}^{({\rm{e}})}}+\frac{{{\rm{dI}}}_{{\rm{h1}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{u}}}}^{({\rm{e}})}}-\frac{{{\rm{dI}}}_{{\rm{i1}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{u}}}}^{({\rm{e}})}}$$

(66)

$$\frac{{{\rm{dI}}}_{2}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{v}}}}^{({\rm{e}})}}=\frac{{{\rm{dI}}}_{{\rm{a2}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{v}}}}^{({\rm{e}})}}+\frac{{\rm{d}}}{{\rm{dt}}}\frac{{{\rm{dI}}}_{{\rm{b2}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{v}}}}^{({\rm{e}})}}+\frac{{{\rm{dI}}}_{{\rm{c2}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{v}}}}^{({\rm{e}})}}+\frac{{{\rm{dI}}}_{{\rm{d2}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{v}}}}^{({\rm{e}})}}-\frac{{{\rm{dI}}}_{{\rm{e2}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{v}}}}^{({\rm{e}})}}$$

(67)

$$\frac{{{\rm{dI}}}_{3}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{w}}}}^{({\rm{e}})}}=\frac{{{\rm{dI}}}_{{\rm{a3}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{w}}}}^{({\rm{e}})}}+\frac{{\rm{d}}}{{\rm{dt}}}\frac{{{\rm{dI}}}_{{\rm{b3}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{w}}}}^{({\rm{e}})}}+\frac{{{\rm{dI}}}_{{\rm{c3}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{w}}}}^{({\rm{e}})}}-\frac{{{\rm{dI}}}_{{\rm{d3}}}^{({\rm{e}})}}{{{\rm{d}}\bar{{\rm{w}}}}^{({\rm{e}})}}$$

(68)

$${[{\rm{A}}]}_{123\times 123}\left[\begin{array}{c}{\left[\frac{\partial \bar{{\rm{u}}}}{\partial {\rm{t}}}\right]}_{41\times 1}\\ {\left[\frac{\partial \bar{{\rm{v}}}}{\partial {\rm{t}}}\right]}_{41\times 1}\\ {\left[\frac{\partial \bar{{\rm{w}}}}{\partial {\rm{t}}}\right]}_{41\times 1}\end{array}\right]+{[{\rm{B}}]}_{123\times 123}\left[\begin{array}{c}{\left[\bar{{\rm{u}}}\right]}_{41\times 1}\\ {\left[\bar{{\rm{v}}}\right]}_{41\times 1}\\ {\left[\bar{{\rm{w}}}\right]}_{41\times 1}\end{array}\right]={\left[{\rm{F}}\right]}_{123\times 1}$$

(69)

Concerning the system matrices A and B along system vectors F, the Crank-Nicholson scheme was utilized to solve the temporal derivatives in the FEM.