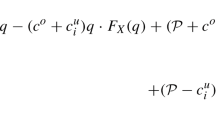1 Introduction

We consider a company, e.g. a retailer sourcing a product with short life cycle to stock using the framework of the celebrated newsvendor model. Traditionally risk-neutral decision makers are considered who optimize the expected value of the cost function or the profit function. Experimental findings state that the actual quantity ordered deviates from the optimal order quantity suggested by the newsvendor model with risk-neutrality. In these findings for high-profit products the order quantity is less than the one of the risk-neutral decisions maker and vice versa (cp. Schweitzer and Cachon 2000; Bolton and Katok 2005). Moreover, empirical observations show that managers tend to order less than the newsvendor solution because they base their decisions on other performance measures besides expected profit (cp. Brown and Tang 2006).

From the perspective of supply chain management the decision maker should control not only internal-facing performance measures of the company like the expected profit or loss and the probability of loss but also customer-related measures like the level of product availability (see Cachon and Terwiesch 2006). E.g. an incentive for an inventory manager to order less is to control the probability of loss. An incentive to order more may be to achieve a high level of product availability resulting in greater customer satisfaction (cp. Narayanan and Raman 2004).

We propose a model to incorporate these experimental and empirical findings: the optimal ordering quantity can be lower or higher than the risk-neutral newsvendor solution depending on the risk preferences of the inventory manager. The objective function of the model is a convex combination of two conditional expected values of profit taking into account the whole probability distribution of profits. One conditional expected value is the conditional value at risk (CVaR) focusing on low profits whereas the other one focuses on high profits.

The main contributions of the paper are:

  • We introduce a newsvendor model with an objective function depending a two risk parameters where different risk preferences can be modelled implying that the optimal order quantity is lower or higher than in the classical newsvendor model.

  • The objective function can be transformed into a mean-deviation decision rule with the coherent measure of risk CVaR.

  • We give a qualitative characterization of the optimal order quantity and its resulting performance measures. A risk-averse inventory manager cannot Pareto-dominate a risk-neutral or risk-taking inventory manager with respect to the expected profit and the level of product availability.

  • The risk preferences can be characterized by the performance measures, level of product availability and probability of loss, respectively.

The paper is organized as follows. In Sect. 2, we briefly review the classical newsvendor model. In Sect. 3 we review some recent papers of related literature. Our newsvendor model with risk preferences is introduced in Sect. 4 where also the risk attitudes of the inventory manager are characterized. In Sect. 5 the optimal order quantity and its resulting performance measures are derived and qualitative properties with respect to the risk parameters are proved. In Sect. 6 we express the risk attitudes by means of the specified cycle service level and the specified probability of loss, respectively. Section 7 concludes the paper and also discusses possible extensions to our model.

2 Notation: the classical newsvendor model

In this section we introduce our notation for the classical newsvendor model and its performance measures.

The random demand X is characterized by the distribution function F. The purchase price per unit of the product is c. During the regular selling season, the product is sold to customers at a unit price p. Unsatisfied demand is lost, and leftover inventory of the product at the end of the selling season is sold in an other distribution channel at the salvage value per unit z. p − c describes the cost of understocking by one unit, whereas c − z describes the cost of overstocking by one unit. It is assumed that p > c > z holds.

Let y denote the order quantity and g the profit. g depends on y and the stochastic demand X and is given by:

$$g(y,X) = (p - c) y - (p - z) (y - X)^{+} $$
(1)

with (y − X)+ = max (0, y − X).

In the classical newsvendor model the optimal order quantity y* is derived by maximizing the expected profit E(g(y, X)). The optimality condition is given by (see, e.g. Cachon and Terwiesch 2006, Sect. 9.4):

$$F(y^{*}) = \frac{p - c}{p - z}.$$
(2)

Here and in the following, we assume that the distribution function F is strictly monotone increasing and continuous; then y* is defined uniquely by

$$y^{*} = F^{{- 1}} {\left({\frac{{p - c}}{{p - z}}} \right)}.$$
(3)

The performance measures implied by y* are denoted in the following as optimal performance measures. The level of product availability is expressed by the cycle service level CSL. The cycle service level CSL* describes the probability that there is no stock-out during the selling season, i.e. that the order quantity y* exceeds demand (see (2)):

$$ \hbox{CSL}^{*} = {F}({y}^{*}) = \frac{{p - c}}{{p - z}}.$$
(4)

CSL* is usually defined as the critical ratio which describes the profit value of the product, i.e. the higher CSL* the higher is the profit value of the product and vice versa. For the optimal order quantity y* given by (3), we can derive the probability of loss

$$\hbox{PL}^{*} = P(g(y^{*},X) \leq 0)=F\left({y^{*} \cdot \frac{{c - z}}{{p - z}}} \right)$$
(5)

as well as the expected loss

$$\hbox{EL}^{*} = E(g(y^{*},X)|g(y^{*},X) \leq 0) = (z - c)y^{*} + \frac{{p - z}}{{PL^{*}}} \cdot {\int\limits_0^{y^{*} \cdot \frac{{c - z}}{{p - z}}}}xdF(x) $$
(6)

(see Appendix D).

2.1 Numerical example

In our numerical study, we choose throughout the paper a so-called newsvendor distribution for the random demand X of a selling season (Braden and Freimer 1991). Such a distribution can deal with exact data and with censored data, which happens to be the case in dynamic newsvendor models. An example of a newsvendor distribution is the Weibull distribution with distribution function

$$F(x) = 1 - \exp (- \delta x^{\gamma}) \quad (x \geq 0)$$

with parameters γ > 0 and δ > 0.

For reference, we choose the following parameters for the classical newsvendor model. The selling price per unit of the product is p = 10, the purchasing cost per unit c = 6, and the salvage value per unit is z = 5. The demand distribution is specified as Weibull distribution with parameters γ = 2 and δ = 0.0001. Thus, the expected demand is 88.6 units.

For these parameter values we have the optimal cycle service level CSL* =80%, the optimal order quantity y* = 126.9 units, the optimal expected profit EP* = 284 currency units, the optimal probability of loss PL* = 6%, and the optimal expected loss EL* = 42.8 currency units.

3 Newsvendor models with risk preferences

The classical newsvendor maximizes expected profit. Within the expected utility theory (and other normative decision theories), this is equivalent to the assumption of risk-neutral behaviour: expected profit derived from the optimal order quantity E(g(y*, X)) is considered indifferent to the random profit g(y*, X).

In decision theory risk-aversion is characterized by the fact that the expected value E(g(y, X)) is preferred to the random variable g(y, X) whereas for risk-taking behaviour g(y, X) is preferred to E(g(y, X)).

Khouja (1999) contains a survey of papers with extensions to different objectives and utility functions. The seminal paper of the newsvendor model within the expected utility framework is Eeckhoudt et al. (1995). For a given monotonically increasing utility function u, the objective is to maximize the expected utility of the profit:

$${\mathop {\max}\limits_y} \quad E(u(g(y,X))$$
(7)

In expected utility theory risk-aversion prevails if and only if the utility function is concave. Let y u be the solution of (7). It can been shown that

$${{y_{u} \leq y^{*} \quad \hbox{for concave}\;u}} $$
(8)

A risk-averse newsvendor will choose an order quantity resulting in a lower cycle service level. Recently, the newsvendor model with objectives different from maximizing expected profit has been an active field of research. Keren and Pliskin (2006) derive for increasing, concave utility functions a closed form solution of the optimal order quantity y u (see (8)) for uniformly distributed demand.

Schweitzer and Cachon (2000) also consider the expected utility approach. They specify several utility functions which represent loss-aversion, waste-aversion, stockout-aversion, underestimation of opportunity costs, preference for minimizing ex-post inventory error, respectively. The special utility functions suggested are consistent with the special preferences assumed. Of course, they represent only one possibility to do so. Moreover, it is shown that only one of the utility functions is consistent with the experimental results (preference for minimizing ex-post inventory error). The objective suggested is

$$ {\mathop {\max}\limits_y} \quad (w_{0} + E(g(y,X)) - {\int\limits_0^{\infty} {q (|y - x|) dF(x))}} $$
(9)

where w 0 represents initial wealth and q is a penalty function to be specified by the decision maker.

A pragmatic approach for modelling non risk-neutral inventory managers is proposed by Chen et al. (2004): The impact of an order quantity y is measured by the conditional value at risk for a given α (0 < α ≤ 1); it is denoted by CVaRα (y). Let F y denote the distribution function of g(y, X). The CVaRα (y) is the conditional expected profit given profit is below F − 1 y (α), in case F − 1 y (α) exists. In this case we have

$$\hbox{CVaR}_{\alpha} (y) = E(g(y,X)|g(y,X) \leq F_{y}^{{- 1}}(\alpha))\quad (0 < \alpha\leq 1).$$
(10)

In the newsvendor model F y is not invertible for some α since F y has a jump discontinuity at (p  − c)y, and therefore we need a more general definition of the CVaR using the generalized inverse of F y (see Appendix A):

$$\hbox{CVaR}_{\alpha} (y) =\frac{1}{\alpha}{\int\limits_0^\alpha F_{y}^{*} (p)dp} \quad (0 < \alpha\leq 1) $$
(11)

In case F − 1 y exists (11) and (10) coincide.

The optimal order quantity y α is the solution of

$$ {\mathop {\max}\limits_y} \quad \hbox{CVaR}_{\alpha} (y). $$
(12)

Therefore, ordering y α implies that the expected profit is maximal provided it is below the α-quantile. It can be shown that the optimal order quantity for the CVaR newsvendor is given by

$$ y_{\alpha} = F^{{- 1}} {\left({\alpha \frac{{p - c}}{{p - z}}} \right)} $$
(13)

(cp. Chen et al. 2004, p. 7). In (13) we get for α = 1 the solution of the classical newsvendor problem (see (3)). For α < 1 the solution y α is smaller than y* and, therefore, the optimal level of product availability is also smaller than in the risk-neutral case. If we consider the example in Sect. 2, we can conclude that decision making by (12) excludes an order quantity which has a cycle service level larger than 80%.

Gotoh and Takano (2007) also derive this analytical solution and extend it to the multi-product newsvendor model with the CVaR criterion. Moreover, they use a mean-CVaR criterion; the focus is to develop a linear programming formulation for solution. Coherent risk measures in general are considered by Ahmed et al. (2006) for the static as well as the multi-period newsvendor problem. Besides the CVaR they propose the mean-absolute deviation as objective function (see also Borgonovo and Peccati 2006).

The identity of the expected value solution and the solution within the mean-variance objective is shown in Collins (2004) for special relations of the cost parameters and/or for special demand distributions.

Brown and Tang (2006) maximize the probability that the profit exceeds some target profit. If the target is relatively low, the optimal order quantity is less than the optimal risk-neutral order quantity.

A possibility to attain a higher level of product availability and thereby a higher optimal order quantity is to include opportunity cost of a stockout. The difficulty of measuring shortage cost and its application to the newsvendor model is addressed by Anderson et al. (2006). Wang and Webster (2006) present a newsvendor model with shortage cost and loss-averse utility function of the form

$$u(g(y,x)) =\left\{{\begin{array}{lll} g(y,x) & \hbox{for} & g(y,x) \geq 0\\ \gamma g(y,x)& \hbox{for} & g(y,x) < 0\\ \end{array}} \right. $$
(14)

where γ ≥ 1 denotes the coefficient of loss aversion. They show that in case of low shortage cost the optimal order quantity is lower than that of the risk-neutral newsvendor and that with increasing loss aversion the optimal order quantity increases. Contrary, the loss-averse newsvendor orders more than y* if the shortage cost is high; this order quantity increases with higher loss aversion.

Like Wang and Webster (2006) we consider also an objective function which results in lower or higher optimal order quantities than y*. To achieve this result we do not have to specify the opportunity cost of a stockout but the proposed objective function is characterised by two risk parameters. This model is formally introduced in the next section.

4 A newsvendor model with two risk parameters

In the following we introduce an objective function of the newsvendor model where risk-averse as well as risk-taking behaviour can be modelled. Consider the CVaR newsvendor (12). Recall that in this case the optimal order quantity y α is obtained by restricting to the α · 100% lowest profits. By (13) the level of product availability reduces to α · CSL*. Contrary, restricting to the (1 − α)· 100% highest profits the optimal order quantity is \({F^{{- 1}} {\left({\frac{{p - c}}{{p - z}} +\alpha \cdot \frac{{c - z}}{{p - z}}} \right)}};\) here the level of product availability increases to CSL* + α (1 − CSL*) (see (21) and (22)).

In each of these two cases only a part of the probability distribution of profits is used for decision-making. Instead, we propose an objective function which is a convex combination of the conditional expected values of low profits and high profits. Thus the whole distribution of profits is taken into account.

Contrary to Eeckhoudt et al. (1995) the newsvendor does not have to specify a utility function to express risk-aversion; moreover in our approach risk-taking behaviour can be modelled, too.

Consider first the case for those α where F −1 y (α) exists. For 0 ≤ λ ≤ 1 the objective is to determine the optimal order quantity y by

$$ {\mathop {\max}\limits_y} \quad \lambda E(g(y,X)|g(y,X) \leq F_{y}^{{- 1}} (\alpha)) + (1 - \lambda)E(g(y,X)|g(y,X) \geq F_{y}^{{- 1}} (\alpha)). $$
(15)

According to the well-known Hurwicz criterion the parameter λ can be interpreted as coefficient of pessimism. The higher λ the more weight the inventory manager puts to low profits. The parameter α defines the set of low profits for each order quantity y.

In the general case we replace in (15) the first conditional expected value by (10) and the second one by \({\frac{1}{{1 - \alpha}}{\int_\alpha^1 }F_{y}^{*} (u)du}.\) Then (15) is a special case of the following problem

$${\mathop {\max}\limits_y} \quad \lambda\frac{1}{\alpha}{\int\limits_0^{\alpha} }F_{y}^{*} (u)du + (1 -\lambda)\frac{1}{{1 - \alpha}}{\int\limits_\alpha^1 }F_{y}^{*}(u)du .$$
(15a)

Since (see Appendix A)

$$E(g(y,X)) ={\int\limits_0^1 }F_{y}^{*} (u)du = \alpha{\text{CVaR}}_{\alpha} (y) + {\int\limits_\alpha^1}F_{y}^{*} (u)du$$

we can rewrite (15a) as

$${\mathop {\max}\limits_y} \quad \lambda {\text{CVaR}}_{\alpha} (y) + \frac{{1- \lambda}}{{1 - \alpha}}(E(g(y,X) - \alpha {\text{CVaR}}_{\alpha} (y))$$
(16)

or

$${\mathop {\max}\limits_y} \quad \frac{{\lambda - \alpha}}{{1 -\alpha}}CVaR_{\alpha} (y) + \frac{{1 - \lambda}}{{1 -\alpha}}E(g(y,X))$$
(17)

If we multiply (17) with (1 − α)/(1 − λ), with λ < 1, we get a mean-deviation rule where risk is measured by −CVaR (see e.g. Müller and Stoyan 2002, p. 274):

$${\mathop {\max}\limits_y} \quad E(g(y,X)) + \beta \cdot {\text{CVaR}}_{\alpha}(y),$$
(17a)

with β = (λ − α)/(1 − λ).

By choosing parameters α and λ in (15) the risk parameter β of the mean-deviation rule (17a) is determined.

Since we would like to include the CVaR criterion (λ = 1), we will use (17) in the following. From (17) we see that for α = λ our approach entails the classical newsvendor model. Note that for all parameters α and λ we have

$$\frac{{\lambda - \alpha}}{{1 - \alpha}} + \frac{{1 - \lambda}}{{1 -\alpha}} = 1 .$$

Thus, for α ≤ λ the objective (17) is defined as a convex combination of the conditional value at risk of the profit CVaRα (y) and the expected profit E(g(y, X)). Decision theoretic implications of (17) as well as applications in finance theory for the case α ≤ λ < 1 are considered in Hanisch (2005).

Since −E(g(y, X)) and −CVaR α (y) represent coherent risk measures and the convex combination of coherent risk measures is coherent, too (see Hanisch 2005; Artzner et al. 1999), the criterion (17) reformulated as:

$${\mathop {\min}\limits_y} \frac{{\lambda - \alpha}}{{1 -\alpha}} (- CVaR_{\alpha} (y)) + \frac{{1 - \lambda}}{{1 - \alpha}} (-E(g(y,X))$$

defines the solution with a coherent risk measure for the case α ≤ λ.

However, the objective function (17) will be applied also in cases where λ < α holds. We shall provide a complete characterization of the newsvendor model (17) in dependence of the risk parameters α and λ.

In the following we analyse the attitudes to risk of an inventory manager using (17). A decision maker is risk-averse if for all random variables the expected value of the random variable is preferred to the random variable itself. Therefore a risk-averse inventory manager would prefer E(g(y, X)) to the stochastic profit g(y, X) for all y. On the other hand a risk-neutral manager is indifferent and a risk-taking manager prefers g(y, X).

Since \(E(g(y, X)) \geq {\text{CVaR}}_{\alpha} (y)\) and the conditional expected value of a constant equals the constant we have for \({0 \leq \lambda \leq 1, 0 < \alpha < 1,\alpha\leq\lambda }\)

$$\begin{aligned}& \frac{{1 - \lambda}}{{1 -\alpha}} E(E(g(y,X)) + \frac{{\lambda - \alpha}}{{1 -\alpha}}\hbox{CVaR}_{\alpha} (E(g(y,X)) \\& \quad {{\geq \frac{{1 - \lambda}}{{1 - \alpha}} E(g(y,X)) +\frac{{\lambda - \alpha}}{{1 - \alpha}}\hbox{CVaR}_{\alpha} (y)} } \\\end{aligned}$$
(18)

Similarly for α ≥ λ we get the opposite relation and for α = λ we get the equality, i.e. the usual expected value criterion.

Summarizing an inventory manager using (15) or (17) as a decision criterion exhibits:

$$\begin{aligned}&\bullet \hbox{risk-averse behaviour for}\;\alpha < \lambda,\\&\bullet \hbox{risk-neutral behaviour for}\;\alpha = \lambda,\\&\bullet \hbox{risk-taking behaviour for}\;\alpha > \lambda.\\\end{aligned}$$
(19)

5 Optimal performance measures

Now we derive the optimal performance measures of the newsvendor model with risk parameters α and λ, namely the optimal order quantity and the resulting optimal cycle service level, the optimal probability of loss, the optimal expected profit and the optimal expected loss. From the objective function (17), we can derive important special cases. If the risk parameters α and λ coincide, then our model is reduced to the classical newsvendor model described in Sect. 2. On the other hand, if in (17) λ = 1 we have the special case of the CVaR criterion (12).

The solution of (17) is denoted by

$$y(\alpha, \lambda) = {\hbox{arg }}{\mathop{\max}\limits_y} \frac{{\lambda - \alpha}}{{1 - \alpha}}\hbox{CVaR}_{\alpha}(y) + \frac{{1 - \lambda}}{{1 - \alpha}}E(g(y,X)).$$
(20)

From Appendix C, it follows that for 0 < α < 1 the optimal order quantity y(α, λ) is given by:

$$y(\alpha, \lambda) = \left\{{\begin{array}{lll} {{F^{{- 1}}{\left({\frac{{p - c}}{{p - z}} + \frac{{\alpha - \lambda}}{{1 -\lambda}} \cdot \frac{{c - z}}{{p - z}}} \right)}, \quad \lambda \leq \frac{{p - c}}{{p - z}}}} \\ {\begin{aligned} & \\ & F^{{-1}} {\left({\frac{{p - c}}{{p - z}} \cdot \frac{\alpha}{\lambda}}\right)}, \quad \quad \lambda \geq \frac{{p - c}}{{p - z}} \\\end{aligned}} \\ \end{array}} \right.$$
(21)

For 0 < α < 1 the optimal cycle service level CSL(α, λ) is given by:

$$CSL(\alpha, \lambda) = F(y(\alpha, \lambda))$$
(22)

Note that for λ = (p − c)/(p − z) the two functions in (21) coincide.

For λ = α the cycle service level CSL(α, λ) is equal to CSL* = (p − c)/(p − z). CSL(α, 1) = αCSL* is the cycle service level for the CVaR criterion, CSL(α, 0) = α + (1 − α)CSL* is the cycle service level for λ = 0.

Also, for λ = α the optimal order quantity is equal to the optimal order quantity y* in the classical newsvendor model.

The risk attitudes of the inventory manager described by α and λ can be characterized by the optimal order quantity y(α,λ).

From (21) we have:

  • • y(α, λ) = y* if α =  λ (risk-neutrality)

  • • y(α, λ) < y* if α < λ (risk-aversion)

  • • y(α, λ) > y*  if α > λ (risk-taking).

The same characterization holds for the cycle service level CSL(α, λ) from (22).

The optimal expected profit EP(α, λ) in dependence of the optimal order quantity y(α, λ) is given by:

$$\hbox{EP}(\alpha, \lambda) = (p - c) y(\alpha, \lambda) - (p -z) {\int\limits_0^{y(\alpha, \lambda)} }(y(\alpha, \lambda) -x) dF(x)$$
(23)

Note that y(α, λ) is differently defined for λ larger or smaller than (p − c)/(p − z).

Furthermore we have for the probability of loss and the expected loss depending on α and λ (see Appendix D):

$$\hbox{PL}(\alpha, \lambda) = F(y(\alpha, \lambda) \cdot \frac{{c - z}}{{p -z}})$$
(24)
$$\hbox{EL}(\alpha, \lambda) = (z - c) y(\alpha, \lambda) + \frac{{p -z}}{{PL(\alpha, \lambda)}} \cdot {\int\limits_0^{y(\alpha, \lambda)\cdot \frac{{c - z}}{{p - z}}} {xdF(x)}}.$$
(25)

We are now able to present structural properties of the optimal performance measures in dependence of the risk parameters α and λ.

  • The optimal order quantity y(α, λ), the optimal cycle service level CSL(α, λ), the optimal probability of loss PL(α, λ), and the optimal expected loss EL(α, λ) are increasing in α and decreasing in λ.

  • The optimal expected profit EP(α, λ) is decreasing in α and as a function of λ increasing for 0 ≤ λ ≤ α and decreasing for α ≤ λ ≤ 1. The maximal value is attained for λ = α: EP(α, α) = EP*, the optimal expected profit of the classical newsvendor.

On the basis of these results, it is possible to show the traditional inventory-service tradeoff in dependence of the risk parameters λ and α. In Fig. 1, the tradeoff between the optimal expected profit and the optimal cycle service level is presented.

Fig. 1
figure 1

Risk preferences in dependence of expected profit and cycle service level

Full size image

We illustrate our approach by the following numerical analysis. For comparison purposes, we use the same parameter values as in Sect. 2 for the classical newsvendor. For this numerical example, Fig. 1 shows the optimal cycle service level CSL(α, λ) and the optimal expected profit EP(α, λ) for all combinations of risk parameters (α, λ) with 0.1 ≤ α ≤ 0.9 and  0 ≤ λ ≤ 1. For fixed α and variable λ (0 ≤ λ ≤ 1) one obtains some part of the curve; for different α these parts may overlap. From Fig. 1 we see that with respect to the optimal expected profit and the optimal level of product availability a risk-averse inventory manager does not Pareto-dominate a risk-taking inventory manager: if a specific value of the expected profit is optimal for a risk-averse and for a risk-taking inventory manager, then the optimal cycle service level will always be larger for the risk taker.

Table 1 contains the optimal performance measures for several values of the risk parameters α and λ. Note that in Table 1 the row with α = λ = 0.5 repeats the performance measures of the risk-neutral inventory manager, i.e. the classical newsvendor of Sect. 2. Additionally, Table 1 contains the performance measures probability of loss and expected loss which are the primary objectives in the risk-averse newsvendor models of Sect. 3.

Table 1 Optimal performance measures for selected risk parameters α and λ
Full size table

From Table 1, we can see the tradeoff between the level of product availability, the order quantity and the expected profit, on the one hand, and the expected loss and the probability of loss on the other hand. The rows with risk parameter λ = 1 represent the performance measures of the most risk-averse inventory manager, the CVaR newsvendor for different values of risk parameter α. As α approaches 1, the CVaR-newsvendor converges to the risk-neutral inventory manager (cp. with Sect. 3). E.g. if α = 0.5 the cycle service level of 0.4 for the CVAR newsvendor is only half of CSL* of the risk-neutral newsvendor. The optimal order quantity is about 71 units compared with 127 units for the classical newsvendor. And finally, the optimal expected profit is about 20% smaller than that of the risk-neutral inventory manager.

Based on these performance measures (CSL, y, EP) an inventory manager could be recommended to express risk-taking behaviour. But this holds only true if the primary objective is the level of product availability, i.e. the order winner is customer service. If, on the other hand, the most important objective of the inventory manager is internally oriented like the expected loss or the probability of loss, then this advice is not always correct.

6 Risk preferences for specified performance measures

In the previous section we have characterized the risk preferences of the newsvendor with respect to the risk parameters α and λ. Based on these results we show in this section how the risk preferences can be related with performance measures like the level of product availability and the probability of loss. For a product with given price and cost structure the risk attitudes of the inventory manager are expressed as a function of the corresponding profit value of the product. We begin the analysis by specifying the cycle service level as measure of the product availability.

First we assume that the inventory manager can specify a cycle service level \({\widehat{{\hbox{CSL}}}}\) which seems to be the appropriate level of product availability for prospective consumers. There is an order quantity \({\hat{y}}\) such that \({\widehat{{\hbox{CSL}}}= F(\hat {y})}.\) Let y* be the order quantity of the risk-neutral inventory manager; from (3) we know \({F(y^{*}) = \frac{{p - c}}{{p - z}} = \hbox{CSL}^{*}}.\) Therefore for \({\widehat{{CSL}} < \hbox{CSL}^{*}}\) we have \({\hat {y} < y^{*}}\) and vice versa. If the specification of \({\widehat{{\hbox{CSL}}}}\) is consistent with (17) we have \({\hat{y} = y(\alpha, \lambda)}\) for some α, λ (see 21). From (21) we conclude that y(α, λ) < y* if and only if α < λ and vice versa. Summarizing, for the decision rule (15) and (17), respectively, we have:

$$\begin{aligned}&\bullet \hbox{an inventory manager with}\ {\widehat{{\hbox{CSL}}} = \hbox{CSL}^{*}}\ \hbox{is risk-neutral},\\&\bullet \hbox{an inventory manager with}\ {\widehat{\hbox{CSL}}\,<\, \hbox{CSL}^{*}} \ \hbox{is risk-averse},\\&\bullet \hbox{an inventory manager with}\ {\widehat{{\hbox{CSL}}}\,>\ \hbox{CSL}^{*}}\ \hbox{is risk-taking.}\\\end{aligned}$$
(26)

For given cycle service level \({\widehat{{\hbox{CSL}}}}\) these results are in accordance with the experimental findings of Schweitzer and Cachon that the newsvendor for high-profit products orders less than the classical, risk-neutral newsvendor and vice versa (Schweitzer and Cachon 2000); if the profit value of a specific product \({\frac{{p - c}}{{p - z}}}\) exceeds the prespecified cycle service level \({\widehat{{\hbox{CSL}}}}\) the newsvendor exploits risk-averse behaviour.

Table 2 shows some results for risk-averse \(({\widehat{{\hbox{CSL}}} = 0.7})\) and risk-taking behaviour \(({\widehat{{\hbox{CSL}}}= 0.9})\) in comparison with the classical newsvendor \(({\widehat{{\hbox{CSL}}} = {\hbox{CSL}}^{*}).}\)

Table 2 Performance measures for different cycle service levels
Full size table

Next we assume that the inventory manager can specify a certain probability of loss \({\widehat{{\hbox{PL}}}};\) let \({\hat {y}}\) now denote the order quantity which implies \({\widehat{{\hbox{PL}}} = P(g(\hat {y},X)\leq0).}\)

The probability of loss for the risk-neutral inventory manager is PL* given by (5) corresponding to y*. Since P(g(y,X) ≤ 0) = F(y(1 − CSL*) (see Appendix D) we have \({\hat {y} < y^{*}\hbox{ for }\widehat{{\hbox{PL}}} < \hbox{PL}^{*}}\) and vice versa. Again, if the specification of \({\widehat{{\hbox{PL}}}}\) is consistent with (15) or (17) we have by the same reasoning as above

$$\begin{aligned}&\bullet \hbox{an inventory manager with}\; {\widehat{{\hbox{PL}}}\,=\,\hbox{PL}^{*}}\ \hbox{is risk-neutral},\\&\bullet \hbox{an inventory manager with} \; {\widehat{{\hbox{PL}}}\,<\,\hbox{PL}^{*}}\ \hbox{is risk-averse},\\&\bullet \hbox{an inventory manager with}\; {\widehat{{\hbox{PL}}}\,>\,\hbox{PL}^{*}}\ \hbox{is risk-taking.}\\\end{aligned}$$
(27)

From (5) we have

$$\hbox{PL}^{*} = F(F^{{- 1}} (\hbox{CSL}^{*})(1 - \hbox{CSL}^{*})).$$
(28)

For the demand given by our numerical example and alternative values for CSL* we get the results shown in Fig. 2.

Fig. 2
figure 2

Risk behaviour in dependence of \({\widehat{{\hbox{PL}}}}\) and CSL*

Full size image

For given probability of loss \({\widehat{{\hbox{PL}}}}\) we conclude from Fig. 2 that for very low-profit products and for very high-profit products the newsvendor is a risk taker, i.e. the order quantity is higher than y*. For the large portion of products with profit level ranging from low to high – e.g. if \({\widehat{{\hbox{PL}}} = 6\%}\) for CSL* from about 8% to about 80% – the newsvendor is a risk averter, i.e. the order quantity is lower than y*.

7 Conclusions

In this paper, we present an inventory model with risk preferences. Based on related models with risk-averse objective function (expected utility, CVaR), we use the newsvendor model and analyze it for an objective function with two risk parameters. The classical newsvendor model as well as the model with CVaR criterion are included as special cases.

In this way, it is possible to characterize a risk-averse inventory manager who orders less than the classical newsvendor but also a risk-taking manager ordering more than the risk-neutral newsvendor. We present a complete description of the risk preferences of the inventory manager in dependence of the performance measures, expected profit and service level. With respect to these two measures, a risk-averse inventory manager cannot Pareto-dominate a risk-neutral or a risk-taking manager. Furthermore, we describe how the inventory manager for a given product can express the risk preferences based on its specified prices and costs with respect to performance measures like service level and probability of loss.

The model presented can be extended in several ways. In addition to the order quantity, the selling price can be chosen as a decision variable. The conjecture is that the optimal inventory-pricing policy is an extended base stock list price policy. Furthermore, the dependence of the demand on the price can be described by general demand functions including a reference selling price besides other market parameters. Also, in a dynamic version of the model the updating of the demand function is a challenging task. As already mentioned in the text, the parameters of a newsvendor distribution like the Weibull distribution can be updated using past sales but also past service levels, to include also sales lost during the past.