Introduction

For the last decade, the extended variation of steel products has led to the development of next-generation, advanced high-strength steels with superior mechanical properties. These steels are referred as transformation-induced plasticity (TRIP) steels and have a composition range of 2–30 wt.% Mn, 1–3 wt.% Al, 1–3 wt.% Si, and < 1 wt.% C with remarkable strength and ductility. Significant research work1,2,3 has focused on investigating the effect of alloying, heat treatment, and deformation on the final mechanical properties of these steels. However, very little knowledge is present that elucidates the effect of steel composition and processing conditions on the final as a solidified microstructure.

Continuous casting is the most common and high yielding casting technology in the steel industry. However, high-strength steels pose a striking challenge in obtaining a good quality final cast product. The casting challenges are further aggravated as most of these high-strength steels are of peritectic grade and the solidification process involves a transformation from BCC δ iron to FCC γ iron. Furthermore, with high casting speed and thin slab castings, volume contraction involved in the peritectic transformation leads to recalescence (detachment of primarily solidified region from the mold) in the meniscus area, leading to surface cracks and breakouts.4,5 The surface quality of the continuous cast steel is dependent on the solidification events that occur during casting. To control the final steel quality, the relationship between casting parameters such as steel compositions, thermal gradient, solidification velocity, cooling rate, and solidification events such as start and finish temperature of peritectic reaction, volume fraction of phases (liquid, FCC, and BCC), and distribution of solute elements in solid phases is imperative to understand. In addition, experimental studies have demonstrated that BCC δ iron to FCC γ iron transformation during solidification can either be diffusion controlled6,7,8,9,10,11 or “massive” like.12,13 Irrespective of the mode of transformation, the volume contraction is inevitable during peritectic transformation, and it directly affects the cast quality. The continuous casting process exhibits both of these modes depending on the local solidification conditions.13 A diffusion-controlled process is more desirable during the solidification as volume contraction is time dependent leading to a smaller probability of surface imperfections and improved cast quality compared to massive transformation.5

Various experimental studies proved BCC to FCC phase transformation as a carbon-controlled diffusion process.6,7,8,9 Matsumiya et al.6,7 performed directional solidification experiments in the Fe-C-Mn-Si-Mo-P system at different carbon concentrations (0.04–0.23 wt.% C) and cooling rates (0.04–0.4 K/s). Choi8 investigated the variation of BCC and FCC phase fractions in Fe-C-Mn-Al alloys solidified at 2 K/s and 8 K/s using a directional solidification technique. Both studies observed diffusion-controlled transformation of BCC to FCC phase. Similar observations were reported by Lee et al.9 during directional solidification of 304 stainless steel. Chuang and Reinisch10 experimentally measured the temperature at which BCC phase disappears during slab casting of Fe-0.39 wt.% C alloy. Cooling curves were experimentally measured at different distances from the mold wall. They observed that a BCC to FCC transformation finish temperature is a complex function of cooling rate and secondary dendrite arm spacing. Shibata et al.11 observed the in situ peritectic transformation for Fe-0.14 wt.% C and 0.42 wt.% C alloys using the confocal laser scanning microscope. They characterized the mechanism of peritectic transformation by observing the formation of a thin layer of FCC phase separating the liquid and BCC phase. The transformation is progressed by the growth of FCC into liquid and BCC phase domains. Moreover, they also reported that growth of FCC phase is governed by the carbon diffusion in case of Fe-0.42 wt.% C, whereas in Fe-0.14 wt.% C, the peritectic transformation is massive or diffusion less in nature. Yasuda et al.12 performed time-resolved in situ observation for the peritectic transformation of BCC to FCC phase by solidifying Fe-0.45 wt.% C alloys in the cooling rate range of 0.16–0.83 K/s. They reported the massive-like transformation in the alloys solidified at 0.33 K/s accompanied by undercooling of 100 K below the liquidus temperature. Griesser et al.13 studied massive-like transformation in Fe-C alloys using a concentric solidified technique aided by in situ confocal scanning microscope. In this technique, the alloy is held in the mushy zone (L + BCC) until a chemical and thermal equilibrium is established followed by solidification under controlled cooling conditions. Three different Fe-C alloys with 0.10 wt.% C, 0.14 wt.% C, and 0.43 wt.% C were isothermally held above peritectic reaction temperature and then cooled at 10 K/s. The authors reported that Fe-0.43 wt.% C undergoes equilibrium peritectic transformation whereas Fe-0.10 wt.% C exhibits massive transformation of BCC to FCC phase. In another set of experiments, Fe-0.43 wt.% C alloy is solidified at 5 K/min, 10 K/min, and 50 K/min using the same technique. The authors reported that higher cooling rates increase the probability of massive transformation.

Matsumiya et al.6,7 presented a one-dimensional (1D) numerical solidification model to predict the solute distribution behavior in liquid, BCC, and FCC phases even accounting for peritectic phase transformation. The transverse section of dendrites was assumed to be a regular hexagon. The calculation domain was set to be a triangular section (part of the hexagon) that was further divided into liquid, BCC, and FCC nodal areas. The solute distribution was calculated by solving flux balance equations in each phase assuming thermodynamic equilibrium at liquid/solid and solid/solid interface. The peritectic transformation was incorporated by explicitly moving BCC/FCC interface to the next node as soon as the global temperature falls below the thermodynamically calculated temperature. This process was repeated until no BCC phase remains in the system. After the transformation was complete, solute distribution was calculated in the liquid and FCC phase until the final eutectic temperature was achieved. The modeling results were validated against the experimental solute distribution data obtained through electron probe micro analyzer (EPMA) analysis of the directionally solidified samples of the Fe-C-Mn-Si-Mo-P-S system. The authors obtained a good agreement between the modeling and experimental results. It is to be noted that in Matsumiya’s model, the BCC phase is explicitly dissolved as it is assumed that BCC phase fraction decreases along the solvus temperature (BCC and FCC phase boundary). Thermodynamically, this is not a generalized case as the BCC phase fraction can increase with decrease in the solvus temperature. Moreover, the solvus temperature calculation in the model is entirely empirical and based on the individual binary systems for a multicomponent system. Lastly, the authors did not present any calculation on the variation of phase fraction (liquid, BCC, and FCC) with the temperature at different cooling rates, which is important for practical applications. Won and Thomas14 used exactly a similar model to predict the microsegregation in steels. Fredriksson and Stjerndahl15 presented a solidification model for the Fe-C system undergoing a peritectic transformation. They calculated the growth of FCC phase by assuming a linearly decreasing carbon profile in FCC phase from the FCC/liquid boundary to the FCC/BCC interface. Moreover, the carbon distribution in BCC and liquid phase was considered to be uniform. Thuinet and Combeau16,17 developed a 1D diffusion-based solidification model considering energy balance. They validated their results using experimental data obtained for Fe-Ni-C alloys.

In the present work, we propose a 1D numerical solidification model for Fe-C system that incorporates peritectic transformation. The length scale of the model is chosen to be the half-length of the secondary arm spacing unlike the triangular section of a hexagon used in previous models.6,7 The model is dynamically linked with thermodynamic databases of FactSage18 for accurate input of boundary carbon concentrations at the liquid/FCC or the FCC/BCC interface. Once the boundary conditions are known, the flux balance equation is solved at the FCC/BCC phase boundary to accurately calculate the growth or dissolution of the BCC phase depending on the system under investigation. This approach is effective compared to Matsumiya’s model6,7 as the kinetics of the BCC phase (growth or dissolution) is automatically calculated by solving flux balance equations while considering accurate thermodynamic boundary conditions. The model can evaluate the influence of cooling rate and alloy composition on the solute distribution in solid phases, evolution of secondary arm spacing, and variation of phase fractions with temperature. The modeling results are compared with the experimental data available for the binary Fe-C system until now. The nomenclature for variables used in the model is provided in Table I.

Table I Nomenclature used for variables used in the model
Full size table

Solidification Model

The present peritectic-based solidification model is based on previous microstructure solidification work on Mg alloys.19,20,21,22 The previous model incorporated the important kinetic features during solidification such as dendrite tip undercooling, coarsening of secondary dendrite arm, and back diffusion of solutes (Al, Zn, Mn, Sn) in the HCP Mg phase. The model was also dynamically linked to the FactSage thermodynamic database through ChemAppV 7.1.423 library for input of accurate thermodynamic data. The experimental data on microstructural features such as cellular-dendritic transition, primary and secondary dendrite arm spacing, total second phase fraction, and microsegregation were correctly predicted by the model. The same model is extended to include the high-temperature peritectic transformation in the Fe-C system. The salient features of the model are outlined as follows:

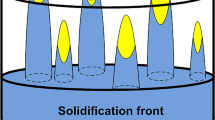
  • The proposed model is 1D. The calculation domain for the model is chosen as the half-length of the secondary arm spacing and schematically shown in Fig. 1. As suggested by Stefanescu24 and further corroborated by Shibata et al.,11 a thin layer of FCC is in contact with BCC and liquid phase at the peritectic temperature. In addition, the peritectic reaction the further growth of FCC phase is progressed by direct solidification from liquid and solid-state transformation of BCC phase. Growth or dissolution of FCC or BCC phase is controlled by carbon diffusion and is automatically calculated by the model. In the Fe-C system, the evolution of secondary arm spacing (SDAS) is a complex function of cooling rate and carbon composition. SDAS has been experimentally investigated by many researchers at different cooling rates and carbon concentrations.14 Typically, SDAS decreases with increasing cooling rate at a fixed composition. This trend is similar to metallic systems such as Mg and Al alloys.21,22 However, the SDAS variation with carbon composition strongly depends on the primary solidified phase. For instance, the SDAS decreases with increasing carbon concentration in the BCC (0–0.15 wt.% C) and FCC (0.53–1 wt.% C) phase domains. However, if the carbon concentration lies in the peritectic region (0.15–0.53 wt.% C), the SDAS is observed to increase with carbon concentration. Won and Thomas14 proposed an empirical equation to ascertain the variation of SDAS as a function of cooling rate (cr) and carbon concentration (C). This was derived by fitting all the available experimental data on SDAS (mentioned as λ) over a wide range of cooling rate and carbon concentration. The same equation is used in the present study for simplification purposes and is given as:

    $$ \lambda = (169.1 - 720.9*C)*{\text{cr}}^{ - 0.4935} \quad 0 < C \le 0.15 $$
    (1.1)
    $$ \lambda = 143.9*{\text{cr}}^{ - 0.3616} *C^{(0.5501 - 1.996*C)} \quad C > 0.15 $$
    (1.2)
    Fig. 1
    figure 1

    Schematics of the peritectic solidification model and the length scale of BCC, FCC, and liquid phase

    Full size image

  • Local thermodynamic equilibrium is assumed at the solid/liquid interface (solidification front). For accurate thermodynamic data at the boundary conditions, the model was dynamically linked with the FactSage thermodynamic database through ChemAppV 7.1.4 library.

  • Complete mixing is assumed in the liquid phase.

  • The impurity diffusivity of carbon in BCC (Dδ) and FCC (Dγ) phase is taken as 1.27E − 6exp(− 19450/RT) m2 s−1 and 7.61E − 6exp(− 32160/RT) m2 s−1, respectively,6 where R is the universal gas constant (Cal/mol). It follows an Arrhenius25 relationship given as:

    $$ D_{{{\text{Solute}}\,{\text{in}}\;{\text{Phase}}}} = D_{0} \exp \left( { - \frac{Q}{\text{RT}}} \right) $$
    (2)

  • No mass flow of solute from the end of the dendrite arm space, i.e., diffusion flux at the end of the dendrite arm is zero.

    $$ D_{\text{s}} \left( {\frac{{\partial C_{\text{s}}^{\text{BCC}} }}{\partial x}} \right) = 0 $$
    (3)

    where \( D_{\text{s}} \) represents the diffusivity of the solute and \( C_{\text{s}}^{\text{BCC}} \) is the solute concentration (carbon) in BCC phase.

  • Coarsening effects are neglected; i.e., it is assumed that the dendritic length does not change with time.

Model Development

The primary phase field (BCC or FCC) is determined on the basis of initial carbon concentration. For example, in the Fe-C binary system, if carbon composition is greater than 0.53 wt.%, FCC is the primary phase to directly precipitate from the liquid phase, and the solidification progresses until the final eutectic temperature is reached. However, if the carbon content is less than 0.53, then BCC is the first phase to form followed by a peritectic reaction at 1767.69 K and then the solidification proceeds by the direct transformation of liquid into FCC and dissolution of BCC to FCC phase. The flowchart of the model is shown in Fig. 2.

Fig. 2
figure 2

Outline of the solidification model

Full size image

In the BCC region, the solute balance in the secondary arm spacing is given as:

$$ \int\limits_{0}^{{x_{\text{s}}^{\text{BCC}} }} {C_{\text{s}}^{\text{BCC}} {\text{d}}x + } \int\limits_{{x_{\text{s}}^{\text{BCC}} }}^{{x_{\text{o}} }} {C_{\text{l}} {\text{d}}x = x_{\text{o}} C_{\text{o}} } $$
(4)

\( C_{\text{l}} \) is the solute concentration (carbon) in liquid, whereas \( C_{\text{o}} \) and \( x_{\text{o}} \) represents the initial carbon concentration and total length scale, respectively. \( x_{\text{s}}^{\text{BCC}} \) denotes the length of BCC solid formed at time t. Considering fixed carbon concentration in liquid at a given time t, the above equation can be written as:

$$ \int\limits_{0}^{{x_{\text{s}}^{\text{BCC}} }} {C_{\text{s}}^{\text{BCC}} {\text{d}}x + } C_{\text{l}} \left( {x_{\text{o}} - x_{\text{s}}^{\text{BCC}} } \right) = x_{\text{o}} C_{\text{o}} $$
(5)

Differentiating the above equation with respect to time (t) and employing Leibniz rule:

$$ \int\limits_{0}^{{x_{\text{s}}^{\text{BCC}} }} {\frac{{\partial C_{\text{s}}^{\text{BCC}} }}{\partial t} + \;C_{\text{s}}^{\text{BCC}} \frac{{{\text{d}}x_{\text{s}}^{\text{BCC}} }}{{{\text{d}}t}}\; + \;\frac{{{\text{d}}C_{\text{l}} }}{{{\text{d}}t}}} \left( {x_{\text{o}} - x_{\text{s}}^{\text{BCC}} } \right)\; + \;\left( {\frac{{{\text{d}}x_{0} }}{{{\text{d}}t}}\; - \;\frac{{{\text{d}}x_{\text{s}}^{\text{BCC}} }}{{{\text{d}}t}}} \right) = 0 $$
(6)

Partitioning coefficient for Liquid/BCC transformation can be given by the expression:

$$ k_{\text{BCC/L}}^{{}} = \frac{{C_{\text{s}}^{\text{BCC}} }}{{C_{\text{l}} }} $$
(7)

It is noted that the solute back diffusion on the solid side of the domain \( 0 \le x \le x_{\text{s}}^{\text{BCC}} \) is governed by Fick’s second law:

$$ \frac{{\partial C_{\text{s}}^{\text{BCC}} }}{\partial t} = D_{\text{s}}^{\text{BCC}} \frac{{\partial^{2} C_{\text{s}}^{\text{BCC}} }}{{\partial x^{2} }} $$
(8)

\( D_{\text{s}}^{\text{BCC}} \) in the above equation represents diffusivity of carbon in BCC Iron. Arranging the terms and expressing the Eq. 6 employing Fick’s law gives:

$$ \int\limits_{0}^{{x_{\text{s}}^{\text{BCC}} }} {D_{\text{s}}^{\text{BCC}} \frac{{\partial^{2} C_{\text{s}}^{\text{BCC}} }}{{\partial x^{2} }}{\text{d}}x + } (k_{\text{BCC/L}} - 1)C_{\text{l}} \frac{{{\text{d}}x_{\text{s}}^{\text{BCC}} }}{{{\text{d}}t}} + \left( {x_{\text{o}} - x_{\text{s}}^{\text{BCC}} } \right)\frac{{{\text{d}}C_{\text{l}} }}{{{\text{d}}t}} = 0 $$
(9)

Considering diffusion flux to be zero at the end of the dendritic arm and diffusivity of solute to be constant for a given temperature:

$$ \left| {D_{\text{S}} \frac{{\partial C_{\text{s}} }}{\partial x}} \right|_{{x = x_{\text{s}} }} + (k_{\text{BCC/L}} - \;1)C_{\text{l}} \frac{{{\text{d}}x_{\text{s}} }}{{{\text{d}}t}} + (x_{\text{o}} - x_{\text{s}} )\frac{{{\text{d}}C_{\text{l}} }}{{{\text{d}}t}} + (C_{\text{l}} - C_{\text{o}}^{{}} )\frac{{{\text{d}}x_{\text{o}} }}{{{\text{d}}t}} = 0 $$
(10)

The time derivative in Eq. 10 can be replaced by the relation obtained from the phase diagram:

$$ \frac{{{\text{d}}C_{\text{l}} }}{{{\text{d}}t}} = \frac{\text{cr}}{m} $$
(11)

Substituting Eq. 11 into the previous expression yields:

$$ \left| {D_{\text{s}}^{\text{BCC}} \frac{{\partial C_{\text{s}}^{\text{BCC}} }}{\partial x}} \right|_{{x = x_{\text{s}} }} + (k_{\text{BCC/L}} - \;1)C_{\text{l}} \frac{{{\text{d}}x_{\text{s}}^{\text{BCC}} }}{{{\text{d}}t}} + \left( {x_{o} - x_{\text{s}}^{\text{BCC}} } \right)\left( {\frac{\text{cr}}{m}} \right) = 0 $$
(12)

Discretizing Eq. 12 with time step using the Euler forward treatment can give:

$$ x_{\text{s}}^{\text{BCC(new)}} = x_{\text{s}}^{\text{BCC(old)}} + \Delta t\left[ {\frac{{\left| {D_{\text{s}}^{\text{BCC}} \frac{{\partial C_{\text{s}}^{\text{BCC}} }}{\partial x}} \right|_{{x = x_{\text{S}}^{\text{BCC}} }}^{\text{old}} + \left( {x_{o} - x_{\text{s}}^{\text{BCC}} } \right)\left( {\frac{\text{cr}}{m}} \right)}}{{(1 - k_{\text{BCC/L}}^{{}} )C_{\text{l}} }}} \right] $$
(13)

The phase fraction of BCC phase at any given time is:

$$ f_{\text{s}}^{\text{BCC}} = {{x_{\text{s}}^{\text{BCC}} } \mathord{\left/ {\vphantom {{x_{\text{s}}^{\text{BCC}} } {x_{\text{o}} }}} \right. \kern-0pt} {x_{\text{o}} }} $$
(14)

The peritectic reaction temperature is determined at each time step by checking the activity of FCC phase using the ChemApp thermodynamic library. As the activity equals to one, FCC phase is introduced in the calculation domain with a predefined thickness of 1 micron. The solute balance when all the three phases, BCC, FCC, and liquid coexist in the system is given as:

$$ \int\limits_{0}^{{x_{\text{s}}^{\text{BCC}} }} {C_{\text{s}}^{\text{BCC}} {\text{d}}x \,+\,} \int\limits_{{x_{\text{s}}^{\text{BCC}} }}^{{x_{\text{s}}^{\text{FCC}} }} {C_{\text{s}}^{\text{FCC}} {\text{d}}x + \int\limits_{{x_{\text{s}}^{\text{FCC}} }}^{{x_{\text{o}} }} {C_{\text{l}}^{{}} {\text{d}}x} = x_{\text{o}} C_{\text{o}} } $$
(15)

where \( C_{\text{s}}^{\text{FCC}} \) is the solute concentration (carbon) in FCC phase and \( x_{\text{s}}^{\text{FCC}} \) denotes the length of total solid formed at time t. In the FCC region, \( x_{\text{s}}^{\text{BCC}} \le x \le x_{\text{s}}^{\text{FCC}} \) the back diffusion term is given by:

$$ \frac{{\partial C_{\text{s}}^{\text{FCC}} }}{\partial t} = D_{\text{s}}^{\text{FCC}} \frac{{\partial^{2} C_{\text{s}}^{\text{FCC}} }}{{\partial x^{2} }} $$
(16)

\( D_{\text{s}}^{\text{FCC}} \) in the above equation represents diffusivity of carbon in FCC Iron. Differentiating Eq. 15 with time and using the same mathematical treatment as in Eqs. 5–13 gives:

$$ x_{\text{s}}^{\text{FCC(new)}} = x_{\text{s}}^{\text{FCC(old)}} + \;\Delta t\;\;\left[ {\frac{\begin{aligned} \left| {D_{\text{s}}^{\text{FCC}} \frac{{\partial C_{\text{s}} }}{\partial x}} \right|_{{X = X_{\text{FCC}}^{\text{s}} }}^{\text{old}} - \left| {D_{\text{s}}^{\text{FCC}} \frac{{\partial C_{\text{s}} }}{\partial x}} \right|_{{X = X_{\text{BCC}}^{\text{s}} }}^{\text{old}} + \left| {D_{\text{s}}^{\text{BCC}} \frac{{\partial C_{\text{s}} }}{\partial x}} \right|_{{X = X_{\text{BCC}}^{\text{s}} }}^{\text{old}} \\ + \left( {\frac{\text{cr}}{m}} \right)\left( {x_{\text{o}} - x_{\text{FCC}}^{\text{old}} } \right) \\ \end{aligned} }{{(1 - k_{\text{FCC/L}} )C_{\text{l}} }}} \right] $$
(17)

where \( k_{\text{FCC/L}} \) denotes the partitioning coefficient for Liquid/FCC transformation. The solute balance at the BCC/FCC interface boundary gives:

$$ x_{\text{s}}^{\text{BCC(new)}} = x_{\text{s}}^{\text{BCC(old)}} + \Delta t\;\;\left[ {\frac{{\left| {D_{\text{s}}^{\text{FCC}} \frac{{\partial C_{\text{s}} }}{\partial x}} \right|_{{X = X_{\text{BCC}}^{\text{s}} }}^{\text{old}} - \left| {D_{\text{s}}^{\text{FCC}} \frac{{\partial C_{\text{s}} }}{\partial x}} \right|_{{X = X_{\text{FCC}}^{{}} }}^{\text{old}} }}{{C_{\text{s}}^{\text{BCC}} - C_{\text{s}}^{\text{FCC}} }}} \right] $$
(18)

At any given time step, the phase fraction of the BCC, FCC, and liquid phase is given as:

$$ f_{\text{s}}^{\text{BCC}} = {{x_{\text{s}}^{\text{BCC}} } \mathord{\left/ {\vphantom {{x_{\text{s}}^{\text{BCC}} } {x_{\text{o}} }}} \right. \kern-0pt} {x_{\text{o}} }} $$
(19.1)
$$ f_{\text{s}}^{\text{FCC}} = {{\left( {x_{\text{s}}^{\text{FCC}} - x_{\text{s}}^{\text{BCC}} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{\text{s}}^{\text{FCC}} - x_{\text{s}}^{\text{BCC}} } \right)} {x_{\text{o}} }}} \right. \kern-0pt} {x_{\text{o}} }} $$
(19.2)
$$ f_{{}}^{\text{Liquid}} = {{(x_{\text{o}}^{{}} - x_{\text{s}}^{\text{FCC}} )} \mathord{\left/ {\vphantom {{(x_{\text{o}}^{{}} - x_{\text{s}}^{\text{FCC}} )} {x_{\text{o}} }}} \right. \kern-0pt} {x_{\text{o}} }} $$
(19.3)

The back diffusion terms \( \left| {D_{\text{s}}^{\text{BCC}} \frac{{\partial C_{\text{s}}^{\text{BCC}} }}{\partial x}} \right|_{{x = x_{\text{s}}^{\text{BCC}} }}^{\text{old}} \) and \( \left| {D_{\text{s}}^{\text{FCC}} \frac{{\partial C_{\text{s}}^{\text{FCC}} }}{\partial x}} \right|_{{x = x_{\text{s}}^{\text{FCC}} }}^{\text{old}} \) can be calculated in the previous time step by solving Eqs. 8 and 16. The back diffusion in BCC or FCC needs to be solved in the domain of \( 0 \le x \le x_{\text{s}}^{\text{BCC}} (t) \) and \( x_{\text{s}}^{\text{BCC}} (t) \le x \le x_{\text{s}}^{\text{FCC}} (t) \). As the domain is not fixed with time, Landau’s transformation26 is employed to fix up the domain length \( \left( {0 \le \eta \le 1} \right) \) where \( \eta = \frac{x}{{x_{\text{s}} \left( t \right)}} \). Landau’s transformation for Fick’s second law is given by the expression:

$$ \frac{\partial C}{\partial t}\; + \;\frac{1}{{x_{\text{s}} \left( t \right)}}\frac{\partial C}{\partial \eta }\frac{{{\text{d}}x}}{{{\text{d}}t}}\; = \;D_{\text{s}} \frac{1}{{x_{\text{s}}^{2} \left( t \right)}}\frac{{\partial^{2} C}}{{\partial \eta^{2} }} $$
(20)

Finite difference control volume formulation was employed to solve equations numerically. In this approach, the calculation domain is divided into a number of overlapping control volumes such that there is one control volume surrounding each element. The differential equation is integrated over each control volume. A fully implicit control volume discretization of the transformed Eq. 20 on a uniform grid of total node point n, leads to the following formulation at a node point P:

$$ \left( {C_{\text{P}} - C_{\text{P}}^{\text{old}} } \right) + \Delta t\;\left[ {\frac{1}{{x_{\text{s}} \left( t \right)}}\frac{{V_{\text{west}} C_{\text{P}} - V_{\text{east}} C_{\text{E}} }}{\Delta \eta }} \right] = D_{\text{s}} \frac{\Delta t}{{x_{\text{s}}^{2} \left( t \right)}}\left( {\frac{{C_{\text{W}} - \;2C_{\text{P}} \; + \;C_{\text{E}} }}{{\Delta \eta^{2} }}} \right) $$
(21)

where \( V_{\text{west}} , V_{\text{east}} \) are the west and east velocity for a node and \( C_{\text{W}} , C_{\text{E}} , C_{\text{P}} \) are the solute concentrations at the node points. The following relationship holds at each of the node points:

$$ a_{\text{P}} C_{\text{P}} \; = \;a_{\text{W}} C_{\text{W}} \; + \;a_{\text{E}} C_{\text{E}} \; + \;d_{\text{P}} $$
(22)

A tridiagonal matrix algorithm is used to calculate the back diffusion term in the solid (BCC or FCC) phases. \( a_{\text{W}} , a_{\text{E}} , a_{\text{P}} \) in the above equation are the coefficients of the matrix. Accordingly, all the terms in Eqs. 13, 17, and 18 are known at a given time step, and the phase fractions can be calculated using Eqs. 14 and 19. The solidification calculations in the three-phase regions are continued until the BCC to FCC transformation is complete. If the BCC phase thickness (\( x_{\text{s}}^{\text{BCC}} \)) calculated by Eq. 18 is less than 1 micron, the transformation is assumed to be finished. It is noted that in our current model, the dissolution of BCC to FCC phase arises naturally from Eq. 18, which is based on the carbon profile in both the phases and the interfacial carbon concentration at the BCC/FCC phase boundary. Once the transformation is complete, the FCC phase is formed from direct solidification from the liquid phase and the governing equation is given as:

$$ x_{\text{s}}^{\text{FCC(new)}} = x_{\text{s}}^{\text{FCC(old)}} + \Delta t\left[ {\frac{{\left| {D_{\text{s}}^{\text{FCC}} \frac{{\partial C_{\text{s}}^{\text{FCC}} }}{\partial x}} \right|_{{x = x_{\text{S}}^{\text{FCC}} }}^{\text{old}} + \left( {x_{\text{o}} - x_{\text{s}}^{\text{FCC}} } \right)\left( {\frac{\text{cr}}{m}} \right)}}{{(1 - k_{\text{FCC/L}}^{{}} )C_{\text{l}} }}} \right] $$
(23)
$$ f_{\text{s}}^{\text{FCC}} = {{\left( {x_{\text{s}}^{\text{FCC}} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{\text{s}}^{\text{FCC}} } \right)} {x_{\text{o}} }}} \right. \kern-0pt} {x_{\text{o}} }} $$
(24)

Equations 23 and 24 are solved until the FCC phase fraction (\( f_{\text{s}}^{\text{FCC}} \)) reaches 1, and at this step, the calculations are terminated. The calculation steps in the solidification model are superimposed in a binary Fe-C phase diagram shown in Fig. 3.

Fig. 3
figure 3

Various stages of solidification model incorporating peritectic transformation in Fe-C alloy. Co stands for initial carbon concentration, \( C_{\text{s}}^{\text{BCC}} \)\( C_{\text{s}}^{\text{FCC}} \), represents carbon concentration at BCC and FCC interphase, \( C_{\text{L}}^{\text{FCC}} \) and \( C_{\text{L}}^{\text{Liq}} \) stands for carbon content at FCC and liquid interphase

Full size image

In the solidification calculations, the composition of carbon at BCC/FCC interface (\( C_{\text{s}}^{\text{BCC}} \) and \( C_{\text{s}}^{\text{FCC}} \)), partitioning coefficient (\( k_{\text{BCC/L}}^{{}} \) and \( k_{\text{FCC/L}}^{{}} \)), and liquidus slope (m) are all calculated using the ChemApp library with the FSteel database containing the optimized model parameters for the Fe-C binary system. The present micro segregation model was tested for the Scheil cooling approximation by setting the diffusion of carbon in BCC and FCC phases to zero. The calculated results in Scheil cooling conditions matched with the Scheil cooling thermodynamic calculations using the FactSage software.18

Results and Discussion

The solidification model presented in the current study is used to explain the experimental data in the Fe-C binary system. It is noted that only the diffusion-based experimental data are used for comparison purposes. The growth of the FCC phase in Fe-0.42 wt.% C alloy is calculated from the solidification model and compared with the experimental results of Shibata et al.,11 who isothermally held the alloy at 1758 K and observed the in situ growth of FCC phase using a confocal scanning microscope. In the present model, the calculation domain and cooling rate were set to be 500 µm and 1 K/min, respectively, which is exactly similar to the experimental conditions. The calculations start with the direct solidification of the BCC phase from the liquid phase. The calculations are continued until 1758 K allowing the system to undercool below the equilibrium peritectic temperature. At this stage, the FCC phase is introduced in the calculation domain and allowed to grow with time. As seen in Fig. 4, the calculated thickness of the FCC phase agrees reasonably well with the experimental results.

Fig. 4
figure 4

Comparison between the calculated FCC phase thickness with the experimental results observed by Shibata et al.11 for Fe-0.42 wt.% C alloy

Full size image

The variation of peritectic transformation finish temperatures with cooling rate for Fe-0.39 wt.% C alloy is compared with the experimental results of Chuang et al.10 in Fig. 5. Chuang et al. experimentally measured the secondary dendrite arm spacing (SDAS) at different distances along the mold. In the present study, the cooling rate was indirectly determined from the SDAS using Eq. 1 and used as input for calculating the peritectic finish temperature. As seen from Fig. 5, BCC to FCC transformation finish temperature decreases with cooling rate at very slow solidification rates (< 1 K/s) and becomes almost constant with further increase in cooling rate. The calculated results reasonably capture this trend. To understand further the relationship of peritectic finish temperature with cooling rate, two separate sets of simulations are performed for Fe-0.39 wt.% C. In the first case, SDAS is fixed at 200 µm and cooling rates are varied between 0.1 K/s and 10 K/s, whereas the cooling rate is kept constant at 10 K/s and SDAS is varied between 200 µm and 400 µm in the second set of calculations. Through these calculations, the combined effect of SDAS and cooling rate on the peritectic finish temperature can be elucidated. The variation of phase fractions of BCC, FCC, and liquid phases at different cooling rates (0.1 K/s, 1 K/s, and 10 K/s) at fixed SDAS of 200 µm is shown in Fig. 6a. As expected, the peritectic transformation finish temperature increases with decreasing cooling rate. The back diffusion terms in Eq. 18 are dominant at lower cooling rates resulting in faster transformation of BCC to FCC phase. The modeling results on the variations of phase fractions with the temperature at a fixed cooling rate of 10 K/s and different SDAS (200 µm, 300 µm, and 400 µm) is shown in Fig. 6b. The calculations suggest that as the SDAS increases (cooling rate is constant), phase transformation of BCC to FCC phase is retarded and the peritectic transformation range increases. Thus, increasing the cooling rate and decreasing SDAS have the opposite effects on the transformation finish temperature, and for this reason, Chuang et al.10 did not observe any appreciable difference in the transformation finish temperatures with an increase in cooling rate. This effect is also reasonably captured by the model.

Fig. 5
figure 5

Comparison between the calculated peritectic finish temperature and experimental results of Chuang et al.10 for Fe-0.39 wt.% C alloy

Full size image
Fig. 6
figure 6

Variation of phase fractions with temperature for Fe-0.39 wt.% C (a) fixed SDAS of 200 µm and varying cooling rate of 0.1 K/s, 1 K/s, 10 K/s. (b) Fixed cooling rate of 10 K/s and varying SDAS of 200 µm, 300 µm, 400 µm

Full size image

The carbon profile in BCC and FCC phases during solidification essentially controls the variation of phase fractions at different cooling rates. The calculated carbon profile in BCC and FCC phase at 1 K/s and 10 K/s for Fe-0.39 wt.% C is shown in Fig. 7. The simulations were performed at 1765 K, which is slightly below the equilibrium peritectic temperature (1767.69 K). As seen in Fig. 7a at 1 K/s (the carbon profile or the concentration gradient of carbon in BCC phase is less steep in comparison to 10 K/s, which leads to faster dissolution of BCC to FCC phase). Interestingly, the carbon profile in FCC phase is exactly similar at both the cooling rates (Fig. 7b). Also, the calculated carbon profile suggests that at a given cooling rate, the carbon diffusion flux is higher in the FCC in comparison to BCC causing the BCC phase to dissolve. Thus, the growth or dissolution of BCC phase naturally arises from the model.

Fig. 7
figure 7

Variation of carbon distribution at 1765 K at different cooling rates (10 K/s, 1 K/s) in (a) BCC phase and (b) FCC phase

Full size image

The relationship between the peritectic range and carbon composition at two different cooling rates (1 K/s, 10 K/s) is presented in Fig. 8. The peritectic range is defined as the difference between the equilibrium peritectic temperature (1767.69 K) and the temperature at which the BCC to FCC transformation is complete. The peritectic range is an important solidification parameter that determines the extent of BCC to FCC phase transformation during the casting. As this volumetric transformation controls the cast product quality, the relationship between the peritectic range, carbon concentration, and cooling rate should be evaluated. As seen in Fig. 8, peritectic range decreases with increasing carbon concentration for a given cooling rate. At fixed carbon concentration, increasing cooling rate increases the peritectic range or BCC to FCC phase transformation temperature. The above calculation provides a qualitative understanding on the formation of as-cast defects during continuous casting at higher rates.8 Casting at higher cooling rates increases the peritectic temperature range as seen in Fig. 8. The results indicate increased possibility of defect formation at higher casting speeds.

Fig. 8
figure 8

Variation of peritectic solidification range with carbon composition in Fe-C alloy and cooling rate (K/s)

Full size image

Conclusion

A numerical solidification model has been developed for the Fe-C system incorporating the peritectic solidification. The model is dynamically linked with thermodynamic software database FactSage18 through ChemAppV 7.1.4 library for input of accurate thermodynamic data. The peritectic transformation involving the dissolution of BCC to FCC phase is a natural outcome of the model. Moreover, the authors have provided sufficient evidence on the validity of the solidification model by comparing the modeling results with the experimental data on the Fe-C system. As mentioned earlier, Griesser et al.13 showed experimental confirmation of massive transformation of BCC to FCC phase in Fe-C alloys. On the other hand, directional solidification experiments on Fe-C alloys6,7,8,9 provide irrefutable evidence of diffusion-controlled transformation process. In both cases, peritectic transformation is accompanied by volume contraction as BCC transforms to FCC phase during solidification. In the case of massive transformation, a volume change is sudden and could lead to massive defects in the cast product compared to diffusion-controlled process.

Griesser et al.13 stated that steeper carbon concentration in the solidified BCC phase (Fe-C binary alloys) results in the undercooling that fulfills the driving force requirement for massive transformation of BCC to FCC phase. Variable thermal gradients in the continuous casting process could result in similar conditions as observed by Griesser et al. In this regard, interrupted directional solidification experiments with variable thermal gradients can aid in determining the effect of thermal gradients on the kinetics of massive transformation. In addition, the present model can be modified to incorporate variable thermal gradients and determine the concomitant carbon profile in the BCC phase along with the total undercooling required for massive transformation.