Introduction

Dendritic structure is commonly formed during the solidification of alloys.1 The growth of morphology has a strong link with the mechanical properties and performance of the final products.2 To control the solidification structure and achieve the desired properties, a fundamental knowledge about the mechanism of microstructure formation is required. Both experimental and theoretical work has been carried out to characterize dendritic growth behavior. Nevertheless, because of its complexity, it is not yet well understood and further research is necessary. In the past few decades, several numerical models, which can solve complicated transport phenomena and phase transformation under different boundary and initial conditions, were developed to characterize the microstructure features of the solidification of materials.3 Currently, the rapid development of computer technology and a thorough understanding of the thermodynamics and kinetics of microstructure evolution have impelled the simulation of microstructure evolution.4 The emergence of simulation methods enables prediction on grain structure and morphological evolution. Among the models for microstructure evolution, Monte Carlo simulations, cellular automata, and phase field are the most widely used.5 Phase-field modeling has been successfully applied for simulating the dendritic structure growth during the solidification of alloys.

The phase-field model was originally proposed for simulating the dendrite growth in undercooled pure melts and has been extended to the solidification of alloys. The first model for alloy solidification was proposed by Wheeler et al.6 The model has been the most widely used and is derived in a thermodynamically consistent way. In the model, any point within the interfacial region is assumed to be a mixture of both solid and liquid with the same composition. The phase-field parameters are determined not only under a sharp interface condition but also under a finite interface thickness condition. Kim et al.7,8 proposed a new phase-field model for binary alloys. The model is similar to the model from Ref. 6 but has a different definition of the free energy density for the interfacial region, and it been widely used to simulate the microstructure evolution during conventional solidification9–11 and rapid solidification.7 Despite the advantage of the phase-field method, it still requires considerable computation time and can only simulate very small domains with a few dendrites.

Modeling of the solidification microstructures in rapid solidification requires an understanding of different aspects of the physical phenomena occurring during the process, which are affected by both processing and material parameters.12 There is some research about the simulation of dendritic morphology growth during the rapid solidification process.13,14 However, the microstructure evolution of the rapid solidification of Ti-6Al-4V alloy has not yet been studied. In addition, the effects of the phase-field parameters on the morphology also have not been investigated.

Electron beam additive manufacturing (EBAM) technology has receiving widespread attention as a means of producing net-shape components, owing to the potential manufacturing benefits. The previous experimental study has investigated the microstructure evolution of Ti-6Al-4V parts processed by EBAM with different scanning speeds.15 The objective of this numerical study is to better understand the microstructural evolution, in terms of phase transformation and solute distribution, affected by the scanning speed in EBAM-built Ti-6Al-4V. A phase-field model was applied to model the dendritic and columnar structure formation with different scanning speeds. Moreover, the effect of the undercooling on the microstructure evolution is also studied. The intent is to predict the microstructure evolution during the solidification process in EBAM.

Model Description

Thermal Process Modeling

The microstructure evolution during EBAM is determined by the thermal history of the materials, which is the result of energy absorption by the materials, heat conduction within the built part and heat losses. With the assumption of negligible molten flow during the solidification process, the governing equation of heat transport during the EBAM process becomes thermal conduction based:16

$$ \nabla (k\nabla T) + \dot{Q} = \frac{{{\text{d}}(\rho c_{\text{p}} {\cdot} T)}}{{{\text{d}}t}} +v_{\rm s} \frac{{\partial (\rho c_{\text{p}}{\cdot} T)}}{\partial x} $$
(1)

where T is temperature, ρ is density, \( \dot{Q}_{{\left( {x,y} \right)}} \) is the absorbed heat flux, c is specific heat capacity, λ is thermal conductivity, and v s is the constant speed of the moving heat source on the scanning surface. The latent heat of fusion L f was considered in this model to track the solid/liquid interface of the molten pool.

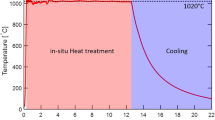
A two-dimensional finite-element analysis (FEA) thermal model was developed and implemented in ABAQUS 6.11 to comprehensively study the thermal process of EBAM. The electron beam heating, simulated as a moving conical body heat source with Gaussian distribution horizontally and decaying linearly, starts at the top powder layer surface and scans along the x-direction. The detailed setting of the model is introduced in the previous research.17

Microstructural Modeling

In the phase-field model, the free energy density \( f(c,{\kern 1pt} \phi ) \), where ϕ is the phase field, is defined as the sum of the free energies of liquid and solid phases with different compositions of c L and c S, respectively, and an imposed double-well potential, w·g(ϕ). The chemical potentials (μ) are defined as the difference between the chemical potentials of solute and solvent.8,18,19

$$ f(c,\phi ) = h(\phi )f^{S} (c_{\text{S}} ) + (1 - h(\phi ))f^{L} (c_{\text{L}} ) + w \cdot g(\phi ) $$
(2)
$$ c = h(\phi )c_{\text{S}} + (1 - h(\phi ))c_{\text{L}} $$
(3)
$$ \mu^{S} (c_{\text{S}} (x,t)) = \mu^{L} (c_{\text{L}} (x,t)) $$
(4)

where h(ϕ) = ϕ 3(6ϕ 2 − 15ϕ + 10) and g(ϕ) = ϕ 2(1 − ϕ)2. The subscripts and superscripts S and L indicate solid and liquid phases, respectively. Note that the chemical potentials μ S and μ L are derived from the free energy densities f S and f L. The free energy density at the interface without the w·g(ϕ) is defined as the fraction-weighted average values of the free energy in solid and liquid phases.

The phase-field model for solidification is based on the Ginzburg–Landau free energy functional. The phase-field and diffusion equations are described as:20

$$ \frac{\partial \phi }{\partial t} = M[\varepsilon^{2} \nabla^{2} \phi - h'(\phi )\{ f^{\text{S}} - f^{\text{L}} \} - w \cdot g'(\phi )] $$
(5)
$$ \frac{\partial c}{\partial t} = \nabla \cdot (\frac{D(\phi )}{{\partial^{2} f/\partial c^{2} }}\nabla \frac{\partial f}{\partial c}) $$
(6)

where M and ε are phase-field parameters, and D(ϕ) is the solute diffusion coefficient. The gradient energy coefficient (ε) and height of double potential (w) are related to the interface energy (σ) and interface width (λ).

In phase-field modeling, the phase field ϕ = 0 means the alloy is liquid, whereas ϕ = 1 means the alloy is solid. Interface cells also possess a solid fraction between ϕ = 0 and 1, whereas all liquid and solid cell have zero and unity solid fractions, respectively. For the solute concentration field, each solid and liquid cell has one solute concentration, whereas the interface cells have both a solid and a liquid solute concentration.

In this model, the ternary Ti-6Al-4V alloy is treated as binary and the solute is the combination of Al and V. The thermophysical parameters used in the phase-field modeling are listed in Table I. It is assumed that the initial temperature and concentration of liquid is uniform in the calculated region. The mesh size is set as 0.1 μm. The programming of dendrite growth was written in the MATLAB(The MathWorks Inc., Natick, MA) to solve partial differential equations and consequently simulate the evolution of the crystal growth. The multiple dendrites growth is also simulated to validate the phase-field modeling. When the calculation for the phase field and the concentration field is finished, the morphology with the phase field and the concentration field could be shown.

Table I Parameters used in the phase-field modeling on Ti-6Al-4V alloy8,20,21
Full size table

Results and Discussions

Single Crystal Growth

Figure 1 shows the simulation results of a single nucleus growing as an equiaxed grain. The preferential growth orientation of the primary dendrites is parallel or perpendicular to the x direction. The simulated results of the phase field and solute concentration field at different time steps are presented in Figs. 1 and 2, respectively. The grain growth morphologies and solute concentration at 0.01 ms, 0.2 ms, 1 ms, and 1.2 ms are shown. The initial seed is put in the center of the domain and applied to simulate the dendrite structure growth, as can be seen in Fig. 1a. In the beginning of growth, the secondary arms are not obvious. With continuous growth, the solutes accumulate at the solid/liquid (S/L) interface more intensely. The primary arms begin to grow from the horizontal and vertical directions, as shown in Fig. 1b. With the subsequent time increase, the dendritic structure is formed. When the solidification is 1.6 ms, the continuous growth of the dendritic structure can be seen in Fig. 1c. It is noted that the current model is applied to model the growth of primary β phase, and the phase has a body-centered cubic crystal structure with fourfold symmetry. The solute concentration profiles shown in Fig. 2 are consistent with the phase-field profile. During the dendritic structure growth, the interface is found to have the highest concentration. The interface is described by a smooth transition of the phase-field variable, which extends in thickness over the range of several grid nodes. The smooth interface in the phase field leads to a much higher computational cost compared with cellular automata method consisting of one layer of cells.19

Fig. 1
figure 1

Simulated dendrite structure growth at different times: (a) 0.01 ms, (b) 0.2 ms, and (c) 1.6 ms

Full size image
Fig. 2
figure 2

Simulated solute concentration during dendrite structure growth at different times: (a) 0.01 ms, (b) 0.2 ms, and (c) 1.6 ms

Full size image

Effect of Undercooling

According to the principle of metal crystallization, undercooling has an important impact on the growth processes of the dendritic structure. To demonstrate the influence of undercooling on dendrite growth, simulations are conducted with different amounts of undercooling values, with corresponding simulation times 0.6 ms. A nucleus is placed at the center of the calculation domain.

Figure 3 illustrates the effect of undercooling on the average velocity of primary arms growth. It is noticed that the larger undercooling helps the formation of the primary arms. A smaller undercooling leads to lower velocity of grain growth, which results in more time for the transfer of solute from the S/L interface to the bulk liquid region. This is the reason that small undercooling results in lower maximum composition. Liptonet al.22 developed an analytical model (the LGK model) that described free dendrite growth at a given melt undercooling. The tip growth velocity with various undercoolings calculated by the LGK theory is shown in Fig. 4. The influence of undercooling on tip growth velocity follows well with the analytical model, which described free dendrite growth at a given melt undercooling.22 Zhu and Stefanescu23 compared the dendritic morphologies for Al dendrites grown at different undercoolings, finding that the dendrite arms at smaller undercooling were thicker than those for the larger undercooling. In the current model, similar results are obtained. In addition, it can be observed that a larger undercooling increases the growth speed of the dendrite and causes the formation of an increased number of secondary dendrite arms. The similar phenomenon is also observed by Zhao et al.24 The increase of secondary dendrite arms reflects the higher instability of the SL interface at large undercoolings, whereas the faster growth of the dendrite at larger undercooling is mainly due to the larger driving force. The increase of the interface instability along with the undercooling is also within the solidification theory predicted by Mullins and Sekerka.25

Fig. 3
figure 3

Dendrite growth at different undercooling temperatures up to 0.6 ms: (a) 47.5 K, (b) 52.5 K, and (c) 55 K

Full size image
Fig. 4
figure 4

Tip growth velocity versus undercooling calculated by the phase-field model

Full size image

Columnar Structure Growth

In EBAM, the solidification of Ti-6Al-4V alloy involves two steps: liquid to primary solid phase of β and solid phase transformation (β to α or α′) depending on the cooling rate. The nucleation and growth of columnar grains of prior β takes place during initial rapid solidification when the temperature is above the β-transus temperature (about 980°C). The size of α after solid phase transformation is also affected by the size of the prior β.15 The larger the prior β columnar structure, the larger the α-lath during the subsequent solid-state transformation. It is important to use the phase model to simulate the columnar structure growth during the EBAM process.

The thermal modeling could provide the temperature history of the EBAM process. Under the equilibrium condition, the cooling rates are calculated when the temperature is below the melting temperature and above the solid phase transformation temperature (about 980°C). For one powder layer in EBAM, three cooling rates (top, middle, and bottom) are calculated. To study the beam scanning speed effects in EBAM, four scanning speeds are applied and the cooling rates are calculated based on the thermal model, as can be seen from Table II. In EBAM, the speed function(SF) is a process parameter setting related to the actual beam scanning speed (Table II).Faster cooling results in a larger undercooling and subsequently contributes to a higher density of the nucleation sites in EBAM.15 A previous study has investigated the influence of scanning speeds on the microstructure of EBAM Ti-6Al-4V specimens. The relationship between the cooling rate and nucleation sites is found based on the regression equation:

$$ \rho = 28.8\exp \left\{ { - \left( {\frac{Cr - 68970}{60120}} \right)^{2} } \right\} $$
(7)
Table II Calculated cooling rate from thermal model
Full size table

To model the growth of the columnar grains, nuclei sites are placed at the bottom wall at the beginning of the simulation. Figure 5 shows the morphology of columnar dendritic growth with different solidification times (0.2, 1, 2 and 4 ms, respectively). The preferential growth orientation of the primary dendrites is parallel or perpendicular to the x direction. The primary arms whose morphology orientations are not parallel to the temperature gradient direction are stopped by the growth of the arm that is parallel to the heat transfer direction. The growth of some main arms is suppressed by nearby dendrites. Figure 6 shows the simulated columnar dendrites under different SFs in EBAM, respectively, at corresponding simulation times of 10 ms. Microstructures with different columnar widths are presented.

Fig. 5
figure 5

Simulated columnar structure growth at different times (SF 36): (a) 0.2 ms, (b) 1 ms, (c) 2 ms, and (d) 4 ms

Full size image
Fig. 6
figure 6

Comparison of phase-field contours across modeling results with different speed functions: (a) SF 20, (b) SF 36, (c) SF 50, and (d) SF 65

Full size image

The experimental results of EBAM parts with different scanning speeds are shown in Fig. 7.15 The microstructure shown in Fig. 7 represents the Ti-6Al-4V alloy after primary solidification and solid phase transformation. However, the columnar structure produced from the primary solidification still existed. The width of the columnar prior β grains was measured from microstructures in Fig. 7. Figure 8 presents a comparison of the characteristic sizes between the experimental and simulated results with various SFs. For a given beam power, increasing the scanning speed would increase the cooling rate and the thermal gradient. A higher cooling rate would result in more nuclei and subsequently finer grains in a long and narrow columnar morphology. The simulation results agree qualitatively well with the experimental studies of a columnar microstructure with different SFs. It is obvious that the current model not only can simulate the dynamic growth of the columnar dendrites but also can be applied to the branching and competition growth processes. Besides the microstructure modeling during EBAM, the current model could also be extended to model of the microstructure evolution for other additive manufacturing systems given the information of thermal history.

Fig. 7
figure 7

Optical microscopy microstructures from X-plane specimens: (a) SF 20, (b) SF 36, (c) SF 50, and (d) SF 6515

Full size image
Fig. 8
figure 8

Measured characteristic sizes from experiments15 and simulated results with various speed functions

Full size image

Conclusion

A phase-field model was developed to model the microstructure evolution in an EBAM-built Ti-6Al-4V alloy. As an input to the phase-field model, the cooling rate was extracted from the simulation of a thermal model. MATLAB code was used to implement and solve the phase-field equations. The major findings are summarized as follows.

  1. (1)

    The phase-field model can model the morphology and solute concentration during solidification.

  2. (2)

    The dendrite morphology at various undercoolings is simulated. The undercooling is shown to affect the columnar dendrite growth significantly, and a greater undercooling will resultin a higher growth speed.

  3. (3)

    The columnar dendritic structure could be simulated using phase-field modeling. The columnar dendritic spacing and the width of dendrites decrease with the increase of the beam scanning speed.