CBS-Based Partitioned Semi-implicit Coupling Algorithms for Fluid–Structure Interaction: A Decade Review

Abstract

Being a general fractional-step solver, the characteristic-based split (CBS) scheme not only works out a broad range of fluid flow problems but also underpins an emerging partitioned semi-implicit coupling framework for fluid–structure interaction (FSI). This article thoroughly summarizes the CBS-based partitioned semi-implicit coupling algorithms going into FSI over the past decade. Full details related to this class of new partitioned solution strategies are given alongside illustrative examples whereby we look to demonstrate a good prospect of the developed methodology.

1 Introduction

1.1 Motivation

Fluid–structure interaction (FSI), which characterizes the mutual dependence between a fluid flow and structural movements through fluid–structure interface(s), is commonplace in nature and engineering. A reliable FSI solver is regarded as a highly useful tool for exploring and understanding many real-world problems [1]. Historically, partitioned coupling algorithm with application to computational FSI simulation may be traced back to the pioneering work conducted by Park et al. [2] on a simplified pressure–structural analysis in the late 1970s. The partitioned approach to transient FSI problems [3] has been mainstreamed nowadays due to its operational simplicity and computational effectiveness. In most instances, a partitioned coupling scheme is readily formulated under the arbitrary Lagrangian–Eulerian (ALE) description [4] that combines a fluid flowing on the Eulerian reference system and structural motion represented from the Lagrangian viewpoint in a unified kinematics framework. As a result, the fluid and structural subsystems can be treated separately with well-established discretization and solution schemes. The program modularity is well preserved and efforts of software development are greatly simplified thereby. Further, the coupled fluid–structure mechanical system comprises a three-field partitioned formulation since the dynamic mesh can be modeled as a pseudo-structural subsystem [5]. Traditionally, the partitioned solution procedures are divided into explicit and implicit coupling schemes. The former is usually known for higher efficiency [6,7,8] while the latter preserves the numerical stability much better [9,10,11]. In short, partitioned solution procedures have for years won popularity with analysts and practitioners in a wide variety of realistic applications.

It has however become clear that traditional partitioned procedures are difficult to arrive at an optimal compromise between the computational efficiency and numerical accuracy. To circumvent this dilemma, Fernández et al. [12] proposed a so-called partitioned semi-implicit coupling method in 2007 to tackle hemodynamic FSI problems with strong added-mass effect [13, 14]. This new semi-implicit concept is totally underpinned by the classic Chorin–Témam projection method [15, 16], hence consisting of two major steps responsible for the non-standard (and also non-physical) multi-field coupling. First, the ALE–advection–diffusion fluid phase is explicitly coupled with the mesh motion in response to a proper extrapolation of the position of the interfaces. Second, the divergence-free velocity and pressure variables, and the structural movement are calculated on the domain mesh that stays provisionally stationary during the course of a sequence of implicit subiterations at each time step. The main procedure of the projection-based partitioned semi-implicit coupling algorithm [12] is recalled below

• Step 1: Initialize field variables

• Step 2: Perform the explicit coupling phase

  • 2.1: Extrapolate the position of the interface $\Sigma$ [17]

    $$\begin{aligned} \bar{\textbf{d}}^{n+1}_\Sigma = \textbf{d}^{n}_\Sigma + \left( \frac{3}{2} \dot{\textbf{d}}^{n}_\Sigma - \frac{1}{2} \dot{\textbf{d}}^{n-1}_\Sigma \right) \Delta t, \end{aligned}$$

    (1)

  • 2.2: Renew the fluid mesh

  • 2.3: Compute the intermediate velocity

    $$\begin{aligned} \dfrac{\textbf{v} - \textbf{u}^n}{\Delta t} + \textbf{c}^n \cdot \nabla \textbf{u}^n - \frac{1}{Re}\nabla ^2 \textbf{u}^n = \textbf{0}, \end{aligned}$$

    (2)

• Step 2: Perform the implicit coupling phase

  • 3.1: Update the pressure

    $$\begin{aligned} \nabla ^2 p^{n+1} - \frac{1}{\Delta t} \nabla \cdot \textbf{v} = \textbf{0}, \end{aligned}$$

    (3)

  • 3.2: Correct the velocity

    $$\begin{aligned} \dfrac{\textbf{u}^{n+1} - \textbf{v}}{\Delta t} + \nabla p^{n+1} = \textbf{0}, \end{aligned}$$

    (4)

  • 3.3: Solve the structural equation

    $$\begin{aligned} \textbf{M} \ddot{\textbf{d}}^{n+1} + \textbf{C} \dot{\textbf{d}}^{n+1} + \textbf{K} \textbf{d}^{n+1} = \textbf{R}^{n+1}(\textbf{v}, p^{n+1}), \end{aligned}$$

    (5)

where the primitive variables denoted by common symbols will be explained later, $\textbf{M}$ is the mass matrix, $\textbf{C}$ is the damping matrix, $\textbf{K}$ is the stiffness matrix and $\textbf{R}$ is the external force vector. The projection-based partitioned semi-implicit coupling method can decrease the computational expense without too much stability loss, in contrast to its full implicit counterpart. This technique is considered to be a wining combination of the explicit and implicit partitioned schemes and thus it probably offers excellent potential for computing large-scale FSI problems. Nevertheless, it appears to be somewhat weird to employ the intermediate velocity (which usually does not meet the divergence-free condition) to evaluate the applied fluid forces, see Eq. (5). Recently, a few variant forms, such as the three-step (i.e. explicit-implicit-explicit) [18, 19] and semi-monolithic [20] coupling formulations, have also been developed in an attempt to enhance some algorithmic properties of the semi-implicit coupling scheme. Despite these accomplishments, there is still room for improvement in the projection-based partitioned semi-implicit coupling method. For example, the method may suffer from the stability issues because the pure projection method lacks a stabilizing mechanism in computing incompressible convective flows. Also, the interface conditions can be reshaped to compensate the intrinsic time lag triggered by the temporally staggered advancement of the fluid and solid fields .

The characteristic-based split (CBS) scheme [21, 22] is a general fractional-step finite element algorithm originally proposed in the trilogy of Zienkiewicz et al. [23,24,25] for computing compressible and incompressible fluid flows. This algorithm effectively combines the characteristic Galerkin method [26] with the projection method [15, 16] to form a new stabilization mechanism. Spurious oscillations in convection-dominated flows are successfully suppressed via a higher-order time stepping due to the characteristic-Galerkin procedure, while the pressure field being decoupled from the velocity field is well stabilized by the projection method. Such distinguishing features make the CBS scheme an obvious candidate for the enhancement of Fernández’s semi-implicit method. Then, a series of CBS-based partitioned semi-implicit coupling algorithms were introduced expressly for that purpose. Their implicit steps are readily iterated via a standard fixed-point algorithm [27, 28], or via a dynamic relaxation scheme [10] if a faster convergence rate is sought. It is thus realized that, the CBS scheme can work not only for the fluid flow in a moving domain but also for the entire multi-physical system. In what follows, we shall go over all the aspects of the CBS-based partitioned semi-implicit coupling method with application to computational FSI simulations.

1.2 Historical Perspective

The basic procedure of the CBS-based partitioned semi-implicit coupling method is described as follow. The first step of the CBS scheme is explicitly coupled with the mesh movement resulting from an extrapolation of the interface’s position. The remaining two steps are implicitly iterated alongside the structural motion on the same mesh which is temporarily frozen, though. In particular, a mass source term (MST) [6] is introduced into the pressure Poisson equation (PPE) at the implicit coupling stage. As the MST has already been updated at the explicit stage, it needs to be re-calculated simply for those elements adhering to the interface during the implicit subiterations. Hence, not only the genuinely semi-implicit coupling fashion but also the geometric conservation law (GCL) [29] is retrieved for the distinctive partitioned solution procedure. Moreover, unlike Fernández et al. [12], the fluid forces loading on the immersed structure are evaluated through the end-of-step velocity rather than the intermediate one. In summary, the developed CBS-based partitioned semi-implicit coupling procedure inherits algorithmic virtues from both the CBS scheme and the projection-based semi-implicit coupling method because it can offer

• a well-stabilized approximate solution to incompressible Navier–Stokes (NS) equations;

• a noticeable reduction in computing time, but without too much stability drop.

For the CBS-based partitioned semi-implicit coupling method, initial investment has gone into reshaping interface conditions in an effort to mitigate the undesirable time lag [30,31,32]. To this end, the conventional interface conditions are individually corrected at explicit and implicit phases by the so-called combined interface boundary condition (CIBC) method [33, 34]. In this series of numerical studies [30,31,32], the modified CIBC (MCIBC) formulae are proposed to adapt quickly to oscillating rigid bodies which the original CIBC method fails to solve. Different shape functions can be used to approximate the fluid and solid equations in space under the semi-implicit coupling framework [31]. Additionally, a dual-time stepping scheme incorporating internal and external time steps [35] is tentatively attempted in the CBS-based partitioned semi-implicit coupling method [30]. However, the results calculated from a transversely oscillating circular cylinder at low Reynolds number [36] are against the inference drawn from a simple Stokes flow on the fixed mesh [35]. To be specific, a large ratio of the internal time step to the external one cannot yet work to the benefit of an incompressible FSI computation. Comparative studies [37, 38] have also been carried out for explicit, implicit and semi-implicit forms of partitioned coupling methods in terms of traditional interface conditions and their MCIBC corrections, respectively. It is found that, the three sets of computed results are nearly identical in large-displacement FSI problems where the mass ratios (i.e., the ratio of the structural density to the fluid one) seem relatively large. Apparently, the conducted comparison gives us a clear direction towards the solvability of the CBS-based partitioned semi-implicit coupling methods in small-mass-ratio FSI problems.

Since the MST is theoretically derived from the movement of three-node triangular (T3) element [6], the CBS-based partitioned semi-implicit coupling method encounters the following limitations: (i) heavy dependence on element type while maintaining its fractional-step modularity; and (ii) inconvenient mathematical management and increased expenditure from the solution of algebraic interface system. To work out the issues, a simple and accurate alternative method [39] is developed based upon an artificial compressibility (AC) scheme [40]. The AC-CBS scheme [41] is not new in computational fluid dynamics (CFD), but the AC-CBS-based partitioned semi-implicit coupling method [39] is a relatively novel solution approach to FSI indeed. What we need to do next is to modify the continuity equation by inserting a pressure time derivative [40] to model a quasi-incompressible fluid flow. A non-iterative AC parameter [40], which is sometimes determined locally [42, 43], is employed herein. The iterated AC parameter decouples the pressure, end-of-step velocity and structural motion at the implicit stage. Thus, we do not have to iteratively solve a set of simultaneous equations of the interface system. Especially, the implicit coupling between the fluid projection step and structural motion merges with the pseudo-time subiterative loops. Consequently, the AC-CBS-based partitioned semi-implicit coupling method is completely matrix-free and has unlimited access to various finite elements. Its computational performance is clearly demonstrated through an oscillating rigid body subjected to uniform laminar flows. Furthermore, a stabilized second-order pressure splitting scheme is developed for the AC-CBS-based coupling algorithm [44] as the erratic fluctuation of pressue may become sensitive to the change of the interface’s position. Because the increased accuracy in pressure prediction probably engenders a reduced stability of both the fluid solution and semi-implicit coupling schemes, the stabilized pressure gradient projection (SPGP) technique [45, 46] is introduced into the second-order CBS scheme in a moving fluid domain. In view of different types of the continuity equations, the CBS-based partitioned semi-implicit coupling algorithms can be categorized as PPE-based and AC-based schemes.

As mentioned above, it makes sense to solve small-mass-ratio FSI problems with the aid of the CBS-based partitioned semi-implicit coupling scheme that is expected to deliver a good balance between the computational efficiency and numerical stability. With this in mind, we shall search a more generic and stable CBS-based algorithm suitable for very small mass ratios that represent the outstanding added-mass effect in quantitative terms [13, 14]. According to Zienkiewicz et al. [47], it is possible to suggest two alternative formulations, namely Split A and Split B, for the CBS scheme. In particular, Split A excludes the pressure gradient from the momentum equation whereas Split B retains the same term in that equation. Though Split B appears to be more accurate in form, it may lose some self-pressure stabilizing properties [47]. Additional measures against undesirable instabilities [45, 46] must be taken to Split B, especially when it serves as a vehicle for the second-order pressure accuracy of the CBS scheme. Following these splits, two simple but effective alternatives to improve the CBS-based partitioned semi-implicit coupling algorithm are proposed accordingly [48]. It should be interpreted that, the $\underline{\hbox {CBS}}$-based $\underline{\hbox {P}}$artitioned $\underline{\hbox {S}}$emi-$\underline{\hbox {I}}$mplicit coupling algorithm integrating Split $\underline{\hbox {A}}$ or Split $\underline{\hbox {B}}$ (including necessary stabilization for the second-order splitting error in pressure) is officially referred to as the CBS(A/B)-$\varPsi$ coupling method [48] in shorthand. Similarly, the AC-CBS-based partitioned semi-implicit coupling method using Split A or Split B [39, 44] is named AC-CBS(A/B)-$\varPsi$ coupling method. A key idea behind the CBS(A/B)-$\Psi$ coupling algorithm lies in introduction of the end-of-step velocity into the implicit stages, which avoids using the MST constructed exclusively by moving T3 elements. The presented algorithms have done very well in many examples so far, even if their implicit phases are calculated via a regular fixed-point procedure without any accelerator. To cater for much smaller mass ratios, the CBS(B)-$\Psi$ coupling algorithm is further stabilized by the SPGP technique [45, 46]. Numerical examples have shown that such a treatment for remarkable added-mass effect is an undoubted success [48].

As expected, the CBS-$\Psi$ coupling method can easily incorporate different spatial discretization schemes. In this semi-implicit coupling scheme, some effort [31, 49] has been spent on a sensible integration of the finite element method (FEM) for fluid flows [47] and the cell-based smoothed FEM (CSFEM) for solid deformation [50]. Smoothed finite element methods (SFEMs) [51] are known as a special subclass of finite element algorithms that are able to produce a more accurate solution to partial differential equations (mainly in solid mechanics, heat transfer and applied acoustics) through the steady alliance between the mesh-free strain smoothing [52] and traditional FEM. However, the existing applications [31, 49] have not provided any settlements tailored for the ALE–NS equations, but rather have replicated the earlier success of the CSFEM in solid mechanics. The improvement of a single-field solution is meaningful to the partitioned semi-implicit computation, though.

Given its attractive merits [50], the CSFEM is additionally expected to model both fluid and solid equations under the CBS-$\Psi$ coupling framework. It is inferred that the most technically straightforward way is to integrate the viscous stress and PPE of the NS equations in smoothed weak form for the CBS-$\Psi$ algorithm [53]. It must be stressed that, multiplication of a variable quantity and the first-order derivative (or gradient) of another variable quantity in the smoothed Galerkin weak form of the NS equations invites the chief difficulty that the SFEM has to face in CFD [54]. To integrate these mixed products in smoothed weak form, we may simply dictate that in each four-node quadrilateral (Q4) element the number and numbering of smoothing cells (SCs) are exactly identical to those of Gaussian points (GPs) [48]. After spatial discretization, both the CBS(A)- and CBS(B)-$\Psi$ coupling schemes are validated against previously published data for benchmark problems. Recently, there follows a mathematical evidence that the gradient smoothing procedure for the CSFEM is highly flexible in each SC [54]. Therefore, all of the entries from the weak form of the NS equations can be acquired in the cell-based smoothing manner. The importance of the recent study [54] consists in the solid conclusion that the CSFEM can be generalized to modeling of the vast majority real-world phenomena hereafter. A genuinely smoothed-finite-element formulation of the CBS(B)-$\Psi$ coupling scheme is easily presented therein. Subsequently, a stabilized CBS(B)-$\Psi$ coupling method [55] is proposed to cope with viscoelastic FSI (VFSI) using the CSFEM. Especially, the discrete elastic-viscous split stress-gradient (DEVSS-G) procedure [56] is introduced to the explicit stage whereas the SPGP technique is used for the implicit stage as before. Stabilization techniques customized for the viscoelastic fluid subproblem are naturally integrated into the partitioned semi-implicit coupling framework whose numerical stability is appropriately boosted. It is noteworthy that, in the CSFEM context, our semi-implicit coupling algorithm saves more than 60% computing time than its implicit counterpart does [57]. Another distinguished member of the SFEM family, i.e. the edge-based SFEM (ESFEM) [58], is found spatially and temporally stable in dynamic analyses. For this reason, the flexibility of the ESFEM in smoothed Galerkin weak-form integral is also proved for FSI modeling more recently [59]. A simple integration scheme is proposed to facilitate the resultant smoothed weak-form approximation over variable-node SCs constructed from T3 elements. A new CBS(B)-$\Psi$ coupling method incorporating the ESFEM is proposed for simulating VFSI shortly [57]. In addition to the DEVSS-G/CBS(B)-SPGP stabilization [55], the MST is re-derived from the modified continuity equation based on T3 element to fulfill the GCL in the ESFEM environment. Again, the higher efficiency is acquired by solving an open cavity flow problem with the GCL-preserving ALE–ESFEM-T3 formulation, in contrast to the expense demanded for the partitioned implicit coupling algorithm.

At the end of this subsection, it is worthwhile to refer briefly to an up-to-date development of the CBS-$\Psi$ coupling algorithms covering the subject of VFSI modeling [55, 57]. VFSI which is generally more complicated than Newtonian FSI (NFSI) often occurs in a rich variety of biological and industrial systems. Although the simple Oldroyd-B fluid model [60] is adopted in our algorithmic studies, this constitutive relation retains extravagant extensional and constant shear viscosities that still render certain unwanted difficulties of getting accurate numerical approximations [61]. Furthermore, improper communications of the triple fluid variables and structural responses possibly take place along moving and deformable interfaces since the contrived semi-implicit decoupling procedure appears to be non-physical among cut modules. However, as stated above, several computational benefits can be obtained in the CBS-$\Psi$ coupling algorithm being equipped with appropriate stabilization mechanisms.

1.3 Outline

Since the non-linear three-field formulation of a partitioned FSI system consists of the fluid flow, structural movement and mesh deformation, respectively, the reminder of this article is organized in terms of these components. Section 2 gives a general description of different fluid flows. The conceptual frameworks of the first- and second-order CBS schemes are accordingly presented therein. Subsequently, computational structural dynamics governing both rigid-body motion and finite solid deformation is illustrated in Sect. 3. Section 4 briefly describes the coupling conditions as well as their MCIBC corrections. A cost-effective moving mesh scheme along with the MST structured for the GCL is then articulated in Sect. 5. After that, the principle of the CSFEM and ESFEM is discussed in Sect. 6 for spatial and traction approximations. Next, various CBS-$\Psi$ coupling algorithms are detailed in Sect. 7 where explanatory notes are provided correspondingly. Section 8 presents selected numerical examples so as to highlight the advantages of the proposed methodology. Finally, some concluding remarks as well as prospective directions are drawn in Sect. 9.

2 Fluid Flows in Moving Domain

2.1 Incompressible Newtonian Fluid

Given a moving domain $\Omega _\textrm{f} \subset \mathbb {R}^2$ and time $t \in (0, \ t_\infty )$, the unsteady, isothermal, laminar flow of an incompressible viscous Newtonian fluid is governed by the ALE–NS equations written below

$$\begin{aligned}{} & {} \nabla \cdot \textbf{u} = 0 \quad \text {on} \quad \Omega _\textrm{f} \times (0, \ t_\infty ), \end{aligned}$$

(6)

$$\begin{aligned}{} & {} \rho _\textrm{f} \left( \frac{\partial \textbf{u}}{\partial t} + \textbf{c} \cdot \nabla \textbf{u} - \textbf{g} \right) -\nabla \cdot \varvec{\sigma }_\textrm{f} = \textbf{0} \quad \text {on} \quad \Omega _\textrm{f} \times (0, \ t_\infty ), \end{aligned}$$

(7)

where $\rho _\textrm{f}$ is the fluid density, $\textbf{u}$ the flow velocity, $\textbf{c} = \textbf{u} - \textbf{w}$ the convective velocity, $\textbf{w}$ the mesh velocity, $\textbf{g}$ the gravitational acceleration, and $\varvec{\sigma }_\textrm{f}$ the Cauchy stress. For a Newtonian fluid, its Cauchy stress is written as the sum of the volumetric and deviatoric stresses, namely

$$\begin{aligned} \varvec{\sigma }_\textrm{f} = -p \mathbb {I} + 2\mu _\textrm{s} \varvec{\epsilon } \quad \text {and} \quad \varvec{\epsilon } = \frac{1}{2} \left( \nabla \textbf{u} + (\nabla \textbf{u})^\textrm{T}\right) , \end{aligned}$$

(8)

where p denotes the pressure, $\mathbb {I}$ the identity tensor, $\mu _\textrm{s}$ the Newtonian dynamic viscosity, $\varvec{\epsilon }$ the deformation rate tensor and the superscript T the transpose. The fluid subproblem should be completed by imposing proper initial and boundary conditions.

Using the free-stream velocity $U_\infty$ and characteristic length L, we may define the following non-dimensional scales

$$\begin{aligned} \textbf{x}^* = {} & \frac{\textbf{x}}{L}, \ t^* = \frac{t U_\infty }{L}, \ \textbf{u}^* = \frac{\textbf{u}}{U_\infty }, \ \textbf{c}^* = \frac{\textbf{c}}{U_\infty }, \nonumber \\ p^* = {} & \frac{p}{\rho _\textrm{f} U^2_\infty }, \ \textbf{g}^* = \frac{\textbf{g} L}{U^2_\infty }. \end{aligned}$$

(9)

After introducing Eq. (9) into Eqs. (6)–(8) and dropping the asterisks for brevity, the continuity, momentum and constitutive equations can be readily non-dimensionalized as follows

$$\begin{aligned}{} & {} \nabla \cdot \textbf{u} = 0, \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \frac{\partial \textbf{u}}{\partial t} + \textbf{c} \cdot \nabla \textbf{u} - \nabla \cdot \varvec{\sigma }_\textrm{f} - \textbf{g} = \textbf{0}, \end{aligned}$$

(11)

$$\begin{aligned}{} & {} \varvec{\sigma }_\textrm{f} = -p\mathbb {I} + \frac{1}{Re} \left( \nabla \textbf{u} + (\nabla \textbf{u})^\textrm{T}\right) , \end{aligned}$$

(12)

where $Re = \frac{\rho _\textrm{f} U_\infty L}{\mu _\textrm{s}}$ is the Reynolds number.

2.2 Quasi-Incompressible Newtonian Fluid

Let us consider in this subsection a quasi-incompressible viscous Newtonian fluid flow. Based on a non-iterative AC model suitable for unsteady flow [40], Eq. (10) is modified by inserting a pressure time derivative such that

$$\begin{aligned} \frac{1}{a^2} \dfrac{\partial p}{\partial t}+ \nabla \cdot \textbf{u} = 0 \quad \text {on} \quad \Omega _\textrm{f} \times (0, \ t_\infty ), \end{aligned}$$

(13)

where a is the AC coefficient ($a \rightarrow \infty$ for fully incompressible flow) that connects the fluid projection step to the implicit phase. As the pseudo-time step is set equal to the physical time step in Eq. (13), recovering a real transient solution (or dual time stepping) [41, 62] is not needed any more. Consequently, the AC-CBS(A/B)-$\Psi$ coupling algorithm avoids the triple nested-loops which may be very costly. Here, a locally varying AC parameter [42] is recommended below

$$\begin{aligned} a^2 = \text {max}(\varepsilon ^2, \ 2.5| \textbf{u} |^2), \end{aligned}$$

(14)

where $\varepsilon$ is typically chosen to be 1. Additionally, the following inequality may be respected

$$\begin{aligned} a^2 \gg \left( 1 + \frac{4L}{Re} \right) ^2 - 1, \end{aligned}$$

(15)

for low-speed incompressible flows [43].

2.3 Incompressible Viscoelastic Fluid

The Cauchy stress of a viscoelastic fluid normally contains three parts; that is to say,

$$\begin{aligned} \varvec{\sigma }_\textrm{f} = -p\mathbb {I} + 2\mu _\textrm{s} \varvec{\epsilon } + \varvec{\tau }, \end{aligned}$$

(16)

where $\varvec{\tau }$ is the viscoelastic stress. Further, the constitutive equation of an Oldroyd-B fluid [60] is formulated as follow

$$\begin{aligned} \varvec{\tau } + \lambda {\mathop {\varvec{\tau }}\limits ^{\triangledown }} = 2 \mu _\textrm{p} \varvec{\epsilon }, \end{aligned}$$

(17)

where $\lambda$ denotes the relaxation time, $\mu _\textrm{p}$ the polymer viscosity and ${\mathop {\bullet }\limits ^{\triangledown }}$ the upper-convected time derivative of $\bullet$. Under the ALE description, ${\mathop {\varvec{\tau }}\limits ^{\triangledown }}$ is given by

$$\begin{aligned} {\mathop {\varvec{\tau }}\limits ^{\triangledown }} = \frac{\partial \varvec{\tau }}{\partial t} + \textbf{c} \cdot \nabla \varvec{\tau } - \left( (\nabla \textbf{u})^\textrm{T} \cdot \varvec{\tau } + \varvec{\tau } \cdot \nabla \textbf{u} \right) . \end{aligned}$$

(18)

It is important to note that the polymeric contribution can be recast in terms of the conformation tensor $\mathbb {C}$ [63], i.e.

$$\begin{aligned} \varvec{\tau } = \frac{\mu _\textrm{p}}{\lambda } (\mathbb {C} - \mathbb {I}), \end{aligned}$$

(19)

in order to strengthen the positive definite properties of the flow system. For the Oldroyd-B model, the introduction of Eq. (19) into Eq. (17) admits the following representation

$$\begin{aligned} \frac{\partial \mathbb {C}}{\partial t} + \textbf{c} \cdot \nabla \mathbb {C} - \left( (\nabla \textbf{u})^\textrm{T} \cdot \mathbb {C} + \mathbb {C} \cdot \nabla \textbf{u} \right) + \frac{1}{\lambda } (\mathbb {C} - \mathbb {I}) = \textbf{0}, \end{aligned}$$

(20)

which makes the set of viscoelastic flow equations be well-posed in a mathematical sense.

In addition to Eq. (9), we define one more variable $\mathbb {C}^*= \mathbb {C}$ to non-dimensionalize the governing equations of the Oldroyd-B fluid flow. After dropping the asterisks, we obtain the non-dimensional form of the momentum and constitutive equations below

$$\begin{aligned} \frac{\partial \textbf{u}}{\partial t} + \textbf{c} \cdot \nabla \textbf{u} + \nabla p - \frac{\eta }{Re} \nabla ^2 \textbf{u} - \frac{1 - \eta }{Re W\!i} \nabla \cdot \mathbb {C} - \textbf{g} = \textbf{0}, \end{aligned}$$

(21)

$$\begin{aligned} {\mathop {\mathbb {C}}\limits ^{\triangledown }} + \frac{1}{W\!i} (\mathbb {C} - \mathbb {I}) = \textbf{0}, \end{aligned}$$

(22)

where $\eta = \frac{\mu _\textrm{s}}{\mu }$ is the viscosity ratio, $\mu = \mu _\textrm{s} + \mu _\textrm{p}$ the total shear viscosity, $Re = \frac{\rho _\textrm{f} U_\infty L}{\mu }$ the Reynolds number and $W\!i = \frac{\lambda U_\infty }{L}$ the Weissenberg number. Note that the continuity equation (17) remains unchanged in the viscoelastic fluid flow.

The DEVSS-G method introduces a stabilizing elliptic operator into the discrete momentum equation and avoids the objective derivative of the deformation rate tensor [56]. For this reason, an $L^2$-projection of the velocity gradient [64]

$$\begin{aligned} \mathbb {G} - \nabla \textbf{u} = \textbf{0}, \end{aligned}$$

(23)

is defined, which allow us to recast Eq. (21) into

$$\begin{aligned} \frac{\partial \textbf{u}}{\partial t} + \textbf{c} \cdot \nabla \textbf{u} - \textbf{g}= & {} -\nabla p + \frac{\eta + \theta }{Re} \nabla ^2 \textbf{u} - \frac{\theta }{Re} \nabla \cdot \mathbb {G}\nonumber \\{} & {} + \frac{1 - \eta }{Re W\!i} \nabla \cdot \mathbb {C}, \end{aligned}$$

(24)

where $\theta$ is the stabilizing parameter that is typically equal to $1 - \eta$. It is clear that the elliptic operator vanishes automatically once the exact solution is recovered.

2.4 Solution Procedures

For all the illustrative purposes, only Eqs. (10)–(12) are solved with the first- and second-order CBS schemes in this subsection. Application of the CBS procedures to the other two cases is straightforward nevertheless. Full technical details are easily accessible in the previously published papers [39, 44, 55, 65].

2.4.1 CBS(A) Scheme

In most cases, we prefer the semi-implicit version of the CBS(A) scheme [25]. This solution procedure largely consists of the following steps

• Step 1: Velocity prediction

  $$\begin{aligned} \dfrac{\textbf{v} - \textbf{u}^n}{\Delta t}= -\textbf{c}^n \cdot \nabla \textbf{u}^n + \frac{1}{Re} \nabla ^2 \textbf{u}^n + \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla (\textbf{c}^n \cdot \nabla \textbf{u}^n), \end{aligned}$$

  (25)

• Step 2: Pressure update

  $$\begin{aligned} \nabla ^2 p^{n+1} = \dfrac{1}{\Delta t} \nabla \cdot \textbf{v}, \end{aligned}$$

  (26)

• Step 3: Velocity correction

  $$\begin{aligned} \dfrac{\textbf{u}^{n+1} - \textbf{v}}{\Delta t} = -\nabla p^{n+1} + \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla ^2 p^n, \end{aligned}$$

  (27)

where $\textbf{v}$ is the intermediate velocity, $\Delta t$ denotes the time step, and the third-order terms and gravity force are neglected.

It is of interest to remark that the semi-implicit CBS(A/B) scheme remains conditionally stable [21, 47]. Hence, the general time-step limitations are recommended below

$$\begin{aligned}{} & {} \texttt {Newtonian \, fluid:} \quad \Delta t \leqslant \text {min}(\Delta t_\textrm{con}, \ \Delta t_\textrm{dif}), \end{aligned}$$

(28a)

$$\begin{aligned}{} & {} \texttt {Oldroyd-B \, fluid:} \quad \Delta t \leqslant \text {min}(\Delta t_\textrm{con}, \ \Delta t_\textrm{dif}, \ \Delta t_\textrm{vis}), \end{aligned}$$

(28b)

where the convection, diffusion and viscoelasticity limits are given as

$$\begin{aligned} \Delta t_\textrm{con} = \frac{h}{| \textbf{u} |}, \quad \Delta t_\textrm{dif} = \frac{1}{2} h^2 Re, \quad \Delta t_\textrm{vis} = h \sqrt{Re W\!i}, \end{aligned}$$

(29)

where h is the characteristic size of a local element.

2.4.2 CBS(B) Scheme

The CBS(B) scheme is of the second-order accuracy in both time and pressure, but its pressure stability may be corrupted by the pressure difference included in the momentum equation [46]. The reduced pressure stability is the penalty for increasing the order of splitting error in pressure. To suppress this instability, Nithiarasu and Zienkiewicz [46] suggested the SPGP technique [45] for stabilizing the CBS(B) scheme. The stabilization mechanism is briefly recalled in the following.

First, we shall define an auxiliary variable $\textbf{q}$ satisfying

$$\begin{aligned} \textbf{q} - \nabla p = \textbf{0}, \end{aligned}$$

(30)

whereby Eq. (10) is accordingly modified as

$$\begin{aligned} \nabla \cdot \textbf{u} + \phi \nabla \cdot \textbf{q} - \phi \nabla ^2 p = 0, \end{aligned}$$

(31)

where $\phi$ denotes the stabilization parameter being discussed elsewhere [66].

For simplicity, the effect of gravity is omitted in the law of momentum conservation. The time-discrete form of the modified continuity and momentum equations can be expressed as

$$\begin{aligned}{} & {} \nabla \cdot \textbf{u}^{n+1} + \phi \nabla \cdot \textbf{q}^n - \phi \nabla ^2 p^{n+1} = 0, \end{aligned}$$

(32)

$$\begin{aligned}{} & {} \dfrac{\textbf{u}^{n+1} - \textbf{u}^n}{\Delta t} = -\textbf{c}^n \cdot \nabla \textbf{u}^n - \nabla p^{n+1} + \nabla p^n - \nabla p^n + \frac{1}{Re}\nabla ^2 \textbf{u}^n. \end{aligned}$$

(33)

Following the CBS procedure, the main steps of the stabilized CBS(B) scheme are thus finalized as follows

• Step 1: Velocity prediction

  $$\begin{aligned} \dfrac{\textbf{v} - \textbf{u}^n}{\Delta t} = -\textbf{c}^n \cdot \nabla \textbf{u}^n - \nabla p^n + \frac{1}{Re} \nabla ^2 \textbf{u}^n + \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla (\textbf{c}^n \cdot \nabla \textbf{u}^n + \nabla p^n), \end{aligned}$$

  (34)

• Step 2: Pressure update

  $$\begin{aligned} \nabla ^2 p^{n+1} = \dfrac{1}{\Delta t + \phi } \left( \nabla \cdot \textbf{v} + \Delta t \nabla ^2 p^n + \phi \nabla \cdot \textbf{q}^n \right) , \end{aligned}$$

  (35)

• Step 3: Velocity correction

  $$\begin{aligned} \dfrac{\textbf{u}^{n+1} - \textbf{v}}{\Delta t} = \nabla (p^{n+1} - p^n) - \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla ^2 (p^{n+1} - p^n), \end{aligned}$$

  (36)

• Step 4: Auxiliary variable

  $$\begin{aligned} \textbf{q}^{n+1} = \nabla p^{n+1}. \end{aligned}$$

  (37)

3 Structural Motions

We assume that, an immersed structure seizes a continuous domain $\Omega _\textrm{s} \subset \mathbb {R}^2$ and it owns the isotropic material properties. The structural kinematics is expressed under the purely Lagrangian description.

3.1 Rigid-Body Dynamics

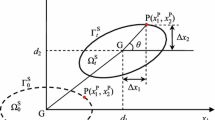
Without loss of generality, an elastically mounted rigid body is free to undergo translation and rotation in Fig. 1. The flow–body system can be modeled as a spring-damper-mass mechanism where each degree of freedom (DOF) is uncoupled from the others. The structural dynamics equation governing the planar rigid-body motion reads

$$\begin{aligned} \begin{bmatrix} m_1 &{} &{} \\ &{} m_2 &{} \\ &{} &{} m_\theta \end{bmatrix} \ddot{\textbf{d}} + \begin{bmatrix} c_1 &{} &{} \\ &{} c_2 &{} \\ &{} &{} c_\theta \end{bmatrix} \dot{\textbf{d}} + \begin{bmatrix} k_1 &{} &{} \\ &{} k_2 &{} \\ &{} &{} k_\theta \end{bmatrix} \textbf{d} = \textbf{R}, \end{aligned}$$

(38)

where $\textbf{d} = \{ d_1, \ d_2, \ \theta \}^\textrm{T}$ is the displacement of the body, $d_1$, $d_2$ and $\theta$ are the horizontal, vertical and rotational components prescribed at the center of gravity G, the dot indicates a time derivative in Newton’s notation, $m_i$, $c_i$ and $k_i$ ($i = 1, \ 2 \ \text {and} \ \theta$) are the mass, damping and stiffness of the body, respectively, and $\textbf{R} = \{ F_\textrm{d}, \ F_\textrm{l}, \ F_\textrm{m} \}^\textrm{T}$ is the applied fluid forces whose components are the drag, lift and pitching moment. In the case of torsional motion, the compatibility condition [67] must be respected to relate those variables defined on a surface point P and DOFs defined at G.

Fig. 1

Schematic view of the planar rigid-body motion

To non-dimensionalize Eq. (38), we define the non-dimensional scales

$$\begin{aligned} \begin{aligned}&\textbf{x}^* = \frac{\textbf{x}}{L}, \ t^* = \frac{tU_\infty }{L}, \ d_1^* = \frac{d_1}{L}, \ d_2^* = \frac{d_2}{L}, \\ & m_1^* = \frac{m_1}{\rho _\textrm{f} L^2}, \ m_2^* = \frac{m_2}{\rho _\textrm{f} L^2}, \ m_\theta ^* = \frac{m_\theta }{\rho _\textrm{f} L^4}, \\ & C_\textrm{d} = \frac{2F_\textrm{d}}{\rho _\textrm{f} U_\infty ^2 L}, \ C_\textrm{l} = \frac{2F_\textrm{l}}{\rho _\textrm{f} U_\infty ^2 L}, \ C_\textrm{m} = \frac{2F_\textrm{m}}{\rho _\textrm{f} U_\infty ^2 L^2}, \end{aligned} \end{aligned}$$

(39)

and the reduced parameters

$$\begin{aligned} \xi _1 = {} & \frac{c_1}{2 \sqrt{m_1 k_1}}, \ \xi _2 = \frac{c_2}{2 \sqrt{m_2 k_2}}, \ \xi _\theta = \frac{c_\theta }{2 \sqrt{m_\theta k_\theta }}, \nonumber \\ f_\textrm{r1} = {} & \frac{f_\textrm{n1} L}{U_\infty }, \ f_\textrm{r2} = \frac{f_\textrm{n2} L}{U_\infty }, \ f_{\textrm{r}\theta } = \frac{f_{\textrm{n}\theta } L}{U_\infty }, \end{aligned}$$

(40)

where $C_\textrm{d}$, $C_\textrm{l}$ and $C_\textrm{m}$ are the drag, lift and moment coefficients, respectively, $m^*_i$ the mass ratio, $\xi _i$ the damping ratio, $f_{\textrm{r}i}$ the reduced natural frequency and the natural frequency $f_{\textrm{n}i} = \frac{1}{2\pi } \sqrt{ k_i / m_i }$. Introducing these variables to Eq. (38), we may write the non-dimensional governing equation of the rigid-body motion as follow

$$\begin{aligned}{} & {} \ddot{\textbf{d}} + 4\pi \begin{bmatrix} f_\textrm{r1} \xi _1 &{} &{} \\ &{} f_\textrm{r2} \xi _2 &{} \\ &{} &{} f_\mathrm {r \theta } \xi _\theta \end{bmatrix} \dot{\textbf{d}} + 4\pi ^2 \begin{bmatrix} f_\textrm{r1}^2 &{} &{} \\ &{} f_\textrm{r2}^2 &{} \\ &{} &{} f_\mathrm {r \theta }^2 \end{bmatrix} \textbf{d} \nonumber \\{} & {} \quad = \frac{1}{2} \begin{Bmatrix} \dfrac{C_\textrm{d}}{m^*_1} \\ \dfrac{C_\textrm{l}}{m^*_2} \\ \dfrac{C_\textrm{m}}{m^*_\theta } \end{Bmatrix}, \end{aligned}$$

(41)

which retains the asterisk to identify the mass ratio.

3.2 Non-linear Elastodynamics

The conservation of linear momentum of an elastic solid may be formulated in the absence of structural damping as follow

$$\begin{aligned} \rho _\textrm{s} \left( \ddot{\textbf{d}} - \textbf{g} \right) - \nabla \cdot \varvec{\sigma }_\textrm{s} = \textbf{0} \quad \text {on} \quad \Omega _\textrm{s} \times (0, \ t_\infty ), \end{aligned}$$

(42)

where $\rho _\textrm{s}$ is the structural density, $\textbf{d} = \{ d_1, \ d_2 \}^\textrm{T}$ and $\varvec{\sigma }_\textrm{s}$ the Cauchy stress. We may translate the stress tensor via the geometric transformation

$$\begin{aligned} \varvec{\sigma }_\textrm{s} = \frac{1}{J} \textbf{F} \textbf{S} \textbf{F}^\textrm{T}, \end{aligned}$$

(43)

where $\textbf{F}$ is the deformation gradient, $J = \textrm{det} (\textbf{F})$ the Jacobian and $\textbf{S}$ the second Piola–Kirchhoff stress. The stress-strain relation is given by assuming a Saint Venant–Kirchhoff material as follow

$$\begin{aligned} \textbf{S} = \textbf{D} : \textbf{E} \quad \text {and} \quad \textbf{E} = \frac{1}{2}(\textbf{F}^\textrm{T} \textbf{F} - \mathbb {I}), \end{aligned}$$

(44)

where $\textbf{D}$ is the elastic constitutive matrix and $\textbf{E}$ the Green–Lagrange strain. Besides, Young’s modulus E, Poisson’s ratio $\nu$, and proper boundary and initial conditions need to be supplied for the elastodynamics problem.

Similarly, the following non-dimensional scales

$$\begin{aligned} \textbf{x}^* = {} & \frac{\textbf{x}}{L}, \ t^* = \frac{t U_\infty }{L}, \ \textbf{d}^* = \frac{\textbf{d}}{L}, \ E^*= \frac{E}{\rho _\textrm{f} U^2_\infty }, \nonumber \\ \textbf{g}^* = {} & \frac{\textbf{g} L}{U^2_\infty }, \ m^* = \frac{\rho _\textrm{s}}{\rho _\textrm{f}}, \end{aligned}$$

(45)

are defined to non-dimensionalize Eq. (42) as

$$\begin{aligned} m^*\left( \ddot{\textbf{d}} - \textbf{g} \right) - \nabla \cdot \varvec{\sigma }_\textrm{s} = \textbf{0}. \end{aligned}$$

(46)

Depending on the inherent non-linearity of the solid system, it is imperative to linearize Eq. (46) via the modified Newton–Raphson procedure under the total Lagrangian description [68] in association with a proper time marching scheme.

3.3 Time Marching

Step-by-step time integration algorithms have been easily accessible to structural dynamics equations for years. Two of them are the well-known Newmark-$\beta$ and generalized-$\alpha$ methods [69, 70]. The Newmark approximations to the structural unknowns are given by

$$\begin{aligned} \dot{\textbf{d}}^{n+1} = \dot{\textbf{d}}^n + \Delta t ((1 - \gamma )\ddot{\textbf{d}}^n + \gamma \ddot{\textbf{d}}^{n+1} ), \end{aligned}$$

(47)

$$\begin{aligned} \textbf{d}^{n+1} = \textbf{d}^n + \Delta t \dot{\textbf{d}}^n + (\Delta t)^2 \left( \left( \frac{1}{2} - \beta \right) \ddot{\textbf{d}}^n + \beta \ddot{\textbf{d}}^{n+1} \right) , \end{aligned}$$

(48)

where $\gamma \geqslant \frac{1}{2}$ and $\beta \geqslant \frac{1}{4}$ are the two Newmark parameters. By contrast, the structural unknowns being temporally discretized at the generalized midpoints are derived from

$$\begin{aligned} \ddot{\textbf{d}}^{n+1-\alpha _\textrm{m}} = {} & \dfrac{1 - \alpha _\textrm{m}}{\beta (\Delta t)^2}(\textbf{d}^{n+1} - \textbf{d}^n) - \dfrac{1 - \alpha _\textrm{m}}{\beta \Delta t}\dot{\textbf{d}}^n\nonumber \\{} & {} - \dfrac{1 - \alpha _\textrm{m} - 2\beta }{2\beta }\ddot{\textbf{d}}^n, \end{aligned}$$

(49)

$$\begin{aligned} \dot{\textbf{d}}^{n+1-\alpha _\textrm{f}} = {} & \dfrac{(1 - \alpha _\textrm{f})\gamma }{\beta \Delta t}(\textbf{d}^{n+1} - \textbf{d}^n) - \dfrac{(1 - \alpha _\textrm{f})\gamma - \beta }{\beta }\dot{\textbf{d}}^n\nonumber \\{} & {} - \dfrac{(\gamma - 2\beta )(1 - \alpha _\textrm{f})}{2\beta }\Delta t \ddot{\textbf{d}}^n, \end{aligned}$$

(50)

where the control parameters are determined by the spectral radius $\rho _\infty \in [ 0, \ 1 ]$

$$\begin{aligned} & \beta = \frac{1}{4} (1 - \alpha _\textrm{m} + \alpha _\textrm{f})^2, \ \gamma = \frac{1}{2} - \alpha _\textrm{m} + \alpha _\textrm{f}, \nonumber \\ & \alpha _\textrm{m} = \dfrac{2\rho _\infty - 1}{\rho _\infty + 1}, \ \alpha _\textrm{f} = \dfrac{\rho _\infty }{\rho _\infty + 1}. \end{aligned}$$

(51)

Furthermore, the internal force of the elastic solid discretized at the general midpoint $n+1-\alpha _\textrm{f}$ is approximated in accordance with the suggestion of Kuhl and Crisfield [71].

4 Interface Conditions

4.1 Traditional Interface Conditions

The interplay between the fluid flow and structural movement is accomplished by enforcing the velocity continuity and stress equilibrium on the interface

$$\begin{aligned} \textbf{u} = \dot{\textbf{d}} \quad \text {and} \quad \textbf{t}_\textrm{f} = \textbf{t}_\textrm{s} \quad \text {on} \quad \Sigma , \end{aligned}$$

(52)

where $\textbf{t}_\textrm{f} = \varvec{\sigma }_\textrm{f} \textbf{n}_\textrm{s}$ and $\textbf{t}_\textrm{s} = \varvec{\sigma }_\textrm{s} \textbf{n}_\textrm{s}$ denote the fluid and structural tractions, respectively, $\textbf{n}_\textrm{s}$ represents the unit outward normal of the interface $\Sigma$ pointing from the structure to the fluid and $\textbf{n}_\textrm{f} = -\textbf{n}_\textrm{s}$. Besides, the geometric continuity should be satisfied due to the instantaneous mesh motion

$$\begin{aligned} \textbf{x} = \textbf{d} \quad \text {and} \quad \textbf{u}_\textrm{m} = \dot{\textbf{d}} \quad \text {on} \quad \Sigma . \end{aligned}$$

(53)

As the external force acting on a vibrating rigid body by the surrounding fluid is a concentrated load vector, the stress equilibrium on $\Sigma$ is rewritten as

$$\begin{aligned} \int \nolimits _{\Sigma } \textbf{t}_\textrm{f} \textrm{d}\Gamma = \int \nolimits _{\Sigma } \textbf{t}_\textrm{s} \textrm{d}\Gamma \quad \text {and} \quad \int \nolimits _{\Sigma } \Delta \textbf{x} \times \textbf{t}_\textrm{f} \textrm{d}\Gamma = \int \nolimits _{\Sigma } \Delta \textbf{x} \times \textbf{t}_\textrm{s} \textrm{d}\Gamma , \end{aligned}$$

(54)

where $\Delta \textbf{x} = \{ \Delta x_1, \ \Delta x_2 \}^\textrm{T}$ is the distance between a surface point and the center of gravity (refer to Fig. 1).

4.2 Modified Interface Conditions

The conventional interface conditions may be corrected by the MCIBC method [38] in the semi-implicitly staggered manner. To this end, the interface conditions after time discretization may be modified as

$$\begin{aligned} \textbf{t}_\textrm{s}^{n+1}= \, & {} \textbf{t}_\textrm{f}^{n+1} + \delta \textbf{t}^n, \end{aligned}$$

(55a)

$$\begin{aligned} \textbf{u}_\Sigma ^{n+1}= \, & {} \dot{\textbf{d}}_\Sigma ^{n+1} + \delta \textbf{u}^{n+1}, \end{aligned}$$

(55b)

where $\delta \textbf{t}$ and $\delta \textbf{u}$ indicate, respectively, the MCIBC corrections to the velocity and traction on $\Sigma$. As for the rigid-body rotation, the applied moment is implicitly corrected via

$$\begin{aligned} \int \nolimits _{\Sigma } \Delta \textbf{x} \times \textbf{t}_\textrm{s} \textrm{d}\Gamma {} & {} = \int \nolimits _{\Sigma } \Delta \textbf{x} \times ( \textbf{t}_\textrm{f} + \delta \textbf{t} ) \textrm{d}\Gamma \nonumber \\{} & {} = \int \nolimits _{\Sigma } \Delta \textbf{x} \times \textbf{t}_\textrm{f} \textrm{d}\Gamma + \int \nolimits _{\Sigma } \Delta \textbf{x} \times \delta \textbf{t} \textrm{d}\Gamma . \end{aligned}$$

(56)

The MCIBC method acts through a small positive coupling parameter that provides a suitable acceleration-traction joint to ensure the stable interfacial energy. As the two increments added into Eq. (55) vary in form, the interested reader is referred to the review article [38] for more details.

5 Mesh Deformation

5.1 Two-Level Mesh Updating Approach

Since the mesh motion cannot be prescribed a priori in transient FSI, a cost-effective mesh updating method is employed to capture the moving interface and rearrange dynamic grids. This method marries the moving submesh approach (MSA) [72] with the ortho-semi-torsional spring analogy method (OST-SAM) [73]. The basic procedure of the two-level mesh updating technique is written below

• the OST springs assimilate a layer of coarse T3 submesh (i.e. the background mesh) to the structural movements;

• the MSA creates a mapping between the submesh and the deforming fluid mesh via area coefficients (i.e. the shape functions of T3 element).

When interior points arise in a submesh, the quasi-static equilibrium equations of the small-scale pseudo-structural system are iterated with a simple successive over-relaxation algorithm [74]. It is reported that the present method can save much more time consumption on mesh updating than the OST-SAM [39].

We would also like to mention that, the matching meshes are deployed on both sides of the interface such that the coupling conditions and mesh deformation are directly handled in the node-to-node fashion.

5.2 Enforcing GCL

The GCL states that any ALE computation should preserve the trivial solution of a uniform flow on a moving mesh [29, 75]. Sometimes we find it helpful to stabilize the time integrator of a fluid solver implemented on a moving mesh. It is nontrivial to enforce this constraint in a fractional-step fluid solver, however. Here, the MST [6] is introduced into the second step of the semi-implicit CBS(A) scheme on the element-by-element basis [34]

$$\begin{aligned} \nabla ^2 p^{n+1} = \frac{1}{\Delta t} \nabla \cdot \textbf{v} + Q^{n+1}_e, \end{aligned}$$

(57)

together with

$$\begin{aligned} Q^{n+1}_e = {} & \frac{1}{2 \bar{A}^{n+1}_e} \begin{vmatrix} w^2_1 - w^1_1&w^2_2 - w^1_2 \\ w^3_1 - w^1_1&w^3_2 - w^1_2 \end{vmatrix}^{n+1}_e \quad \text {and} \nonumber \\ \textbf{w}^{n+1}_e= {} & \frac{\textbf{x}^{n+1}_e - \textbf{x}^n_e}{\Delta t}, \end{aligned}$$

(58)

where $Q_e$ denotes the MST of Element e, $\bar{A}_e$ is the element’s area, $\textbf{w}_e$ is the mesh velocity, the superscripts in w indicate the local numbering of nodes, the subscripts in w represent the axes of a Cartesian coordinate system, and $\textbf{x}_e$ means the coordinates of the element.

6 Smoothed Finite-Element Discretization

The SFEM [51, 76] offers a new paradigm for FEM modeling with a number of advantages. Since the CSFEM and ESFEM have been proved exceptionally flexible in smoothed Galerkin weak-form integral [54, 59], the ease with which we use them for spatial discretization of both fluid and solid fields is astonishing. To be specific, the coordinates of an integration point can be arbitrarily placed in an SC. It is stressed that, the presented proofs are mathematically universal, considering the constant smoothing kernel. Importantly, the rest models, such as the node-based and face-based SFEMs [77, 78], can be readily proved to enjoy the same flexibility of smoothed Galerkin weak-form integral. In addition to those flow/transport problems [79,80,81,82], the outreach of the SFEM towards a broader range of realistic phenomena grows increasingly visible.

6.1 Gradient Smoothing

Let $\widetilde{\Omega } \subset \mathbb {R}^2$ be a continuous and smoothed SC bounded by $\widetilde{\Gamma }$, as is depicted in Fig. 2. We define in $\widetilde{\Omega }$ a scalar-valued function f at $\textbf{x}_\textrm{c}$ for simplicity. According to Liu et al. [50], the smoothed gradient of f at the point of interest may be structured as

$$\begin{aligned} \widetilde{\nabla } f(\textbf{x}_\textrm{c}) = \int \nolimits _{\widetilde{\Omega }} \nabla f(\textbf{x}) W(\textbf{x} - \textbf{x}_\textrm{c}) \, \textrm{d}\Omega , \quad \forall \ \textbf{x}_\textrm{c} \in \widetilde{\Omega }, \end{aligned}$$

(59)

where $\widetilde{\nabla }$ is the smoothed gradient operator and W is the smoothing kernel. Given the SC’s area $A_\textrm{c}$, W may take the form of Heaviside function [50, 52]

$$\begin{aligned} W(\textbf{x} - \textbf{x}_\textrm{c}) = {\left\{ \begin{array}{ll} \dfrac{1}{A_\textrm{c}}, &{} \textbf{x} \in \widetilde{\Omega }, \\ 0, &{} \textbf{x} \notin \widetilde{\Omega }, \end{array}\right. } \end{aligned}$$

(60)

which indeed meets the positivity and unity requirements [83].

Fig. 2

Sketch of a generic SC

Applying integration by parts into the right-hand side of Eq. (59) and after some arithmetic operations, we can get

$$\begin{aligned} \widetilde{\nabla } f(\textbf{x}_\textrm{c}) = \frac{1}{A_\textrm{c}} \int \nolimits _{\widetilde{\Gamma }} f(\textbf{x}) \textbf{n} (\textbf{x}) \, \textrm{d}\Gamma , \end{aligned}$$

(61)

where $\textbf{n}$ is the unit outward normal to $\widetilde{\Gamma }$. Eq. (61) is readily transformed into its algebraic form

$$\begin{aligned} \widetilde{\nabla } f(\textbf{x}_\textrm{c}) = \frac{1}{A_\textrm{c}} \sum _{i=1}^{n_\textrm{l}} f(\textbf{x}^\textrm{m}_i) \textbf{n}(\textbf{x}^\textrm{m}_i) l_i, \end{aligned}$$

(62)

where $n_\textrm{l}$ means the number of segments that make up $\widetilde{\Gamma }$, $\textbf{x}^\textrm{m}_i$ represents the coordinates of the midpoint on the i-th segment $\widetilde{\Gamma }_i$ and $l_i$ is the length of $\widetilde{\Gamma }_i$.

6.2 Numerical Integration

In the finite-element approximation procedure, a computational domain $\Omega$ is typically discretized into $n_\textrm{e}$ elements such that $\Omega = \overline{\Omega }_1 \cup \overline{\Omega }_2 \cup \cdots \cup \overline{\Omega }_{n_\textrm{e}}$ and $\overline{\Omega }_i \cap \overline{\Omega }_j = \varnothing$ where $1 \leqslant i, j \leqslant n_\textrm{e}$ and $i \ne j$. For the SFEM, we further establish a group of non-overlapping and non-gap SCs instead of traditional elements. The alternative mesh generation is thus represented by $\Omega = \widetilde{\Omega }_1 \cup \widetilde{\Omega }_2 \cup \cdots \cup \widetilde{\Omega }_{n_\textrm{g}}$ and $\widetilde{\Omega }_i \cap \widetilde{\Omega }_j = \varnothing \ (1 \leqslant i, j \leqslant n_\textrm{g} \ \text {and} \ i \ne j)$ where $n_\textrm{g}$ is the total number of the SCs. The integration rule of the SFEM is explicitly explicated on an SC-by-SC basis

$$\begin{aligned} \int \nolimits _{\Omega } f(\textbf{x}) \, \textrm{d}\Omega = \sum _{i=1}^{n_\textrm{g}} \int \nolimits _{\widetilde{\Omega }_i} f( \textbf{x} ) \, \textrm{d}\Omega = \sum _{i=1}^{n_\textrm{g}} f(\textbf{x}_\textrm{c}) A_i, \quad \textbf{x}_\textrm{c} \in \widetilde{\Omega }_i, \end{aligned}$$

(63)

which is free from the isoparametric mapping between the Cartesian and natural coordinates and also maintains some mesh-free properties in association with the above gradient smoothing treatment [54, 84, 85].

6.3 SC Configuration and Shape Functions

In general, there is a wide range of possibilities that we can deploy different SCs in a discrete domain, provided that the arrangement satisfies the stability condition of the resultant smoothed Galerkin weak-form integral [51]. Since the SCs are all constructed on a given finite-element mesh, extra DOFs have never been brought into the original discretized system. Here the CSFEM and ESFEM are taken into account based on Q4 and T3 elements, respectively. A brief interpretation on SC configurations and shape functions of the two different stencils shall be given below.

Fig. 3

Configuration of SCs and values of shape functions

In the CSFEM, each Q4 element is usually subdivided into four SCs by connecting the midpoints of a pair of opposite sides of the quadrangle. Such an SC partition can reach an excellent balance between the accuracy and efficiency. As plotted in Fig. 3 (a), five dummy nodes are generated to compute the shape functions by simply averaging those values at four corners. Fig. 3 (b) shows a mesh of T3 elements which are represented by the colored triangles. An SC is constructed by connecting the two endpoints of an edge with the center(s) of adjacent T3 element(s) of the edge. The assembly of two neighboring triangles of an interior edge produces a quadrilateral SC. By contrast, a triangular SC stems from the element attached to an segment of the boundaries. Both types of the edge-based SCs are displayed in Fig. 3 (b). To facilitate the weak-form computation, the shape functions are intentionally calculated at the centroids of interior and boundary SCs as follows

$$\begin{aligned} \textbf{N} = {\left\{ \begin{array}{ll} \left\{ \frac{1}{4}, \ \frac{1}{4}, \ \frac{1}{4}, \ \frac{1}{4} \right\} &{} \texttt {for \, interior \, SCs}, \\ \left\{ \frac{1}{3}, \ \frac{1}{3}, \ \frac{1}{3} \right\} &{} \texttt {for \, boundary \, SCs}. \end{array}\right. } \end{aligned}$$

(64)

6.4 Smoothed Interface Conditions

The stress equilibrium on $\Sigma$ can also be formulated through a smoothed finite-element representation [86]. The fluid traction passed on to the immersed structure can be numerically derived from the cell-based or edge-based gradient smoothing concept. In Fig. 4 (a), either of the two SCs next to the interface is available for the fluidic excitation computation thanks to the constant strain in the bilinear Q4 element. Fig. 4 (b) illustrates a diagram of the triangular SCs sticking to the interface. Below is the weak-form formulation of smoothed fluid forces $\widetilde{\textbf{R}}$ acting on rigid and elastic bodies all over the boundary SCs

$$\begin{aligned}{} & {} \begin{aligned} \begin{bmatrix} 2 m^*_1 &{} \\ &{} 2 m^*_2 \\ \end{bmatrix} \widetilde{\textbf{R}}&= \int \nolimits _{\Sigma } \widetilde{\textbf{t}}_\textrm{f} \, \textrm{d}\Gamma \\&= \int \nolimits _{\Sigma } \left( -p \mathbb {I} + \frac{1}{Re} \left( \widetilde{\nabla } \textbf{u} + (\widetilde{\nabla } \textbf{u})^\textrm{T} \right) \right) \textbf{n}_{\Sigma _\textrm{s}} \, \textrm{d}\Gamma \\&= \sum _{i=1}^{n_\textrm{fs}} \left( -p(\textbf{x}^\textrm{m}_i) \mathbb {I} + \frac{1}{Re} \left( \widetilde{\nabla } \textbf{u} (\textbf{x}^\textrm{m}_i) + (\widetilde{\nabla } \textbf{u} (\textbf{x}^\textrm{m}_i))^\textrm{T} \right) \right) \textbf{n}_{\Sigma _\textrm{s}} (\textbf{x}^\textrm{m}_i) l_i, \end{aligned} \end{aligned}$$

(65a)

$$\begin{aligned}{} & {} \begin{aligned} \widetilde{\textbf{R}}&= \int \nolimits _{\Sigma } \textbf{N}^\textrm{T} \widetilde{\textbf{t}}_\textrm{f} \, \textrm{d}\Gamma \\&= \int \nolimits _{\Sigma } \textbf{N}^\textrm{T} \left( -p \mathbb {I} + \frac{1}{Re} \left( \widetilde{\nabla } \textbf{u} + (\widetilde{\nabla } \textbf{u})^\textrm{T} \right) \right) \textbf{n}_{\Sigma _\textrm{s}} \, \textrm{d}\Gamma \\&= \sum _{i=1}^{n_\textrm{fs}} \textbf{N}^\textrm{T} (\textbf{x}^\textrm{m}_i) \left( -p(\textbf{x}^\textrm{m}_i) \mathbb {I} + \frac{1}{Re} \left( \widetilde{\nabla } \textbf{u} (\textbf{x}^\textrm{m}_i) \right. \right. \\&\quad \left. \left. + (\widetilde{\nabla } \textbf{u} (\textbf{x}^\textrm{m}_i))^\textrm{T} \right) \right) \textbf{n}_{\Sigma _\textrm{s}} (\textbf{x}^\textrm{m}_i) l_i, \end{aligned} \end{aligned}$$

(65b)

where $\Sigma _\textrm{s}$ refers to the dry interface and $n_\textrm{fs}$ defines the number of constituent segments of $\Sigma$. Moreover, it is trivial to calculate the smoothed fluid moment and viscoelastic traction from the gradient smoothing notion.

Fig. 4

Evaluation of fluidic excitation on the interface

7 Conceptual Frameworks of Semi-implicit Algorithms

The fluid–structure coupled problem embraces a set of nonlinear algebraic equations to be solved at each time step. After addressing all the ingredients in previous sections, the present section is intended as a detailed introduction to a variety of the CBS-$\Psi$ coupling methods for computational FSI solution. The resulting algorithmic implementation contains substantial improvements and numerical techniques introduced subsequently. The subiterations per time step are under-relaxed by a predefined constant factor for the sake of simplicity; however, any dynamic relaxation scheme [87, 88] can be utilized to accelerate the convergence rate. The spatial discretization scheme can have access to either the standard FEM or an SFEM. In what follows, a detailed account of different CBS-based partitioned semi-implicit coupling algorithms will be given.

7.1 Basic CBS(A)-$\Psi$ Coupling Algorithm

Following the projection-based partitioned semi-implicit coupling procedure [12], the basic CBS(A)-$\Psi$ coupling algorithm is written in the following steps

• Step 1: Initialize field variables and set the iteration count $k = 0$

• Step 2: Perform the explicit coupling step

  • 2.1: Extrapolate the position of the interface

    $$\begin{aligned} \bar{\textbf{d}}^{n+1(k)}_\Sigma = \textbf{d}^{n}_\Sigma + \left( \frac{3}{2} \dot{\textbf{d}}^{n}_\Sigma - \frac{1}{2} \dot{\textbf{d}}^{n-1}_\Sigma \right) \Delta t, \end{aligned}$$

    (66)

  • 2.2: Move the dynamic fluid mesh

  • 2.3: Gain the mesh velocity and geometric quantities

    $$\begin{aligned} \textbf{w}^{n+1} = \dfrac{\bar{\textbf{d}}^{n+1(k)} - \textbf{d}^n}{\Delta t}, \end{aligned}$$

    (67)

  • 2.4: Compute the intermediate velocity

    $$\begin{aligned} \dfrac{\textbf{v} - \textbf{u}^n}{\Delta t}= & {} -\textbf{c}^n \cdot \nabla \textbf{u}^n + \frac{1}{Re} \nabla ^2 \textbf{u}^n \nonumber \\{} & {} + \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla (\textbf{c}^n \cdot \nabla \textbf{u}^n), \end{aligned}$$

    (68)

• Step 3: Perform the implicit coupling step

  • 3.1: Start fixed-point iterations and set $k \leftarrow k + 1$

  • 3.2: Update the pressure

    $$\begin{aligned} \nabla ^2 p^{n+1(k)} = \dfrac{1}{\Delta t} \nabla \cdot \textbf{v}, \end{aligned}$$

    (69)

  • 3.3: Correct the velocity

    $$\begin{aligned} \dfrac{\textbf{u}^{n+1(k)} - \textbf{v}}{\Delta t} = \nabla p^{n+1(k)} - \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla ^2 p^n, \end{aligned}$$

    (70)

  • 3.4: Solve the structural dynamics equation

  • 3.5: Obtain the interfacial residuals

  • 3.6: Check the convergence: if not convergent, then go ahead; otherwise, proceed to the next time step

  • 3.7: Relax the interface

    $$\begin{aligned} \bar{\textbf{d}}^{n+1(k)}_\Sigma = \omega \textbf{d}^{n+1(k)}_\Sigma + (1 - \omega ) \bar{\textbf{d}}^{n+1(k-1)}_\Sigma , \end{aligned}$$

    (71)

  • 3.8: Calculate the mesh velocity on $\Sigma$ as new boundary condition

  • 3.9: Return

where the applied fluid forces are evaluated in terms of the corrected velocity and $\omega$ is the relaxation factor. One may notice that, the PPE is actually excluded from the implicit stage unless a monolithic coupling method is adopted to resolve the interface system. This reality is identical to the procedure of Fernández et al. [12], as mentioned before. It is necessary to include the PPE inside iterative loops for boosting the numerical stability of the entire coupling algorithm. Some measures to strengthen the implicit phase will be presented subsequently to reach a truly semi-implicitly staggered coupling style.

7.2 Enhanced CBS(A)-$\Psi$ Coupling Algorithms

For obvious reasons, the MST is introduced to the PPE within the CBS-based coupling framework as a default configuration in several numerical studies [37, 49]. In addition, the CBS(A)-$\Psi$ coupling algorithm can employ the MCIBC method [30,31,32] to impose the interface conditions. After being equipped with these techniques, the main steps of the enhanced CBS(A)-$\Psi$ coupling algorithm are given as

• Step 1: Initialize field variables and set $k = 0$

• Step 2: Perform the explicit coupling step

  • 2.1: Extrapolate the position of the interface

  • 2.2: Move the dynamic fluid mesh

  • 2.3: Gain the mesh velocity and geometric quantities

  • 2.4: Compute the MST in the specified zone that moves

    $$\begin{aligned} Q^{n+1(k)}_e = \frac{1}{2 \bar{A}^{n+1}_e} \begin{vmatrix} w^2_1 - w^1_1&w^2_2 - w^1_2 \\ w^3_1 - w^1_1&w^3_2 - w^1_2 \end{vmatrix}^{n+1(k)}_e, \end{aligned}$$

    (72)

  • 2.5: Compute the intermediate velocity (see Eq. (68))

• Step 3: Perform the implicit coupling step

  • 3.1: Start fixed-point iterations and set $k \leftarrow k + 1$

  • 3.2: Update the pressure

    $$\begin{aligned} \nabla ^2 p^{n+1(k)} = \dfrac{1}{\Delta t} \nabla \cdot \textbf{v} + Q^{n+1(k-1)}_e, \end{aligned}$$

    (73)

  • 3.3: Correct the velocity (see Eq. (70))

  • 3.4: Apply the MCIBC correction to the structural traction (optional)

    $$\begin{aligned} \textbf{t}_\textrm{s}^{n+1(k)} = \textbf{t}_\textrm{f}^{n+1(k)} + \delta \textbf{t}^n, \end{aligned}$$

    (74)

  • 3.5: Solve the structural dynamics equation

  • 3.6: Apply the MCIBC correction to the fluid velocity (optional)

    $$\begin{aligned} \textbf{u}_\Sigma ^{n+1(k)} = \dot{\textbf{d}}_\Sigma ^{n+1(k)} + \delta \textbf{u}^{n+1(k)}, \end{aligned}$$

    (75)

  • 3.7: Obtain the interfacial residuals

  • 3.8: Check the convergence: if not convergent, then go ahead; otherwise, proceed to the next time step

  • 3.9: Relax the interface

  • 3.10: Calculate the mesh velocity on $\Sigma$ as new boundary condition

  • 3.11: Renew the MST for interface elements

  • 3.12: Return.

It is observed that the MST is continuously calculated during the implicit stage for those elements sticking to the interface so that the PPE stays inside the iterative loops all the time [31]. Hence, the update of the MST is viewed as not only the enhanced necessity to iterate the field unknowns at each time step but also the key to recovery the genuinely semi-implicit coupling fashion. While only the T3 element is valid for the MST, the resulting algorithmic procedure is quite simple and time-saving. Moreover, the MCIBC formulations may slightly vary on account of different assumptions [30, 31]. For instance, a weak treatment regarding the displacement increment is proposed to prevent the numerical instability caused by the two-sided corrections [31]. A further analysis based on the theory of general inverse matrix reveals that the MCIBC method is freely applicable to the generalized planar rigid-body motion involving both translation and rotation [32]. In summary, the increment corrections for both Dirichlet and Neumann interface conditions fit the MCIBC method perfectly for the CBS(A)-$\Psi$ coupling algorithms. On the other hand, the results gained from vortex-induced vibration (VIV) of a flexible circular cylinder [30] suggest that the dual time stepping initially developed for the CBS scheme [35] is not suitable for use in the current semi-implicit coupling methods.

7.3 Improved CBS(A)-$\Psi$ Coupling Algorithm

The core of this variant rests with introduction of the end-of-step velocity into the implicit coupling phase [48]. Correspondingly, the intermediate velocity serves as the initial guess of the ongoing subiterations where the MST can be dropped from the PPE. An obvious benefit is that the semi-implicit coupling algorithm has unlimited access to different finite elements. Such a simple treatment also boosts the algorithmic performance considerably, as will be demonstrated later. The main steps of the improved CBS(A)-$\Psi$ coupling algorithm are described as follows

• Step 1: Initialize field variables and set $k = 0$

• Step 2: Perform the explicit coupling step

  • 2.1: Extrapolate the position of the interface

  • 2.2: Move the dynamic fluid mesh

  • 2.3: Gain the mesh velocity and geometric quantities

  • 2.4: Compute the intermediate velocity

    $$\begin{aligned}\dfrac{\textbf{u}^{n+1(k)} - \textbf{u}^n}{\Delta t} = & {} -\textbf{c}^n \cdot \nabla \textbf{u}^n + \frac{1}{Re} \nabla ^2 \textbf{u}^n\nonumber \\ & {} + \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla (\textbf{c}^n \cdot \nabla \textbf{u}^n), \end{aligned}$$

    (76)

• Step 3: Perform the implicit coupling step

  • 3.1: Start fixed-point iterations and set $k \leftarrow k + 1$

  • 3.2: Update the pressure

    $$\begin{aligned} \nabla ^2 p^{n+1(k)} = \dfrac{1}{\Delta t} \nabla \cdot \textbf{u}^{n+1(k-1)}, \end{aligned}$$

    (77)

  • 3.3: Correct the velocity

    $$\begin{aligned} \dfrac{\textbf{u}^{n+1(k)} - \textbf{u}^{n+1(k-1)}}{\Delta t} = \nabla p^{n+1(k)} - \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla ^2 p^n, \end{aligned}$$

    (78)

  • 3.4: Solve the structural dynamics equation

  • 3.5: Obtain the interfacial residuals

  • 3.6: Check the convergence: if not convergent, then go ahead; otherwise, proceed to the next time step

  • 3.7: Relax the interface

  • 3.8: Calculate the mesh velocity on $\Sigma$ as new boundary condition

  • 3.9: Return.

The explanation for the better stability behavior of the above algorithm is given as follow. The latest velocity variables are always iterated during the implicit coupling phase, hence resulting in the block-Gauss–Seidel-type iterations of the interface system. Earlier semi-implicit schemes [30,31,32] constantly adopt the velocity variables at last time step for the implicit phase, so they actually experience the block-Jacobi-type iterations by comparison. It is known that the convergence rate of the former can become twice higher than that of the latter under certain conditions [27].

7.4 Improved CBS(B)-$\Psi$ Coupling Algorithm

The CBS(A)-$\Psi$ coupling scheme is found to be inadequate in solving small-mass-ratio problems, despite some success [32]. The stabilized CBS(B)-$\Psi$ coupling algorithm is proposed to account for exceptionally low mass ratios which are of practical interest in many biological and industrial systems. Before proceeding any further, we may write the time-discrete form of Eq. (32) as follow

$$\begin{aligned} \nabla \cdot \textbf{u}^{n+1(k)} + \phi \nabla \cdot \textbf{q}^{n+1(k-1)} - \phi \nabla ^2 p^{n+1(k)} = 0, \end{aligned}$$

(79)

which stabilizes the PPE via the up-to-date auxiliary variable from last subiteration. Using Eq. (79), we can elaborate the procedure of the CBS(B)-$\Psi$ coupling algorithm below

• Step 1: Initialize field variables and set $k = 0$

• Step 2: Perform the explicit coupling step

  • 2.1: Extrapolate the interface

  • 2.2: Move the dynamic fluid mesh

  • 2.3: Gain the mesh velocity and geometric quantities

  • 2.4: Compute the intermediate velocity

    $$\begin{aligned} \dfrac{\textbf{u}^{n+1(k)} - \textbf{u}^n}{\Delta t}= & {} -\textbf{c}^n \cdot \nabla \textbf{u}^n - \nabla p^n + \frac{1}{Re} \nabla ^2 \textbf{u}^n \nonumber \\{} & {} + \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla (\textbf{c}^n \cdot \nabla \textbf{u}^n + \nabla p^n), \end{aligned}$$

    (80)

• Step 3: Perform the implicit coupling step

  • 3.1: Start fixed-point iterations and set $k \leftarrow k + 1$

  • 3.2: Update the pressure

    $$\begin{aligned} \nabla ^2 p^{n+1(k)}= & {} \ \dfrac{1}{\Delta t + \phi } \left( \nabla \cdot \textbf{u}^{n+1(k-1)} \right. \nonumber \\{} & {} \left. + \ \Delta t \nabla ^2 p^n + \phi \nabla \cdot \textbf{q}^{n+1(k-1)} \right) , \end{aligned}$$

    (81)

  • 3.3: Correct the velocity

    $$\begin{aligned} \dfrac{\textbf{u}^{n+1(k)} - \textbf{u}^{n+1(k-1)}}{\Delta t}= & {} \nabla (p^{n+1(k)} - p^n)\nonumber \\{} & {} - \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla ^2 (p^{n+1(k)} - p^n), \end{aligned}$$

    (82)

  • 3.4: Renew the auxiliary variable

    $$\begin{aligned} \textbf{q}^{n+1(k)} = \nabla p^{n+1(k)}, \end{aligned}$$

    (83)

  • 3.5: Solve the structural dynamics equation

  • 3.6: Obtain the interfacial residuals

  • 3.7: Check the convergence: if not convergent, then go ahead; otherwise, proceed to the next time step

  • 3.8: Relax the interface

  • 3.9: Calculate the mesh velocity on $\Sigma$ as new boundary condition

  • 3.10: Return.

Seen from the above steps, the SPGP technique not only stabilizes the CBS(B) scheme, but also alleviates the adverse low-mass-ratio effect [13, 14] for the non-physical semi-implicit coupling style. As a matter of course, the achieved balance between the computational accuracy and numerical stability is essential to diminish the pressure sensitivity along the moving interfaces due to the second-order splitting error in pressure. It is important to note that, even without incorporating any accelerators for fixed-point iterations at the implicit stage, the CBS(A/B)-$\Psi$ coupling algorithm scheme can engender visible improvements versus the previously published data for several benchmarks [48].

7.5 AC-CBS(A)-$\Psi$ Coupling Algorithm

In the PPE-based semi-implicit algorithms, the fluid projection step is fully coupled with the structural movement through the divergence-free constraint. Here, a simple and accurate AC-CBS(A)-$\Psi$ coupling method is proposed based upon an AC method [40] for fast computing of the coupled interface system [39]. The procedure of the AC-based semi-implicit algorithm is particularized below

• Step 1: Initialize field variables and set $k = 0$

• Step 2: Perform the explicit coupling phase

  • 2.1: Extrapolate the position of the interface

  • 2.2: Move the dynamic fluid mesh

  • 2.3: Gain the mesh velocity and geometric quantities

  • 2.4: Compute the intermediate velocity (see Eq. (68))

• Step 3: Perform the implicit coupling phase

  • 3.1: Start fixed-point iterations and set $k \leftarrow k + 1$

  • 3.2: Assess the AC coefficient $a^{n+1(k-1)}$

  • 3.3: Update the fluid pressure

    $$\begin{aligned} \left( \frac{1}{a^2} \right) ^{n+1(k-1)} \dfrac{p^{n+1(k)} - p^n}{\Delta t} = -\nabla \cdot \textbf{v} + \Delta t \nabla ^2 p^n, \end{aligned}$$

    (84)

  • 3.4: Correct the fluid velocity

    $$\begin{aligned} \dfrac{\textbf{u}^{n+1(k)} - \textbf{v}}{\Delta t} = \nabla p^n - \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla ^2 p^{n+1(k)}, \end{aligned}$$

    (85)

  • 3.5: Solve the structural dynamics equation

  • 3.6: Obtain the interfacial residuals

  • 3.7: Check the convergence: if not convergent, then go ahead; otherwise, proceed to the next time step

  • 3.8: Relax the interface

  • 3.9: Calculate the mesh velocity on $\Sigma$ as new boundary condition

  • 3.10: Return.

Since the fully explicit AC-CBS scheme [41] is adopted for the solution of the approximate PPE, the time-discrete form of the fluid correction step slightly varies from its counterpart of the PPE-based scheme. Especially for the fluid–rigid body interaction, the solution procedure of the AC-CBS(A)-$\Psi$ coupling algorithm becomes completely matrix-free when the mass matrices are lumped [39]. The presented algorithm is technically available for any finite elements as it does not necessarily need the MST. The GCL may be still met for a stabilized ALE–FEM formulation where the mid-point rule is applied to the mesh velocity [75]. It is remarked that, triple iterative loops are avoided in the whole coupling scheme as the dual-time stepping recommended for the quasi-incompressible flow has already been incorporated into the implicit coupling stage. Given the AC coefficient iterated during the implicit phase, there is no need to fulfill multiple convergence criteria for different field quantities [89, 90].

7.6 AC-CBS(B)-$\Psi$ Coupling Algorithm

Similar to its PPE-based counterpart, the AC-based algorithm can also achieve the second-order splitting error in pressure. To this end, we modify Eq. (13) with the SPGP technique after temporal discretization

$$\begin{aligned} \left( \frac{1}{a^2} \right) ^n \dfrac{p^{n+1} - p^n}{\Delta t} + \nabla \cdot \textbf{u}^{n+1} + \phi \nabla \cdot \textbf{q}^n - \phi \nabla ^2 p^{n+1} = 0, \end{aligned}$$

(86)

where the end-of-step velocity is not introduced. Then the main procedure of the AC-CBS(B)-$\Psi$ coupling algorithm is interpreted as follow

• Step 1: Initialize field variables and set $k = 0$

• Step 2: Perform the explicit coupling phase

  • 2.1: Extrapolate the position of the interface

  • 2.2: Move the dynamic fluid mesh

  • 2.3: Gain the mesh velocity and geometric quantities

  • 2.4: Compute the intermediate velocity

    $$\begin{aligned}\dfrac{\textbf{v} - \textbf{u}^n}{\Delta t} = & {} -\textbf{c}^n \cdot \nabla \textbf{u}^n - \nabla p^n + \frac{1}{Re} \nabla ^2 \textbf{u}^n \nonumber \\ & {} + \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla (\textbf{c}^n \cdot \nabla \textbf{u}^n + \nabla p^n), \end{aligned}$$

    (87)

• Step 3: Perform the implicit coupling phase

  • 3.1: Start fixed-point iterations and set $k \leftarrow k + 1$

  • 3.2: Assess the AC coefficient $a^{n+1(k-1)}$

  • 3.3: Update the fluid pressure

    $$\begin{aligned}{} & {} \left( \frac{1}{a^2} \right) ^{n+1(k-1)} \dfrac{p^{n+1(k)} - p^n}{\Delta t} \nonumber \\{} & {} \quad = -\nabla \cdot \textbf{v} + \Delta t \nabla ^2 (p^{n+1(k-1)} - p^n)\nonumber \\{} & {} \quad - \phi \nabla \cdot \textbf{q}^{n+1(k-1)} + \phi \nabla ^2 p^{n+1(k-1)}, \end{aligned}$$

    (88)

  • 3.4: Correct the fluid velocity

    $$\begin{aligned} \dfrac{\textbf{u}^{n+1(k)} - \textbf{v}}{\Delta t} = {} & {} \nabla (p^{n+1(k)} - p^n) \nonumber \\ & {} - \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla ^2 (p^{n+1(k)} - p^n), \end{aligned}$$

    (89)

  • 3.5: Evaulate the auxiliary variable

  • 3.6: Solve the structural dynamics equation

  • 3.7: Obtain the interfacial residuals

  • 3.8: Check the convergence: if not convergent, then go ahead; otherwise, proceed to the next time step

  • 3.9: Relax the interface

  • 3.10: Calculate the mesh velocity on $\Sigma$ as new boundary condition

  • 3.11: Return.

In the given steps, the AC coefficient serves a vehicle to exchange information between the explicit and implicit coupling stages. As before, a single convergence criterion is specified herein because the AC dual-time stepping has already been merged with the implicit subiterations per time step. The observed merits of the presented scheme live in: (i) the fractional-step modularity with the second-order splitting error in pressure; (ii) simple mathematical management and matrix-free calculation; and (iii) no limitations on finite elements.

7.7 Stabilized CBS(B)-$\Psi$ Coupling Algorithm

Likewise, the viscoelastic fluid–structure system is partitioned into the explicit and implicit coupling phases to comply with the stabilized CBS(B) scheme. A stabilized CBS(B)-$\Psi$ coupling algorithm is thereby proposed to deal with VFSI based on the CSFEM [55]. Because the Oldroyd-B constitutive equation is more complicated than the Newtonian one, the DEVSS-G/CBS(B)-SPGP stabilization [65] is developed to enhance the stabilities of the seim-implicit coupling algorithm where the stabilized fluid solution is achieved accordingly. Starting from the intermediate velocity, the end-of-step velocity is favorably iterated during the implicit phase as well. Consequently, the main steps of the stabilized CBS(B)-$\Psi$ coupling algorithm are written as follows

• Step 1: Initialize field variables and set $k = 0$

• Step 2: Perform the explicit coupling step

  • 2.1: Extrapolate the position of the interface

  • 2.2: Move the dynamic fluid mesh

  • 2.3: Gain the mesh velocity and geometric quantities

  • 2.4: Calculate the two auxiliary variables

    $$\begin{aligned} \mathbb {G}^n = \nabla \textbf{u}^n \quad \text {and} \quad \textbf{q}^n = \nabla p^n, \end{aligned}$$

    (90)

  • 2.5: Predict the velocity

    $$\begin{aligned} \begin{aligned} \dfrac{\textbf{u}^{n+1(k)} - \textbf{u}^n}{\Delta t} =&-\textbf{c}^n \cdot \nabla \textbf{u}^n - \nabla p^n + \frac{\eta + \theta }{Re} \nabla ^2 \textbf{u}^n \\&- \frac{\theta }{Re}\nabla \cdot \mathbb {G}^n + \frac{1 - \eta }{Re W\!i} \nabla \cdot \mathbb {C}^n \\&+ \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla \left( \textbf{c}^n \cdot \nabla \textbf{u}^n + \nabla p^n \right. \\&\left. + \frac{\theta }{Re}\nabla \cdot \mathbb {G}^n - \frac{1 - \eta }{Re W\!i} \nabla \cdot \mathbb {C}^n \right) , \end{aligned} \end{aligned}$$

    (91)

  • 2.6: Determine the conformation tensor

    $$\begin{aligned} \begin{aligned} \dfrac{\mathbb {C}^{n+1} - \mathbb {C}^n}{\Delta t} = &-\textbf{c}^n \cdot \nabla \mathbb {C}^n + \left( (\nabla \textbf{u})^\textrm{T} \cdot \mathbb {C} + \mathbb {C} \cdot \nabla \textbf{u} \right) ^n \\& - \frac{1}{W\!i} (\mathbb {C}^n - \mathbb {I}) + \frac{\Delta t}{2} \textbf{c}^n \cdot \nabla \left( \textbf{c}^n \cdot \nabla \mathbb {C}^n -\right. \\&\left. \left( (\nabla \textbf{u})^\textrm{T} \cdot \mathbb {C} + \mathbb {C} \cdot \nabla \textbf{u} \right) ^n + \frac{1}{W\!i} (\mathbb {C}^n - \mathbb {I}) \right) , \end{aligned} \end{aligned}$$

    (92)

• Step 3: Perform the implicit coupling step

  • 3.1: Start fixed-point iterations and set $k \leftarrow k + 1$

  • 3.2: Update the pressure

    $$\begin{aligned} \nabla ^2 p^{n+1} = & {} \ \frac{1}{\Delta t + \phi } \left( \nabla \cdot \textbf{u}^{n+1(k-1)} \right. \nonumber \\{} & {} \left. + \ \Delta t \nabla ^2 p^n + \phi \nabla \cdot \textbf{q}^n \right) , \end{aligned}$$

    (93)

  • 3.3: Correct the velocity (see Eq. (82))

  • 3.4: Solve the elastodynamics equation

  • 3.5: Obtain the interfacial residuals

  • 3.6: Check the convergence: if not convergent, then go ahead; otherwise, proceed to the next time step

  • 3.7: Relax the interface

  • 3.8: Compute the mesh velocity on $\Sigma$ as new boundary condition

  • 3.9: Return.

The DEVSS-G/CBS(B)-SPGP stabilization, which is originally proposed for stabilizing the viscoelastic flow [65], is of vital importance in computing VFSI semi-implicitly. Again, it is seen that, even without invoking any accelerators, the simple fixed-point procedure shows very good performance during the subiterations per time step [55].

7.8 GCL-Preserving CBS(B)-$\Psi$ Coupling Algorithm

The present algorithm utilizes both the DEVSS-G/CBS(B)-SPGP stabilizer and the end-of-step velocity for the semi-implicit multi-physical coupling, but its spatial approximation makes use of the ESFEM. As a result of the use of T3 element, the GCL can be preserved through the MST being implanted into the modified PPE in the smoothed-finite-element context. The proposed GCL-preserving semi-implicit algorithm is now expatiated by the following steps

• Step 1: Initialize field variables and set $k = 0$

• Step 2: Perform the explicit coupling step

  • 2.1: Extrapolate the position of the interface

  • 2.2: Move the dynamic fluid mesh

  • 2.3: Compute the mesh velocity and geometric quantities

  • 2.4: Gain the MST $Q^{n+1}_e$ on the element-by-element basis (see below for details)

  • 2.5: Calculate the two auxiliary variables (see Eq. (90))

  • 2.6: Predict the velocity (see Eq. (91))

  • 2.7: Determine the conformation tensor (see Eq. (92))

• Step 3: Perform the implicit coupling step

  • 3.1: Start fixed-point iterations and set $k \leftarrow k+1$

  • 3.2: Update the pressure in tandem with the GCL contribution

    $$\begin{aligned} \nabla ^2 p^{n+1} = & {} \ \frac{1}{\Delta t + \phi } \left( \nabla \cdot \textbf{u}^{n+1(k-1)} + \Delta t \nabla ^2 p^n\right. \nonumber \\{} & {} \left. + \ \phi \nabla \cdot \textbf{q}^n + \Delta t Q^{n+1}_e \right) . \end{aligned}$$

    (94)

  • 3.3: Correct the velocity (see Eq. (82))

  • 3.4: Solve the elastodynamics equation

  • 3.5: Obtain the interfacial residuals

  • 3.6: Check the convergence: if not convergent, then go ahead; otherwise, proceed to the next time step

  • 3.7: Relax the interface

  • 3.8: Compute the mesh velocity on $\Sigma$ as new boundary condition

  • 3.9: Return.

A variant of the above algorithm can also be developed by including the MST within the implicit stage where velocities of those intefacial nodes are continuously updated at each subiteration. This minor modification possibly enhances the information exchange during the implicit coupling step, to an extent.

As mentioned above, the ESFEM is able to respect the GCL over moving T3 elements by introducing the MST into the approximate incompressibility condition. For this purpose, the original PPE needs to be revised in line with the SPGP formulation applied for the CBS(B) scheme [45, 46]. According to Jan and Sheu [6], the continuity equation is rewritten as follow, for a single element e

$$\begin{aligned} \frac{1}{\bar{A}_e} \int \nolimits _{\overline{\Omega }_e} \nabla \cdot \textbf{u} \, \textrm{d}\Omega = \langle \nabla \cdot \textbf{u} \rangle _e = -\Delta t Q_e. \end{aligned}$$

(95)

Correspondingly, the time-discrete form of the modified continuity equation is locally re-derived from the SPGP formulation as follow

$$\begin{aligned} \langle \nabla \cdot \textbf{u}^{n+1} + \phi \nabla \cdot \textbf{q}^n - \phi \nabla ^2 p^{n+1} \rangle _e = -\Delta t Q^{n+1}_e, \end{aligned}$$

(96)

which leads to the modified PPE after some simple operations

$$\begin{aligned} \langle \nabla ^2 p^{n+1} \rangle _e = & {} \ \frac{1}{\Delta t + \phi } \left( \langle \nabla \cdot \textbf{v} + \Delta t \nabla ^2 p^n + \phi \nabla \cdot \textbf{q}^n \rangle _e \right. \nonumber \\{} & {} \left. + \ \Delta t Q^{n+1}_e \right) . \end{aligned}$$

(97)

Using the Galerkin approximation procedure, we may integrate in weak form Eq. (97) over the fluid domain of interest

$$\begin{aligned}{} & {} \sum _{i=1}^{n_\textrm{e}} \int \nolimits _{\bar{\Omega }_i} \textbf{N}^\textrm{T}_\textrm{e} \left( \nabla ^2 p^{n+1} \right) \, \textrm{d}\Omega \nonumber \\{} & {} \quad = \frac{1}{\Delta t + \phi } \sum _{i=1}^{n_\textrm{e}} \int \nolimits _{\bar{\Omega }_i} \textbf{N}^\textrm{T}_\textrm{e} \left( \nabla \cdot \textbf{v} + \Delta t \nabla ^2 p^n + \phi \nabla \cdot \textbf{q}^n + \Delta t Q^{n+1}_i \right) \, \textrm{d}\Omega , \end{aligned}$$

(98)

where $\textbf{N}_\textrm{e}$ is the shape function of T3 element. Since the number of DOFs of the discrete system keeps unchanged, Eq. (98) can be recast below

$$\begin{aligned}{} & {} \sum _{i=1}^{n_\textrm{g}} \int \nolimits _{\widetilde{\Omega }_i} \textbf{N}^\textrm{T} \left( \widetilde{\nabla }^2 p^{n+1} \right) \, \textrm{d}\Omega \nonumber \\{} & {} \quad = \frac{1}{\Delta t + \phi } \sum _{i=1}^{n_\textrm{g}} \int \nolimits _{\widetilde{\Omega }_i} \textbf{N}^\textrm{T} \left( \widetilde{\nabla } \cdot \textbf{v} + \Delta t \widetilde{\nabla }^2 p^n + \phi \widetilde{\nabla } \cdot \textbf{q}^n \right) \, \textrm{d}\Omega \ + \frac{\Delta t}{\Delta t + \phi } \sum _{j=1}^{n_\textrm{e}} \int \nolimits _{\bar{\Omega }_j} \textbf{N}^\textrm{T}_\textrm{e} Q^{n+1}_j \, \textrm{d}\Omega . \end{aligned}$$

(99)

By doing this, the GCL contribution to the modified PPE is easily integrated into the discrete subsystem on grounds of totally different support domains (i.e. SCs and T3 elements). Its computation is actually confined to the dynamic part of the fluid domain, seeing that $Q_e$ naturally disappears on stationary grids. A GCL-preserving ALE-ESFEM-T3 formulation is thereby developed under the stabilized CBS(B)-$\Psi$ coupling framework for VFSI simulation [57].

8 Numerical Examples

The CBS(A/B)-$\Psi$ coupling algorithms have succeeded in solving a number of NFSI and VFSI problems over the past decade. This section is by no means an exhaustive list of those numerical tests, but it gives an indication of several selected examples clearly stating the performance and advantages of various developed semi-implicit coupling methods. Some necessary details involving the mesh generation and sensitivity tests for grids and time-step sizes are not given either, but all of them are readily consulted from the referenced papers.

8.1 Cross-Flow Oscillations of a Circular Cylinder

The first test case is cross-flow oscillations of an elastically mounted circular cylinder in the fully laminar flow regime. The geometry and boundary conditions of the problem is shown in Fig. 5. The system parameters are taken from the experimental investigation: [36] $90 \leqslant Re \leqslant 140$, $m^*_2 = 116.37$, $\xi _2 = 1.237 \times 10^{-3}$ and $f_\textrm{r2} = 17.961 / Re$. The enhanced CBS(A)-$\Psi$ and improved CBS(B)-$\Psi$ coupling algorithms [30, 54] are applied on the basis of the FEM and CSFEM, respectively.

Fig. 5

Problem setup of a transversely oscillating circular cylinder

Fig. 6

Amplitudes and frequency ratios of the vibrating cylinder at different Re

The cross-flow amplitude $Y = \frac{1}{2} (d_\textrm{2max} - d_\textrm{2min})$ and frequency ratio $r_2 = \left. f_\textrm{v} / f_\textrm{n2} \right.$ calculated at different Re are displayed in Fig. 6, where $d_\textrm{2max}$ and $d_\textrm{2min}$ are the positive and negative peaks of $d_2$, respectively, and $f_\textrm{v}$ is the vortex-shedding frequency. They are also compared with previously published data [36, 91,92,93] in the Figure. A dashed line connecting the scattered points [54] is plotted to illustrate the general trend of the computed quantities towards the Re effect. Identical to the experimental study [36], the well-known lock-in phenomenon [94] has been successfully captured by various numerical methods in Fig. 6 (a). The cylinder undergoes large-scale, violent motions during lock-in but otherwise its motions become fairly faint outside the lock-in region. In Fig. 6 (b), the frequency ratio $r_2$ becomes extremely close to unity in lock-in, clearly indicating the synchronization of the vortex-shedding and natural frequencies. Normally, the Re–St relation of an oscillating cylinder deviates from the following fitting formula

$$\begin{aligned} St = 0.212\times \left( 1.0 - \frac{21.2}{Re} \right) , \end{aligned}$$

(100)

for a stationary circular cylinder [95] (refer to the solid line in Fig. 6 (b)), where $St = f_\textrm{v} L/U_\infty$ is the Strouhal number. Furthermore, the time history of $d_2$ gained at $Re = 105$ by the improved CBS(B)-$\Psi$ coupling algorithm [54] is shown in Fig. 7, corresponding to the direct observation of violent oscillations due to lock-in. The stable, periodic oscillations of the cylinder have been fully established for a long time. The recent result [54] seems to be in better agreement with the VIV experiment [36] as the wider lock-in range and the larger amplitude are acquired at resonance.

Fig. 7

Time history of the cross-flow displacement at $Re = 105$

What interests us is that the AC-CBS(A)-$\Psi$ coupling method is indeed less costly than its PPE-based counterpart. We can now quantify time costs of the two techniques by solving the $Re = 100$ flow under the same conditions [39]. With reference to Fig. 8, it is clearly seen that the AC-CBS(A)-$\Psi$ coupling method makes a saving of roughly 13% run time.

Fig. 8

Time consumption generated by the two schemes

8.2 Free Oscillations of a Circular Cylinder with Low Mass Ratios

The second example is concerned with free oscillations of a circular cylinder with very low mass ratios. The geometry and boundary conditions are exactly the same as those of the first example. The cylinder has equal elastic properties in both the cross-flow and stream-wise directions. The physical properties of the coupled flow-body system are set as follows: [96] $Re = 100$, $0.188 \leqslant m^*\leqslant 0.471$, $\xi = 0$ and $f_\textrm{r} = 0.2$. The improved CBS(B)-$\Psi$ coupling algorithm [48] is employed in conjunction with the CSFEM for spatial approximation.

For verification, the time histories of a few important parameters are first calculated in Fig. 9 for $m^*= 0.408$. It is clearly seen from the two pictures that the highly stable and smooth responses of the light-weight cylinder have been established for a long time. Subsequently, the vorticity fields at $m^*= 0.393 \ \text {and} \ 0.298$ are displayed in Fig. 10. The 2S vortex-shedding mode [97] is evidently observed in the wake of the cylinder at such a low Re. The longitudinal spacings between two rows of parallel shedding vortices remain almost equal in the two cases. That is because the cylinder goes through comparative cross-flow motions which are dominant at the given mass ratios.

Fig. 9

Time history of computed parameters at $m^*= 0.408$

Fig. 10

Vorticity contours behind the wake for different $m^*$

The $x_1$-$x_2$ trajectories of the oscillating light cylinder with varying $m^*$ are shown in Fig. 11 where a very low mass ratio $m^*= 0.188$ is considered. It is noticed that, because of the self-limiting VIV process at low Re [98], the cylinder takes on the nearly symmetrical trajectory shaping the classical Lissajous figure of “8". Basically, these Lissajous figures are distributed along the horizontal axis and the magnitude of the stream-wise oscillation is far smaller than that of its cross-flow counterpart. When a flexibly supported circular cylinder is inspired to vibrate freely, the common frequencies of the structural oscillations and driving forces in their respective directions may result in lock-in and the cylinder’s axis traces the path of the Lissajous figure [99]. These eight-type loops are caused by the substantial change in drag force during the large-scale flow-induced vibrations. As a result of the action of the mean drag force imposed on the cylinder, the equilibrium position of the structural oscillations is not situated at the origin in the stream-wise direction.

Fig. 11

8-profile trajectories of the circular cylinder at various $m^*$

Interestingly, another focal point is the expenditure of computing time demanded by the proposed semi-implicit coupling approaches. Here, time costs of two CBS-$\Psi$ coupling methods [31, 48] are collectively discussed for 2-DOF VIV of a circular cylinder in different working conditions. In Fig. 12 (a), the improved CBS(A)-$\Psi$ coupling method saves nearly 10% overheads for the $m^*= 0.471$ case [48]. He [31] further reports in Fig. 12 (b) that the enhanced CBS(A)-$\Psi$ coupling method saves almost 20% computing time in the $m^*= 2.5\pi$ case [100]. When $m^*$ becomes larger, the added-mass effect will be weakened and less subiterations per time step are needed accordingly. Hence, the expenditure of the explicit coupling phase accounts for the more part of total cost. This clearly explains why the CBS-$\Psi$ coupling method is faster at $m^*= 2.5\pi$.

Fig. 12

Time consumption generated by the semi-implicit and implicit schemes

8.3 VIV of a Cantilever Behind an Obstacle

This subsection is devoted to VIV of an elastic cantilever attached to the downstream face of a fixed square cylinder [101]. The problem settings are illustrated in Fig. 13. A measuring point is put at the center of the right side of the cantilever. The material parameters are given as: [101] $Re = 332.6$, $m^*= 84.75$, $E = 8.05 \times 10^5$ and $\nu = 0.35$. The enhanced CBS(A)-$\Psi$, improved CBS(A)-$\Psi$ and improved CBS(B)-$\Psi$ coupling algorithms in collaboration with the FEM and/or SFEM [31, 32, 48, 54] are employed to solve this benchmark problem, respectively.

Fig. 13

VIV of a cantilever attached to a square cylinder

Table 1 summarizes the tip deflection Y and the oscillation frequency $f_\textrm{o}$ documented in the open literature [9, 31, 32, 42, 48, 54, 101,102,103,104,105,106,107]. Overall, a good agreement is realized between the results obtained from the semi-implicit methods and other numerical techniques. Apparently, the flexible cantilever is excited to reach large-amplitude oscillations since $f_\textrm{o} = 0.0579$ is fairly close to the first eigenfrequency of the elastic cantilever $f^1_\textrm{n} = 0.0591$ (details are given in the Appendix of the recent paper [108]). Namely, the cantilever vibrates in resonance with the incoming flow. Furthermore, Fig. 14 shows the time history of the tip displacement in the cross-flow direction [54]. The smooth and undamped curve indicates that the transient, long-term, periodic oscillations of the flexible cantilever have been completely stimulated after a growth stage.

Table 1 Comparison between the previous and present results

Fig. 14

Time history of the tip deflection

Fig. 15 displays three snapshots of the vorticity and pressure fields at typical time slices when the structural oscillations are fully built up. During one period of vibration, the unsteady features of flow patterns and structural oscillations differ at the three stages. Thanks to the flow separation, the swirling vortices are shedding from the salient edges of the square cylinder with a certain frequency. The vortex formation in the wake causes the time-varying drag and lift forces which are constantly working on the elastic cantilever. Correspondingly, the structural oscillations alter the flow pattern near the cantilever such that $f_\textrm{o}$ starts to deviate from $f^1_\textrm{n}$. Once the fluid flow develops fully, the cantilever begins strong and large oscillations. On this occasion, the pressure distribution on the solid surface opposite to the direction of the structural deflection is negative but results in the lower suction.

Fig. 15

Instantaneous contours of the elastic cantilever

Fig. 16 illustrates the time costs of the CBS-based partitioned semi-implicit and implicit coupling schemes based on two different convergence tolerances, respectively. For simplicity, the convergence criterion is calculated in terms of the $L_\infty$ norm of residuals of the interfacial displacement. Given a relatively loose tolerance $tol = 1.0 \times 10^{-6}$, the semi-implicit coupling method merely makes very limited saving of computing time in Fig. 16 (a). Fig. 16 (b) suggests that the semi-implicit coupling method [31] significantly improves the computational efficiency for a tight tolerance $tol = 1.0 \times 10^{-7}$.

Fig. 16

Time consumption generated by the semi-implicit and implicit schemes

8.4 Viscoelastic Flow in a Leaky Cavity

Flow of an incompressible fluid in a leaky square cavity mounted on a flexible thin bottom [109] has been one of benchmark problems aiming at algorithmic developments of both NFSI and VFSI [10, 106, 110, 111]. Fig. 17 depicts the initially undeformed configuration and boundary conditions of the leaky cavity. The inlet and outlet conditions are set in accordance with the previous installation [106]. For quantitative analysis, three measuring points are located at the upper surface of the bottom, namely $P1(0.25, \ 0)$, $P2(0.5, \ 0)$ and $P3(0.75, \ 0)$. The material properties of the Oldroyd-B fluid and elastic solid are prescribed as follows: $Re = 100$, $W\!i = 0.1$, $\eta = 0.5$, $m^*= 500$, $E = 250$ and $\nu = 0$. Here, two stabilized CBS(B)-$\Psi$ coupling algorithms are utilized in conjunction with the CSFEM and ESFEM [55, 57], respectively.

Fig. 17

Lid-driven open cavity with an elastic bottom

To highlight the stabilizing effect, Fig. 18 monitors the time-dependent profiles of $d_2$ calculated at P2 by the CBS(A/B)-$\Psi$ coupling methods with and without the DEVSS-G/CBS(B)-SPGP stabilizer [55]. Here, the CBS(A)-$\Psi$ and CBS(B)-$\Psi$ coupling algorithms proposed by He et al. [31, 48] are also run for the purpose of comparison. It is clearly seen from Fig. 18 that the first-order CBS(A)-$\Psi$ scheme fails to give correct flow-induced responses of the flexible bottom. Moreover, the second-order CBS(B)-based scheme, even equipped with the DEVSS-G technique, has under-performed this test since the exposed oscillations of P2 show some destabilizing characteristics. Xue et al. [112] explained that, for transient viscoelastic fluid flows with inertia force, those stabilizers aimed at steady-state cases may alter the equation type or overly diffuse the velocity field in the presence of the solvent viscosity. Not surprisingly, inaccurate prediction of VFSI phenomena is a very definite possibility. As indicated by Fig. 18, the CBS(B)-SPGP method is a good remedy to both the DEVSS-G formulation and second-order pressure splitting error such that the combined DEVSS-G/CBS(B)-SPGP stabilization has shown a valuable capability to considerably improve inferior results.

Fig. 18

Computation of $d_2$ with and without DEVSS-G/CBS(B)-SPGP stabilizer

Table 2 summarizes a few parameters computed at P2, including Y, $f_\textrm{o}$, $d_\textrm{2max}$, the mean value of vertical displacement $d_\textrm{2mean}$ and its root-mean-square (RMS) error $d_\textrm{2rms}$. Generally speaking, the difference among all sets of computational data is fairly small in the table. It is also found that the oscillation frequencies are very close to the driving frequency of the top lid. Among these cited studies, the predicted deflections of the thin bottom away from the horizontal axis seem relatively large and remain reasonable as well.

Table 2 Summary of computed parameters

Fig. 19 displays the time evolution of $d_2$ extracted from the three measuring points [57]. The stable, periodic oscillations of the bottom are evidently observed after a growth phase. Due to the viscoelastic fluid flow, P1, P2 and P3 go through large deflections away from the horizontal axis. Further, the displacement of P2 is much larger than those of P1 and P3. The positive structural movement towards the interior of the cavity is excited owing to the inertia of the elastic thin bottom [114]. However, the deflections collected at the same three points are underestimated in some NFSI cases [114, 115]. Beside, the negative deflection may take place because the numerical solution to the open cavity flow seems sensitive to the boundary conditions [116, 117].

Fig. 19

Time history of vertical displacement at the measuring points

Computational expenses of different coupling methods are quantitatively compared in Fig. 20. We consider in this example $t = 100$ which is sufficient to arouse enough stable periodic oscillations of the flexible beam. Seen from Fig. 20, the GCL-preserving CBS(B)-$\Psi$ coupling algorithm demands less overheads than its implicit counterpart [113] does. Nevertheless, there is an obvious contrast in time consumption between the two recent works employing the ESFEM and CSFEM [55, 57], respectively. Based on the semi-implicit coupling notion, the GCL-preserving CBS(B)-$\Psi$ algorithm is twice as costly as the stabilized CBS(B)-$\Psi$ algorithm [55]. The reasons for this fact are given as follows: (i) the edge-based gradient smoothing treatment is somewhat more complicated than its cell-based counterpart; and (ii) the number of Q4 elements is half that of T3 elements for a mesh with the same DOFs. However, if the ESFEM-T3 formulation takes over the CBS-based partioned implicit coupling algorithm [113] for spatial approximation, the corresponding semi-implicit coupling method is capable of cutting down on computing time substantially as well.

Fig. 20

Comparison of computational efficiency of different algorithms

Typical streamline contours are chronologically displayed in Fig. 21 [57]. These streamlines confined in the cavity result from the viscoelastic flow driven by the moving lid. The internal flow circulation stimulates finite deformation of the elastic bottom accordingly. As the Oldroyd-B fluid has the constant shear viscosity [61], the flow phenomena look very much like those in the NFSI situation [106, 114]. For instance, the vortices are identified at left- and right-lower corners of the square cavity.

Fig. 21

Streamlines inside the cavity at different time instants

9 Concluding Remarks and Future Work

This article has given an overview on various CBS-$\Psi$ coupling algorithms with applications to computational FSI simulations in the past decade. The CBS-$\Psi$ coupling algorithm is inspired by the pioneering work of Fernández et al. [12], and also is viewed as a credible improvement on the original projection-based partitioned semi-implicit coupling method. In particular, two different criteria are presented for classifying the CBS-based partitioned semi-implicit solution algorithms based on the split scheme and the way to treat the PPE, namely

• the CBS(A)-$\Psi$ and CBS(B)-$\Psi$ schemes;

• the PPE-based and AC-based schemes.

We have first looked over the theoretical bases of individual fields as well as the CSFEM and ESFEM for spatial approximation, respectively. We have then focused on up to eight intriguing variants of the CBS-$\Psi$ coupling algorithms that are known to win the desirable stabilizing effect and higher efficiency at the same time. The resulting algorithmic implementation is described together with some necessary details. Especially, those numerical techniques used for the CBS scheme are almost perfectly applicable to the developed semi-implicit coupling framework. The performance and advantages of the CBS-$\Psi$ coupling methods are clearly acknowledged through a number of selected examples. Although the presented methods are applied to two-dimensional low-Re FSI problems, they are free to be extended three-dimensional and/or high-Re cases. Furthermore, other effects such as heat transfer, turbulence, free surface and material non-linearities of complex fluids and solids are very likely to be taken into account, provided that more robust CBS-based semi-implicit schemes are properly devised. Dynamic acceleration techniques applicable to the implicit coupling step are also welcome as the convergence of this non-physical coupling scheme probably becomes very slow in some difficult situations. We believe that this class of new semi-implicit coupling methods has the potential to become an appealing tool, in view of the stabilizing effect and lower overall cost, for a wider range of realistic FSI problems.