Introduction

Dispersion of flammable substances is considered extremely dangerous in industrial settings due to the high risk of fires and explosions. The concern is not only related to large-scale releases resulting from catastrophic failures, but also to the occurrence of small leaks during normal operation that can lead to major accidents. Along these lines, it is paramount to accurately define the area where control of ignition sources is necessary to, e.g., safely install electrical equipment in the operational environment [1]. Area classification studies aim at determining the dimensions and volumes of hazardous releases, ensuring that the specification and installation of electrical equipment meet the requirements of applicable technical standards [2]. It is important to note, however, that classified areas should have the smallest possible size, while maintaining some level of safety, avoiding situations that can generate unnecessary risks.

Understanding the mechanism of cloud dispersion is fundamental as it defines the properties needed for the determination of the hazardous area extent. In some situations, the material released to the environment can only partially vaporize, giving rise to a two-phase flow system where the liquid breaks up into fine droplets producing an aerosol cloud, whose behavior in the atmosphere affects dispersion distances. This complex system is the result of such phenomena as expansion of the material released to ambient pressure, liquid atomization to form the aerosol cloud, and (possibly) rainout of liquid droplets. The use of rigorous mathematical models capable of describing these processes appears as a reliable alternative to empirical criteria described in specific standards [3]. In fact, the use of standardized diagrams, such as those found in the IEC 60079-10-1 [4] and in the API RP 505 [5] standards, can produce dubious results due to the oversizing of the classified areas, increasing the cost of the project and sometimes creating a false impression of safety.

These mathematical models should be able to explain both the mechanisms at the origin of the release as well as the dispersion of the material into the environment. Thus, once the release scenario is defined, source models are used to describe how materials are released from an orifice. A dispersion model subsequently describes how the material is transported and dispersed, producing concentration profiles that ultimately determine the extent of the hazardous area [6]. Several models have been proposed in the literature to represent the two-phase dispersion phenomenon. Many of these originated from rigorous multidimensional mass, energy, and momentum balances applied to multicomponent, multiphase systems via Computational Fluid Dynamics (CFD). Others involve simplifications thereof, generating preferable easy-to-understand low-dimensional models that can be solved more easily. However, the latter showed poor agreement to available experimental data, probably due to the lack of adjustment of parameters inherent to the phenomenon, or the absence of important terms in the balance equations.

Taking that into account, this work proposes a systematic procedure to determine the extent of hazardous areas in two-phase dispersions with important modifications to the mathematical modeling. Models applied to gas jets were adapted to two-phase releases by considering the expansion region characterized by the flashing phenomenon. In this sense, an alternative for the decay constants for the calculation of the velocity, concentration, and temperature profiles along the centerline was derived. Another important aspect was the gas temperature along the centerline. For far-field gas jets, it is usually determined by the normalization principle of Thring and Newby [7, 8]. However, for two-phase systems, this principle may not produce good results. Therefore, a new normalization ratio for the centerline temperature was proposed, resulting in a model that conforms quite well to experimental data. Moreover, during construction of the model, it was observed that the degree of subcooling of the stored liquid influenced the entrainment of air in the single-phase region. By assuming the typical value of the entrainment coefficient, \({\alpha }_{1}\), available in the literature for single-phase calculations, the model failed to predict experimental gas temperature profiles on the centerline, possibly because \({\alpha }_{1}\) did not generate the expected contribution to the heat exchange involved in two-phase flow dispersions. A new correlation for \({\alpha }_{1}\) as a function of the orifice Reynolds number was then obtained from those experimental temperature profiles. The results showed the model with the adjusted parameter estimated quite accurately the experimental data.

The remainder of this manuscript is organized as follows. Sect. “Background” gives an overview of the main results on two-phase flow releases related to this contribution. Sect. “Fundamental concepts” discusses some important definitions and concepts in hazardous area classification. Sect. “Methodology” describes the proposed systematic algorithm and the underlying mathematical model with the important modifications. Sect. “Results and discussions” elaborates on the novel correlation for the entrainment coefficient, compares the relevant outputs of the tuned-up mathematical model with available experimental data, and tests its applicability on a few pertinent cases. Conclusions and some future directions are considered in Sect. “Conclusions.”

Background

There are experimental as well as theoretical results in the open literature on two-phase flow releases of hazardous materials. Though this work is not intended to give a thorough survey on the subject, this section provides a brief overview of some of the main results in the field that are somehow related to this contribution.

Kukkonen [9] proposed a mathematical model for the initial dispersion of two-phase jet releases of ammonia and water. The model predicted the mass fraction of materials deposited on the ground and the influence of water vapor in the ambient air was also considered. Fauske and Epstein [10] computed the release rate for subcooled, saturated, and two-phase flow conditions, investigated the behavior of the expanded jet, including aspects of air entrainment, vaporization, and cooling, as well as calculated the size of the two-phase jet for ammonia and hydrofluoric acid under various conditions. Anjos [11] proposed a systematic methodology based on the Homogeneous Equilibrium Model (HEM) and on the studies of Bakkum and Duijm [12], Fauske and Epstein [10], and Kukkonen [9]. The method did not make use of balance equations, but derived an analytical model based on empirical correlations to predict the size of the two-phase region coupled with a gas jet model.

Dunbar et al. [13] studied the dispersion and evaporation of droplets formed from accidental releases of materials to calculate the concentration profiles of the components into the environment. They concluded that proper correlations for the formation of droplets were still an important source of uncertainty. Papadourakis et al. [14] examined the limits of evaporation of droplets of pure components in two-phase jets resulting from the release of superheated liquids by developing two models based on mass, momentum, and energy balances. The first model is used to calculate the upper limit of evaporation which assumes that liquid droplets travel through stagnant atmospheric air without back pressure and with a non-zero relative velocity. A second model is then used for the calculation of the lower limit of evaporation, assuming that the liquid droplets of the released material are transported along with the vapor phase and that there was no relative movement between the phases.

Lacome et al. [15] developed a new mathematical model to simulate a two-phase jet resulting from a leak in a pipeline containing a liquefied gas. The work focused especially on the effect of the vaporization and boiling process in the jet. They tested the model in a two-phase release of butane from a circular orifice. Lacome et al. [3] used experimental data and a mathematical model to investigate the two-phase jet resulting from any release of liquefied gases to deepen the understanding of the flashing phenomena. The studies focused especially on the cooling effect evidenced by large-scale experiments on butane and propane releases carried out during the Flashing Liquids in Industrial Environment (FLIE) test project.

Coldrick [16] described the Computational Fluid Dynamics (CFD) modeling of small-scale propane flashing jets and compared with experimental data and integral model predictions. Their results provided a good fit to experimental temperature and velocity profiles. Based on simulations of an experimentally validated CFD model, Souza et al. [17] developed an analytical correlation to estimate the extent of the classified area applied to fugitive gas emissions. Oliveira et al. [18] used a parametrized CFD model to predict the extent and volume of the hazardous area resulting from two-phase releases. The influence of wind and release conditions on area classification was considered and they proposed a new formula based on the volume and length of the jet. Barros [19] employed CFD techniques to obtain a model to predict the two-phase flow of pure components to compute the volume and extent of the resulting flammable cloud. Her work evaluated two different approaches to obtain release conditions for classification of hazardous areas: two-phase equilibrium jet, in which the homogeneous equilibrium model is assumed, and unbalanced jet, in which an orifice overheating condition is considered. More recently, Barros et al. [20] discussed the influence of the magnitude and direction of wind speed on the classification of hazardous areas. The authors evaluated the extent and volume of methane, propane, and hydrogen leaks using a CFD model and showed that these parameters, as well as the type of zone, were substantially influenced by wind speed. Lim and Ng [21] built a model to predict flashing leaks of liquefied natural gas. The leak model consisted of nine equations and quantified leak parameters for risk assessment. A potential use of the model was to provide an equivalent boundary condition for CFD simulations to predict gas dispersion properties. According to the authors, additional validation with risk analysis tools and actual experimental data was needed to confirm the suitability of the model.

Aiming at increasing accuracy, many works made use of CFD to model and consequently determine the extent and volume of classified areas. Although it is a reliable tool that in some cases can be used as an alternative to experiments, CFD modeling requires a lot of knowledge and user experience in the difficult subject of transport phenomena applied to two-phase flow. In addition, CFD simulations can take a very long time to converge at a very high computational cost. In that regard, low-dimensional, simpler models capable of capturing the most significant aspects of the two-phase release phenomenon are an alternative to the more complex CFD counterpart. However, some works that propose these simpler mathematical models do not conform to experimental data, maybe because some parameters are not properly estimated or because some key terms are not considered in the balance equations.

Therefore, this original contribution proposes (1) a novel algorithm to compute the extent of hazardous areas; (2) an important modification to the energy balance of the two-phase jet model that accounts for the influence of the vapor component; (3) new correlations for the decay constants to compute velocity, concentration of species, and temperature along the centerline; (4) a new normalization ratio for temperature on the centerline; and (5) a new correlation for the entrainment coefficient. Altogether, these important modifications produced a systematic algorithm based on an improved mathematical model that fitted quantitatively well to experimental data.

Fundamental Concepts

Area classification is key to maintaining safety and understanding the potential hazards arising from flammable releases into a given environment. Along these lines, experts assess and classify scenarios prone to generate explosive atmospheres, creating a framework for designing safety procedures to minimize risk levels.

According to the IEC 60079-10-1 [4] standard, a classified area is one in which an explosive atmosphere is present, or may be present, in such quantities as to require special precautions for the design, manufacture, installation, use, inspection and maintenance of equipment. The classification concerns internal and external areas of the process equipment and is closely related to the release and dispersion phenomena [22]. Schram et al. [2] defined classified areas as places, areas, or spaces where there is a likelihood of danger of fire or explosion due to the presence of gases or vapors, liquids, combustible dust, or flammable fibers in suspension.

A substance can be released and dispersed in different ways, as can be seen in the flowchart of Fig. 1 [6]. The release scenario will depend on the physical state, the thermodynamic, fluid-mechanical and transport properties of the substance, as well as the storage conditions [23].

Fig. 1
figure 1

Adapted from CCPS [6]

Configuration for release and dispersion of hazardous materials.

Full size image

Initially, the vapor fraction of the release is determined. In the case of liquid release, evaporation can occur with consequent formation of aerosol. If that does not happen, a suitable model should be used either for two-phase or liquid-only dispersion [24]. Particularly, the presence of droplets in the plume can form a pool from the phenomenon known as rainout [25,26,27]. If there is no rainout, then all droplets have evaporated, and hence a model of aerosol transport and evaporation must be used [14, 28]. Regardless of the type, all releases will eventually result in the formation and dispersion of a vapor cloud to which the related mathematical model will depend, among other factors, on the relative density of the gas. Thus, dispersion models can be used for dense, neutral, or light gases, depending on the properties of the cloud. Notice that if the cloud behaves as a free turbulent jet, a particularly specific dispersion model is required.

Based on the above discussion, suppose now that a liquefied gas contained in a control volume is discharged through a small diameter orifice and that it partially evaporates, giving rise to a two-phase jet, as illustrated in Fig. 2. The escaping liquid is subjected to a sudden decrease in pressure resulting in the formation of a jet of vapor laden with droplets. Previous studies [10, 29,30,31,32] showed that the configuration of this release basically depends on the conditions of the jet at the orifice outlet (plane “e”), at the end of the expansion region (plane “f”), and after the total evaporation of the droplets (plane “j”).

Fig. 2
figure 2

Schematic of the two-phase jet release and dispersion into the environment

Full size image

In the expansion region between planes “e” and “f,” the liquefied gas at subcooled conditions expands as pressure decreases. When the pressure drops below saturation, a two-phase cloud composed of vapor and liquid droplets (aerosol) of various sizes and speeds is formed: these are projected in different directions into the air. The expansion takes place until the pressure equals the ambient pressure. In this region, the process of formation of the first droplets is called primary separation. Subsequent rupture forms new particles from the collapse of previous ones due to high relative velocities in the vapor/liquid interface [33]. The available mathematical models for the expansion region do not consider the dynamics and evaporation of these droplets. It is believed that the breaking process overlaps that of evaporation since the droplets move with increasing speed, causing the size reduction effect. In addition, several authors assume that the size of this region is very small, the entrainment of air is negligible, and the vapor and the droplets have the same velocity and temperature [3, 12, 34, 35]. Under these assumptions, the conditions at the end of the expansion at plane “f” can be calculated from the initial conditions at plane “e.”

At the region between planes “f” and “j,” the moving cloud of vapor and liquid droplets is diluted by the entrainment of ambient air. Due to the temperature difference between the air and the two-phase jet, heat transfer causes the evaporation of droplets and, hence, the cooling of the entrained air. Further cooling may also result by moisture condensation from the air inside the jet.

Droplets that only partially evaporate will eventually reach the ground (rainout) and form a liquid pool. This phenomenon is limited by the energy and mass transfer between the gas, composed of the component's vapor and the air drawn into the jet, and the dispersed particles. The most common consideration is to limit droplet evaporation to a critical diameter [28], i.e., rainout will only occur if the droplet size after flashing is greater than the calculated critical diameter. In this work, the occurrence of rainout is determined by solving a set of ordinary differential equations describing the transport of momentum, heat, and mass between the gas and the droplet surface. Droplets that do not reach the ground will continue to evaporate and decrease in size until they disappear completely, forming a vapor cloud that will ultimately disperse into the atmosphere (region beyond plane “j” in the Figure) [26].

These fundamental concepts are important for the understanding of the developments discussed in the next section.

Methodology

The proposed systematic algorithm designed to compute the extent of hazardous areas for two-phase releases is better depicted as the flowchart of Fig. 3.

Fig. 3
figure 3

Proposed systematic algorithm to calculate the extent of hazardous areas for two-phase releases

Full size image

It relies on an improved low-dimensional (simple) dispersion mathematical model that will be detailed in the next subsection. It starts by calculating all the relevant information at the release orifice corresponding to plane “e” in Fig. 2. Then, it moves on to compute the value of important variables after the expansion zone at plane “f.” These are the initial conditions for the set of balance equations that describes the spatial profiles of the droplets and gas of the two-phase jet in the entrainment region between planes “f” and “j.” Initially, an elevated jet, i.e., the one for which the y-coordinate at plane “f” is suitably above ground, is computed by considering droplet dynamics and evaporation, as well as the entrainment of air. If certain conditions are met, the jet may eventually touch the ground at some horizontal coordinate. From this point on in the two-phase region, the balance equations describing this new configuration must be adequately adjusted. Rainout, or the complete evaporation of droplets, is always checked to determine the start of the single-phase region, corresponding to plane “j.” Like the two-phase region, it starts by computing information of the elevated jet, and if eventually the jet touches the ground, the describing equations must be switched. Regardless of the region where computations are conducted, the algorithm always checks whether the LEL is reached, in which case the process is halted, and the extent of the hazardous area calculated.

Modeling Approach

This section briefly describes the mathematical modeling of the two-phase release of pure substances used in this work. The focus is to describe the phenomena taking place at the orifice after the expansion of the two-phase jet, at the entrainment zone when air is dragged into the jet, and at the single-phase dispersion region. More details are given as Supplementary Information.

The variables of interest at the orifice are the mass flow rate, the release velocity, and the vapor fraction. These are computed via the Homogeneous Equilibrium Model (HEM) using the omega method [36,37,38,39]. This method applies to substances stored as saturated or subcooled liquid at various degrees. Algorithm 1 is a high-level overview description of its implementation.

figure afigure a

Algorithm 1. A high-level overview of the homogeneous equilibrium Model (HEM) using the omega method

In Algorithm 1, \({T}_{s}\) and \({P}_{s}\) are the storage temperature and pressure, respectively; \({\phi }_{v,s}\) is the storage mass vapor fraction; \({v}_{lg,s}\) is the difference between the specific volume of the vapor and liquid phases at storage conditions; \({v}_{s}\) is the specific volume of the material at storage conditions (with \({\rho }_{s}=\frac{1}{{v}_{S}}\) as the corresponding density); \({Cp}_{l,s}\) is the specific heat of the liquid phase; \({L}_{v,s}\) is the latent heat of vaporization at \({T}_{s}\); \({P}_{a}\) is the room pressure; \({T}_{e}\) e \({P}_{e}\) are the temperature and pressure at the orifice, respectively; \(G\) is the mass flux at the orifice; \({\rho }_{l,s}\) is the density of the liquid phase; \({\phi }_{v,e}\) is the vapor fraction at the orifice; \({L}_{v,e}\) is the latent heat of vaporization at \({T}_{e}\); \({C}_{d,e}\) is the discharge coefficient at the orifice; \({q}_{e}\) is the mass flow rate at the orifice; \({A}_{e}\) is the orifice cross-sectional area; \({\rho }_{e}\) is the density at the orifice; \({\rho }_{l,e}\) is the density of the liquid phase at the orifice; \({\rho }_{v,e}\) is the density of the vapor phase at the orifice; and \({u}_{e}\) is the velocity at the orifice.

The velocity (\({u}_{f}\)), vapor mass fraction (\({\phi }_{v,f}\)), and cross-sectional area (\({A}_{f}\)) after expansion, corresponding to plane “f,” when \({P}_{f}={P}_{a}\), are computed by solving steady-state momentum, mass, and energy balance equations. At this location, the initial droplet diameter is also computed.

After the expansion zone, droplet dispersion can be described by momentum conservation balances in the x- and y-directions [14, 40] giving the droplet velocities and leading to equations for the droplet trajectory; by an evaporation model [41]; and by an energy balance to give the temperature profile [14]. Note that rainout occurs if there is some x-coordinate \({X}_{d}\) such that the respective y-coordinate \({Y}_{d}=0\) and the droplet diameter \({d}_{d}\ne 0\), and that the complete vaporization of the droplets occurs if there is some \({X}_{d}\) such that \({Y}_{d}\ne 0\) and \({d}_{d}=0\).

Balance equations with respect to the centerline curvilinear coordinate \(s\) applied to the two-phase jet after expansion, between locations “f” and “j” in Fig. 2, give profiles for (1) the two-phase jet flow rate, (2) the momentum in the horizontal and vertical directions, (3) the entrainment of air flow rate, (4) the centerline jet trajectory coordinates, and (5) the gas phase temperature, which is different from the droplet temperature [42,43,44].

The entrainment of air into the two-phase jet is given by [43]

$$\frac{d{q}_{a}}{ds}={2\pi R}_{jet}{\rho }_{a,\infty }\left({\alpha }_{1}\sqrt{\frac{{\rho }_{jet}}{{\rho }_{a,\infty }}}\left|{u}_{jet}-{u}_{w}{\text{cos}}\theta \right|+{\alpha }_{2}{u}_{w}{\text{cos}}\theta \left|{\text{sin}}\theta \right|\right),$$
(11)

where \({R}_{jet}\), \({\rho }_{jet}\) and \({u}_{jet}\) are the cross-sectional radius, density, and velocity of the two-phase jet, respectively; \({\rho }_{a,\infty }\) is the air density; \({u}_{w}\) is the wind velocity; and \(\theta\) is the (local) angle of the jet with respect to horizontal. Typical values for the entrainment coefficient and the coefficient for a thermal plume are, respectively, \({\alpha }_{1}=0.0806\) and \({\alpha }_{2}=0.5\) [43]. Notwithstanding, \({\alpha }_{1}\) largely influences the gas temperature for liquids stored at high subcooling conditions and hence needs to be adjusted.

From the energy balance, it is possible to obtain an expression for the gas phase temperature (\({T}_{g}\)) profile. To the authors’ surprise, no model has considered the influence of the component vapor on the energy balance. For example, the model developed by Nikmo et al. [45] accounted only for the effect of droplet evaporation and entraining of air in the two-phase jet. Therefore, one very important original contribution proposed by the present work is to include the total enthalpy term due to the component vapor (\({h}_{vc,jet}\frac{d{q}_{v,c}}{ds}\)) in the energy balance equation yielding,

$$\frac{d{T}_{g}}{ds}=\frac{\left({h}_{a,\infty }-{h}_{a,jet}\right)\frac{d{q}_{a}}{ds}+\left({h}_{vc,jet}-{h}_{lc,jet}\right)\frac{d{q}_{l,c}}{ds}+{C}_{pl,d}{q}_{l,c}\frac{d{T}_{d}}{ds}}{{Cp}_{v,a}{q}_{a}+{Cp}_{v,c}{q}_{v,c}}.$$
(12)

Note that the capacitance of the component vapor (\({Cp}_{v,c}{q}_{v,c}\)) is also considered. In the above equation, \({h}_{a,\infty }\) is the air specific enthalpy calculated at the air temperature, \({T}_{a}\); \({h}_{a,jet}\), \({h}_{vc,jet}\), and \({h}_{lc,jet}\) are the specific enthalpy of air and the component in the vapor and liquid phases, respectively; \({q}_{v,c}\) and \({q}_{l,c}\) are the vapor and liquid phase mass flow rate of the component; and \({C}_{pl,d}\), \({Cp}_{v,a}\), and \({Cp}_{v,c}\) are the droplet, air and component vapor heat capacity, respectively.

The proposed refinement is particularly important for high volatile components since their increasing concentration in the vapor phase can significantly influence the character of the heat effect interactions between the gas and the droplet. As will be seen, this modified gas temperature profile greatly improves the predictive capability of the model when compared to experimental data.

The two-phase jet touches the ground if the height with respect to the centerline is such that \({Y}_{jet}\le {R}_{jet}{\text{cos}}\theta\), as illustrated in Fig. 4 [46].

Fig. 4
figure 4

Adapted from Epstein et al. [46]

Trajectory of the two-phase jet as it touches the ground.

Full size image

According to Epstein et al. [46], from that point at ground-level the jet cross section is rectangular, with height \(2{Y}_{jet}\) and half-width \({R}_{jet}\). The ground-level dispersion is handled in the same way as the elevated dispersion, except that the momentum and kinematic equations account for gravity compaction and the consequent sideways spreading. No heat exchange between the jet and the ground is assumed.

The balance equations for the elevated and ground-level single-phase dispersion region are similar to the developments for the two-phase region and are given as Supplementary Information.

The main purpose is to determine the size of the hazardous area. Therefore, the concentration profile along the centerline (the curvilinear coordinate \(s\)) is paramount. The correlations of Chen and Rodi [47] for the component concentration (\({\phi }_{vc,cent,TP}(s)\)) and gas velocity \(({u}_{g,cent,TP}(s))\) in the two-phase region in the below equations are used.

$$\frac{{\phi }_{vc,cent,TP}(s)}{{\phi }_{vc,0}}={C}_{\phi ,TP}\left(\frac{{d}_{f}}{{X}_{jet}}\right)\sqrt{\frac{{\rho }_{f}}{{\rho }_{a,\infty }}},$$
(13)
$$\frac{{u}_{g,cent,TP}(s)}{{u}_{g,0}}={C}_{u,TP}\left(\frac{{d}_{f}}{{X}_{jet}}\right)\sqrt{\frac{{\rho }_{f}}{{\rho }_{a,\infty }}},$$
(14)

where \({\phi }_{vc,0}\) and \({u}_{g,0}\) are the initial component vapor mass fraction in the gas and the initial gas velocity corresponding to the conditions at the beginning of the two-phase region. Since at this location there is no entrainment of air, \({\left.{\phi }_{vc,cent,TP}(s)\right|}_{f}={\phi }_{vc,0}=1\). Moreover, \({u}_{g,0}={u}_{f}\), and the profiles can be simplified.

$${\phi }_{vc,cent,TP}\left(s\right)={C}_{\phi ,TP}\left(\frac{{d}_{f}}{{X}_{jet}}\right)\sqrt{\frac{{\rho }_{f}}{{\rho }_{a,\infty }}},$$
(15)
$$\frac{{u}_{g,cent,TP}(s)}{{u}_{f}}={C}_{u,TP}\left(\frac{{d}_{f}}{{X}_{jet}}\right)\sqrt{\frac{{\rho }_{f}}{{\rho }_{a,\infty }}},$$
(16)

where \({d}_{f}\) is the diameter of the jet at location “f.”

The decay constants \({C}_{\phi ,TP}\) and \({C}_{u,TP}\) can assume different values for gas jets, especially in the range of 5 to 6.3 [47,48,49,50,51,52]. These values, however, can produce unrealistic results for the concentration and velocity profiles in two-phase jet flows. In this work, a new value for these constants is therefore proposed. It goes like this: Since the Reynolds number is considered high at location “f,” the velocity profile is flat, which leads to \({\left.{u}_{g,cent,TP}\left(s\right)\right|}_{f}={u}_{f}\). Moreover, \({\left.{\phi }_{vc,cent,TP}\left(s\right)\right|}_{f}=1\). Hence,

$${C}_{\phi ,TP}={C}_{u,TP}={\left(\frac{{d}_{f}}{{\left.{X}_{jet}\right|}_{f}}\right)}^{-1}{\left(\frac{{\rho }_{f}}{{\rho }_{a,\infty }}\right)}^{-1/2}.$$
(17)

In the above equation, the computation of \({\left.{X}_{jet}\right|}_{f}\) will make use of the concept of virtual source [53]. Laboratory investigations reveal that all circular turbulent jets have the same opening angle of 23.6°, regardless of the type of fluid, orifice diameter, or release velocity [53, 54]. Consequently, the origin of the x-coordinate must be counted not from the orifice but from a certain distance back from the orifice. This point of origin is called virtual source. Accordingly, \({\left.{X}_{jet}\right|}_{f}\) would be given by \({\left.{X}_{jet}\right|}_{f}={\text{tan}}\left(\frac{{23.6}^{o}}{2}\right){R}_{f}\cong 5{R}_{f}\). However, this last argument is valid only when neutral buoyancy occurs, i.e., when \({\rho }_{f}={\rho }_{a,\infty }\), which may not be the case for two-phase jets. For this reason, the buoyancy correction proposed by Ricou and Spalding [55] is applied to this expression, leading to the following formula.

$${\left.{X}_{jet}\right|}_{f}=5{R}_{f}\sqrt{\frac{{\rho }_{f}}{{\rho }_{a,\infty }}}.$$
(18)

Upon substitution in Eq. 17, \({C}_{\phi ,TP}={C}_{u,TP}=\frac{5}{2}\). This is the new value for the decay constants. This simple result greatly improves model predictions when compared to experimental data.

The gas temperature profile along the centerline in the two-phase region is calculated by an adaptation of the normalization principle of Thring and Newby [7, 8]. This principle was originally developed for gas jets but does not conform well to two-phase jets. The present work then proposes a new normalization strategy that considers the intrinsic characteristics of the two-phase axisymmetrical jet. Accordingly, the maximum gas temperature is the component’s bubble temperature, and the minimum is the droplet’s temperature at the same curvilinear location \(s\). Therefore, the expression for the gas profile temperature becomes:

$$\frac{{T}_{g,cent,TP}(s)-{T}_{d}(s)}{{T}_{b}-{T}_{d}(s)}={C}_{T,TP}\left(\frac{{d}_{f}}{{X}_{jet}}\right)\sqrt{\frac{{\rho }_{f}}{{\rho }_{a,\infty }}}.$$
(19)

The decay constant \({C}_{T,TP}\) assumes the same value as \({C}_{\phi ,TP}={C}_{u,TP}\). As will be seen later, this corrected normalization substantially improves model predictions when compared to experimental data.

For the single-phase region, the dispersion region beyond location “j” in Fig. 2, the centerline profile expressions are analogous to the correlations for the two-phase region, namely,

$$\frac{{\phi }_{vc,cent,SP}(s)}{{\phi }_{vc,cent,TP,j}}={C}_{\phi ,SP}\left(\frac{{d}_{j}}{{X}_{jet,g}}\right)\sqrt{\frac{{\rho }_{j}}{{\rho }_{a,\infty }}},$$
(20)
$$\frac{{u}_{g,cent,SP}(s)}{{u}_{g,cent,TP,j}}={C}_{u,SP}\left(\frac{{d}_{j}}{{X}_{jet,g}}\right)\sqrt{\frac{{\rho }_{j}}{{\rho }_{a,\infty }}},$$
(21)
$$\frac{{T}_{g,cent,SP}(s)-{T}_{a}}{{T}_{g}(s)-{T}_{a}}={C}_{T,SP}\left(\frac{{d}_{j}}{{X}_{jet,g}}\right)\sqrt{\frac{{\rho }_{j}}{{\rho }_{a,\infty }}}.$$
(22)

The conditions that \({\left.{\phi }_{vc,cent,SP}\left(s\right)\right|}_{j}={\phi }_{vc,cent,TP,j}\) and \({\left.{u}_{g,cent,SP}(s)\right|}_{j}={u}_{g,cent,TP,j}\) ensure seamless transition through plane “j.” Therefore, the concentration and velocity decay constants in the dispersion region are given below.

$${C}_{\phi ,SP}={C}_{u,SP}={\left(\frac{{d}_{j}}{{\left.{X}_{jet,g}\right|}_{j}}\right)}^{-1}{\left(\frac{{\rho }_{j}}{{\rho }_{a,\infty }}\right)}^{-1/2},$$
(23)

where \({\left.{X}_{jet,g}\right|}_{j}\) is simply the final value of the x-coordinate of the two-phase region. Similarly, \({\left.{T}_{g,cent,SP}(s)\right|}_{j}={T}_{g,cent,TP,j}\), and the decay constant related to temperature is easily obtained.

$${C}_{T,SP}=\frac{{T}_{g,cent,TP,j}-{T}_{a}}{{T}_{g}(s)-{T}_{a}}{\left(\frac{{d}_{j}}{{\left.{X}_{jet,g}\right|}_{j}}\right)}^{-1}{\left(\frac{{\rho }_{j}}{{\rho }_{a,\infty }}\right)}^{-1/2}.$$
(24)

From Eqs. (15) and (20), the hazardous area extent (\(hae\)) can be calculated at the x-direction location \({X}_{LEL}\) (\({X}_{jet}\) or \({X}_{jet,g}\)), for which \({\phi }_{vc,cent}\left(s\right)=LEL\). Assuming an elevation \({h}_{0}\) of the point of release, the extent is given below.

$$hae=\sqrt{({h}_{0}-{Y}_{LEL}{)}^{2}+{X}_{LEL}^{2}},$$
(25)

where \({Y}_{LEL}\) is the vertical coordinate corresponding to \({X}_{LEL}\).

An equally important variable to represent the size of hazardous areas is the volume of the flammable gas cloud. In the present work, it is the volume of the geometric shape of the jet bounded by the isopleths at the LEL. An isopleth is the line connecting points of equal concentration around the cloud boundary [56]. The geometric shape of the jet is assumed to have circular cross-sectional area, for which the radius \({R}_{c}\) is given by the following equation.

$${R}_{c}\left(s\right)=\frac{s}{{C}_{c}}\sqrt{{\text{ln}}\left(\frac{{\phi }_{vc,cent,SP}\left(s\right)}{{\phi }_{isopleth}}\right)},$$
(26)

where \({\phi }_{isopleth}\) is the concentration of interest and \({C}_{c}=5\) [57]. Integration of \({R}_{c}\) along the curvilinear coordinate \(s\) gives the required volume.

All physical property correlations and parameters of the mathematical model are given as Supplementary Information.

Solution Strategy

Implementation of the algorithm boils down to the solution of decoupled systems of algebraic or differential algebraic equations (DAE).

The variables at the release orifice are computed by Algorithm 1, which is basically a structured way to solve a set of explicit nonlinear algebraic equations. Some of these variables, namely \({P}_{e}\), \({T}_{e}\), \({\phi }_{v,e}\), \({q}_{e}\), \({\rho }_{e}\), and \({u}_{e}\), are then passed to the nonlinear set of algebraic equations describing the phenomena at the expansion zone, to which the solution is implicit in nature.

The solution of the model equations of the expansion zone produces the initial conditions for the DAE system describing the behavior of the two-phase region. These values are given in Table 1.

Table 1 Initial conditions for the DAE model of the two-phase region
Full size table

Integration of this DAE system proceeds until rainout is detected, i.e., for all remaining droplets when \({Y}_{d}=0\) with \({d}_{d}\ne 0\), or after complete evaporation when \({Y}_{d}\ne 0\) and \({d}_{d}=0\), for all droplets. If either of these two conditions is met, the model equations switch to those of the single-phase region, and the state of plane “j” is ultimately defined. Note that the model equations describing the behavior of the two-phase region switches if the jet touches the ground, which happens if the condition that \({Y}_{jet}\le {R}_{jet}{\text{cos}}\theta\) is met.

The initial conditions for the DAE model of the single-phase region correspond to the final values of the respective variables from the two-phase region. Namely, \({T}_{g,g}\left({s}_{j}\right)={\left.{T}_{g}\right|}_{j}\), \({X}_{jet,g}\left({s}_{j}\right)={\left.{X}_{jet}\right|}_{j}\), \({Y}_{jet,g}\left({s}_{j}\right)={\left.{Y}_{jet}\right|}_{j}\), \({P}_{x,g}\left({s}_{j}\right)={\left.{P}_{x}\right|}_{j}\), \({P}_{y,g}\left({s}_{j}\right)={\left.{P}_{y}\right|}_{j}\), and \({q}_{a,g}\left({s}_{j}\right)={\left.{q}_{a}\right|}_{j}\). Here, \({s}_{j}\) is the curvilinear coordinate at location “j.” Likewise, if the jet touches the ground, i.e., if \({Y}_{jet,g}\le {R}_{jet,g}{\text{cos}}{\theta }_{g}\), then the equations switch to model ground-level jets.

Despite the region where computations are conducted, the DAE solver must be able to detect when the LEL is reached, and flag, within reasonable accuracy, where it happens. In other words, it should halt solution whenever \({\phi }_{vc,cent}=LEL\), for some curvilinear coordinate \({s}_{LEL}\). For best accuracy, the solver should (ideally) automatically adjust the integration step size as \({\phi }_{vc,cent}\left(s\right)\to LEL\), which could be implemented by defining a neighborhood around \({\phi }_{vc,cent}\left(s\right)\) such that \({\Vert {\phi }_{vc,cent}\left(s\right)-LEL\Vert }_{p}\le \epsilon\), for some suitable \(\epsilon \in {\mathbb{R}}\). In case this strategy is not doable, simply create the event \({\Vert {\phi }_{vc,cent}\left(s\right)-LEL\Vert }_{p}\le \epsilon\) under the current integration step and try reducing tolerances to improve accuracy. Alternatively, place an upper bound on the step size.

One very powerful option to the full numerical solution of the DAE system described above is the use of the Adomian Decomposition Method (ADM) [58]. This very efficient strategy solves the underlying DAE system in a semi-analytical manner. The fundamental concept behind the ADM is to break down the unknown equation \(Fu=g(t)\), which encompasses a wide array of linear and nonlinear equations, ranging from ordinary and partial differential equations to integral equations, into a series of constituent solutions, each corresponding to varying degrees. Subsequently, the objective is to determine these solutions at each order. By summing up these solutions, one can then achieve an approximation of the actual solution with a precision tailored to the desired level of accuracy [59]. A highly efficient and user-friendly algorithm has been devised, drawing upon a hybrid analytical–numerical approach known as the Multistage Adomian Decomposition Method (MADM). This technique proves invaluable for tackling nonlinear differential equations, especially in cases where the conventional ADM struggles to yield precise and convergent solutions across the entire semi-infinite time spectrum. By incorporating two finely tuned precision adjustment parameters, the MADM excels at providing solutions of optimal accuracy for both transient and steady-state temporal domains. This versatility empowers the MADM to seamlessly deliver solutions tailored to the specific degree of accuracy required [60].

Results and Discussions

In this section, the main results of the application of the proposed algorithm to compute the extent of hazardous areas for two-phase releases are discussed. The purpose is to compare important output variables of the algorithm with the rather scarce experimental data available in the open literature. The algorithm was implemented in Matlab® version R2019b.

The experimental data are those of Allen [61] and the ones of the Flashing Liquids in Industrial Environments (FLIE) test series described in Ichard et al. [62] and Lacome et al. [3]. The experimental conditions are given in Table 2, in addition to some relevant information.

Table 2 Experimental parameters for the test cases
Full size table

Note the row of Table 2 that defines the storage condition of the material. Recall that, according to Leung [36], when a liquid is subcooled, there are degrees of subcooling to consider, namely, if \({\eta }_{sat}\ge {\eta }_{sc}\) then the liquid is on a low subcooling state; otherwise, it is said to be on a high subcooling state, where:

$${\omega }_{s}=\frac{{Cp}_{l,s}\cdot {T}_{s}\cdot {P}_{sat}({T}_{s})}{{v}_{s}}{\left(\frac{{v}_{lg,s}}{{L}_{v,s}}\right)}^{2}.$$
(5)
$${\eta }_{sat}=\frac{{P}_{sat}({T}_{s})}{{P}_{s}}.$$
(6)
$${\eta }_{sc}=\frac{2{\omega }_{s}}{1+2{\omega }_{s}}.$$
(7)

For materials stored as saturated or slightly subcooled liquids, the entrainment coefficient of 0.0806 suggested by Muralidhar et al. [43] is used in this work. For highly subcooled liquids, however, this value for \({\alpha }_{1}\) results in poor agreement with the experimental data. Ricou and Spalding [55] established that the entrainment rate correlates with the orifice Reynolds number (\({Re}_{e}\)), and since \({\alpha }_{1}\) can be chosen to match these experimentally entrainment rates [43], it was decided to seek a relation between \({\alpha }_{1}\) and \({Re}_{e}\).

Entrainment coefficients were found to best fit the temperature profiles in the experiments for highly subcooled liquids of the FLIE project (see Table 2). In such manner, cases 2, 3, 4 and 8 were chosen as the training set used to build the regressed line of Fig. 5, and cases 5, 6, and 7 were defined as the test set.

Fig. 5
figure 5

Entrainment coefficient \({\alpha }_{1}\) as a function of the orifice Reynolds number \({Re}_{e}\) for the FLIE project test cases

Full size image

The linear relation of Eq. (26) was then used to predict \({\alpha }_{1}\) for the test set.

$${\alpha }_{1}=0.5547-7.6203\bullet {10}^{-5}{Re}_{e}.$$
(27)

Note from Fig. 5 that the regressed line matches fairly well the observed values (with a coefficient of determination \({R}^{2}>0.98\)), particularly the unseen data, indicating that values of \({\alpha }_{1}\) obtained by the above equation should considerably improve model predictions.

With this relation for \({\alpha }_{1}\), the model is now complete and ready for application to predict relevant experimental information as per the test cases in Table 2. The focus is on temperature profiles and comparison with other model implementations. Particularly, for the FLIE test cases, Fig. 6 depicts the position of the thermocouples placed in three lines along the jet axis, where each line contains six thermocouples. The temperature field on the background of Fig. 6 is just to give an idea of the relative locations.

Fig. 6
figure 6

Location of thermocouples for the FLIE test cases [3]

Full size image

Figure 7 depicts the temperature profiles at the centerline of the model without and with the important changes proposed on this contribution against the experimental data. In that Figure, the relative squared error, \(RSE=\frac{\sum_{i=1}^{n}{({Y}_{i}-{\widehat{Y}}_{i})}^{2}}{\sum_{i=1}^{n}{({Y}_{i}-\overline{Y })}^{2}}\) (where \({Y}_{i}\) is the experimental data and \(\overline{Y }\) its mean, and \({Y}_{i}\) is given by the algorithm), computed on unseen data is a goodness-of-fit measure. The closer to 0, the better the predictive capacity of the underlying algorithm. The x-distance is the distance from the plane “f” in the horizontal direction. Actually, the distance between planes “e” and “f” is quite small if compared to the hazardous extent, and therefore can be safely disregarded [3, 12, 35]. The data in Table 3 confirm this hypothesis, where the length of the expansion region given by \(5{R}_{f}\sqrt{\frac{{\rho }_{f}}{{\rho }_{a,\infty }}}-5{R}_{e}\) was computed based on the concept of virtual source, with \({R}_{e}\) as the radius of the orifice.

Fig. 7
figure 7

Temperature profiles at the centerline against experimental data. Blue line: model with the important modifications. Red line: model with no changes. Small circles: experimental data

Full size image
Table 3 Calculated length of the expansion region
Full size table

The inflection points of the blue lines in Fig. 7 flag the transition to the single-phase region. As expected, the model with the proposed modifications is in very good agreement with the experimental data with very small relative squared error \(RSE<0.10\), while the model with no changes does not correctly describe the jet behavior up to the end of the two-phase region, and barely fits the data after that. In special, the extent of the two-phase region is accurately predicted by the proposed algorithm.

The sharp drop in temperature observed in all cases is due to the evaporation of droplets created by jet fragmentation, and by the entrainment of air, which, according to Lacome et al. [3], contributes to reducing the partial pressure of the released material. Thus, the system formed by air, vapor, and liquid droplets tends to reach equilibrium as the temperature decreases. Moreover, there is a competing effect between the endothermic process of droplet evaporation and the heating of the jet by the entrained air: The spray jet cools down until the vaporization of the liquid no longer influences the flow, and then the temperature eventually increases toward ambient.

The deviation of the proposed algorithm relative to the two-phase region of the FLIE Case 1 data is due to measurement saturation [62]. However, the temperature is dropping below the normal boiling temperature of propane due to the evaporation of liquid droplets. For the remaining cases with butane, the experiments predicted a minimum temperature of approximately -42°C, which is also predicted by the simulations carried out in this work.

Coldrick [16] reported CFD and Phast results applied to the Allen [61] test case, as seen in Fig. 8. Phast is a prestigious commercial software package for consequence modeling of accidental releases of toxic or flammable chemicals to the atmosphere [35].

Fig. 8
figure 8

Comparison of centerline temperature profiles of the Allen (1998) test case for different models. Small circles: experimental data

Full size image

Notably, the algorithm proposed in this contribution better fitted the experimental data. In addition, the model used by Coldrick did not reach the minimum temperature obtained by the experiments of Allen [61]. The Phast model with no moisture predicted a smaller extent of the two-phase region and considerably missed the profile of the single-phase region. The other Phast model improved prediction on this region at the expense of poor estimation of the complete evaporation of droplets.

Ichard et al. [62] developed a model and simulated FLIE cases 1 to 4, and Fig. 9 gives a comparison of the results. It can be seen that the proposed algorithm performs better. In fact, the model by Ichard et al. [62] considered thermal equilibrium between the phases, while the model proposed in this contribution assumed the droplet and gas temperatures were calculated from two different energy balances, which is a more realistic assumption.

Fig. 9
figure 9

Temperature profiles at the centerline against the model by Ichard et al. [62]. Blue line: model with the important modifications. Red line: model of Ichard et al. [62]. Small circles: experimental data

Full size image

The measured release rates can also be compared with the algorithm’s predictions, as shown in Table 4. The differences are in general within what one would expect for such a complex phenomenon: the calculated release rates were only (on average) 9% off from measured data. Note that release rates in such systems are inherently difficult to measure in practice, which may produce inaccurate results.

Table 4 Measured against calculated release rates for the test cases in Table 2
Full size table

Fauske and Epstein [10] suggested that, for subcooling conditions, the flow in the orifice can be obtained based on the Bernoulli equation adjusted for two-phase releases [12]. Therefore, the mass flux is calculated by the following relation.

$$G=\sqrt{2{\rho }_{e}\left({P}_{s}-{P}_{e}\right)},$$
(28)

where \({P}_{e}\) is given by Algorithm 1 and \({\rho }_{e}\) by the below equation.

$${\rho }_{e}=\frac{1}{\frac{\left(1-{\phi }_{v,e}\right)}{{\rho }_{l,e}}+\frac{{\phi }_{v,e}}{{\rho }_{v,e}}}.$$
(29)

For the Allen [61] case, the release rate of 0.0614 kg/s computed by the method of Leung [36] resulted in a larger deviation than the release rate determined by the proposed algorithm. For the low subcooling FLIE case 1, the release rate by Leung’s [36] method was equal to 0.4766 kg/s, even far from the experimental estimation. For the other (high subcooling) cases, both methods gave similar results and compared well with experimental data.

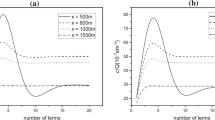
Rainout is determined by evaluating the diameter and elevation profiles of the droplets: If the droplet reaches the ground before complete evaporation, then rainout with possible formation of a pool has occurred. Figure 10 presents these profiles for the test cases as a function of the x-distance. Figure 11 provides a clearer picture of the phenomenon.

Fig. 10
figure 10

Diameter and elevation profiles of the droplets for the test cases as a function of the x-distance

Full size image
Fig. 11
figure 11

Droplet diameter vs. elevation plots to detect rainout for the test cases

Full size image

Clearly, for all test cases, no rainout was detected by the proposed algorithm, which is in accordance with the experimental findings. The effect of the degree of subcooling on the distance required for the evaporation of the droplets was also examined. As the degree of subcooling increased, so does the distance required for complete evaporation. This was evident for the Allen [61] and first FLIE cases where the droplets completely evaporated at the initial height. Note also from Fig. 9 that for the case with the highest degree of subcooling, the model by Ichard et al. [62] underestimated the evaporation distance compared to the more accurate prediction of the proposed algorithm.

In the present work, the dispersion model did not assume thermal equilibrium between phases, which represents a more realistic description of the phenomenon. Figure 12 shows that the gas temperature is always higher than the droplets’ because of the entrainment of warmer air.

Fig. 12
figure 12

Gas and droplet temperature profiles along the centerline

Full size image

From the gas concentration profiles at the centerline, the extent of the classified area can be estimated with respect to the LFL (\({X}_{LEL}\)) by Eq. (25).

Figure 13 depicts the concentration profiles and the extents at the UFL (upper flammability limit), LFL, 1/2 LFL, and 1/4 LFL. The UFL and LFL for propane and butane are, respectively, 9.5 and 8.4%, and 2.1 and 1.8% by volume in air.

Fig. 13
figure 13

Concentration profiles along the centerline for hazardous extent computations

Full size image

The hazardous extents in Fig. 13 coincided with the x-distances because the jet elevation changed very little. However, it is reasonable to conclude that as the elevation gets higher, the extent of the classified area can be significantly greater than the x-distance. For the propane cases, the estimated extent in Allen [61] was considerably lower than that obtained in the FLIE test because the release rate was small, and no wind was considered. The extents are otherwise larger for the remaining cases because of the amount of component released and the influence of wind velocity in the direction of the dispersion. Also notice the sharp drop of concentration as a result of the dilution with air.

Another important measure of the hazardous area is the volume of the flammable gas cloud. For the nine cases tested in this contribution, the calculated volumes at the LFL, and also at 1/2 LFL and 1/4 LFL are shown in Table 5. An average reduction of about 55% in the hazardous extent vis-à-vis the computations by the ubiquitous IEC 60079–10-1 was observed.

Table 5 Computed volume of flammable gas clouds for the test cases in Table 2
Full size table

Note that, in general, the volume does not necessarily increase with the extent. It depends on the shape of the cloud, especially if it touches the ground. A look at the isopleths in Figs. 14 and 15 helps to better understand this lack of relation: some clouds (FLIE Case 2 and 3) are wider than others (FLIE Case 7), producing larger volumes with smaller extents

Fig. 14
figure 14

Cross-sectional isopleths at the orifice plane. The red, blue, and green contours refer to the isopleths at the LFL, 1/2 LFL, and 1/4 LFL, respectively, and the black line is the centerline trajectory

Full size image
Fig. 15
figure 15

Top view isopleths at the orifice plane. The red, blue, and green contours refer to the isopleths at the LFL, 1/2 LFL, and 1/4 LFL, respectively

Full size image

It can be seen from Fig. 14 that for the Allen [61] case and the FLIE cases 1 and 8, the ground up to the hazardous extent is not considered classified area. For the other cases, the cloud touched the ground at the LFL. Another important observation was that for the Allen [61] case and the FLIE cases 1, 7, and 8 the cloud rose after some distance from the origin due to the reduced gas density as compared to the air density. When touching the ground, the isopleths for butane tended to increase the critical radius resulting in a larger contour at 1/4 LFL. It is reasonable to assume that, since the cross-section is rectangular for the situations where the cloud touches the ground, the plume should also have approximately the same rectangular shape.

The importance of the isopleths cannot be underemphasized as these contours help establish the locations in the flammable volume where equipment that may cause sparks should be avoided. In addition, they are beneficial in identifying possible situations of side wind that could otherwise change the trajectory of the jet.

Table 5 also shows the hazardous extents as given by the IEC 60079-10-1 [4] standard calculated for heavier-than-air vapors since for all cases the density of the cloud is greater than the air, as evidenced by the isopleths spreading along the ground. As seen in Table 5, the extents are much larger than the ones computed by the proposed algorithm, oversizing the classified areas, and possibly increasing the cost of the project.

Conclusions

This contribution proposed a novel algorithm to determine the extent of hazardous areas for two-phase releases of pure components based on a one-dimensional model that took into consideration: (1) the influence of the vapor component on the energy balance of the two-phase jet model; (2) new decay constants to calculate velocity, concentration, and temperature profiles; (3) a new normalization ratio for the temperature along the centerline; and (4) a new correlation for the entrainment coefficient in the two-phase region. Were it not for the meager experimental data available in the open literature, one would expect a better fit for the entrainment coefficient that could result in a model with even broader predictive capabilities. Be that as it may, those improvements resulted in a simple model that fitted well to measured release rates and temperature profiles. It is therefore believed that the algorithm can compute hazardous extent, volume, and shape of the resulting dispersions with satisfactory accuracy. However, more work should be done toward fitting in a methodology for pool computations to be coupled with the existing model as this is important when considering releases that produce significant rainout. Adapting the proposed algorithm for multicomponent systems is also a most desirable result. Just as important is the availability of more experimental data in the open literature, particularly the 94 cases and related profiles of the FLIE test series [62].