Mathematical Modeling of Micro-/Nanoparticles Transport in Blood Vessels: A Review

Abstract

Targeted drug delivery using drug-carrying nanoparticles has emerged as a promising approach for the treatment of diseases such as cancer. This review paper provides an overview of the current state of the art in modeling the transport and margination of micro-/nanoparticles in blood vessels. The review examines single-particle models, which consider a single micro-/nanoparticle, and multi-particle models, which consider a large number of particles in the bloodstream. The models are assessed based on factors such as the geometry of the blood vessel, the type, shape, size, and concentration of micro-/nanoparticles, the type of blood flow, the mathematical modeling approach, investigated parameters, and observed results. By analyzing the literature, this review aims to identify the desired properties of micro-/nanopharmaceuticals and to highlight the limiting factors of particle transport in the vascular system. The findings of this review can provide useful insights for researchers working on the development of more effective drug delivery strategies.

Introduction

Nanomaterials have been successfully employed in drug delivery for fighting diseases such as cancer, thrombosis, atherosclerosis, and cerebrovascular amyloid angiopathy [1,2,3,4]. Drug-carrying nanoparticles (NPs) can increase the drug’s circulation half-life by altering the pharmacokinetics of the drug cargo [5]. Nanocarriers can also be designed to deliver targeted drug cargos, so that the drug remains trapped inside the NPs until certain external or physiological stimuli such as temperature, pH, electromagnetic radiation, or enzymes trigger its release [6].

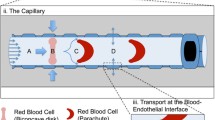
In cancer treatment, the process by which NPs enter the bloodstream to reach the target tumor cells involves three stages: transport and margination¹ of particles in the blood vessels, binding of particles to the vessel walls, and transfer of particles into the tumor matrix. Each of these three stages involves several physical, biochemical, biophysical, and mechanical phenomena [7]. Figure 1 shows the three stages of the drug delivery process by the NPs. As seen in this figure, blood is made up of several substances: plasma, white blood cells (WBCs or leukocytes), red blood cells (RBCs or erythrocytes) and platelets (thrombocytes). Plasma (~ 54% of blood volume) is composed of water (~ 91.5% of plasma volume) and particles (~ 8.5% of plasma volume), including organic molecules, electrolytes, proteins (albumin, fibrinogen and globulins), and more. RBCs (~ 45% of blood volume) carry oxygen, WBCs (~ 1% of blood volume) fight infection, and platelets (< 0.5% of blood volume) help to form blood clots [8, 9].

Fig. 1

Three stages of drug delivery process by NPs: Transport and margination of particles in the blood vessels, binding of particles to the vessel walls, and transfer of particles into the tumor matrix

Although different types of organic and inorganic nanoparticles have been proposed for drug delivery to tumors, and some NPs are currently in clinical use [10,11,12,13,14], there are remaining challenges and uncertainties that must be addressed before NPs can be used clinically [6, 15]. Due to the costly and time-consuming nature of empirical studies, the possibility of severe side effects of potential new drugs, and the extent of variables controlling the drug delivery process, mathematical modeling is strongly suggested prior to laboratory studies. Mathematical modeling and simulation of the transport of NPs in the body can help to optimize the design and find the desired physical and chemical properties of nanomedicines, as well as to identify the limiting factors of NP transport in the vascular system and cancerous tissues [16].

Liu et al. [16] reviewed some multi-scale computational approaches to targeted drug delivery by NPs. First, they investigated a number of continuum-based models for the dissolution, transport, and binding of drugs based on mass conservation and chemical reaction kinetic equations. Second, they discussed particle modeling based on the coupled Brownian adhesion dynamics method [16]. Ramezanpour et al. [17] reviewed some biophysical and computational approaches to study nanocarriers used in drug delivery research. In a review article, Afkhami and Renardy [18] studied three different mathematical models: the transport of superparamagnetic NPs in the drug delivery process, the breakage of a ferrofluid thin film, and the motion of a ferrofluid droplet [18]. Ye et al. [19] discussed the effect of different forces (inter-particle collisions, deformation-induced lift force, and shear gradient-induced lift force) and physiochemical properties (size, shape, surface functionality, and stiffness of NPs) on NP transport behavior and extravasation to tumors. They also studied the application of external stimuli (mainly magnetic stimulation) in targeted drug delivery [19]. Karolak et al. [20] investigated some in silico three-dimensional (3D) tumor models, including multicellular spheroids, normal and tumor spheroids and organoids, multicomponent tissues and epithelial acini, for studying drug delivery [20]. Dogra et al. [6] reviewed some kinetic models, discrete, hybrid, or continuum approaches, pharmacodynamics and pharmacokinetic models, and coarse-grained molecular dynamics simulations [21, 22] used to describe the transport of NPs in the body, including the three stages of the drug delivery process [6]. To evaluate the effect of NPs characteristics and tumor environment on the transport process, Gao et al. [7] reviewed different mathematical models used for active targeting of NPs to tumor cells. Eckmann et al. [23] reviewed some multi-scale modeling of protein membrane interactions for targeted drug delivery by NPs. Hadjicharalambous et al. [24] studied some in silico cancer models of tumor growth to identify the strengths and weaknesses of these models in clinical oncology [24]. Sahai et al. [25] discussed various mathematical models, including phenomenological and physiologically based pharmacokinetic (PBPK) models [26, 27], used to understand the biological interactions of nanodrugs [25]. These review articles have investigated either the second and/or third stages of the drug delivery process by NPs, or a specific NP (such as magnetic NPs), or briefly studied the three stages of the drug delivery by NPs.

The main purpose of the present study is to comprehensively review the mathematical modeling and simulation of transport and margination of different kinds of micro-/nanoparticles in the blood vessels (the first stage of the drug-carrying NPs delivery process). Modeling this stage of the drug delivery process is important not only for the design of vascular-targeted micro-/nanocarriers [28,29,30,31,32], but also for devices designed based on the margination process to separate particles and cells from the blood flow (e.g. separation of leukocytes, Malaria-infected RBCs, and circulating tumor cells) [33,34,35,36,37]. Understanding the properties of micro-/nanoparticles (material type, size, shape, and surface properties) and the hemodynamics of blood flow in the vascular system is essential for modeling this stage [8, 9, 38, 39]. The geometric shape and characteristics of the vessels and their branches (capillaries, arteries and veins) as well as the knowledge of blood constituents and their characteristics are also among the important parameters in the study of hemodynamics [8, 9]. It is clear that simultaneous consideration of random and unpredictable movements of NPs in the bloodstream (Brownian motion of NPs), interactions of NPs with blood components and vessel walls, inter-NPs interactions, interactions between blood components, characteristics of NPs (material type, shape, size, and surface properties), blood vessel characteristics (diameter, length, and degree of wall permeability), and blood rheology are among several variables that control the transport and margination of NPs and make it challenging to accurately predict their behavior in the bloodstream and to model the drug delivery process by NPs [16, 40].

In our previous articles, transport phenomena in various nanofluids were extensively investigated in different geometries and under different flow conditions [41,42,43,44,45,46,47,48,49,50,51]. Mathematical modeling and simulation have become important tools for investigating the transport of micro-/nanoparticles in blood vessels and designing drug delivery systems that can efficiently target specific tissues or organs. In this review, we aim to provide a comprehensive overview of the current state of research on the mathematical modeling and simulation of particle transport in blood vessels. By examining the various models and approaches that have been developed, we hope to identify key challenges and opportunities for future research in this field. In the present research, mathematical models and simulations of transport and margination of micro-/nanoparticles in blood vessels are divided into two main categories: (“Single-particle models” section) and (“Multi-particle models” section). Single-particle models refer to models considering one micro-/nanoparticle in the bloodstream over a flat plate or through a rectangular channel. In these models, the effect of blood cells has not been considered and the blood flow has been studied as a Newtonian fluid. Multi-particle models consider a large number of micro-/nanoparticles in the bloodstream. This group includes two categories: (“Models without considering blood cells” section) and (“Models with considering blood cells” section). Models without considering blood cells include two sub-categories: (“Models with Newtonian behavior of blood” section) and (“Models with non-Newtonian behavior of blood” section). In each category and sub-category, various published articles are studied based on the geometry of blood vessel, type, shape, size and concentration of micro-/nanoparticles, type of blood flow, mathematical modeling, and investigated parameters. Finally, in “Future aspects” section, approaches that can be useful in the future for modeling the transport and margination of micro-/nanoparticles are mentioned. Figure 2 shows how the different models studied in this article are categorized.

Fig. 2

Categories of different models studied in this article

Single-Particle Models

Single-particle models are a common tool used to study the transport and margination of micro-/nanoparticles in blood vessels. These models typically consider the interaction between a single particle and the surrounding fluid and vessel wall and can provide valuable insights into the behavior of individual particles. In this section, we discuss the advantages and limitations of single-particle models and their applications in drug delivery. Decuzzi et al. [52] investigated the margination of a spherical particle in a laminar bloodstream over a horizontal flat plate. They assumed blood to be a Newtonian fluid without blood cells and studied particle margination at different particle densities and sizes. The authors considered the contribution of various forces, including hemodynamic and buoyancy forces, van der Waals forces based on Lifshitz theory [53], and electrostatic and steric interactions according to Derjaguin approximation [53] between the particle and the endothelium. They ignored ligand–receptor interactions and assumed the particle was far from the vessel wall. To gain insight into the process of particle margination, Decuzzi et al. [52] employed a nonlinear differential equation of force equilibrium (Eq. 1) to solve for the trajectory of a spherical particle moving near the endothelial wall in a laminar flow [52].

$$ \begin{gathered} 6\underbrace {{\pi \mu R\left[ { - \frac{1}{{1 - \frac{R}{z}}} + \frac{1}{8}\log \left( {1 - \frac{R}{z}} \right)} \right]v_{z} }}_{{\text{Hemodynamic Force}}} + \underbrace {{64\pi R\frac{{kTnz^{2} }}{\kappa }\tanh \left( {\frac{{e\psi_{2} }}{4kT}} \right)\tanh \left( {\frac{{e\psi_{1} }}{4kT}} \right)e^{{ - \kappa \left( {z - R} \right)}} }}_{{\text{Electrostatic Force}}} + \hfill \\ \underbrace {{0.36\pi \frac{R}{{R_{{\text{g}}}^{2} }}kTe^{{{{ - \left( {z - R} \right)} \mathord{\left/ {\vphantom {{ - \left( {z - R} \right)} {R_{{\text{g}}} }}} \right. \kern-0pt} {R_{{\text{g}}} }}}} }}_{{\text{Steric Repulsive Interaction}}} = \underbrace {{\frac{4\pi }{3}gR^{3} \Delta \rho }}_{{\text{Buoyancy Force}}} + \underbrace {{A\frac{{R^{3} }}{{\left( {z - R} \right)^{4} }}}}_{{\text{van der Waals Interaction}}} \hfill \\ \end{gathered} $$

(1)

In this equation, $\mu$, $R$, $z$, $v_{z}$, $k$, $T$, $n$, $\kappa$, $e$, $\psi_{i}$, $R_{{\text{g}}}$, $g$, $\Delta \rho$ and $A$ , respectively, represent blood viscosity, the radius of the particle, relative particle position with respect to the endothelial wall, the velocity component along z, the Boltzmann constant, the absolute temperature of the system, the number density of ions in the unperturbed region of the solution, the characteristic Debye length of the solution, the electron charge, the electrostatic potential at the surface i, the unperturbed radius of gyration of polymer chains grafted onto the particle surface, the acceleration of gravity, density of the particle relative to blood, and the Hamaker constant. Decuzzi et al. [52] estimated the speed and time of particle margination as a function of the difference between particle and blood density, the Hamaker constant, and the particle radius. Their findings revealed that the particle has a critical radius with a maximum margination time. Based on their results, particles used for drug delivery should have a radius smaller than the critical value to enhance margination. The authors also observed that the critical radius decreased with increasing Hamaker constant and the difference between particle and blood density. Decuzzi et al. [52] showed that when designing practical drug delivery systems, it is crucial to consider the role of buoyancy, hemodynamic forces, and van der Waals interactions in particle margination. However, electrostatic repulsion and steric repulsion are only significant within very short distances from the endothelium, typically on the scale of tens of nanometers [52].

Lee et al. [54] extended a two-dimensional (2D) mathematical model developed by Gavze and Shapiro [55, 56] to investigate the transport of a single NP in blood (or air) flow on a horizontal or vertical flat surface in the presence of gravity. They investigated the motion of ellipsoidal rigid particles made of either silica or iron oxide, with a length-to-width ratio of 2c:2b and an aspect ratio of b/c = 0.5, in a laminar bloodstream. They solved the Navier–Stokes equation (Eq. 2) and the mass conservation equation (Eq. 3) for the fluid by using a pressure-based solver with the SIMPLEC algorithm in the FLUENT software. They employed the QUICK scheme for both space and time discretizations [54].

$$ \rho \left( {\frac{\partial V}{{\partial t}} + \left( {V \cdot \nabla } \right)V} \right) = - \nabla P + \mu \nabla \cdot \left( {\nabla V} \right) $$

(2)

$$ \nabla \cdot V = 0 $$

(3)

where $\rho$ and $\mu$ are the density and viscosity of the fluid, respectively. $V$ is the fluid velocity vector, $t$ is the time, and $P$ is the fluid pressure. Lee et al. [54] also described the motion of the particle using Newton’s laws as follows [54]:

$$ m_{{\text{p}}} \frac{{{\text{d}}v_{{\text{p}}} }}{{{\text{d}}t}} = F $$

(4)

$$ I\frac{{{\text{d}}\omega }}{{{\text{d}}t}} - I\omega \times \omega = T $$

(5)

where $m_{{\text{p}}}$ and $I$ are the mass and rotational inertia of the particle, respectively; $v_{{\text{p}}}$ is the particle velocity vector; $\omega$ is the particle rotational velocity vector; and F and T are the net force vector and net torque exerted on the particle, respectively. The forces include surface forces such as hydrodynamic forces, as well as external volume forces, such as gravitation. In their study, Lee et al. [54] considered the perturbation generated by the particle motion to be insignificant when the Reynolds (${\text{Re}} = {{\rho_{{}} c^{2} S} \mathord{\left/ {\vphantom {{\rho_{{}} c^{2} S} \mu }} \right. \kern-0pt} \mu }$) and Stokes (${\text{St}} = {{\rho_{p} c^{2} S} \mathord{\left/ {\vphantom {{\rho_{p} c^{2} S} \mu }} \right. \kern-0pt} \mu }$) numbers were sufficiently small. $\rho_{p}$, $c$ and $S$ are, respectively, the particle density, major semi-length of the elliptic particle and a linear unidirectional shear flow rate. To model the motion of the particle, they used a Runge–Kutta scheme in the MATLAB environment to numerically integrate Newton’s laws. Their model gave good results for Re <  = O(0.1) and St < O(1) in the context of cardiovascular applications and for St < O(10³) in pulmonary applications. Lee et al. [54] concluded that a proper balance between the particle-to-fluid density ratio, particle size, and shape can lead to sufficiently large Stokes numbers (St > 1) and enhance particle margination in capillaries. Additionally, they observed that in pulmonary applications, much larger Stokes numbers can be achieved due to the lower viscosity of air compared to blood [54].

In a separate study utilizing similar mathematical modeling, Lee et al. [57] predicted the margination behavior of a micro-/nanoparticle with spherical, elliptical, hemispherical, or disc-like shapes in blood or air flow over a horizontal or vertical flat plate. Their results revealed that the margination speed is dependent on the normalized buoyancy force and the Stokes number of the particle, and increases with the rotational inertia, density and size of the particle. The authors also found that in the absence of external forces, margination occurs spontaneously for the critical Stokes number of 0.1. Additionally, they observed that the maximum margination speed is achieved at a Stokes number of 20, which is independent of both the normalized buoyancy force and the particle shape. Their results also revealed that disc-like particles with low aspect ratios exhibit the strongest tendency to marginate in a laminar flow. In blood microcirculation and at very low shear rates (< 100 s⁻¹, such as tumor microcirculation), Lee et al. [57] found that the margination of micro-/nanoparticles can only occur by applying external forces, whereas microparticles can reach margination speeds of 1–10 μm/s at high shear rates (> 1000 s⁻¹). In addition, they observed that margination occurs for both micro- and nanoparticles in the pulmonary circulation, due to the lower density and viscosity of air [57].

Shah et al. [58] developed a model to study the margination of a single NP in a laminar bloodstream through a rectangular channel (5 × 2 μm) and its subsequent binding to the channel wall. Their model combined an adhesion kinetics model (Eq. 6) [59], Brownian dynamics of NPs (Eqs. 7, 8), and the Navier–Stokes and mass conservation equations for fluid (Eqs. 2, 3), and the governing equations were solved using immersed finite element method (IFEM) [60,61,62].

$$ \frac{{\partial N_{{\text{b}}} }}{\partial t} = k_{{\text{f}}} \left( {N_{{\text{l}}} - N_{{\text{b}}} } \right)\left( {N_{{\text{r}}} - N_{{\text{b}}} } \right) - k_{{\text{r}}} N_{{\text{b}}} $$

(6)

where $N_{{\text{b}}}$, $N_{{\text{l}}}$ and $N_{{\text{r}}}$ are the bond, ligand and receptor densities; $k_{{\text{r}}}$ and $k_{{\text{f}}}$ are the reverse and forward reaction rates, respectively. The Brownian motion and rotation of a NP are caused by random forces $R(t)$ and torque $T(t)$, which follow the fluctuation–dissipation theorem [63]:

$$ \left\langle {R_{i} \left( t \right)} \right\rangle = 0,\left\langle {T_{i} \left( t \right)} \right\rangle = 0 $$

(7)

$$ \left\langle {R_{i} \left( t \right)R_{j} \left( {t^{\prime } } \right)} \right\rangle = 2k_{B} T\beta_{{\text{t}}} \delta_{ij} \delta \left( {t - t^{\prime } } \right)\delta ,\left\langle {T_{i} \left( t \right)T_{j} \left( {t^{\prime } } \right)} \right\rangle = 2k_{B} \beta_{{\text{r}}} \delta_{ij} \delta \left( {t - t^{\prime } } \right)\delta $$

(8)

The Brownian motion and rotation of a NP are influenced by factors such as the unit-second-order tensor $\delta$, Kronecker delta $\delta_{ij}$, Dirac delta function $\delta \left( {t - t^{\prime } } \right)$, thermal energy $k_{B} T$, and translational and rotational friction coefficients $\beta_{{\text{t}}}$ and $\beta_{{\text{r}}}$, respectively. Shah et al. [58] derived the friction coefficient of non-spherical particles numerically through IFEM and empirically.

They assumed the NP as a rigid body and ignored the influence of particle motion on the fluid flow. Shah et al. [58] employed the Navier–Stokes equations for the fluid phase and solved the equations through finite element method. The authors obtained the Petrov–Galerkin weak form of the equations by applying integration by parts and the divergence theorem, which was then solved using the Newton–Raphson method. To improve computational efficiency, they further employed the generalized minimum residual (GMRES) iterative algorithm and computed residuals using matrix-free techniques. Considering a spherical NP (with a diameter of 380 nm) and a nanorod with the same volume (200 nm in diameter and 1000 nm in length), Shah et al. [58] found that under the same fluid flow conditions, rod-shaped nanoparticles had faster binding to the channel wall due to its rolling motion. In addition, by considering two nanorods with aspect ratios of 5 and 10, they found that the higher the aspect ratio, the better the NPs binding to the channel wall. They also observed that the probability of particle binding increases with decreasing flow shear rate and channel height, and the Brownian motion of NP greatly enhances its binding to the vessel wall [58].

Table 1 shows the single-particle models investigated in this article. While single-particle models provide a useful tool for studying the behavior of individual micro-/nanoparticles in blood vessels, they have limitations when it comes to understanding the behavior of a large population of NPs. These models focus on the interaction between a single particle and the surrounding fluid and vessel wall, typically assuming idealized conditions, such as uniform flow, a rectangular channel and a flat plate. They can be useful for investigating the effects of particle shape, size, and surface properties on transport and margination, but their results may not be applicable to the complex and heterogeneous environment of the bloodstream. In particular, single-particle models may not accurately capture the effects of particle–particle interactions, such as aggregation and repulsion, which can significantly impact the behavior of NPs in the bloodstream. To overcome these limitations, more complex models that consider a large number of NPs and account for particle–particle interactions, as well as the heterogeneity of the bloodstream, are required. These models can provide insights into the collective behavior of NPs and their distribution in the bloodstream, which are important factors in drug delivery applications. In the following sections, we review some of these models and their applications in drug delivery.

Table 1 Single-particle models

Multi-Particle Models

The behavior of micro-/nanoparticles in blood vessels is influenced by a number of factors, including the presence of other particles in the bloodstream. Multi-particle models provide a more comprehensive approach to studying this behavior, as they consider the effects of a large number of particles. In this section, we will explore some of the key multi-particle models that have been developed to study NP transport and margination in blood vessels.

Models Without Considering Blood Cells

Many multi-particle models for NP transport and margination in blood vessels treat blood as a homogeneous fluid, without considering the effects of blood cells. In this section, we will examine some of the key models that fall within this category, focusing on those that consider the blood flow as either a Newtonian or non-Newtonian fluid.

Models with Newtonian Behavior of Blood

In this section, we will examine some of the key models that have been developed for blood-based nanofluids as Newtonian fluids without considering blood cells as separate objects and discuss their underlying assumptions, methods, and results. Grief and Richardson [64] studied the transport of magnetic particles in the bloodstream through a 2D vascular network and determined the fraction of magnetic particles that were able to reach the walls of the network [65]. They investigated the effects of particle size, vessel size, and magnetic field on the particle transport in the bloodstream. They considered spherical particles with diameters of 1, 2 and 4 μm and a volume percentage of 10% and applied the Navier–Stokes equations for fluid transport and the advection–diffusion model for particle concentration in MATLAB environment. The following equation shows the advection–diffusion model for NPs [64]:

$$ \frac{\partial c}{{\partial t}} + \nabla \cdot \left( {cv_{{{\text{ep}}}} } \right) = \nabla \cdot \left( {D\nabla c} \right) $$

(9)

$$ v_{{\text{p}}} = v_{{\text{b}}} + v_{{{\text{mag}}}} ,{\text{where }}v_{{{\text{mag}}}} = \frac{{F_{{{\text{mag}}}} }}{6\pi \mu a} $$

(10)

$$ D = \underbrace {{\frac{{k_{B} T}}{6\pi \mu a}}}_{{\text{Brownian Diffusivity}}} + \underbrace {{K_{{{\text{sh}}}} \left( {r_{{{\text{RBC}}}} } \right)^{2} \dot{\gamma }}}_{{\text{Shear - Induced Diffusivity}}} $$

(11)

where $c$, $v_{{\text{p}}}$, $v_{{\text{b}}}$, $F_{{{\text{mag}}}}$, $a$, $K_{{{\text{sh}}}}$, $r_{{{\text{RBC}}}}$ and $\dot{\gamma }$ are, respectively, particle concentration, particle velocity in the blood stream, blood velocity, the magnetic force on the particle, hydrodynamic radius, a dimensionless coefficient that depends on the blood cell concentration, the blood cell radius and the local value of the fluid shear rate. $D$ is the combined diffusivity of magnetic particles in blood, which includes Brownian diffusivity (for small particles) and shear-induced diffusivity (for vessels larger than capillaries). The Brownian diffusivity can be calculated by introducing a particle diffusivity using the Einstein relation. The shear-induced diffusivity takes interactions and collisions between moving red blood cells in the bloodstream into account, resulting in a diffusive motion of the magnetic particles that is much greater than that caused by standard Brownian diffusion [64].

The model proposed by Grief and Richardson [64] relies crucially on a dimensionless parameter, denoted by $S$, as defined in Eq. (12). This parameter represents the ratio of the advective and diffusive flux across the channel and plays a critical role in the model’s predictions [64].

$$ S = \alpha \delta {\text{Pe}}_{{{\text{sh}}}} = \frac{{F_{{{\text{mag}}}} d^{2} }}{{16\pi \mu aUK_{{{\text{sh}}}} r_{{{\text{RBC}}}}^{2} }} $$

(12)

The equation above involves several variables, including the dimensionless magnetic velocity ($\alpha$), aspect ratio of the vessel ($\delta$), half the width of the channel ($d$), mean blood velocity ($U$), and the shear Peclet number (${\text{Pe}}_{{{\text{sh}}}}$). The shear Peclet number is a dimensionless parameter that represents the ratio of the advective flux along the channel to the combined diffusive fluxes resulting from shear-induced motion and Brownian motion. When S <  < 1, the magnetic force has minimal influence compared to the effects of shear-induced diffusion, and this can significantly affect the deposition of particles in arterioles and venules. Under these conditions, the diffusive flux may play a dominant role in particle transport, leading to substantial disruption in deposition patterns [64].

Furlani and Ng [66] developed an analytical model for predicting the transport of drug-carrying Fe₃O₄ NPs in laminar bloodstream through a cylindrical vessel under the effect of an external magnetic field. Taking into account the predominant magnetic and fluidic forces (Eqs. 13, 14) in the Newton’s second law (Eq. 4), they predicted the motion of magnetic particles [66].

$$ F_{{{\text{mag}}}} = \mu_{{\text{f}}} \left( {m_{{\text{p,eff}}} \cdot \nabla } \right)H_{{\text{a}}} $$

(13)

$$ F_{{\text{f}}} = - 6\pi \mu R\left( {v_{{\text{p}}} - v_{{\text{b}}} } \right) $$

(14)

where $\mu_{{\text{f}}}$ is the permeability of the transport fluid, $m_{{\text{p,eff}}}$ is the effective dipole moment of the particle, and $H_{{\text{a}}}$ is the (externally) applied magnetic field intensity. They also obtained the particle number density based on an advection–diffusion model (Eq. 9) [66].

Furlani and Ng [66] investigated the effect of microvessel size, flow velocity, magnet position and properties, nanoparticle size and properties, and blood hematocrit level on NP transport. They also considered the effect of blood cells on effective bulk viscosity, and used their proposed model to estimate the required size of NPs for better capture. The results of their analysis suggest that submicron particles can be effectively guided to tumors located several centimeters away from the source of the magnetic field [66].

Decuzzi et al. [67] studied the effective longitudinal diffusion of spherical nanovectors in impermeable and permeable cylindrical capillaries. Depending on the organ, the capillary wall can be impermeable (such as brain–blood endothelium), or it can be highly permeable (such as the capillary wall of the developing tumor masses or kidney) [67, 68]. Decuzzi et al. [67] investigated the effect of spherical particle size (with radii less than 1000 nm) and various hemodynamic conditions on the longitudinal diffusion of particles in a one-dimensional (1D) laminar flow. They took into account the blood as a Newtonian and incompressible fluid and obtained the diffusion of particles using the Taylor–Aris approach [69, 70].

Decuzzi et al. [67] presented the relationship between the effective diffusivity ($D_{{{\text{eff}}}}$) and the mean fluid velocity ($U$), channel radius ($R_{e}$), viscosity ($\mu$), and particle radius ($R$) for both non-permeable (Eq. 15) and permeable capillaries (Eqs. 16, 17) as follows [67]:

$$ D_{{{\text{eff}}}} = \frac{{k_{B} T}}{6\pi \mu R} + \frac{{R_{e}^{2} U_{{}}^{2} }}{{8k_{B} T}}\pi \mu R $$

(15)

$$ D_{{{\text{eff}}}} = \frac{{k_{B} T}}{6\pi \mu R} + \frac{{R_{e}^{2} U_{0}^{2} }}{{8k_{B} T}}\pi \mu Rf\left( {\Omega ,\Pi ,\overline{z}} \right) $$

(16)

$$ f\left( {\Omega ,\Pi ,\overline{z}} \right) = \left[ {\frac{{\left( {1 + e^{{2\overline{z}\Pi }} } \right) - e^{\Pi } \left( {1 + e^{{2\left( {\overline{z} - 1} \right)\Pi }} } \right)\Omega }}{{2 - e^{\Pi } \left( {1 + e^{ - 2\Pi } } \right)\Omega }}e^{{ - \Pi \overline{z}}} } \right]^{2} $$

(17)

The variables $U_{0}$, $\overline{z}$, $\Omega$ and $\Pi$ in the equation above represent the inlet mean velocity, axial normalized coordinate, pressure parameter and permeability parameter, respectively [67].

Their results showed that NPs have a critical radius that depends on the vessel size and hemodynamic conditions, such that their effective longitudinal diffusion is minimal at that radius. The critical radius ($R_{{{\text{cr}}}}$) is given by the following equations for non-permeable (Eq. 18) and permeable capillaries (Eq. 19) [67]:

$$ R_{{{\text{cr}}}} = \frac{2}{\pi \sqrt 3 }\frac{{k_{B} T}}{{\mu R_{e} U}} $$

(18)

$$ R_{{{\text{cr}}}} = \frac{2}{\pi \sqrt 3 }\frac{{k_{B} T}}{{\mu R_{e} U_{0} }}\frac{1}{{f\left( {\Omega ,\Pi ,\overline{z}} \right)}} $$

(19)

According to their results, at radii smaller than the critical radius, the diffusion coefficient decreases as the particle radius increases. In this range, the particles are mainly diffused by the Brownian diffusion. At radii larger than the critical radius, the effective diffusion coefficient increases with increasing the particle radius. In this range, the particles are mainly diffused by the convection mechanism. Decuzzi et al. [67] also found that the higher product of the flow velocity and the vessel radius, the smaller critical radius of the NPs. Furthermore, they observed that in the permeable vessels, the effective diffusion was significantly reduced compared to the usual impermeable vessels [67].

Li et al. [71] modeled the transport of ferrofluid in a 2D rectangular channel under the influence of a high-gradient magnetic field using the mass conservation (Eq. 3) and Navier–Stokes equations (Eq. 20) for fluid and advection–diffusion equation (Eq. 9) for the particle concentration.

$$ \rho \left( {\frac{\partial V}{{\partial t}} + \left( {V \cdot \nabla } \right)V} \right) = \nabla \cdot \left[ { - {\text{PI}} + \mu \nabla V - {{2\mu } \mathord{\left/ {\vphantom {{2\mu } {3\left( {\nabla \cdot V} \right)I}}} \right. \kern-0pt} {3\left( {\nabla \cdot V} \right)I}}} \right] + F $$

(20)

The variables $I$ and $F$ represent the identity tensor and the volume force term, respectively. Li et al. [71] assumed that the volume force term is equal to the magnetic force on a single particle multiplied by the number of particles per unit volume. They investigated the effect of the intensity, gradient, and susceptibility of the magnetic field, flow velocity, and vessel size (10 × 50 mm and 1 × 20 mm) on particle accumulation, streamlines, and contours of nanoparticle concentration [71].

Mahmoudi et al. [72] dealt with simulating the 2D dynamic behavior of superparamagnetic iron oxide NPs in a rectangular blood vessel under the effect of an external magnetic field. They took into account blood-based nanofluids as incompressible and Newtonian fluids and solved the Maxwell and Navier–Stokes equations [73, 74] for nanofluid transport based on the finite element method (FEM) in the COMSOL platform. Mahmoudi et al. [72] took into account the magnetic volume force and gravity in the Navier–Stokes equations and used an FEM model to investigate how the interactions between magnetic properties of superparamagnetic iron oxide NPs and the strength of the applied field affect the amplitude and shape of the resulting ferrofluid velocity field. Based on their simulation results, it appears that the strength of the applied magnetic field and the magnetic properties of superparamagnetic iron oxide NPs have an impact on the velocity field fluctuations (flow turbulence) and amplitude (peak velocity). The authors found that an increased external field leads to a more turbulent flow, and a velocity field with less fluctuation and higher amplitude, particularly in the direction normal to the tissue, is advantageous for promoting drug delivery [72].

Kayal et al. [75] performed a CFD simulation based on ANSYS-FLUENT software to model the transport of the drug-carrying magnetic NPs (Fe₃O₄) in a laminar bloodstream through a 2D rectangular channel under the influence of an external magnetic field. They used the continuity equation (Eq. 3), the Navier–Stokes equation of motion (Eq. 20) and the species balance equation (Eq. 9) and studied the effect of size and properties of NPs and the strength, position and shape (rectangular and cylindrical cross section) of the external magnet on the motion of NPs [75]. They found that the retention of magnetic carrier NPs has been significantly influenced by the fluid flow behavior resulting from the position and shape of the magnet, magnetic properties and size of the magnetic carrier NPs, and the magnetic field strength [75]. David et al. [76] performed a 2D simulation of the transport of blood-based nanofluids in a tube with a circular cross section under the effect of an externally applied magnetic field at low Reynolds numbers (Re < 1). They considered spherical magnetic NPs with diameters ranging from 10 to 800 nm and solved the Newton’s second law, considering drag and magnetic forces, in the MATLAB environment. Using the proposed model, David et al. [76] estimated the fractional retention of magnetic NPs, NP accumulation areas, the effect of NPs size and their position relative to the magnet on drug delivery. Their findings indicate that the probability of particle retention at any point in the capillary is directly proportional to the ratio of magnetic to drag forces acting on particles that are in a resting state on a wall [76].

Yue et al. [77] used a stochastic ODE model to simulate the transport of a superparamagnetic cluster under the influence of an external magnet. They considered the spherical clusters in the radius range from 10 to 200 nm, and evaluated the effect of injection position, strength of the magnetic field, blood flow, stochastic effects, and number of clusters on the transport of clusters. They applied Newton’s second law, considering Stokes drag force and magnetic force (based on Maxwell’s equations). For particles with radii less than 20 nm, they also considered Langevin’s Brownian motion model [78]. Yue et al. [77] found that the cluster capture rate is highly dependent on the magnetic moment, the distance between the vessel wall and the magnet, and the cluster size, and weakly depends on the flow velocity [77].

Hossain et al. [79] presented a mathematical model for mass transport of drug-carrying NPs and drug and solved the equations by isogeometric finite element analysis [80]. In their work, the authors expressed the advection–diffusion–reaction equations for the drug-encapsulated NPs (species I) and the drug (species II) in cylindrical coordinates as follows [79]:

$$ \begin{aligned} \frac{{\partial C_{{\text{I}}} }}{\partial t} = & \frac{1}{r}\frac{\partial }{\partial r}\left( {D_{{{\text{r}},{\text{I}}}} r\frac{{\partial C_{{\text{I}}} }}{\partial r}} \right) + \frac{1}{{r^{2} }}\frac{\partial }{\partial \theta }\left( {D_{{\theta ,{\text{I}}}} \frac{{\partial C_{{\text{I}}} }}{\partial \theta }} \right) + \frac{\partial }{\partial z}\left( {D_{{z,{\text{I}}}} \frac{{\partial C_{{\text{I}}} }}{\partial z}} \right) \\ & \quad - \left[ {\frac{1}{r}\frac{{\partial \left( {rV_{r} C_{{\text{I}}} } \right)}}{\partial r} + \frac{1}{r}\frac{{\partial \left( {V_{\theta } C_{{\text{I}}} } \right)}}{\partial \theta } + \frac{{\partial \left( {V_{z} C_{{\text{I}}} } \right)}}{\partial z}} \right] - \sigma_{{\text{I}}} C_{{\text{I}}} \\ \end{aligned} $$

(21)

$$ \begin{gathered} \frac{{\partial C_{{{\text{II}}}} }}{\partial t} = \frac{1}{r}\frac{\partial }{\partial r}\left( {D_{{\text{r,II}}} r\frac{{\partial C_{{{\text{II}}}} }}{\partial r}} \right) + \frac{1}{{r^{2} }}\frac{\partial }{\partial \theta }\left( {D_{{\theta ,{\text{II}}}} \frac{{\partial C_{{{\text{II}}}} }}{\partial \theta }} \right) + \frac{\partial }{\partial z}\left( {D_{{z,{\text{II}}}} \frac{{\partial C_{{{\text{II}}}} }}{\partial z}} \right) - \hfill \\ \left[ {\frac{1}{r}\frac{{\partial \left( {rV_{r} C_{{{\text{II}}}} } \right)}}{\partial r} + \frac{1}{r}\frac{{\partial \left( {V_{\theta } C_{{{\text{II}}}} } \right)}}{\partial \theta } + \frac{{\partial \left( {V_{z} C_{{{\text{II}}}} } \right)}}{\partial z}} \right] - \sigma_{{{\text{II}}}} C_{{{\text{II}}}} + C_{{\text{I}}} f \hfill \\ \end{gathered} $$

(22)

For simplicity, the subscripts I and II are omitted, and $D_{{\text{r}}}$, $D_{\theta }$ and $D_{z}$ represent the diffusivities of the respective species in radial, circumferential, and axial directions. $\sigma$ is metabolism rate constant, and $f$ is the drug release rate by each NP. They performed the simulations on a patient-specific coronary artery geometry and analyzed the inhomogeneity effect of artery. They considered spherical polymeric NPs with a diameter range of 20–500 nm. Hossain et al. [79] found the number of NPs that bind to the artery wall depends on the surface properties [79].

Applying the isogeometric finite element analysis [80, 81], Hossain et al. [82] also coupled the advection–diffusion–reaction equation (Eq. 23), the continuity equation (Eq. 3) and the Navier–Stokes (Eq. 20) equation to simulate the transport of blood-based micro/nanofluids in the coronary artery of a patient-specific vascular network. They considered blood flow as an incompressible Newtonian fluid and studied the effect of vessel geometry, wall shear rate and spherical particle size (with diameters less than 7 μm) on particle transport. The following equation shows the advection–diffusion-reaction model [82].

$$ \frac{\partial c}{{\partial t}} + V \cdot \nabla c - \nabla \cdot \left( {D \cdot \nabla c} \right) + \sigma c = 0 $$

(23)

where $\sigma$ is the reaction coefficient. Hossain et al. [82] found that smaller NPs (less than 2 μm in diameter) tend to bind to areas with larger shear rates, while larger NPs tend to bind to locations with medium shear rates [7, 82].

Tan et al. [83] developed a 2D computational model to describe the transport and distribution of NPs in branched vessels by coupling the Brownian dynamics of NPs (Eqs. 7, 8), the continuity equation (Eq. 3), the Navier–Stokes equation (Eq. 2) and the receptor–ligand binding model (Eq. 6) and studied the effect of particle shape and size, shear rate, and vessel geometry. In their study, the Navier–Stokes equations were solved using the finite element method and the nonlinear system was solved using the Newton–Raphson method. Additionally, the authors employed the generalized minimum residual (GMRES) iterative algorithm to improve computation efficiency and compute residuals based on matrix-free techniques, as described by Saad and Schultz [84]. They investigated spherical NPs (with diameters of 100 and 200 nm) and nanorods with the same volume as spheres (with aspect ratios of 3 and 5). They found that the adhering rates were higher for nanorods with smaller sizes (due to lower drag force and larger contact surface) at vessel bifurcations and at lower shear rates. Their results also revealed that the adhering dynamics of nanorods depended on the initial contact points and the orientations to the wall, and the ratio of bound NPs between the bifurcation zone and the straight zone depended on the Peclet number [83].

Tan et al. [85] modeled the transport and delivery of NPs in the bloodstream in straight and bifurcated rectangular channels by presenting a combined particulate and continuum models. In the particle model, they coupled the ligand–receptor bonding dynamics (Eq. 6), the Brownian dynamics (Eqs. 7, 8), the Navier–Stokes equations (Eq. 2) and the continuity equation (Eq. 3). In the continuum model, they paired a convection–diffusion–reaction model (Eq. 9) with the adhesion occurring on the reaction surface. They solved their equations using the finite element method and studied the effect of vascular geometry, particle size, and shear rate. Tan et al. [85] considered spherical NPs with diameters of 50, 100, and 200 nm and observed that smaller particles diffused faster than larger particles and had shorter reaction times and faster bonding speeds. Furthermore, their simulation results showed that the binding rate of NPs first increases with the shear rate and then decreases, and the binding rate of the particles enhances with increasing ligand density and receptor density [85].

Sharma et al. [86] tracked a cluster of spherical iron oxide (Fe₃O₄) NPs in a 2D laminar bloodstream under the effect of a magnetic field. To describe the motion of NPs, they solved Newton’s second law, taking into account buoyancy, drag, and magnetic forces, using the classical fourth-order Runge–Kutta method. The authors also used their model to optimize the positioning of an external magnet for magnetic particle capture at the tumor site, to improve the effectiveness of drug targeting. To validate their model, Sharma et al. [86] conducted simulations using COMSOL software. Their findings indicated that magnetic particles can be captured up to a distance of 4.5 cm between the blood vessel and the magnet, but beyond this distance, the particles are free to move [86].

Elnaqeeb et al. [87] studied the transport of blood flow containing copper NPs through a catheterized mild stenotic artery. They used the single-phase model for incompressible steady flow and solved the governing equations of mass (Eq. 24), momentum (Eqs. 25, 26), and energy (Eq. 27) using the Wolfram Mathematica 10 program [87].

$$ \frac{\partial u}{{\partial r}} + \frac{u}{r} + \frac{\partial w}{{\partial z}} = 0 $$

(24)

$$ \rho_{{{\text{nf}}}} \left( {u\frac{\partial u}{{\partial r}} + w\frac{\partial u}{{\partial z}}} \right) = - \frac{\partial P}{{\partial r}} + \mu_{{{\text{nf}}}} \left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{{\partial r}} + \frac{{\partial^{2} u}}{{\partial z^{2} }} - \frac{{u^{2} }}{{r^{2} }}} \right) $$

(25)

$$ \rho_{{{\text{nf}}}} \left( {u\frac{\partial w}{{\partial r}} + w\frac{\partial w}{{\partial z}}} \right) = - \frac{\partial P}{{\partial z}} + \mu_{{{\text{nf}}}} \left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{{\partial r}} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right) + g\left( {\rho \gamma } \right)_{{{\text{nf}}}} \left( {T - T_{0} } \right) $$

(26)

$$ u\frac{\partial T}{{\partial r}} + w\frac{\partial T}{{\partial z}} = \frac{{K_{{{\text{nf}}}} }}{{\left( {\rho c_{p} } \right)_{{{\text{nf}}}} }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) + \frac{{Q_{0} }}{{\left( {\rho c_{p} } \right)_{{{\text{nf}}}} }} $$

(27)

In Eqs. 24–27, u and w represent radial and axial velocity components, respectively, while Q₀ is defined as the constant heat absorption or heat generation. The nanofluid viscosity is denoted by μ_nf, the thermal conductivity of the nanofluid is represented by K_nf, the nanofluid density is given by ρ_nf, the heat capacity of the nanofluid is indicated by (ρcp)_nf, and the thermal expansion coefficient of the nanofluid is denoted by γ_nf. T₀ is the temperatures at the wall of the artery. Elnaqeeb et al. [87] derived expressions for axial velocity, temperature, stream function, resistance impedance, and wall shear stress. They considered the effect of NP volume fractions (ranging from 0.01 to 0.06) and observed that the velocity increases with increasing NPs concentration, but the trapping phenomena and resistance impedance decrease [87].

Chapal Hossain et al. [88] applied an unsteady two-phase flow model to describe the hemodynamic and thermal behaviors of blood-based nanofluids in a bifurcation structure with a flexible membrane wall under the influence of a wire magnetic field. They considered spherical Fe₃O₄ NPs with a diameter of 10 nm and assumed a 2D, incompressible, viscous and Newtonian bloodstream at low Reynolds numbers (Re < 100, laminar flow). Chapal Hossain et al. [88] discretized the conservation equations of momentum (Eq. 29), energy (Eq. 31), and mass (Eqs. 28, 30) using a finite-volume method in a CFD platform [88].

Mixture conservation equation of mass:

$$ \frac{\partial }{\partial t}\left( {\rho_{{\text{m}}} } \right) + \nabla \cdot \left( {\rho_{{\text{m}}} u_{m} } \right) = 0 $$

(28)

Mixture conservation equation of momentum:

$$ \begin{aligned} \frac{\partial }{\partial t}\left( {\rho_{{\text{m}}} u_{m} } \right) + \nabla \cdot \left( {\rho_{{\text{m}}} u_{m} u_{m} } \right) = & - \nabla P + \nabla \cdot \left[ {\mu_{{\text{m}}} \left( {\nabla u_{m} + \nabla u_{m}^{T} } \right)} \right] \\ \quad + \nabla \cdot \left( {\sum\limits_{q = p,f} {\alpha_{q} \rho_{q} u_{{{\text{dr}},q}} u_{{{\text{dr}},q}} } } \right) + \rho_{m} g + F \\ \end{aligned} $$

(29)

Volume fraction equation for particle phase:

$$ \frac{\partial }{\partial t}\left( {\alpha_{p} \rho_{p} } \right) + \nabla \cdot \left( {\alpha_{p} \rho_{p} u_{m} } \right) = - \nabla \cdot \left( {\alpha_{p} \rho_{p} u_{{{\text{dr}},p}} } \right) $$

(30)

Mixture conservation equation of energy:

$$ \frac{\partial }{\partial t}\left( {\sum\limits_{q = p,f} {\alpha_{q} \rho_{q} c_{p,q} T} } \right) + \nabla \cdot \left( {\sum\limits_{q = p,f} {\alpha_{q} u_{q} \left( {\rho_{q} c_{p,q} T + P} \right)} } \right) = \nabla \cdot \left( {k_{{\text{m}}} \nabla T} \right) $$

(31)

Here, $\rho_{{\text{m}}}$ denotes the mixture density, while $q$ represents either $p$ (nanoparticles) or $f$ (biofluid). The volume fraction for phase q is denoted by α_q ($\alpha_{p} + \alpha_{f} = 1$). The mass-averaged velocity is represented by $u = {{\left( {\alpha_{p} \rho_{p} u_{p} + \left( {1 - \alpha_{p} } \right)\rho_{f} u_{f} } \right)} \mathord{\left/ {\vphantom {{\left( {\alpha_{p} \rho_{p} u_{p} + \left( {1 - \alpha_{p} } \right)\rho_{f} u_{f} } \right)} {\rho_{{\text{m}}} }}} \right. \kern-0pt} {\rho_{{\text{m}}} }}$, the drift velocity for phase $q$ is $u_{{{\text{dr,}}q}} = u_{q} - u_{m}$. Other parameters include $\mu_{{\text{m}}}$ for the mixture dynamic viscosity, $k_{{\text{m}}}$ for the mixture thermal conductivity, $c_{p}$ for the specific heat, and $F$, which specifies the Kelvin force relying on the existence of the applied magnetic field. The researchers found that the streamlines, velocity magnitude contours, and isotherms were reasonably affected by the applied magnetic field of the wire [88].

Zaman et al. [89] investigated the transport of NPs in an unsteady, laminar, incompressible, pulsatile blood flow through a curved channel with stenosis and aneurysm. The authors considered copper or silver NPs and developed mass, momentum, and thermal energy equations using curvilinear coordinates. The authors solved the governing equations for Grashof and Reynolds numbers smaller than one using an explicit finite difference scheme based on the assumption of mild stenosis and validated their results using a finite element method. Their findings indicated that the flow rate, shear stress, and velocity increase, but the flow resistance decreases with increasing volume fraction of NPs [89].

Manshadi et al. [90] applied a numerical model to study the transport of clusters of drugs and drugs/cargoes in a luminal artery under the influence of a magnetic field. They used the continuity equation (Eq. 3) and the Navier–Stokes equation (Eq. 32) for the bloodstream through vessels, the Darcy-Brickman momentum equation (Eq. 33) [91] for the bloodstream through tissues, and the Newton’s second law for the motion of particles (Eq. 4) (considering drag and magnetophoretic forces) in the COMSOL Multiphysics framework [90].

$$ \rho \left( {V \cdot \nabla } \right)V = - \nabla P + \mu \nabla \cdot \left( {\nabla V} \right) + F $$

(32)

$$ \frac{1}{\varphi }\rho \left( {V \cdot \nabla } \right)\frac{V}{\varphi } = - \nabla P + \frac{\mu }{\varphi }\nabla \cdot \left( {\nabla V} \right) - \frac{\mu }{k}V + F $$

(33)

The symbols $\varphi$ and $k$ represent porosity and tissue permeability, respectively. To determine the drag force, Manshadi et al. [90] utilized the Schiller–Naumann model, which can be expressed by the following equation [90]:

$$ F_{d} = \frac{{3\mu C_{{\text{D}}} {\text{Re}}_{{\text{b}}} }}{{4\rho_{b} d_{{\text{p}}}^{2} }}m_{p} \left( {V - v_{p} } \right) $$

(34)

$$ C_{{\text{D}}} = \frac{24}{{{\text{Re}}_{{\text{b}}} }}\left( {1 + 0.15{\text{Re}}_{{\text{b}}}^{0.687} } \right) $$

(35)

$$ {\text{Re}}_{{\text{b}}} = \frac{{\rho \left| {V - v_{p} } \right|d_{{\text{p}}} }}{\mu } $$

(36)

The symbols $\rho_{{\text{p}}}$ and $C_{{\text{D}}}$ represent particle density and drag coefficient, respectively. The blood Reynolds number is denoted by ${\text{Re}}_{{\text{b}}}$, and the particle diameter by $d_{{\text{p}}}$. The magnetophoretic force is calculated using the following equation [90]:

$$ F_{{{\text{mag}}}} = 2\pi r_{{\text{p}}}^{3} \mu_{0} \mu_{{\text{r}}} \left( {\frac{{\mu_{{\text{r,p}}} - \mu_{{\text{r}}} }}{{\mu_{{\text{r,p}}} + 2\mu_{{\text{r}}} }}} \right)\nabla H^{2} $$

(37)

where $r_{{\text{p}}}$ is particle radius, $\mu_{0}$ represents magnetic permeability of space, $\mu_{{\text{r}}}$ is the relative magnetic permeability, $H$ is the induced magnetic field, and $\mu_{{\text{r,p}}}$ represents particle magnetic relative permeability. Manshadi et al. [90] investigated the impact of magnet size, magnetic field strength, relative magnetic permeability of particles, initial position of particles, and particle size on drug delivery efficiency. The authors concluded that an increase in the size of the cargo/particles/drug and the strength of the magnetic field resulted in greater capture of cargo/particles/drug in the tissue [90].

In a 2D numerical study, Sharifi et al. [92] investigated the transport of drug-carrying spherical Fe₃O₄ NPs in aneurysm vessels under the influence of a magnetic field at a Reynolds number of 200. Sharifi et al. [92] took into account the flow of blood-based nanofluids as an unsteady, incompressible, laminar and Newtonian fluid with a NPs concentration of 0.33 mg/cc. They used the equations of continuity, momentum, and mass transfer to investigate the effect of parameters such as NP diameter (2, 5, 10, and 15 nm) and magnet location on the drug delivery process. Sharifi et al. [92] employed the finite-volume method in conjunction with C +  + programming to numerically solve continuity, momentum, and mass transfer equations. The transient terms of the equations were discretized using the Euler first-order central scheme. In addition, they utilized second-order central difference and second-order upwind methods for diffusion and advection terms of the equations, respectively. To handle the time derivative, an implicit scheme was utilized. Sharifi et al. [92] also applied the PISO algorithm with double correction for pressure–velocity coupling. The first-order Gauss linear scheme was used to discretize the gradient terms. They observed the maximum retention time for NPs with a diameter of 10 nm during their study [92]. Shahzadi and Kousar [93] dealt with modeling the hybrid mediated blood flow through atherosclerotic bifurcated artery with considering slip effect, compliant wall impacts and convective heat transfer effects [93]. They modeled the laminar bloodstream in a bifurcated stenosed artery in the presence of copper and copper oxide NPs (Cu–CuO/blood and Cu-blood) based on continuity, momentum and energy conservation equations using the single-phase approach. They investigated the effect of Cu or Cu/CuO particles concentration (volume fractions less than 0.05) on velocity and temperature profiles. Shahzadi and Bilal [94] observed that Cu–CuO–blood nanofluid had higher velocity profiles compared to pure blood and Cu-blood flows [94]. Kolitsi and Yiantsios [65] numerically simulated the transport of iron oxide NPs during three stages of microcirculation: to vessel walls, through their pores and into the interstitium. They studied the share of different forces based on an order-of-magnitude method. To model the flow of blood-based nanofluid in a vascular network, they used the convection–diffusion equation and applied the simulations using the Galerkin finite element method. Kolitsi and Yiantsios [65] investigated spherical NPs with diameters ranging from 50 to 200 nm and found that the main resistance to NP transport was respectively in the interstitium, inside the wall pores and during the microcirculation stage to the vessel walls [65]. Majee and Shit [95] studied 2D transport of magnetic particles in Newtonian, unsteady blood flow in a diseased arterial segment with atherosclerosis. They investigated the effect of particle concentration and magnetic field on NP aggregation and flow pattern. They used the vorticity-stream function formulations to solve the conservation equations of mass, momentum and energy [95].

Ali et al. [96] investigated Newtonian, laminar and incompressible bloodstream containing magnetic NPs in a capillary under the effect of a constant magnetic field. They solved the governing mass and momentum equations for fluid, as well as Newton’s second law for particles (considering drag and magnetic forces), based on finite element method and a hybrid CPU-GPU approach in the MATLAB platform. The following equation shows the momentum conservation equation for the fluid [96].

$$ \rho \frac{\partial V}{{\partial t}} = \mu \left( {\frac{{\partial^{2} V}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial V}{{\partial r}}} \right) + \frac{NA}{\rho }\left( {v_{p} - V} \right) - \frac{\partial P}{{\partial z}} $$

(38)

where $N$ represents the numeral density of suspended particles and $A$ is Stoke’s coefficient.

Ali et al. [96] considered the effect of capillary radius, pressure, magnetic field intensity and NPs radius on the nanofluid flow. Their observations showed that there is a direct relationship between the magnetic field and the flow pattern, where an increase in the former corresponds to an upsurge in the latter. Additionally, the distance between the magnet and capillary wall has a direct effect on velocity and can aid in attracting magnetic NPs to the capillary wall [96].

Salem and Tuchin [97] investigated the transport of magnetic NPs in the bloodstream through a capillary tube under the effect of a magnetic field perpendicular to the direction of flow. They performed the magnetic equation for the permanent magnet and the Navier–Stokes equation for the nanofluid, and solved the governing equations in the COMSOL Multiphysics® framework. They found the strength of the magnetic field and the distance between the capillary wall and the magnet surface affect the capture and accumulation of NPs, which could potentially be used to optimize the delivery of nanofluid-based therapies [97].

Al-Qamdi et al. [98] modeled 2D laminar blood-based nanofluids composed of copper or/and copper oxide NPs (copper/blood and copper + copper oxide/blood) in a rectangular deformable channel with permeable walls. They studied the effect of magnetohydrodynamics and heat source/sink on the flow pattern at low Reynolds numbers (Re < 100) and wrote the equations of continuity, energy and momentum based on the single-phase model [99]. Al-Qamdi et al. [98] used elegant homotopy analysis method (HAM) to obtain analytic approximations for the resulting system of nonlinear differential equations. Their results showed that hybrid nanofluids (copper + copper oxide/blood) were more useful than Cu/blood nanofluids for drug delivery in contracting/expanding channels [98]. Meschi et al. [100] used a combination of an image-based computational fluid dynamics method (FEniCS-based open-source finite element solver Oasis [101]) with continuum transport models to study the NP transport or transfer of microcarriers containing NPs in the bloodstream through the coronary arteries. They obtained the concentration of micro-carriers and NPs by solving a coupled system of continuum advection–diffusion–reaction equations. They considered spherical NPs with a radius of 90 nm and spherical microcarriers with a radius of 1.5 μm. Furthermore, Meschi et al. [100] assumed that blood behaves as a Newtonian fluid, although they took into account the impact of hematocrit² (0.4) on the calculation of the particle diffusion coefficient (NP or microcarrier anisotropic diffusion tensor) in their modeling [100].

Khazayinezhad et al. [102] studied the transport of graphene NPs in blood flow through a vessel under the influence of an angled magnetic field. They took into account the blood vessel as a porous medium having walls with peristaltic waves. Considering the Joule heating and viscous dissipation effects, Khazayinezhad et al. [102] solved the governing equations by Optimal Collocation Method and investigated the influence of NPs concentration and inclination angle of magnetic field on the temperature profile. Nuwairan and Souayeh [103] simulated the transport of gold-blood nanofluid flow in a micro-channel, taking into account the effects of bioconvection, gyrotactic microorganisms, activation energy and radiation. They also considered the bloodstream as an electro-magneto-hydrodynamic peristaltic flow and investigated the influence of different shapes of NPs, such as bricks, platelets, and cylinders. Nuwairan and Souayeh [103] solved the conservation equations of momentum, mass, and energy based on low Reynolds number, long wavelength, and Debye–Hückel linearization assumptions in the MATLAB environment. They found that nanofluid velocity was higher for brick-shaped NPs compared to cylindrical- and platelet-shaped NPs. Furthermore, they found that NP concentration increased with an increase in radiation and Brownian motion parameters [103]. The models studied in this section are summarized in Table 2 for easy reference and comparison.

Table 2 Multi-particle models with Newtonian behavior of blood and without considering blood cells

Although, in large vessels, because of the high shear rates, blood can be assumed as a Newtonian fluid. But, non-Newtonian behavior of blood is more likely in microcirculation (arteries, capillaries and veins). In microcirculation, the fast-moving RBCs tend to force WBCs, platelets and NPs laterally, accumulate in the central core region of the vessels, and form a marginal “red blood cell-free layer” (RBC-FL). The presence of this layer can significantly alter the velocity profile in small vessels, deviating from the parabolic shape seen in Poiseuille flow. In this case, the velocity profile is flat (plug flow) in the center of the vessel, and the radius of the plug increases with an increase in hematocrit. Therefore, in the microcirculation, careful consideration of the non-Newtonian behavior of blood is required for the development of accurate models for the transport of nanoparticles in blood flow [68, 104, 105]. Figure 3 illustrates the presence of the RBC-FL and non-Newtonian behavior of blood flow in microcirculation. In the following section, some research studies that have considered the non-Newtonian behavior of blood flow in the microcirculations are mentioned.

Fig. 3

Red blood cell-free layer and non-Newtonian behavior of blood flow

Models with Non-Newtonian Behavior of Blood

Some research has shown that blood-NP suspensions can exhibit non-Newtonian behavior, which can greatly impact nanoparticle transport and margination in blood vessels. In this section, we will examine some of the key models that have been developed to study the non-Newtonian behavior of blood-NP suspensions, focusing on their assumptions, methods, and results.

In a study conducted by Gentile et al. [68], the transport of spherical NPs with a diameter of 200 nm in cylindrical blood vessels was investigated by considering blood as a Casson fluid. Modifying the Taylor–Aris theory [69, 70], Gentile et al. [68] studied the longitudinal diffusion of NPs in blood vessels at different values of the blood rheological parameter of ξ_c (ratio of plug to vessel radius) and permeability parameters of the blood vessel (hydraulic conductivity and pressure drop). Equation (39) shows the effective longitudinal diffusion of NPs (D_eff) comprises two terms: a molecular diffusion term D_m and a convective term proportional to P_e0², where Pe₀ is the Peclet number at the inlet [68].

$$ D_{{{\text{eff}}}} = D_{{\text{m}}} \times \left[ {1 + \frac{{P_{e0}^{2} }}{48}\left( {\frac{{\cosh \left( {\overline{z} \Gamma \left( {\xi_{c} } \right)} \right) - \Omega \cosh \left( {\Gamma \left( {\xi_{c} } \right) - \overline{z} \Gamma \left( {\xi_{c} } \right)} \right)}}{{1 - \Omega \cosh \left( {\Gamma \left( {\xi_{c} } \right)} \right)}}} \right)^{2} \times G\left( {\xi_{c} } \right)} \right] $$

(39)

$\Gamma$ is a function of the permeability and the rheology of blood and $G$ is a function of the rheology of blood. The molecular diffusion term D_m has been given in Eq. (11). Gentile et al. [68] found that an increase in either the vascular permeability parameters or rheological parameters of blood can reduce the longitudinal diffusion of NPs [7, 68].

Haverkort et al. [106] investigated the transport of spherical magnetic particles in a laminar bloodstream (Re <  = 200) under the effect of a magnetic field. They studied particle motion and blood flow in a straight cylindrical channel and a 90-degree-bended tube. In addition, they performed unsteady simulations in a carotid artery and a left coronary artery. They considered the blood as a power-law fluid (Eq. 41) and solved the momentum conservation equations (Eq.

particles 40) for the blood flow, and Newton’s second law (Eq. 4) for the particle trajectory (considering magnetization and drag forces) using ANSYS FLUENT [106].

$$ \rho \left( {\frac{\partial V}{{\partial t}} + \left( {V \cdot \nabla } \right)V} \right) = - \nabla P + \nabla \cdot \left( {\mu \left( {\dot{\gamma }} \right)\nabla V} \right) $$

(40)

where

$$ \mu (\dot{\gamma }) = \lambda \left| {\dot{\gamma }} \right|^{n - 1} $$

(41)

$$ \mu (\left| {\dot{\gamma }} \right|) = \mu_{\infty } + \Delta \mu \exp \left[ { - \left( {1 + \frac{{\left| {\dot{\gamma }} \right|}}{a}} \right)\exp \frac{ - b}{{\left| {\dot{\gamma }} \right|}}} \right] $$

(42)

$$ n(\left| {\dot{\gamma }} \right|) = n_{\infty } - \Delta n\exp \left[ { - \left( {1 + \frac{{\left| {\dot{\gamma }} \right|}}{c}} \right)\exp \frac{ - d}{{\left| {\dot{\gamma }} \right|}}} \right] $$

(43)

where $\dot{\gamma }$ is the strain rate, $\mu_{\infty } = 0.0035\;{\text{Pa}}\;{\text{s}}$, $n_{\infty } = 1$, $\Delta \mu = 0.025\;{\text{Pa}}\;{\text{s}}$, $\Delta n = 0.45\;{\text{Pa}}\;{\text{s}}$, $a = 50\;{\text{s}}^{{ - {1}}}$, $b = 3\;{\text{s}}^{{ - {1}}}$, $c = 50\;{\text{s}}^{{ - {1}}}$, and $d = 4\;{\text{s}}^{{ - {1}}}$ [106].

Haverkort et al. [106] implicitly solved the Navier–Stokes equation (Eq. 2) with a quadratic upwind discretization (QUICK) of the nonlinear term. They also solved Newton’s second law numerically by integrating it with a sixth order Runge–Kutta scheme. Investigating with diameters less than 4 µm, they found that a significant fraction of 4-micron particles could be trapped in a portion of artery by applying a magnet placed a few centimeters from the artery [106, 107]. Habibi and Ghasemi [108] investigated the transport of laminar magnetic NPs-blood flow in a 2D channel (W = 0.001 m, L = 0.02m) under the effect of an external magnetic field. They described the non-Newtonian behavior of blood flow by a power-law viscosity model and solved the momentum and mass conservation equations using a finite-volume method based on the SIMPLE algorithm. For the mass conservation of NPs, they used the advection–diffusion model, considering the influence of hydrodynamic and magnetic forces on the velocity of particles. They found that the NPs accumulation improved with increasing magnetic strength and particle size [108].

Kenjeres and Righolt [109] studied the transport of spherical magnetic particles in the bloodstream through a brain’s vascular system designed based on a MRI image of a patient at fluid Re <  = 460. They described the continuous phase (blood flow) based on the conservation equations of mass and momentum for a power-law fluid (Eq. 41), and used the Lagrangian tracking of particles (discrete-phase model) to estimate the particle accumulation on the arterial wall in the presence of magnetic field gradients. They used the Newton’s second law (taking into account drag, virtual mass, and magnetization forces) to track the trajectory of spherical magnetic particles in the fluid. Kenjeres and Righolt [109] solved the governing equations using a second-order finite-volume numerical solver [107, 109].

Doig et al. [110] simulated a blood flow containing spherical NPs through a bifurcated carotid artery with a stenosis.³ They modeled the transport of NPs based on a discrete particle approach and a simple one-way Lagrangian coupling in FLUENT software. They considered the Brownian force component as a Gaussian white noise (Eq. 44), the Saffman lift due to shear based on Li and Ahmadi’s formulation (Eq. 45) [111], and the drag force on the particles based on the Stokes–Cunningham formulation (Eq. 46).

$$ F_{{{\text{bi}}}} = \zeta_{i} \sqrt {\frac{{\pi S_{0} }}{\Delta t}} $$

(44)

$$ F_{l} = \frac{{2K\nu^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \rho d_{ij} }}{{\rho_{p} d_{p} \left( {d_{lk} d_{kl} } \right)^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}}} }}\left( {u - v_{p} } \right) $$

(45)

$$ F_{D} = \frac{18\mu }{{d_{p}^{2} \rho_{p} C_{{\text{c}}} }} $$

(46)

where $\zeta_{i}$ are zero-mean, unit-variance-independent Gaussian random numbers and $S_{0}$ is the spectral intensity. Also, $K = 2.594$, $d_{ij}$ is the deformation tensor and $C_{{\text{c}}}$ is the Cunningham correction based on the molecular mean free path. Doig et al. [110] used a PREssure Staggering Option (PRESTO) scheme for pressure discretization and a power law expression for the momentum term. They studied the effect of NPs size (diameters ranging from 50 to 500 nm) on particle–wall interaction and particle residence time at low NPs concentrations (< 1 vol%) and low Reynolds numbers (less than 1). They found that smaller particles had more considerable ability to reach the target zone [110].

Cherry and Eaton [107] simulated the transport of magnetic particles with a diameter of one micrometer in the bloodstream through a straight tube and a bifurcating tube, based on the mathematical model proposed by Carrier [112]. They derived the advection–diffusion equation for the particle concentration, and the momentum and continuity equations for the mixture. Cherry and Eaton [107] incorporated Brownian diffusion and diffusion resulting from collisions between particles and red blood cells into their mathematical model. Their mathematical model also took into account the dispersion caused by collisions between particles and red blood cells, as well as the influence of various forces, including pressure, gravity, the bulk magnetic force from an external magnetic field gradient, viscous force, and inter-particle magnetic force. Using the built-in laminar, second-order upwind solver in Fluent, Cherry and Eaton [107] conducted simulations and analyzed the impact of applied magnetic field gradients, particle cluster concentration, and particle diffusion on the transport of magnetic particles. The simulation results indicated that while it is possible to decelerate a particle cluster in a straight tube, it cannot be brought to a complete stop, and steering the cluster toward a specific branch of a bifurcation is more successful. Furthermore, the study revealed that particle diffusion plays a crucial role in restraining the effectiveness of magnetic control [107].

Varmazyar et al. [113] investigated the distribution of spherical magnetic NPs in a laminar pulsatile blood flow within the lumen. They considered the blood flow as power-law fluid under the influence of a vein stenosis and a non-uniform magnetic field and solved the conservation equations of mass (Eq. 3), momentum (Eq. 47) and NPs concentration (Eq. 9) based on a finite-volume approach implemented in a FORTRAN code [113].

$$ \rho \left( {\frac{\partial V}{{\partial t}} + \left( {V \cdot \nabla } \right)V} \right) = \rho g - \nabla P + \nabla \cdot \tau + F_{{{\text{mag}}}} $$

(47)

where $\tau$ is the tangential shear stress. The authors addressed the coupling of velocity and pressure in their mathematical model by utilizing the Semi-Implicit Method for Pressure Linked Equation (SIMPLE) algorithm over a staggered grid. The resulting equations were then solved iteratively using the tridiagonal matrix algorithm at each time step of the simulation [113]. Varmazyar et al. [113] examined the effect of vein geometry, the number of stenosis, vein stenosis severity, and NPs size (with diameters ranging from 200 to 2000 nm) on the drug delivery process. They found that the non-Newtonian behavior of the bloodstream played a considerable role in decreasing the effects of vein stenosis. They also observed that particle absorption decreased as the magnetic field strength decreased and that magnetic forces increased when the effect of momentum forces diminished, which pulled drugs toward the tissue [113].

The computational simulation by Abu-Hamdeh et al. [114] modeled the transport of magnetic NPs in a laminar bloodstream between parallel plates under the influence of a magnetic field. They considered the blood flow as both Newtonian and non-Newtonian fluids, as described by the power-law model, and solved the conservation equations of momentum and mass using a finite-volume method in the Open-FOAM framework. Their study revealed the necessity of considering the non-Newtonian behavior in modeling vascular blood flow. Additionally, Abu-Hamdeh et al. [114] observed that the intensity and the permeability coefficient of the magnetic field played a major role in the accumulation of magnetic NPs on the walls of the parallel plates [114].

Jafarzadeh et al. [8] examined the persistence and distribution of drug-carrying iron oxide NPs in a laminar bloodstream through an abdominal aortic aneurysm. Using a two-phase modeling approach, they used the Brownian diffusion to describe the relative motion of the blood flow and NPs and solved the equations of momentum (Eq. 50), continuity (Eq. 48), and drug concentration (Eq. 9) using the finite-volume method in the OpenFOAM platform [8].

$$ \frac{{\partial \rho_{{{\text{nf}}}} }}{\partial t} + \nabla \cdot \left( {\rho_{{{\text{nf}}}} V} \right) = 0 $$

(48)

$$ \rho_{{{\text{nf}}}} = \left( {1 - C} \right)\rho_{f} + C\rho_{np} $$

(49)

$$ \frac{{\partial \left( {\rho_{{{\text{nf}}}} V} \right)}}{\partial t} + \rho_{{{\text{nf}}}} V \cdot \nabla V = - \nabla P + \nabla \cdot \tau $$

(50)

Jafarzadeh et al. [8] incorporated the shear-thinning nature of blood in their mathematical model based on the model proposed by Ameenuddin et al. [115]. They related blood viscosity to the hematocrit and strain rate, and drug dispersion in the blood to the NP diameter and hematocrit. They studied the effect of different hematocrits (30, 40 and 50%) and different diameters of spherical NPs (5, 10 and 15 nm) on drug persistence, blood flow pattern and shear stress. Their study revealed that increasing the hematocrit level reduced the strength of vorticity and drug concentration while increasing the wall shear stress. Additionally, Jafarzadeh et al. [8] found that the drug concentration decreased with increasing NP diameter and that the NP diameter had no significant effect on vorticity and wall shear stress [8].

Sodagar et al. [116] modeled the transport of spherical magnetic microparticles (with diameters ranging from 1 to 6 μm) in a turbulent bloodstream through a 3D aortic arch in the presence of a magnetic field. They considered transient, non-Newtonian, and incompressible blood flow with oscillating velocity profiles at the inlet. They used a discrete-phase model that treats blood and particles as continuous and discrete phases, respectively. To simulate turbulent blood flow, they applied the continuity equation (Eq. 3), equation of motion (Eq. 51), and Newton’s second law (incorporating drag, magnetic, and buoyancy forces), along with the k-ω model (Eqs. 52, 53), in the ANSYS FLUENT platform [116].

$$ \rho \frac{Du}{{Dt}} = \frac{\partial P}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \mu_{{\text{t}}} } \right)\left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{i} }}{{\partial x_{i} }}} \right)} \right] + S_{v} $$

(51)

$$ \rho \frac{Dk}{{Dt}} = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \frac{{\mu_{{\text{t}}} }}{{\sigma_{k} }}} \right)\frac{\partial k}{{\partial x_{j} }}} \right] + G_{{\text{k}}} - Y_{{\text{k}}} $$

(52)

$$ \rho \frac{D\omega }{{Dt}} = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \frac{{\mu_{{\text{t}}} }}{{\sigma_{\omega } }}} \right)\frac{\partial \omega }{{\partial x_{j} }}} \right] + G_{\omega } - Y_{\omega } $$

(53)

Here, $\mu_{{\text{t}}}$ and $S_{v}$ are turbulence viscosity and source term, respectively. G_k and G_ω represent the turbulent kinetic energy rate and the production of vorticity (ω), respectively. Y_k and Y_ω denote the dissipation rates of k and ω, respectively. Sodagar et al. [116] solved the equations for blood flow in a transient state over one cardiac cycle. They applied the second-order upwind method to discretize the diffusion terms and the second-order central method for the advection terms. Sodagar et al. [116] considered the effect of oscillating input, non-Newtonian viscosity, direction of magnetic field, and diameter of microparticles on drug delivery. They found that the efficiency of particle capture enhanced with increasing diameter of microparticles [116].

Table 3 provides a brief overview of the mathematical models that incorporate the non-Newtonian behavior of blood flow. However, these models have only corrected the terms of shear stress or NP diffusion coefficient without considering the role of the blood components and their interactions with each other and with nanodrugs. Therefore, these models are still not comprehensive enough to accurately describe the complex conditions that occur during the transport and margination of nanodrugs in the circulatory system. To date, only a limited number of mathematical models have considered the role of the blood components and their interactions in the bloodstream containing nanodrugs. The following section presents these models in more detail.

Table 3 Multi-particle models with non-Newtonian behavior of blood and without considering blood cells

Models with Considering Blood Cells

Micro-/nanoparticles’ transport and margination in blood vessels can be significantly affected by the presence of blood cells. Consequently, some models have been developed to consider the impact of blood cells on particle behavior. In this section, we will explore some of the key models that take into account the presence of blood cells, with a focus on their assumptions, methods, and findings.

Due to the significant length-scale discrepancy between the blood cells ∼ O (10 μm) and the NPs ∼ O (10 nm), analyzing the transport of nanoparticles in the presence of blood cells is a significant challenge. Furthermore, the complex dynamics of nanoparticles, which depend heavily on Brownian motion, inter-particle hydrodynamic interactions (HI), and particle–cell interactions, increase the complexity of modeling NP transport and margination in the bloodstream [40]. In the following studies, although the base fluid (blood plasma) is simulated as a Newtonian fluid, the non-Newtonian behavior arises from modeling RBCs and micro-/nanoparticles as separate components.

Fullstone et al. [9] used a combination of flexible large-scale agent-based modeling (FLAM) and computational fluid dynamics (CFD) to predict the distribution of drug-carrying spherical NPs in cylindrical blood capillaries [123]. They considered the blood plasma as an incompressible, laminar, and Newtonian nanofluid flow and wrote the continuity equation (Eq. 3) and the Navier–Stokes equation (Eq. 2) for it. They applied a finite element approach, using Galerkin/least squares (GLS) methods to solve the Navier–Stokes equations. In their model, RBCs were treated as separate objects that create transient moving wall boundaries to influence flow. To predict the motion of NPs, the researchers applied Newton’s second law, taking into account Brownian and laminar flow forces. They considered the vessel wall to be a reflective boundary in the event of an NP-vessel wall collision and neglected interactions between NPs as well as those between NPs and RBCs. Fullstone et al. [9] investigated the effect of NP size (ranging from 10 to 160 nm in diameter) and hematocrit level (0, 10.7% and 38%) on drug diffusion. They found that the moderate hematocrit range resulted in the highest diffusion of NPs toward the vessel wall [8, 9].

Freund and Shapiro [117] developed a model to study the transport of spherical magnetic microparticles (with a diameter of 0.56 μm) under the influence of an external magnetic field in the bloodstream through a cylindrical vessel (with a diameter of 16.9 μm and a length of 33.9 μm). They modeled 10 magnetic particles and 19 red blood cells (equivalent to a hematocrit level of 0.22) as rigid spheres and fluid filled elastic shells, respectively. Freund and Shapiro [117] used the particle-mesh-Ewald algorithm, which was proposed for suspensions by Saintillan et al. [118], to perform their modeling. They solved the equations using the generalized minimal residual algorithm (GMRES) [119]. They considered blood to be a Newtonian fluid and investigated the effect of applying a vertical and parallel magnetic field on fluid flow. They found that the magnetic field could enhance the margination of particles toward the vessel wall [117].

Tan et al. [30] developed a hybrid particle-cell approach to model the transport, dispersion and binding dynamics of polymer-drug conjugates based spherical NPs (with diameters ranging from 10 to 200 nm and a volume concentration of 0.08%) in a blood microvessel. They considered the motion and deformation of RBCs through the immersed finite element method (IFEM) [60,61,62] and the motion and adhesion of NPs through Brownian adhesion dynamics (Eqs. 7, 8) [30]. Tan et al. [30] employed a computational framework in which RBCs and NPs were treated as Lagrangian solids immersed in an Eulerian fluid domain. The entire transport problem was based on solving a Navier–Stokes equation [30, 122]. In their study, the authors modeled RBCs as flexible, thin membranes enclosing plasma. To represent the material behavior of the RBC membrane, they used a Mooney–Rivlin strain energy function [30]. They modeled motion of blood plasma through continuity and Navier–Stokes equations (Eqs. 2, 3). To model the interaction between individual NPs, they applied a Lennard–Jones potential. They also used a Morse potential to describe the interactions between NPs and RBCs. Tan et al. [30] solved the coupled fluid–structure interaction equations using the finite element method. They obtained the Petrov–Galerkin weak form by performing integration by parts and using the divergence theorem. The nonlinear system was then solved using the Newton–Raphson method. To improve computation efficiency, Tan et al. [30] employed the Generalized Minimum Residual (GMRES) iterative algorithm, which computes residuals based on matrix-free techniques [30]. They investigated the effect of vascular flow velocity, particle size and RBCs on the distribution of NPs and drug delivery efficiency. Tan et al. [30] observed that the distribution of NPs in the capillaries was not uniform, with more particles located near the vessel wall. They also found that the rate of NP binding to the vessel wall in the presence of RBCs was twice that of the case without RBCs. Additionally, they discovered that increasing the shear rate could enhance the tumbling motion of RBCs in the core area of the capillary, leading to the dispersion of NPs [30]. Although the model proposed by Tan et al. [30] includes the Brownian effect, it does not take into account the HI effect. Several studies have shown that HI has a significant impact on the rheological behavior of non-colloidal/colloidal suspensions [40, 120, 121]. Lee et al. [122] applied a similar hydrodynamic approach to all blood components (plasma, RBCs and NPs) which were resolved directly using finite element grids [40]. In addition to the RBCs–NP and NP-NP interactions, they also considered RBC-RBC-RBC interactions based on Morse potential. They investigated the transport of 100 spherical fluorescent beads with diameters ranging from 10 to 1000 nm in a blood vessel with a diameter of 20 μm and a length of 60 μm at various blood hematocrit levels (0, 15% and 30%). They estimated the radial dispersion coefficient of NPs as a function of particle size and hematocrit level [122]. Unlike the margination behaviors observed by Tan et al. [30], the simulation results showed a relatively small margination of NPs [40].

Tan et al. [124] also conducted a 2D simulation using an immersed boundary fluid–structure interaction method based on the lattice Boltzmann model for fluid, an elastic cell membrane model for RBCs, and a particle motion model for NPs (Langevin dynamics). They investigated the impact of different flow conditions and hematocrit levels on the dispersion of 100 nm spherical nanoparticles in a rectangular channel measuring 50 × 25 μm [40, 124].

Li et al. [104] also presented a computational model for the 2D simulation of NPs transport in a microvessel using the molecular electrodynamic finite element method (IMEFEM) [125]. They meshed the fluid domain and solid domain by Eulerian unstructured and Lagrangian nonlinear finite element, respectively. The Navier–Stokes equation was used for the fluid domain and is given as follows [104]:

$$ \rho \left( {\frac{\partial V}{{\partial t}} + V \cdot \nabla V} \right) = \nabla \cdot \sigma + f^{{{\text{FSI}}}} + \nabla \cdot \sigma^{{\text{M}}} + \nabla \cdot \overline{S} $$

(54)

where $\sigma$, $f^{{{\text{FSI}}}}$, $\sigma^{{\text{M}}}$ and $\overline{S}$ are, respectively, the Cauchy stress tensor, the FSI force, the Maxwell stress tensor and the stochastic stress tensor.

In their modeling, the governing equation of the immersed solids was given as follows:

$$ \rho^{{\text{s}}} \left( {\frac{{\partial^{2} u^{{\text{s}}} }}{{\partial t^{2} }}} \right) - \nabla \cdot \sigma^{{\text{s}}} = f^{{\text{FSI,s}}} + f^{{{\text{ext}}}} $$

(55)

where $\rho^{{\text{s}}}$, $u^{{\text{s}}}$, $\sigma^{{\text{s}}}$, $f^{{\text{FSI,s}}}$ and $f^{{{\text{ext}}}}$ , respectively, represent the density of solid, the displacement field of solid, the Cauchy stress tensor of solid, the FSI force applied on the solid surface and the external force [104]. They also used Gauss’s law or Poisson’s equation to describe the electric field and considered the deformation of RBCs using a Mooney–Rivlin strain energy function. In addition, they modeled RBC–RBC interactions using a Morse-type potential and RBC–NP and NP–NP interactions using a Lennard–Jones potential. They examined the effect of NPs size (diameter less than 1000 nm) and NPs shape (spherical, capsular and elliptical) on their distribution in the blood vessels. Their results demonstrated that the nanoparticles in the bloodstream tend to accumulate in regions near the vessel wall and as the size of NPs increases, the number of NPs near the vessel wall gradually increases. Furthermore, they discovered that spherical NPs have a lower lateral drift velocity compared to capsular and elliptical NPs [7, 104]. It is evident that 2D models do not provide a comprehensive understanding of the actual 3D margination behavior of NPs [40].

Müller et al. [126] used the dissipative particle dynamics (DPD) [127, 128] and the smooth dissipative particle dynamics (SDPD) [129] to, respectively, simulate the two- and three-dimensional transport of NPs in the bloodstream. They studied the impact of particle shape (spherical and elliptical) and particle size (ranging from one hundred nanometers to several micrometers), blood hematocrit, channel size, and blood flow rate on particle margination. Müller et al. [126] found that spherical particles showed slightly better margination than elliptical particles, but elliptical particles had a much higher chance of adhesion due to their larger surface area for adhesive interactions and reduced rotational dynamics within the RBC-FL. They also found that smaller vessel sizes, larger particle sizes and higher blood hematocrits were more effective for particle margination. Therefore, Müller et al. [126] suggested the use of micron-sized elliptical particles instead of sub-micron spheres for the particle margination and adhesion steps [126].

In another study, Müller et al. [130] used the same mathematical modeling to investigate the margination of spherical NPs in two- and three-dimensional bloodstream. Their study demonstrated that, as long as the particle size was not too small in comparison with the thickness of the RBC–FL, margination increased with increasing particle size and hematocrit level, as well as decreasing channel width and shear rate. They observed the best margination results for particles with diameters ranging from 2 to 3 μm. Müller et al. [130] also discovered that deformable particles were more effective at low shear rates and low thickness of the RBC-FL, but rigid particles showed better margination properties in other cases. Based on their results, the size of NPs and their collision with erythrocytes determine particle distribution in the RBC-FL, while hydrodynamic interactions between particles and erythrocytes affect the margination velocity [130]. Based on some research, methods based on the dissipative particle dynamics can only accurately describe the behavior of hundreds of RBCs for a short period of time (0.1 s) [104].

Despite the significant impact of Brownian motion on NP dynamics, none of the above-mentioned studies have comprehensively analyzed NP Brownian motion [40]. To overcome the limitations of the aforementioned models, Liu et al. [40] investigated NP diffusion in blood flow through a microvessel using a 3D approach based on the lattice Boltzmann method [131,132,133] for the fluid phase, the coarse-grained Spectrin-link method [134, 135] for the RBCs and the Langevin dynamics method [40] for the NPs. Their model enabled the consideration of interactions between components at different scales by providing comprehensive two-way coupling schemes. They considered spherical NPs with diameters ranging from 1 to 500 nm, volumetric concentrations of 0.5% and 13% in the bloodstream, and a hematocrit level of 20%. Liu et al. [40] discovered that for particles with diameters ranging from 1 to 100 nm, Brownian diffusion is the primary radial diffusion mechanism, whereas for 500 nm particles, both RBC-enhanced diffusion and Brownian diffusion are effective on radial diffusion [40]. Using the same mathematical modeling, Liu et al. [136] calculated the diffusion tensor of NPs in the bloodstream at various hematocrit levels and shear rates [136].

Ye et al. [137] investigated the margination of nanoworms and magnetic NPs in the bloodstream through rectangular channels under the influence of an external magnetic field. They described the NP-fluid interface (PFI) and RBC-fluid interface (CFI) using the IBM-based force coupling and the Immersed boundary method (IBM)-based velocity coupling, respectively. After validating the CFI and PFI schemes, Ye et al. [137] integrated these two schemes within the parallelized molecular dynamics platform of the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) [138]. They also utilized the parallelized lattice Boltzmann simulator within LAMMPS to simulate fluid flow. They observed that the magnetic field could enhance NP margination toward the vessel wall [137]. A summary of multi-particle models that consider blood cells is available in Table 4.

Table 4 Multi-particle models with considering blood cells

In this section, we discussed models that take into account the effect of RBCs on the transport and margination of micro-/nanoparticles in the bloodstream. These models are more complex than the previous ones as they require a detailed understanding of the interactions between the micro-/nanoparticles and the blood cells. However, they offer a more realistic representation of the blood flow and can provide insights into the behavior of micro-/nanoparticles in more physiologically relevant conditions. It is worth noting that these models do not yet account for the effect of platelets and white blood cells in the presence of micro-/nanoparticles. The simultaneous margination of micro-/nanoparticles, platelets, and white blood cells, along with their comparable concentrations and sizes, can increase the likelihood of cell-particle interactions, especially in the red blood cell-free layer (RBC-FL). Therefore, future models should aim to incorporate the effect of not only RBCs, but also platelets and white blood cells to provide a more comprehensive understanding of the behavior of micro-/nanoparticles in the bloodstream. Such models can also help in the development of more effective drug delivery strategies that take into account the complex interactions between particles and blood cells.

Future Aspects

Some studies have shown that the micrometer and submicrometer particles tend to accumulate more near the vessel wall in the RBC-FL [122, 126]. In contrast, small particles like NPs or other particles with diameters below a few micrometers can penetrate deeper into the cancerous mass more easily by overcoming the network of proteins and other molecules that make up the complex tumor matrix, as well as the pressure exerted by the fluid in the spaces between cells in the tumor, known as the adverse interstitial fluid pressure [122, 139, 140]. As a result, the concept of multistage drug delivery carriers [141, 142], which involve larger microparticles carrying smaller nanocarriers, appears to be very promising in enhancing drug delivery to tumors. NP-carrying microparticles can be used to marginate and adhere to a specific site within the microvasculature, which is then followed by the diffusion of NPs into the cancerous tissue [126]. In terms of particle shape, elliptical and rod-shaped particles have been shown to exhibit better binding to the vessel wall [7, 126]. However, overall, spherical particles have better margination in blood vessels and better diffusion into the cancerous tumor matrix and seem to be more appropriate for the entire process of drug delivery. Additionally, rigid particles have been found to exhibit better margination [7]. Furthermore, magnetic particles are highly attractive for drug delivery because they can be directed to the target tissue using an external magnetic field and have a longer circulation time than conventional drugs [40, 107].

Although many researchers have studied the transport and margination of micro-/nanoparticles in the bloodstream, there is still a lack of mathematical models that can simultaneously consider a large number of controlling variables that affect this process. In most of the studies, deformation of red blood cells has not been considered. A red blood cell is a biconcave disk in its resting form, but under shear stress it can deform into several shapes that are desirable for reducing flow resistance, particularly in bounded geometries [9, 143, 144]. In addition, mathematical modeling of the transport and margination of particles in the bloodstream has not yet considered the effect of platelets and white blood cells in the presence of micro-/nanoparticles. The simultaneous margination of the micro-/nanoparticles, platelets and white blood cells, along with their comparable concentrations and sizes (especially in the case of microparticles and platelets), increases the likelihood of cell-particle interactions, particularly in the RBC–FL. In addition, it is important to consider all blood components in modeling the transport and margination of particles in the bloodstream, as the concentrations of these components can vary in different diseases. For example, in the case of thrombosis, a disease characterized by the formation of blood clots in the circulation, the number of platelets may increase greatly, and their impact on the transport and margination of particles will be more pronounced.

In future studies, it will be important to investigate the effect of different concentrations of NPs and different dimensions of blood vessels on particle transport and margination. Even in the most comprehensive models reviewed above (“Models with considering blood cells” section), these effects have been investigated in a very limited way [40, 124].

Most current research has focused on modeling the transport of micro-/nanoparticles in idealized blood vessels, such as straight or branched channels, which do not fully represent the complex geometries and flow conditions found in the human body. However, to accurately simulate and model drug delivery in vivo, it is important to consider the actual physiological conditions of blood vessels. By designing vascular geometries based on CT/MRI scanned images, we can come closer to reconstructing the true vascular geometry and flow conditions, allowing for more accurate modeling of drug delivery [16]. In the near future, integrating patient data such as MRI scans can help scientists develop computational models of tumor growth and provide a pathway for personalized treatment with drug-carrying NPs, optimized for each individual’s specific conditions [145,146,147].

The three stages of NP transport within the body from the injection site to the desired site are associated with different phenomena across a wide range of longitudinal and temporal scales. Therefore, providing multi-scale models that simultaneously examine all of these phenomena is very valuable [23]. Beyond the molecular dynamics models (such as Ab initio quantum mechanical simulations, coarse-grained models), the dissipative particle dynamics and the computational fluid dynamics, multi-scale modeling can also be performed using high-performance software tools such as MUSCLE [148], the VPH hyper model framework [149] or TAVERNA [150]. To increase accuracy and speed-up performance, machine-learning method [151, 152] can also be promising [23].

Summary

In this study, we reviewed models of the transport and margination of micro-/nanoparticles in the bloodstream. The models were divided into two main categories: single-particle models and multi-particle models. We studied various published articles in each category, considering factors such as the geometry of the blood vessel, the type, shape, size, and concentration of micro-/nanoparticles, the type of blood flow, mathematical modeling, investigated parameters, and observed results. Based on our literature review, current studies support the hypothesis of multistage drug delivery carriers [141, 142], in which larger microparticles carry a number of small nanocarriers. This approach allows NP-carrying microparticles to marginate and adhere to a specific target inside the microvasculature, followed by the diffusion of NPs into the cancerous tissue. Additionally, spherical particles appear to have better margination in the blood vessels and better diffusion into the cancerous tumor matrix, making them more suitable for the whole process of drug delivery [7, 126].

Although many studies have examined the transport of micro-/nanoparticles in the bloodstream, there is still a lack of mathematical models that can simultaneously the numerous variables that control this process. For example, the effect of platelets and white blood cells in the presence of micro-/nanoparticles in the bloodstream has not yet been fully considered. Even in the most comprehensive models reviewed above (“Models with considering blood cells” section), the deformation of red blood cells and the effects of different NP concentrations and blood vessel dimensions have only been investigated in a limited way. An accurate computational model should reflect the actual physiological conditions of drug delivery. Additionally, there is a need for more multi-scale modeling and simulations that are based on CT/MRI scanned images of real vascular environments [16, 145]. These simulations can be performed using high-performance software such as MUSCLE [148], the VPH hyper model framework [149], TAVERNA [150], and machine-learning method [151, 152] [23].