DEM-CFD Analysis of Fluid Flow in Packed Bed Under the Small Column-to-Particle-Diameter Ratios

Abstract

In this study, a novel three-dimensional DEM-CFD numerical method was used to simulate the void fraction, pressure drop, velocity, and local flow in the packed bed under the small column-to-particle-diameter (D/d) ratios. The pseudo-continuum model method is used in the interior of particles, and for the simulation of the fluid outside the particles, the models are established based on DEM to avoid the wall effect. The simulation results of void fraction and pressure drop show that the void fractions generated by the DEM method are consistent with the ones calculated from the empirical correlations; and the empirical correlations used for pressure drop in this work are basically consistent with the results of the pressure drop predicted by DEM-CFD method. The simulation results of velocity and local flow show that velocity distribution is related to the void fraction distribution; the radial velocity distribution depends mainly on the structure of the packed bed and is independent of the inlet velocity; and the velocity uniformities of fluid flow are improved with the increasing of D/d ratio.

Introduction

The application of packings of particles has been widely exploited in several industrial processes, especially in energy engineering [1,2,3], powder engineering [4,5,6], nuclear engineering [7,8,9], and chemical engineering. In the field of chemical engineering, packed beds can be widely used in diverse processes, such as gasification [10, 11], catalysis [12, 13], distillation [14, 15], and adsorption [16], stripping [17], or cooling [18]. In these processes, packing layers are needed to provide large contact surfaces or to ensure a high holdup for the liquid phase to enhance the heat and mass transfer processes, the efficiency of these chemical engineering processes depends strongly on the complex porous structures formed by solid particles. Hence, some efforts have been made to provide an insight into packing geometries and fluid flow among them aimed at further improvements of existing technologies.

The structures in the porous media area can be visualized intuitively [19, 20] with the experimental measurement techniques, but the flow state of the fluid cannot be observed. With the rapid development of computing technology, numerical simulation has become a good choice to study fluid flow in packed beds. The pseudo-continuum model is normally used in numerical simulation to simulate the flow characteristics of the fluid, and many empirical correlations have been proposed to predict the void fraction and pressure drop [21,22,23,24,25]. However, when the D/d (column diameter/particle diameter) ratio is low and the particles are relatively large, the phenomena caused by local pressure and velocity, such as channeling, backflow, or stagnation, cannot be observed, which is the limitation of the pseudo-continuum model. For some chemical process, like filtration or adsorption, local phenomena are of great importance for the appropriate description of the process [26].

The application of computational fluid dynamics (CFD) simulation combined with the discrete element method (DEM) has been widely used to assess the performance of the fluid flow [27, 28]. The CFD-DEM approach simulates the processes inside the packed bed similarly to experiments, which makes it an alternative to experiments. Moreover, the local phenomena of the particle of the packed bed can also be described by simulation using CFD-DEM. A three-dimensional DEM-CFD numerical method was used in the current work to simulate the fluid in the packed bed with a relatively lower D/d ratio, and the conventional pseudo-continuum models are used only in the interior of particles. The pseudo-continuum model method is still used in the interior of particles in the current work, for the local phenomenon like channeling and backflow has little effect on the internal flow of particles. However, for the simulation of the fluid outside the particles, to avoid the wall effect, the models are established based on DEM. DEM is an explicit scheme of numeration that treats particulate materials as an assembly of distinct granules governed by the fundamental rules of physics and mechanics.

Ookawara et al. [29] proposed a high-fidelity DEM-CFD model, using DEM to randomly stack several spheres in a cylindrical tube. Based on the change in D/d, it was verified that DEM can construct a packed bed void ratio that is consistent with the literatures, and the conceptual proof of the model capability of process enhancement was provided. David Hund et al. [30] also used the DEM-CFD coupling method, using a three-dimensional cylindrical pore model, to conduct a numerical study of particle deposition, obtaining the time for spherical particles to form a bridge on the filter hole at different concentrations and inlet velocities, and studying the impact of the interaction between filter media, particles, and fluids on the total filtration resistance. In addition, Hua Bai et al. [31] conducted a simulation process at both factory and laboratory scales, introducing the concept of ‘void correction coefficient’ to compensate for the void ratio deviation between the actual filler and the CFD model. By using the CFD-DEM coupling method, the pressure drop obtained from the simulation was compared with the laboratory data, with high consistency. Most of the available research papers focus on the studies of solid particles without considering the complexity inside the pores. However, in several practical cases like adsorption processes, solid particles may consist of thousands of tiny porous particles which make up complex porous skeletons, therefore, the flow inside the pores also has a great influence on the process. In this paper, not only the fluid flow between particles is considered, but the fluid flow in pores inside particles is also further analyzed.

It is not possible to perform a three-dimensional simulation of a complete full-scale industrial packed bed device with an adequate resolution in a reasonable amount of time. In this paper, cross-links are established between detailed simulation and classical modeling methods, and a new solution is proposed, which is, that DEM is used to simulate the particles as a whole in three dimensions, while the details of the particles are treated by pseudo-continuum models.

In the current study, a three-dimensional CFD-DEM numerical method is proposed to study the flow field of packed beds with different D/d ratios. Under different ratios of D/d (2.86, 3.08, 3.33, and 4), the void fraction distribution and fluid flow characteristics of particle accumulation were studied. In CFD simulations, the flow within the pores of the particles was simulated by a porous media model, assuming that spherical particles in the packed bed consist of several tiny particles. Moreover, detailed flow field information, including a variation of pressure drop at different Reynolds numbers and variation of velocity, was also simulated. CFD simulations were analyzed and compared with the correlations of the researchers. Local flow characteristics including distribution of radial and axial velocity were also studied with the contour, vector, and streamline.

Methods

Considered System and Material Properties

DEM is an explicit numerical scheme in which forces are calculated based on the particles' interaction and the entities' physical properties to simulate the dynamic and static behavior of assemblies of particles. The commercial DEM software package EDEM was used in this work.

EDEM is an internationally recognized CAE software that simulates and analyzes particle system processes and production operations based on DEM. EDEM provides a solution for the motion and power transfer of particle flows. EDEM is the world's first DEM software that can be coupled with CFD (Computational Fluid Dynamics) software, which can be used to model particle level solid–liquid systems. Therefore, the application of EDEM can greatly reduce the costs and time of the development.

DEM is employed to simulate the random packing process to obtain a good numerical representation of the realistic particle arrangement in the experiment. DEM simulation stops when it reaches a steady state which means that the force balance is reached and the velocity of each particle is virtually zero.

The DEM simulation parameters are set according to Table 1. Restitution coefficient and particle density correspond to the typical values of activated carbon spheres.

Table 1 Parameters for DEM simulations

A cluster of particles is randomly placed at the top of the column and allowed to fall due to gravity. Several clusters are used to fill the column to an approximate height of H = 50 mm. For the DEM simulations, the particle–particle and the particle–wall interactions are considered. The Hertz–Mindlin model [32] was used in this simulation, which is calculated based on the interaction of particles and the physical properties of the entities to simulate the dynamic and static behavior of assemblies of particles.

The transient filling procedure for D/d = 4 is shown in Fig. 1. It can be observed that the particles are settled at 0.4 s and stable afterward. However, for all the other D/d ratios, the simulations are continued at least till 0.6 s, which assures the maximum velocity becomes zero. Due to the random character of the particle generation process, initialization of the random falling position results in a slightly different packing each time, i.e., the relative positions of the spheres are slightly different.

Fig. 1

Transient snapshots of the DEM simulations for D/d = 4

A total of four particles diameter are used with d = 14, 13, 12, and 10 mm, respectively. The four packed beds composed of different sizes of particles are presented in Fig. 2, corresponding to the D/d ratios 2.86, 3.08, 3.33, and 4.

Fig. 2

Packing structures inside packed bed with different diameters

The particles of the packed bed are predicted with DEM and then incorporated into CFD to simulate the flow through the packed bed. The schematic overview of the column and the fluid is displayed in Fig. 3. In addition to the packed bed, an upstream and downstream region is also generated to minimize the influence of the boundary conditions.

Fig. 3

Reference bed used for the development of the methodology, with L₁ = L₂ = 40 mm, and H = 50 mm

Mesh Generation

Generating a numerical packed bed using DEM regularly results in little distance between the two adjacent particles, which is not a favorable condition for mesh generation. The main issue with the creation of a computational mesh is to treat the contact points where the surfaces of spheres force the creation of cells with very small angles and high skewness, which might lead to low-quality mesh and low computational accuracy. Various methodologies to avoid low-quality mesh generation has been developed to solve the issue. To avoid the contact point problem, the method of scaling from the literature [33] is used in this work. Particles are scaled to introduce the gap between the particles, which makes the coordinates of their centers preserved.

Figure 4 shows a part of the generated mesh in the packed bed. Due to the complex geometry of the randomly packed bed, an unstructured tetrahedral mesh was used for the discretization of the computational domain. And, prism layers were imposed on the surfaces of the particles and container wall with a thickness increment of 20% per layer in the normal direction to improve the resolution of fluid velocity variations in the boundary layer. Particles are scaled and the gap width between two particles is equal to one percent of the particle diameter.

Fig. 4

Mesh design of the computational domain

Grid Independence Study

To ensure the accuracy of the simulation results, it is essential to make a grid independence test. The grid independence of the solution was checked by varying the grid density. Six sets of grids with a different number of grid cells were generated to evaluate the effect of grid density on the simulation results without considering the internal porosity structure of the particles. Results of the grid independence test are shown in Fig. 5. It can be observed that grid independence can be achieved when the total elements are higher than 2.5 million. Therefore, the setting of the marked mesh (2.5 million) can meet the requirements of computational accuracy.

Fig. 5

Results of grid independence test

Numerical Solution Technique and BOUNDARY Conditions

The fluid is assumed to be isothermal and incompressible with the physical properties of water in this study. The walls of the column, as well as the surfaces of the particles, are defined as ‘no-slip’ walls, and the inlet is defined as ‘velocity-inlet’ and the outlet is defined as ‘pressure-outlet.’ Inlet values of turbulent intensity I and hydraulic diameter were set to specify the initial turbulence. The turbulent intensity was calculated by Eq.

$$I=0.16{{\text{Re}}}^{-1/8}$$

(1)

where Re is the Reynolds number based on the hydraulic diameter D_h.

The parameters of the fluid are shown in Table 2. The SIMPLEC algorithm is employed to couple the velocities and pressure. The second-order upwind scheme was employed for the convective terms in the momentum and turbulence equations.

Table 2 Parameters for CFD simulations

In this study, there is no divergence and oscillation state, so the relaxation factor is the default value. During the iteration process, by monitoring the flow rate at the inlet and outlet, it is considered that the calculation has converged when the flowrate no longer changes with the iteration.

Governing Equations

For the current calculation, the equations of conservation of mass and momentum are adopted to estimate the pressure and velocity fields of the fluid flow. The governing differential equations are presented as follows.

The Reynolds-averaged equation:

$$\frac{{\partial u}_{i}}{{\partial x}_{i}}=0$$

(2)

where the vectors u_i and x_i are velocity and position.

The Reynolds equations with Boussinesq hypothesis:

$${u}_{j}\frac{{\partial u}_{i}}{{\partial x}_{j}}=-\frac{1}{\rho }\frac{\partial P}{{\partial x}_{i}}+\frac{\partial }{{\partial x}_{j}}(\upsilon \left(\frac{{\partial u}_{i}}{{\partial x}_{j}}+\frac{{\partial u}_{j}}{{\partial x}_{i}}\right)+{\upsilon }_{t}\left(\frac{{\partial u}_{i}}{{\partial x}_{j}}+\frac{{\partial u}_{j}}{{\partial x}_{i}}\right)-\frac{2}{3}{\delta }_{ij}k$$

(3)

where P is the mean pressure, ${\upsilon }_{t}$ is the turbulence kinematic viscosity, ${\delta }_{ij}$ is the Kronecker delta, and $k$ is the turbulence kinetic energy:

$${\text{k}} = \frac{1}{2}\overline{{{\text{u}}^{\prime } _{i} {\text{u}}^{\prime } _{i} }}$$

(4)

where ${u^{\prime}}_{i}$ are the fluctuations of the velocity components around their mean values.

In addition, it is to be noted that the object of this study is the fluid flow characteristics of water flowing through a packed bed, and the heat transfer between the water and the packed bed is outside the scope of consideration for the time being. Therefore, the energy equation was not solved in this study.

Numerical Methods and Solution Strategy

turbulence Model

Due to the complex structure in the packed bed and the large inlet flow velocity used in the calculation, the flow of fluid in the particle gap is in a transition state, which causes the exchange of momentum between the fluid media and is no longer a simple laminar flow or turbulent flow. To meet it, ‘turbulence models’ have been invented.

The RNG k–ε turbulence model, accruing from the renormalization group mathematical theory, is supposed to correct the k–ε model’s deficiency in determining the turbulence kinetic energy, by adding an extra source term to the turbulence kinetic energy dissipation ε transport equation and having slightly different constants compared to k–ε model’s. k–ε turbulence model lacks effectiveness in simulating complex flows with strong pressure gradients and swirling problems. However, RNG k–ε model can simulate complex flows like swirling flow. In the small-scale vortex of porous media, the vortex generated by the flow is inevitable, so RNG k–ε model is a good choice.

The RNG k–ε turbulence model is usually employed to simulate flow characteristics in the case of turbulent regime.

The equations of the RNG k–ε model used in this study are as follows,

$$\frac{\partial k}{\partial t}+{u}_{j}\frac{\partial k}{\partial {x}_{j}}=\frac{\partial }{\partial {x}_{j}}\left[\left(v+\frac{{v}_{t}}{\sigma k}\right)\frac{\partial k}{\partial {x}_{j}}\right]+{\upsilon }_{t}\left(\frac{{\partial u}_{i}}{{\partial x}_{j}}+\frac{{\partial u}_{j}}{{\partial x}_{i}}\right)\frac{{\partial u}_{i}}{{\partial x}_{j}}-\varepsilon$$

(5)

$${v}_{t}={C}_{\mu }\frac{{k}^{2}}{\varepsilon }$$

(6)

where ${C}_{\mu }$ is a constant, taken equal to 0.09.

$$\frac{\partial \varepsilon }{\partial t}+{u}_{j}\frac{\partial \varepsilon }{\partial {x}_{j}}=\frac{\partial }{\partial {x}_{j}}\left[\left(v+\frac{{v}_{t}}{{\sigma }_{\varepsilon }}\right)\frac{\partial \varepsilon }{\partial {x}_{j}}\right]+{C}_{{\varepsilon }_{1}}\frac{\varepsilon }{k}{\upsilon }_{t}\left(\frac{{\partial u}_{i}}{{\partial x}_{j}}+\frac{{\partial u}_{j}}{{\partial x}_{i}}\right)\frac{{\partial u}_{i}}{{\partial x}_{j}}-{C}_{{\varepsilon }_{2}}\frac{{\varepsilon }^{2}}{k}-{C}_{\mu }{\eta }^{3}\frac{1-\eta /{\eta }_{0}}{1+\beta {\eta }^{3}}\frac{{\varepsilon }^{2}}{k}$$

(7)

$$\eta =\left(\frac{k}{\varepsilon }\right){\left(\frac{{\upsilon }_{t}\left(\frac{{\partial u}_{i}}{{\partial x}_{j}}+\frac{{\partial u}_{j}}{{\partial x}_{i}}\right)\frac{{\partial u}_{i}}{{\partial x}_{j}}}{{v}_{t}}\right)}^{0.5}$$

(8)

where $\beta$=0.012 and ${\beta }_{0}$=4.38.

The constants, which are ${C}_{\mu }$=0.085, ${C}_{{\varepsilon }_{1}}$=1.42, ${C}_{{\varepsilon }_{2}}$=1.68, ${\sigma }_{k}$=0.7194, and ${\sigma }_{\varepsilon }$= 0.7194, are derived from the RNG theory. The RNG model with these constants has been successfully used in the past in urban flow and dispersion simulations.

Porous Media Models

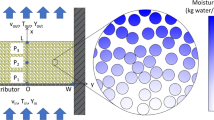
A porous media model is used to simulate the particle layers in a packed bed in the current study. A spherical particle is composed of countless tiny particles, as shown in Fig. 6a, and the actual simulation of each tiny part would greatly increase the difficulty of the task, which cannot be realized with the current computing power for such a volume of simulation calculations. Therefore, the porous media model is used to simulate the internal pore structure of the particles, and the actual models are converted into porous media models for the treatment, as shown in Fig. 6b.

Fig. 6

Simplified treatment of particle model

The momentum source term ${S}_{i}$ on the right side of the momentum equation Eq. (3) can express the hysteresis effect of pores on the fluid in the porous media model. ${S}_{i}$ is the source term due to the presence of the porous media and is only considered when using the porous media model.

Superficial velocity, instead of the actual velocity, is used in the porous media model in CFD inside the porous media. Thus, pressure drop, instead of real velocity, can be predicted with the model inside the media.

If the positive direction of the $i$-axis is assumed to be along the main direction of flow, ${S}_{i}$ can be expressed as follows

$${S}_{i}=\left(\frac{\mu }{\alpha }{u}_{i}+{C}_{2}\rho \left|u\right|{u}_{i}\right)$$

(9)

where α represents the permeability. $\frac{1}{\alpha }$ and ${C}_{2}$ represent the viscous resistance coefficient and the inertial resistance coefficient, respectively.

For different known conditions, these coefficients can be determined by different methods. For example, it is possible to derive the porous coefficient from experimental results and empirical correlations. In this study, the resistance coefficients for the porous media are derived based on the Ergun correlation [21].

Equation (10) and (11) can be obtained by combining the Ergun correlation and Eq. (9)

$$\frac{1}{\alpha }=\frac{150}{{d}_{p}}\frac{{\left(1-\theta \right)}^{2}}{{\theta }^{3}}$$

(10)

$${C}_{2}=\frac{3.5}{{d}_{p}}\frac{1-\theta }{{\theta }^{3}}$$

(11)

where ${d}_{p}$ represents the tiny particle equivalent diameter and $\theta$ is the porosity within particles (${d}_{p}$=0.5 mm, $\theta$=65%).

Results and Discussion

Model Comparison

The void fraction is the most basic and intuitive property of the granular bed. A general method for validating the DEM simulation results is to investigate the void fraction distribution. In this work, for verifying the rationality of the simulation model, the global void fraction and radial void fraction distribution of the simulated packed bed were compared with the empirical equation.

Global Void Fraction

The global void fraction influences significantly the pressure drop calculation of packed beds. Therefore, an accurate prediction of the global bed void fraction is of great importance in the simulations. The global void fraction of the packed bed can be expressed by the ratio of the volume of the void between particles to the volume of the entire packed bed, given in Eq. (12).

$$\varepsilon =\frac{{v}_{poro}}{{v}_{{\text{bed}}}}$$

(12)

where ${v}_{bed}$ is the volume of the whole packed bed and ${v}_{poro}$ is the volume of the void between particles.

For the packed beds filled with spherical particles, a more detailed equation based on Eq. (12) was given by Hua Bai et al. [31], expressed as follows

$$\varepsilon =1-\frac{2N{d}^{3}}{3{D}^{2}H}$$

(13)

where N is the total number of particles in the packing.

The empirical equation of the global void fraction distribution in packed bed was obtained through experiments by Dixon [34], shown as follows

$${{\upvarepsilon}} = 0.4 + 0.05\left( {\frac{d}{D}} \right) + 0.412\left( {\frac{d}{{\text{D}}}} \right)^2$$

(14)

Dixon's equation, applicable to the simulation of the global void fraction of the packed bed with spherical particles, is used to compare with the global void fraction of the packed bed established by CFD in the current study.

The results of comparing the CFD simulation with the Dixon equation are shown in Table 3.

Table 3 Global void fraction comparison

It is found that the global void fraction of the particle bed generated by using DEM is consistent with the expected value of Dixon's experiment, with a maximum relative error of 6.19%, mainly due to the restriction of particles on the pipe wall at small D/d ratios. When D/d > 3, the maximum relative error is 3.345%. It can be seen that the overall error of the global void fraction is less than 7%, confirming that the value of the packed bed void fraction simulated in this study is consistent with the value of the Dixon correlation, indicating that the model generated through DEM meets the filling standards in the actual process.

Radial Void Fraction

The void fraction in the radial direction profile ε(r) is an important parameter related to flow channeling near the wall and the homogeneity of the packed bed. In this study, the radial void fraction of the packed bed is checked and verified with the empirical correlation by Mueller [35] and experimental results reported by de Klerk [36].

Mueller [35] obtained through experiments the following empirical correlation of radial void fraction which can predict accurately the radial void fraction distribution of a packed bed with spherical particles.

$$\varepsilon (r)={\varepsilon }_{b}+\left(1-{\varepsilon }_{b}\right){J}_{0}\left(a^{\prime}z\right){e}^{-b^{\prime}z}$$

(15)

$$a^{\prime}=7.45-\frac{3.15}{D / d}$$

(16)

$$b^{\prime}=0.315-\frac{0.735}{D / d}$$

(17)

where z is the nondimensional distance from the wall and ${\varepsilon }_{b}$ is the bulk void fraction of the packed bed undisturbed by wall effects.

$${\varepsilon }_{b}=0.365+\frac{0.22}{D / d}$$

(18)

While the Mueller proposed correlation equation has worked well, its drawback is the use of the intuitively poor and large computational Bessel function in the calculation equation. de Klerk (2003) proposed the empirical equation that is averaged in the axial and azimuthal directions, shown as follows

$$\varepsilon \left(r\right)=\left\{\begin{array}{l}2.14{z}^{2}-2.53z+1, \quad z\le 0.637\\ {\varepsilon }_{b}+0.29{\text{exp}}\left(-0.6z\right)\cdot \left[{\text{cos}}\left(2.3\pi \left(z-0.16\right)\right)\right]\\ +0.15{\text{exp}}\left(-0.9z\right), \quad z>0.67\end{array}\right.$$

(19)

To ensure the accuracy of the validation results, this work chooses the calculation results of the above two correlations to compare with the CFD results for validation.

To study the radial void fraction distribution, which has been generated by DEM methods, the packed bed was divided into several cylindrical subsurfaces at different radial positions. The intersected bulk of each sphere was calculated and the void volume was calculated by subtracting the intersected volume from the total volume between two adjacent cylinders (see Fig. 7).

Fig. 7

Subsurfaces along the radial direction

Figure 8 shows the void fraction of the DEM-generated bed compared within different D/d ratios with experimental data by Mueller (1992) and a more general correlation by de Klerk (2003):

Fig. 8

Radial void fraction distribution for different D/d ratios

The maximum radial void fraction is obtained at the position near the wall, due to the contact mode between the particles and the wall is point contact. With the extension to the inside of the packed bed, the oscillation amplitude of the radial void fraction decreases.

The radial void fraction calculated by DEM is slightly different from the calculated value obtained by Klerk and Mueller’s empirical formula. The possible reason is that the particle is not vibrated and compacted after falling into the column by gravity, and so, the bed is not very tightly filled.

Although some slight deviations can be observed on some local details of the profiles due to the stochastic nature of random packing, amplitude and peak–valley positions of the void fraction profile are effectively reproduced. It confirms that the DEM simulation in this study is reliable for the subsequent CFD study.

Spherical Particle Position Distribution

Analysis for the structure of the packed bed is an important basis for understanding the interaction between fluid flow and porous media in packed beds. As shown in Fig. 9, the centroids of all particles are plotted on the x–y plane.

Fig. 9

Particle centroids distribution in x–y plane: N = 22, 30, 37, 68

The annular structure of the particle centroid can be found near the tube wall with different particle numbers (N), and the circular region becomes more obvious as the number of particles increases. When the particle centroid is away from the tube wall of the packed bed, the regular annular structure gradually disappears as the distance increases. By comparing the distribution of particle centroids under different particle numbers, it can be seen that the order and clarity of the centroid rings may depend on the number of particles. For example, when the number of particles reaches 68, the second ring is more pronounced than when the number of particles is low.

In addition, as shown in Fig. 9, there are several isolated particles between the particles near the wall surface and the inner layer. This is also the reason why in Fig. 8 (near z = 1) the variation in void fraction of different particles stacked is random compared to Klerk and Mueller’s empirical formula, and it also indicates that there may be partial overlap between inner layer particles and outer layer particles when stacked. The figure shows that the distribution of particle centroids is basically consistent with the radial porosity amplitude change rule in Fig. 8.

Pressure Drop

The crucial factors that affect the pressure drop are fluid flow velocity and void fraction, and a common model to describe the pressure drop under different bed characteristics is given in Eq. (20). For the study of pressure drop, a large number of empirical correlations have been summarized by some researchers, and the four empirical correlations are listed in Table 4.

$$\frac{\Delta p}{L}={f}_{k}\rho \frac{\left(1-\varepsilon \right)}{{\varepsilon }^{3}}\frac{{u}^{2}}{d}$$

(20)

$${R}_{{e}_{m}}=\frac{du\rho }{\mu \left(1-\varepsilon \right)}$$

(21)

where ${f}_{k}$ is the friction factor and ${R}_{{e}_{m}}$ is the modified particle Reynolds number.

Table 4 Empirical correlations for pressure drop calculation

Simulation of packed beds with CFD requires the treatment of the particle–particle and particle–wall contact points within the packed bed. Based on the study in the literature [31], the treatment of the contact points had a significant effect on the results of the pressure drop, and a 1% decrease in particle size may result in a 3% error in void fraction, which will yield a 10% error in pressure drop.

To obtain the accurate pressure drop of the packed bed, the CFD calculation is corrected according to Eq. (22). The void fraction correction factor k for the pressure drop was obtained by Eq. (23) [31].

$$\Delta {p}_{c}=k^{\prime}\cdot \Delta p$$

(22)

$$k^{\prime}=\frac{1}{1-3.385\sigma +0.045{\sigma }^{2}}$$

(23)

The relationship between the pressure drop and the velocity at different ratios of D/d is shown in Fig. 10.

Fig. 10

Plot of pressure drop–velocity distribution at different D/d

As shown in Fig. 10, the pressure drop is independent of the D/d ratio, but decreases with the increase in the void fraction (see Table 2), indicating that the pressure drop is influenced by the void fraction. When the void fraction is smaller, the particles are stacked more tightly and the resistance of the particles to the fluid enhances, resulting in a greater change in pressure drop, and vice versa.

Figure 10 shows that the pressure drop increases with the increase in the velocity and the pressure drop fall to zero when the fluid inlet velocity is zero. When the velocity is less than 0.035 m/s, the resistance of particles to the fluid is low, and so, the pressure drop is also low, the change of pressure drop is relatively small. It shows that the velocity has little effect on the pressure drop at this range. As the velocity increases, the resistance of particles to the fluid increases with the increase in the velocity, and the pressure drop increased rapidly. It means that the velocity has a greater effect on the pressure drop at this range.

Comparison between the friction coefficient ${f}_{k}$ calculated by CFD at different D/d ratios is shown in Fig. 11 and the ${f}_{k}$ calculated by empirical correlation in Table 4. It can be seen from the plots that an oscillating decline can be observed in Foumeny and Cheng's correlations [38, 39] plot because wall effects are considered in the correlations. The calculation of the Ergun correlation [23] is significantly higher than that of other correlations when the Reynolds number is greater than 300. The reason is that the second term of the friction factor, which is constant in Ergun correlation, is independent of the Reynolds number. Therefore, the Ergun correlation is unsuitable under the condition of higher Reynolds numbers.

Fig. 11

Variations of friction factors upon D/d ratios using empirical correlations

In addition, although wall effects are not taken into account, the Carman correlation [37] is of great consistency with predictions of Cheng's correlation, which is due to Re_m being taken into account in the second term of the Carman correlation.

To further explore the applicability of the empirical correlations, the variation of the relative error (RE), calculated with Eq. (24) between the simulation results and the empirical correlations is displayed in Fig. 12.

Fig. 12

RE of pressure drop for different D/d ratios

$$RE=\frac{{f}_{kCFD}-{f}_{kEmp}}{\Delta {f}_{kEmp}}\times 100\%$$

(24)

Figure 12 shows that the prediction of the Ergun correlation has a relatively larger RE value in predicting the CFD results than the other three correlations. The RE increases with the increase in the Reynolds number. With the increased Reynolds number, in particular, when the Reynolds number is higher than 900, the RE between the correlation calculated values and the CFD of over 50% results. Due to the excessive RE, Ergun correlation can no more predict the pressure drop variation inside porous media. However, the Foumeny correlation predicts the least computational error for CFD. The RE distribution of Carman and Cheng displays a similar tendency of decrease (Table 5).

Table 5 Range of Reynolds numbers of empirical correlations (RE < 40%)

Velocity Profile

The velocity distribution is an important characteristic of the flow through a packed bed. In this section, to investigate the effect of different D/d ratios on the velocity magnitude of the fluid in the packed bed, the velocity distribution is studied at different D/d ratios with an inlet velocity of 0.02 m/s.

In the present study, the D/d ratio of the packed bed is relatively small (2.86 ≤ D/d ≤ 4), and the wall effect on the flow would be obvious. A typical longitudinal section is selected to analyze the local fluid velocity and flow in the packed bed, as shown in Fig. 13.

Fig. 13

Illustration of selected longitudinal section

The local velocity in a cross section perpendicular to the column axis at different D/d ratios is shown in Fig. 14. The flow direction is from bottom to top. Figure 12 shows that the fluid velocity distribution in the column is not the same for different d/D ratios with the same inlet velocity.

Fig. 14

Axial velocity distribution for different D/d ratios: D/d = 2.86, 3.07, 3.33, and 4

It can be seen that fluid tends to flow into the voids of particles and the velocity distribution is related to the void distribution. The velocity is relatively greater through the pore and in some areas near the wall, where the local void fraction is relatively high.

In Fig. 14, several acceleration zones can be seen in the particle–particle and particle–wall regions. When the ratio of D/d is 2.86, the void fraction in the packed bed is relatively large and there are fewer acceleration zones and the distribution of velocity is uneven, see Fig. 14a. As the D/d ratio increases, the particle layer is more evenly arranged, and more flow channelings are formed, see b, c, d in Fig. 14. Therefore, there are more acceleration zones and the velocity distribution is more even.

The velocity vector inside the particles is also shown in Fig. 14. As shown in the figure, the particles have a porous structure, and fluid flow can be observed inside the particles. The flow velocity of the fluid is higher at the radial boundary inside the particle.

The flow path lines in the packed bed under various D/d ratios are given in Fig. 15, and deflection of the flow around the particles and jet flow can be seen at the gap between two particles.

Fig. 15

Axial streamline distribution for different D/d ratios: D/d = 2.86, 3.07, 3.33, and 4

When the column diameter is relatively small, low-velocity fluids and wake and eddying zones appear behind the particles and at the exit of the packed bed, even leading to backflow. As the D/d ratio increases, the eddying zones gradually shrink or even disappear, but the wake can still be observed. The appearance of wake and eddying zones at the exit may be caused by the sudden widening of the flow channel from a narrow void, resulting in a sudden reduction in the local resistance to fluid flow. Boundary layer separation occurs at the particle surface at the exit of the bed, leading to the appearance of eddying and consequently backflow. With an increase in the D/d ratio, the velocity distribution is more even and eddies are less likely to form.

The influence of the fluid flow velocity of the liquid on the radial subsurfaces can be observed in Fig. 16 with the inlet velocity of 0.02 m/s. The averaged axial velocity profile over radial position is shown in Fig. 17. It can be seen that velocity distribution has the same trend as the change of radial void fraction. It is found that the average velocity of the near-wall region is higher than that of the inner column region in the packed bed. The first velocity peak can be observed at the location near the wall. This is since the contact points of the particles were treated by the shrinking method in this study, which resulted in narrow flow channelings between the particles and the wall. In addition, particles near the wall are highly ordered and the void fraction in the vicinity of the wall is larger, which makes the flow velocity higher. This behavior of the velocity profiles is quite typical and has been observed in the studies of the literature [2, 40].

Fig. 16

Subsurfaces along the radial direction

Fig. 17

Radial velocity distribution for different D/d ratios

As the distance from the wall increases, the regularity of the particle configuration drops, flow channeling occurs at the position of about 1 particle diameter, and the second peak is observed.

At the center of the column, for D/d = 4, flow channeling occurs and another velocity peak can be observed, which indicates that the smaller the particles are, the more flow channelings form, depending on the random geometric arrangement of the packed bed.

To gain insight into the flow field around the particles, sample contour maps of the instantaneous flow velocity magnitude are presented in Fig. 18 without showing the packing structure and column walls, to make it clear. Characteristics of the flow around the cross section along the column axis, and the local increase in the velocity in narrow channels can be observed in the figure.

Fig. 18

Radial velocity contour for different D/d ratios: D/d = 2.86, 3.07, 3.33, 4

Velocity inhomogeneity within the cross section as well as differences between the three sections is shown in Fig. 18 which are directly related to the geometry of the packed bed. The hindering effect of the bed structure leads to the inhomogeneity of flow at the bed bottom and top, which will change the fluid flow velocity in the packed bed.

As it can be seen from the contour, the maximum value of the velocity distribution occurs at the particle–particle and particle–wall regions, and several velocities exceed 0.05 m/s, which is also shown in Fig. 14.

At the solid wall, the velocity is zero, whereas, inside the voids, the local velocity is more than 3 times the superficial velocity. The strong correlation between the void fraction and the fluid velocity can also be seen. The fluid velocity goes down to zero due to the no-slip condition at the wall.

With the increase in the D/d ratio, the fluid velocity distribution is more uniform, which indicates that the bed uniformity is being improved when the D/d ratio increases. Therefore, for the packed bed, the method of the increasing D/d ratio can be used to reduce the effect of the wall effect and to achieve the homogeneity of flow inside the bed.

Conclusions

A new three-dimensional CFD-DEM numerical method is proposed to simulate porous particle packed beds with different D/d ratios and to identify the internal fluid flow of particles by defining appropriate parameters of the porous media model.

The simulation results show that the predicted void fraction is consistent with the prediction results of the empirical correlation. The overall error of the global void fraction is less than 7%, and the radial void fraction oscillation trend is consistent with the empirical formula, which proved that the DEM method can be used to simulate the random packing structure of the packed bed. The order and clarity of the centroid rings may depend on the number of particles.

The friction factor value of the CFD simulation is calculated based on the predicted pressure drop and then compared with the results predicted by the empirical correlations of Ergun, Carman, Foumeny, and Cheng. Results show that the empirical correlations can be used to predict the pressure drop through the packed bed, and their applicability is related to the range of D/d ratio and Reynolds number. The empirical correlation of Ergun has a larger error value compared with the prediction results of the other three correlations, and Foumeny’s empirical correlation has the best applicability.

Channeling occurs mainly in the near-wall areas and some local internal areas of the packing. In the inner area of the packed bed, the fluid velocity distribution of different D/d ratios is related to the void fraction distribution. The radial velocity distribution of different D/d ratios depends on the structure of the packed bed and is independent of the inlet velocity.