Brauer and Geršgorin Locations of Zeros of Perturbed Chebyshev Polynomials of the Second Kind by Dilation

Abstract

We consider some perturbations of Chebyshev polynomials of the second kind obtained by modifying by dilation one of its recurrence coefficients at an arbitrary order. By applying Brauer and Geršgorin theorems to Jacobi matrices associated with such perturbed sequences we obtain some locations of their zeros.

1 Introduction

It is well known that a polynomial sequence $\{P_n(x)\}_{n\ge 0}$ is orthogonal if and only if it satisfies a recurrence relation of order two (see (1)-(2)) defined by two sequences of coefficients $\{\beta _n\}_{n\ge 0}$ and $\{\gamma _{n+1}\}_{n\ge 0}$, the so-called recurrence coefficients. If we modify, at the order r, the $\beta$-coefficient by translation, $\beta _r\rightarrow \beta _r+\mu _r$, or the $\gamma$-coefficient by dilation, $\gamma _r\rightarrow \lambda _r\gamma _r$, by means of some parameters $\mu _r$ or $\lambda _r$, we obtain a perturbed orthogonal sequence, the so-called in-literature generalized co-recursive or co-dilated polynomials, respectively [16]. In recent years, several authors have worked on perturbed orthogonal polynomials often taking as a study case the fundamental example of the Chebyshev sequence of polynomials of second kind (see (3)). With no attempt of completion, we cite [4, 16,17,18, 21]. The study of zeros of orthogonal polynomials, and in particular zeros of Chebyshev families, constitutes an important topic, because they are used in several methods in numerical analysis and have applications in applied sciences [11, 14, 19, 21]. With respect to properties of zeros of perturbed orthogonal polynomials, see in particular [2, 3, 15]. Furthermore, these families have some applications, in which their zeros play a role (see, for instance, [10]. I have also studied these perturbed sequences in the papers [5,6,7,8], where the reader can find further references about this subject. In the present article, I investigate the location of zeros of perturbed Chebyshev sequence of the second kind by dilation; the translation case is treated in another work [9]. Indeed, it is interesting to know how the above perturbations change the location of zeros of the original sequence. We furnish some answers to this question by applying Geršgorin [12, 13, 20] and Brauer theorems [1, 20] to Jacobi matrices associated with such perturbed sequences, finding in this way some locations of perturbed zeros. Those general results by Geršgorin and Brauer provide a simple way to determine certain intervals, circles, or ovals whose union contains the eigenvalues of any $n\times n$ matrix. Jacobi matrices $J_n$ (18) are defined from the recurrence coefficients $\{\beta _n\}_{n\ge 0}$ and $\{\gamma _{n+1}\}_{n\ge 0}$ of any orthogonal polynomial sequence in such a way that $P_n(x)$ is the characteristic polynomial of $J_n$ (19). In other words, the eigenvalues of $J_n$ are the zeros of $P_n(x)$ [4].

This article is organized as follows. In Sect. 2, we define perturbed Chebyshev polynomials of the second kind by dilation, and we give some of their properties. We keep the same type of notation adopted in previous works [7, 8]. In Sect. 3, from some connection relations derived in [7], we deduce a location of real perturbed zeros in terms of Chebyshev zeros. In the next section, we consider the associated Jacobi matrices, and we determine their Geršgorin and Brauer sets. In Sect. 5, we deduce the Geršgorin location of perturbed zeros. We begin by fixing the order r of perturbation, and then for each r, we should consider separately some initial values of the degree n, after that, we obtain results for all the other values of n. In each case, locations depend on the value of $\lambda _r$, the parameter of perturbation. In the next section, we accomplished the Brauer location. In Sect. 7 we compare Geršgorin and Brauer locations, and we conclude about the advantage of the last one in some cases. Also, we present a definition for the sharpness of the locations we have obtained. In the next section, we give some symbolic, numerical, and graphical results to clarify and illustrate the results of this work. We finish this article with some conclusions.

2 Perturbed Chebyshev Polynomials of the Second Kind by Dilation

Let $\mathcal {P}$ be the vector space of polynomials with coefficients in $\mathbb {C}$ and let $\mathcal {P}^{\prime }$ be its topological dual space. We denote by $\langle u,p\rangle$ the effect of the form $u\in \mathcal {P}^{\prime }$ on the polynomial $p\in \mathcal {P}$. In particular, $\langle u,x^{n}\rangle :=\left( u\right) _{n},n\ge 0$, represent the moments of u. A form u is said to be regular [17] if and only if there exists a polynomial sequence $\{P_{n}\}_{n\ge 0}$, such that

$$\begin{aligned} \left\langle u,P_{n}P_{m}\right\rangle= & {} {} 0\ ,\ n\ne m\ , \ n,m\ge 0\ , \\ \left\langle u,P^2_{n}\right\rangle =k_n\ne & {} {} 0\ , \ n\ge 0. \end{aligned}$$

Consequently $\deg P_n=n$, $n\ge 0$, and any $P_n$ can be taken monic (that is, with unit leading coefficient, $P_n(x)=x^n+\ldots$); then $\{P_{n}\}_{n\ge 0}$ is called a monic orthogonal polynomial sequence (MOPS) with respect to u. The sequence $\{P_{n}\}_{n\ge 0}$ is regularly orthogonal with respect to u [17] if and only if there exist two sequences of coefficients $\{\beta _{n}\}_{n\ge 0}$ and $\{\gamma _{n+1}\}_{n\ge 0}$, with $\gamma _{n+1}\ne 0,\;n\ge 0$, such that $\{P_{n}\}_{n\ge 0}$ satisfies the following initial conditions and linear recurrence relation of order 2

$$\begin{aligned}{} & {} P_{0}(x)=1,\quad P_{1}(x)=x-\beta _{0}, \end{aligned}$$

(1)

$$\begin{aligned}{} & {} P_{n+2}(x) =(x-\beta _{n+1})P_{n+1}(x) -\gamma _{n+1}P_{n}(x),\quad n\ge 0. \end{aligned}$$

(2)

Furthermore, the recurrence coefficients $\{\beta _{n}\}_{n\ge 0}$ and $\{\gamma _{n+1}\}_{n\ge 0}$ satisfy

$$\begin{aligned} \beta _{n} =\frac{\left\langle u,xP_{n}^{2}(x) \right\rangle }{k_n}, \quad \gamma _{n+1} =\frac{k_{n+1}}{k_n},\quad n\ge 0. \end{aligned}$$

As usual, we suppose that $\beta _{n}=0$, $\gamma _{n+1}=0$, and $P_{n}(x)=0$, for all $n<0$.

A form $u\in {\mathcal {P}}'$ is said to be positive definite if and only if $<u,p>>0$, $\forall p\in {\mathcal {P}}$: $p(x)\ge 0$, $p\not \equiv 0$, $x\in \mathbb {R}$. A form $u\in {\mathcal {P}}'$ is symmetric if and only if $(u)_{2n+1}=0,\ n\ge 0.$ A polynomial sequence $\{P_{n}\}_{n\ge 0}$ is symmetric if and only if $P_n(-x)=(-1)^nP_n(x), \ n\ge 0$. Then $P_{2n+1}(0)=0$, and zeros of $P_n(x)$ are symmetric with respect to the origin. If $\{P_{n}\}_{n\ge 0}$ is a MOPS with respect to u, the symmetry of $\{P_{n}\}_{n\ge 0}$ is equivalent to $\beta _n=0$, $n\ge 0$, and the positive definiteness of u is equivalent to $\beta _n,\ \gamma _{n+1}\in {\mathbb {R}}$, $\gamma _{n+1}>0$, $n\ge 0$ [4]. If $\{P_{n}\}_{n\ge 0}$ is a symmetric MOPS, then $P_{2n}(0)\ne 0$, $n\ge 0$.

In this work, our starting point is the well-known monic Chebyshev polynomial sequence of second kind $\{P_n(x)\}_{n\ge 0}$ [19] defined by the following recurrence coefficients

$$\begin{aligned} \beta _{n}=0\quad ; \quad \gamma _{n+1}={\frac{1}{4}},\ n\ge 0. \end{aligned}$$

(3)

This is a symmetric and positive definite example. We are going to perturbe this sequence as follows. For some fixed order $r\ge 1$, we modify the recurrence coefficient $\gamma _r$ by multiplying it by a parameter $\lambda _r\in {\mathbb {R}}$, $\lambda _r\ne 0$, $\lambda _r\ne 1$, that is, we consider the following recurrence coefficients

$$\begin{aligned} \beta _n^{d}=0;\ \gamma _{r}^d=\frac{\lambda _r}{4},\ \gamma _{n+1}^d =\frac{1}{4},n\ne r-1,n\ge 0, r\ge 1, \end{aligned}$$

(4)

that determine the so-called r-th perturbed Chebyshev sequence of the second kind by dilation, noted by $\{P^{d}_n\left( \lambda _r;r\right) (x)\}_{n\ge 0}$. This perturbation modifies the Chebyshev polynomials from the degree $r+1$, as stated by the following relations

$$\begin{aligned}&{} P^{d}_{k}(\lambda _r;r)(x)=P_k(x)\ , \ 0\le k\le r\ , \\{}&{} P^{d}_{r+1}(\lambda _r;r)(x)=xP_r(x) -\frac{\lambda _r}{4}P_{r-1}(x)\ ,\\{}&{} P^{d}_{n+r+2}(\lambda _r;r)(x)=xP^{d}_{n+r+1} (\lambda _r;r)(x)-\frac{1}{4}P^{d}_{n+r}(\lambda _r;r)(x)\ , \ n\ge 0. \end{aligned}$$

From (4), we see that $\{P^{d}_n\left( \lambda _r;r\right) (x)\}_{n\ge 0}$ is symmetric; in addition, if $\lambda _r>0$, then it is also positive definite.

The monic Chebyshev polynomial sequence of first kind $\{T_n(x)\}_{n\ge 0}$ [19] defined by the following recurrence coefficients

$$\begin{aligned} \beta _{n}=0,\ n\ge 0 ; \quad \gamma _{1} =\frac{1}{2},\ \gamma _{n+1}={\frac{1}{4}},\ n\ge 1, \end{aligned}$$

(5)

can be naturally considered as perturbed of $\{P_n(x)\}_{n\ge 0}$ as follows [6]

$$\begin{aligned} r=1\ ,\ \lambda _r=2\ ,\ T_n(x)=P^{d}_n\left( \lambda _r;r\right) (x). \end{aligned}$$

(6)

We recall the trigonometric definition of the monic Chebyshev sequence of the second kind

$$\begin{aligned} P_n(x)=\frac{1}{2^n}\frac{\sin (n+1)t}{\sin t}\ , \ n\ge 0\ , \end{aligned}$$

with $x=\cos t$, $t\in [0,\pi ]$. The explicit formula of its zeros in increasing size is [19]

$$\begin{aligned} \xi ^{(n)}_{k}=\cos \left( \frac{n-k+1}{n+1}\pi \right) , \ 1\le k\le n. \end{aligned}$$

(7)

Let us summarize some well-known properties of zeros of orthogonal polynomial sequences $\displaystyle \{P_n(x)\}_{n\ge 0}$. In the positive definite case previously defined, all zeros are distinct real numbers [4]. In addition, in the case the form has an integral representation through a positive measure, zeros are located in the interior of the convex hull of the corresponding support [4]. Also, there exists an interlacing property between zeros of polynomials of consecutive degrees, $P_n(x)$ and $P_{n+1}(x)$, that is,

$$\begin{aligned} \displaystyle \xi _k^{(n+1)}<\xi _k^{(n)}<\xi _{k+1}^{(n+1)}\ , \ 1\le k\le n\ , \ n\ge 1. \end{aligned}$$

Moreover, there are some monotonicity properties, namely, for fixed $k\ge 1$, $\displaystyle \{\xi _k^{(n)}\}_{n=k}^{\infty }$ is a decreasing sequence, and $\displaystyle \{\xi _{n-k+1}^{(n)}\}_{n=k}^{\infty }$ is an increasing sequence. Also,

$$\begin{aligned} \displaystyle \lim _{n\rightarrow +\infty }\xi _k^{(n)}=\rho _k, \quad \displaystyle \lim _{n\rightarrow +\infty }\xi _{n-k+1}^{(n)}=\eta _k\ , \end{aligned}$$

being $\displaystyle [\rho _1,\eta _1]$ the smallest closed interval that contains all zeros of $\displaystyle \{P_n(x)\}_{n\ge 0}$.

Zeros of Chebyshev polynomials satisfy all those properties in the interval $\displaystyle [-1,1]$ [19]. Perturbed Chebyshev polynomials of the second kind by dilation, $\{P^{d}_n\left( \lambda _r;r\right) (x)\}_{n\ge 0}$, with $\displaystyle \lambda _r\in {\mathbb {R}}$, $\lambda _r>0$, satisfy those properties as well in some intervals. If $\lambda _r<0$, we are not in the positive definite case, then zeros can have different behavior namely there exist some conjugate pairs of complex zeros. In any case, perturbed Chebyshev polynomials are semi-classical sequences [18], consequently their zeros are always simple [17, p.123].

3 A Location of Real Zeros of Perturbed Chebyshev Polynomials of the Second Kind by Dilation

We begin this section by recalling a result needed for obtaining the location given in Proposition 2 (see below) of real zeros of perturbed polynomials in terms of Chebyshev zeros.

Proposition 1

[7, p.107] If $\{P_n(x)\}_{n\ge 0}$ is the monic Chebyshev polynomial sequence of the second kind, and $\{P^{d}_n(\lambda _r;r)(x)\}_{n\ge 0}$ is its r-th perturbed sequence by dilation, with $\lambda _r\ne 0$, $\lambda _r\ne 1$, $r\ge 1$, then the following connection relations hold

$$\begin{aligned}{} & {} P^{d}_{k}(\lambda _r;r)(x)=P_k(x)+\frac{1-\lambda _r}{4} \sum _{i=1}^{k-r}\frac{1}{4^{i-1}}P_{k-2i}(x), \ r+1 \le k\le 2r-1, \end{aligned}$$

(8)

$$\begin{aligned}{} & {} P^{d}_{n+2r}(\lambda _r;r)(x)=P_{n+2r}(x) +\frac{1-\lambda _r}{4}\sum _{i=1}^{r}\frac{1}{4^{i-1}} P_{n+2(r-i)}(x), \ n\ge 0. \end{aligned}$$

(9)

Proposition 2

If $\displaystyle \{P_n(x)\}_{n\ge 0}$ is the monic Chebyshev polynomial sequence of the second kind, being $\xi _i^{(k)}$, $1\le i \le k$, the zeros of $P_k(x)$ by increasing size, and $\{P^{d}_n(\lambda _r;r)\}_{n\ge 0}$ is its r-th perturbed sequence by dilation, with $\lambda _r\in \mathbb {R}$, $\lambda _r\ne 0$, $\lambda _r\ne 1$, being $\displaystyle \xi _i^{(k)}(\lambda _r;r)$, $1\le i \le k$, the zeros of $\displaystyle P^{d}_k(\lambda _r;r)(x)$ by increasing size, then for $k\ge r+1$ and $r\ge 1$, it holds

• 1. $sgn\big [P^{d}_{k}(\lambda _r;r) (\xi _{k}^{(k)})\big ]=sgn(1-\lambda _r)$.

• 2. $sgn\big [P^{d}_{k}(\lambda _r;r) (\xi _{1}^{(k)})\big ]=(-1)^k sgn(1-\lambda _r)$.

• 3. If $\lambda _r<1$, then

  • (a) $\forall y\ge \xi _{k}^{(k)}$, $P^{d}_{k}(\lambda _r;r)(y)>0$. Thus there are no real zeros of $P^{d}_{k}(\lambda _r;r)(x)$ greater than or equal to $\xi _{k}^{(k)}$.

  • (b) $\forall z\le \xi _{1}^{(k)}$, $(-1)^kP^{d}_{k}(\lambda _r;r)(z)>0$. Thus there are no real zeros of $P^{d}_{k}(\lambda _r;r)(x)$ less than or equal to $\xi _{1}^{(k)}$.

  • (c) All real zeros of $P^{d}_{k}(\lambda _r;r)(x)$ belong to the interval ${\mathcal {Z}}_k=\left]\xi _{1}^{(k)},\xi _{k}^{(k)}\right[$.

• 4. If $\lambda _r>1$, then the number of (real) zeros of $P^{d}_{k}(\lambda _r;r)(x)$ less than $\xi _{1}^{(k)}$, or greater than $\xi _{k}^{(k)}$, is odd. In particular,

  $$\begin{aligned} \xi _1^{(k)}(\lambda _r;r)<\xi _{1}^{(k)}, \quad \xi _k^{(k)}(\lambda _r;r)>\xi _{k}^{(k)}. \end{aligned}$$

  (10)

Proof

Recall that if $\lambda _r>0$, all zeros are real. We shall use the properties of Chebyshev zeros mentioned above and the trivial fact that for any monic polynomial, it holds

$$\begin{aligned} \lim _{x\rightarrow +\infty }P_n(x)=+\infty , \ \lim _{x\rightarrow -\infty }P_{2n}(x)=+\infty , \ \lim _{x\rightarrow -\infty }P_{2n+1}(x)=-\infty . \end{aligned}$$

(11)

As perturbed polynomials $P^{d}_{k}(\lambda _r;r)(x)$ are symmetric, their real zeros are symmetric with respect to the origin. This fact is important in parts 3 and 4. We are going to deal with the recurrence relation (8). The same can be done with (9). We remark that in (8) the polynomials under sum have degrees smaller than the degree k of $P_k(x)$ and have the same parity of it; moreover all their zeros belong to ${\mathcal {Z}}_k$. Next, we will evaluate (8) at the smallest and the biggest zeros of $P_k(x)$, and at certain y and z, and we note the signs of polynomials at those points using (11).

$$\begin{aligned} P^{d}_{k}(\lambda _r;r)(\xi _{k}^{(k)})&= \underbrace{P_k(\xi _{k}^{(k)})}_{=\ 0} +(1-\lambda _r)\sum _{i=1}^{k-r}\frac{1}{4^{i}} \underbrace{P_{k-2i}(\xi _{k}^{(k)})}_{>\ 0}, \end{aligned}$$

(12)

$$\begin{aligned} P^{d}_{k}(\lambda _r;r)(y)&= \underbrace{P_k(y)}_{>\ 0} +(1-\lambda _r)\sum _{i=1}^{k-r}\frac{1}{4^{i}} \underbrace{P_{k-2i}(y)}_{>\ 0},\ \forall y> \xi _{k}^{(k)}, \end{aligned}$$

(13)

$$\begin{aligned} P^{d}_{2k}(\lambda _r;r)(\xi _{1}^{(2k)})&= \underbrace{P_{2k}(\xi _{1}^{(2k)})}_{=\ 0} +(1-\lambda _r)\sum _{i=1}^{2k-r}\frac{1}{4^{i}} \underbrace{P_{2k-2i}(\xi _{1}^{(2k)})}_{>\ 0}, \end{aligned}$$

(14)

$$\begin{aligned} P^{d}_{2k+1}(\lambda _r;r)(\xi _{1}^{(2k+1)})=&{} \underbrace{P_{2k+1}(\xi _{1}^{(2k+1)})}_{=\ 0} +(1-\lambda _r)\!\sum _{i=1}^{2k-r+1} \frac{1}{4^{i}}\underbrace{P_{2k-2i+1} (\xi _{1}^{(2k+1)})}_{<\ 0} \end{aligned}$$

(15)

$$\begin{aligned} P^{d}_{2k}(\lambda _r;r)(z)=&{} \underbrace{P_{2k}(z)}_{>\ 0} +(1-\lambda _r)\sum _{i=1}^{2k-r}\frac{1}{4^{i}} \underbrace{P_{2k-2i}(z)}_{>\ 0},\ \forall z < \xi _{1}^{(2k)}, \end{aligned}$$

(16)

$$\begin{aligned} P^{d}_{2k+1}(\lambda _r;r)(z)=&{} \underbrace{P_{2k+1}(z)}_{<\ 0} + (1-\lambda _r)\!\sum _{i=1}^{2k-r+1}\frac{1}{4^{i}} \underbrace{P_{2k-2i+1}(z)}_{<\ 0}, \forall z < \xi _{1}^{(2k+1)}. \end{aligned}$$

(17)

From the above considerations, we can easily deduce the following conclusions. Part 1 follows from (12), and part 2 follows from (14)–(15). If $\lambda _r<1$, then (12) $\Longrightarrow$ $P^{d}_{k}(\lambda _r;r)(\xi _{k}^{(k)})>0$, and (13) $\Longrightarrow$ $P^{d}_{k}(\lambda _r;r)(y)>0$, then we get part 3(a); (14)–(17) $\Longrightarrow$ 3(b); parts 3(a) and 3(b) $\Longrightarrow$ part 3(c). If $\lambda _r>1$, then (12) $\Longrightarrow$ $P^{d}_{k}(\lambda _r;r)(\xi _{k}^{(k)})<0$, and $P^{d}_{k}(\lambda _r;r)(\xi _{k}^{(k)})<0\Longrightarrow$ part 4 by (11) and the symmetry. $\square$

4 Brauer and Geršgorin Sets of Jacobi Matrices

4.1 Brauer and Geršgorin Sets of any Matrix

We begin by recalling Geršgorin [12, 13, 20] and Brauer [1, 20] theorems to locate the eigenvalues of any matrix $A_n=(a_{ij})_{1\le i,j\le n}\in {\mathbb {C}}^{n\times n}$.

Geršgorin disks (G-disks) are defined by

$$\begin{aligned} {\mathcal {D}}^{(n)}_i=\left\{ z\in {\mathbb {C}}: \left| z-a_{ii}\right| \le r_i^{(n)} \right\} , \ r_i^{(n)}=\sum _{j=1,j\ne i}^n|a_{ij}|,\ 1\le i\le n. \end{aligned}$$

Geršgorin set (G-set) is the union of all G-disks, that is,

$$\begin{aligned} {\mathcal {D}}^{(n)}=\bigcup _{i=1}^{n} {\mathcal {D}}^{(n)}_{i}, \ n\ge 1. \end{aligned}$$

Geršgorin circle theorem [12] states that the set of eigenvalues of $A_n$, the so-called spectra of $A_n$, $\sigma (A_n)$, satisfies $\sigma (A_n) \subseteq {\mathcal {D}}^{(n)}.$ Furthermore, if there exist $m<n$ G-disks disjoint from the remaining ones, then their union contains exactly m eigenvalues of $A_n$.

Brauer-Cassini ovals of $A_n$ [1] (B-ovals) are defined by

$$\begin{aligned} {\mathcal {B}}^{(n)}_{ij}=\left\{ z\in {\mathbb {C}}: \left| z-a_{ii}\right| \left| z-a_{jj}\right| \le r_{ij}^{(n)}\right\} , \ r_{ij}^{(n)}=r_i^{(n)}r_j^{(n)}, \end{aligned}$$

for $1\le i<j\le n$, $n\ge 2$, and the Brauer set (B-set) is

$$\begin{aligned} {\mathcal {B}}^{(n)}=\bigcup _{\begin{array}{c} i,j=1\\ i<j \end{array}}^{n}{\mathcal {B}}^{(n)}_{ij}, \ n\ge 2. \end{aligned}$$

We remark that there exist $\left( {\begin{array}{c}n\\ 2\end{array}}\right) =n(n-1)/2$ B-ovals. The Brauer theorem [1] states that

$$\begin{aligned} \sigma (A_n)\subseteq {\mathcal {B}}^{(n)} \subseteq {\mathcal {D}}^{(n)}. \end{aligned}$$

More precisely

$$\begin{aligned} {\mathcal {B}}^{(n)}_{ij}\subseteq \left( {\mathcal {D}}^{(n)}_{i} \cup {\mathcal {D}}^{(n)}_{j}\right) . \end{aligned}$$

Furthermore, there exists an analogous of Geršgorin result on disjoint subsets for Brauer-Cassini ovals. In the sequel, we will refer to B-ovals as B-subsets.

4.2 Brauer and Geršgorin Sets of Jacobi Matrices Associated with Monic Orthogonal Polynomials

Let us consider the sequence of Jacobi matrices $\{J_n\}_{n\ge 1}$ associated with any monic orthogonal polynomial sequence $\{P_n(x)\}_{n\ge 0}$ given by (1)-(2), taking $\alpha _{n}$ such that

$$\begin{aligned}{} & {} \alpha _{n}^2=\gamma _{n}\ne 0,\ n\ge 1,\nonumber \\{} & {} J_n= \left( \begin{array}{ccccccc} \beta _0 &{} \alpha _1 &{} &{} &{} &{} &{} \\ \alpha _1 &{} \beta _1 &{}\alpha _2 &{} &{} &{} &{}\\ &{} \ddots &{} \ddots &{} \ddots &{} &{} &{}\\ &{} &{} \alpha _{i-1} &{} \beta _{i-1} &{} \alpha _ i &{} &{}\\ &{} &{} &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} &{} &{} \alpha _{n-2} &{} \beta _{n-2} &{} \alpha _{n-1} \\ &{} &{} &{} &{} &{} \alpha _{n-1} &{} \beta _{n-1} \end{array}\right) , \ n\ge 1. \end{aligned}$$

(18)

It can be proved that $P_n(x)$ is the characteristic polynomial of $J_n$, that is,

$$\begin{aligned} P_n(x)=\det (xI_n-J_n), \ n\ge 1, \end{aligned}$$

(19)

where $I_n$ is the identity matrix of order n. Thus, zeros of $P_n(x)$ are eigenvalues of $J_n$. In this work, we are going to apply Geršgorin [12] and Brauer [1] theorems to the Jacobi matrix $J_n$ in order to obtain some locations of zeros of $P_n(x)$.

G-disks of $J_n$, for $n\ge 2$, are

$$\begin{aligned} {\mathcal {D}}^{(1)}_1=\{\beta _0\}\ ;\ {\mathcal {D}}^{(n)}_i=\{z\in {\mathbb {C}}:|z-\beta _{i-1}| \le r^{(n)}_i\},\ 1\le i\le n, \end{aligned}$$

with radius given by

$$\begin{aligned}{} & {} r^{(1)}_1=0;\nonumber \\{} & {} r^{(n)}_1=|\alpha _{1}|, r^{(n)}_i=|\alpha _{i-1}| +|\alpha _{i}|, 2\le i\le n-1,r^{(n)}_n=|\alpha _{n-1}|. \end{aligned}$$

(20)

We remark that $r^{(1)}_1\ne r^{(1+m)}_1$ and $r^{(n)}_n\ne r^{(n+m)}_n$, $m\ge 1$, thus the upper index in the notation is necessary.

B-subsets of $J_n$, for $n\ge 2$, are

$$\begin{aligned} {\mathcal {B}}^{(n)}_{ij}=\{z\in {\mathbb {C}}:|z -\beta _{i-1}||z-\beta _{j-1}|\le r^{(n)}_{ij}\}, \ r^{(n)}_{ij}=r^{(n)}_{i}r^{(n)}_{j},\ 1\le i<j\le n. \end{aligned}$$

Denoting the zeros of $P_n(x)$ by $\xi ^{(n)}_k$, $1\le k\le n$, Geršgorin and Brauer theorems allow us to conclude that

$$\begin{aligned} Z^{(n)}=\left\{ \xi ^{(n)}_k\right\} _{k =0}^{n} \subseteq {\mathcal {B}}^{(n)}\subseteq {\mathcal {D}}^{(n)}. \end{aligned}$$

(21)

It is easy to see that in the symmetric case ($\beta _n=0$, $n\ge 0$) G-sets and B-sets are the following disks

$$\begin{aligned}{} & {} {\mathcal {D}}^{(n)}=\left\{ z\in {\mathbb {C}}: \left| z\right| \le g^{(n)} \right\} ,g^{(n)} =\max \left\{ r_{i}^{(n)},1\le i\le n\right\} ,n\ge 1; \end{aligned}$$

(22)

$$\begin{aligned}{} & {} {\mathcal {B}}^{(n)}\!=\!\left\{ z\in {\mathbb {C}}: \left| z\right| \le b^{(n)} \right\} ,b^{(n)}\!\! =\!\! \sqrt{\max \left\{ r_{ij}^{(n)},1\le i<j \le n\right\} },n\ge 2. \end{aligned}$$

(23)

Furthermore, from (21), we have

$$\begin{aligned} b^{(n)} \le g^{(n)} ,\ n\ge 2. \end{aligned}$$

(24)

We remark that if $\exists i$, $1\le i\le n-1$: $\gamma _i<0$, then $\alpha _i$ is a complex number and $J_n$ is not an hermitian matrix since $J_n \ne {(\overline{J_n}})^{T}$. In the symmetric positive definite case ($\beta _n=0$, $\gamma _{n+1}>0$, $n\ge 0$), disks (22)-(23) are reduced to the following intervals since all zeros (eigenvalues) are real numbers

$$\begin{aligned} {\mathcal {D}}^{(n)}=\left[ -g^{(n)},\ g^{(n)}\right] , \ {\mathcal {B}}^{(n)}=\left[ -b^{(n)},\ b^{(n)}\right] . \end{aligned}$$

4.3 Brauer and Geršgorin Sets of Jacobi Matrices Associated with Chebyshev Polynomials of the Second Kind

From (3) and (18), we obtain the sequence of Jacobi matrices $\{{\mathcal {J}}_n\}_{n\ge 1}$ associated with the monic Chebyshev sequence of the second kind

$$\begin{aligned} {\mathcal {J}}_n= \left( \begin{array}{cccccc} 0 &{} 1/2 &{} &{} &{} &{} \\ 1/2 &{} 0 &{} 1/2 &{} &{} &{}\\ &{} &{} \ddots &{} \ddots &{} \ddots &{}\\ &{} &{} &{} 1/2 &{} 0 &{} 1/2 \\ &{} &{} &{} &{} 1/2 &{} 0 \end{array}\right) , \ n\ge 1. \end{aligned}$$

(25)

Radius of G-disks of ${\mathcal {J}}_n$ are given by

$$\begin{aligned} r_1^{(1)}=0;\ r_1^{(2)}=r_2^{(2)}=\frac{1}{2};\ r_1^{(n)} =r_n^{(n)}=\frac{1}{2},\ r_i^{(n)}=1,\ 2\le i\le n-1,\ n\ge 3. \end{aligned}$$

(26)

Radius of G-sets and radius of B-sets of ${\mathcal {J}}_n$ are given by

$$\begin{aligned} g^{(1)}=0; \ g^{(2)}=\frac{1}{2}; \ g^{(n)}=1,\ n\ge 3 \ ; \ b^{(2)}=\frac{1}{2}; \ b^{(3)}=\frac{\sqrt{2}}{2}; \ b^{(n)}=1, \ n\ge 4. \end{aligned}$$

With the notation

$$\begin{aligned} {\mathcal {I}}_{c}=\left[ -c,\ c\right] , \ c>0 , \end{aligned}$$

(27)

G-sets and B-sets are the following intervals

$$\begin{aligned}&{} {\mathcal {D}}^{(1)}=\{0\}\ ,\ {\mathcal {D}}^{(2)} ={\mathcal {I}}_{\frac{1}{2}}\ ,\ {\mathcal {D}}^{(n)} ={\mathcal {I}}_{1}\ ,\ n\ge 3 \ ; \\{}&{} {\mathcal {B}}^{(2)}={\mathcal {I}}_{\frac{1}{2}}\ , \ {\mathcal {B}}^{(3)}={\mathcal {I}}_{\frac{\sqrt{2}}{2}} \,\ {\mathcal {B}}^{(n)}={\mathcal {I}}_{1}\ ,\ n\ge 4\ , \end{aligned}$$

and we recover the well-known location of zeros of Chebyshev polynomials of the second kind [19]. We consider that ${\mathcal {J}}_n$ is constituted by the first n rows and n columns of an infinite dimensional Jacobi matrix ${\mathcal {J}}$ corresponding to the entire sequence $\{P_n\}_{n\ge 0}$.

4.4 Geršgorin Disks of Jacobi Matrices Associated with Perturbed Chebyshev Polynomials of the Second Kind by Dilation

From recurrence coefficients (4), and the definition (18) of $J_n$, we obtain the following Jacobi matrix associated with the sequence $\left\{ P^{d}_n(\lambda _r;r)(x)\right\} _{n\ge 0}$

$$\begin{aligned} J^{d}(\lambda _r;r)= \left( \begin{array}{ccccccccc} 0 &{} \frac{1}{2} &{} &{} &{} &{} &{} &{} &{} \\ \frac{1}{2} &{} 0 &{} \frac{1}{2} &{} &{} &{} &{} &{} &{} \\ &{} \ddots &{} \ddots &{} \ddots &{} &{} &{} &{} &{} \\ &{} &{} \frac{1}{2} &{} 0 &{} \frac{\sqrt{\lambda _r}}{2} &{} &{} &{} &{} \\ &{} &{} &{} \frac{\sqrt{\lambda _r}}{2} &{} 0 &{} \frac{1}{2} &{} &{} &{} \\ &{} &{} &{} &{} \ddots &{} \ddots &{} \ddots &{} &{} \\ &{} &{} &{} &{} &{} \frac{1}{2} &{} 0 &{} \frac{1}{2} &{} \\ &{} &{} &{} &{} &{} &{} \ddots &{} \ddots &{} \ddots \\ \end{array}\right) , \begin{array}{l} \leftarrow \textrm{row} \ r\\ \leftarrow \textrm{row} \ r+1 \end{array}. \end{aligned}$$

(28)

$J_n^{d}(\lambda _r;r)$, $n\ge 1$, denotes the matrix constituted by the first n rows and n columns of $J^{d}(\lambda _r;r)$. For $1\le n\le r$, $J_n^{d}(\lambda _r;r)\equiv {\mathcal {J}}_n$ given by (25).

Let us introduce some notation related to $\displaystyle J_n^{d}(\lambda _r;r)$. We note G-disks by $\displaystyle {\mathcal {D}}^{d(n)}_i(\lambda _r;r)$ with radius $\displaystyle r_i^{d(n)}(\lambda _r;r)$, G-set by $\displaystyle {\mathcal {D}}^{d(n)}(\lambda _r;r)$ with radius $g^{(n)}(\lambda _r;r)$, B-set by ${\mathcal {B}}^{d(n)}(\lambda _r;r)$ with radius $b^{(n)}(\lambda _r;r)$, and the set of zeros of $P_n^{d}(\lambda _r;r)$ by

$$\begin{aligned} Z^{(n)}(\lambda _r;r)=\left\{ \xi _k^{(n)}(\lambda _r;r) \right\} _{k=1}^{n}. \end{aligned}$$

Thus, Brauer and Geršgorin theorems applied to $\displaystyle J_n^{d}(\lambda _r;r)$ state that

$$\begin{aligned} Z^{(n)}(\lambda _r;r)\subseteq {\mathcal {B}}^{(n)}(\lambda _r;r) \subseteq {\mathcal {D}}^{(n)}(\mu _r;r). \end{aligned}$$

(29)

From (28), we see that such a perturbation modifies rows of orders r and $r+1$ of ${\mathcal {J}}$, the Jacobi matrix associated with the monic Chebyshev sequence of the second kind. Consequently, it modifies G-disks of the same orders. The radius of those two perturbed G-disks depends if $n=r+1$ or if $n\ge r+2$, and also if $r=1$ or if $r\ge 2$. With the notation

$$\begin{aligned} A_r:=A(\lambda _r;r)=\frac{\sqrt{|\lambda _r|}}{2}, \quad C_r:=C(\lambda _r;r)=\frac{1+\sqrt{|\lambda _r|}}{2}, \end{aligned}$$

(30)

we have

$$\begin{aligned} n=r+1&\Longrightarrow \left\{ r=1 \Rightarrow \left\{ r_1^{d(2)}(\lambda _1;1)=r_2^{d(2)}(\lambda _1;1) =A_1\right\} ,\right. \end{aligned}$$

(31)

$$\begin{aligned}&\quad \left. r\ge 2 \Rightarrow \left\{ r_r^{d(r+1)}(\lambda _r;r)=C_r, \ r_{r+1}^{d(r+1)}(\lambda _r;r)=A_r \right\} \ \right\} ;\nonumber \\ n\ge r+2&\Longrightarrow \left\{ r=1 \Rightarrow \left\{ r_1^{d(n)}(\lambda _1;1)=A_1\ ; \ r_2^{d(n)} (\lambda _1;1)=C_1\right\} \right. ,\nonumber \\&\quad \left. \ \ r\ge 2 \Rightarrow \left\{ r_{r}^{d(n)} (\lambda _r;r)=r_{r+1}^{d(n)}(\lambda _r;r)=C_r\ \right\} \right\} . \end{aligned}$$

(32)

The other G-disks remain unchanged. Thus, with $r^{(n)}_{i}$ given by (26), we have

$$\begin{aligned} r^{d(n)}_{i}(\lambda _r;r)=r^{(n)}_{i},\ i\ne r,\ i\ne r+1, \ 1\le i\le n,\ n\ge 1,\ r\ge 1. \end{aligned}$$

(33)

5 Geršgorin Location of Zeros of Perturbed Chebyshev Polynomials of the Second Kind by Dilation

Proposition 3

The radius $\displaystyle g^{(n)}(\lambda _r;r)$ of the Geršhgorin set ${\mathcal {D}}^{(n)}(\lambda _{r};r)$ of the Jacobi matrix $J_n^{d}(\lambda _{r};r)$ (28), for $\lambda _r\in {\mathbb {R}}$, $\lambda _r\ne 0$, $\lambda _r\ne 1$, $r\ge 1$, and $n\ge r+1$, is given next with the notation (30). By (21), ${\mathcal {D}}^{(n)}(\lambda _{r};r)$ constitutes a location of zeros of $P_n(\lambda _{r};r)(x)$, the r-th perturbed Chebyshev polynomial of the second kind by dilation of degree n.

• For $r=1$,

  $$\begin{aligned}&{} g^{(1)}(\lambda _1;1)=0,\ n=1\ ;\ g^{(2)}(\lambda _1;1)={A_1},\ n=2\ ;\\{}&{} g^{(3)}(\lambda _{1};1)={C_1},\ n=3. \end{aligned}$$

  - If $-1\le \lambda _1<0$ or $0<\lambda _1<1$, then $g^{(2)}(\lambda _1;1)<\frac{1}{2}$ and $g^{(3)}(\lambda _1;1)<{1}$.

  - If $|\lambda _1|>1$, then $g^{(2)}(\lambda _1;1)>{\frac{1}{2}}$ and $g^{(3)}(\lambda _1;1)>{1}$.

• For $r=2$,

  $$\begin{aligned}&{} g^{(1)}(\lambda _2;2)=0,\ n=1\ ;\ g^{(2)}(\lambda _2;2)={\frac{1}{2}},\ n=2.\\{}&{} g^{(3)}(\lambda _2;2)=g^{(4)}(\lambda _2;2)={C_2},\ n=3\ ,\ n=4. \end{aligned}$$

  - If $-1\le \lambda _2<0$ or $0<\lambda _2<1$, then $g^{(3)}(\lambda _2;2)=g^{(4)}(\lambda _2;2)<1$.

  - If $\left| \lambda _2\right| >1$, then $g^{(3)}(\lambda _2;2)=g^{(4)}(\lambda _2;2)>1$.

• For $r\ge 3$,

  $$\begin{aligned}&{} g^{(1)}(\lambda _r;r)=0,\ n=1\ ;\ g^{(2)}(\lambda _r;r)={\frac{1}{2}}\ ,\ n=2\ ;\\{}&{} g^{(k)}(\lambda _r;r)={1}\ ,\ n=k\ ,\ 3\le k\le r. \end{aligned}$$

• For $r=1$ and $n\ge 4$, or for $r=2$ and $n\ge 5$, or for and $r\ge 3$ and $n\ge r+1$,

  $$\begin{aligned} g^{(n)}(\lambda _{r};r)=\max \left\{ 1,C_r\right\} . \end{aligned}$$

  - If $-1\le \lambda _r<0$ or $0<\lambda _r< 1$, then $g^{(n)}(\lambda _{r};r)=1$.

  - If $|\lambda _r|>1$, then $g^{(n)}(\lambda _{r};r)= {C_r}>1$.

Proof

Let us begin by determining the radius of perturbed G-disks from formulas (31) and (32). For $r\ge 1$ and $n=1$, $\displaystyle r^{d(1)}_{1}(\lambda _r;r)=0$. For $r=1$ and $n\ge 2$, $\displaystyle r^{d(n)}_{1}(\lambda _1;1)={A_1}$. For $r\ge 2$ and $n\ge r+1$, $\displaystyle r^{d(n)}_{r}(\lambda _{r};r)={C_r}$. For $r\ge 1$ and $n= r+1$, $\displaystyle r^{d(r+1)}_{r+1}(\lambda _{r};r)={A_r}$. For $r\ge 1$ and $n\ge r+2$, $\displaystyle r^{d(n)}_{r+1}(\lambda _{r};r)={C_r}$. For $r\ge 1$ and $n=1$, $\displaystyle r^{d(1)}_{1}(\lambda _r;r)=0$. For $r=1$ and $n\ge 2$, $\displaystyle r^{d(n)}_{1}(\lambda _1;1)={A_1}$. For $r\ge 2$ and $n\ge r+1$, $\displaystyle r^{d(n)}_{r}(\lambda _{r};r)={C_r}$. For $r\ge 1$ and $n= r+1$, $\displaystyle r^{d(r+1)}_{r+1}(\lambda _{r};r)={A_r}$. For $r\ge 1$ and $n\ge r+2$, $\displaystyle r^{d(n)}_{r+1}(\lambda _{r};r)={C_r}$. Then, taking into account the radius of other disks given by (33), we apply (22) for obtaining the given formulas of $\displaystyle g^{(n)}(\lambda _r;r)$. In each case, we also indicate some information about the magnitude of $\displaystyle g^{(n)}(\lambda _r;r)$ according to the value of $\lambda _r$. $\square$

Corollary 1

Geršhgorin sets of Jacobi matrices associated with the monic Chebyshev sequence of the first kind $\displaystyle \{T_n(x)\}_{n\ge 0}$ (6), with notation (30), are

$$\begin{aligned}&{} {\mathcal {D}}^{d(1)}(2;1)=\{0\},\ g^{(1)}=0, \ n=1;\\{}&{} {\mathcal {D}}^{d(2)}(2;1)=\left[ -g^{(2)},g^{(2)}\right] , \ g^{(2)}=A_1(2;1)=\frac{\sqrt{2}}{2},\ n=2;\\{}&{} {\mathcal {D}}^{d(n)}(2;1)=\left[ -g^{(n)},g^{(n)}\right] \supset {\mathcal {I}}_{1}, \ g^{(n)}=C_1(2;1)=\frac{1+\sqrt{2}}{2}>1, \ n\ge 3. \end{aligned}$$

Proof

In the last proposition, take $r=1$ and $\lambda _r=2$. $\square$

Remark that the well known location of zeros of $\displaystyle \{T_n(x)\}_{n\ge 0}$ is the interval ${\mathcal {I}}_1$ [19], thus in this case Geršgorin location is not sharp.

Proposition 4

If $\lambda _r>1$, then the extremal zeros $\displaystyle \xi _1^{(n)}(\lambda _r;r)$ and $\displaystyle \xi _n^{(n)}(\lambda _r;r)$ of $P_n(\lambda _{r};r)(x)$ have the following location in terms of extremal zeros $\xi _1^{(n)}$ and $\xi _n^{(n)}$ of $P_n(x)$. With notation (30), it holds

• For $r=1$ and $n=2$,

  $$\begin{aligned} \displaystyle -A_r \le \xi _1^{(n)}(\lambda _r;r)< \xi _1^{(n)} , \quad \xi _n^{(n)}<\xi _n^{(n)} (\lambda _r;r)\le A_r. \end{aligned}$$

• For $r=1$ and $n\ge 3$, or for $r\ge 2$ and $n\ge r+1$,

  $$\begin{aligned} -C_r \le \xi _1^{(n)}(\lambda _r;r)< \xi _1^{(n)} , \quad \xi _n^{(n)}<\xi _n^{(n)}(\lambda _r;r)\le C_r. \end{aligned}$$

Proof

Apply (10), the last part of Proposition 2, and Proposition 3.$\square$

6 Brauer Location of Zeros of Perturbed Chebyshev Polynomials of the Second Kind by Dilation

Proposition 5

The radius $\displaystyle b^{(n)}:=b^{(n)}(\lambda _r;r)$ of the Brauer set ${\mathcal {B}}^{(n)}(\lambda _{r};r)$ of the Jacobi matrix $J_n^{d}(\lambda _{r};r)$ (28), for $\lambda _r\in {\mathbb {R}}$, $\lambda _r\ne 0$, $\lambda _r\ne 1$, $r\ge 1$, and $n\ge r+1$, is given next with the notation (30), and the following one

$$\begin{aligned}&{} A'_r:=A'_r(\lambda _r;r)=\sqrt{|\lambda _r|},\ B_r:=B_r(\lambda _r;r)=\sqrt{A'_r}=\root 4 \of {|\lambda _r|}\ , \end{aligned}$$

(34)

$$\begin{aligned}&{} C'_r:=C'_r(\lambda _r;r)=2C_r=1+\sqrt{|\lambda _r|}\ , \nonumber \\{}&{} D_r:=D_r(\lambda _r;r)=\sqrt{C'_r}= \sqrt{1+\sqrt{|\lambda _r|}}. \end{aligned}$$

(35)

By (29), ${\mathcal {B}}^{(n)}(\lambda _{r};r)$ constitutes a location of zeros of $P_n(\lambda _{r};r)(x)$, the r-th perturbed Chebyshev polynomial of the second kind by dilation of degree n.

• For $r=1$, $b^{(n)}:=b^{(n)}(\lambda _1;1)$,

  $$\begin{aligned}&{} \bullet \ \, b^{(2)} =\frac{1}{2}A'_1=A_1\ , \ n=2; \\ {}&{} \bullet \ \, b^{(3)}=\max \left\{ \ \frac{1}{2}D_1\ , \ \frac{1}{2}B_1D_1\right\} , \ n=3, \\ {}&{} -1\le \lambda _1<0 \ \textrm{or}\ 0< \lambda _1<1 \Rightarrow b^{(3)}=\frac{1}{2}D_1;\ |\lambda _1|>1\Rightarrow b^{(3)}=\frac{1}{2}B_1D_1; \\{}&{} \bullet \ \, b^{(4)}=\max \left\{ \frac{1}{\sqrt{2}}D_1\ , \ \frac{1}{2}B_1D_1\right\} , \ n=4, \\{}&{} -4\le \lambda _1< 0 \ \textrm{or}\ 0<\lambda _1< 1\ \textrm{or}\ 1<\lambda _1 \le 4 \Rightarrow b^{(4)}= \frac{1}{\sqrt{2}}D_1, \\{}&{} |\lambda _1|>4\Longrightarrow b^{(4)}=\frac{1}{2}B_1D_1; \\{}&{} \bullet \ \, b^{(n)}=\max \left\{ 1\ , \ \frac{1}{\sqrt{2}}D_1\ , \ \frac{1}{2}B_1D_1\right\} ,\ n\ge 5, \\{}&{} -1\le \lambda _1<0 \ \textrm{or}\ 0< \lambda _1<1 \Rightarrow b^{(n)}=1; \\{}&{} -4\le \lambda _1< -1 \ \textrm{or}\ 1< \lambda _1 \le 4 \Rightarrow b^{(n)}=\frac{1}{\sqrt{2}}D_1;\\{}&{} |\lambda _1|>4\Rightarrow b^{(n)}= \frac{1}{2}B_1D_1. \end{aligned}$$

• For $r=2$, $b^{(n)}:=b^{(n)}(\lambda _2;2)$,

  $$\begin{aligned}&{} \bullet \ \, b^{(3)}=\max \left\{ \frac{1}{2}D_2\ , \ \frac{1}{2}B_2D_2\right\} , \ n=3, \\{}&{} -1\le \lambda _2<0 \ \textrm{or}\ 0< \lambda _2 <1 \Rightarrow b^{(3)}= \frac{1}{2}D_2;\\{}&{} |\lambda _2|>1\Rightarrow b^{(3)}= \frac{1}{2}B_2D_2; \\{}&{} \bullet \ \, b^{(4)}=b^{(5)}=\frac{1}{2}C'_2=C_2; \ n=4\, \ n=5. \end{aligned}$$

• For $r=3$, $b^{(n)}:=b^{(n)}(\lambda _3;3)$,

  $$\begin{aligned}&{} \bullet \ \, b^{(4)}=\max \left\{ \frac{1}{\sqrt{2}}B_3\ , \ \frac{1}{\sqrt{2}}D_3\ ,\ \frac{1}{2}B_3D_3\right\} , \ n=4, \\{}&{} -4\le \lambda _3< 0 \ \textrm{or}\ 0<\lambda _3< 1\ \textrm{or}\ 1<\lambda _3 \le 4 \Rightarrow b^{(4)}= \frac{1}{\sqrt{2}}D_3,\\{}&{} |\lambda _3|>4\Rightarrow b^{(4)}=\frac{1}{2}B_3D_3; \\{}&{} \bullet \ \, b^{(5)}=\max \left\{ \frac{1}{\sqrt{2}}\ , \ \frac{1}{2}C'_3\ ,\ \frac{1}{\sqrt{2}}D_3\right\} , \ n=5, \\{}&{} -1\le \lambda _3<0 \ \textrm{or}\ 0< \lambda _3 <1 \Rightarrow b^{(5)} = \frac{1}{\sqrt{2}}D_3;\\{}&{} |\lambda _3|>1\Rightarrow b^{(5)}=\frac{1}{2}C'_3=C_3. \end{aligned}$$

• For $r\ge 4$, $b^{(n)}:=b^{(n)}(\lambda _r;r)$,

  $$\begin{aligned}&{} \bullet \ \, b^{(r+1)}=\max \left\{ 1\ , \ \frac{1}{\sqrt{2}}B_r\ ,\ \frac{1}{\sqrt{2}}D_r \ , \ \frac{1}{2}B_rD_r\right\} , n=r+1, \nonumber \\{}&{} -1\le \lambda _r<0 \ \textrm{or}\ 0< \lambda _r<1 \Rightarrow b^{(r+1)}= 1;\nonumber \\{}&{} -4\le \lambda _r< -1 \ \textrm{or}\ 1< \lambda _r\le 4 \Rightarrow b^{(r+1)}=\frac{1}{\sqrt{2}}D_r.\nonumber \\{}&{} |\lambda _r|>4 \Rightarrow b^{(r+1)}= \frac{1}{2}B_rD_r. \end{aligned}$$

  (36)

• For $r=2$ or $r=3$, and $n\ge 6$; or for $r\ge 4$ and $n\ge r+2$, $b^{(n)}:=b^{(n)}(\lambda _r;r)$,

  $$\begin{aligned}&{} \bullet \ \, b^{(n)}=\max \left\{ 1\ ,\ \frac{1}{2}C'_r\ , \ \frac{1}{\sqrt{2}}D_r\right\} . \\{}&{} -1\le \lambda _r<0 \ \text {or}\ 0< \lambda _r <1 \Rightarrow b^{(n)}= 1\ ;\ |\lambda _r|>1\Rightarrow b^{(n)}=\frac{1}{2}C'_r=C_r. \end{aligned}$$

Proof

By (23), we have

$$\begin{aligned}{} & {} b^{(n)}(\lambda _r;r) =\sqrt{\max \left\{ r_{ij}^{(n)}(\lambda _r;r), \ 1\le i<j\le n\right\} }, \\{} & {} r_{ij}^{(n)}(\lambda _r;r)=r_{i}^{(n)}(\lambda _r;r)r_{j}^{(n)} (\lambda _r;r), \end{aligned}$$

with $r_{i}^{(n)}(\lambda _r;r)$ given by (31)-(33). In order to determine the maximum, observe that $B_r<D_r$, $C_r>1$, and $D_r<C_r$. Next, we demonstrate the case for $n=r+1$. Other cases are similar. The equality (36) is obtained by direct computations. If $|\lambda _r|\le 1$, then the maximum is 1, because

$$\begin{aligned} \left\{ \left( B_r\le 1\Rightarrow \frac{B_r}{\sqrt{2}}<1\right) \wedge \left( D_r\le \sqrt{2}\Rightarrow \frac{D_r}{\sqrt{2}} \le 1\right) \right\} \Longrightarrow \frac{1}{2}B_rD_r<1. \end{aligned}$$

If $1<|\lambda _r|< 4$, then the maximum is $\displaystyle \frac{D_r}{\sqrt{2}}$, because

$$\begin{aligned} \left( \frac{B_r}{\sqrt{2}}<1 \Rightarrow \frac{B_r}{\sqrt{2}}\frac{D_r}{\sqrt{2}} =\frac{1}{2}B_rD_r<\frac{D_r}{\sqrt{2}}\right) \ \wedge \ \frac{B_r}{\sqrt{2}}<\frac{D_r}{\sqrt{2}}. \end{aligned}$$

If $|\lambda _r|\ge 4$, then the maximum is $\displaystyle \frac{1}{2}B_rD_r$, because

$$\begin{aligned} \frac{B_r}{\sqrt{2}}\ge 1 \Rightarrow \frac{B_r}{\sqrt{2}} \frac{D_r}{\sqrt{2}}=\frac{1}{2}B_rD_r\ge \frac{D_r}{\sqrt{2}} > \frac{B_r}{\sqrt{2}}. \end{aligned}$$

$\square$

Corollary 2

Radius $b^{(n)}:=b^{(n)}(2;1)$ of Brauer sets of Jacobi matrices associated with the Chebyshev sequence of the first kind $\displaystyle \{T_n(x)\}_{n\ge 0}$ (6) are the followings, being $g^{(n)}:=g^{(n)}(2;1)$ the radius of Geršgorin sets given by Corollary 1,

$$\begin{aligned}&{} b^{(2)}=\frac{\sqrt{2}}{2}=g^{(2)} \ ;\ b^{(3)} =\frac{1}{2} \root 4 \of {2}\sqrt{1+\sqrt{2}} =\frac{1}{\root 4 \of {2}}\sqrt{g^{(3)}}; \end{aligned}$$

(37)

$$\begin{aligned}&b^{(n)}=\frac{1}{\sqrt{2}} \sqrt{1+\sqrt{2}} =\sqrt{g^{(n)}}, \ n\ge 4. \end{aligned}$$

(38)

Then,

$$\begin{aligned} b^{(n)}< g^{(n)},\ n\ge 3\ ;\ b^{(n)}>1 ,\ n\ge 4. \end{aligned}$$

(39)

Proof

In Proposition 5, taking $r=1$ and $\lambda _r=2$, we obtain the first equalities of (37)-(38); the second ones are by straightforward consequences of the expressions of $g^{(n)}$ given by Corollary 1. That result states, in particular, that $g^{(n)}>1$, $n\ge 3$, then from (37)-(38), we get (39). Also, direct computations give

$$\begin{aligned} g^{(n)}\approx 1.207,\ n\ge 3\ ;\ b^{(3)}\approx 0.934\,\ b^{(n)}\approx 1.099, \ n\ge 4. \end{aligned}$$

Thus, we conclude that Brauer location is better than the Geršgorin one, but is not sharp, because it is well known that zeros of $\displaystyle \{T_n(x)\}_{n\ge 0}$ belong to ${\mathcal {I}}_1$ [19]. $\square$

7 Comparison Between Geršgorin and Brauer Locations

In the sequel, our goal will be to evaluate how much better is the Brauer location with respect to the Geršgorin one. For that, in each case of Propositions 3 and 5, we are going to compare the radius of G-sets with the radius of B-sets.

Proposition 6

The radius $\displaystyle g^{(n)}:=g^{(n)}(\lambda _r;r)$ of the Geršgorin set given by Proposition 3, and the radius $\displaystyle b^{(n)}:=b^{(n)}(\lambda _r;r)$ of the Brauer set given by Proposition 5, of the Jacobi matrix $\displaystyle J_n^{d}(\lambda _r;r)$ (28), for $\lambda _r\in {\mathbb {R}}$, $\lambda _r\ne 0$, $\lambda _r\ne 1$, $r\ge 1$, and $n\ge r+1$, satisfy the following with notation (30) and (34)–(35).

• For $r=1$, $g^{(n)}:=g^{(n)}(\lambda _1;1)$, $b^{(n)}:=b^{(n)}(\lambda _1;1)$, $n\ge 2$,

  $$\begin{aligned}&{} \bullet \ { For} \ n=2:\ b^{(2)} =g^{(2)}=A_1.\\{}&{} \bullet \ { For} \ n=3: \\{}&{} - \ { If } -1\le \lambda _1<0 \ \textrm{or}\ 0< \lambda _1<1,\ { then}\ b^{(3)} =\frac{1}{\sqrt{2}}\sqrt{g^{(3)}}< g^{(3)}; \\{}&{} -\ { If }\ |\lambda _1|> 1, \ { then} \ b^{(3)}=\frac{B_1}{\sqrt{2}}\sqrt{g^{(3)}}<g^{(3)}. \\{}&{} \bullet \ { For} \ n=4: \\{}&{} \ - { If }\ \lambda _1=-1, \ { then}\ b^{(4)} =g^{(4)}=1 \ ;\\{}&{} \ - { If } -1<\lambda _1<0 \ \textrm{or}\ 0< \lambda _1<1, \ { then}\ b^{(4)}=\sqrt{C_1}<g^{(4)}=1; \\{}&{} \ - { If }\ 1<|\lambda _1|\le 4, \ { then} \ b^{(4)}=\sqrt{g^{(4)}}<g^{(4)};\\{}&{} \ - { If }\ |\lambda _1|> 4, \ { then} \ b^{(4)}=\frac{B_1}{\sqrt{2}}\sqrt{g^{(4)}}<g^{(4)}. \\{}&{} \bullet \ { For} \ n\ge 5:\\{}&{} - \ { If } -1\le \lambda _1<0 \ \textrm{or}\ 0< \lambda _1<1, \ { then}\ b^{(n)}= g^{(n)}=1;\\{}&{} -\ { If }\ 1<|\lambda _1|\le 4, \ { then}\ b^{(n)} =\sqrt{g^{(n)}}<g^{(n)};\\{}&{} -\ { If }\ |\lambda _1|> 4, \ { then}\ b^{(n)} =\frac{B_1}{\sqrt{2}}\sqrt{g^{(n)}}<g^{(n)}. \end{aligned}$$

• For $r=2$, $g^{(n)}:=g^{(n)}(\lambda _2;2)$, $b^{(n)}:=b^{(n)}(\lambda _2;2)$,

  $$\begin{aligned}{} & {} \bullet \ { For} \ n=3: \\{} & {} -\ { If } -1\le \lambda _2<0 \ \textrm{or} \ 0< \lambda _2<1,\ { then}\ b^{(3)} =\frac{1}{\sqrt{2}}\sqrt{g^{(3)}}< g^{(3)}=C_2; \\{} & {} -\ { If }\ |\lambda _2|> 1, \ { then} \ b^{(3)}=\frac{B_2}{\sqrt{2}}\sqrt{g^{(3)}}<g^{(3)}=C_2. \\{} & {} \bullet \ { For} \ n=4: \ b^{(4)}=g^{(4)}=C_2. \\{} & {} \bullet \ { For} \ n=5: \\{} & {} -\ { If }\ \lambda _2=-1, \ { then}\ b^{(5)}=g^{(5)}=1;\\{} & {} -\ { If } -1<\lambda _2<0 \ \textrm{or}\ 0< \lambda _2<1, \ { then}\ b^{(5)}=C_2<g^{(5)}=1;\\{} & {} -\ { If }\ |\lambda _2|>1, \ \textrm{then} \ b^{(5)}=g^{(5)}=C_2. \end{aligned}$$

• For $r=3$, $g^{(n)}:=g^{(n)}(\lambda _3;3)$, $b^{(n)}:=b^{(n)}(\lambda _3;3)$,

  $$\begin{aligned}{} & {} \bullet \ { For} \ n=4: \\{} & {} -\ { If }\ \lambda _3=-1, \ \textrm{then}\ b^{(4)}=g^{(4)}=1;\\{} & {} -\ { If } -1<\lambda _3<0 \ \textrm{or} \ 0< \lambda _3<1, \ { then}\ b^{(4)} =\frac{1}{\sqrt{2}}D_3<g^{(4)}=1; \\{} & {} -\ { If }\ 1<|\lambda _3|\le 4, \ { then}\ b^{(4)}=\sqrt{g^{(4)}}<g^{(4)};\\{} & {} -\ { If }\ |\lambda _3|> 4, \ { then} \ b^{(4)}=\frac{B_3}{\sqrt{2}}\sqrt{g^{(4)}}<g^{(4)}. \\{} & {} \bullet \ { For} \ n=5: \\{} & {} -\ { If }\ \lambda _3=-1, \ \textrm{then}\ b^{(5)}=g^{(5)}=1;\\{} & {} -\ { If } -1<\lambda _3<0 \ \textrm{or}\ 0< \lambda _3<1, \ { then}\ b^{(5)}=\frac{1}{\sqrt{2}}D_3<g^{(5)}=1;\\{} & {} - \ { If} \ |\lambda _3| >1, \ { then}\ b^{(5)} =g^{(5)}=C_3. \end{aligned}$$

• For $r\ge 4$, and n= r+1, $g^{(r+1)}:=g^{(r+1)}(\lambda _r;r)$, $b^{(r+1)}:=b^{(r+1)}(\lambda _r;r)$,

  $$\begin{aligned}{} & {} -\ { If} \ -1\le \lambda _{r}<0 \ \textrm{or} \ 0< \lambda _{r}<1, \ \textrm{then}\ b^{(r+1)}=g^{(r+1)}=1;\\{} & {} -\ { If }\ 1<|\lambda _r|\le 4, \ { then}\ b^{(r+1)} =\sqrt{g^{(r+1)}}<g^{(r+1)}=C_r;\\{} & {} -\ { If }\ |\lambda _r|> 4, \ { then}\ b^{(r+1)} =\frac{B_r}{\sqrt{2}}\sqrt{g^{(r+1)}}<g^{(r+1)}=C_r. \end{aligned}$$

• For $r=2$ or $r=3$, and $n\ge 6$; or for $r\ge 4$ and $n\ge r+2$, $g^{(n)}:=g^{(n)}(\lambda _r;r)$, $b^{(n)}:=b^{(n)}(\lambda _r;r)$,

  $$\begin{aligned}{} & {} -\ { If}\ -1\le \lambda _{r}<0 \ \textrm{or}\ 0< \lambda _{r}<1, \ \textrm{then}\ b^{(r+1)}=g^{(r+1)}=1;\\{} & {} -\ { If}\ |\lambda _r| >1, \ { then}\ b^{(n)}=g^{(n)} =C_r. \end{aligned}$$

Fig. 1

Graph of M, given in Definition 1, as a function of $\lambda _r\in [-30,\ 30]$, for $r=6$ and $n=18$. Remark that there is no symmetry of M with respect to the parameter of perturbation. The behavior of zeros is very different for positive and negative values of $\lambda _r$. We have obtained similar graphs for other values of r

Fig. 2

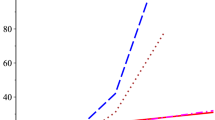
Illustration of Proposition 6. Graphs of radius of G-sets, $g^{(n)}:=g^{(n)}(\lambda _r;r)$ (blue trace), and radius of B-sets, $b^{(n)}:=b^{(n)}(\lambda _r;r)$ (dashed red trace), as functions of $\lambda _r$, for $-10\le \lambda _r\le 10$

Fig. 3

Continuation of the previous figure

Proof

Let us prove some parts of the case $r=1$. For $n=3$, if $-1\le \lambda _1<0$ or $0\le \lambda _1<1$, then $\displaystyle b^{(3)}=\frac{1}{2}\sqrt{1+\sqrt{|\lambda _1|}}< \frac{1+\sqrt{|\lambda _1|}}{2}=g^{(3)},$ since $\displaystyle 1+\sqrt{|\lambda _1|}>1$. If $|\lambda _1|>1$, then $\displaystyle b^{(3)}=\frac{1}{2}\root 4 \of {|\lambda _1|}\sqrt{1+\sqrt{|\lambda _1|}}< \frac{1+\sqrt{|\lambda _1|}}{2}=g^{(3)}\Longleftrightarrow 0<1+\sqrt{|\lambda _1| }\,$ which is a true proposition. For $n=4$, if $-1\le \lambda _1<0$ or $0<\lambda _1<1$, then $g^{(4)}=1$, and $b^{(4)}=\frac{1}{\sqrt{2}}\sqrt{1+\sqrt{|\lambda _1|}}$. If $\lambda _1=-1$, then $b^{(4)}=g^{(4)}$. If $\lambda _1\ne - 1$, then $b^{(4)}<1$ and consequently $b^{(4)}<g^{(4)}$. If $-4\le \lambda _1<-1$ or $1<\lambda _1\le 4$, then $\displaystyle b^{(4)}=\frac{1}{\sqrt{2}}\sqrt{1+\sqrt{|\lambda _1|}} =\sqrt{g^{(4)}}<g^{(4)}\,$ since $g^{(4)}>1$. Other parts or cases are similar to the one we just proved (Fig. 1). $\square$

From this proposition, we conclude about the advantage of the Brauer location for $r=1$, $|\lambda _1|>1$, and $n\ge 5$; also for other values of r and some initial values of n, as can be seen from graphical representations of $g^{(n)}(\lambda _r;r)$ and $b^{(n)}(\lambda _r;r)$ presented in Figs. 2 and 3.

Definition 1

A measure of the sharpness of Geršgorin or Brauer location of zeros $\xi _k^{(n)}(\lambda _r;r)$, $1\le k\le n$, of $P_n(\lambda _r;r)(x)$, for $\lambda _r\in {\mathbb {R}}$, $\lambda _r\ne 0$, $\lambda _r\ne 1$, $r\ge 1$, and $n\ge r+1$, is defined by

$$\begin{aligned} {\mathcal {S}}^{(n)}(\lambda _r;r)=\left( R^{(n)}(\lambda _r;r)-M\right) /M\ ,\ M=\max \left\{ \left| \xi _k^{(n)}(\lambda _r;r)\right| : 1\le k\le n\right\} , \end{aligned}$$

where $R^{(n)}(\lambda _r;r)$ is equal to radius $g^{(n)}(\lambda _r;r)$ or $b^{(n)}(\lambda _r;r)$ of Geršgorin or Brauer sets ${\mathcal {B}}^{(n)}(\lambda _{r};r)$ or ${\mathcal {D}}^{(n)}(\lambda _{r};r)$ of the Jacobi matrix $J_n^{d}(\lambda _{r};r)$ (28). See Fig. 1 for $r=6$ and $n=18$.

We observe that the sharpness measures the relative error between the radius M of the smallest circle or interval that contains all perturbed zeros and the radius of the G-set or the B-set that locates them. It is worth mentioning here that M is equal to the spectral measure of $J_n(\lambda _r;r)$.

Fig. 4

Illustration of Propositions 2, 3, and 4. Zeros (blue dots) and G-sets ${\mathcal {G}}$ (traced in red) for order $r=6$, degree $n=18$, and several values of $\lambda _6$. Zeros of $P_{18}(\lambda _6;6)(x)$ are denoted by $\xi _{k}^{d(18)}$. Zeros of Chebyshev polynomial $P_{18}(x)$ are denoted by $\xi _{k}^{(18)}$. ${\mathcal {S}}:={\mathcal {S}}_{G}^{(18)}(\lambda _6;6)$ is the sharpness of Geršgorin location

Fig. 5

Continuation of the previous figure

Fig. 6

Numerical evolution of sharpness ${\mathcal {S}}_{G}^{(n)}(\lambda _r;r)$ of G-sets (blue dots), and sharpness ${\mathcal {S}}_{B}^{(n)}(\lambda _r;r)$ of B-sets (red squares) with the degree $2\le n\le 25$, for order $r=1$ and several negative values of the perturbation parameter $\lambda _1$. In each case, ranges of sharpnesses are indicated next to the value of $\lambda _1$

Fig. 7

Continuation of the previous figure for positive values of $\lambda _1$. For $\lambda _1=1\pm \frac{1}{4}$, that is, for $\lambda _1=\frac{3}{4}$ and $\lambda _1=\frac{5}{4}$, we represent also sharpness of G-sets for Chebyshev polynomials of second kind (brown diamonds)

Fig. 8

Zeros $\xi _k^{(n)}(\lambda _r;r)$, $1\le k\le n$, for $r=6$, $n=18$, and $\lambda _r =-50,-48,...,-2$

8 Symbolic, Numerical, and Graphical Results

In this section, we give some symbolic, numerical, and graphical results obtained with the software Mathematica^® to clarify and illustrate the main results of this work. These kinds of experiments are useful in the investigation of this topic because they can serve as a verification tool, as a way to get negative answers, to formulate conjectures, or to make some discoveries, and therefore allow to direct some aspects of the theoretical study.

To get concrete results, we should begin by fixing the order r of perturbation and the degree n. Taking, as in [8], $r=6$, $n=18$, and a symbolic parameter of perturbation $\lambda _6$, starting from initial conditions (1), using the recurrence relation (2) with recurrence coefficients (4), we compute recursively polynomials with increase degrees until obtaining $P_{18}^{d}(6;\lambda _6)(x)$ presented next. We applied the command Expand to get polynomials in the canonical basis.

$$\begin{aligned}{} & {} P_{18}^{d}(\lambda _6;6)(x) = x^{18}-\frac{1}{4} \left( \lambda _6+16\right) x^{16}+\frac{1}{8} \left( 7 \lambda _6+53\right) x^{14}\\{} & {} \qquad \qquad -\frac{1}{64} \left( 79 \lambda _6+376\right) x^{12}+\frac{1}{256} \left( 230 \lambda _6+771\right) x^{10}-\frac{\left( 367 \lambda _6+920\right) }{1024}x^8\\{} & {} \qquad \qquad +\frac{\left( 157 \lambda _6+305\right) }{2048}x^6-\frac{3 \left( 43 \lambda _6+67\right) }{16384}x^4+\frac{9 \left( 2 \lambda _6+3\right) }{65536}x^2-\frac{1}{262144}. \end{aligned}$$

Fixing the value of the parameter of perturbation, taking for example $\lambda _6=-2$, we obtain polynomials that can be plotted and studied numerically.

$$\begin{aligned}{} & {} P_{18}^{d}(-2;6)(x) = x^{18}-\frac{7 x^{16}}{2} +\frac{39 x^{14}}{8}-\frac{109 x^{12}}{32}+\frac{311 x^{10}}{256}-\frac{93 x^8}{512}\\{} & {} \qquad \qquad -\frac{9 x^6}{2048}+\frac{57 x^4}{16384}-\frac{9 x^2}{65536}-\frac{1}{262144}. \end{aligned}$$

We compute their zeros with the command NSolve, and we get some conjugate complex zeros.

$$\begin{aligned}{} & {} \{\xi ^{(18)}_k(-2;6)\}_{k=1}^{18}=\left\{ -0.967703, -0.877088 - 0.0130199 I, -0.877088 + 0.0130199 I, \right. \\{} & {} \qquad \qquad -0.719435,-0.535283 - 0.053851 I, -0.535283 + 0.053851 I, \\{} & {} \qquad \qquad -0.27156, 0. - 0.13711 I, 0. + 0.13711 I, 0. - 0.338328 I, 0. + 0.338328 I, \\{} & {} \qquad \qquad 0.27156, 0.535283 - 0.053851 I, 0.535283 + 0.053851 I, 0.719435, \\{} & {} \qquad \qquad \left. 0.877088 - 0.0130199 I, 0.877088 + 0.0130199 I, 0.967703\right\} . \end{aligned}$$

Recall that for $r=6$ and $n\ge 8$, Brauer location coincides with the Geršhgorin one. In Figs. 4 and 5, we give some representations of zeros and G-sets for $P_{18}^{d}(\lambda _6;6)(x)$, with values of $\lambda _6$ corresponding to last part of Proposition 3. Also, we give measures of sharpness of G-sets, numerical values of extremal zeros, and some comments. We notice the existence of pairs of close zeros which is a source of numerical instability (see Figs. 4 and 5).

Figures 6 and 7 represent numerical evolution of sharpnesses of Geršgorin and Brauer locations with the degree n, for $r=1$ and several values of $\lambda _1$. It is worth mentioning that the higher the degree, the more the locations are relevant because computing zeros of high-degree polynomials is imprecise and time-consuming. We remark that sharpnesses decrease, so locations become more accurate, which means that some zeros approach the limits of G-sets and B-sets as n increases. Note that G-sets and B-sets are constant for $n\ge r+2$ and $\lambda _r$ fixed. Furthermore, we can observe that the larger $|\lambda _1|$, the less the sharpness decreases with n, which means that for those values of $\lambda _1$ zeros of the highest absolute value vary very little. We have tested other values of r, and we have obtained similar results.

At last, in Fig. 8, we show the zeros of $P_n(\lambda _r;r)$, for $r=6$, $n=18$, and some negative and consecutive values of the parameter of perturbation $\lambda _r$. We remark that zeros describe special trajectories as functions of $\lambda _r$, a fact that deserves further study.

9 Conclusions

We consider that we have obtained by this method quite good locations of zeros of perturbed Chebyshev polynomials of the second kind by dilation. The Brauer location is better in some cases. The methodology applied in this article constitutes a starting point for treating more complicated perturbed orthogonal sequences and getting some locations for their zeros.