Introduction

The assessment of thermodynamic data for application in computer simulations is commonly based on the knowledge of the amount and composition of individual phases in thermodynamic equilibrium. Together with basic thermo-physical data, such as single phase enthalpies, specific heat capacities, and enthalpies of solution, parameters are obtained from least-squares optimization that describe the Gibbs free energy of the individual phases and, thus, the thermodynamic equilibrium state of multi-component multi-phase systems. Computer simulation of multi-phase equilibria, so-called ‘computational thermodynamics’, as well as simulation of phase transformation kinetics are standard tools in materials development and research nowadays.[1]

In recent times, computational thermodynamics has been coupled with theoretical models for the kinetics of phase transformations, utilizing the multi-component chemical driving forces and potentials from thermodynamic engines. A prominent approach of this kind is realized in the software package DICTRA.[2] The thermodynamic data needed in the kinetic model is obtained directly from the thermodynamic engine of the software ThermoCalc.[3] Based on the local thermodynamic equilibrium hypothesis together with the solution of the long-range diffusion problem surrounding the moving phase boundary, the kinetics of diffusion-controlled phase transformations can be simulated.

More recently, an alternative approach has been developed,[4,5] which describes the evolution of precipitates in multi-component, multi-phase systems based on the thermodynamic extremal principle of maximum entropy production.[6-8] Since this new model is based on a mean-field representation of the precipitation problem, it is particularly useful in complex systems where the numerical solution of the classical moving boundary problem becomes increasingly difficult.

One of the major features of the new model is that the thermodynamic forces are formulated in terms of chemical potentials only and no information on thermodynamic equilibrium is processed in the kinetic simulation. The evolution of the system is solely determined by the thermodynamic extremal principle. The kinetic pathway towards the final equilibrium state can proceed through numerous metastable states. Another feature is that the simulations can be performed without arbitrary fitting parameters. The necessary input data for the simulation are entirely derived from thermodynamic and kinetic databases, which have been assessed in independent experiments.

One of the prerequisites for accurate kinetic simulations is accuracy of the thermodynamic and kinetic input data. Since the kinetic pathway of the simulation can be far away from thermodynamic equilibrium, knowledge of the Gibbs free energy must be accurate over the entire compositional range. Unfortunately, precise thermodynamic data for hypothetical states of pure compounds; for instance, fcc-iron at room temperature, are often not readily accessible by experiment. Nevertheless, their numerical values need to be defined for computational reasons. In practice, these parameters are frequently estimated from some theoretical consideration, e.g., lattice stabilities obtained from first-principle calculations.[9] However, sometimes they are simply guessed.

The problem of accurate data for hypothetical states is schematically illustrated in Fig. 1. Consider a phase α consisting of the two components A and B. From experiment, thermodynamic quantities, such as solution enthalpies, are measured to obtain a description of the Gibbs energy of this phase. However, experimental data is available only in a limited composition range, because, in equilibrium, this phase α only dissolves a certain amount of B. On performing a thermodynamic assessment by least-squares fitting of the experimental data, different curves can give a good representation of the results. All of these describe the equilibrium properties of the compound well. For thermodynamic equilibrium calculations, the chosen extrapolation into the metastable region will have little or no effect.

Fig. 1
figure 1

On the difficulty in extrapolating thermodynamic data into metastable regions

Full size image

Now consider a situation where this phase α precipitates from a solid solution with 99% B atoms and 1% A atoms. Due to kinetic reasons, in the initial stages of the reaction, the precipitates are highly enriched in B with a composition indicated by the grey bar in Fig. 1.

In this case, the shape of the curves in the extrapolation to the B-rich side is essential and the results of kinetic simulations will strongly depend on the choice of extrapolation.

When looking at this problem from the opposite direction, however, proper kinetic simulations provide a huge potential for assessing and improving these unknown parameters. Given the availability of a ‘predictive’ model for describing the kinetic process, e.g., the nucleation and growth of precipitates, thermodynamic parameters can be optimized even in non-equilibrium regions. This aspect is discussed in the following sections based on two recent examples of application of the new precipitation kinetics model to heat treatments of steels. Beforehand, the model is outlined and it is demonstrated how the necessary input parameters for the kinetic simulation can be obtained from thermodynamic and kinetic databases. No real thermodynamic assessment is carried out in this paper, but the potential for doing so is emphasized.

The Kinetic Model

The model for simulation of precipitation kinetics that is applied in this work consists of two major parts, i.e., a module for precipitate nucleation and a module for the evolution of the radius and chemical composition of the precipitates. These have been described in detail elsewhere.[10,11] The models are implemented in the software MatCalc.[12]

It is important to emphasize that the following simulations are performed without any of the classical fitting parameters, such as interfacial energy and/or nucleation site density. All input quantities are determined from either the microstructure of the material or from the thermodynamic and kinetic databases. Since the latter parameters have been determined from independent experiments, the present simulations are considered as having ‘predictive character’ at least within the accuracy of the experimental information and the theoretical models.

Precipitate Nucleation

Precipitate nucleation in solid-state systems can be conveniently described by classical nucleation theory (CNT). Accordingly, the transient nucleation rate J is given as[13]

$$ J=Z\beta ^\ast N_{\rm C} \exp \left( {-\frac{\Delta G^\ast }{kT}} \right)\exp \left( {-\frac{\tau }{t}} \right)=J_{\rm S} \exp \left( {-\frac{\tau }{t}} \right) $$
(1)

where J S is the steady state nucleation rate, Z is the Zeldovich factor, β* is the atomic attachment rate, N C is the number of potential nucleation sites, δG * is the critical nucleation energy, k is the Boltzmann constant, T is the absolute temperature, t is the time and τ is the incubation time.

For application to multi-component systems, the mathematical formulation has recently been extended.[4,10] Table 1 summarizes the multi-component expressions for nucleation as used in the present study.

Table 1 Expressions for multi-component precipitate nucleation
Full size table

When analyzing the equations in Table 1, it is recognized that all parameters (including the interfacial energy) for evaluation of the nucleation rate J are given quantities. The methodology for estimating the interfacial energy γ is presented later.

Evolution of Radius and Composition of Precipitates

Once a precipitate has nucleated, further evolution of its radius and chemical composition is evaluated with the novel model for precipitation kinetics in multi-component multi-phase systems described by Svoboda et al.[4] and Kozeschnik et al.[11] Basis of this model is a mean-field formulation of the precipitation problem and application of the thermodynamic extremal principle of maximum entropy production. Accordingly, the total Gibbs free energy (G) of a system with m precipitates and n components is expressed as

$$G=\sum\limits_{i=1}^{n} N_{0i} \mu_{0i}+\sum\limits_{k=1}^{m}\frac{4\pi\rho_{k}^{3}}{3}\left(\lambda_{k}+\sum\limits_{i=1}^{n} c_{ki}\mu_{ki}\right)+ \sum\limits_{k=1}^{m}4\pi\rho_{k}^{2}\gamma_{k}$$
(2)

N 0i and μ0i are number of moles and chemical potential of component i in the matrix; μ ki and c ki are the chemical potential and the concentration of component i in the precipitate k; ρ k is the radius; γ k is the interfacial energy; and λ k takes into account elastic and plastic energy contributions. It is then assumed that three dissipative processes are operative during growth of the precipitate. These are: (a) diffusion inside the precipitate, (b) diffusion in the matrix and (c) interface movement. Application of the extremum principle leads to evolution equations that describe the change of the radius and of the mean chemical composition of each single precipitate on the basis of a linear system of equations. The development of the entire system is obtained by numerical integration of these evolution equations as described in Ref 5.

Evaluation of Interfacial Energies

In simulation of nucleation and growth of precipitates, the interfacial energy γ and the effective driving force F play dominant roles. These quantities appear in the numerator and denominator of the CNT expression for the critical nucleation energy ΔG * in cubic and quadratic form (see Table 1), which itself is in the exponent of the expression for the steady state nucleation rate J S. In contrast to F, which is frequently well known from thermodynamic databases, γ is not accessible by direct experimental measurement and it is therefore often considered as a fitting parameter.[14]

In the present work, the attempt is made to determine all input parameters of the kinetic simulation from independent sources. Thus, γ is determined from an extended formulation of the ‘nearest-neighbor broken-bond’ model (see Fig. 2), which has been introduced by Becker[15] and Turnbull.[16] Accordingly, based on the assumption of pairwise bonding between neighboring atoms, γ can be related to the solution enthalpy ΔE sol of the precipitate with:

$$\gamma =\frac{n_{\rm S} \cdot z_{\rm S} }{N\cdot z_{\rm L} }\cdot \Delta E_{\rm sol}$$
(3)

where z L is the number of nearest neighbors per atom, z S the number of broken bonds across the interface per atom. n S denotes the number of atoms per m2 interface and N is the Avogadro constant. In an fcc lattice, the values determined by the structure of the crystal lattice are z S = 4 and z L = 12. E sol is computed from standard thermodynamic databases with:

$$\Delta E_{\rm sol} =\frac{\partial H}{\partial f_{\rm P}}$$
(4)

where H denotes the molar system enthalpy and f P is the precipitate phase fraction.

Fig. 2
figure 2

Matrix-precipitate interface in the ‘nearest-neighbor broken-bond’ model. In this 2D example, z L = 6, z s = 2

Full size image

Results and Discussion

How ‘Predictive’ Can Kinetic Simulations Be?

In a recent thesis,[17] the above described methodology for a ‘predictive’ precipitation kinetics simulation has been applied to a number of alloy systems. The simulations included binary alloys such as Fe-C and Fe-Cu as well as complex systems, such as \({2\frac{1}{4}\hbox{Cr}}\) steels and 9-12% Cr steels. In several instances, it has been found that experiment and prediction are in good agreement. In some instances, it has been necessary to adapt some of the thermodynamic parameters to correctly represent the experimentally determined equilibrium state.[18] One of the conclusions has been that in systems where the thermodynamic data is well established, ‘predictive’ kinetic simulations can be performed with good success. In systems where the thermodynamic data is less accurate (e.g., in some types of tool steels[19]), the kinetic simulation is also inaccurate and the predictions do not correspond to the experimental finding.

Figure 3 presents the results of a simulation of the evolution of precipitates in the 9% Cr-steel CB8 (from the European COST 522 action) together with some experimental data points from Ref. [20]. The thermodynamic and kinetic input data for this simulation are taken from the TCFE3 database[21] and the mobility database of the software DICTRA.[2] The chemical composition of this steel is summarized in Table 2.

Fig. 3
figure 3

Kinetic simulation of the precipitate evolution during processing of a 9% Cr-steel for power plant application. R, precipitate radius, f, phase fraction, T, temperature

Full size image
Table 2 Chemical composition of the steel CB8 used in the heat treatment simulation
Full size table

To compensate for inaccuracies in the thermodynamic data of Laves phase, the description of this phase had to be modified slightly. This was necessary to match the predicted and measured Si-content of these precipitates.[17] Still, in kinetic simulations, the predicted interfacial energy of Laves phase had to be decreased by 25%. It is important to emphasize that these were the only modifications that had to be made to obtain accordance between the present simulation and experiment. All details for this kind of simulation are described in Rajek.[17]

The first graph in Fig. 3 shows the temperature profile applied in experiment and simulation. It consists of the cooling phase after casting, austenitization, and multiple annealing cycles. The middle and lower graphs summarize the evolution of the phase fractions and mean radii of the individual precipitate populations. The experimental points represent the mean experimental radii weighted by the precipitate volume.

This example demonstrates that even in highly complex alloys and with multi-stage heat treatments, the quality of the simulations can be excellent, provided that the thermodynamic equilibrium and mobility data are of sufficient accuracy. Under these circumstances, the ‘predictive’ potential of the kinetic simulations can be utilized to improve thermodynamic data outside the well-known regions of thermodynamic equilibrium.

How Sensitive Are Kinetic Simulations to Variations in Thermodynamic Data?

On recalling the expressions for the critical nucleation energy ΔG * and the steady state nucleation rate J S, we have:

$$ \Delta G^\ast \sim \frac{\gamma^{3}}{F^{2}}\; {\hbox{and}}\; J_{\rm S} \sim \exp \left( -\frac{\Delta G^\ast }{kT} \right) $$
(5)

Since the interfacial energy γ occurs in cubic form and the driving force F occurs in quadratic form, and both appear in the exponent of the steady state nucleation rate J S, F or γ are very sensitive parameters to the nucleation kinetics and even small variations can have tremendous impact. If the critical nucleation energy ΔG * is in the order of kT or is even higher, nucleation is strongly retarded or completely suppressed.

It is important to emphasize that, in the present work, both quantities are closely related and they are evaluated from the same thermodynamic database. However, when investigating the physical origin of these quantities, it becomes clear that the (chemical part of the) driving force F chem is related to the Gibbs free energy of the precipitate phase, with:

$$ F_{\rm chem}=\sum\limits_i {X_i^\alpha \mu_i^{\rm mat}} -G_{\rm m}^\alpha $$
(6)

where as the interfacial energy γ is related to the enthalpy of solution according to Eq 4. The index i denotes the number of components, X α i is the mole fraction of element i in the precipitate and μ mat i is the chemical potential of element i in the matrix. Entropy does not occur in the expression for γ, because entropy is neglected in the derivation of this relation due to the assumption of an infinitely narrow precipitate/matrix interface. Within reasonable limits, γ and F can thus be adjusted independently.

Evaluation of Extrapolated Thermodynamic Parameters: Cementite Precipitation in Fe-Si-C Austenite

In this section, the potential for improvement of the thermodynamic parameter G(CEM,Si:C) of the metastable (FeSi)3C compound is investigated. ‘CEM’ stands for the cementite phase and the parameter notation is oriented on the standard notation for CALPHAD-type thermodynamic databases.[22] G(CEM,Si:C) describes the Gibbs energy of a hypothetical Si3C compound with orthorhombic cementite structure.

It is well known that silicon is virtually insolvable in cementite and, therefore, the thermodynamic interaction between Si and C in the orthorhombic cementite structure is not directly accessible by experiment. Consequently, since Si does not occur in cementite in equilibrium, Si is usually omitted in the thermodynamic modeling of this phase. However, when analyzing the initial stages of cementite precipitation at lower temperatures, it is found that cementite nucleates and grows with a chemical composition of substitutional elements that is close to that of the parent matrix.[23] This special relationship is usually denoted as para-equilibrium.[24]

When dealing with situations where Si occurs in cementite in significant amount, such as para-equilibrium nucleation, the parameter G(CEM,Si:C) is essential because Si increases the Gibbs energy of the precipitate and, thus, significantly retards the precipitation of cementite.[25,26] Recently, this parameter has been estimated ‘by a trial-and-error method utilizing the known phase equilibria in Fe-Si-C and Co-Si-C’.[25] A value of G(CEM,Si:C) = 250,000 J · mol has been suggested in this paper.

Based on this parameter, simulations of the para-equilibrium cementite precipitation kinetics in austenite have been performed (see Fig. 4) with the model described previously. The simulation is based on the experimental conditions given by Jaques et al.[27] In this work, an Fe-1.4Mn-1.5Si-0.29C (wt.%) steel was annealed in the intercritical range at 760 °C and then rapidly cooled to bainite transformation temperatures between 360 and 410 °C. Cementite precipitation in the retained austenite plates has been studied, with the carbon content of the retained austenite observed with 0.58 wt.%. It was demonstrated that 1.5 wt.% Si was sufficient to completely suppress precipitation of cementite in the retained austenite between the ferrite plates of the bainitic structure. In a similar steel with only 0.38 wt.% Si, rapid cementite formation was observed[27] simultaneously with the bainite reaction.

Fig. 4
figure 4

Predicted isothermal TTP curves for cementite precipitation in the retained austenite lamellae of a bainitic Fe-1.4Mn-1.5Si-0.29C-steel. The interaction parameter G(CEM,Si:C) is 250,000 (left image) and 100,000 (right image)

Full size image

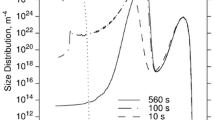
The left graph in Fig. 4 shows the calculated TTP diagram for para-equilibrium of cementite in austenite based on the G(CEM,Si:C) parameter with a value of 250,000 as suggested by Ghosh and Olson.[25] In the figure, the experimental temperature range for the isothermal annealing is indicated with grey bars and comparison with the simulation shows good agreement. According to the experiment, no cementite precipitation occurs in the steel with 1.5 wt.% Si, whereas rapid precipitation takes place in the steel with 0.38 wt.% Si.

The right graph in Fig. 4 presents the results of a simulation with a G(CEM,Si:C) value of 100,000, which shows that this lower value of the parameter can also reproduce the experimental finding of Ref. [27]. On repeating the experiment for steel with intermediate Si-content, e.g., 1 wt.%, and comparison with the predicted TTP curves, the present methodology could provide further information for limiting the uncertainty range of the Gibbs energy parameter G(CEM,Si:C).

Estimation of Uncertain Equilibrium Parameters: 9-12% Cr Steels and the Z-Phase

In the second example, precipitation of the so-called Z-phase (or modified Z-phase) in 9-12% Cr steels for power plant application is analyzed. Z-phase occurs in many alloy variants of this group of materials after long time of thermal exposure.[28] It is held responsible for the deterioration of the superior creep resistance of 9-12% Cr-steels because few but large Z-phase precipitates gradually dissolve a high number of small VN precipitates.[20] Simultaneously, the strength of the material strongly decreases because the small but numerous VN precipitates effectively pin grain boundaries and dislocations. Z-phase in the steel CB8 (see Table 2) has been observed in samples annealed for 16,000 h at 650 °C.[20] It has not (yet) been identified in earlier samples.

In a recent work by Danielsen and Hald,[28] thermodynamic parameters for the Z-Phase have been assessed. The data reported in this reference have been included into the thermodynamic database and simulations have been carried out to study the precipitation kinetics of this phase in CB8 in the course of the typical manufacturing process of cast 9-12% Cr steels. Details on the simulation parameters are summarized in Ref. [17].

Figure 5 shows the results of the kinetic simulation with the original data of Danielsen and Hald[18] together with a possible modification of the data to match better the kinetic simulation with experimental evidence. The results with the original data are indicated with dark solid lines and the subscript ‘org’, the modified data is represented by dark dashed lines and the subscript ‘mod’. The light grey curves represent data for the other precipitate phases, which are almost unaffected by modification of the Z-phase thermodynamic parameters.

Fig. 5
figure 5

Precipitation kinetics during production of 9% Cr-steel CB8. The images show the temperature T, phase fraction f, mean radius R and number density N of Z-phase. Dark solid lines: original thermodynamic data; dark dashed lines: modified data

Full size image

Simulation with the original thermodynamic data shows that precipitation of Z-phase occurs much earlier than observed experimentally. Z-phase reaches its maximum phase fraction already during heating to the first 730 °C quality heat treatment cycle at around 80 h. In practice, the Z-phase with such a high number density close to 1021 m−3 and a radius between 10 and 20 nm should be clearly observable in TEM. Since this has not been the case[20] we conclude that the original combination of interfacial energy and driving force yields a critical nucleation energy too low to effectively suppress precipitation of this phase during heat treatment.

When investigating the origin of the thermodynamic parameters and having in mind that the stoichiometry of Z-phase in this type of steel is (CrV)2N, with equal proportions of Cr and V, the parameter G(ZET,Cr:V:N) is identified as the major contributor to the Gibbs energy of this phase. ‘ZET’ denotes the Z-phase. In the original assessment,[28] a value of:

$$\hbox{G(ZET,Cr:V:N)}= -349,000+200*\hbox{T}+\hbox{GHSERFE}+\hbox{GHSERVV}+\hbox{GHSERNN} $$
(7)

has been suggested. GHSERFE, GHSERVV and GHSERNN are the Gibbs energies of the reference states of Fe, V and N at 298 K and 1 atm. In a test simulation, this parameter is modified such that the value of the total Gibbs energy remains unchanged at approximately 650 °C. The enthalpy contribution has been decreased while, simultaneously, the entropy contribution has been increased. The modified parameter reads:

$$ \hbox{G(ZET,Cr:V:N)}= -400,000+255*\hbox{T}+\hbox{GHSERFE}+\hbox{GHSERVV}+\hbox{GHSERNN} $$
(8)

With this modification, the driving force for Z-phase precipitation remains almost unaltered, i.e., in the order of 60,000 J · mol−1 in the supersaturated state and 8000 J · mol−1 in the state where all VN particles have precipitated, but no significant amount of Z-phase has yet been formed. However, the calculated interfacial energy changes from originally 0.69-0.72 J · m−2 to 0.77-0.82 J · m−2.

Although the impact of this modification on the equilibrium phase diagram is small, the influence on the Z-phase precipitation kinetics is enormous. In Fig. 5, the dashed lines represent the results of the simulation with the modified thermodynamic parameter. Now, the phase fraction of Z-phase reaches its maximum much later, at approximately 20.000 h. Simultaneously, the VN precipitates dissolve. The number density of Z-phase is also much smaller and with approximately 1017 m−3 so low that identification in TEM becomes difficult. These results are in good accordance with the experimental observation that Z-phase is not easy to detect and it is usually only found in long-term annealed specimens.

An alternative strategy to optimize the Z-phase thermodynamics would be to increase the value of the critical nucleation energy ΔG * by decreasing the chemical driving force F. Corresponding kinetic simulations have been carried out and similar results to the ones presented earlier could be obtained with a reduction in Gibbs energy of 5000 J · mol−1. A value of 5500 J · mol−1 has completely suppressed Z-phase nucleation. However, in both of these cases, the equilibrium phase diagram is no longer in accordance with experimental finding.

Summary and Conclusions

In this paper, the potential for improving thermodynamic databases with the help of kinetic simulations is explored. On the basis of a recent model for the simulation of precipitation kinetics in multi-component multi-phase materials, simulations have been performed with the aim of determining metastable or uncertain thermodynamic parameters that are difficult to obtain by direct experiment. The model is briefly outlined. The ‘predictive’ character of the modeling approach is emphasized, which means that all input parameters of the simulation are obtained from independent experiments, i.e., thermodynamic and kinetic databases. Based on this model, the attempt is made to derive estimates of thermodynamic parameters in regions that are not easily accessible by direct experimental observation.

In a first application example, an estimate for the Gibbs energy parameter of the metastable Si3C compound in orthorhombic cementite structure is derived from comparison of the predicted TTP diagram for cementite precipitation in austenite with experimental data. Reasonable agreement is observed with a parameter that has been suggested in literature using a trial-and-error method. It is shown that a smaller value of this parameter can also represent the experimental evidence and it is concluded that further experiment should be undertaken and compared to the simulation to improve the estimate of this parameter.

In a second example, improvement of the thermodynamic description of the so-called Z-phase in 9-12% Cr steels is explored. It is shown that chemical driving force F and interfacial energy γ have different relationship to the Gibbs energy of the phase and that both parameters can be adjusted independently. Whereas the chemical driving force is directly related to the Gibbs energy, the interfacial energy is evaluated on basis of the enthalpy of solution, thus ignoring the contribution of entropy. Adjustment of the corresponding thermodynamic parameter for the Z-phase can give significantly improved agreement between kinetic simulation and experiment, while the equilibrium phase diagram is affected only slightly by these modifications.

The strategies that are outlined in this paper demonstrate that there is substantial potential for improving thermodynamic assessments with the use of kinetic simulations. It must, nevertheless, be warned that all kinetic models, including the one used in this work, are based on assumptions and simplifications, such as the mean field approximation, the classical homogeneous nucleation model, and the coherent interfacial energy model, that introduce uncertainties into the analysis. There is always some risk that improper application of this methodology can also reduce the quality of thermodynamic data, i.e., if thermodynamic data is only modified to correct shortcomings of the kinetic models.