Optimization Method for Gear Heat Treatment Process Oriented to Deformation and Surface Collaborative Control

Abstract

Carburizing and quenching can endow the gear with a hardening depth, improving the part's hardness and contact fatigue strength while distorting the part, resulting in increased or uneven subsequent grinding allowances and reduced part precision. Therefore, cooperative control of hardening depth and distortion is critical. Here, the temperature, phase transition, hardness of carburizing and quenching, and the numerical strain model after die unloading were analyzed to predict the hardening depth and deformation of die quenching. Numerical model is the mathematical essence of finite element model (FEM), based on numerical model, a face gear die-quenching FEM was established to predict the hardening depth and deformation of die quenching, which was verified through carburizing and die-quenching experiments. Based on the FEM, the simulation results under multiple process parameters can be obtained. Further, using the results can built a neural network surrogate model to describe the relationship between carburizing and quenching process parameters and hardening depth and deformation. Additionally, the non-dominated sorting genetic algorithm (NSGA-II) was used to optimize the parameters of the heat treatment process, which are able to control the deformation under the condition of satisfying hardening depth. Finally, a “simulation-surrogation-optimization” model was proposed to simulate the process of carburizing and die quenching of parts, predict the deformation and hardening depth of parts, and give the optimal process parameters under certain process requirements. The results revealed that the martensite content and the deformation of the face gear increased as the carbon content increased from the surface to the center of the face gear. As the die pressure increased, the overall deformation of the face gear using die quenching decreased gradually. However, the excessive pressure caused severe distortion to the tooth height. Using appropriate pressure for die quenching not only controlled the face gear's warping but also reduced its diameter shrinkage.

1 Introduction

Gears working under high-speed and heavy-load conditions require tooth surface precision, hardness, and wear resistance. Therefore, the gears are usually carburized and quenched or even pre-shot peening (Ref 1,2,3) to improve the gear surface hardness and wear resistance. Carburization increases the carbon content of the gear surface and the pearlite content on the surface, consequently improving the gear surface's hardness and wear resistance. However, the increase in carbon reduces the transformation temperature of martensite and bainite during subsequent quenching. Consequently, more martensite and bainite are transformed in the carburized layer after quenching, making the volume and phase transition latent heat of the carburized layer larger than that of the non-carburized layer, causing transformation and thermal stress. Under the action of transformation stress and thermal stress, the tooth surface gets warped and distorted, resulting in increased or uneven subsequent grinding allowances that affect the precision and service life of the tooth surface. An important issue in gear's heat treatment is minimizing distortion while maintaining satisfying tissue performance.

There are two primary heat treatment-induced distortion control methods: (1) adjusting process parameters through trial-and-error experiments in small batches. This method is time-consuming and laborious, and obtaining accurate and quantitative control is difficult. (2) Simulating the heat treatment process and optimizing the parameters according to the simulated data (Ref 4,5,6,7). This method helps to reduce trial-and-error costs, improve production efficiency, and achieve quantitative control.

The heat treatment mathematical model is the basis for the finite element simulation of the heat treatment process. Currently, the mathematical model of carburization simulation is rather mature and is mainly used in studying carburizing process factors such as the material's diffusion coefficient and the atmosphere's transfer coefficient (Ref 8). The quenching process is more complex than the carburizing process, with more influencing factors, and its mathematical model is not yet mature. Some complex multi-field coupled models (Ref 9,10,11) have been proposed in quenching simulation, including electric-magnetic-thermal-organization-coupled model in induction quenching (Ref 12, 13) and gas flow field-temperature organization in gas quenching furnace-coupled model of stress (Ref 14). The heat treatment theory is still under development, and new models are being proposed for different heat treatment processes. For instance, Kang et al. (Ref 15) gave the heat transfer models to simulate the heat treatment processes of workpieces in furnace, and the heat conduction model between components for massive workpieces of different shapes is presented. Dou et al. (Ref 16) proposed a rolling and quenching heat transfer model for simultaneous quenching of strip steel; Zhang et al. (Ref 17) combined carburizing field, temperature field, and phase transition dynamic analysis, establishing a model of the hardness field after carburizing and quenching for low-carbon alloy steel gear; Tong et al. (Ref 18) established a thermo-elasto-plastic constitutive model related to transformation stress and phase transition-induced plasticity for positive gear asynchronous dual-frequency induction quenching process.

Finite element models have been established to perform high-precision simulations on the carburizing and quenching processes based on various mathematical models of heat treatment. Using the DANTE software, Li et al. (Ref 19) investigated the die-quenching-induced deformation of the spiral cone gear; the results revealed that changing the tire's shape by increasing its size controlled the spline deformation. Zhang et al. (Ref 20) established a finite element analysis model for the phase transition deformation process of the spiral cone gear during carburizing and quenching and studied the relationship between hardenability, phase transition, and deformation. The simulation results indicated that the ultimate structure of high-hardenability steel is a mixture of bainite and ferrite. Compared with the low-hardenability gear, the high-hardenability gear has smaller deformation. Liu et al. (Ref 21) reported a simulation of the die-quenching process of aviation face gear using the Deform software. The simulation results revealed that the gear produced contraction–expansion–contraction deformation; the tooth top was saddle-shaped at the end of the quenching; the inner ring die controlled the rib contraction deformation.

The relationship between heat treatment parameters and part quality after heat treatment is nonlinear, making it challenging to establish a mathematical model and obtain a numerical solution. However, machine learning methods do not need to consider the nonlinear relationship between heat treatment parameters and part quality. Rather, these methods obtain the mapping relationship between the two through many reliable sample data. It takes about 10 hours to simulate the carburizing and die quenching of the face gear by the FEM, while using the neural network surrogate model to obtain deformation and hardening depth only takes 1 minute, which is a significant reduction in time. Additionally, it is easier to use the neural network surrogate model for parameter optimization, while it is difficult to optimize the results obtained by FEM. Tong et al. (Ref 22) used artificial neural network (ANN) to establish the relationship between the mechanical properties of Zr alloy tubes and annealing parameters. Ding et al. (Ref 23) used a data-driven method to propose a model for predicting and optimizing the heat treatment deformation of a spiral-bevel gear tooth surface. Liang et al. (Ref 24) used oblique gear heat treatment simulation data to establish a prediction model for predicting carbon concentration distribution and microstructure.

As described above, there have been many reports on deformation prediction and on deformation optimization after heat treatment. Usually, the way to reduce the heat treatment deformation of parts is to reduce the quenching temperature or increase the temperature of the quenching medium, which will lead to a decrease in martensite content and eventually lead to a decrease in hardness; on the contrary, the opposite measures are taken to increase the hardness of carburizing. In summary, for heat treatment deformation and hardening depth, simply controlling one index will cause the other to fail to meet the design requirements, so it is necessary to coordinate process optimization. But there are some studies on coordinating conflicting heat treatment optimization objectives. This manuscript proposes a "simulation-surrogation-optimization" method based on the finite element method, artificial neural network, and a multi-objective optimization algorithm to control the hardness and deformation of heat-treated parts synergistically. By establishing the numerical model of the unloading process after die quenching, the elastic recovery mechanism of the part is clarified, and a finite element simulation model for die quenching of face gear is obtained. This surrogation model and multi-objective optimization method can predict the distortion and the hardening depth of the part under the specific heat treatment parameters. It can also obtain the optimized heat treatment parameters through the simultaneous constraints, improving the hardening depth of part and reducing the deformation.

2 Simulation Model

2.1 Carburizing Process and Heat Transfer in Quenching

Assuming that the atmosphere in the furnace is uniform, the diffusion of carbon into the part obeys Fick's second law, that is (Ref 24)

$$\frac{\partial C}{{\partial t}} = D \cdot \left( {\frac{{\partial^{2} C}}{{\partial x^{2} }} + \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{\partial^{2} C}}{{\partial z^{2} }}} \right)$$

(1)

Carburizing boundary condition is

$$J = \beta (C_{{\text{e}}} - C_{{\text{s}}} )$$

(2)

where $C$ is carbon concentration; $t$ is time; $D$ is diffusion coefficient; $J$ is carbon flux; $\beta$ is transfer coefficient of carbon atoms; $C_{{\text{e}}}$ is carbon content of furnace atmosphere; $C_{{\text{s}}}$ is carbon content in the part surface.

Assuming that the temperature is uniform at the beginning of the quenching, the temperature field governing the quenching process is:

$$\lambda_{{\text{m}}} \cdot \nabla^{2} T + q_{{\text{v}}} = \rho_{{\text{m}}} c_{{{\text{pm}}}} \frac{\partial T}{{\partial t}}$$

(3)

The boundary condition in convective heat transfer is:

$$- \lambda_{{\text{m}}} \cdot \nabla T = h_{{\text{c}}} (T - T_{{\text{c}}} )$$

(4)

where $\lambda_{{\text{m}}}$ is the thermal conductivity of the material; $T$ is the part temperature; $q_{{\text{v}}}$ is the latent heat of phase transition; $\rho_{m}$ is the material density; C_pm is the specific heat capacity of the material at constant pressure; h_c is the coefficient for the heat exchange; T_c is the temperature of the cooling medium. q_v is the heat released or absorbed during the phase transition:

$$q_{{\text{v}}} = \Delta H \cdot \frac{\Delta V}{{\Delta t}}$$

(5)

where $\Delta H$ is the enthalpy difference per unit volume between the generated new phases (martensite, bainite, ferrite, and pearlite) and the parent phase (austenite); $\frac{\Delta V}{{\Delta t}}$ is the volume fraction change of the new phase over a period of time.

2.2 Microstructure and Hardness

In the quenching process, the microstructure transformation from austenite to pearlite(P), ferrite(F), and bainite(B) is classified as a diffusion-type transformation. Diffusion-type transformation is an isothermal transformation consisting of two stages: gestation stage and growth stage. The former is a process from the beginning of cooling to the occurrence of phase transition, in which the required time is the gestation period. The latter is a process from the beginning of transformation to the end. The transformation amount in the entire diffusion transformation process is calculated by:

$$\begin{array}{*{20}c} {V_{{{\text{ph}}}} = 1 - \exp ( - bt^{m} )} & {{\text{ph}} = {\text{ F, P}}} \\ \end{array} {\text{,B}}$$

(6)

where ${\text{ph}}$ is the short for ‘phase’, which stands for the phase of the austenite transition;$V_{{\text{F}}}$, $V_{{\text{P}}}$, and $V_{{\text{B}}}$ are the transformation amount of ferrite, pearlite, and bainite, respectively (expressed in volume fraction); t is the isothermal time; b and m are coefficients and exponents related to the temperature and the material, respectively.

The diffusion-type phase transition model described by Eq 6 is under an isothermal condition, which is not suitable for the continuous cooling process in quenching. To solve the problem, the time during the continuous cooling process is discretized based on the Scheil superposition principle. Let $\Delta t_{i}$ be a tiny time period for cooling until a certain temperature, and $\tau_{i}$ be the gestation period in the TTT (time, temperature, transformation) curve under this temperature. $\frac{{\Delta t_{i} }}{{\tau_{i} }}$ is hence the gestation rate under this temperature. When the superposition of the gestation rate under the different temperatures is 1, the gestation period ends, and the phase transition begins, namely

$$\sum\limits_{i = 1}^{n} {\frac{{\Delta t_{i} }}{{\tau_{i} }} = 1}$$

(7)

The transition in each small period can be considered an isothermal transition. Based on the Scheil superposition principle, the transformation in each period is superposed to obtain the transformation in continuous cooling in quenching. The superposition process is shown in Fig. 1, in which the start time of phase transition is $t_{i}$, the temperature is $T_{i}$, and after the holding time $\Delta t_{i}$ the transformation amount is $V_{i}$. To calculate the transformation amount at the next temperature $T_{i + 1}$ and after the holding time $\Delta t_{i + 1}$, it is necessary to convert the transformation amount $V_{i}$ to that at $T_{i + 1}$. The time required for the transition is called virtual time $t_{{{\text{i}} + 1}}^{*}$,

$$t_{i + 1}^{*} = [\frac{{ - \ln (1 - V_{i} )}}{{b_{i + 1} }}]^{{\frac{1}{{m_{i + 1} }}}}$$

(8)

where $b_{i + 1}$ and $m_{i + 1}$ are the coefficient and the exponent under $T_{i + 1}$, respectively. Next, the transformation amount from $t_{i + 1}^{*}$ after $\Delta t_{i + 1}$ at $T_{i + 1}$ can be calculated by:

$$V_{i + 1} = 1 - \exp ( - b_{i + 1} (t_{i + 1}^{*} + \Delta t_{i + 1} ))^{{m_{i + 1} }}$$

(9)

Fig. 1

Scheil superposition principle

In the quenching process, the phase transition from austenite to martensite is a non-diffusion transformation and the amount of transformation does not depend on the time but on the difference between the temperature $M_{S}$ at which the martensite begins to transform and the actual temperature $T$ of the part, and the amount of martensite transformation is:

$$V_{{\text{M}}} = 1 - \exp ( - \alpha_{{\text{M}}} (M_{{\text{s}}} - T))$$

(10)

where $\alpha_{{\text{M}}}$ is a material-dependent coefficient reflecting the martensite transition rate.

The hardness (HV) after quenching of the mixed tissue is obtained by summing and averaging the hardness of each phase, that is,

$$HV = V_{{\text{M}}} \cdot HV_{{\text{M}}} + V_{{\text{B}}} \cdot HV_{{\text{B}}} + \left( {V_{{\text{F}}} + V_{{\text{P}}} } \right) \cdot HV_{{\text{F - P}}}$$

(11)

where $HV_{{\text{M}}}$, $HV_{{\text{B}}}$, and $HV_{{\text{F - P}}}$ are the hardness of martensite, bainite, and ferrite/pearlite, respectively.

2.3 Die-Quenching Strain

In quenching, the increments of strain due to elasticity, plasticity, temperature, phase transition, and phase transition plasticity are ${\text{d}}\varepsilon^{{\text{e}}}$, ${\text{d}}\varepsilon^{{\text{p}}}$, ${\text{d}}\varepsilon^{{\text{T}}}$, ${\text{d}}\varepsilon^{{{\text{Tr}}}}$, and ${\text{d}}\varepsilon^{{{\text{tp}}}}$, respectively. These strain increments will add up to the full strain increments (${\text{d}}\varepsilon$) (Ref 25),

$${\text{d}}\varepsilon = {\text{d}}\varepsilon^{{\text{e}}} + {\text{d}}\varepsilon^{{\text{p}}} + {\text{d}}\varepsilon^{{\text{T}}} + {\text{d}}\varepsilon^{{{\text{Tr}}}} + {\text{d}}\varepsilon^{{{\text{tp}}}}$$

(12)

where ${\text{d}}\varepsilon^{{\text{e}}}$ and ${\text{d}}\varepsilon^{{\text{p}}}$ are

$${\text{d}}\varepsilon^{{\text{e}}} { = }\frac{1 + \mu }{E}d\sigma$$

(13)

$${\text{d}}\varepsilon^{{\text{p}}} { = }\frac{3}{2}\frac{{d\overline{{\varepsilon^{{\text{p}}} }} }}{{\overline{\sigma } }}\sigma_{ij}^{\prime }$$

(14)

where $\mu$ is the Poisson's ratio, $E$ is the modulus of elasticity, $\sigma$ is the stress, $\overline{{\varepsilon^{{\text{p}}} }}$ is effective strain, $\overline{\sigma }$ is equivalent stress, $\sigma_{ij}^{\prime }$ is deviator stress tensor, ${\text{d}}\varepsilon^{{\text{T}}}$ and ${\text{d}}\varepsilon^{{{\text{Tr}}}}$ are

$${\text{d}}\varepsilon^{{\text{T}}} { = }\sum {V_{{{\text{ph}}}} \xi_{{{\text{ph}}}} {\text{d}}T}$$

(15)

$${\text{d}}\varepsilon^{{{\text{Tr}}}} { = }\sum {\beta_{{{\text{ph}}}} {\text{d}}V_{{{\text{ph}}}} }$$

(16)

where ph refers to a certain phase, $V_{{{\text{ph}}}}$ is its volume fraction, $\xi_{{{\text{ph}}}}$ is its thermal expansion coefficient, and $\beta_{{{\text{ph}}}}$ is its phase transition expansion coefficient. Considering that phase transition plasticity is proportional to the stress, the Greenwood–Johnson model can be modified to obtain ${\text{d}}\varepsilon^{{{\text{tp}}}}$,

$${\text{d}}\varepsilon^{{{\text{tp}}}} { = }3KS(1 - V_{{{\text{ph}}}} ){\text{d}}V_{{{\text{ph}}}}$$

(17)

where $K$ is the phase transition plastic coefficient, and $S$ is the partial stress tensor.

The die-quenching process can be regarded as a quasi-static process with transient temperature. When using the finite element method to analyze stress, the governing equation is (Ref 26)

$$\iiint {\left[ B \right]}^{{\text{T}}} \left\{ \sigma \right\} \cdot {\text{d}}V = \iiint {\left[ N \right]}^{{\text{T}}} \left\{ {F_{{\text{b}}} } \right\} \cdot {\text{d}}V + \iint {\left[ N \right]}^{{\text{T}}} \left\{ {F_{{\text{t}}} } \right\} \cdot {\text{dS = }}\left[ K \right]\left\{ U \right\} = \left\{ F \right\}$$

(18)

$$\left[ K \right] = \iiint {\left[ B \right]}^{{\text{T}}} \left[ {D_{{{\text{ep}}}} } \right]\left[ B \right] \cdot {\text{d}}V$$

(19)

where $\left[ B \right]$ is the strain rate matrix, $\left[ N \right]$ is the shape function matrix describing the relationship between the strain and the node displacement, and $F_{b}$ is the external force on the internal unit body. $F_{t}$ is the external force on the surface, $\left[ K \right]$ is the overall stiffness matrix, $\left\{ U \right\}$ is the node displacement vector, $\left\{ F \right\}$ is the force, and $\left[ {D_{{{\text{ep}}}} } \right]$ is the elastic–plastic constitutive matrix.

The pre-stress loaded during die quenching is unloaded after quenching, which will affect the calculation of the stress–strain due to a certain rebound of the workpiece. Equation 18 shows that the stress–strain under the load of quenching die can be obtained from the elastic–plastic constitutive equation. Since there is only elastic deformation while unloading, the stress–strain after unloading is calculated by the difference between the strain before unloading and the rebound strain after unloading. Assuming that the strain before unloading is $\varepsilon_{{\text{s}}}$, a total of unloading steps is $s$, the load amount reduced by each unloading step is $\Delta F_{i}$ ($i = 1,2,3,...,s$), and the material is in a uniform elastic state during unloading, and then, the displacement increment and strain increment after each unloading step are $\Delta \delta_{i}$ and $\Delta \varepsilon_{i}$, respectively.

$$\sum\limits_{i = 1}^{s} {\Delta F_{i} } = \left[ D \right]\sum\limits_{i = 1}^{s} {\Delta \delta_{i} }$$

(20)

$$\sum\limits_{i = 1}^{s} {\Delta \varepsilon_{i} } = \left[ B \right]\sum\limits_{i = 1}^{s} {\Delta \delta_{i} }$$

(21)

where $\left[ D \right]$ is the elastic stiffness matrix. Combining Eq 20 and 21, it can be obtained that:

$$\varepsilon_{{\text{d}}} = \sum\limits_{i = 1}^{s} {\Delta \varepsilon_{i} } = \left[ B \right]\left[ D \right]^{ - 1} \sum\limits_{i = 1}^{s} {\Delta F_{i} }$$

(22)

$$\varepsilon_{{\text{e}}} = \varepsilon_{{\text{s}}} - \varepsilon_{{\text{d}}}$$

(23)

where $\varepsilon_{{\text{d}}}$ is the rebound strain after die quenching is unloaded, and $\varepsilon_{{\text{e}}}$ is the ultimate strain after unloading.

2.4 Simulation-Surrogation-Optimization-Integrated Model

Figure 2 shows the shaped-oriented simulation-surrogation-optimization integrated model. Carburizing and quenching simulation subroutine was developed based on the carburizing and quenching numerical model. In the simulation calculation of Abaqus software, the STEP module can define the calculation property (heat transfer or coupled temp-displacement) and quenching time, and the Interaction module can define the heat transfer coefficient, which will be stored as a function of temperature and called during the calculation. The Load module can define the temperature of the cooling medium, the temperature of the part and the temperature of the furnace. Consequently, the quenching sequence and heat treatment parameters can be determined by the definition of the three modules. For instance, the interface DFLUX was used to define the boundary conditions for carbon atom diffusion, and a subroutine was written to obtain the distribution of carbon concentration after carburization. The interface USDFLD was used to customize field variables such as temperature field, phase field, and carbon concentration; the GETVRM subroutine in this interface read all field variables on the integration point so that the carburization concentration was read and written in the quenched structure calculation. By using the subroutine interface of Abaqus software HETVAL and TTT curve of AISI9310 steel, the subroutine defines the time and temperature of the beginning transformation and the time and temperature of the end transformation of pearlite, bainite, and martensite. When the finite element main program calculates the values of temperature and time according to the set boundary conditions, the subroutine receives these parameters and calculates the transition amounts of pearlite, bainite and martensite according to the formulas mentioned in Sect. 1.2 which have been written into the subroutine. The interface UEXPAN defined the thermo-elasto-plastic constitutive model, and a subroutine was written to calculate the strain of carburizing and quenching and to obtain the stress and deformation.

Fig. 2

Flow of shaped-oriented simulation-surrogation-optimization integrated model

The carburizing and quenching simulation models were used to obtain a large amount of sample data. Based on these sample data, artificial neural networks were used to establish a surrogation model between process parameters and heat treatment quality. The prepared model could predict the quality of heat treatment. Additionally, heat treatment process parameters were optimized based on the multi-objective constraints of hardening depth and deformation.

3 Model Validation

3.1 Experiment Setup

Figure 3 shows a face gear part that verifies the carburizing and quenching simulation model. The part material is AISI 9310 steel; its chemical composition is shown in Table 1. The geometric parameters are as follows: the number of teeth: 142, normal modulus: 3.9, normal pressure angle: 25°, the coefficient of addendum: 1, the coefficient of dedendum: 1, and the coefficient of bottom clearance: 0.25.

Fig. 3

Photograph of face gear

Table 1 Material chemical composition (mass fraction, %) (Ref 27)

When solving the temperature field and thermodynamic coupling problems, the thermal physical properties of materials are required: density, Young's modulus, Poisson's ratio, specific heat capacity at constant pressure, coefficient of thermal expansion and thermal conductivity. The thermal property parameters of materials will change with the change of microstructure content and temperature as shown in Figure 4.

Fig. 4

The physical performance parameters of AISI9310. (a) Density, (b) Young's modulus, (c) Poisson's ratio, (d) heat capacity, (e) thermal expansion, (f) thermal conductivity

The TTT curve as shown in Fig. 5 was obtained by using the performance simulation software. B (0.01%) curve indicates the transition curve of 9310 steel bainite, that is, after holding at a certain temperature for a certain time, austenite begins to transform into bainite. The B (99.9%) curve represents the end transformation curve of 9310 steel bainite, that is, after holding at a certain temperature for a certain time, austenite is completely transformed into bainite. The same is true for F (0.01%), P (0.01%), and P (99.9%). $M_{S}$ is the martensite transition temperature curve.

Fig. 5

The thermodynamic performance parameters of AISI 9310

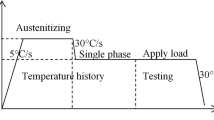
The teeth of the face gear are faced up and put into the furnace stably, heated, and kept warm in the vacuum furnace. The heat treatment process is shown in Fig. 6.

Fig. 6

Face gear heat treatment flow chart

During carburization, the face gear was heated to 927 °C, and the carbon concentration in the furnace was maintained at 1.03% and infiltrated for 7 h. After 7 h, the carbon concentration in the furnace was reduced to 0.75% and diffused for 3 h. After carburization, the part was cooled to room temperature under N₂. When annealing at high temperature, the face gear was reheated to 620 °C, kept for 4 h, and then cooled to room temperature under nitrogen protection after annealing.

A specific die was used to apply pressure in quenching to the face gear to reduce deformation. First, the face gear and the die were heated to 820 °C and kept for 2 h. The die applied pressure to the face gear and cooled it down to 50 °C with a quenching solution. The die was unloaded after cooling. Figure 7 illustrates the schematic diagram of the face gear clamped on the die. The outer ring acts on the tooth top, and the inner ring acts on the end face of the inner spline shaft. The die pressure was set according to the material and the part size. In the test, the pressure of the outer and inner rings was set to 100 psi and 30 psi, respectively.

Fig. 7

Face gear and die assembly position

After quenching, the face gear was cooled to − 100 °C in a cryogenic box and held for 2 h to convert the residual austenite into martensite. After cold treatment, it was returned to normal temperature and low -temperature annealed at 150 °C for 4 h.

3.2 Hardness Validation

Due to the large size of the face gear sample and the symmetrical part, 1/4 of the face gear was used for analysis to reduce the simulation time. The face gear 1/4 model is shown in Fig. 8(a), and the single-tooth geometric model is shown in Fig. 8(b). Carburization usually requires the depth of carburized layer to be around 1-2 mm. Thus, the depth of the carburized layer was only effectively reflected by dividing dense grids while performing finite element analysis. However, the over-dense meshing for the entire part will lead to substantial calculation and difficulty in convergence. Therefore, the carburized layer was simulated by using a finer mesh of the face gear single tooth to observe the distribution of carbon concentration. In the simulation, the tooth face, two end faces, and the tip of the tooth of the face gear were in contact with the carburizing gas. The gear body was not in contact with the carburizing gas. The gas contact of the single-gear FE model is shown in Fig. 9. After carburizing, the single tooth was cut off from the middle of the tooth, and the path from the tip to the center of the tooth is regarded as path1, the path from the surface to the center of the tooth is regarded as path2, and the path from the root to the center of the tooth is regarded as path3, as shown in Fig. 10(a). Moreover, the carbon concentration changes of tooth along the three paths were measured, as shown in Fig. 10(b). The highest concentration of single tooth at the edge and tip of the single tooth, with the carbon content reaching 0.796%, is consistent with the given carbon concentration. Taking 0.35% as the effective carburization concentration, the effective carburizing layer depths of the three paths were, respectively, 1.83mm, 1.05mm, and 2.18mm.

Fig. 8

Geometric model of 1/4 section of the face gear and single-tooth model of face gear. (a) 1/4 of the face gear. (b) Single tooth of face gear

Fig. 9

The face gear single-tooth FEM model

Fig. 10

Carbon concentration of the single tooth in three paths. (a) Three paths of middle section of the tooth and (b) concentration of three paths

After the simulation of carburizing and quenching, the single-tooth model was cut off to obtain the tooth surface, the middle section of the tooth and the middle section of the tooth is shown in Fig. 11(a), and the martensite content of each section is shown in Fig. 11(b), (c) and (d). For different cross sections, a vertical downward path along the tooth tip was selected, and the martensite content was measured. The variation of martensite content with the distance from the tooth tip under different cross sections is shown in Fig. 12. The results showed that the lower the martensite content was in the middle of the tooth, the higher the martensite content was on the tooth surface than in the core and in the outer and inner circle than in the middle of the tooth surface, consistent with the real situation of the quenched structure transformation. The surface of the face gear was more in contact with the cooling medium than the core of tooth, maintaining a faster cooling rate. Consequently, more martensite structure was produced on the tooth surface than the core. The inner and outer circles were sharp-angled and thin-walled, and their cooling rate was higher than the middle part of the tooth surface. Hence, these positions reached the martensite transformation temperature faster and had higher martensite content.

Fig. 11

Martensite content of different sections. (a) Martensite content in the single tooth of face gear. (b) Surface of the tooth. (c) Secondary middle of the tooth. (d) Middle of the tooth

Fig. 12

Variation trend of martensite content under different sections

In the experiment, vacuum carburizing furnace was used for carburizing, special equipment was used for die quenching, and metallographic microscope was used to measure the microstructure after the experiment. Part of the experimental equipment and testing equipment are shown in Fig. 13. The metallographic diagram of the surface-permeable layer structure and the heart tissue of 9130 steel was obtained through metallographic microscope measurement, as shown in Fig. 14. After carburizing and quenching, the surface of 9310 steel has a large number of black acicular martensite and a small amount of residual austenite, and the core is a large number of lath martensite and a small amount of bainite. The simulation results agree well with the experimental results.

Fig. 13

Part of the experimental equipment. (a) Vacuum carburizing furnace. (b) Metallographic microscope

Fig. 14

Metallographic photographs of the face gear after carburizing and quenching. (a) Microstructure of tooth surface. (b) Microstructure of tooth center

The simulated tissue content is substituted into Eq 11 to obtain the value of the hardness of the face gear. A comparison of the simulated value, experimental value, and design value is shown in Fig. 15. The design, experimental, and simulated values of the hardness of the face gear core were 65~71 HRA, 69.5-70.5 HRA, and 321 HV (converted to 66.5 HRA), respectively. The difference between the simulated and experimental values was about 4.3%. The simulated value of the surface hardness of the face gear was 65.2 HRC (converted to 92.2 HR15N), while the experimental value was 90.5-91 HR15N. The results demonstrate that the established carburizing and quenching simulation model could effectively simulate the part hardness.

Fig. 15

Hardness obtained by simulation, experiment, and design

3.3 Deformation Validation

Figure 16 shows the cloud of deformation of face gear obtained by using the die-quenching simulation model. Figure 16(a) shows that after die quenching and annealing, warpage deformation occurred on the outer circle, inner circle, and tooth root of the inner circle. The warping deformation of the inner circle was the largest, with a value of 0.04 mm. Under the pressure of the inner ring and outer ring, quenching thermal stress, and tissue stress, the web experienced a certain degree of depression; the maximum depression was 0.15 mm. Figure 16(b) shows that the overall thermal deformation occurs in the axial direction in the face gear heat treatment due to the axial warping and the concave of the web, leading to the reduction of the radial dimension of the face gear. The part size was reduced due to quenching and cooling. However, since the density of the generated martensite was lower than that of the original microstructure, the volume of the part increased, resisting the size reduction. Compared with the outer circle, the cooling rate of the inner bore was slower, lesser martensite was produced, and the ability to resist cold shrinkage was weaker. Hence, the radial shrinkage at the inner hole was the largest.

Fig. 16

Cloud of deformation in die quenching. (a) Axial. (b) Radial

Table 2 lists the quenching-induced deformation of face gear obtained by simulation, experiment, and design. Before the simulation, three nodes on the outer circle and the inner bore were selected, respectively, to record the coordinates of the three nodes. After the simulation, three coordinates were recorded again, and the diameter of the circle after deformation was calculated according to the coordinates. It was calculated that after the simulation of carburizing and quenching, the outer diameter was 609.96 mm and experimental value of the outer diameter was 610.113 mm, a difference of 0.025%. The simulated value of aperture reduction was 0.04 mm, while the experimental value was − 0.011 ~ 0.056 mm; the simulated value was within the range of the experimental value. For the calculation of tooth surface height before and after simulation, 10 nodes at different positions on a single tooth were selected, and the height difference before and after the nodes was calculated, and the range of tooth height change was − 0.03 ~ 0.01, which were also within the range of the experimental values. Thus, the good agreement between the simulated and experimental values suggested that the established finite element simulation model accurately predicted the deformation induced by carburizing and die quenching.

Table 2 Workpiece size before and after quenching

The load of the outer ring was set to 0, 50, 100, and 150 psi in the simulation model. Figure 17 shows the warping deformation under different pressures. The end face warpage was the largest during pressure-free quenching. The tooth height deformation decreased as the pressure increased from 0 to 100 psi. However, the tooth height deformation increased when the load exceeded a certain level (150 psi) as the outer ring part was deformed due to pressure, causing tooth shape distortion. Therefore, it was necessary to optimize the design of the die pressure to determine the appropriate pressure.

Fig. 17

Axial deformation and radial distribution of the lower tooth top under different pressures

4 Optimization

4.1 Surrogate Model of Hardening Depth

The data samples of the hardness simulation model were used to train the network model with carburizing and quenching process parameters (boost time $t_{{\text{b}}}$, boost temperature $T_{{\text{b}}}$, boost carbon concentration $C_{{\text{b}}}$, diffusion time $t_{{\text{d}}}$, diffusion carbon concentration $C_{{\text{d}}}$, quenching temperature $T_{{\text{q}}}$, and cooling temperature $T_{{\text{c}}}$) as input and the hardening depth $h$ as the output (Fig. 18); a surrogation model was established between hardening depth and process parameters. There were 576 groups of data samples, in which 560 groups were used for training and 16 groups were used for verification. Table 3 shows some training samples involved.

Fig. 18

Structure of surrogation model of hardening depth

Table 3 Hardening depths under different heat treatment parameters

The surrogation and simulation models were used to predict the hardening depth. The results (Fig. 19a) revealed that the difference between the two was < 5%, confirming that the established hardening depth surrogation model has a high prediction precision.

Fig. 19

Hardening depth obtained by prediction and simulation. (a) Prediction result. (b) Relative error

4.2 Surrogate Model of Deformation

The simulation data of the training model of pressed quenching were taken as the sample to train the network model with the main process parameters of die quenching (outer ring pressure $P$, quenching temperature $T_{{\text{q}}}$, and cooling temperature $T_{{\text{c}}}$) as input, and the maximum deformation $\delta_{\max }$ as the output (Fig. 20); the surrogation model was obtained between deformation surrogate and process parameters.

Fig. 20

Structure of maximum deformation surrogation model

There were 24 groups of data samples, 20 of which were used for training and 4 for verification. Table 4 shows some of the training samples involved in this study.

Table 4 Maximum deformation under different heat treatment parameters

Figure 21 shows the maximum deformations predicted by the surrogation and the simulation models. Although there were some differences, the trend of changes was essentially the same and $\delta_{\max }$ < 0.15 mm, which was within the allowable error range.

Fig. 21

Deformation obtained by prediction and simulation. (a) Prediction. (b) Training set relative error

4.3 Multi-objective Optimization

The process parameters of heat treatment were as follows: boost time $t_{{\text{b}}}$, boost temperature $T_{{\text{b}}}$, boost carbon concentration $C_{{\text{b}}}$, diffusion time $t_{{\text{d}}}$, diffusion carbon concentration $C_{{\text{d}}}$, quenching temperature $T_{{\text{q}}}$, cooling temperature $T_{{\text{c}}}$, and outer ring pressure $P$; these were used as design variables, i.e., $X = [t_{{\text{b}}} ,T_{{\text{b}}} ,C_{{\text{b}}} ,t_{{\text{d}}} ,C_{{\text{d}}} ,T_{{\text{q}}} ,T_{{\text{c}}} ,P]$:

$$\left\{ \begin{gathered} y_{1} = \min (\left| {h - h_{{\text{d}}} } \right|) \hfill \\ y_{2} = \min (t_{{\text{d}}} + t_{{\text{b}}} ) \hfill \\ y_{3} = \min (\delta_{\max } ) \hfill \\ X^{{\text{L}}} \le X \le X^{{\text{U}}} \hfill \\ \end{gathered} \right.$$

(24)

where $h$ is the hardening depth, $h_{{\text{d}}}$ is the design value of the hardening depth, and $\delta_{\max }$ is the maximum deformation. Optimization objectives $y_{1}$ implied that the closer to $h$ and $h_{{\text{d}}}$, the better. Optimization objectives $y_{2}$ meant a shorter carburization time was preferred from a cost-saving perspective. Optimization objectives $y_{3}$ indicated that a smaller $\delta_{\max }$ was preferred. According to the commonly used range of heat treatment parameters $X^{L}$ and $X^{U}$ were the upper and lower limits of the design variables, respectively.

$$\left\{ \begin{gathered} X^{U} = [43200,950,1.05,18000,0.85,860,60,150] \hfill \\ X^{L} = [21600,850,0.95,10800,0.75,830,25,0] \hfill \\ \end{gathered} \right.$$

(25)

According to the established hardening depth and deformation network surrogation model, in the objective equation (Eq 22), the NSGA-II algorithm was used for multi-objective optimization to obtain an optimized solution set of heat treatment process parameters.

According to different requirements, three optimization parameter combinations were designed: hardening depth deviation and carburization time, hardening depth deviation and warping deformation, and carburization time and warping deformation. The parameters of the NSGA-II algorithm were set as follows: population size: 100, the maximum number of evolutionary generations: 200. According to the hardening depth, the design value and $h_{{\text{d}}}$ were taken as 1.10-1.30 mm and 1.20 mm, respectively.

For the three optimization parameter combinations designed, the closer the point on the Pareto front is to the origin of the coordinate system, the better the solution is. By calculating the distance from the point on the Pareto front to the origin of the coordinate system, point A, point B, and point C are selected, respectively, in Fig. 22(a), (b), and (c). The optimized solution set was evenly and smoothly distributed within the range of process parameters, indicating that the correlation between optimization objectives was obvious, and the optimized solution set has a certain representativeness. When the carburization time was shortened, the hardening depth could not reach the design value (Fig. 22(a)). Thus, point $A$ was used as the optimized process parameter to ensure that the carburization time was short and the hardening depth deviation was small. According to Fig. 22(b), minimizing the hardening depth deviation and deformation contradicts each other. The deformation and hardening depth deviation were small if point $B$ was used as the optimized process parameters. According to Fig. 22(c), the minimization of carburization time and the minimization of deformation checked and balanced each other. If point $C$ was the optimized parameter, the carburization time could be shortened while the deformation was small. The dual-objective optimization results of heat treatment process parameters are shown in Table 5.

Fig. 22

Pareto frontier optimized solution set obtained by dual-objective optimization. (a) Hardening depth deviation and carburizing time; (b) hardening depth deviation and maximum deformation; (c) carburizing time and maximum deformation

Table 5 Optimization of the parameters of the dual-objective heat treatment process

5 Conclusions

This study established a simulation model for carburizing and quenching of face gear, based on the numerical model of established carburizing and die quenching, which could predict the hardening depth and deformation of die quenching of face gear. The proposed simulation model was verified, and a surrogation model of heat treatment process parameters, depth, and deformation was established. Based on the surrogation model and objective equation, a multi-objective optimization algorithm was used to obtain the optimized heat treatment process parameters that controlled the distortion under the condition of satisfying the hardening depth. The following are the salient features of the study:

• (1) A multi-field coupled finite element simulation model was established for carburizing and quenching, which could simulate the heat treatment process and predict the carbon concentration, organization, hardness, and deformation of workpiece after heat treatment.

• (2) A simulation model was established according to the numerical model. The hardness and deformation prediction results revealed by the model were close to the experimental measurement results. Compared with the experimental results, the hardness of the simulation of the tooth core differed by 4.3%-5.7%, and the hardness of the tooth surface differed by 1.7%. The difference between the experimental and the simulation in the outer diameter deformation was 0.153 mm, and in the aperture, deformation was 0.029-0.096 mm.

• (3) An optimization model of die-quenching process parameters was proposed based on a neural network surrogation model, which could optimize heat treatment process parameters and die pressure. The results revealed an optimized solution set with short carburization time, small deviation of hardening depth, and small maximum deformation, providing a reference for the design of process parameters in actual production.