Introduction

With the gradual requirement of fuel savings and structural weight reduction in the aerospace and automobile industries, lightweight materials such as aluminum alloy, titanium alloy, and magnesium alloy have gotten more and more applications (Ref 1, 2). However, lightweight materials are more difficult to be pressed than deep drawing steel due to their limited plasticity at room temperature. The forming of these metal alloy sheets has taken a challenge to the conventional forming methods. The phenomenon that superimposed hydrostatic pressure can improve the plasticity of metal has been found by Bridgman (Ref 3). Over past decades, many researchers have conducted extensive research on how the hydrostatic pressure affects the mechanical behavior of various engineering materials and how to use this effect to benefit the forming of low-plasticity lightweight materials (Ref 3-5).

In recent years, the influences of hydrostatic pressure on the formability of sheet metal have been gradually investigated. Academic analysis and experimental investigations have shown that superimposed hydrostatic pressure can significantly improve the formability of sheet metal (Ref 6-9). Based on this founding, some double-sided pressure forming processes have been proposed to improve the formability of sheet metal, especially for lightweight metal alloy sheet. Matin and Smith (Ref 8) carried out the double-sided high-pressure hydraulic bulge tests on 1018 CR low carbon steel sheets and found that the bulge depth increases as counter pressure increases. Smith et al. (Ref 10) and Jain and Wang (Ref 11) developed a double-sided high-pressure tubular hydroforming processes (DSHP THF), in which hydraulic pressure is imposed on both the inside and outside of the expanding tube, as shown in Fig. 1(a). The presence of the external pressure is shown to delay the onset of plastic instability and lead to increased formability relative to that observed for the traditional single-sided high-pressure (SSHP) process. Double-sided viscous pressure forming (DSVPF) is another double-sided pressure forming process, in which a kind of semi-solid, flowable, and high viscous materials are used as pressure-carrying medium and applied on both sides of sheet metal (Ref 12). Figure 1(b) shows schematically the principle of a typical DSVPF. Double-sided viscous pressure bulge (DSVPB) tests for titanium alloy TC1 sheet and aluminum alloy AA1060 sheet have been carried out by the authors. Experimental results showed that imposing the counter pressure increases the limit bulge height and fracture strain (Ref 13, 14). Abovementioned results have proved that employing the double-sided pressure benefits to the forming of lightweight metal alloy sheet with low plasticity. However, the fundamental mechanical analysis of the biaxially stretched tension under superimposed double-sided pressure has not yet been reported, such as formability, void evolution, fracture locus and fracture strain, and so on.

Fig. 1
figure 1

Schematical principle of two double-sided forming processes (a) double-sided high-pressure tubular hydroforming (Ref 11) and (b) double-sided viscous pressure forming (Ref 12)

Full size image

In conventional sheet forming processes, the sheet metal is usually assumed to be state of plane stress. Based on this assumption, many methods have been developed to predict the formability of sheet metal. In general, these methods can be divided into three categories, namely phenomenological ductile fracture criterion, damage model, and plastic instability theory. A great deal of ductile fracture criteria have been proposed in the past and have been used to predict the failure of sheet metal in stretching (Ref 15, 16), deepdrawing (Ref 17), hydroforming (Ref 18), and so forth. These criteria assume that the failure takes place once the damage variable reaches its critical value. However, most of these criteria cannot be used to predict the whole forming limit curve (FLC) according to the comparison of various ductile fracture criteria done by Jain et al. (Ref 19). The second methodology is damage model. The Gurson’s continuum damage model is the most commonly used one. Based on the assumption of either the existence of an initial defect in the form of microvoids or the continuous nucleation of voids during the straining process, the Gurson’s continuum damage material model was developed and then modified by Tvergaard and Needleman (Ref 20) to the Gurson-Tvergaard-Needleman (GTN) damage model. The GTN damage model is extensively used in sheet metal forming, such as predicting formability, analyzing the void evolution, and so on (Ref 21-24). However, the GTN damage model cannot accurately predict the forming limit for the condition of large stress triaxiality \( \upeta > 1/\sqrt 3 , \) namely biaxial tension state (Ref 25). The third methodology is plastic instability theory, especially the localizing necking theory developed by Marciniak and Kuczynski (Ref 26, 27). Over past decades, M-K model has been widely used to predict the formability of sheet metal. Assempour et al. (Ref 28) developed a methodology based on the M-K model to predict the forming limit diagram (FLD) and forming limit stress diagram (FLSD) of low carbon steel ST12 and investigated the effect of strain path on FLD and FLSD. Ahmadi et al. (Ref 29) successfully predicted the FLD of AA3003-O aluminum sheet by using the BBC yield criteria and M-K model. Needleman and Triantafylidis (Ref 30) combined the M-K model with porous metal plasticity to study the effect of void growth on the formability of sheet metal under in-plane loading. Simha et al. (Ref 31) used a similar model to study the onset of necking in sheet metal under three-dimensional loading. Zadpoor et al. (Ref 25) compared these three kinds of methodologies and found that the M-K model and the M-K model combined with GTN damage model can accurately predict the forming limit of sheet metal for the condition of biaxial strain state, namely the right-hand side of FLD.

For double-sided pressure forming, the effect of normal pressure cannot be neglected any more. Predicting the formability of sheet metal under double-sided pressure is important for designing the reasonable forming process. Gotoh et al. (Ref 6) investigated the effect of out-of-plane stress on forming limit strain using the classical Swift’s or Hill’s criterion of instability and predicted the FLD under out-of-plane stress through modifying the Storen and Rice’s theory. However, these results are mostly of qualitative nature. Smith et al. (Ref 7) and Matin and Smith (Ref 8) proposed analytical modifications to FLC to account for the effect of transverse normal stress on sheet metal formability. Banabic and Soare (Ref 32) predicted the FLD under loading normal pressure using the M-K model combined with Poly6 plane stress yield criterion. These abovementioned investigations proved that imposing the normal pressure on sheet metal are beneficial to improving the formability of sheet metal.

In the present study, the GTN damage model combined with finite element method is used to investigate the influence of superimposed double-sided pressure on the formability of sheet metal. Nucleation and growth of microvoids in sheet metal under superimposed double-sided pressure are predicted. The M-K localized necking model is used to predict the FLD and failure locus of sheet metal at plane stress state and three-dimensional stress state. Finally, the effect of superimposed double-sided pressure on the fracture strain is also studied.

Mechanics of Biaxial Tension Strain State Under Double-Sided Pressure

In this section, the stress triaxiality expression of sheet metal under constant superimposed double-sided pressure is derived. Similar works have been done by Smith et al. (Ref 7).

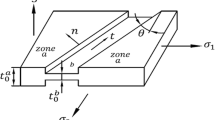
The stress state of biaxially stretched sheet metal under superimposed double-sided pressure is shown in Fig. 2. Employing the Hill’s 48 yield criterion (Ref 33), the effective stress is expressed

$$ \bar{\upsigma } = \left[ {{\frac{{R\left( {\upsigma_{1} - \upsigma_{2} } \right)^{2} + \left( {\upsigma_{2} + p} \right)^{2} + \left( {\upsigma_{1} + p} \right)^{2} }}{R + 1}}} \right]^{{\frac{1}{2}}} , $$
(1)

where R is the normal anisotropy coefficient, p is the value of normal pressure, and σ i (i = 1,2) is stress component at x i direction.

Fig. 2
figure 2

Stress state of biaxially stretched sheet metal under double-sided pressure

Full size image

In order to facilitate building the stress triaxiality expression, three ratios are defined as follows:

$$ \upalpha \equiv {\frac{{\upsigma_{2} }}{{\upsigma_{1} }}},\quad \upgamma \equiv {\frac{p}{{\upsigma_{1} }}},\quad \uprho \equiv {\frac{{\upvarepsilon_{2} }}{{\upvarepsilon_{1} }}}, $$
(2)

where ɛ i (i = 1,2) is the strain component at x i directions.

Substituting Eq 2 into Eq 1, the effective stress can be rewritten as

$$ \bar{\upsigma } = \upsigma_{1} \left[ {{\frac{{R\left( {1 - \upalpha } \right)^{2} + \left( {\upalpha + \upgamma } \right)^{2} + \left( {1 + \upgamma } \right)^{2} }}{R + 1}}} \right]^{{\frac{1}{2}}} $$
(3)

The stress triaxiality is defined as

$$ {\frac{{\upsigma_{\text{m}} }}{{\bar{\upsigma }}}} = {\frac{1 + \upalpha + \upgamma }{{3\left[ {{\frac{{R\left( {1 - \upalpha } \right)^{2} + \left( {\upalpha + \upgamma } \right)^{2} + \left( {1 + \upgamma } \right)^{2} }}{R + 1}}} \right]^{{\frac{1}{2}}} }}}, $$
(4)

where σm is mean stress, σm = (σ1 + σ2 + σ3)/3.

According to associated flow rule and assuming a linear proportional loading path, the strain ratio is expressed as

$$ \uprho = {\frac{{ - R\left( {1 - \upalpha } \right) + \left( {\upalpha + \upgamma } \right)}}{{R(1 - \upalpha ) + \left( {1 + \upgamma } \right)}}} $$
(5)

The stress ratio can be defined in terms of ρ and γ

$$ \upalpha = {\frac{{\left( {R + 1} \right)\uprho - \upgamma + \upgamma \uprho + R}}{R\uprho + R + 1}} $$
(6)

Substituting Eq 6 into Eq 4 and neglecting the normal anisotropy of sheet metal (namely R = 1), the relationship between stress triaxiality and strain path and normal pressure ratio is derived.

$$ {\frac{{\upsigma_{\text{m}} }}{{\bar{\upsigma }}}} = {\frac{1 + \upgamma + \uprho }{{\left( {1 - \upgamma } \right)\sqrt {3\left( {1 + \uprho + \uprho^{2} } \right)} }}} $$
(7)

When γ = 0, Eq 7 represents the stress triaxiality of sheet metal under plane stress state. The stress triaxiality is constant for given linear strain path. When γ ≠ 0, Eq 7 represents the stress triaxiality of sheet metal under the three-dimensional stress state. The stress triaxiality of sheet metal varies with stress ratio ρ for given linear strain path.

Finite Element Analysis Model

GTN Continuum Damage Material Model

This section briefly outlined the GTN damage model and the detailed description can be seen in Ref 34.

Different from the constitutive laws that follow the classic J 2 criterion and are independent of hydrostatic pressure, the yield function of GTN continuum damage material model is a pressure-sensitive yield function and can be expressed as (Ref 20)

$$ \Upphi = \left( {{\frac{q}{{\upsigma_{y} }}}} \right)^{2} + 2q_{1} f^{ * } \cosh \left( { - q_{2} {\frac{3p}{{2\upsigma_{y} }}}} \right) - \left( {1 + q_{3} f^{ * 2} } \right) = 0, $$
(8)

where q denotes the macroscopic Von Mises equivalent stress, \( q = \sqrt {{{3S_{ij} S_{ij} } \mathord{\left/ {\vphantom {{3S_{ij} S_{ij} } 2}} \right. \kern-\nulldelimiterspace} 2}} , \), S ij is the deviatoric part of the Cauchy stress tensor σ ij , S ij  = σ ij  − σ kk δ ij /3, δ ij represents the Kronecker delta, σ y is the equivalent flow stress which represents the actual microscopic stress state in the matrix material, p is the hydrostatic stress, q 1, q 2, q 3 are introduced by Tvergaard to make the predictions of Gurson’s equations agree with numerical studies of materials containing periodically distributed circular cylindrical voids. When q 1 = q 2 = q 3 = 1, the GTN model recovered to Gurson model.

f* is the damage parameter introduced by Tvergaard and Needleman, which denotes the total effective void volume fraction (VVF) (Ref 20, 34). It accounts for the gradual loss of stress carrying capability of the material due to void coalescence. f* = 0 implies that the material is fully dense, and the Gurson yield condition reduces to the Von Mises yield condition. f* = 1 implies that the material is completely voided and has no stress carrying capacity. This function is defined in terms of the VVF:

$$ f^{ * } = \left\{ {\begin{array}{lll} f \hfill & {\text{if}} \hfill & {f \le f_{\text{c}} } \hfill \\ {f_{\text{c}} + {\frac{{\bar{f}_{\text{F}} - f_{\text{c}} }}{{f_{\text{F}} - f_{\text{c}} }}}\left( {f - f_{\text{c}} } \right)} \hfill & {\text{if}} \hfill & {f_{\text{c}} < f < f_{\text{F}} } \hfill \\ {\bar{f}_{\text{F}} } \hfill & {\text{if}} \hfill & {f \ge f_{\text{F}} } \hfill \\ \end{array} } \right. $$
(9)

in which

$$ \bar{f}_{\text{F}} = {\frac{{q_{1} + \sqrt {q_{1}^{2} - q_{3} } }}{{q_{3} }}}, $$
(10)

where f is the VVF, f c is a critical value of the VVF, f F is the value of VVF at which there is a complete loss of stress carrying capacity in the material. The user specified parameters f c and f F model the material failure when f c < f < f F, due to mechanisms such as microfracture and void coalescence. When f ≥ f F, total failure at the material point occurs. In ABAQUS/Explicit, an element is removed once all of its material points have failed (Ref 35).

The increased rate of total VVF \( \dot{f} \) is partly due to the growth of existing voids \( \dot{f}_{\text{g}} \) and partly due to the nucleation of new voids \( \dot{f}_{\text{n}} \) as

$$ \dot{f} = \dot{f}_{\text{g}} + \dot{f}_{\text{n}} $$
(11)

The growth rate of voids \( \dot{f}_{\text{g}} \) is proportional to the hydrostatic component of the plastic strain rate \( \dot{\upvarepsilon }_{kk}^{p} , \) as follows:

$$ \dot{f}_{\text{g}} = (1 - f)\dot{\upvarepsilon }_{kk}^{p} $$
(12)

The nucleation rate of new voids can be expressed by a plastic strain-controlled nucleation rule through assuming that voids nucleate at second-phase particles and there exists a normal distribution of nucleation strain for the total population of particles (Ref 36):

$$ \dot{f}_{\text{n}} = {\frac{{f_{N} }}{{s_{N} \sqrt {2\pi } }}}\exp \left[ { - \frac{1}{2}\left( {{\frac{{\bar{\upvarepsilon }^{p} - \upvarepsilon_{N} }}{{s_{N} }}}} \right)} \right]\dot{\bar{\upvarepsilon }}^{p} , $$
(13)

where f N represents the volume fraction of void-nucleating particles, ɛ N and s N are the average and standard deviation of the strains at which particles nucleate voids.

M-K Localized Necking Model

In the M-K localized necking model, an initial imperfection zone is assumed to be present in the sheet metal. The imperfection zone is modeled by a band which is weaker than other zone. The imperfection zone can be a band with lower strength or smaller thickness than the rest zone of the sheet metal. In the present study, the GTN continuum damage material model is used to describe the deformation behavior of sheet metal. A certain initial volume fraction of voids at the imperfection zone are assumed. Thus, this zone has a lower strength than other zone and is called inhomogeneous zone. This method is different from the approach assumed a geometric inhomogeneity and avoid the effect of normal pressure on the material deformation of geometrically inhomogeneous zone at the initial stage of biaxially stretching under superimposed double-sided pressure (Ref 31). The schematic presentation of M-K model used in the present study is shown in Fig. 3(a). A narrow band with width of 0.2 mm is defined as inhomogeneous zone. Double-sided pressure is imposed on both homogeneous zone and inhomogeneous zone. The loading displacements at two principal directions are adjusted to obtain the various strain paths. Due to predicting the right-hand side of FLD, it is assumed that the inhomogeneous zone is perpendicular to the principal axis 1. During the biaxially stretching processes, both zones deform continuously. Because of the relative low strength in inhomogeneous zone, the plastic strain in this zone is larger than that in homogeneous zone. At a certain point, the plastic strain in the homogeneous zone begins to rise rapidly. The failure is assumed to take place once the plastic strain increment in the inhomogeneous zone is 10 times larger than that in the homogeneous zone. The major strain and minor strain in the homogeneous zone is assumed to be the critical strain and is used to plot the FLD.

Fig. 3
figure 3

M-K model and the corresponding finite element model (a) schematic presentation of M-K model and (b) finite element model

Full size image

The commercial FEA software package ABAQUS/Explicit is used to conduct the numerical investigations. Figure 3(b) shows the finite element analysis model of M-K method. It consists of a homogenous zone and an inhomogeneous zone that contains voids and is used to initiate a neck. Due to symmetry, only one-eighth of the entire model is constructed. Three symmetrical planes are constrained. The sheet metal is modeled by the solid type of element C3D8R and is divided into multiple layers along the thickness direction. Three double-sided pressure conditions are applied to investigate its influence on the deformation behavior of sheet metal, p = 0, 80, and 160 MPa.

The material used in this study is an aluminum alloy AA6111-T4. A Ludwik-type hardening law is used to describe the plastic behavior of the matrix of both zones.

$$ \bar{\upsigma } = \upsigma_{\text{s}} + K\bar{\upvarepsilon }^{n} , $$
(14)

where \( \bar{\upsigma } \) is flow stress, \( \bar{\upvarepsilon } \) is effective plastic strain.

The mechanical properties of AA6111-T4 aluminum alloy are summarized in Table 1. The parameters for GTN damage model are shown in Table 2. Two sets of GTN model parameters taken from Aravas (Ref 37) and Lievers et al. (Ref 22) are used to study of the sensitivity of FLD to the GTN model parameters.

Table 1 Mechanical properties of AA6111-T4 aluminum alloy (Ref 23)
Full size table
Table 2 GTN damage model parameters for AA6111-T4 aluminum alloy (Ref 22, 37)
Full size table

Results and Discussion

Identification of the Initial Void Volume Fraction of Inhomogeneous Zone

In the M-K analysis, the initial imperfection factor f 0 has greatly effect on the prediction accuracy of FLD. In the present study, the initial imperfection factor f 0 lies on the initial VVF f a0 of inhomogeneous zone. The FLD of the model material can be varied through varying the initial VVF f a0 of inhomogeneous zone. f a0 is indentified by comparing the predicted FLD with experimental ones. When the predicted FLD without double-sided pressure matches the experimental FLD through adjusting the f a0, the value of f a0 is determined. Figure 4 shows the comparisons of the predicted FLD using the two sets of GTN model parameters and experimental measurement. The FLD predicted by using the GTN model parameters taken from Aravas (Ref 37) agreed well with the experimental result when the value of f a0 is 0.007. Hence, this set of GTN model parameters are used to conduct the numerical investigations.

Fig. 4
figure 4

FLDs obtained by varying the initial void volume fraction of inhomogeneous zone f a0 (a) GTN parameters No. 1 and (b) GTN parameters No. 2

Full size image

Effect of Double-Sided Pressure on the Formability of Sheet Metal

Void Evaluation

Ductile fracture of engineering materials can be attributed to the nucleation, growth, and coalescence of microvoids. Figure 5(a) shows the evolution of total VVF of homogenous zone and inhomogeneous zone. The evaluation of microvoids has a similar trend with the evaluation of plastic strain. At the initial stage of deformation, the total VVF slowly increases in both zones and the total VVF of the inhomogeneous zone is larger than that of the homogenous zone. When the deformation proceeds to a critical degree, the total VVF of the inhomogeneous zone drastically increases till fracture occurs. Imposing the double-sided pressure decreases the total VVF of both zones and thus delays the occurrence of fracture. In order to deeply analyze the influence of normal pressure on the void evaluation, the nucleation and growth of void are investigated, respectively. Figure 5(b) and (c) represents the evaluation of VVF due to growth and nucleation in both zones. The evaluation of VVF due to growth is similar to that of the total VVF. Void growth is suppressed when applying normal pressure on both sides of sheet metal. However, the evolution of VVF due to nucleation has a different rule. At the initial stage of deformation, some new voids have been nucleated drastically. After proceeding to a certain deformation, the VVF due to nucleation becomes invariable and almost no new microvoids nucleate. Furthermore, the normal pressure has no effect on the nucleation of new microvoids. Hence, it can be said that the decreasing of VVF due to the superimposed double-sided pressure is mainly owing to suppressing void growth but not nucleation.

Fig. 5
figure 5

Influence of superimposed double-sided pressure on the evaluation of microvoids (a) void volume fraction, (b) void volume fraction due to growth, and (c) void volume fraction due to nucleation

Full size image

Formability of Sheet Metal

A formability increase factor (FIF) is defined by Smith et al. (Ref 7) as Φ = ε1/e 1 to represent the increased ability of formability affected by normal pressure, in which e 1 is maximum principle strain under the plane stress state and ε1 is maximum principle strain under superimposed the double-sided pressure. Figure 6 shows the predicted FIF under double-sided pressure of 80 and 160 MPa. It is found that the FIF increases with the double-sided pressure for any biaxial tension strain state. Furthermore, the FIF is sensitive to the strain state. The FIF in equi-biaxial tension strain state is larger than that in in-plane plane strain tension state. Figure 7 shows the predicted FLDs under double-sided pressure. It is observed that superimposed the double-sided pressure increases the formability of sheet metal.

Fig. 6
figure 6

Effect of double-sided pressure on FIF

Full size image
Fig. 7
figure 7

Influence of double-sided pressure on FLDs

Full size image

Stress Triaxiality and Fracture Loci

Ductile fracture strongly depends on the stress triaxiality. Bao and Wierzbicki (Ref 38) found that a cut-off value of the stress triaxiality exists and equals to −1/3. Fracture never occurs when the stress triaxiality is lower than this value. This finding is consistent with the tensile test under hydrostatic pressure reported by Bridgman. In conventional sheet metal forming processes, according to Eq 7, the stress triaxiality is constant for given strain path, as shown in Fig. 8(a). As shown in Fig. 8(b) and (c), it is noted that imposing the normal pressure on sheet metal changes the value of stress triaxiality. The stress triaxiality decreases with increasing the value of normal pressure. The predicted loci are shown in Fig. 9. Experimental fracture locus is obtained through transferring the experiment FLD according to Eq 7. The increasing of the predicted fracture strain and the decreasing of stress triaxiality causes the entire fracture locus shift to the left.

Fig. 8
figure 8

Relationship of stress triaxiality and equivalent strain (a) p = 0 MPa, (b) p = 80 MPa, and (c) p = 160 MPa

Full size image
Fig. 9
figure 9

Influence of double-sided pressure on the predicted fracture loci

Full size image

Fracture Thickness

Figure 10 shows the effect of superimposed double-sided pressure on the fracture thickness. It can be seen that the fracture thickness is obviously reduced through imposing the double-sided pressure. Furthermore, the fracture thickness is sensitive to the strain state. The fracture thickness in equi-biaxial tension strain state is smaller than that in-plane strain tension state.

Fig. 10
figure 10

Effect of double-sided pressure on the fracture thickness

Full size image

Conclusions

In the present work, the deformation behavior of biaxially stretched aluminum alloy AA6111-T4 sheet under superimposed double-sided pressure are investigated via numerical simulations. Imposing the double-sided pressure on sheet metal can suppress the growth of microvoids, but make no significant difference on the nucleation of microvoids. With increasing the value of superimposed double-sided pressure, the formability of biaxially stretched aluminum alloy AA6111-T4 sheet is improved. The superimposed double-sided pressure decreases the stress triaxiality and increases the forming limit strain. The FLC of the biaxially stretched AA6111-T4 sheet metal under superimposed double-sided pressure is improved and the fracture locus shifts to the left. Furthermore, the formability increase value is sensitive to the strain path.