Introduction

The consumption of thermal energy from traditional fossil fuels is currently the most important means of electricity generation worldwide. However, the disadvantages of this form of electricity generation, which include low efficiency and environmental pollution, are becoming increasingly prominent. As a result, there is an urgent need to replace this conventional method of energy generation with novel clean energy generation schemes. Thermoelectric materials provide a type of green electricity that meets this requirement.1,2,3 The thermoelectric conversion capacity of these materials can be measured in terms of the optimal value of thermoelectricity, which can be expressed as \(ZT = {{S^{2} T\sigma } \mathord{\left/ {\vphantom {{S^{2} T\sigma } \kappa }} \right. \kern-\nulldelimiterspace} \kappa }\).4,5 In this formula, \(S\) is the Seebeck coefficient, \(\sigma\) is the electrical conductivity, \(T\) is the absolute temperature, and \(\kappa\) is the thermal conductivity. Note that both the electronic thermal conductivity \(\kappa_{e}\) and the lattice thermal conductivity \(\kappa_{l}\) contribute to the total thermal conductivity distribution.6

A large number of theoretical and experimental studies have been conducted over more than a decade on the thermoelectric properties of nanomaterials. Two-dimensional (2D) layered nanomaterials possess good electronic, mechanical, and chemical properties, such as a large surface area and abundant active centers,7 and are therefore extremely interesting to the scientific community.8,9,10 For example, a 2004 study showed that peeled-off single-layer graphene exhibited excellent physical properties, such as high fluidity and enhanced mechanical and chemical stability. However, the standard thermoelectric applications of graphene are limited by a small electron gap. Consequently, intensive research is being conducted to enlarge the graphene band gap.11,12 At the same time, there is considerable demand for the development of novel types of two-dimensional (2D) graphene-like materials for fabricating novel thermoelectric materials. One such graphene-like material that has been attracting increasing interest from the scientific community consists of low-dimensional layered transition metal halide (TMD) structures, especially Janus TMD structures.13,14,15

There are different chalcogenide elements of the Janus TMD on the two sides of the transition metal, which breaks the mirror symmetry of the structure. Interestingly, this asymmetry increases the carrier mobility and lowers the thermal transport capacity, enhancing the thermoelectric properties. Patel et al. carried out first-principles calculations based on the semiclassical Boltzmann transport theory to investigate WSSe and WSTe Janus monolayers.16 The WSTe Janus monolayers exhibited the highest ZT of 2.56 at a high temperature. This effect was ascribed to the combination of the high electrical conductivity, high Seebeck coefficient and very low lattice thermal conductivity of the Janus WSTe monolayers.16 Chaurasiya et al. investigated the impact of strain on the thermoelectric properties of Janus WSeS monolayers by using a self-consistent method in conjunction with the single-mode relaxation time approximation (RTA).17 The extracted outcomes showed that the ZT of n(p) carriers increased from 0.72 (0.73) to 1.06 (1.08) at concentrations of \(5 \times 10^{20} {\text{cm}}^{ - 3}\) (\(7 \times 10^{20} {\text{cm}}^{ - 3}\)) under an applied biaxial strain. This effect is attributed to the characteristics of the valence band and the valence band edges obtained under a biaxial strain, few valleys in the energy band structure, and an enhanced power factor.17 Holt et al. employed the advanced planar linearization (FP-LAPW) method and Boltzmann’s semiclassical transmission theory to study the HfSSe-Janus structure, where a first principles calculation was used to determine the electronic structure and optical and thermoelectric properties of a single layer.18 Under the application of a −4% compressive strain, the power factor (PF) value of the n-doped materials was 4.570 Wm−1 K−2 s (\(PF = S^{2} \sigma\)) at 800 K, because metals with free electrons exhibit relatively high electrical conductivity under stress.

All the abovementioned studies were performed on materials with excellent thermoelectric properties, whereas there have been no reports of the thermoelectric properties of Janus-based WSeS bilayer structures with different stacking modes. Thus, three combination modes of WSeS bilayer configurations, namely, SWSe/SWSe (SeS stacking), SWSe/SeWS (SeSe stacking), and SeWS/SWSe (SS stacking), are investigated in this study by conducting first-principles calculations based on the relaxation time approximation method. The thermal conductivity, electrical conductivity, and Seebeck coefficient of the three structures are systematically investigated at different temperatures and doping concentrations. The calculation results demonstrate that the WSeS bilayers with SeSe stacking possesses the highest ZT and can be employed as a candidate material for future thermoelectric applications.

Computational Methods

Calculations were performed in this study using the Vienna Ab Initio Simulation Package (VASP) with the generalized gradient approximation and the Perdew–Burke–Ernzerhof (PBE) exchange–correlation (XC) functional.19,20 The Heyd–Scuseria–Ernzerhof (HSE06) static self-consistent hybridization generalization method was used to accurately calculate the energy band structure.21 The Seebeck coefficients and electrical transport properties of the investigated materials were calculated by the BoltzTrap2 program using the semiclassical Boltzmann transport equation (BTE) and RTA method.22,23 The relaxation times of the carriers were estimated using deformation potential (DP) theory.24 The semiempirical corrections in the GRIMME DFT-D3 model were utilized to describe the weak van der Waals (vdW) interactions between two layers of the Janus WSeS nanostructure.25 In the optimized simulation, a cutoff energy of 500 eV and a 15 × 15 × 1 k-point grid were used to model the Brillouin zone. The electron transport properties were estimated using a 30 × 30 × 1 Monkhorst–Pack special k-point grid. The phonon dispersion and transport properties were calculated using a 3 × 3 × 1 supercell and a 3 × 3 × 1 Monkhorst–Pack special k-point grid by the Phonopy and Phono3py software packages.26,27 The moment of the \(a\)-th generalized transmission coefficient \(\pounds^{(a)}\) was calculated as

$$ \pounds^{(a)} (u;T) = q^{2} \int {\sigma (\varepsilon ,T)} (\varepsilon - u)^{\alpha } \left( { - \frac{{\partial f^{(0)} (\varepsilon ;u,T)}}{\partial \varepsilon }} \right)d\varepsilon $$
(1)

where \(\varepsilon\), \(q\), \(u\) and T are the band energy, charge, chemical potential, and temperature, respectively. The transport distribution function \(\sigma (\varepsilon ,T)\) is given by

$$ \sigma (\varepsilon ,T) = \int {\sum\limits_{b} {{\mathbf{v}}_{{b,{\mathbf{k}}}} } } \otimes {\mathbf{v}}_{{b,{\mathbf{k}}}} \tau_{{b,{\mathbf{k}}}} \delta (\varepsilon - \varepsilon_{{b,{\mathbf{k}}}} )\frac{{d{\mathbf{k}}}}{{8\pi^{3} }} $$
(2)

where the summation over \(b\) bands is integrated over the \({\mathbf{k}}\) points. \({\mathbf{v}}_{{b,{\mathbf{k}}}}\) and \(\tau_{{b,{\mathbf{k}}}}\) represent the carrier velocity and relaxation of the \(b\) th band at the \({\mathbf{k}}\) th point, respectively.

The deformation potential (DP)24 is typically used to estimate the carrier relaxation time \(\tau \), which can be expressed as follows:

$$ \tau = \frac{{\mu m^{ * } }}{e} = \frac{{2\hbar^{3} C}}{{3k_{B} Tm^{ * } E_{l}^{2} }} $$
(3)

where \(\mu\),\(\hbar\),\(m*\), \(C\), \(E_{l}\) and \(k_{B}\) are the carrier mobility, reduced Planck constant, effective mass, elastic constant, deformation potential constant, and Boltzmann constant, respectively. The effective mass of the carrier is defined as \(m^{ * } = {{\hbar^{2} } \mathord{\left/ {\vphantom {{\hbar^{2} } {\left( {{{\partial^{2} E} \mathord{\left/ {\vphantom {{\partial^{2} E} {\partial^{2} k}}} \right. \kern-\nulldelimiterspace} {\partial^{2} k}}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{{\partial^{2} E} \mathord{\left/ {\vphantom {{\partial^{2} E} {\partial^{2} k}}} \right. \kern-\nulldelimiterspace} {\partial^{2} k}}} \right)}}\), and the elastic constant is given by \(C = {{\left[ {{{\partial^{2} E} \mathord{\left/ {\vphantom {{\partial^{2} E} {\left( {\partial \varepsilon } \right)^{2} }}} \right. \kern-\nulldelimiterspace} {\left( {\partial \varepsilon } \right)^{2} }}} \right]} \mathord{\left/ {\vphantom {{\left[ {{{\partial^{2} E} \mathord{\left/ {\vphantom {{\partial^{2} E} {\left( {\partial \varepsilon } \right)^{2} }}} \right. \kern-\nulldelimiterspace} {\left( {\partial \varepsilon } \right)^{2} }}} \right]} {S_{0} }}} \right. \kern-\nulldelimiterspace} {S_{0} }}\), where \(E\) is the total energy of the system, \(\varepsilon = {{\Delta l} \mathord{\left/ {\vphantom {{\Delta l} {l_{0} }}} \right. \kern-\nulldelimiterspace} {l_{0} }}\) is the lattice strain under stress along the long x- or y-direction, and \(l_{0}\) is the equilibrium lattice constant. \(E_{l}\) is calculated as \(E_{l} = {{\partial E_{edge} } \mathord{\left/ {\vphantom {{\partial E_{edge} } {\partial \varepsilon }}} \right. \kern-\nulldelimiterspace} {\partial \varepsilon }}\), where \(E_{edge}\) is the shift of the band edge.

The rigid band approximation can be used to determine an electrical transport coefficient at a specified temperature \(T\) and chemical potential \(\varepsilon\). The carrier concentration can be calculated by the following equation:

$$ n(\varepsilon ) = \int {\sum\limits_{b} {\delta (\varepsilon - \varepsilon_{{b,{\mathbf{k}}}} )} } \frac{{d{\mathbf{k}}}}{{8\pi^{3} }} $$
(4)

where the sum is performed over \(b\) bands; the deviation from charge neutrality is then calculated as

$$ C\left( {\mu ,T} \right) = N - \int {n\left( \varepsilon \right)} f^{\left( 0 \right)} \left( {\varepsilon ;\mu ,T} \right)d\varepsilon $$
(5)

where \(N\) is the nuclear charge and \(f^{\left( 0 \right)}\) is the Fermi distribution function.

The electrical conductivity \(\sigma\), electronic thermal conductivity \(\kappa_{e}\), and Seebeck coefficient \(S\) can be written as follows:

$$ \kappa_{e} = \frac{1}{{q^{2} T}}\left[ {\frac{{\left( {\pounds^{(1)} } \right)^{2} }}{{\pounds^{(0)} }} - \pounds^{(2)} } \right] $$
(6)
$$ \sigma = \pounds^{(0)} $$
(7)
$$ S = \frac{1}{qT}\frac{{\pounds^{(1)} }}{{\pounds^{(0)} }} $$
(8)

Results and Discussion

Geometric Structure and Phonon Spectrum

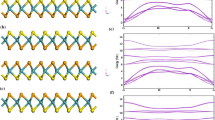
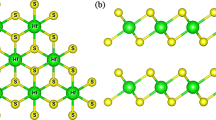
An in-depth analysis of three different combination modes of WSeS-based bilayer structures is performed in this study, namely, SWSe/SWSe (SeS stacking), SWSe/SeWS (SeSe stacking), and SeWS/SWSe (SS stacking), which are schematized as ball-and-stick models in Fig. 1a–c. These three structures exhibit 2D hexagonal lattice symmetry. Thus, each minimum cell contains six atoms. An analysis of the results of VASP calculations with GGA-PBE shows that the lattice parameters for the SeS, SeS, and SS structures are almost the same in the a- and b-directions, with approximate values of 3.22 Å. The thicknesses of the SeS, SeSe, and SS structures are 9.51 Å, 9.59 Å, and 9.45 Å, respectively. The layer spacings of the SeS, SeSe, and SS structures are 2.99 Å, 3.05 Å, and 2.92 Å, respectively. Figure 1 shows the dynamical photon properties determined after performing the optimization process. Figure 1e and f show the phonon spectra of the three structures of the Janus WSeS bilayer membrane. An analysis of the extracted outcomes shows that the entire frequency band is above 0, indicating that these three structures are stable. Ab initio molecular dynamics (AIMD) simulations demonstrated the thermodynamic stabilities of the three structures, as presented in supplementary Figs. S1–S4 in the Supplementary Materials.

Fig. 1
figure 1

Janus WeSeS bilayer structures with (a) SeS, (b) SeSe, and (c) SS stacking modes. The blue, brown, and yellow balls represent W, Se, and S atoms, respectively. Phonon spectra of the (d) SeS, (e) SeSe, and (f) SS stacking structures (Color figure online).

Full size image

Energy Band Structure and Electronic Density of States

The energy band structure and electron projected density of states (PDOS) were determined for the three types of WSeS bilayers. Figure 2 shows the energy band structure and PDOS of the WSeS bilayer determined by carrying out static self-consistent calculations based on the HSE06 hybridization generalization function with the VASP package.28 The calculated energy band structure lies along the ΓKMΓ high-symmetry direction due to the formation of a planar hexagonal structure.29 Figure 2a, b, and c show that the three Janus WSeS structures have an indirect band gap. The band gaps of the SeS, SeSe, and SS structures are 1.58 eV, 1.93 eV, and 1.66 eV, respectively. The peaks of the valence bands of the three structures are parabolic and flatter than those of the conduction bands, indicating the existence of relatively large hole effective masses,30 as shown in Table I.

Fig. 2
figure 2

Band structures of the (a) SeS, (b) SeSe, and (c) SS stacking structures calculated by HSE06. Projected DOS values for the (d) SeS, (e) SeSe, and (f) SS stacking structures.

Full size image
Table I Calculated effective mass, elastic modulus, deformation potential constant, and relaxation time of electrons and holes for the Janus WSeS bilayer
Full size table

The band gap of the SeS structure is smaller than that of the SeSe and SS structures. This result is obtained because the different polar charge distributions of the layers create a difference between the electronegativity of the atoms at the two ends of W, resulting in electrostatic attraction between the two layers and thereby reducing the energy band gap.32 To further analyze the electronic structure of the 2D WSeS bilayer, the PDOS of the three structures was determined and is shown in Fig. 2d, e, and f. The d orbital of the W atom plays a very important role in the conduction band of the investigated structures. This d orbital also makes a large contribution to the major valence band near the Fermi level. The p orbitals of the W atom and the S and SeS atoms make relatively small contributions to the major valence band near the Fermi level of the WSeS structure. The influence of the s orbitals of W, Se, and S on both the valence and conduction bands is negligible and occurs far from the Fermi level. Note that there are many locations outside the Fermi energy level where the d orbitals of the W atoms overlap with the p orbitals of Se and S. These orbitals are not in the vicinity of the Fermi energy level and do not contribute to the transport of charge carriers.

Seebeck Coefficients

Figure 3a, b, and c show the variation in the n-type doping Seebeck coefficient with the concentration at different temperatures for the WSeS-based structures with SeS, SeSe, and SS stacking. Figure 3d, e, and f show the variation in the p-type doping Seebeck coefficient with the concentration at different temperatures for the WSeS structures with SeS, SeSe, and SS stacking. The calculated outcomes lead us to conclude that the Seebeck coefficient decreases with increasing carrier concentration. The Seebeck coefficient can be related to the carrier concentration as follows:\(S = {{k_{B} \left[ {\ln \left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N n}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$n$}}} \right) + 2.5 - r} \right]} \mathord{\left/ {\vphantom {{k_{B} \left[ {\ln \left( {{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N n}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$n$}}} \right) + 2.5 - r} \right]} e}} \right. \kern-\nulldelimiterspace} e}\), where \(N\), \(n\), \(r\), and \(e\) are the effective DOS near the Fermi level, carrier concentration, scattering mechanism parameter, and electron charge, respectively.33 The aforementioned equation shows that the Seebeck coefficient decreases with increasing concentration.34 In addition, the impact of the temperature on the Seebeck coefficient cannot be neglected. Within the free-electron theory approximation, the Seebeck coefficient \(S\) is directly related to the temperature \(T\) as follows: \(S = \left( {{{8\pi^{2} k_{B}^{2} } \mathord{\left/ {\vphantom {{8\pi^{2} k_{B}^{2} } {3eh^{2} }}} \right. \kern-\nulldelimiterspace} {3eh^{2} }}} \right)m * T\left( {{\pi \mathord{\left/ {\vphantom {\pi {3n}}} \right. \kern-\nulldelimiterspace} {3n}}} \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}\). Note that this equation shows that the Seebeck coefficient is proportional to the temperature, and Fig. 3 shows that the Seebeck coefficients increase with the temperature.

Fig. 3
figure 3

Seebeck coefficients for the (a) SeS, (b) SeSe, and (c) SS stacking structures with n-type doping at different temperatures. Seebeck coefficients for the (d) SeS, (e) SeSe, and (f) SS stacking structures with p-type doping at different temperatures.

Full size image

Electrical Conductivity

\({\sigma \mathord{\left/ {\vphantom {\sigma \tau }} \right. \kern-\nulldelimiterspace} \tau }\) can be obtained using Boltztrap2, and the relaxation time \(\tau = {{2\hbar^{3} C} \mathord{\left/ {\vphantom {{2\hbar^{3} C} {\left( {3k_{B} Tm^{ * } E_{l}^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {3k_{B} Tm^{ * } E_{l}^{2} } \right)}}\) can be determined from Eq. 3. These two results can be used to determine the electrical conductivity. Figure 4 shows the relationship between the electrical conductivity and the doping concentration. Figure 4a, b, and c show the electrical conductivity of the SeS, SeSe, and SS structures versus the n-type doping concentrations, respectively. Figure 4a, b, and c show that at a constant temperature, the electrical conductivity increases with the carrier concentration. Figure 4d, e and f show the electrical conductivity of the Se, SeSe, and SS structures as a function of the p-doping concentration. The extracted results lead us to conclude that the carrier conduction paths between the atoms increase with the carrier concentration, which effectively changes the carrier transport properties.32 Thus, it is reasonable that a high doping concentration produces a strong conductive pattern.

Fig. 4
figure 4

Conductivity of the (a) SeS, (b) SeSe, and (c) SS stacked structures with n-type doping at different temperatures. Conductivity of the (d) SeS, (e) SeSe, and (f) SS stacked structures with p-type doping at different temperatures.

Full size image

Figure 4 shows that holding all other conditions fixed, the SeS structure with p-type doping has the highest electrical conductivity and the SS structure with n-type doping has the lowest electrical conductivity. This effect is attributed to the difference in the relaxation times of these structures: the electrical conductivity can be related to the relaxation time as \(\sigma = {{e^{2} \int {\tau \left( {\vec{k}} \right)v\left( {\vec{k}} \right)v\left( {\vec{k}} \right)\left[ {{{ - \partial f^{0} \left( {\varepsilon_{k} } \right)} \mathord{\left/ {\vphantom {{ - \partial f^{0} \left( {\varepsilon_{k} } \right)} {\varepsilon_{k} }}} \right. \kern-\nulldelimiterspace} {\varepsilon_{k} }}} \right]{\text{d}}\varepsilon } } \mathord{\left/ {\vphantom {{e^{2} \int {\tau \left( {\vec{k}} \right)v\left( {\vec{k}} \right)v\left( {\vec{k}} \right)\left[ {{{ - \partial f^{0} \left( {\varepsilon_{k} } \right)} \mathord{\left/ {\vphantom {{ - \partial f^{0} \left( {\varepsilon_{k} } \right)} {\varepsilon_{k} }}} \right. \kern-\nulldelimiterspace} {\varepsilon_{k} }}} \right]{\text{d}}\varepsilon } } \Omega }} \right. \kern-\nulldelimiterspace} \Omega }\), where \(\Omega\) represents the volume of the unit cell, \(\tau \left( {\vec{k}} \right)\) represents the relaxation time, \(v\left( {\vec{k}} \right)\) represents the group velocity, \(\varepsilon_{f}\) represents the Fermi energy, and \(f^{0}\) is the Fermi–Dirac distribution function.35 The results presented in Table I show that the SeS structure with p-type doping has the greatest relaxation time and therefore the highest electrical conductivity, and vice versa. Thus, the electrical conductivity is positively correlated with the carrier relaxation time: the larger the carrier relaxation time, the higher the electrical conductivity.

Thermal Conductivity

Electronic Thermal Conductivity

The influence of the carrier concentration on the thermal conductivity of the material is also analyzed. Notably, the total thermal conductivity has two components: the electronic thermal conductivity (\(\kappa_{e}\)) and the lattice thermal conductivity (\(\kappa_{l}\)). The change in the electronic thermal conductivity distribution with the carrier concentration is calculated at different temperatures. These results are presented graphically in Fig. 5, showing trends with the doping concentration. Figure 5a, b, and c show the electronic thermal conductivity of the n-doped material as a function of the carrier concentration at different temperatures. Figure 5d, e, and f show the total thermal conductivity and the electronic thermal conductivity of the p-doped material as a function of the carrier concentration at different temperatures. The extracted outcomes show that the electrical thermal conductivity of the Janus-based WSeS gradually increases with the doping concentration. The Boltzmann transport equation can be used to calculate the electronic thermal conductivity as \(\kappa_{e} = {{\pi^{2} nk_{B}^{2} T\tau_{e} } \mathord{\left/ {\vphantom {{\pi^{2} nk_{B}^{2} T\tau_{e} } {3m_{0} }}} \right. \kern-\nulldelimiterspace} {3m_{0} }}\).36 Hence, it can be concluded that a high doping concentration leads to high electronic thermal conductivity. The electronic thermal conductivity decreases with increasing temperature. The electronic thermal conductivity and electrical conductivity are related by the Wiedemann–Franz law37,38 \(\kappa_{e} = L\sigma T\), where \(L\) is the Lorentz constant. The electronic thermal conductivity depends on the temperature and electrical conductivity. Figure 5 shows that the electronic conductivity decreases with increasing temperature. In summary, the electronic thermal conductivity of electrons decreases with increasing temperature.

Fig. 5
figure 5

Electronic thermal conductivity of the (a) SeS, (b) SeSe, and (c) SS stacked structures with n-type doping at different temperatures. Electronic thermal conductivity of the (d) SeS, (e) SeSe, and (f) SS stacked structures with p-type doping for electronic thermal conductivity at different temperatures.

Full size image

Lattice Thermal Conductivity

The phonon kinetic theory can be used to express the lattice thermal conductivity as \(\kappa_{l} = {{C_{\lambda } \upsilon_{\lambda }^{2} \tau_{\lambda } } \mathord{\left/ {\vphantom {{C_{\lambda } \upsilon_{\lambda }^{2} \tau_{\lambda } } 3}} \right. \kern-\nulldelimiterspace} 3}\), where \(\upsilon_{\lambda }\) is the phonon velocity, \(\tau_{\lambda }\) is the phonon relaxation time, \(C_{\lambda } = \sum\limits_{\lambda } {9R\left( {{T \mathord{\left/ {\vphantom {T {\Theta_{D} }}} \right. \kern-\nulldelimiterspace} {\Theta_{D} }}} \right)^{3} \int\limits_{0}^{{\Theta_{D} }} {{{y^{4} e^{y} } \mathord{\left/ {\vphantom {{y^{4} e^{y} } {\left( {e^{y} - 1} \right)^{2} }}} \right. \kern-\nulldelimiterspace} {\left( {e^{y} - 1} \right)^{2} }}} dy}\) is the heat capacity distribution, \(R\) is the ideal gas constant, \(\lambda\) is the phonon mode, \(\Theta {}_{D}\) is the Debye temperature, and \(y = {{\Theta_{D} } \mathord{\left/ {\vphantom {{\Theta_{D} } T}} \right. \kern-\nulldelimiterspace} T}\).39

The group velocity of phonons is one of the determining factors for the thermal conductivity of phonons. Figure 6a, b, and c show the trend in the phonon group velocity with the frequency for the three structures of Janus-based WSeS bilayers. The phonon group velocity along the x- and y-direction is approximately 150 THz*Angstrom for the SeS structure and has a higher value of approximately 300 THz*Angstrom for the SeSe and SS structures.

Fig. 6
figure 6

Frequency-dependent velocities of phonon groups for the (a) SeS, (b) SeSe, and (c) SS stacking modes.

Full size image

The phonon relaxation time also influences the thermal conductivity of phonons. Thus, the phonon relaxation times of the three structures vary across the frequency range, as shown in Fig. 7a, b, and c. The phonon relaxation time of the SeS structure is considerably larger than that of the SeSe and SS structures. The relaxation time of the SeSe structure is lower than that of the SS structure. Figure 7 shows that the SeS structure has a relatively large relaxation time in the high-frequency range. The phonon relaxation time can be expressed as follows:\({1 \mathord{\left/ {\vphantom {1 {\tau = {1 \mathord{\left/ {\vphantom {1 {\tau_{PP} }}} \right. \kern-\nulldelimiterspace} {\tau_{PP} }}}}} \right. \kern-\nulldelimiterspace} {\tau = {1 \mathord{\left/ {\vphantom {1 {\tau_{PP} }}} \right. \kern-\nulldelimiterspace} {\tau_{PP} }}}} + {1 \mathord{\left/ {\vphantom {1 {\tau_{PB} + {1 \mathord{\left/ {\vphantom {1 {\tau_{PD} }}} \right. \kern-\nulldelimiterspace} {\tau_{PD} }}}}} \right. \kern-\nulldelimiterspace} {\tau_{PB} + {1 \mathord{\left/ {\vphantom {1 {\tau_{PD} }}} \right. \kern-\nulldelimiterspace} {\tau_{PD} }}}}\), where \({1 \mathord{\left/ {\vphantom {1 {\tau_{pp} }}} \right. \kern-\nulldelimiterspace} {\tau_{pp} }}\),\({1 \mathord{\left/ {\vphantom {1 {\tau_{PB} }}} \right. \kern-\nulldelimiterspace} {\tau_{PB} }}\), and \({1 \mathord{\left/ {\vphantom {1 {\tau_{PD} }}} \right. \kern-\nulldelimiterspace} {\tau_{PD} }}\) are the contributions from phonon–phonon scattering, phonon-boundary scattering, and phonon-defect scattering, respectively.40,41

Fig. 7
figure 7

Frequency dependence of the phonon relaxation time for the (a) SeS, (b) SeSe, and (c) SS stacking modes.

Full size image

The Grüneisen constant can be used to evaluate the anharmonicity of materials and as a general measure of the scattering rate. Consequently, the higher the Grüneisen constant, the lower the thermal conductivity of the phonons.42 Figure 8a, b, and c show the frequency-dependent Grüneisen constants of the SeS, SeSe, and SS structures. The SeSe structure has the highest Grüneisen constant over the entire frequency range, followed by the SS structure and then the SeS structure. Therefore, the phonon relaxation time is the largest for the SeSe structure, followed by the SS structure and then the SeS structure.

Fig. 8
figure 8

(a) Variation in the Grünigsen constant with frequency for the (a) SeS, (b) SeSe, and (c) SS stacking structures.

Full size image

Figure 9 shows the lattice thermal conductivity \(\kappa_{l}\) of the SeS, SeSe, and SS structures, where \(\kappa_{l}\) decreases with increasing temperature. Note that the SeSe structure has the highest phonon group velocity and the shortest phonon relaxation time; by comparison, the SeS structure possesses the lowest phonon group velocity and the longest phonon relaxation time, which leads to the largest \(\kappa_{l}\). Similarly, at a fixed temperature, the configuration of SeSe results in the lowest \(\kappa_{l}\), as shown in Fig. 9. This effect is ascribed to the significant enhancement of phonon–phonon interactions at elevated temperatures. Thus, the higher the temperature, the stronger the phonon–phonon interaction, whereas phonons are prevented from participating in heat transfer from high-temperature to low-temperature regions.42 Therefore, the lattice thermal conductivity decreases as the temperature increases.

Fig. 9
figure 9

The lattice thermal conductivity versus the temperature for the SeS, SeSe, and SS stacking structures.

Full size image

Figures of Merit

As all the transport properties have been determined, the figure of merit, ZT, of the WSeS can be calculated. Figure 10 shows the variation in ZT for the n- and p-type doped materials in the x- and y-direction as a function of the carrier concentration at different temperatures. As the carrier concentration increases, ZT first rises to a peak and then decreases. ZT increases with the temperature. ZT is higher for n-type doping than p-type doping, holding all other conditions constant. The highest ZT peak for n-type doping is obtained for the SeSe structure, which possesses the lowest thermal conductivity and highest electrical conductivity. In conclusion, the SeSe structure exhibits a ZT of 2.4 with an n-type doping concentration of \(5 \times 10^{11}\)\({\text{cm}}^{ - 3}\) at a temperature of 900 K. Patel et al. determined the thermoelectric properties of monolayer WSeS using first-principles calculations based on the semiclassical Boltzmann transport theory.16 A ZT of approximately 0.25 was determined at 900 K due to the extraordinary Seebeck coefficient and high electrical conductivity of the material. Kumar et al. used the same methods to calculate a ZT of 0.8 for monolayer WSe2 at 1200 K, which results from the low thermal conductivity of the material.43 Huang et al. determined the ZT of WSe2 at 500 K using ab initio calculations and ballistic transport theory.44 These results can be explained in terms of the presence of additional valleys in the electron energy band structure near the k-point at high temperatures. The results of our study show that the Janus WSeS bilayer has superior thermoelectric properties to those of WSe2 or WSeS monolayers.

Fig. 10
figure 10

ZT of the (a) SeS, (b) SeSe, and (c) SS stacked structures with n-type doping at different temperatures. ZT of the (d) SeS, (e) SeSe, and (f) SS stacked structures with p-type doping at different temperatures.

Full size image

Conclusion

In summary, first-principles calculations and the Boltzmann semiclassical transport theory were employed to systematically investigate the geometry, band structure distribution, electrical conductivity, thermal conductivity, Seebeck coefficient, and figures of merit of Janus-based WSeS bilayers with SeS, SeSe, and SS stacking. The small deformation potential constant and large elastic modulus of a monolayer results in an enhanced carrier relaxation time; thus, Janus-based WSeS bilayer structures possess excellent electrical transport capability and thermoelectric properties. Moreover, n-type doping of the SeSe structure results in excellent thermoelectric performance, with a ZT of 2.4 due to high electrical conductivity and low thermal conductivity at 900 K at an n-doping concentration of \(5 \times 10^{11} {\text{cm}}^{ - 3}\). These calculated outcomes can be used for other two-dimensional materials and can provide useful theoretical guidance for optimizing various thermoelectric properties.