Effect of Phase Transformation and Recalescence on the Squareness of Steel Beams in Water-Jet Quenching

Abstract

Quenching and self-tempering (QST) is an advanced thermo-mechanical process for “H” shaped steel beams. QST is an intensive surface cooling and self-tempering process that provides the grain refinement needed for high strength of low-carbon steels. However, the application of quenching often results in substantial deformation due to the formation of the martensitic microstructure at a high cooling rate. Quench deformation has been a complex metallurgical phenomenon that is difficult to accurately control in the beam-making process. A correlation between shape distortion and temperature distribution was therefore investigated through a lab-scale test. The thermal deformation was also analyzed numerically by using a commercial finite element program ANSYS APDL to explain the thermal expansion and contraction mechanisms of quenched steel beams. A metallurgical effect was sub-coded to follow a phase transformation in the quenching simulation. The theoretical approach and numerical simulation of the H-beam quenching are compared to the experimental findings.

Introduction

Recent demands for the high strength and toughness of steel beams have increased gradually in the construction market. A quenching and self-tempering (QST) technique after finishing rolling has been used to strengthen steel beams since its development by ARBED, CRM and British Steel.^[1] A QST process is primarily designed for long products, e.g., rails and reinforcing bars, as Matlock and Speer indicated.^[2] Quenching in QST is an intensive surface cooling technique which releases high-pressure water as a cooling medium for a few seconds, as indicated by Degtyarev.^[3] Self-tempering is a process of reheating the cold surface through the heat transferred from the hot core. The main objective of quenching is to lower manufacturing costs by reducing the alloying elements and to improve mechanical properties by refining the microstructure. Kumar et al. has observed a considerable improvement in hardness, tensile strength and yield strength after heat treatment.^[4] Esterl et al. investigated the effect of quenching on the texture and mechanical properties of ultra-high strength steels.^[5] Lu et al. reported that the cooling method was more critical than the rolling temperature in determining the mechanical properties.^[6] Ning et al. studied how the cooling rate affects the mechanical properties and precipitation behavior of carbides.^[7] They found an optimum cooling rate could make the desired distribution of carbides, which in turn leads to improved mechanical behaviors. Thus, quenching has been considered as an efficient beam-making process for improving mechanical properties.

However, the application of quenching was very limited because of the undesired distortion despite the advantages. A few studies have been carried out to understand the deformation behavior and to avoid the undesirable distortion during quenching. Abouaf et al. suggested a two-dimensional (2D) finite element analysis while assuming that constant curvature dominates rail deflection.^[8] The same authors further developed a technique called 2D idealization which predicted bending perpendicular to the 2D plane using nonlinear material properties on temperature.^[9] These early studies focused mainly on 2D numerical computation for quantitative analysis and compared to experimental findings. Pernía et al. simulated the thermal deformation of H-beams in the cooling bed by utilizing the computation fluid dynamics (CFD) and finite element methods (FEM).^[10] Reyes et al. investigated the thermal deformation of a ring-shaped steel by immersing it in a mixture of water and polymer.^[11] Huiping et al. has developed a FEM model showing the relationship between temperature, phase transformation and stress/strain during quenching.^[12] But, their conclusions were limited to developing a sample-based model rather than understanding large-scale deformation due to quenching. Kamak proposed a model to compute the residual stress of an advanced high-strength steel (AHSS) including phase transformation kinetics.^[13] Their studies on quenching application were however similar to watering or liquid dipping rather than high pressure spraying, although all were based on the thermal, mechanical and metallurgical domains. Two of my previous research were related to the quenching process: one was for quantification of quenching effect,^[14] the other for localized longitudinal deflection.^[15] None of the above studies focused on sectional torsion, e.g., squareness, due to the thermal loads after quenching.

Mróz et al. indicated that the materials would be heated unevenly or cooled locally before the rolling process.^[16] But, more precisely, the heat losses on the H beams are not uniform because of a "H" shape which causes a separate thermal behavior above and below the web. The upper half of the H-beams generally dissipates heat much faster than the lower half because it is an open system. While the upper half easily emits heat without obstacles, the heat dissipation of the lower half is disrupted by a transfer roller located beneath the beam. Heavy section steels shall be subjected to a sufficiently high degree of quenching for adequate heat treatment, but the strong application results in severe shape deformation due to uneven heat dissipation. As Gür and Tekkaya reported in their numerical quenching study, quenching was expected to have a significant effect on non-uniform plastic deformation.^[17] Figure 1 shows the possible shape defects observed after quenching. Operation at the maximum quenching rate was therefore prohibited on large beams due to significant thermal deformation. It was necessary to optimize the quenching parameters which minimize the thermal deformation in quenching. Only a limited method, e.g., computational approximation, was however more readily available than experimental observations. In this study, lab-scale experiments were carried out for the structural behavior of quenched beams using self-developed quenching facilities. Experimental observations have been analyzed to estimate a correlation between quenching and deformation. A thermo-mechanical analysis was then conducted using ANSYS and compared against the empirical results.

Fig. 1

Out-of-squareness due to strong quench

Experimental Setup

A research material was an A36 hot-rolled H-shaped steel beam. The beam size was W24 × 12¾ × 192 according to its cross-sectional geometries described in American Society for Testing and Materials (ASTM) Standard A6/A6M.^[18] The web and flange were 646.9 mm and 328.9 mm long, their thickness was 20.6 mm and 37.1 mm respectively. The material required a minimum yield strength (YS) of 250 MPa and a tensile strength (TS) of 400 to 550 MPa in accordance with ASTM A36/A36M.^[19] Table I shows the chemical composition of grade A36 steels. ${t}_{2}$ corresponds to the flange thickness given at 37.1 mm in this study.

Table I Chemistry Requirements of A36 in ASTM Standard

A lab-scale QST simulator consists of a heating oven, a transfer system, an air blower, and a quenching device. The simulator is depicted schematically in Figure 2. A test sample was a “⊢” shape that was the half-symmetry of an H-beam. A measure of surface temperature was a primary concern, but it was difficult to maintain the contact due to the high pressure of the water-jet in quenching. The inner temperature was therefore measured in place of the surface temperature. A number of thermocouples (TCs) were inserted into the beam sample with prefabricated holes and then sealed to prevent wetting. The sample was initially loaded in the oven and heated up to 1200 °C for 2 to 3 hours to reach the overall uniform temperature. It was mounted on a transfer device after being taken out of the oven. It was then transferred to an air spray to remove the scales prior to quenching. Finally, the sample moved to a quenching device when the temperature reached a preset value during air cooling. In general, the H-beams exhibit unequal temperature profiles above and below the web due to differences in heat convection and radiation. The preset value was therefore checked in relation to the upper flange surface temperature. The travel speed was between 0.01 and 1.0 m/s in the quenching device, and the maximum coolant flow rate was 800 m³/h. The sample was rapidly tempered by itself after quenching and slowly air-cooled down to room temperature. The beam was then observed to analyze the degree of deformation and microstructure.

Fig. 2

QST simulator configuration

Theoretical Studies

Estimation of Heat Transfer in Quenching

A quenching effect is dependent on the water flow rate and the duration of exposure to the water jet. An estimate of the heat transfer coefficient (HTC) is based on a heat exchange relationship between the hot steel beam and the cold water. Figure 3 shows the thermal boundary where the heat exchange occurs. The heat would be released from the beam surface into the water via convective heat transfer because the beam had higher thermal energy. The expression of convection is stated in Eq. [1].

$${q}_{\rm{conv}}=h\left({T}_{\rm{s}}-{T}_{i}\right){A}_{\rm{s}},$$

(1)

$h$ is the HTC due to forced convective quenching, and ${A}_{\rm{s}}$ is a hypothetical surface of the thermal contact. ${T}_{\rm{s}}$ and ${T}_{i}$ are a beam temperature at the surface and an initial water temperature before quenching. The water temperature rises from room temperature ${T}_{i}$ to the boiling point ${T}_{f}$, some water evaporates instantaneously from the hot surface. Eq. [2] accounts for the temperature increase due to the amount of heat exchanged as the water flows. This includes thermal energy obtained and liquid-vapor transition energy.

$$q={c}_{\rm{w}}\dot{m}\Delta T={\rho }_{\rm{w}}\left[{c}_{\rm{w}}\left({T}_{f}-{T}_{i}\right)+\Delta {H}_{v}\right]\dot{Q},$$

(2)

${c}_{\rm{w}}$, ${\rho }_{\rm{w}}$, and $\dot{m}$ are the specific heat, the density, and the mass flow rate of water. $\Delta {H}_{v}$ represents the latent heat of evaporation when water evaporates, and $\dot{Q}$ is the volumetric flow rate. The symbols and the thermo-physical properties required are given in Table II. The heat released would be the same as the heat transferred assuming there is no loss. The quantity of thermal energy in Eqs. [1] and [2] should be identical according to the energy conservation principle. Therefore, the HTC can be obtained as in Eq. [3] by using the law of energy conservation.

Fig. 3

Heat exchange between hot and cold media

Table II Thermo-physical Properties for Calculating Transferred Heat

$$h=\frac{{\rho }_{\rm{w}}\left[{c}_{\rm{w}}\left({T}_{f}-{T}_{i}\right)+\Delta {H}_{\rm{v}}\right]\dot{Q}}{\left({T}_{\rm{s}}-{T}_{i}\right){A}_{\rm{s}}}.$$

(3)

Shape Deformation in Quenching

Steels generally exhibit a plastic deformation behavior as a result of temperature change and phase transformation in quenching. The plastic deformation due to thermal effect varies according to the coefficient of thermal expansion over temperature, and it can be expressed as follows.

$$\Delta l=\alpha \cdot {l}_{0}\cdot \Delta T,$$

(4)

${l}_{0}$ stands for the initial length of an object, and $\Delta l$ is the change in length which is proportional to the change in temperature $\Delta T$. $\alpha$ is the coefficient of linear expansion which is a function of temperature and has a separate profile depending on a material phase, e.g., ferrite, bainite, or martensite.

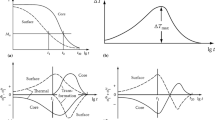
The transformation of austenite into ferrite, bainite and martensite depends on the cooling rate of the steels. The plastic deformation occurs due to the difference in phase volume. This expansion or contraction is referred to as phase change deformation and is illustrated schematically in Figure 4 using a linear expansion. Bainite (or martensite) is usually formed at the surface layer because the QST is an intensive surface quenching process. A quenched part expands in an explosive manner due to the sudden phase transition, while an uncooled region gradually shrinks in the stable phase state. The imbalance in the expansion rate therefore causes a permanent deformation of the quenched steels.

Fig. 4

Linear expansion curve according to a cooling rate

A material used in this study was considered isotropic since steels have identical material features in all directions. Hooke's law ($E=\sigma {\varepsilon }_{\rm{e}}$) indicates the relationship between stress and deformity, and steels in the elastic range obey the following expression.

$${\varepsilon }_{ij}=\frac{1+\nu }{E}{\sigma }_{ij}-\frac{\nu }{E}{\sigma }_{\rm{kk}}.$$

(5)

The index $e$ denotes elasticity. $i$, $j$, and $k$ are indices indicating the x, y and z components in the Cartesian coordinates. $\nu$ is Poisson’s ratio, $E$ is the elastic modulus, and $\sigma$ corresponds to the stress in the elastic range. Structural analysis in heat treatment is a study about permanent resistance due to the increase in internal stress against deformation. Assuming that the material is isotropic, a thermal expansion occurs in all directions. Since a volume change is directly related to the change in temperature, the thermal stress proportional to the change in temperature was given as follows.

$${\varepsilon }_{\rm{t}}=\alpha \Delta T,$$

(6)

where ${\varepsilon }_{t}$ is a thermal strain, and $\alpha$ is a coefficient of thermal expansion. $\Delta T$ is the temperature change that can be measured experimentally or calculated numerically in the FEM simulation. Plastic behavior has a significant influence on the change in residual stress because steels are strain-hardened by thermal distortion in heat treatment. Plastic strain ${\varepsilon }_{\rm{p}}$ was therefore necessary to explain stress evolution since the strengthening is assumed to take place in cooling. The plastic portion of the strain is described as the difference between the total and the elastic strain. The bilinear isotropic hardening used for the calculation is as follows.

$$d{\varepsilon }_{\rm{p}}=d\varepsilon -d{\varepsilon }_{\rm{e}}=\frac{E-{E}_{T}}{E\cdot {E}_{T}}d\sigma .$$

(7)

A material starts to deform plastically as it goes beyond the elastic region. The isotropic hardening model means that a yield surface expands in all directions proportionally when the stress exceeds the yield strength ${\sigma }_{y}$. Young's modulus represents the ratio of stress versus strain in the elastic range. ${E}_{\rm{T}}$ is the tangent modulus that is the slope of the stress–strain curve in the inelastic region. The use of ${E}_{\rm{T}}$ is simple and useful in describing the behavior of materials if there are no continuous high loads resulting in ultimate failure. During the quenching process, the total strain can be expressed as the sum of the strain components as follows.

$$\varepsilon ={\varepsilon }_{\rm{e}}+{\varepsilon }_{\rm{t}}+{\varepsilon }_{\rm{p}}.$$

(8)

The components of this equation represent strain due to elastic, thermal, and plastic loading respectively. Residual stress and strain are the cumulative results of the calculation until the material is cooled to room temperature. The materials were expected to comply with von Mises yield criterion. Mechanical properties, e.g., yield strength and tensile strength, were subject to change during quenching. Changes in thermophysical characteristics due to ferrite, bainite and martensite have therefore been taken into account by using a user developed subroutine in ANSYS APDL. A commercial software JMatPro was used to derive thermophysical properties due to the lack of exact experimental data. A specific phase was defined in terms of cooling rate and temperature, and a decision was made whether or not it had undergone austenite-ferrite, -bainite, and -martensite transformation. For each element which has been transformed into a new phase, the physical characteristics have been replaced by those of the designated.

Phase Transformation

A quenching process and subsequent thermal deformation were analyzed using ANSYS APDL. The thermo-structural behavior of quenched steels depends on the rate of heat treatment and the phase change according to the alloying composition. A coupled-computational model including thermo-structural behavior and metallurgical features was therefore applied to this quenching study as shown in Figure 5. Phase transformation properties were obtained from JMatPro.

Fig. 5

Thermo-metallurgical-mechanical coupled analysis

A phase transformation is a multi-physical process that a phase turns into a new or different one. Steels are transformed into a different phase during quenching depending on the cooling rate. Temperature and cooling rate are important thermodynamic parameters which indicate the physical properties of the steels. Phase transformation typically has a significant effect on the thermophysical properties, e.g., density, specific heat, the coefficient of thermal expansion, etc. Beam quenching is a rapidly changing process, not an isothermal operation. A time temperature transformation (TTT) approach is therefore not favorable to quenching heat treatment. The TTT curve is only capable of providing an isothermal estimate of phase information. As a result, continuous cooling transformation (CCT) curves are used to anticipate phase transformation over time.

Recalescence is a metallurgical phenomenon which emits heat during phase change as Gao et al. described.^[20]. Austenite can transform quickly when quenched, and the fraction of the transformed phase varies depending on the rate of cooling. Therefore, a new transformed phase releases a different amount of latent heat based on the thermodynamic conditions. Using the CCT curve, Figure 6 illustrates how quenching leads to austenite-martensite transformation and heat generation. The temperature of the hot-rolled workpiece is generally above A_r3 because quenching occurs after hot-rolling. Ouchi et al. introduced the starting temperature of γ-α transformation, and they had developed a regression equation of A_r3 for Si–Mn–Nb microalloyed steels^[21] Schacht et al. designed material properties in various forming processes and proposed a formula for A_r1 temperature depending on the carbon, manganese, and silicon content.^[22] A_r3 was estimated between 820 and 850 °C, and A_r1 was expected to be between 720 and 740 °C.

Fig. 6

Austenite to martensite transformation and heat release on the CCT curve

$${A}_{r3}\left(^\circ{\rm C} \right)=910-310\rm{C}-80\rm{Mn}-20\rm{Cu}-15\rm{Cr}-80\rm{Mo},$$

(9)

$${A}_{r1}\left(^\circ{\rm C} \right)=739-22\rm{C}-7\rm{Mn}+2\rm{Si}.$$

(10)

Density and latent heat change when austenite is converted into a different phase during the quenching process. The transformed phase fraction is estimated based on temperature and cooling rate. The heat released in quenching is therefore defined as the product of the phase fraction, density, and latent heat.

$$q\left({T}_{i},C{R}_{i}\right)=\Delta f\left({T}_{i},{CR}_{i}\right)\rho \left({T}_{i}\right)L\left({T}_{i},C{R}_{i}\right)/\Delta t,$$

(11)

$i$ is the index representing a specific time. $T$ and $CR$ represent the temperature and cooling rate at the time. $\Delta f$ is the volume fraction which has been phase-transformed in the given temperature and cooling rate. $\rho$ is the density, and $L$ is the latent heat of transformation. $\Delta t$ is the small-time interval used to convert heat energy into power.

It was assumed that phase transformation would occur continuously during quenching as the quenching process promoted phase transformation. The evolution of the volume fraction of each phase due to the continuous transition was estimated using the additivity rule. Accordingly, a corresponding latent heat was applied proportional to the change in the volume fraction of the transformed phase. Guo et al. used Avrami theory to state the overall phase transformation kinetics,^[23] and the model was modified to present a volume fraction of the transformed phase as of Eq. [12].

$$\Delta {f}_{i}=1-\frac{{f}_{i}-{f}_{i-1}}{{f}_{tot}},$$

(12)

$$\Delta f=1-\sum \Delta {f}_{n},$$

(13)

${f}_{i}$ is a volume fraction of the transformed phase at a specific time step $i$. ${f}_{\rm{tot}}$ is the total volume fraction, and $\Delta {f}_{i}$ is an instantaneous volume fraction during phase change. $\Delta f$ is an infinitesimal volume fraction related to a specific phase, and $\sum \Delta {f}_{n}$ represents the rest.

The latent heat below 1 × 10⁶ [J/m³] was considered insufficient to produce a noticeable temperature rise at a cooling rate of 100 to 200 °C/s. Through many simulation trials, the latent heat over 1 × 10⁷ [J/m³] appeared to be well suited for making a significant temperature change. Figure 7 shows a latent heat profile calculated at various cooling rates. The heat is formulated based on temperature and cooling rate, and is linked to the conservation of energy principle to calculate the temperature affected by the recalescence in the transient simulation. The latent heat released during the transition to a new phase was easily recognized by the transformation temperature range, as shown in the figure. Heat allocation in a specific phase has therefore become easier in a numerical way.

Fig. 7

Latent heat calculated at various cooling rates

Results and Discussion

Experimental Results and Discussion

A laboratory-scale quenching test was performed to determine the effect of quenching on the beam deformation. The quenching zone is divided into 3 sections: a side section to quench the external flange, an upper section to quench the inner flange and upper web, and a lower section to quench the inner flange and lower web. A start-cooling temperature (SCT) was set to 900 °C, and temperature during quenching was measured continuously through a thermocouple (TC). As forementioned, the temperature within the beam was measured instead of the surface due to the risk of a TC being detached from the surface by high-pressure water jet. The figure shows the location of the TCs inserted for temperature measurement. The TC insert holes were located 1/6 of the flange thickness and 1/6 of the flange length, as shown in Figure 8. The preheated sample was exposed to a pressurized water jet for 9 seconds, and the test parameters are presented in Table III. The difference in cases 1, 2, and 3 was the quenching coolant flow rate and the applied position. The flow rate applied to the outer flange was identical in all cases, but the rate to the inner flange and web was variable. The sample was macro-etched and then optically measured for microstructure analysis.

Fig. 8

H-beam sample for quenching simulation

Table III Experimental Quenching Setup

Empirical simulations comparing quenched and unquenched were conducted to verify the quenching effect on beam deformation. The first attempt (Case #1) was to cool the outer flange, the lower-inner flange, and the lower web. The second trial (Case #2) was intended to cool the outer flange, the upper-inner flange, and the upper web. The last experiment (Case #3) involved cooling all beam surfaces. Figure 9 shows the temperature measures of the quenching experiments. The TC3 and TC6 profiles indicate that the upper and lower flange have not been quenched in cases #1 and #2 respectively, resulting in a gradual decrease in temperature over time.

Fig. 9

Temperatures measured in quenching experiments

The level of deformation was investigated by measuring the distorted distance at room temperature. The sample was cut to an appropriate size to measure the deformed length in the transverse section. A thermal deformation of case #3, which had identical cooling patterns for the upper and lower half, was barely noticeable. However, the different cooling schemes of cases #1 and #2 resulted in a form "A" and "V" respectively at the end. The A-shaped beam means its flanges are bent inwards, and the V-shaped beam represents the shape of the flanges which are avulsed outwards. According to the expansion pattern in Figure 4, a rapid volume expansion occurs when austenite is converted to martensite with an increase in the cooling rate. An air-cooled surface that was not water-quenched would gradually shrink with a smooth austenite-ferrite phase transition due to a slow cooling rate. The results in Figure 10 explain the effect of the difference in the cooling pattern on material expansion.

Fig. 10

Deformation measured in quenching experiments

The temperature was measured inside the material, but the microstructure was observed on the surface layer. The lowest internal temperature measured was between 500 °C and 600 °C; the surface temperature is expected to be far below 500 °C. Consequently, the martensite, which is generally obtained at a high cooling rate, has been found on the quenched surface. Observation of the microstructure at room temperature revealed that martensite was present on the quenched surface and ferrite-perlite was found on the unquenched surface.

Modeling Results and Discussion

Heat transfer during quenching was calculated using a finite element (FE) program ANSYS. A half-symmetry of an H-beam was modeled similar to the experimental configurations, and the calculation was performed using a 2D symmetry model. In the FE analysis, rectangular elements of 2 × 2mm² were applied evenly throughout the model. The number of elements for an FE calculation was approximately 5000 based on the W24 × 12¾ × 192 beam size. The 2D thermal analysis included both radiation and convection, considering heat dissipation to the vicinity before and after quenching.

Figure 11 shows the temperature distribution, the estimated martensitic microstructure and the deformation obtained by numerical quenching simulation. The heat analysis indicates the lowest surface temperature at the end of the quench. Phase estimates using the cooling rate and temperature show the result of low temperature martensitic transformation. The residual stress was computed using the Von Mises yield criterion, and the deformation was represented along with the color-coded stress distribution. As shown by the structural analysis of cases #1 and #2, the half-beam inclined toward the direction of the water-jet due to the contraction of the cooled surface at first. A sudden change in volume begins with the phase transition when the quenched beam reaches the starting temperature of the austenite-martensite transformation (or austenite-bainite at a low cooling rate). The quenched surface usually begins to expand when austenite falls below the transformation start temperature. The half-beam thus inclined in the opposite direction of the water-jet due to the volume expansion by quenching-induced phase transformation. As the quench is processed, the phase transformation is progressively extended to the remaining area which is not yet quenched. The earlier deformation is consequently restored due to the counter-expansion of the later one over time. Cases #1 and #2 produced A- and V-shaped beams respectively due to inconsistent quenching on the upper and lower portions. The third case that quenched all the surfaces in a balanced way had nearly perfect beam squareness having the flange and the web perpendicular to each other. In conclusion, the computed deformation was well agreed with the experimental findings.

Fig. 11

Thermal, microstructural, and structural analyses in quenching and self-tempering

Expansion due to phase transformation usually results in additional strain hardening,^[24] so subsequent deformation may not guarantee full restoration to the initial position. The QST technique therefore requires a delicate control of the quenching and tempering effect for a perfect beam shape. Case #1 was one of the shape defects commonly observed when applying maximum cooling in beam manufacturing. However, the incidence of squareness defects decreased dramatically when the improved condition of case #3 was applied. The thermal contraction due to non-uniform quenching and the change in the volume corresponding to the phase transformation were important factors determining the deformation behavior. It was confirmed that the deformation behavior could be adjusted depending on the microstructure of the beam surface. These characteristics have been verified through experiments and analyses.

The only difference between the experiment and the calculation was the degree of deformation. The FE analysis resulted in about 2 times less distortion than the experimental observations as shown in Figure 12. Although the analytical approach was less accurate yet, it was significant that distortion due to non-uniform quenching could be predicted quantitatively.

Fig. 12

Comparison of calculations against experiments

Conclusion

QST has been used for several decades, but there are still theoretical uncertainties associated with quantification. The quenching behavior was primarily experimental, so the objective of this study is to use theoretical approaches to quantify the quenching effect. There are still many practices required to improve the precision of mathematical implementations, but one major accomplishment of this study is that QST becomes more predictable in theory.

Laboratory experiments were conducted to determine the cooling deviation and deformation behavior using a user-developed quenching simulator. The quench deformation mechanism was successfully verified with FE analysis which included transformation kinetics, recalescence phenomenon, and transient heat transfer. Optimum quenching conditions will be further investigated to minimize excessive shape defects. Modeling and simulation study will also be pursed and enhanced to predict the exact displacement of quenching deformation. The results of the study are summarized as follows:

• Non-uniform quenching leads to an out-of-squareness defect that makes 'A' or 'V' shaped flange beams.

• H-beam quench deformation is determined by thermal contraction during cooling and volumetric expansion during phase transformation.

• The thermal deformation can be caused by the cooling deviations of the upper and lower flange, and the beam squareness has been improved by uniform quenching.