Introduction

Because of the outstanding properties of TiAl alloys, for instance, their high specific strength, low density, excellent corrosion and creep resistance, as well as good oxidation resistance at higher temperatures,[1,2] researchers regard it as the most promising light material to replace the Ni-based high-temperature alloys partly in the range of 873 K to 1273 K (600 °C to 1000 °C).[3,4] Therefore, TiAl alloys are the materials with the most potential for reciprocating and rotating components used at elevated temperatures, such as aero engine blades, car turbo-charge blades and engine valves.[5,6] Alloying is one of the most effective methods to improve the properties of TiAl alloys but have a higher requirement for melting[7,8] and could result in segregation. Moreover, TiAl alloys can react with the mold during the melting process because of their high activity, which obviously results in decreasing of properties.[9,10,11] Therefore, to satisfy the requirement of alloying and processing of TiAl alloys, a new method for obtaining homogeneous and low-contamination large-scale ingots with a directionally solidified microstructure and superior properties is needed. The directionally solidified gas turbine blades manufactured by the Bridgman process have been widely used in the aeronautical and energy industries.[12] Saari et al.[13] found that the directional solidification technique is a promising manufacturing method for processing TiAl alloys.

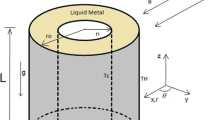
Magnetic fields have been widely used in metallurgical processing to improve the energy efficiency and purity of melt.[14,15,16,17,18] Based on Faraday’s law of electromagnetic induction and Maxwell’s equation, the cold crucible directional solidification (CCDS) technique is an effective and new method for purity and superior properties of TiAl processing.[19,20] The schematic diagram of CCDS is presented in Figure 1. The EMCC is installed in a vacuum cavity connecting the high-frequency current and cold water. Then, a primer and feeding rod with the same composition are put into the EMCC at the appropriate position and connected with the pulling and feeding system, respectively. Increasing the power on coils progressively, the primer will be melted until a steady meniscus is formed. After that, the directionally solidified ingot can continuously grow by turning on the pulling and feeding system. The coils of the EMCC with AC motivate an induction electromagnetic field inside the crucible, as a consequence generating heating energy for melting because of ohmic losses[21] and kinetic energy for stirring as well as the “soft contact” of melt results from the Lorenz force.[22,23] During the directional solidification process, the flow and thermal fields in the melt are the factors most concerned for good surface quality and uniformity of the macro-/microstructure of the directional solidification ingots.[24,25,26,27,28]

Fig. 1
figure 1

Schematic diagram of the cold crucible directional solidification equipment

Full size image

It has been found that the uniformity of the magnetic field significantly influences the DS process by the Joule heat and Lorenz force, especially at the solid/liquid (S/L) interface. For instance, an uneven B distribution at a given height induces a non-uniform EM pressure acting on the melt. A higher EM pressure in turn constrains the liquid meniscus more than lower EM pressure,[29] which further results in a curved S/L interface, and columnar crystal growth is disturbed during the DS process. Bui et al.[30] found that a uniform magnetic distribution could generate uniform temperature distribution. Similarly, a uniform magnetic field is beneficial to a uniform thermal field and solute field in the vicinity of the S/L interface during the CCDS process, which further results in a planar S/L interface and well directionally solidified TiAl alloys. Therefore, investigation of the magnetic field in the charge inside the EMCC is necessary for successful directional solidification of TiAl alloys by the EMCC. So far, there have been many reports on the magnetic flux density distribution in the cold crucible used for melting and continuous casting without a charge,[31,32,33,34,35,36] but infrequent ones on the magnetic flux density distribution in the charge inside the cold crucible for directional solidification.

The aim of this article was to study the magnetic field, temperature field and fluid flow in the charge during directional solidification by the EMCC and to provide a guideline for directionally solidifying TiAl alloys with excellent performance. Because of the poor symmetry of the square crucible for solving Maxwell’s equations, a 3D EMCC model was established to calculate the magnetic field in the charge using the T-Ω finite element method. The distribution and uniformity of magnetic flux density in a charge with different dimensions and positions in the square EMCC, as well as diverse power input parameters, were calculated and analyzed. Based on the calculated results, a selected example of its successful applicability for directionally solidifying the TiAlNb alloy by the square EMCC was experimentally and numerically analyzed.

Mathematical Model Description

3D Model of the EMCC

As shown in Figure 2(a), a square electromagnetic cold crucible with 12 segments and section size of 30 × 30 mm was designed for continuous melting and directional solidifying (DS) TiAl alloys, which was described in the prevision investigation.[37] A cylindrical TiAl charge with a height of h 2 and diameter of d was installed in the crucible; h 1 represented the vertical height of charge from the bottom of the crucible. The 3D model and mesh were generated using ANSYS (distributed by ANSYS HIT), as shown in Figure 2. The magnetic flux density (B) along the red, green and blue lines as shown in Figure 2(b) were calculated, the red line was located at the center of charge, the green line was located at the mid-radial of the charge, and the blue line was located at the wall of the charge, respectively. The physical properties of the materials in the EMCC model are listed in Table I.

Fig. 2
figure 2

(a) Bottomless square EMCC used for directional solidification, (b) 3D FE model and (c) mesh for calculation

Full size image
Table I Material Properties of EMCC for Magnetic Field FEM Analysis
Full size table

The Mathematical Model of the CCDS Process

During the process of CCDS, a bottomless EMCC encircled with coils is used for melting and heating materials, while a longitudinal temperature gradient in the melt is formed because of the intensive cooling by the Ga-In liquid pool at the bottom. Coils with high-frequency alternating current (AC) generate a magnetic field (B) and induce an alternating current (J) in the conductive metals. Due to the skin effect, the B and J are confined to a thin layer, where the induced current causes Joule heat in the metals to melt and overheat, and the interaction of B and J results in the Lorentz force stirring and shaping the liquid metals.[38] The confined meniscus and concentrated Joule heat in skin layer reduces and compensates the heat loss to the cold wall, which makes it possible to eliminate the radial thermal gradient during directional solidification.

Following consideration of the methods applicable to 3D eddy current problems, the combined electric vector potential (T) and scalar magnetic potential (Ω) approach, commonly known as the “T-Ω method,” was selected for development. The basis of the method was originally described by Carpenter et al..[39] It has been found to be a robust and efficient method, which generally gives a better ICCG performance than H-φ.[40]

In eddy current problems, neglecting the electric charge and displacement current, the steady-state time harmonic electromagnetic field is governed by Maxwell’s equations:

$$ \nabla \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H} = - \nabla \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H}_{\text{C}} $$
(1)
$$ \nabla \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} = 0 $$
(2)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} = \mu \cdot \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H}_{\text{C}} } \right) $$
(3)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {T} + \nabla \varOmega $$
(4)
$$ \nabla \times \left( {\frac{1}{\sigma }\nabla \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {T} } \right) + \frac{d}{dt}\left( {\mu \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {T} + \mu \nabla \varOmega } \right) = 0 $$
(5)
$$ \nabla \left( {\mu \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {T} + \mu \nabla \varOmega } \right) = - \nabla $$
(6)
$$ \nabla \cdot \mu \nabla \varOmega = - \nabla \cdot \left( {\mu \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H}_{\text{C}} } \right) $$
(7)

where \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H} \) is the magnetic field intensity, \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H}_{\text{C}} \) is the magnetic field intensity produced by an imaginary monopole, \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} \) is the magnetic flux density, \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {T} \) is the electric vector potential, Ω is the scalar magnetic potential, σ is the electric conductivity, and μ is the magnetic permeability.[41]

$$ \nabla \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} = - \frac{{\partial {\mathop{B}\limits^{\rightharpoonup}}}}{\partial t} $$
(8)
$$ \nabla \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} = \mu \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {J} $$
(9)

When the conducting melt flows with velocity \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v} \), the current density \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {J} \) can be expressed as:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {J} = \sigma \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} } \right) $$
(10)

Therefore, the governing equation of magnetic flux density \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} \) is:

$$ \frac{{\partial {\mathop{B}\limits^{\rightharpoonup}}}}{\partial t} = \lambda \nabla^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} + \nabla \times \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} } \right) $$
(11)

where \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} \) is the electric field intensity, \( \lambda = \frac{1}{\sigma \mu } \) is the diffusion coefficient of the magnetic field, the first term on the right side represents the diffusion term of \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} \), and the second term on the right side represents the convection term. Generally, the diffusion term is much bigger than the convection term in the liquid metal. Therefore, the governing equation of \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} \) and \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {J} \) can be simplified as:

$$\frac{{\partial {\mathop{B}\limits^{\rightharpoonup}}}}{\partial t} = \lambda \nabla^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} $$
(12)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {J} = \sigma \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {E} $$
(13)

The electromagnetic heat source Q caused by the eddy currents can be expressed as:

$$ Q = \frac{{J^{2} }}{\sigma } $$
(14)

In addition, the Lorentz force \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{EM} \) can be calculated as follows:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{EM} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {J} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} $$
(15)

The electromagnetic force of Eq. [15] is very important for conducting the melt convection in the crucible and therefore can be discussed more in detail. Equation [15] can be written using Ampere’s law:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{EM} = \frac{1}{\mu }\left( {\nabla \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} } \right) \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} $$
(16)

This can be decomposed into a pressure term \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{p} \) and a driving part \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{d} \):

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{EM} = - \nabla \left( {\frac{{\mathop{B}\limits^{\rightharpoonup}}^{2} }{2\mu }} \right) + \frac{1}{\mu }\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} \cdot \nabla } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{p} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{d} $$
(17)

\( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{p} \) represents the electromagnetic pressure gradient, the driving (rotational) part \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{d} \) caused by non-uniform of current density along radial direction, which drives fluid motion from regions of low magnetic pressure to regions of high pressure. It was reported that the flow driving by the electromagnetic force in melt is turbulent, which is a benefit for transporting induction heat and makes the solute more homogenized.

The induction heating process before melting in the EMCC can be described by a classical transient heat transfer equation as follows:

$$ \rho C_{p} \frac{\partial T}{\partial t} = \nabla \left( {k\nabla T} \right) + Q $$
(18)

where \( \rho \) is the density of TiAl alloys, C p is the specific heat of TiAl alloys, k is the thermal conductivity, T is the temperature, and t is the time. The directional solidification process in EMCC combines the fluid dynamics and the induction heating. The melting TiAl melt flow is assumed to be turbulent, and the flow can be considered incompressible. The mathematical basis of the present model is the continuity equation for the conservation of mass, the time-dependent Navier-Stokes equations for the conservation of momentum and the thermal energy equation for the conservation of heat. The solved Lorenz force field and Joule heat field were incorporated as the momentum source term and energy source term in the CFD calculations, respectively.[42,43]

Continuity equation:

$$ \nabla \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v} = 0 $$
(19)

Momentum equation:

$$ \frac{{\partial{\rho{\mathop{v}\limits^{\rightharpoonup}}}}}{\partial t} + \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v} \cdot \nabla } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v} = \mu_{v} \nabla^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v} - \nabla p + \rho \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} \beta_{\text{T}} \Delta T + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {F}_{\text{EM}} $$
(20)

Energy equation:

$$ \rho C_{p} \left( {\frac{\partial T}{\partial t} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v} \cdot \nabla T} \right) = \nabla \left( {k\nabla T} \right) + Q $$
(21)

where μ v is the viscosity, p is the pressure, g is the gravitational acceleration, and β T is the thermal expansion coefficient.

Boundary Conditions

Eddy current problems:

The eddy current problem consists of a vortex region and a non-eddy region. A boundary condition gives the normal flux density ΓB:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} = 0 $$
(22)

A boundary condition gives the tangential magnetic field strength ΓH:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n} = 0 $$
(23)

The boundary between the vortex and non-vortex regions Γ12 is:

$$ \left\{ \begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B}_{1} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n}_{1} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {B}_{2} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n}_{2} = 0 \hfill \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H}_{1} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n}_{1} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {H}_{2} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {n}_{2} = 0 \hfill \\ \end{aligned} \right. $$
(24)

Thermal radiation and heat flux to the Ga-In liquid:Heat is lost from the top and bottom of the ingot via radiation and heat flux, respectively. The radiative heat transfer may be described by the Stefan-Boltzmann relationship as in Eq. [25]:

$$ q_{\text{rad}} = \varepsilon \sigma_{\text{rad}} \left( {T^{4} - T_{\text{ref}}^{4} } \right) $$
(25)

where ε denotes the emissivity, σ rad is the Stefan-Boltzmann constant, T ref is the reference temperature for radiation, and T is the free surface temperature. Heat loss from the bottom of the meniscus to the Ga-In liquid can be expressed as:

$$ q_{\text{hf}} = h_{\text{w}} (T_{\text{w}} - T_{\text{c}} ) $$
(26)

where h w denotes the coefficient of thermal conductivity, T w is the average temperature of meniscus, and T c is temperature of Ga-In liquid.

There are two types of fluid boundaries used to simplify the mathematical models: a smooth solid wall of the crucible and a free surface of the fluid. No fluid may pass through the wall, and therefore the velocity component normal to the boundary must be equal to the velocity of the wall:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v} \cdot n = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}_{s} \cdot n $$
(27)

where \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}_{s} \) is the velocity of the wall and n is the surface normal vector. The tangential velocity component on the wall must be zero (no-slip boundary condition). The fluid next to the boundary, which allows the existence of the tangential velocity component, can be described as:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v} \times n = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}_{s} \times n $$
(28)

Solution Procedure

The computational domain was discretized using tetrahedron and hexahedron elements, and there were 326,508 elements in the whole domain for solving the electromagnetic field by ANSYS (distributed by ANSYS HIT) and 981,114 elements in the meniscus domain for solving the flow field using Fluent. The electromagnetic field was first solved by using the finite element method, and then the Lorenz force and induction heat were transferred into fluid dynamics differential equations via the source term and solved using the finite volume method. A standard k-ε two-equation model was used to solve the turbulent flow; for each simulation, convergence to steady state was usually accomplished in 2000 iterations, and 5 hours was required on a single EV5 processor of a Dell T7810 workstation.

Results and Discussion

Calculated Results and Experimental Verification

It is difficult to measure the magnetic flux density in the charge; consequently, the magnetic field in the EMCC with no-load was experimentally and numerically investigated to test the validity of the 3D model. The experimental and calculated results at the center of the crucible along the symmetry axis are shown in Figure 3(a). The specific measurement method of magnetic flux density is described in Reference 44. Assuming that the magnetic flux density along axial (B z ) is uniform within the sensor coil, based on Faraday’s law of electromagnetic induction, the magnetic flux density can be described as follows:

$$ B_{z} = \frac{E}{4.44NfS} $$
(29)

where B z is the magnetic flux density in the axial direction, E is the induced electromotive force, f is the frequency of AC, N is the turns of the coils, and S is the cross-sectional area of the coils.

Fig. 3
figure 3

Verification of the magnetic field and temperature field: (a) B z at the center of the crucible; (b) temperature at the center of the TiAl charge during the induction heating process

Full size image

When the effective input power on coils is 1.8 kW with current frequency of 30 kHz, the measured and calculated B z at the center of the crucible is shown in Figure 3. It can be observed that although there is a difference between the calculated and measured results, the distribution of B z is similar, and the values are almost equal in the induction coil zone. Due to a limitation of the device, the magnetic flux density under the coils is not measured, but these could be ignored because of the small effect on the induction heating beyond the coil region. The measured and calculated temperature with an input power of 3 kW is shown in Figure 3(b); it indicates that the calculated time to reach steady state and temperature at steady state agrees well with the experimental measurements.

Calculated Magnetic Field in the Charge Inside the EMCC

The magnetic field distribution in the EMCC used for directional solidification with no load has been reported previously. However, when a charge was fixed in the crucible, based on Faraday’s law of electromagnetic induction and Maxwell’s equation, the induced current with an opposite direction to that in the coils will be generated in the charge, as shown in Figure 4(a).

Fig. 4
figure 4

Distribution of (a) the current density vector at the cross section; (b) magnetic flux density vector at the longitudinal section of the charge

Full size image

The induced current decreases from the wall to the center of the charge because of the skin effect and generates a weakened magnetic field in the charge but an enhanced magnetic field between the charge and crucible wall. Therefore, the magnetic flux density (B) decreases in the charge and increases out of the charge. Figure 4(b) shows the orientation of B in the charge; it parallels the surface at the wall of the charge and deflects at the bottom and top, and the deflection increases with increasing distance from the wall. Taking the charge as an ideal conductor, consequently, the magnetic flux density will jump according to the distinction of the electromagnetic parameters at the interface of the air and charge.

The electromagnetic boundary conditions result in a changed orientation of B at the interface of two distinguished electromagnetic media. The time-varying magnetic field must be tangential to the interface and only exists there. Nevertheless, as to the practice conductor, a magnetic field will be generated in the charge’s interface with a finite distance because of the skin effect. The orientation of B tends to be tangential to the interface where it is located; however, it deflects near two intersecting interfaces as a superposition. Because of the weakened magnetic force generated in the charge, the intensity of B decreases from wall to center. Therefore, if the diameter of the charge is big enough, there must has a position where the magnetic flux density will recede to zero. Beyond this position, there will be an opposite magnetic field in the charge.

Because of the non-uniform magnetic field in the crucible and the skin effect in the charge discussed above, the magnetic field in the charge is complicated and non-uniform. Figure 5 shows the magnetic flux density contours inside the charge. It indicates that the magnetic field in the charge is inhomogeneous along the axial direction because of the non-uniformity of the magnetic field in the axial line of the crucible. Therefore, the relative position of the charge in the EMCC will result in different intensities of the B in the charge. Along the radial direction, the B increases from the center to the wall of the charge because of the increasing of the B from the symmetry axis to crucible wall. Therefore, the maximum B appears at the wall of the charge and increases with increasing of the charge diameter.

Fig. 5
figure 5

Magnetic flux density contours inside the charge: (a) 3D view; (b) top view; (c) side view

Full size image

Due to the slits in the EMCC wall, the distribution of B along the circumferential direction is also non-uniform. The B is stronger close to the slits and decreases far from it, and it increases with extension of the slit width.[33] The non-uniformity is owing to the superposition of the magnetic flux density induced by the opposite eddy currents at two sides of the slits and the current in coils.[45] In conclusion, the dimensions and positions of the charge affect the uniformity and distribution of magnetic field in it, which will result in inhomogeneous induction heat and electromagnetic force during the melting and directional solidification of the TiAl alloys.[30] The uniformity of the magnetic field in a given domain can be quantitatively analyzed by statistical methods,[36] and it is expressed as:

$$ u = \frac{1}{{\bar{B}}}\sqrt {\frac{{\sum\nolimits_{i = 1}^{n} {\left( {B_{i} - \bar{B}} \right)^{2} } }}{n}} $$
(30)

Equation [30] reflects the deviation of the magnetic flux density from the mean value. A smaller value of u yields a more uniform magnetic field in the analyzed domain.

Magnetic Field Distribution in the Charge Under Different Currents

A TiAl ingot (h 1 = 32 mm, h 2 = 21 mm and d = 20 mm) was installed in the crucible, and the B in it was calculated under different currents. The calculated results are shown in Figure 6. The calculated results indicate that the B in the charge increases with increasing current intensity. Jiang and Zhu[46,47] proved that the billet center segregation declines continuously as the current intensity increases in the continuous billet casting process with final electromagnetic stirring. However, the B has different distribution characteristics at each position. As presented in Figure 6(a), the B at the center of the charge decreases with increasing of the height near the bottom of the charge; after it reaches the minimum then increases continually to the maximum at half of the charge, the distribution of B in the upper part is symmetrical with the lower part.

Fig. 6
figure 6

Distribution of B in the charge under different currents: (a) at the center of the charge; (b) at the midpoint in the radial of the charge; (c) at the wall of the charge; (d) the uniformity of B in the charge

Full size image

Due to the skin effect in the bottom and top of the charge, the B at the midpoint in the radial of the charge decreases from both sides to the middle of the charge, as shown in Figure 6(b). The distribution of B along the wall of the charge is presented in Figure 6(c). It increases continuously until it decreases a little near the top of the charge. This is the reason for the non-uniform B along the axial line and the superposition of the magnetic field close to the wall and top of the charge. The curve of “E500A” represents the B in the EMCC without the charge. Compared with the magnetic flux density in the empty crucible, the intensity of B in the charge is smaller than that in the empty EMCC.

The uniformity of B in the TiAl charge along the axial, circumferential and radial directions was calculated under different currents, and the results are shown in Figure 6(d). It indicates that the uniformity of B along the radial direction is the worst as a consequence of the skin effect, and the change in the currents has no influence on the uniformity of B in the charge.

Magnetic Field Distribution in the Charge Under Different Frequencies

The distribution of B in the charge will be significantly affected by the frequency of the current as a consequence of the skin effect. A TiAl ingot (h 1 = 32 mm, h 2 = 21 mm and d = 20 mm) was installed in the EMCC, and the B in the charge was calculated under different current frequencies. The calculated results are shown in Figure 7.

Fig. 7
figure 7

Distribution of B in the charge under different current frequencies: (a) at the center of the charge; (b) at the midpoint in the radial of the charge; (c) at the wall of the charge; (d) the uniformity of B in the charge

Full size image

The skin layer thickness in the charge decreased with an increase of the current frequency. Figure 7(a) shows the B at the center of the charge; it indicates that the B increases with increasing frequency at low values because of the change of the skin depth. Gross et al.[48] proved that when the skin depth equals half of the charge radius, only a small percentage of the overall power is lost in the copper coil and crucible. As the frequency increases further, the intensive skin effect restrains the diffusion of the magnetic field into the charge, which leads to a decrease of B at the center of the charge as discussed above in Section III–C.

Because of the decreasing of the skin layer thickness with increasing frequency, the intensity of B decreases at half of the radius but increases at the side wall,[49] as shown in Figures 7(b) and (c), which is the inverse of B decreasing with an increase of frequency in the empty EMCC.[34,35] When a charge was placed in the EMCC, the oscillating magnetic field generated in the crucible diffused through the charge according to Eq. [12]. The curve of “E30 kHz” represents the B in the EMCC without a charge. Compared with the magnetic flux density in the empty crucible, the intensity of B in the charge is smaller than that in the empty EMCC.

The magnetic field is periodically injected into, and extracted from, the conductor. As successive waves of the positive and negative magnetic field difference diffuse inward from the boundary, there is a tendency for them to overlap and cancel. In the limit of a high angular frequency, the field will only penetrate a finite distance into the charge, so a thinner skin layer will have a higher B in it. Figure 7(d) shows that the uniformity of B in the charge decreases with increasing frequency because of the skin effect.

Magnetic Field Distribution in the Charge with Different Diameters

The magnetic field distributions in charges (h 1 = 32 mm, h 2 = 21 mm) with different diameters are shown in Figure 8. The charge diameter in the EMCC will affect the magnetic field in it for two reasons: first, a certain current frequency generates a constant skin layer thickness. As a consequence, the relative size between the charge and skin layer changed with changing of the charge’s dimensions, leading to a heterogeneous magnetic field as discussed in Section III–D. On the other hand, because of the inhomogeneous magnetic field along the radial and circumferential direction in the empty EMCC, the intensity of B is stronger at the crucible wall, especially the slits more than other positions, which will result in a non-uniform magnetic field in charges with different diameters. As shown in Figure 8(a), the intensity of B at the wall of the TiAl charge increased with an increase of the charge’s diameter, which results in a higher energy efficiency.[50] The uniformity of B with different charge diameters is presented in Figure 8(b), which shows that with increasing diameters the uniformity becomes worse.

Fig. 8
figure 8

Distribution of B in charges with different diameters: (a) at the wall of TiAl charge; (b) the uniformity of B in the charge

Full size image

Magnetic Field Distribution in The charge with Different Heights and Positions in the EMCC

As discussed above, the intensity of B is non-uniform along the axial direction in the empty EMCC and could affect the magnetic field in the charge. Therefore, the B in charges with different heights and positions in the EMCC was calculated under I = 500 A, f = 30 kHz, and the results are shown in Figure 9.

Fig. 9
figure 9

Distribution of B in charges (a) at different positions in the EMCC; (b) charges with different heights

Full size image

As shown in Figure 9(a), when the charges are fixed under different positions in the EMCC, the intensity of B in the charge is in proportion to B in the EMCC, except the region close to the top of the charge, because of the superposition of the magnetic field in the charge and the non-uniform magnetic field in the EMCC. With increasing height of the charge in the EMCC, the maximum B increases first; it reaches the peak value of 26.38 mT when h 1 = 36 mm at the height of the middle of coils (h c = 53 mm) in the EMCC.

Figure 9(b) shows that the B increases along the axial direction from the bottom of the charge first, after it reaches the maximum and then decreases as the distribution of B in the EMCC. Moreover, with increasing charge height, the location of the maximum point increases first and then decreases. On the one hand, B is in proportion to the intensity of B at the same position in the EMCC. On the other hand, the superposition of B due to the skin effect at both ends and the wall of the charge is also important. When the height of the charge is less than 26 mm, the first reason plays a leading role, and then both of them play a significant role as the height is more than 26 mm. With an increase of charge height, the maximum of B increases first, reaches a peak value of 26.2 mT when h 2 = 26 mm at h c = 53 mm in the EMCC and then decreases as the superposition effect is weaker there. Therefore, the maximum of B in the charge can be obtained at the height of the middle of the coils when the relationship \( h_{\text{c}} < h_{2} + h_{1} < h_{\text{c}} + \delta \) is satisfied, which is caused by the superposition of the magnetic field in the skin layer and the maximum B in the EMCC.

Melting and Directional Solidification of TiAlNb Alloys in the Square EMCC

During the process of induction melting of the TiAlNb alloy in the square EMCC, the induction heating rate per unit surface can be expressed as[51]:

$$ \dot{q} = \left( {{{B_{h}^{2} } \mathord{\left/ {\vphantom {{B_{h}^{2} } {4\mu }}} \right. \kern-0pt} {4\mu }}} \right)\omega \delta $$
(31)

here B h is the surface magnetic flux density at different heights of the ingot, μ is the permeability of the TiAlNb alloy, \( \omega \) is the angle frequency, and \( \delta \) is the thickness of the skin layer. According to the Eq. [31], the higher magnetic flux density and frequency benefit from induction heating. Therefore, the TiAlNb primer with h 1 = 36 mm, h 2 = 21 mm and d = 20 mm was placed in the EMCC (h c = 54 mm) for directional solidification. Figure 10(a) shows the calculated temperature field in the half meridian plane of the primer and the magnetic flux density at the edge of the primer. It indicates that the B increases from the bottom to the upper position and reaches the maximum at h c, where the melting temperature will first be reached. Therefore, the TiAlNb primer edge will first melt, as shown in Figure 10(b), as Yang et al.[37] reported.

Fig. 10
figure 10

Induction melting of TiAlNb alloy in the square EMCC under power of 15 kW (a) calculated temperature field and B at the edge of ingot; (b) induction melting image

Full size image

Based on the calculated results above, the TiAlNb alloy was successfully melted with lower power consumption of 15 kW in the 30 × 30 mm square EMCC under optimized operating parameters. Subsequently, the molten TiAlNb alloys were constrained and stirred with increasing coil current. At steady state of directional solidification, the S/L interface gradually moves forward with heat and mass transfer in the meniscus. The physical properties of molten TiAlNb alloys and operating conditions of directional solidification in the square EMCC are listed in Table II. A relatively low frequency of the current was chosen, not only satisfying the requirement of induction heating but also improving the uniformity of the magnetic field in the charge.

Table II Physical Properties of Molten TiAlNb Alloys and Operating Conditions in this Work[52]
Full size table

At steady state (neglecting the influence of pulling velocity) of the directional solidification of TiAl alloys in the square EMCC, the complex physical phenomenon in the molten pool due to the high frequency current is shown in Figure 11. The mean flow driven by the high frequency electromagnetic field (shown in Figure 11(a)) and the turbulence kinetic energy in the meniscus are shown in Figure 11(b). It shows that there are two mean eddies in the half meridian plane of the meniscus, and the maximum velocity appears near the surface of the meniscus at the upper eddies. The oscillations of convection between the upper and lower eddies promote the homogenization of mass and heat in the axial, where the maximum turbulence kinetic energy exists. Because of the uniform fluid flow induced by a uniform magnetic field, smaller flowing velocity and turbulence kinetic energy in the vicinity of the S/L interface led to stabilized conditions for the continuous growth of the columnar crystal with a homogeneous microstructure.

Fig. 11
figure 11

Directional solidification of TiAl alloys in the square EMCC at steady state: (a) magnetic field intensity distribution in the meniscus; (b) turbulence kinetic energy contours and streamlines of the flow field in the meniscus; (c) temperature field contours in the meniscus

Full size image

The calculated temperature fields in the meniscus with electromagnetic stirring are shown in Figure 11(c). Under the influence of electromagnetic stirring, the joule heat generated in the skin layer was continuously transported to the bulk of the meniscus. At the surface of the meniscus, the average temperature is smaller than in the bulk of the melt because of the extensive radiative and convective heat loss there. The two mean flows in the half median plane result in two high temperature regions in the upper and lower area of the half median plane. The high-temperature region in the vicinity of the S/L interface is important for the unidirectional crystal growth as it determines the temperature gradient and the temperature fluctuation in front of the S/L interface. In the present case, the temperature field in the vicinity of the S/L interface is uniform, especially in the interior region of the meniscus, which results in well paralleled and continuous crystal growth. However, the inclined temperature gradient will be formed near the surface of the meniscus because of the lower temperature there, which leads to an inclined columnar crystal.

As the current frequency strongly affects the uniformity of the magnetic field in the charge, the influence of the uniformity of the magnetic field on the flow field and temperature field in the melt was calculated under different frequencies. The calculation parameters, results of temperature uniformity and maximum turbulence kinetic energy in the vicinity of the S/L interface are shown in Table III. The temperature uniformity can be expressed as:

$$ u_{T} = \frac{1}{{\bar{T}}}\sqrt {\frac{{\sum\nolimits_{i = 1}^{n} {\left( {T_{i} - \bar{T}} \right)^{2} } }}{n}} $$
(32)
Table III Comparison of Temperature Uniformity (uT) and the Maximum Turbulence Kinetic Energy (kmax) in the Vicinity of the S/L Interface Under Different Frequencies
Full size table

Equation [32] reflects the deviation of the temperature from the mean value. A smaller value of u T yields a more uniform temperature field in the vicinity of the S/L interface. The results in Table III indicate that improving the uniformity of the magnetic field could weaken the turbulence and improve the temperature uniformity in the vicinity of the S/L interface, which is beneficial to forming the planar S/L interface and continuous columnar grains during directional solidification.

The as-cast TiAlNb alloy was directionally solidified by the square EMCC under the different currents (50 kHz) and pulling velocity of 1 mm/min at steady state. The specific experimental process was described in Reference 53, and the macro-/microstructure is shown in Figure 12. The as-cast TiAlNb alloy exhibits equiaxed grains as shown in Figure 12(a), and it can be clearly seen that the macro-/microstructure of the TiAlNb alloys changed from equiaxed grains to columnar grains after being processed by the EMCC as presented in Figure 12(b). The DS macrostructure shown in Figure 12(b) can be divided into three regions from the top down: the mushy layer, stable DS region and initial solidification region. A near planar S/L interface was formed during the DS process, except a slight deflection that appears close to the cold wall. The microstructure of the TiAlNb ingot was homogeneous and exhibited typical β-solidification characteristics, since the secondary dendritic arms were perpendicular to the primary dendritic arms.[54] In the stable DS region, the columnar crystals are continuous and parallel to the pulling direction in the interior region, while some inclined columnar crystals appear at the periphery of the ingot. However, the continuously growing columnar crystals were blocked, and the columnar to equiaxed transition (CET) ahead of the stable DS region occurred with a current of 140 A, as shown Figure 12(c). In our case, the higher current used in Figure 12(c) could induce a stronger magnetic field as discussed above, which drives the intensive melt flow in the bulk of the melt. Dong et al.[55] reported that the intensive electromagnetic stirring drives the fusing of the columnar grains during the directional solidification process, therefore leading to the CET.

Fig. 12
figure 12

Macro-/microstructure of the TiAlNb ingot (a) as cast; (b) directionally solidified by the square EMCC with the current of 125 A; (c) directionally solidified by the square EMCC with the current of 140 A

Full size image

Conclusions

A 3D EMCC model was established and verified to calculate the magnetic flux density in the charge inside a square EMCC designed for directional solidification. The distribution and uniformity of B in the charge under different electrical parameters, positions and dimensions of the charge were numerically evaluated using the T-Ω finite element method. Based on the calculated results, a TiAlNb alloy was selected to melting and directionally solidifying using the square EMCC under optimized operating parameters. The temperature field and fluid flow induced by the magnetic field were calculated during the melting and directionally solidifying process. In the light of the present investigations and analyses, the following conclusions can be drawn:

  1. 1.

    Due to the skin effect of the high frequency electromagnetic field in the EMCC, the magnetic field concentrates in the skin layer of the charge and the intensity of B is augmented with increasing frequency, charge diameter and current.

  2. 2.

    The maximum B in the charge is affected by the position of the charge in the EMCC (h 1) and charge height (h 2). It can be obtained at the middle of the coils (h c) when the relationship of h c < h 1 + h 2 < h c + δ is satisfied, which results in lower power consumption during induction melting of TiAl alloys by the EMCC.

  3. 3.

    Relatively lower frequency and smaller charge diameter can improve the uniformity of the magnetic field in the charge. Further, the induced uniform electromagnetic stirring weakens the turbulence and improves the temperature uniformity in the vicinity of the S/L interface.

  4. 4.

    Based on the calculated results above, the TiAlNb alloy was fixed at the optimized position and successfully melted in the square EMCC with lower power consumption of 15 kW. Finally, it was directionally solidified with a planar S/L interface and continuous columnar grains because of the stabilized flow and uniform temperature in the vicinity of the S/L interface.