Introduction

Integrated steel plants have always been challenged with newer ideas to develop high-quality steels. In such cases, these ideas are bound to include the use of secondary steelmaking processes such as VOD and Ruhrstahl–Heraeus (RH) degasser. These processes are also considered to be more efficient and reliable currently. Several such processes are studied by developing a cold model on the basis of similarity principles. The RH vacuum recirculation degasser is one of the most widely used vacuum decarburization units. It is used to treat molten steel for decarburization in order to lower the carbon content and also for deoxidation, desulfurization, H and N removal, or alloy additions. Modeling studies pave the way to show the effects of operational parameters (RH vacuum pressure, lift gas flow rate, O2 blowing rate, O2 blowing time, and dimensions of the RH apparatus) on the dynamics of reactions occurring in the RH process and the evolution of the bulk composition with time. Several mathematical and physical modeling studies have been done to understand the RH degassing process. Van Ende et al.[1] studied the RH process with the help of a numerical model where the effective reaction equilibrium zones were considered to evaluate the decarburization profile. One of the finest mathematical modeling studies on the RH was done by Kuwabara et al.,[2] where the decarburization profile was obtained by the concept of reaction zones and considering the conditions for CO formation, i.e., static and evolution pressure of the CO gas bubbles. An effort has also been made to understand the effect of oval-shaped snorkels on the circulation rate of steel as well as the application of argon gas blowing from the bottom of the vessel. However, in order to study the effects of different operational and nonoperational parameters on the RH degasser, cold modeling studies have proven to be very helpful. Seshadri and De Souza Costa[3] and Seshadri et al.[4] developed a physical model to understand the effect of three different liquid levels in the vessel on the circulation rate and then developing relationships between the nondimensional parameters. Based on that, relations were obtained between the nondimensional parameters. Li et al.[5] developed an empirical relation between the circulation rate of the liquid and the different parameters such as nozzle diameters, snorkel diameters, the lift gas flow rate, and the injection depth. Lin et al.[6] also studied the RH process by developing a cold model and recording the effects of different parameters such as submerged depth, nozzle diameters, bubble travel, and nozzle blockage. They performed a regression analysis to determine a relation between the circulation rate and these variables. The current study will focus on the effect of submerged depth for different lift gas flow rates as well as validation of these studies with the help of a current conductivity experiment. The circulation rate of the liquid water in the cold model is calculated from the velocity of water at the down snorkel. Sonin[7] explained the dimensional analysis in which the relationship between nondimensional parameters for a physical model as well as the industrial unit can be achieved with the help of the Buckingham π theorem. The same is used by Seshadri and De Souza Costa[3] to develop a relationship for the RH degasser, as follows:

$$ \frac{{v^{2} }}{gd} = C\left( {\frac{d\rho v}{\mu }} \right)^{x} \left( {\frac{G}{{d^{2} v}}} \right)^{y} $$
(1)
$$ Fr = C*{Re}^{x} *{{V}}_{\text{a}}^{y} $$
(2)

where Fr, Re, and V a are the dimensionless numbers. Per the similarity principles concerned, these numbers do not change for either the industrial unit or the model. The development of the cold model studied on the basis of earlier works.[8–10]

Physical Model

Design Parameters of the Physical Model

The physical model was already applied at IEHK, RWTH-Aachen, by Rakotobe et al.[11] on the basis of an arbitrary scale factor of 1:3 for a 160- to 170-ton RH vessel. Table I shows the design parameters of the cold model. Equation [1] is derived on the basis of the Buckingham \( \pi \) theorem. The operational parameters, which are discussed in Section II–B, are set up with the help of Eq. [1].

Table I Dimensional Parameters of the Physical Model
Full size table

Operational Parameters of the Physical Model

Equation [1] involves three nondimensional parameters, as follows:

$$ Fr = \frac{{v^{2} }}{gd} $$
(3)
$$ \text{Re} = \frac{d\rho v}{\mu } $$
(4)
$$ V_{\text{a}} = \frac{G}{{d^{2} v}} $$
(5)

These three numbers are, respectively, the Froude number (Fr), the Reynolds number (Re), and the ratio of the lift gas flow rate to the circulation rate of liquid (V a). Now the lift gas flow rate to be used for the physical model is obtained from the similarity; i.e., these three numbers remain the same for the model and the industrial unit.

The following equations are obtained on the basis of similarity:

$$ \frac{{v_{\text{p}}^{2} }}{{gd_{\text{p}} }} = \frac{{v_{\text{m}}^{2} }}{{gd_{\text{m}} }} $$
(6)
$$ \frac{{v_{\text{m}} }}{{v_{\text{p}} }} = \sqrt {\frac{{d_{\text{m}} }}{{d_{\text{p}} }}} $$
(7)
$$ \frac{{G_{\text{p}} }}{{d_{\text{p}}^{2} v_{\text{p}} }} = \frac{{G_{\text{m}} }}{{d_{\text{m}}^{2} v_{\text{m}} }} $$
(8)
$$ G_{\text{m}} = \frac{{d_{\text{m}}^{2} v_{\text{m}} G_{\text{p}} }}{{d_{\text{p}}^{2} v_{\text{p}} }} $$
(9)

Using Eqs. [7] and [9], a relationship can be derived for the lift gas flow rates between the model and the industrial unit. The lift gas flow rate for the industrial unit\( \left( {G_{\text{p}} } \right) \) is injected at room temperature but undergoes expansion when it attains the metal temperature. If we simply calculate the lift gas flow rate to be applied to the model, the following relation is derived:

$$ G_{\text{m}} = 0.06415*G_{\text{p}} $$
(10)

Table II shows the operational parameters of the cold model. The lift gas flow rate to be applied to the cold model on the basis of Eq. [10] with a consideration of bubble expansion is found to be between 10 and 40 NL/min. The lift gas used here is nitrogen. Seshadri and De Souza Costa[3] used a modified Froude number to evaluate the orifice diameter (f), which is commonly used for fluid in submerged gas injection.

Table II Operational Parameters of the Cold Model
Full size table
$$ Fr^{\prime} = \frac{{u^{2} \rho_{\text{g}} }}{{gf\rho_{\text{l}} }} $$
(11)
$$ G_{\text{p}} = u_{\text{p}} f_{\text{p}}^{2} $$
(12)
$$ G_{\text{m}} = u_{\text{m}} f_{\text{m}}^{2} $$
(13)

On comparison of the industrial unit and physical model, by taking into consideration the densities of water, steel, nitrogen, and argon gases and with Eqs. [10] through [13], the ratio of orifice diameters of the industrial unit to those of the model is obtained. This ratio is approximately equal to unity:

$$ \frac{{u_{\text{p}}^{2} \rho_{{{\text{g}}_{\text{p}} }} }}{{gf_{\text{p}} \rho_{{{\text{l}}_{\text{p}} }} }} = \frac{{u_{\text{m}}^{2} \rho_{{{\text{g}}_{\text{m}} }} }}{{gf_{\text{m}} \rho_{{{\text{l}}_{\text{m}} }} }} $$
(14)
$$ \frac{{f_{\text{p}} }}{{f_{\text{m}} }} \approx 1 $$
(15)

So the inner orifice diameter is taken to be the same as that of the industrial unit, i.e., 3 mm.

Circulation Rate Measurement

The circulation rate is defined here as the amount of liquid or water (in this case) that passes through a plane perpendicular to the flow of water in the down snorkel per unit of time. Generally, it is measured in L/min, m3/min, or tons/h. Different methods are used to measure the circulation rate of the liquid. Li et al.[5] used a velocity instrument, Seshadri and De Souza Costa[3] and Seshadri et al.[4] used a conductivity experiment, and Lin et al.[6] used an ultrasonic wave flow meter. The method used here, in order to measure the circulation rate, is measuring the velocity of the water flowing downward in the down snorkel. According to Bernoulli’s principle, a pressure change exists due to the downward flow of the water in the down leg. The velocity of the water through the down leg is calculated, and in turn, the volumetric flow of water is determined by knowing the circumferential area of the down leg. The velocity of water flow in the down leg is measured from the pressure drop achieved at the bottom of the down leg. A tube with a digital barometer connected at its bottom is used in order to measure the pressure drop. This tube is a simpler version of the pitot tubes used in aircrafts. By applying Bernoulli’s principle (difference in height does not have a large effect),

$$ \frac{1}{2}\rho_{{{\text{l}}_{\text{m}} }}{ v^{\prime }}^{2} + p^{\prime } = {\text{constant}} $$
(16)

If we assume the velocity of water flow in the down leg as v′1 and the velocity at the top of the up leg as v′2, then by the application of Bernoulli’s principle at these two points, we obtain

$$ \frac{1}{2}\rho_{{{\text{l}}_{\text{m}} }} {v_{2}^{\prime }}^{2} + p_{2}^{\prime } = \frac{1}{2}\rho_{{{\text{l}}_{\text{m}} }} {v_{1}^{\prime}}^{2} + p_{1}^{\prime } $$
(17)
$$ {v_{2}^{\prime }}^{2} - {v_{1}^{\prime }}^{2} = 2\frac{{\left( {p_{1}^{\prime } - p_{2}^{\prime } } \right)}}{{\rho_{{{\text{l}}_{\text{m}} }} }} $$
(18)
$$ \bar{v}^{\prime} = \sqrt {2\frac{{\Delta p^{\prime}}}{{\rho_{{{\text{l}}_{\text{m}} }} }}} $$
(19)

This change of pressure \( \Delta p^{\prime} \) is measured by the digital barometer. When \( \bar{v}^{\prime} \) is plotted against \( \Delta p^{\prime} \), we obtain a parabola that increases with decreasing rate. So, if we measure the change in pressure \( \Delta p^{\prime} \), we can obtain the velocity of water in the down leg and also the circulation rate of water.

Experimental Procedure

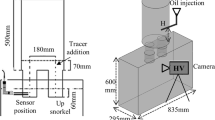
The experimental setup is such that the nitrogen gas from the cylinder flows through a flow meter that is attached to it to give the flow rate of N2 in terms of NL/min. The N2 gas is distributed by connecting the flow meter to a central chamber and then distributing to 12 small tubes. The gas is injected at the up snorkel (up leg) through 12 nozzles equally distributed along the circumference of the up leg. Six nozzles are at a height of 150 mm from the bottom of the up leg, and the other six are at a height of 200 mm. These six nozzles, which are at the top of the other six nozzles, are at alternate positions compared to those that are below. To have a better understanding of the setup, a schematic diagram of the arrangement is shown in Figure 1(b). The vacuum vessel is connected to the vacuum pump with a barometer attached to it in order to measure the vacuum pressure. The setup to measure the pressure drop at the down leg is attached to the down snorkel with a digital barometer. To understand the mixing characteristics, conductivity experiments are also done. A digital power source with constant voltage is used to drive a measurable current, which can be changed accordingly, and an amount of 30 mL of 3M NaCl solution is injected from the bottom of the up leg. The two open terminals, one being positive and the other being negative, are connected just below the down leg, i.e., 600 mm from top of the down leg, to measure the conductivity of the water coming through the down leg in terms of current flow between these two terminals. The level of water in the ladle is kept 1 m from ground level, and the level of water in the vacuum vessel is kept constant and can be changed per the requirement.

Fig. 1
figure 1

(a) Photograph of a single tube and nozzle used in the up leg. (b) Schematic diagram for the arrangement of nozzles in the up leg

Full size image

Experimental Setup

The experimental setup is shown in Figure 2.

Fig. 2
figure 2

Schematic diagram of the cold model set up at IEHK, RWTH–Aachen University

Full size image

Results and Discussion

The effects of different parameters on the circulation rate of water were studied. In this section, effects of these parameters are discussed.

Effects of h vac and p vac on Q cir Keeping h sub Constant

This experiment is done by maintaining the submerged depth of the snorkels constant (100 mm). It was observed that as the water level (h vac) in the vacuum vessel increases, the circulation rate also increases and the vacuum pressure drops gradually. The drop in vacuum pressure is shown in Figure 3. From previous studies, it has been determined that the lift gas expands after entering the up leg and bubbling upward because of the decrease in pressure in the vacuum vessel. As a result, the average density of the mixed flow of water and gas is reduced; because of this, the water in the vessel swells at the top of the up leg. This swelling of water above the up leg leads to the flow of water through the down leg due to gravity. Seshadri and De Souza Costa[3] also considered different aspects of the work done by gas and liquid during water circulation and used them to calculate the circulation velocity theoretically. Lin et al.[6] also showed the same effect by using the concept of the work done by gas and liquid water.

Fig. 3
figure 3

Effect of vacuum pressure on the circulation rate of water

Full size image

As the vacuum pressure is decreased slowly to 920 mbar, the bubbles are pulled up, or we can say that they travel faster than they used to, when no pressure is applied. This decreases the dual-phase flow density \( \rho_{\text{gl}} \) and increases the holding up of gas and lifting level of water in the vessel, and the work done by expansion of gas increases. As is clear from Figure 4, there is an abrupt increase in the circulation rate when the level of water in the vacuum chamber changes from 50 to 100 mm; then it remains constant for some time before increasing after 200 mm of water level. Simultaneously, the vacuum pressure decreases with an increase in the water level. The circulation rate increases and then stays level as the vacuum pressure decreases. However, the circulation rate increases rapidly when the vacuum pressure reaches 920 mbar.

Fig. 4
figure 4

Effect of water level in the vessel on the circulation rate

Full size image

Effect of h sub on Q cir Keeping h vac Constant

Another experiment is done by keeping the level of water in the vessel constant (200 mm with respect to the top of the up leg) and changing the submerged depth of the snorkels. It has been observed that the circulation rate increases with increasing the submerged depth. Figure 5 shows three different curves, which are obtained for three different lift gas flow rates. An interesting observation can be drawn out from this plot when this experiment is done. For the N2 flow rate of 12.04 NL/min, the curve increases almost linearly in the beginning and then increases with decreasing rate.

Fig. 5
figure 5

Effect of lift gas flow rate on the circulation rate of water for different submerged depths of snorkels

Full size image

As the flow rate changes to a slightly higher value, i.e., 24.08 NL/min, the circulation rate increases but the curve shifts downward and increases with increasing rate. Furthermore, when the flow rate increases to a much higher value, i.e., 36.12 NL/min, the plot surpasses all the above curves by shifting upward and then increases with decreasing rate but with a higher magnitude as compared with that of 12.04 NL/min. This observation gives an idea of the effect of three different lift gas flow rates on the circulation rate by changing the submerged depth. When these data are plotted the other way around, a nice effect of submerged depth on circulation rate is observed. Figure 6 shows that the curve shifts upward as the submerged depth is increased further; i.e., the circulation rate increases with respect to the depth of snorkels. This observation is in good agreement with the one obtained by Lin et al.[6]

Fig. 6
figure 6

Effect of submerged depth of snorkels on the circulation rate of water

Full size image

Changing Lift Gas (N2) Flow Rate (NL/min)

It is found that the lift gas flow rate has a profound effect on the circulation rate of water. In this model, a certain water height of 105 mm (with respect to the top of the up leg) is taken in the vacuum chamber. Figure 7 is obtained.

Fig. 7
figure 7

Effect of lift gas flow rate on the circulation rate of water for a water level in a vacuum of 105 mm

Full size image

Figure 7 shows that the circulation rate increases with the increasing lift gas flow rate, but after a certain flow rate, the circulation rate then saturates or becomes constant. As the lift gas flow rate increases, the gas penetration depth increases and, in turn, the holding up of gas increases. Because of this, the work done by bubble floatage increases, which, in turn, increases the circulation rate. As the nitrogen gas flow rate increases, it reaches a certain penetration depth and the bubbles can go to the central part of the up leg, due to which the holding up of gas in the up leg gets saturated and the circulation rate also gets saturated. This observation is also in good agreement with the one obtained by Lin et al.[6] for the lift gas bubble travel effect on the circulation rate. Note that there is no control of submerged depth here. From Figure 8, it can be observed that the curve goes up as the water level draws near the top of the up leg.

Fig. 8
figure 8

Effect of lift gas flow rate on the circulation rate for two different water levels in the vessel

Full size image

Conductivity Experiment to Understand the Mixing Behavior

This current conductivity experiment is done to understand the mixing characteristics in the RH degasser. The water goes up through the up leg and comes down through the down leg. Just below the down leg, i.e., 600 mm from the top of the down leg, two wires are connected—one being positive and the other at negative potential. Under the application of constant voltage of 25 V, a flow rate of 30.10 NL/min, 30 mL of 3M NaCl solution is injected at the bottom of the up leg. After a certain amount of time, there is a sudden rise in current, which attains a peak value and then decreases to a nominal value, as explained in Figure 9. The current increases from 0.03 to 0.07 A, then decreases to 0.05 and 0.04, and finally back to 0.03 A. This shows that the NaCl salt solution disintegrates into ions in the water and conducts current as soon as these ions pass through the open circuit and makes a complete circuit by conducting current. After a certain point of time, this rise in current is observed again but less in order. This shows that after the salt ions reach the ladle, the salt gets diluted and the concentration of ions circulated this time is less as compared to the previous circuit. The mixing characteristics determined in this case are taken to be the time gap between the beginning of the current hike, arriving at the highest peak, and then coming back to the nominal value. The nominal value here is 0.03 A, which is assumed to be a default, as the water may have some free ions, which give a constant current flow between the terminal. This is because the water used is normal water.

Fig. 9
figure 9

Current conductivity measurement showing the mixing effect of water in the ladle

Full size image

The effect of the lift gas flow rate on current conductivity is shown in Figure 10. The current hike observed for 36.12 NL/min flow rate is higher than that for 33.70 NL/min. The mixing characteristics also change with change in flow rate. There is a more rapid mixing for a higher flow rate, i.e., 36.12 NL/min, than that with 33.70 NL/min. This can be derived from the figure, as the current peak obtained in the case of 36.12 NL/min is faster, that is, the current started rising before the twentieth second, whereas the rise in current in the case of 33.70 NL/min takes place at the fourtieth second. In other words, we can say that the water with NaCl in it stays in the vacuum vessel for a little more time in the case of 33.70 NL/min than in the case of 36.12 NL/min, due to which the salty water gets diluted, and as a result, we obtain less conduction of current. This observation gives proof of what has been observed in the past couple of experiments.

Fig. 10
figure 10

Current conductivity vs time for different flow rates

Full size image

In Figure 11, for a constant value of lift gas flow rate, i.e., 33.70 NL/min, it is observed that the current hike is greater for a lower level of water, i.e., 100 mm, in the vessel rather than that of 150 mm. With the same lift gas flow rate, the circulation rate should remain constant, but with lowering the water level in the vacuum vessel, the salt added has a lesser possibility of getting mixed or diluted. The circulation rate depends on how fast the current peak is obtained, as shown in the previous plot for two different gas flow rates, but it also depends on how high the value of the current is no matter if the current starts increasing at the same time. This finding has been similarly observed in Section III–C Figure 8, where the maximum circulation rate is achieved as the water level drops and draws near the top of the up leg. In other words, it can also be stated that the amount of water/water window is greater in the case of the 150-mm water level in the vacuum vessel for the salt to get diluted than that of 100 mm. So the peak is higher in the case of the 100-mm water level, as the water coming down through the down leg is less diluted than that of the 150-mm water level (Figure 11).

Fig. 11
figure 11

Current conductivity vs time for different water levels

Full size image

Changing h vac (mm) Keeping the Distance Between the Water Level in the Vessel and the Submerged Depth, i.e., h′ Constant

In this experiment, the distance (h′) between the water level in the vacuum chamber and the submerged depth level is kept constant, as shown in Figure 12. Three sets of experiments are done with three different levels of water in the vacuum vessel (with respect to the top of the up leg). The plot indicates that as soon as the water level decreases the top of the up leg to 50 mm, the circulation rate becomes 0. This explains that if there is no steel in the vessel, no matter how much gas is blown, the circulation rate should be 0, which is in agreement with the explanation given by Li et al.[5] Also, as the water level increases further to 50 mm, the circulation rate increases rapidly with respect to the lift gas flow rate, but after a certain height, e.g., 200 mm, the curve shifts downward.

Fig. 12
figure 12

Schematic diagram showing the distance h′

Full size image

The relation between the dimensionless numbers is derived for 50- and 200-mm heights of water in the vessel, per the plot in Figure 13. The equations are derived for each plot by putting values of all the known entities, such as g, d, μ, and ρ, the velocity of water (v) in the down leg, and the corresponding lift gas flow rate (G), and calculating the unknown values of C, x, and y, as depicted in Eq. [1]. Equations are derived using a limited number of data points (five data points). Regression was not possible with so few data points. However, three equations were solved simultaneously using these data points to arrive at reasonable coefficients, as represented by these same data points to the best possible extent. The derived equations qualitatively represent the effect of nondimensional parameters in a reasonable way. However, more data sets may help to derive a more accurate equation. Still, the derived equations may be used well for practical purpose. The equations are as follows:

  1. Case 1:

    For 50-mm height of water in vacuum vessel,

    $$ \frac{{v^{2} }}{gd} = \left( {5.64 \times 10^{ - 12} } \right)\left( {\frac{d\rho v}{\mu }} \right)^{2.05} \left( {\frac{G}{{d^{2} v}}} \right)^{0.23} $$
    (20)
    $$ {\text{Fr}} = \left( {5.64 \times 10^{ - 12} } \right){\text{Re}}^{2.05} {\text{Va}}^{0.23} $$
    (21)
  2. Case 2:

    For 200-mm height of water in vacuum vessel,

    $$ \frac{{v^{2} }}{gd} = \left( {7.54 \times 10^{ - 12} } \right)\left( {\frac{d\rho v}{\mu }} \right)^{2.09} \left( {\frac{G}{{d^{2} v}}} \right)^{0.016} $$
    (22)
    $$ {\text{Fr}} = \left( {7.54 \times 10^{ - 12} } \right){\text{Re}}^{2.09} {\text{Va}}^{0.016} $$
    (23)
Fig. 13
figure 13

Effect of lift gas flow rate on circulation rate of water for different water levels in vessel keeping the distance h′ constant

Full size image

As Figure 13 shows, the circulation rate is higher in the case of a 50-mm water level in the vacuum vessel rather than the one with 200 mm. So Eqs. [20] and [21] hold well.

Conclusions

On the basis of cold model-based experiments, the following conclusions are derived:

  1. 1.

    The circulation rate, Q cir, increases with increasing the level of water in the vessel (h vac) and decreasing the vacuum pressure (p vac) by keeping the submerged depth (h sub) constant to 100 mm in this experiment.

  2. 2.

    By keeping the water level in the vessel (h vac) constant, i.e., 200 mm, in this experiment and by dipping the snorkels more or, in other words, by increasing the submerged depth (h sub), the circulation rate (Q cir) increases. For a larger lift gas flow, i.e., 36.12 NL/min, the curve obtained has an increasing behavior but with a decreasing rate, whereas in the case of a lift gas flow rate of 24.08 NL/min, the curve obtained has an increasing behavior with an increasing rate.

  3. 3.

    The effect of lift gas flow rate at a particular height of water in the vessel and submerged depth shows a nice effect on the circulation rate (Q cir). The curve increases at first, but for higher values of gas flow rate, it saturates, showing the limiting behavior of gas flow due to the bubble trap.

  4. 4.

    The effect of different lift gas flow rates and water levels is studied by current conductivity measurements. It is clearly shown that the higher value of lift gas flow rate decreases the mixing time as that for lower flow rates. The water level of 100 mm in the vessel shows a hike in current but takes a longer time, as compared to that with 150 mm where the current hike is less but the mixing time decreases.

  5. 5.

    The relations between dimensionless parameters Re, Fr, and Va are obtained for different heights of water in the vessel keeping the distance h′ constant. Equations [20] and [21] for the curve obtained for the 50-mm water level in the vacuum vessel, which shows a larger circulation rate than the other curves, are proposed to be the governing equations for the RH degassing process.