1 Introduction

Directionally solidified eutectics are self-organized composite materials of great prospective interest for advanced engineering.[1,2,3,4,5] In practice, however, good control of their multiphased microstructures comes up against complex pattern formation phenomena that are still incompletely understood.[6] Among them, the dependence of eutectic solidification microstructures on the orientation of the growing crystals is of primary importance.[7,8,9] We consider coupled-growth patterns during the solidification of a nonfaceted binary eutectic alloy at an imposed velocity V in a fixed temperature gradient G. The two-phased solidification dynamics is primarily controlled by solute diffusion in the liquid and capillary effects at the involved interfaces. The shape of the interphase boundaries in the solid, and thus the two-phase growth microstructure imprinted in the bulk alloy, is a frozen trace of the trajectories of the triple lines (trijunctions) at which the two solids and the liquid are in contact. In a lamellar eutectic, the solid presents a spatial alternation of platelet-like crystals, or lamellae, of the two eutectic solid phases. This results from the formation of banded patterns at the growth front. For a given V value, the (interlamellar) spacing \(\lambda \) usually falls close to a scaling length, the so-called minimum-undercooling spacing \(\lambda _m\), which is proportional to \(V^{-1/2}\). This delineates the bases of the Jackson-Hunt (JH) theory of steady periodic eutectic patterns in regular eutectics.[10]

One of the major hypotheses in the JH calculation is that the involved interfaces are fully isotropic. This essentially holds true for the solid-liquid interfaces in a nonfaceted system. In contrast, the free energy \(\gamma \) of the interphase boundaries in the solid can be markedly anisotropic, in particular in eutectic alloys that present special crystal orientation relationships (ORs). The question arises then of how the anisotropy of the interphase boundary enters into play in the diffusion-controlled growth dynamics of eutectic solidification patterns. Recently, new light has been cast on that issue by focusing on the so-called locked lamellar eutectic patterns.[11,12,13,14,15] Experimentally, eutectic lamellae are often observed to grow tilted with respect to the solidification axis and keep a fixed inclination that is insensitive to changes of the ordinary control parameters. This inclination commonly corresponds, or nearly so, to that of a low-energy, coincidence plane that characterizes an OR. A theory of this effect has been proposed on the basis of a semi-empirical conjecture, called symmetric-pattern (sp) approximation, which states that, in the presence of an anisotropy of the interphase boundaries, the steady-state shape of the solid-liquid interfaces in tilted-lamellar patterns keeps the same mirror symmetry as for an isotropic system.[12] The sp approximation was inspired by in situ directional solidification experiments of a model transparent alloy, namely, the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) eutectic, in thin samples.[12] Its relevance has been essentially confirmed by numerical simulations by Ghosh et al.[14] In the latter study, for general demonstration purposes, a virtual symmetric eutectic alloy with identical thermodynamical properties of the two eutectic phases was considered. In a recent phase-field simulation study using more realistic alloy parameters, a substantial departure from the sp approximation was found in certain conditions.[16] However, a quantitative study aiming at a direct comparison of numerical results with experimental observations is still lacking.

In this article, we present a numerical study of locked lamellar eutectic growth patterns in the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) system. We used a dynamic boundary-integral (BI) code with model interfacial-anisotropy functions, as in Reference 14. The parameters of the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) alloy were taken from Karma and Sarkissian[17] (also see 18 and 19). The sp approximation was again found to be qualitatively relevant, and a strong locking effect close to a deep \(\gamma \) minimum was reproduced. For deeper insight, we carried out a systematic investigation of the dependence of the tilt angle \(\theta _t\) of the lamellar patterns on the main control parameters. We found that the departure \(\delta = \theta _{sp}-\theta _t\) from the tilt angle \(\theta _{sp}\) predicted by the sp approximation depends substantially on two prevailing factors of influence, namely, the G/V ratio and the volume phase fraction in the solid \(\eta \) (thus, the average concentration of the alloy). The effect of the latter is all the stronger as the two phases have different capillary lengths—which is actually the case for the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) alloy. The value of the pinning angle between the interfaces at the trijunction also enters into play, at least for a weak anisotropy. We finally reproduced numerically some experimental observations of locked lamellar patterns in the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) alloy by adjusting the parameters of the model interfacial anisotropy function by following an empirical, iterative approach.

The scientific context of the study is presented in Section II. The BI method for the numerical simulation of 2D eutectic patterns is summarized in Section III. Detailed information on the thin-sample directional solidification method has been abundantly provided in previous papers (see, e.g., References 19, 20) and is not repeated here. The results are presented in Section IV, and a short discussion is proposed in Section V, along with the main conclusions. Symbols used in this article are listed in Appendix A, with definitions and units.

2 Background

2.1 Eutectic Growth: Isotropic System

During directional solidification of a nonfaceted binary eutectic alloy in a thin sample, the dynamics is assumed to occur in 2D geometry. The temperature gradient G (frozen temperature approximation) is directed along the z axis. The sample is pulled at a velocity V towards negative z values. We note x as the (longitudinal) axis perpendicular to z. In the reference frame of the laboratory (which moves at velocity V along z compared to the reference frame of the solid), the temperature field T(z, t) reads:

$$\begin{aligned} T(z,t) = T_E + Gz \, . \end{aligned}$$
(1)

We shall note \(\alpha \) and \(\beta \), the two eutectic solid phases. The dimensionless concentration field u in the liquid is defined by:

$$\begin{aligned} u({\varvec{r}},t) = \frac{C({\varvec{r}},t)-C_E}{{C}_\beta -C_{\alpha }}, \end{aligned}$$
(2)

where \(\mathbf {r}\) is the position vector in the (x, z) plane, \(C(\mathbf {r},t)\) the solute concentration in the liquid (L), and \(C_\alpha \), \(C_\beta \), and \(C_E\) are the equilibrium compositions of the coexisting \(\alpha \), \(\beta \), and liquid phases, respectively, at \(T=T_E\). We assume a one-sided solidification problem (no diffusion in the solid). The diffusion field in the liquid obeys:

$$\begin{aligned} \partial _t u = D \mathbf {\nabla }^2 u + V\partial _z u \,\, , \end{aligned}$$
(3)

where D is the solute diffusion coefficient in the liquid. The diffusion length \(l_d\) is defined as \(l_d=D/V\).

At the \(\alpha \)- and \(\beta \)-liquid interfaces, the conservation of solute imposes:

$$\begin{aligned} V_n u_\nu = -D {\hat{n}}_\nu \cdot \mathbf {\nabla }u|_\nu \,\, , \end{aligned}$$
(4)

where \(V_n\) is the normal growth velocity of the solid-liquid interface, \({\hat{n}}_\nu \) the unit normal vector to the \(\nu \)-liquid interface pointing into the liquid (\(\nu =\alpha ,\beta \)), \(\mathbf {\nabla }u|_\nu \) the concentration gradient at the interface, and \(u_\nu = (C_\nu - C_E)/(C_\alpha -C_\beta )\). The liquidus and solidus lines are assumed to be parallel to each other.

Let us note \(\zeta (x)\) as the shape of the (isotropic) solid-liquid interface. We define the thermal length \(l_t^\nu \) and the capillary length \(d_0^\nu \) of phase \(\nu \) by:

$$\begin{aligned} l_t^\nu = \frac{|m_\nu |(C_\beta -C_\alpha )}{G} \,\, , \end{aligned}$$
(5)

and

$$\begin{aligned} d_0^\nu = \frac{\gamma _{\nu } T_E}{L_\nu |m_\nu | (C_\beta -C_\alpha )} \,\, , \end{aligned}$$
(6)

where \(m_\nu \) is the liquidus slope at \(T_E\), \(L_\nu \) the latent heat of melting per unit volume of phase \(\nu \), and \(\gamma _{\nu }\) the surface free energy of the \(\nu \)-L interface. The local equilibrium can then be written as:

$$\begin{aligned} u_\mathrm{int} = \left\{ \begin{array}{cl} -\zeta (x)/l_t^\alpha - d_0^\alpha \kappa \,\,, & \alpha \hbox {{ -L interface}} \\ \zeta (x)/l_t^\beta + d_0^\beta \kappa \,\,, & \beta \hbox {{ -L interface} \,\, ,} \end{array}\right. \end{aligned}$$
(7)

where \(u_\mathrm{int}\) is the value of the field u at the interfaces and \(\kappa \) the interface curvature, counted positive for a solid bulging into the liquid.

For a fully isotropic system, the local equilibrium at the trijunction reads (Young’s law):

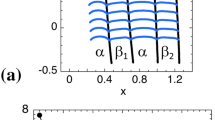
$$\begin{aligned} \gamma _{\alpha } {\hat{t}}_{\alpha } + \gamma _{\beta } {\hat{t}}_{\beta } + \gamma {\hat{t}} = 0, \end{aligned}$$
(8)

where \(\gamma \) is the surface free energy of the \(\alpha \)-\(\beta \) interphase boundary, and the unit vectors tangent to the \(\nu \)-liquid interfaces and the interphase boundary (pointing away from the trijunction) are noted as \({\hat{t}}_{\nu }\) and \({\hat{t}}\), respectively. A pair of \(\alpha \) and \(\beta \) lamellae in a steady periodic eutectic growth pattern is schematically represented in Figure 1(a).

Fig. 1
figure 1

Schematic representation of steady-state lamellar eutectic patterns. (a) Regular pattern (isotropic system). (b) Steady-state tilted-lamellar pattern with anisotropic interphase boundaries. (c) Tilted-lamellar pattern in the symmetric-pattern configuration (anisotropic system). Symbols: see text

Full size image

Equations [1] to [8] form the regular-eutectic growth problem as it was considered a long time ago by Jackson and Hunt (JH).[10] The main conclusions of the JH work were, in brief, that for usual values of the temperature gradient G (typically on the order of \(100~\mathrm{Kcm^{-1}}\)),[21] and values of the Péclet number \(Pe= \lambda /l_d\) much smaller than 1, the eutectic growth dynamics is poorly sensitive to G and depends on a single parameter, namely the dimensionless spacing \(\varLambda = \lambda /\lambda _m\), which is proportional to \(\lambda V^{1/2}\). The scaling length \(\lambda _m\) varies proportionally to \((d_0l_d)^{1/2}\), where \(d_0=2 [ \eta d_0^\alpha \sin\phi _\alpha + (1-\eta ) d_0^\beta \sin\phi _\beta ]\), with \(\phi _\nu \) the pinning angle of the \(\nu \)-liquid interface at a trijunction (Figure 1(a)) and \(\eta \) the volume fraction of the \(\beta \) phase in the solid. The latter quantity is essentially determined by the average concentration of the alloy \(C_0\), and, assuming that the molar volumes of the two solid phases are equal (which is approximately the case for \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\)), one can write:

$$\begin{aligned} \eta = \frac{C_0-C_\alpha }{C_\beta -C_\alpha } \, \, . \end{aligned}$$
(9)

2.2 Anisotropic Interphase Boundaries

In this section, along with the following one, we summarize a theoretical work that has been previously developed in References 12 and 14. The goal was to determine how to predict the effect of anisotropic interphase boundaries in an \(\alpha \beta \) eutectic grain of uniform crystal orientation during eutectic solidification (Figure 1(b)). For the sake of simplicity, we will note \({\hat{n}}\) and \({\hat{t}}\) as the normal and tangent unit vectors of the interphase boundary, respectively. We note \(\theta \) as the inclination angle of the interphase boundary in an arbitrary configuration, which we define as the angle between \({\hat{n}}\) and the x axis (\(n_x=\cos \theta \) and \(n_z=\sin \theta \) are the x and z components of \({\hat{n}}\), respectively). The lamellar tilt angle \(\theta _t\) designates the value of \(\theta \) in a steady-state pattern (Figure 1(b)). One has: \({\hat{t}} = - \mathrm{d}{\hat{n}}/\mathrm{d}\theta \). The angle between the interface and the z axis is also equal to \(\theta \). The anisotropic interphase boundary energy can be written as:

$$\begin{aligned} \gamma (\theta ) = \gamma _0 [1-a_c(\theta )], \end{aligned}$$
(10)

where \(\gamma _0\) is a constant and \(a_c(\theta )\) is a dimensionless function. In two dimensions, the Hoffman-Cahn \(\mathbf {\xi }\) and \(\mathbf {\sigma }\) vectors[22] are defined by

$$\begin{aligned} \mathbf {\xi }= \gamma {\hat{n}} - \gamma '{\hat{t}} \end{aligned}$$
(11)

and

$$\begin{aligned} \mathbf {\sigma }= \gamma {\hat{t}} + \gamma '{\hat{n}}, \end{aligned}$$
(12)

where \( \gamma ' = \mathrm{d} \gamma (\theta )/\mathrm{d}\theta \).

The \(\gamma \) plot is defined by \(\mathbf {\rho }(\theta ) = \gamma (\theta ){\hat{n}}\) in a polar representation. The minimum-energy shape (Wulff shape) of a \(\beta \) crystal in an \(\alpha \) matrix—in a uniform temperature field—is given by the vector \(\mathbf {\xi }(\theta )\) (\(\xi \) plot). It is useful to define the surface stiffness \(\tau (\theta ) = \gamma (\theta )+\gamma ''(\theta )\). A “weak” or “smooth” anisotropy satisfies \(\tau (\theta )>0\) for all orientations. In contrast, with a “large” anisotropy such that the quantity \(\tau \) is negative for a range of \(\theta \),[23] the \(\xi \) plot has self-intersections. The segments with \(\tau <0\) in the \(\xi \) plot correspond to Herring-unstable inclinations of the interface.

The local equilibrium condition at the trijunction (Young-Herring equation) now becomes

$$\begin{aligned} \gamma _{\alpha } {\hat{t}}_{\alpha } + \gamma _{\beta } {\hat{t}}_{\beta } + \mathbf {\sigma }= 0, \end{aligned}$$
(13)

with \(\mathbf {\sigma }\) given by Eq. [12]. That equation replaces Eq. [8] in the anisotropic coupled-growth problem. As it is written, it (reasonably) assumes that the solid-liquid interfaces are isotropic. Generally speaking, the \(\mathbf {\sigma }\) vector is not parallel to the interphase boundary.

In directional solidification, the orientation of a given eutectic grain with respect to the reference frame of the axial temperature field must be specified. In two dimensions, it is practical to define a rotation angle \(\theta _R\), measured from a reference configuration, so that one can write:

$$\begin{aligned} \gamma (\theta ) = \gamma _0 [1-a_c(\theta -\theta _R)] \, . \end{aligned}$$
(14)

We shall set \(\theta _R =0\) in such a way that a \(\gamma \) minimum of interest is located for \({\hat{n}}\) perpendicular to z. For \(\theta _R =0\), one expects the interphase boundary to align with z (\(\theta _t=0\)), for symmetry reasons, during steady-state growth. A lamellar locking effect then corresponds to \(\theta _t\approx \theta _R\) for a finite range of \(\theta _R\) about \(\theta _R=0\). This occurs when the \(\gamma \) minimum in question is sharp enough. The angle \(\theta _R\) was called the rotation angle in reference to the experimental rotating directional solidification method.[13]

As in Reference 14, we will use anisotropy functions \(a_c(\theta )\) of the form

$$\begin{aligned} a_c(\theta ) = \epsilon _g \exp \left[ -(\theta /w_g)^2\right] - \epsilon _2\cos 2\theta - \epsilon _4\cos 4\theta \, , \end{aligned}$$
(15)

where \(\epsilon _m\) (\(m=2,4\)) is the m-fold anisotropy coefficient, \(\epsilon _g\) the amplitude, and \(w_g\) the width of a Gaussian that is used to model a localized minimum of \(\gamma (\theta )\). In this way, we “regularized” the system and avoided numerical issues associated to a singular minimum.

2.3 Symmetric Pattern Approximation

A steady periodic lamellar pattern with a finite tilt angle \(\theta _t\) induced by an anisotropy of the interphase boundary is represented schematically in Figure 1(b). For the sake of realism, the solid-liquid interfaces are represented with a broken mirror symmetry, two neighboring trijunctions with slightly different z positions (or, equivalently, slightly different temperatures), and the \(\mathbf {\sigma }\) vector making a finite angle \(\delta \) with the z axis. We recall that tilted interphase boundaries in the solid result from a lateral drifting motion of the coupled growth pattern along the x axis. If one notes \(v_d\), the lateral drift velocity, one has \(\mathrm{tan}\theta _t=v_d/V\). Such a drifting motion obviously breaks the parity (\(x \leftrightarrow -x\) symmetry) of the system. In general, this entails a breaking of the mirror symmetry of the solid-liquid interfaces with respect to the middle planes between two neighboring trijunctions. The diffusion field in the liquid also presents an asymmetric, drifting component.

Based on experimental observations during thin sample directional solidification of the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) alloy (see Reference 12, and Section IV–E below), a semi-empirical conjecture, the so-called sp approximation (Figure 1(c)) has been emitted, which assumes that the \(\alpha \) liquid and the \(\beta \) liquid interfaces keep a mirror-symmetric shape with respect to the mid-plane of the lamellae.[12] In this configuration, the contact angles of the solid-liquid interfaces at the trijunctions are the same on both sides of a lamella—and the trijunctions at the same temperature. The Young-Herring condition (Eq. 13) imposes then that the surface tension vector \(\mathbf {\sigma }\) is strictly aligned with z. This yields:

$$\begin{aligned} \gamma (\theta -\theta _R) \sin \theta + \gamma '(\theta -\theta _R)\cos \theta = 0 \, . \end{aligned}$$
(16)

This equation has a unique solution if the stiffness \(\tau \) is positive for all angles. If \(\tau \) becomes negative, there are intervals of \(\theta _R\) for which Eq. [16] admits three solutions: one belongs to the convex Wulff shape, another to the unstable segment, and the third to a metastable segment with \(\tau >0\). As mentioned above, we note \(\theta _{sp}\), the solution(s) of Eq. [16], and \(\theta _t\), the computed (or measured) lamellar tilt angle.

The semiquantitative relevance of the sp approximation has been demonstrated for a symmetric eutectic alloy with the help of numerical simulations (both with the BI code and with a phase-field method).[14] The lamellar locking effect could be reproduced in the presence of a strong anisotropy with a sharp \(\gamma \) minimum. However, in the simulations (and in the experiments), the solid-liquid interfaces of tilted lamellar patterns are obviously not strictly mirror symmetric, as schematically represented in Figure 1(b). A measure of the actual asymmetry is given by the angle \(\delta \), knowing that \(\delta =\theta _t-\theta _{sp}\). The sp approximation is equivalent to \(\delta =0\). In the symmetric alloy,[14] the angles \(\delta \) and \(\theta _t\) were systematically of opposite signs—the diffusion field opposes a resistance to the crystallographic effect, and \(\theta _t\) is lower than \(\theta _{sp}\) (in absolute values)—but \(\delta \) was found to be relatively small. The phase-field study of Reference 16 showed that, for a eutectic alloy with dissimilar characteristics of the two eutectic solid phases, the departure angle \(\delta \) could be rather large. The present study aims at casting clearer light onto this issue.

3 Methods

The BI method assumes that the term \(\partial _t u\) can be neglected in the diffusion equation, Eq. [3] (quasistationary approximation).[17] In brief, it uses Green’s function techniques that transform the diffusion equation along with the boundary conditions at the interface [Eqs. 4 and 7] into a single integro-differential equation at the solid-liquid boundary. The calculation starts with a suitable guess of the (discretized) \(\zeta (x)\) shape of a pair of \(\alpha \) and \(\beta \) lamellae. The boundary integral equation is used to calculate the concentration gradient at the solid interface, and the interface velocity is obtained from Eq. [4] for each interface point, but the trijunctions. The interface points are moved accordingly (given a predefined time step). The position of each trijunction is found by solving Eq. [13] with the help of a relaxation scheme. The interfacial anisotropy intervenes at that stage only. More details can be found in References 14 and 17 (also see 24).

The BI code uses dimensionless variables and parameters. The reference scale for the space variables is the width of the simulation box (here, \(\lambda \)) and \(\lambda /V\) for the time. Dimensionless parameters are defined as follows. The eutectic concentration is \(u_E=0\). The edge of the eutectic plateau on the \(\alpha \) (\(\beta \)) side is noted as \(u_\alpha \) (\(u_\beta \)), and \(u_\beta -u_\alpha = 1\). The average concentration of the alloy (that is, the concentration of the liquid for \(z\rightarrow \infty \)) is noted as \(u_0\). The \(\beta \)-phase volume fraction \(\eta \) is equal to the width of the \(\beta \) lamella divided by \(\lambda \) in a steady-state pattern and is given by \(\eta =u_0-u_\alpha \). Two dimensionless parameters are introduced for each phase \(\nu \), namely, \(P_c^\nu =d_0^\nu /l_d\) (capillary Péclet number), and \(\mu ^\nu =l_d/l_t^\nu \), which is proportional to G/V (we recall \(l_d=D/V\)). The lamellar spacing \(\lambda \) appears in the (spacing) Péclet number \(Pe=\lambda /l_d\). Coupled growth patterns are commonly such that \(Pe<<1\). The pinning angles are set by the values of the ratios \(\gamma _\alpha /\gamma \) and \(\gamma _\beta /\gamma \).

The relevant physical constants of the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) eutectic, extracted from Reference 17, are given in Table I. Here, for efficiency, we simply took \(\phi _\alpha =\phi _\beta =\phi =61^o\), while the pinning angles at the trijunction have been previously estimated as \(\phi _\alpha =70\pm 4^o\), and \(\phi _\beta =67\pm 5^o\).[18] Considering the experimental error, taking \(\phi _\alpha =\phi _\beta \) was justified. In addition, slightly decreasing the \(\phi \) value made the simulations faster and the convergence less sensitive to the departure of the initial guess from the steady-state regime at large tilt angles. The thus entailed inaccuracy margin was imperceptible compared to experimental errors. Moreover, as reported in Section IV–E below, we mostly compared simulated and experimental shapes with a large anisotropy. Then, the value of \(|\mathbf {\sigma }|\) that enters into play at the trijunctions substantially departed from \(\gamma \), and the equilibrium angles at the trijunctions varied according to the actual configuration. In the eutectic growth problem, the capillary effects at the solid-liquid interfaces are included in the Gibbs-Thomson equation via the capillary lengths \(d_0^\alpha \) and \(d_0^\beta \) (given in Table I). As concerns the equilibrium at the trijunctions, one only needs to know the two ratios \(\gamma _\alpha /\gamma \) and \(\gamma _\beta /\gamma \), which presently were both set to 0.5717 (isotropic system) according to the chosen \(\phi \) value. Those quantities are sufficient for running the present simulations and for both the Wulff construction and the comparison with the sp approximation. In Reference 18, the values of the \(\alpha \)-liquid and \(\beta \)-liquid surface energies were calculated from the estimates of the capillary lengths (for completion, we shall mention the values of the latent heats, namely, \(L_\alpha \approx 28~\mathrm{Jcm^{-3}}\) and \(L_\beta \approx 26~\mathrm{Jcm^{-3}}\)). Incidentally, in the phase-field study of Reference 16, the authors, while explicitly mentioning the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) system, have been using a set of alloy parameters that differed markedly from those listed in Table I.

Table I Useful Physical Constants of the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) Alloy. See Text
Full size table

We will also present some results obtained with a symmetric alloy for comparison. By definition, one has then \(u_\alpha =-u_\beta =-0.5\). We set the pinning angle to \(\phi _\alpha =\phi _\beta =\pi /6\) (\(\gamma _\alpha =\gamma _\beta =\gamma \)), unless otherwise stated, which is substantially smaller than that in the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\)—and in most of the few other eutectic alloys where \(\phi \) was estimated, to the best of our knowledge (see, e.g., Reference 25 for Al-\(\mathrm{Al_2Cu}\)). In Section IV–D, some of the above parameters of the symmetric alloy will be varied for the sake of comparison with the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) alloy, while respecting the symmetry between the two solid phases.

A thorough description of the preparation of thin \(\mathrm {CBr_4}\)-\(\mathrm {C_2Cl_6}\) samples and the directional solidification method can be found in previous papers.[19,20]

In the following, the symmetric eutectic alloy will be conveniently renamed “SE alloy” and the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) alloy into the “CB alloy.”

4 Results

4.1 Isotropic System

We first simulated a steady-state lamellar pattern with the experimental V, G, \(\eta \), and \(\lambda \) values corresponding to the snapshot of Figure 2—and with isotropic interfaces. The CB alloy was hypoeutectic (\(C_0<C_E\)). In this case, as in the rest of the article, we computed a single pair of lamellae, with periodic lateral boundary conditions. The experimental and numerical shapes superimposed well on each other, which provided an additional piece of confidence in the accuracy of the physical constants of Table I.

Fig. 2
figure 2

Steady periodic lamellar eutectic growth pattern observed in situ during thin-sample directional solidification (\(V = 0.5~\mu \mathrm{ms^{-1}}\), \(G=110~\mathrm{Kcm^{-1}}\), \(\lambda =29~\mu \mathrm{m}\)) of a hypoeutectic \(\mathrm {CBr_4}\)-\(\mathrm {C_2Cl_6}\) alloy (\(\eta = 0.26\), \(C_0=0.114~\)mol pct). Isotropic eutectic grain. Bar: \(20~\mu \mathrm{m}\). Inset: numerical simulation with the BI code (\(Pe=0.029\), \(P_c^\alpha =1.050\times 10^{-5}\), \(\mu ^{\alpha }=1.40\), \(P_c^\beta =0.350\times 10^{-5}\), \(\mu ^{\beta }=0.68729\), \(u_0=-0.028\)) superimposed on the framed detail of the pattern

Full size image

4.2 Weak Interfacial Anisotropy

We considered first a smooth anisotropy function of the form \(a_c(\theta ) = 1 - \epsilon _2\cos 2(\theta - \theta _R)\), with \(\epsilon _2=0.05\). We varied \(\theta _R\) between 0 and \(\pi /2\) (the rest of the diagram can be obtained by symmetry). The output values of the lamellar tilt angle \(\theta _t\) are reported in Figure 3(a) as a function of \(\theta _R\). Representative patterns are also shown in Figure 3(b). We used two sets of parameters for the CB alloy. The first one (filled squares in Figure 3(a)) corresponds to a thin-sample directional solidification experiment in a hypereutectic alloy with equal phase volume fractions in the solid (\(\eta =0.5\)), ordinary values of the control parameters (\(G=110~\mathrm{Kcm^{-1}}\), \(V=0.5~\mu \mathrm{ms^{-1}}\)), and \(\lambda = \lambda _m\) (\(\varLambda =1\)). In those conditions, the tilt angle was markedly lower than \(\theta _{sp}\), and that obtained for the SE alloy (same BI data as in Figure 8 of Reference 14) as well.

Fig. 3
figure 3

(a) Lamellar tilt angle \(\theta _t\) (BI simulations) and sp approximation angle \(\theta _{sp}\) (thick continuous line) as a function of the rotation angle \(\theta _R\) for a weak, twofold anisotropy of the interphase boundary [\(a_c(\theta ) = 0.05\cos 2(\theta - \theta _R)\)]. Symmetric eutectic alloy: (\(\circ \)) \(Pe=0.03129\), \(P_c^\alpha =P_c^\beta =1.9531\times 10^{-5}\), \(\mu ^{\alpha }=\mu ^{\beta }=0.25\), \(\phi = 30^o\) (\(\varLambda =1\)); (□) same parameters, but \(\phi = 60^o\). \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) eutectic alloy: (■) \(Pe=0.018609\), \(P_c^\alpha =1.05\times 10^{-5}\), \(\mu ^{\alpha }=1.40003\), \(P_c^\beta =0.35\times 10^{-5}\), \(\mu ^{\beta }=0.68729\), \(u_0=0.2\) (\(\eta =0.5\), \(G=110~\mathrm{Kcm^{-1}}\), \(V=0.5~\mu \mathrm{ms^{-1}}\), \(\varLambda =1\)); (\(\bullet \)) \(Pe=0.007\), \(P_c^\alpha =2.10\times 10^{-5}\), \(\mu ^{\alpha }=7.0001\), \(P_c^\beta =0.7\times 10^{-6}\), \(\mu ^{\beta }=3.4364\), \(u_0=-0.028\) (\(\eta =0.261\), \(G=110~\mathrm{Kcm^{-1}}\), \(V=0.1~\mu \mathrm{ms^{-1}}\), \(\varLambda =0.766\)). (b) Four simulated patterns corresponding to data points labeled 1, 2, 3, and 4 in the graph, respectively—in this figure, and all the figures below, the \(\alpha \) (\(\beta \)) lamella is on the left (right)

Full size image

However, with a different set of parameters (filled disks in Figure 3(a)) that would correspond to a hypoeutectic CB alloy (\(\eta =0.261\)), a lower pulling velocity (\(V=0.1~\mu \mathrm{ms^{-1}}\)), and a smaller spacing (\(\varLambda =0.766\)), the lamellar tilt angle was significantly larger—thus (fortuitously) coinciding with the \(\theta _t(\theta _R)\) data for the \(\mathrm{SE}\) alloy. The data points corresponding to the SE alloy with a pinning angle of \(\phi = 60^o\) in Figure 3(a) will be commented later on in Section IV–D.

4.3 Large Interfacial Anisotropy

We tested a large anisotropy of the form of Eq. [15] with \(\epsilon _g=0.2\), \(w_g=0.1\), \(\epsilon _2=0.0854\), and \(\epsilon _4=0.0221\) (same as in Figure 10 of Reference 14). The \(\gamma \) plot and the \(\xi \) plot are both shown as an inset in Figure 4(a). The Gaussian term in \(a_c(\theta )\) creates a deep and sharp minimum, associated with a large (quasi) facet and a large range of forbidden inclinations. As explained above, this entails a large interval of \(\theta _R\) values within which the \(\theta _{sp}(\theta _R)\) curve presents three solutions, including an unstable one (Figure 4(a)). We implemented the same two sets of parameters for the CB alloy as in the previous section. For the sake of completeness, we displayed the weak-locking part of the curve (large values of \(\theta _R\)). In this region, the behavior was again typical of smooth anisotropy and, disregarding the details of the anisotropy function, qualitatively similar to that illustrated in Figure 3(a).

Fig. 4
figure 4

(a) Lamellar tilt angle \(\theta _t\) (BI simulations) as a function of the rotation angle \(\theta _R\). Strong lamellar locking (anisotropy function: see text). Thick line: \(\theta _{sp}\) (blue, dotted, and green parts: quasi facet, unstable inclinations, and unlocked branch, respectively). \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) alloy. ■ and ●: see Figure 3 for the respective parameters. Inset: \(\gamma \) plot (blue line) and \(\xi \) plot (red line; dotted-line branches: \(\tau <0\)). (b) Two simulated patterns corresponding to the data points labeled 1 and 2 on the graph, respectively. Color online

Full size image

More interestingly, the locking effect (\(\theta _t\approx \theta _R\)) along the facet was well reproduced by the BI simulations (Figure 4(a)). Lamellar tilt angles as large as \(40^o\) could be reached with the hypoeutectic alloy (circles), but the simulations did not converge toward a steady-state for \(\theta _R\) larger than about \(27^o\) in the hypereutectic alloy. The simulated patterns shown in Figure 4(b) make it clear that, with the present anisotropy parameters, a strong locking still goes along with a substantial asymmetry of the shape of the \(\beta \)-liquid interface—and, to a much lesser extent, of the \(\alpha \)-liquid interface. The deformation of the solid-liquid interface is, as expected, larger for the solid phase that presents the lesser capillary length, namely, the \(\beta \) phase (pattern label 1 in Figure 4(b)). The asymmetry of the shape of both the \(\alpha \)- and \(\beta \)-liquid interfaces became however hardly perceptible in the simulated hypoeutectic alloy (pattern label 2 in Figure 4(b)). The next section aims at clarifying the quantitative influence of the alloy and control parameters on the tilted lamellar dynamics.

4.4 Influence of Individual Parameters

We studied first the variation of the tilt angle \(\theta _t\) as a function of the Pe number (Figure 5) within a range that actually corresponds to a variation of \(\varLambda \) between 0.8635 and 1.4266 for the CB alloy—these are accessible values in usual thin-sample directional solidification experiments. As in the SE alloy, the crystallographic effect is stronger for \(\varLambda \) values well below 1, that is, when capillary effects dominate. The tilt angle \(\theta _t\) decreases as a function of Pe for low Pe values, presents a minimum, and re-increases for Pe larger than about 0.035. Above this Pe value, the system closely approaches the threshold of a spontaneous tilt bifurcation[26]—this is beyond the scope of the present paper.

Fig. 5
figure 5

Lamellar tilt angle \(\theta _t\) as a function of Pe =\(\lambda /l_d\). \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) alloy with \(P_c^\alpha =2.1\times 10^{-5}\), \(\mu ^{\alpha }=0.070\), \(P_c^\beta =0.350\times 10^{-5}\), \(\mu ^{\beta }=0.68729\), \(u_0=0.2\) (\(\eta =0.5\), \(G=110~\mathrm{Kcm^{-1}}\), \(V=1.0~\mu \mathrm{ms^{-1}}\)). Same anisotropy function as in Fig. 3, with \(\theta _R=30^o\) (\(\theta _{sp}=4.58^o\))

Full size image

We then checked the influence of the pulling velocity V and the temperature gradient G, that is, more specifically, the G/V ratio. The calculations were performed by keeping \(\varLambda =1\). The results are shown in Figure 6 in the form of a graph that gives \(\theta _t\) as a function of the average quantity \(\mu = (\mu ^\alpha +\mu ^\beta )/2\), which is proportional to G/V. This permits a comparison with the SE alloy. It can be seen that, in the SE alloy, \(\theta _t\) is close to \(\theta _R\) over the whole range of explored \(\mu \) values and poorly sensitive to the G/V ratio. In contrast, in the CB alloy, the lamellar tilt angle increases substantially and gets closer to \(\theta _{sp}\) when \(\mu \) increases. By observing the tilted-lamellar patterns corresponding to the two extreme data points of the graph (insets in Figure 6), one can see that the solid-liquid interfaces are quite rounded at low \(\mu \) values, but considerably flatten at higher \(\mu \) values. This goes along with a lesser opposing effect of the diffusion field. For the sake of realism, we identified three groups of data points (with different symbols in Figure 6) that can be associated to three values of V, namely, 11.95, 1.0, and \(0.1~\mu \mathrm{ms^{-1}}\), respectively, and G values varying, for each of them, within a \(40-200~\mathrm{Kcm^{-1}}\) range. In thin-sample experiments, the values of the pulling velocity and the temperature gradient most usually remain on the order of, say, \(V=0.1-1~\mu \mathrm{ms^{-1}}\), and \(G=50-12~\mathrm{Kcm^{-1}}\), respectively, which corresponds to \(\mu \) ranging from 0.2 to 4, typically. The parameters used in the KS study,[17] namely, \(V=11.95~\mu \mathrm{ms^{-1}}\), and \(G=188~\mathrm{Kcm^{-1}}\) (\(\mu =0.074596\)), were thus unusually large.

Fig. 6
figure 6

Lamellar tilt angle \(\theta _t\) as a function of the parameter \(\mu \sim G/V\). Anisotropy function: \(a_c(\theta )=0.05\cos 2(\theta -\pi /6)\). Circles: symmetric alloy. Light gray, dark gray, and black squares: \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) alloy with \(\eta = 0.5\), and \(\varLambda =1\) (\(V=11.95, 1.0\) and \(0.1~\mu \mathrm{ms^{-1}}\); \(Pe=0.0923, 0.0267\) and 0.008424, respectively). Dotted horizontal line: \(\theta _{sp}=4.60^o\). Insets: simulated patterns for \(\mu = 0.0160\) (on the left) and 5.220 (on the right)

Full size image

We measured the influence of the pinning angle \(\phi \) at the trijunction by simulating tilted-lamellar patterns in the SE alloy (thus smoothing out the influence of other specific parameters) with various values of \(\phi \) within a \(10-60^o\) range. The \(\theta _t(\phi )\) data are shown in Figure 7. In Figure 7, we considered a weak anisotropy. This allowed us to report the \(\theta _t\) data as a function of the value of \(\phi \) calculated with \(\gamma =\gamma _0\). For small values of \(\phi \), \(\theta _t\) was found to be very close to \(\theta _{sp}\): the solid-liquid interfaces are quasi-planar. In contrast, when \(\phi \) increases, \(\theta _t\) decreases much. Interestingly enough, when \(\phi \) was set close to \(60^o\), the lamellar tilt angle (in the SE alloy) reached down the value of \(\theta _t\) found in the CB alloy with ordinary control parameters. This trend is made clearer in the graph in Figure 3(a): the \(\theta _t\) data calculated for the SE alloy with \(\phi \approx 60^o\) (instead of \(30^o\)) as a function of \(\theta _R\) nearly superimpose with the data obtained with the hypereutectic (\(\eta =0.5\)) CB alloy. In other words, and rather intuitively, the larger the amplitude of the deviation of the solid-liquid interface from a planar shape, the stronger the coupling with the diffusion field.

Fig. 7
figure 7

Lamellar tilt angle \(\theta _t\) as a function of the pinning angle \(\phi \) of the solid-liquid interfaces at the trijunction. Symmetric eutectic (SE) alloy. Anisotropy function: \(a_c(\theta )=0.05\cos 2(\theta -9\pi /48)\). Horizontal dotted line: \(\theta _{sp}=5.53^o\)

Full size image

In Figures 3 and 4, the impact of the asymmetry of the CB alloy phase diagram was indirectly demonstrated. Further evidence is given in Figure 8. We varied \(u_0\) within an interval that corresponds to \(\eta \) between 0.2 and 0.7—those values are accessible experimentally by using CB alloys of different concentrations about the eutectic point. It can be seen that \(\theta _t\) decreases when \(\eta \) increases. It is larger for hypoeutectic (\(\eta <0.3\)) than for hypereutectic alloys. In other words, the angle \(\delta \) nearly vanishes when the \(\beta \) lamella becomes narrower. This is certainly related to the dissemblance between the capillary lengths of the two solid phases (\(d_0^\alpha >d_0^\beta \)): the \(\beta \)-liquid interface deforms easier than the \(\alpha \)-liquid interface, and can present concave shapes under the effect of the diffusion field. This is evidenced by comparing the shapes of the lamellar patterns for markedly hypo- versus hyper-eutectic alloys, respectively (insets of Figure 8).

Fig. 8
figure 8

Lamellar tilt angle \(\theta _t\) as a function of the \(\beta \) phase volume fraction \(\eta \). \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) alloy (\(V= 1.0~\mu \mathrm{ms^{-1}}\), \(G=110~\mathrm{Kcm^{-1}}\), \(\varLambda \approx 0.8\)). Anisotropy function: \(a_c(\theta )=0.05\cos 2(\theta -\pi /6\)). Insets: simulated patterns (arrows: corresponding points in the graph)

Full size image

4.5 Locked Lamellar Patterns, and Experimental Observations

The quantitative agreement between the experimental observations of steady periodic lamellar patterns during thin-sample directional solidification of CB alloys and the BI simulations with the relevant physical parameters has been illustrated in Figure 2—in that case, a fully isotropic situation was considered. In the following, we report on our attempts to reproduce, with the BI code, the shape of locked, or nearly locked, lamellar patterns observed experimentally in two different anisotropic eutectic grains. We selected experiments that provided large-magnification images with a good optical quality, showing steady periodic (or smoothly modulated) lamellar patterns in large eutectic grains that presented a bistable behavior. Again, we used the parameters of Table I without further adjustment in the simulations. The phase fraction \(\eta \) was estimated in situ during the experiments and \(u_0\) set accordingly. Concerning the interfacial anisotropy, we used anisotropy functions of the same type as those in Eq. [15]—taking, in practice, the \(a_c(\theta )\) function of Figure 4 as a first guess—and tuned the anisotropy coefficients with an iterative approach to simulate a shape that reasonably matches with the experimental one. The value of the orientation angle \(\theta _R\) of the eutectic grain was set to the inclination of the locked lamellae in the eutectic grain.

Let us consider the eutectic growth pattern of Figure 9(a). It was observed in a single eutectic grain (see the continuity of the lamellae in the solid), in a slightly hypereutectic \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) alloy (\(u_0=0.085\)). On the right-hand side, the growth behavior was typically that of a weakly locked tilted-lamellar pattern, and the lamellar tilt angle, while remaining close to about \(10^o\), slightly varied and followed a floating-like spatiotemporal dynamics. The interphase boundaries also smoothly oscillated under the effect of an external (here, accidental) perturbation. On the left-hand side of the pattern, the growth dynamics was markedly unsteady, but straight facets with an inclination of about \(51^o\) could be easily identified.

Fig. 9
figure 9

(a) Lamellar eutectic growth pattern during directional solidification of a slightly hypereutectic \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) alloy in a thin sample. \(V = 0.25~\mu \mathrm{ms^{-1}}\), \(G=110~\mathrm{Kcm^{-1}}\). Dotted line: accidental variation of the pulling velocity. Bar: \(100~\mu \mathrm{m}\). (b) Detail of the weakly locked lamellar pattern, on the right-hand side of the image in (a), observed at a larger magnification. \(\lambda =18.8 ~\mu \mathrm{m}\). \(\eta \approx 0.37\). Bar: \(20~\mu \mathrm{m}\). Inset: detail of the same pattern and BI simulation (blue profile) with \(Pe=0.0094\), \(P_c^\alpha =5.25\times 10^{-6}\), \(\mu ^{\alpha }=2.80\), \(P_c^\beta =0.175\times 10^{-5}\), and \(\mu ^{\beta }=1.37457\). Coefficients in the anisotropy function (Eq. 15): \(\epsilon _g=0.2\), \(w_g=0.1\), \(\epsilon _2=0.104\), \(\epsilon _4=0.02208\) (\(\theta _R=51^o\)). Color online

Full size image

A detail of the weakly locked region of the same lamellar pattern as in Figure 9(a), but observed a few minutes later at a larger magnification, is shown in Figure 9(b). It provides a clear example of a lamellar pattern with a relatively large tilt angle (\(\theta _t\approx 10.5^o\)) and an essentially symmetric shape of the solid-liquid interfaces. In the BI simulation, we implemented an anisotropy function of the form of Eq. [15] (also see Figure 11 in Appendix B). The anisotropy parameters (slightly different from those of Figure 4) were selected in such a way that, by setting \(\theta _R=51^o\), two metastable solutions were predicted by the sp approximation. Good agreement was found between the numerical and experimental profiles in the weakly locked region (inset of Figure 9(b)). The value of \(\theta _{sp}\) (\(\approx 14^o\)) was substantially larger than \(\theta _t\), as expected for a hypereutectic alloy (see Figure 8). Nevertheless, a nearly symmetric shape of the solid-liquid interfaces was favored by a low value of Pe (Figure 5) and a large value of the \(l_d/l_t\) ratio (Figure 6). By construction, the sp approximation predicts another solution that corresponds to a locked lamellar pattern aligning with the facets (\(\theta _t\approx \theta _R=51^o\)) in the region on the left of Figure 9(a). The BI simulations however did not converge toward a steady state, which was more or less expected for a \(\theta _R\) value > \(40^o\). This is also in agreement with the unsteadiness of the left-hand side of the pattern in Figure 9(a).

The three snapshots in Figure 10 were observed in the same sample as in Figure 2, but in another eutectic grain. The images in Figures 10(a) and (b) were recorded at two different locations, distant by a few \(\mathrm{100~\mu m}\) from each other, in a large region of the eutectic grain that exhibited a weakly locked behavior. In that region, the lamellar spacing varied smoothly along the x axis. We measured, on average, \(\lambda =20.1~\mu \mathrm{m}\) and \(27.0~\mu \mathrm{m}\), and \(\theta _t=18.0\pm 0.3^o\) and \(19.5\pm 0.5^o\) in the two images, respectively. The large-\(\lambda \) lamellar pattern in Figure 10(b) was slightly oscillatory. The locked lamellar pattern of Figure 10(c) was observed in the same eutectic grain (at a different V, which is of marginal importance as concerns a locked lamellar pattern). As in the precedent case, we used an anisotropy function in the form of Eq. [15] and set \(\theta _R=35.0^o\) (\(=\theta _t\) in Figure 10(c)) in the BI code (also see Figure 12 in Appendix B). In this way, the weakly locked patterns of Figures 10(a) and (b) were reproduced—including the slightly different average tilt angles for the two different lamellar spacings in Figures 10(a) and (b) and the oscillations in Figure 10(b). The locked lamellar pattern of Figure 10(c) was also reproduced numerically for the very same set of parameters by using a convenient initial guess.

Fig. 10
figure 10

Tilted lamellar growth patterns observed during thin-sample directional solidification. The \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) sample is the same as in Figure 2 (\(G=110~\mathrm{Kcm^{-1}}\)), but the eutectic grain is different. (a) \(V = 1.2~\mu \mathrm{ms^{-1}}\), \(\lambda =20.1~\mu \mathrm{m}\), \(\theta _t\approx 18.0^o\) (\(Pe=0.04824\), \(Pc_{\alpha }=2.52\times 10^{-5}\), \(\mu ^{\alpha }=0.583\), \(Pc_{\beta }=8.40\times 10^{-6}\), \(\mu ^{\alpha }=0.2864\)). (b) Same parameters as in (a) but \(\lambda =27.0~\mu \mathrm{m}\), \(\theta _t\approx 19.5^o\) (\(Pe=0.0648\)). c) \(V = 0.5~\mu \mathrm{ms^{-1}}\), \(\lambda =26.75~\mu \mathrm{m}\), \(\theta _t\approx 35.0^o\) (\(Pe=0.02675\), \(Pc_{\alpha }=1.05\times 10^{-5}\), \(\mu ^{\alpha }=1.40\), \(Pc_{\beta }=3.5\times 10^{-6}\), \(\mu ^{\alpha }=0.68729\)). Bar: \(20~\mu \mathrm{m}\). Insets: simulated profiles (blue lines) superimposed to details of the patterns. Coefficients in the anisotropy function (Eq. 15): \(\epsilon _g=0.2\), \(w_g=0.005\), \(\epsilon _2=0.2\), \(\epsilon _4=0.06\) (\(\theta _R=35.0^o\)). Color online

Full size image

5 Discussion and Conclusion

We performed quantitative numerical simulations of steady-state lamellar-eutectic patterns with anisotropic interphase boundaries, by using a dynamic boundary-integral code. We compared the simulations with experimental observations of locked and weakly locked lamellar patterns during thin-sample directional solidification of a nonfaceted transparent alloy, namely, the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) eutectic. We investigated the relevance of an approximate theory based on the symmetric-pattern (sp) approximation for a real alloy, upon varying the value of the main control parameters within experimentally accessible intervals. We brought clear evidence that the sp approximation is quite accurate for a low solidification rate, large temperature gradient, and small lamellar spacing. Otherwise, the actual lamellar tilt angle can depart substantially from the one predicted by the sp approximation, and the shape of the solid-liquid interface becomes then clearly asymmetric. Due to the difference in the capillary lengths associated with the interfaces between the liquid and the two kinds of eutectic solids—which is obviously absent in a symmetric eutectic—the lamellar tilt also depends on the phase volume fraction in the solid and thus the average concentration of the alloy. In addition to the above conclusions, we succeeded in a direct comparison of the simulations with experimental observations in the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) system. For this purpose, as a proof-of-concept exercise, we considered two eutectic grains in which two dynamically metastable tilted lamellar patterns, one locked and the other weakly locked, were observed experimentally. In this way, locked and weakly locked patterns could be reproduced in BI simulations by adjusting the parameters of the model anisotropy function of the interphase boundary. Those results also bring further support to the assumption that the lamellar-locking phenomenon in nonfaceted eutectic alloys is largely dominated by the effect of an anisotropy of the interphase boundaries in the solid and that the solid-liquid anisotropy can be neglected.

Several remarks are in order:

(1) We considered the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) eutectic for two main reasons: (a) the relevant physical constants are known with accuracy, and (b) the shape of the solid-liquid interfaces can be observed in real time. This was crucial for a quantitative demonstration. Reproducing a similar study for a metallic eutectic alloy of (near-)industrial interest would be desirable. In particular, the Al-\(\mathrm{Al_2Cu}\) eutectic alloy could be considered. The relevant physical parameters of this alloy are known (see 25, 27 and References therein). Moreover, an estimate of the \(\gamma \) plot has been obtained by molecular dynamics calculations for two prevailing ORs of the Al-\(\mathrm{Al_2Cu}\) system.[28] A direct comparison of the shape of the solid-liquid interfaces could be made with optical micrographs of longitudinal cross sections in quenched ingots.

(2) The BI code presents the great advantage of being quantitatively reliable and can be used with real values of key parameters such as the capillary lengths. However, the BI method still remains limited to two-dimensional simulations and cannot be used for bulk solidification. For that, phase-field models are needed[29,30]—and for ternary eutectics as well.[31,32]

(3) It would be interesting to extend the present study to transient regimes in systems of a larger spatial extension and investigate, in particular, the so-called spacing diffusion process in the presence of an interfacial anisotropy.[33]

(4) The present numerical study could also motivate new thin-sample directional solidification experiments at low V, large G, and small \(\lambda \), in hypoeutectic \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\) samples, thus targeting conditions that would bring a better agreement with the sp approximation. This may also be important for optimizing rotating directional solidification experiments aiming at measuring the interfacial anisotropy of the interphase boundaries.[13]

(5) In a recent analytical study,[34] the authors used a simplified description of the solid-liquid interfaces with a sawtooth shape with linear segments, thus extending a previous work by Valance et al.[35] to large, anisotropy-induced tilt angles of the lamellae (symmetric eutectic alloy). Interestingly, this analysis succeeded in capturing an interplay between the diffusion field and the drifting motion of the lamellar pattern and predicted not only the lamellar-locking effect for a strong anisotropy, but also the departure of the actual lamellar tilt angle from the sp approximation. This model represents an interesting step beyond a Jackson-Hunt, planar-front calculation (see, e.g., Reference 33). It is, however, limited to convex shapes of the solid-liquid interfaces and becomes inaccurate for large values of the lamellar spacing.

Finally, it could be interesting to explore symmetry-breaking instabilities with anisotropic interphase boundaries. The question is, in other words, to determine to what extent the morphology diagram of lamellar eutectics[17,19] is modified by the interfacial anisotropy. Some attempts have been presented in Reference 16: oscillatory tilted-lamellar patterns were simulated in anisotropic grains with a phase-field model. In the case of the so-called tilt bifurcation, which was observed to occur spontaneously in isotropic eutectic grains in the \(\mathrm CBr_4\)-\(\mathrm C_2Cl_6\), the mirror symmetry of the lamellar pattern is broken, and the lateral traveling motion of the growth pattern strongly coupled with the diffusion field.[26] The sp approximation is then no longer appropriate, and a numerical simulation study would be of deep interest.[36]