Abstract
Aluminum- and magnesium-based metal matrix nano-composites with ceramic nano-reinforcements promise low weight with high durability and superior strength, desirable properties in aerospace, automobile, and other applications. However, nano-particle agglomerations lead to adverse effects on final properties: large-size clusters no longer act as dislocation anchors, but instead become defects; the resulting particle distribution will be uneven, leading to inconsistent properties. To prevent agglomeration and to break-up clusters, ultrasonic processing is used via an immersed sonotrode, or alternatively via electromagnetic vibration. A study of the interaction forces holding the nano-particles together shows that the choice of adhesion model significantly affects estimates of break-up force and that simple Stokes drag due to stirring is insufficient to break-up the clusters. The complex interaction of flow and co-joint particles under a high frequency external field (ultrasonic, electromagnetic) is addressed in detail using a discrete-element method code to demonstrate the effect of these fields on de-agglomeration.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Metal matrix composites (MMC) form a class of advanced materials typically based on light metals such as Al and Mg and ceramic reinforcements including but not limited to Al2O3, AlN, SiC, etc. Combining the light weight and ductility of Al and Mg with high strength and high modulus of ceramic materials makes MMC desirable for applications in aerospace and automotive industries. A good review of the development of MMCs is given in Reference 1. Metal matrix nano-composites (MMNC) are a recently developed subclass of MMCs based on nano-particle reinforcements.
Recent papers showed a clear increase in aluminum Young’s modulus (by up to 100 pct) and in hardness (by up to 50 pct) with the addition of carbon nano-particles.[2] Another study indicated a slight enhancement in Brinell hardness of aluminum-, magnesium-, and copper-based MMNCs with Al2O3 and AlN nano-particles.[3] The study suggested that a better dispersion of nano-particles is needed. Other researchers also report agglomerations of nano-particles made visible using high-definition scanning electron microscopy (SEM).[4] The effect of uneven distribution of NPs on the final properties of MMNCs is explained by the fact that large-size clusters no longer act as dislocation anchors, but instead become defects, leading to inconsistent properties.
The agglomeration of particles in MMNCs is related to the fact that nano-sized inclusions have a larger ratio of surface area to the volume than, e.g., micro-sized particles. This causes surface forces such as van der Waals interaction and adhesive contact to dominate over the volume forces such as, e.g., inertia or elastic repulsion in the case of nano-particles.
Various mechanisms of detachment of adhered particles have been reported in the literature,[5] which includes turbulent flow. It is expected that drag and shear forces in turbulent flow can improve separation of the particles and thus contribute to de-agglomeration. However, the drag force alone is not sufficient to de-agglomerate the nano-particles. This can be qualitatively illustrated by comparing the Stokes equation for the drag force with the force required to break two spherical particles apart, known as the pull off force, given by, e.g., Bradley:[6]
where μ f and vf are the velocity and dynamic viscosity of the melt and γ sl is the solid–liquid interfacial energy. For the case of aluminum melt, the dynamic viscosity is μ f = 0.0013 Pa s. Assuming the interfacial energy γ sl = 0.2 to 2.0 J/m2, Eq. [1] yields v f = 100 to 1000 m/s. Such fluid velocity values can be locally achieved as a result of the collapse of cavitation bubbles induced by ultrasonic field. Indeed, applying an electromagnetic stirring in combination with ultrasonic vibrations was found beneficial for nano-particle dispersion in metal melt.[2–5,7–9]
This paper concerns the investigation of forces causing the agglomeration of nano-particles and the conditions favoring breaking up of these agglomerations. A numerical model has been developed that simulates the behavior of the cluster of nano-particles under various conditions. The collisions of the particles are treated individually as opposed to the kinetic theory of granular flow used in e.g.,[8] It is proposed to investigate the behavior of NPs in metal melts subjected to electromagnetic[9] and other external fields using a coupled CFD-DEM model similar to that developed by Goniva et al.[10] and Hager et al.[11] While a fully coupled CFD-DEM solver is under development, this paper presents results obtained at the scale of a single nano-particle cluster subjected to forces equivalent to those caused by ultrasonic cavitation.
2 Review of Contact Theories with Adhesion
Bradley[6] first described the van der Waals force acting between two rigid spheres in contact and calculated the pull off force as P c = 4πγR, where γ is interfacial energy of the contacting materialsFootnote 1 and R is the radius of the sphere.
Derjaguin[12] pointed out that elastic deformations of the spheres need to be accounted for as well as the adhesive interactions. He presented the first attempt to consider the problem of adhesion between elastic spheres: calculating the deformed shape of the spheres using Hertzian contact theory, he evaluated the work of adhesion assuming only the pair-wise interactions of the closest surface elements. The interaction energy per unit area between small elements of curved surfaces was assumed the same as for parallel planes which is known as the Derjaguin approximation.
On the other hand, Johnson[13] made an attempt to solve the adhesive contact problem by combining the Hertzian spherical contact problem and the problem of a rigid flat-ended punch. Johnson et al.[14] applied Derjaguin’s idea to equate the work done by the surface attractions against the work of deformation in the elastic spheres to Johnson’s[13] combined stress superposition. This resulted in the creation of the famous JKR (Johnson, Kendall, and Roberts) theory of adhesive contact. According to them, the attractive adhesion force is acting only over the contact area and significantly affects the shapes of the contacting spherical bodies. The pull off force calculated using JKR model is P c = 3πγR. The contact area is a circle with radius a, defined as follows:
where P is the applied normal load and E is the combined Young’s modulus. Hertzian theory evaluates the contact radius simply as a 3 = 3PR/4E; therefore, JKR theory is reduced to Hertzian if adhesion is neglected, i.e., γ = 0.
Derjaguin et al.[15] developed a contact theory (DMT—Derjaguin, Müller, Toporov) that combined Bradley’s adhesion force with Hertz elastic contact theory. The attractive intermolecular force is assumed applicable in the contact area as well as in the surrounding annulus zone. The resulting profile of the deformed spheres remains Hertzian and the pull off force is equal to the one derived by Bradley, P c = 4πγR. The contact radius is then given by
Qualitative analysis of both JKR and DMT models performed by Tabor[16] as well as more detailed analysis based on the Lennard–Jones potential conducted by Muller et al.[17] showed that the contradiction between the models lies in the physical principles of adhesive contact assumed by the authors. Both Tabor and Muller concluded that the adhesive contact of larger, softer bodies with stronger surface interaction can be described by the JKR model, while the DMT model is applicable to the smaller, harder bodies with weaker surface interaction. A parameter μ Footnote 2 was introduced to determine which model is more appropriate:
where z 0 is the equilibrium separation distance, typically 0.16 to 0.4 nm. According to Muller if μ < 1 then DMT is applicable, whereas if μ ≫ 1 it is JKR.
Maugis[18] suggested a smooth transition model between JKR and DMT approaches which exploits the principles of fracture mechanics. Greenwood and Johnson[19] suggested an alternative model to Maugis based on a combination of two Hertzian profiles that also connect both the JKR and DMT models in one general theory. These two models use a parameter, which defines the area where the adhesion force is applicable. The necessity to evaluate this parameter at every time step during particle collision makes it impractical to use either Maugis[18] or Greenwood and Johnson[19] theories in a discrete-element method (DEM) solver. Therefore, in the current paper, the JKR and DMT models are implemented, and the Müller parameter μ is used to determine which one is more applicable.
2.1 Oblique Loading With and Without Adhesion
Hertz theory is used in most of the cases of normal impact of spherical bodies. In the case of oblique impact of bodies, tangential contact forces must be incorporated. Mindlin and Deresiewicz[20] developed the main theory connecting normal and tangential forces with normal and tangential displacements. It is assumed that two elastic spheres in tangential contact experience a partial-slip, where the total force is a combination of elastic tangential force and sliding friction. Once the partial-slip tangential force exceeds the sliding friction force, the bodies slide relative to each other. The tangential force is then equivalent to the sliding friction force F s = ηP, where η is the friction coefficient, and P is the normal load. The distribution of contact traction is illustrated in Figure 1.
Thornton and Yin[21] combined all the major cases of the loading/unloading conditions described by Mindlin and Deresievicz[20] and derived the following expression for the tangential stiffness during oblique loading:
where G * is the combined shear modulus, a is the contact radius, η is the friction coefficient, ΔP is the increment of the normal load, Δδ t is the increment of the tangential displacement, and θ is a parameter defining the ratio of the elastic force to the microslip friction force. The parameter θ depends on the loading history and is defined as follows:
where T is current value of the tangential force, and T * and T ** are the load reversal points.
Normal elastic stiffness is defined as k n = 2E * a, which follows from the Hertz theory; see Reference 21 for details.
2.1.1 Oblique contact with JKR adhesion
Savkoor and Briggs[22] extended the JKR contact theory to consider the effect of adhesion in the case of oblique loading. It was suggested that applying the tangential force reduces the potential energy by an amount of Tδ τ /2. Adding this term to the JKR energy balance equation modified the contact radius (1) as follows:
It was concluded that in the presence of tangential force, the contacting spheres peel off each other thus reducing the contact area. The peeling process continues until T reaches the critical value of
For the normal load Thornton and Yin[21] have adopted the JKT theory. The stiffness is then evaluated as
where a c = 9πγR 2 /4Ε is the JKR contact radius at the moment of separation (pull off radius).
In the case of oblique loading Thornton and Yin[21] followed[22] in what concerns the peeling process. They, however, assumed that once the peeling process is complete, the contacting bodies operate in the partial-slip regime as described before with the difference that the normal force P is replaced with P + 6πγR.
2.1.2 Oblique contact with DMT adhesion
In this paper it is suggested to combine the Thornton and Yin[21] partial-slip no-adhesion model with DMT adhesion. The DMT theory assumes that the deformed shapes of the contacting bodies remain within Hertzian elastic theory. Therefore, a no-adhesion model[21] was adopted, where the normal force P is replaced with P + 4πγR to account for the adhesion force.
2.2 Modeling the Breaking Up of Nano-particle Agglomerates
The authors developed a simulation of a nano-particle cluster subjected to various forces. Both normal and tangential contact forces were modeled based on Reference 21 and JKR and DMT models of adhesion were adopted.
Two-dimensional densely packed agglomerates of 36 and 37 mono-sized spherical particles were considered as shown in Figure 2. For simplicity, all the forces were assumed acting in the X and Z direction only, and the problem was modeled in two dimensions. Mass, volume, and surface area were, however, evaluated assuming that particles are spherical rather than circular. It is also assumed that the gaps between the particles are filled with metal melt, which can flow around the particles, despite the fact that the particles arrangement and all the forces are two-dimensional. The flow of liquid metal around the particles induces the drag force even on the particles inside the cluster.
2.2.1 Collapsing of gas bubbles
It is known from various sources that ultrasound has a beneficial effect on de-agglomeration of the nano-particle clusters.[2–5,7] This is explained by the phenomenon of acoustic cavitation, which includes the formation, growth, pulsation, and collapse of gas bubbles. These processes are accompanied by the creation of “hotspots”—zones of high temperature and pressure which explain the beneficial effect of ultrasonic vibrations on breaking the clusters and the dispersing of nano-particles.[4]
As a result of the implosive collapse of the bubbles, high amplitude shockwaves are generated. In Reference 7 authors compare the pressure peak occurring as a result of the collapse with the pressure required to separate two individual nano-particles held together by van der Waals and capillary forces. It is however expected that due to complex pair-wise contact interactions between the particles in a cluster, it is more difficult to de-agglomerate a cluster of particles rather than two individual particles. For this reason, the behavior of a cluster of nano-particles subjected to the shockwave is investigated in this paper.
2.2.2 Lateral and spherical pulses
The behavior of the gas bubbles in the presence of the ultrasonic waves is a complex problem depending on multiple parameters, and is not studied in this paper. For simplicity it is assumed that the shockwave generated by the collapse of a gas bubble can be described as a rapidly decaying disturbance of the local velocity which takes form of a lateral pulse with an exponential time dependency. Expressing the shockwave as a velocity pulse allows the concentration of the particles to be taken into account using the Di Felice drag model. The details of the behavior of the gaseous-fluid interface during the bubble collapse are not studied in this paper; therefore, the duration τ of the pulse is covering a wide range from 5 ns to 5 μs in order to investigate a potential effect of the pulse duration. The magnitude of the pulse is defined by the maximum value v 0 which in this paper is ranging from 1 to 1000 m/s. In Reference 7 authors estimated the cavitation pressure peak as 6 × 107 Pa if a bubble of initial size 100 μm collapses, and 1.5 × 1010 if initial size is 1 μm. Using Bernoulli’s equation, these peak pressure values can be correlated with the peak velocities of 225 and 3575 m/s, respectively.
In this paper a possibility is also investigated that the agglomerates of nano-particles contain gas bubbles inside, originating due to poor wettability of the nano-particles and the specifics of the manufacturing process. In the case of collapsing of a bubble inside of the agglomerate, a spherical shockwave is considered radiating from the center of the cluster. A lateral pulse is shown by the V x field in Figure 2(a), whereas a spherical pulse is shown by the V r field in Figure 2(b). Note that in both lateral and spherical cases, the pulse is assumed propagating through the liquid metal in the gaps between the particles. The pulse is transferred to the particles via the drag force according to Di Felice[23] drag model based on the volume fraction of the fluid.
2.2.3 Viscous drag
The momentum of the fluid is transferred on the particles via the drag force. Di Felice’s[23] theory is used to account for the effect of the presence of other particles on the drag force. This theory is based on the size and relative velocity of the particles, properties of the fluid, and the volume fraction of the fluid in the gaps between the particles. The resulting drag force acting on a particle of radius R p is given as follows:[10]
where v f, v p are the velocities of the fluid and the particle, αf is the void fraction value, C d is the drag coefficient, Rep is the particle Reynolds number, μ f and ρ f are dynamic viscosity and density of the fluid, and χ is empirical function. Empirical relationships for C d and χ were established to fit a wide range of particle Reynolds numbers. The void fraction value α f is typically evaluated based on the density of particles in a mesh cell (see e.g.,[10,11]). In the present model, however, the mesh is not defined, therefore the void fraction is evaluated based on the cubic cell 10R p × 10R p × 10R p centered at the particle center.
2.2.4 Interfacial energy
The interfacial energy γ of the contacting particles can be evaluated from the van der Waals attraction force acting between two parallel flat surfaces separated by an equilibrium distance z 0:
where A is the Hamaker constant of the material. If particles are interacting in a medium, then Hamaker constant must be modified according to the rule:
where A 1 and A 2 are the properties of the particles and the medium, respectively.[24] The average separation distance z 0 for contacting solids with close-packed atomic structure can be evaluated as σ/2.5, where σ is the interatomic distance. The typical value of σ = 4 Å yields z 0 = 0.165 nm (see Reference 24, p. 277). Equations [11] and [12] can be used to compute the interfacial energy for most solids and liquids.
This theory is however not applicable to the system that involves liquid metals or other highly conducting fluids due to short-range non-additive electron exchange interaction. For this reason, the interfacial energy values for nano-particles in metal melts are taken from experimental values reported in the literature.[25–29] If surface energy values for both the particle γ sv and melt γ lv are known, then the contact angle ω is used to evaluate the interfacial energy γ sl according to the Young’s equation:
The values of surface and interfacial energy depend on many factors, such as temperature, atmosphere, purity of the substances, time, and measurement technique, which explains inconsistency in the experimental data available in the literature. The main goal of the present study is the development of the DEM-based model describing the behavior of the particle cluster in the metal melt subjected to various external forces, and accurate evaluation of the interfacial energy is out of the scope of the present research. The values used in the paper and their sources are provided in Table I.
2.2.5 Brownian motion
Brownian motion is modeled as random velocity fluctuations v b added to the current velocity value of each particle in both X and Z directions. The maximum value of these fluctuations is evaluated by equating the Brownian potential energy with average kinetic energy of the particle:
where T is the temperature of the melt, k = 1.38 × 1023 is the Boltzmann constant, and ρ p and R p are the particle density and radius, respectively. For Al2O3 and SiC particles in Al [melting point T ≈ 933 K (660°C)], the average v b value is given in Table II. It is clear from Table II that Brownian motion is significant for particles of radius below 100 nm.
2.2.6 Test cases
A series of simulation experiments were conducted using Al2O3 and SiC particles in Al melt subjected to the velocity pulse caused by the gas bubble collapse. Sizes of the particles were 10 to 1000 nm. The maximum value and the duration of the pulse ranged from 1 to 1000 m/s and 5 to 5000 ns, respectively. Three models of contact used were, namely JKR, DMT, and no adhesion.
2.2.7 Agglomeration rate
In order to assess the efficiency of the de-agglomeration process, weights are assigned to all pairs of particles according to the distance between them. The agglomeration rate value is then defined as average of these weights:
where n is the number of particles, i, j = 1…n are the particle indices, d ij is the distance between ith and jth particles, and W is the weighting function. Weights are evaluated in such a way that the particles which are in contact or close to each other and therefore are likely to re-agglomerate, contribute the most to the total sum. Weights are provided in Table III. The agglomeration rate of the group of particles after the treatment is then scaled by the agglomeration rate of the initial cluster shown in Figure 2 so that AGR = 1 means no effect of the treatment and AGR = 0 means complete de-agglomeration (i.e., all the pair-wise distances between the particles are >5R). As demonstrated in the results section, agglomeration rate is a good indicator of the global de-agglomeration.
In addition to the agglomeration rate, the number of sub-clusters of particles formed after the incidence of the pulse is counted. Considering the initial cluster of 36 (for spherical pulse) or 37 (for lateral pulse) particles, the number of sub-clusters equal to 1 means no de-agglomeration, while 36 (37) sub-clusters indicate that all the particles are isolated which means total de-agglomeration.
3 Results and Discussion
3.1 The Effect of the Contact Model
Figure 3 shows the agglomeration rate values after the incidence of the velocity pulse. The pulse duration is 50 ns, and SiC particles with γ sl = 0.2 J/m2 and radius 50 nm are considered. Figure 4 illustrates the corresponding positions of the particles. Here and henceforth the particles belonging to the same sub-cluster are colored and numbered for convenience. Individual particles are colored red and have unique numbers. As expected, the no-adhesion model predicts better de-agglomeration, i.e., larger number of isolated particles (Figure 4) and lower agglomeration rate (Figure 3). The agglomeration rate values predicted using DMT are higher than those given by JKR. This is explained by the higher pull off force given by the DMT model. Despite the fact that for the amplitudes of 1 and 10 m/s DMT predict visually better de-agglomeration, the agglomeration rate values indicate that particles are more densely packed and therefore are less likely to be separated. It can be visually observed in Figure 4 that particles tend to form chains of particles in the JKR case and more compact sub-clusters when the DMT model is used. This can be explained by the JKR assumption that bodies do not separate as soon as the pull off force is exceeded, but stretch while maintaining contact. This extends the separation process and allows particles to re-agglomerate. The analysis of the adhesion models clearly demonstrates that choice of the model may significantly affect the prediction of de-agglomeration. Adhesion models were compared in the case of lateral pulse as well, which is not shown in the paper. The agglomeration rate values follow the same trend; however, the difference in the structure of sub-clusters is not observed. This is explained by the dominating motion along the X axis as a response to the propagation of the lateral pulse.
The effect of the adhesion model on de-agglomeration. Spherical pulse, duration 50 ns, maximum velocity 1 to 50 m/s, SiC particles with γ sl = 0.2 J/m2, radius 50 nm. Red filling and unique numbers indicate isolated particles, other colors and non-unique numbers indicate that particles form a sub-cluster
3.2 The Effect of Impulse Duration and Amplitude
Figure 5 shows the agglomeration rate for the case of spherical velocity pulse of maximum velocity values 1 to 1000 m/s and durations of 5 to 5000 ns. The DMT model of adhesion is used and 50 nm SiC particles with hypothetical value γ sl = 0.2 J/m2 are considered. Figure 7 illustrates the corresponding particle positions. The obvious tendency is that better de-agglomeration is achieved for higher maximum velocity values, which can be observed from both Figures 5 and 7. The effect of the duration of the impulse is expected to follow the same tendency, i.e., the pulse of the highest duration is expected to be the most effective in de-agglomeration. This tendency is however broken by the pulses of 5-μs duration, making the 500 ns pulses the most effective. From this observation, it can be concluded that not only the maximum value of the pulse affects the result but also the growth rate. The slow changing velocity in the case of 5 μs pulse does not create conditions for breaking the agglomerate.
Another interesting effect of the duration of the pulse is the local separation of particles. Pulses of 5 and 50 ns durations overall give worse de-agglomeration than the 500 ns one (higher agglomeration rate in Figure 5); however, it is visually observed that the local separation of the particles is better, i.e., more particles are isolated. This can be confirmed by Figure 6, where the number of sub-clusters is shown. Considering a total of 36 particles initially, 36 sub-clusters indicate that all the particles are isolated (Figure 7).
For the pulses of amplitudes 50 and 100 m/s, the durations of 5 and 50 ns are more effective in breaking the individual connections between the particles than the 500 ns pulse, which in turn is more effective in overall de-agglomeration. From this observation it can be concluded that shorter pulses can be more efficient for local de-agglomeration, while longer pulses result in better global de-agglomeration (Figures 5 through 7).
The local de-agglomeration can also be observed in a series of experiments based on lateral pulse of the maximum values 1 to 1000 m/s and duration 5 to 5000 ns using SiC particles of the same size 50 nm and interfacial energy γ sl = 0.2 J/m2. The agglomeration rate and the number of sub-clusters for these cases are given in Figures 8 and 9 respectively, and the corresponding positions of particles in Figure 10. The longest pulse, 5 μs, is the least effective in all of the cases. This is explained by the fact that clusters of nano-particles respond to the lateral pulse by moving as a whole. Short impulses nevertheless are capable of breaking the local connections between the particles as shown by the 50 ns pulse in the cases of 50, 500, and 1000 m/s in Figure 9. It is suggested that the duration of the pulse optimal for local separation depends also on the size of the particles and the number of particles in the cluster.
3.3 The Effect of the Interfacial Energy
In this section, the results are shown for SiC particles of radius 50 nm with various interfacial energy values as given by Table I. Figures 11 and 12 show the agglomeration rate values and the number of sub-clusters, while Figure 13 illustrates the particle positions after the incidence of the spherical velocity pulse with maximum values of 1 to 1000 m/s and duration 5 ns. The DMT model is used. Two main trends can be observed in Figures 11 and 12 as well as visually confirmed in Figure 13. A clear reduction of the agglomeration rate can be observed with increasing the maximum velocity, as well as obvious improvement of de-agglomeration for lower interfacial energy values.
It can also be noted that higher interfacial energy causes the cluster to break into large pieces, whereas lower interfacial energy results in smaller sub-clusters as well as individual particles. This is illustrated by the bars corresponding to γ sl = 0.2 J/m2 in Figure 12.
3.4 The Effect of the Pulse Shape
Figures 14 and 15 show the comparison of the agglomeration rate values due to spherical and lateral pulses of 5-ns duration and the maximum velocity ranging from 1 to 1000 m/s. Al2O3 particles of 50-nm radius are used. The interfacial energy values are γ sl = 0.2 and 2.1 J/m2, respectively. Both figures indicate that spherical pulse is more effective for de-agglomeration than the lateral one. This is explained by the fact that clusters of nano-particles tend to move as a whole when subjected to the lateral pulse. The observation can be confirmed visually in Figures 16 and 17 for γ sl = 0.2 and 2.1 J/m2, respectively. Comparing Figures 16 and 17 also confirm the effect of the interfacial energy on de-agglomeration: lower value γ sl = 0.2 J/m2 clearly demonstrates lower agglomeration rate which means better de-agglomeration of the particles. The tendency of the cluster with lower energy particles to break into smaller pieces or isolated particles, rather than larger pieces in the case of higher interfacial energy, can also be observed. It is also interesting to compare the lower row of Figure 16 with the top row of Figure 13, where the configuration parameters are the same, including the interfacial energy, and the only difference is the particle material. It can be seen that the figures are very similar, from which it can be concluded that elastic properties of the materials play less important role than the interfacial energy.
3.5 The Effect of the Brownian Motion
In this section, the effect of the Brownian motion on de-agglomeration is investigated. The effect of the Brownian motion on the particles of various sizes is estimated in Table II. Figures 18 and 19 compare the de-agglomeration due to spherical pulse including and excluding the effect of the Brownian motion. SiC particles of 10-nm radius, γ sl = 0.2 and 0.9 J/m2 are used in these cases, subjected to the spherical pulses of 5 ns duration and amplitudes 1 to 100 m/s. Figure 18 illustrates the case of the higher interfacial energy, γ sl = 0.9 J/m2. It can be seen, that the Brownian motion has little or no effect on de-agglomeration. Figure 19 illustrates that the lower interfacial energy allows the particles to re-agglomerate and forms new clusters. The particle dispersion is not improved and even worsened by the Brownian motion in Figure 19 for the pulse amplitudes from 1 to 10 m/s. Amplitudes of 50 and 100 m/s, however, demonstrate significant effect of the Brownian motion on dispersion of the particles. It can be concluded therefore that the Brownian motion does not improve de-agglomeration and cannot break-up clusters of nano-particles. If however clusters are broken by the velocity pulse, Brownian motion significantly enhances the separation of the particles.
The effect of the particle size on de-agglomeration in the presence of Brownian motion is illustrated in Figure 20, where particles of sizes from 10 to 500 nm are used. The decreasing effect of the Brownian motion with increasing the particle size can be observed by comparing Figures 20 and 21. It is clear that for particles of radius larger than 100 nm, there is no apparent effect of the Brownian motion, as predicted by Table II.
3.6 The Effect of the Particle Size
Apart from the Brownian motion which clearly depends on the particle size, other driving forces of de-agglomeration are affected as well. Higher surface area to volume ratio of smaller particles is expected to enhance the surface interaction forces. Di Felice drag force is proportional to the cross-section area of the particle and therefore larger particles are expected to experience higher drag than the smaller ones. In addition, the combined elastic and frictional forces between the particles during the oblique impact are affected by the contact area and thus by the particles size. For this reason, the effect of the particle size on de-agglomeration is investigated in this section.
Figure 22 shows the agglomeration rate after applying a spherical pulse of 5-ns duration to the cluster of SiC particles of 10 to 500 nm radii. Figure 23 shows the corresponding particle positions. In Figure 22, the cases of 1, 10, and 50 m/s pulse amplitude demonstrate the clear tendency of the increasing agglomeration rate for increasing radii of the particles. The opposite tendency is observed for the cases of 500 and 1000 m/s amplitude: the smaller particles show higher agglomeration rate, i.e., worse de-agglomeration. In Figure 23, it can be seen that smaller particles form large sub-clusters, while larger particles form smaller sub-clusters or remain isolated. Pulses of amplitude below 100 m/s separate the sub-clusters of smaller particles, which results in low agglomeration rate values. Particles in the sub-clusters, however, remain agglomerated which prevents the agglomeration rate from decreasing further. Similar effect has been observed for lower and higher values of the interfacial energy in Figure 13.
4 Conclusions
A DEM model was developed in order to study the behavior of a nano-particle agglomerate in metal melt under various conditions. In particular, ultrasound processing is considered. It was shown that the high velocity pulses caused by the collapse of the gas bubbles during the ultrasonic treatment are capable of breaking up the agglomerates. The importance of the appropriate adhesive contact model was shown, and the Muller parameter is proposed to determine whether the DMT or JKR model should be used. It was illustrated that de-agglomeration is highly dependent on the interfacial energy values, and that oxidized SiC particles are significantly easier to de-agglomerate than pure SiC. The effects of the duration and the maximum value of the velocity pulse were investigated. It was shown that short pulses are efficient in local separation, while longer pulses result in breaking up the clusters into large pieces. It is suggested that an optimal pulse duration depends on the size of the particles and the number of particles in a cluster. The spherical and lateral pulses were compared which demonstrated that the spherical pulses are more efficient for de-agglomeration than the lateral ones due to the tendency of the cluster to move as a whole if subjected to the lateral pulse. The effect of the particle size has also been investigated. It was shown that clusters of smaller particles are easier to de-agglomerate. Smaller particles, however, form large sub-clusters and result in poor local separation despite showing effective global de-agglomeration. The effect of the Brownian motion on de-agglomeration of particles of various sizes was studied and it was concluded that only de-agglomeration of particles smaller than 100 nm is significantly affected by the Brownian motion. This detailed study of the particle–particle interaction forces under various conditions is expected to help optimizing the electromagnetic stirring and the ultrasonic processing of the metal melt with added nano-particles.
References
I.A. Ibrahim, F.A. Mohamed, E.J. Lavernia, J Mater Sci, 26 (1991), 1137-1156
S. Vorozhtsov, D. Eskin, A. Vorozhtsov, and S. Kulkov: in Light Metals 2014, J. Grandfield, ed., TMS, Warrendale, PA, 2014.
J. Tamayo-Ariztondo, S. Madam, E. Djan, D. Eskin, N. Babu, and Z. Fan: in Light Metals 2014, J. Grandfield, ed., TMS, Warrendale, PA, 2014.
Y. Yang, J. Lan and X. Li, “Study on bulk aluminium MMNC fabricated by ultrasonic dispersion of nano-sized SiC particles in molten aluminum alloy” Materials Science and Engineering A, 380(2004), 378–383.
M. Soltani and G. Ahmadi, “On particle adhesion and removal mechanisms in turbulent flow” Journal of Adhesion Science and Technology, 8(7), (1994), 763-785.
R. S. Bradley, “The Cohesive force between Solid Surfaces and the Surface Energy of solids” Phil. Mag. 13(1932), 853–62,
X. Li. Y. Yang, and D. Weiss: in Ultrasonic Cavitation Based Dispersion of Nanoparticles in Aluminum Melts for Solidification Processing of Bulk Aluminum Matrix Nano-composite: Theoretical Study, Fabrication and Characterization, AFS Transactions, American Foundry Society, Schaumburg, IL (2007)
D. Zhang, L. Nastac, J. Mater. Res. Technol., (2015) doi:10.1016/j.jmrt.2014.09.001.
G. Djambazov, V. Bojarevics, B. Lebon, and K. Pericleous: in Light Metals 2014, J. Grandfield, ed., TMS, Warrendale, PA, 2014.
C. Goniva, C. Kloss, A. Hager, G. Wierink, and S. Pirker: 8th International Conference on CFD in Oil & Gas, Metallurgical and Process Industries, SINTEF/NTNU, Trondheim Norway, 21–23 June 2011
A. Hager, C. Kloss, S. Pirker, and C. Goniva: ., “Parallel Resolved Open Source CFD-DEM: Method, Validation and Application” The Journal of Computational Multiphase Flows, 6(1), (2014), 13-27.
Derjaguin, B (1934) Kolloid-Z, 69, 155-164.
Johnson, K. L. “A note on the adhesion of elastic solids”, British Journal of Applied Physics (1958), 9, 199-200.
K.L. Johnson, K. Kendall and A.D. Roberts, “Surface Energy and the Contact of Elastic Solids” Proc. R. Soc. A 324 (1971), 301–13
B.V. Derjaguin, V.M. Muller and Y.P. Toporov, J. Coll. Int. Sci., 53(2) (1975) 314–326
D. Tabor, J. Colloid Interface Sci. 58(1) (1977) 2–13
V.M. Muller, V. S. Yushenko and B.V. Derjaguin, J. Colloid Interface Sci. 77(1) (1980) 91–101
D. Maugis J. Colloid Interface Sci. 150(1) (1992) 243–269
J. A. Greenwood, K. L. Johnson, “An alternative to the Maugis model of adhesion between elastic spheres” J. Phys. D: Appl. Phys., 31(1998), 3279–3290
R. D. Mindlin and H. Deresiewicz, (1953) J. Appl. Mech. Trans. ASME, 20, 327–344.
C. Thornton, K. K. Yin, “Impact of elastic spheres with and without adhesion” Powder Technology, 65(1991),153-166
A.R. Savkoor and G. A. D. Briggs, “The Effect of Tangential Force on the Contact of Elastic Solids in Adhesion” Proc. Roy. Soc. A 356 (1977), 103
R. Di Felice (1994) Int. J. Multiphase Flow 20(I), 153-159
J. N. Israelachvili, Intermolecular and Surface Forces, (Academic Press, New York, 1985), 253.
G.R. Edwards and D.L. Olson: Annual Report, Center for Welding and Joining Research, Colorado School of Mines (1990), pp. 19, 26–27.
S.Y. Oh: Ph.D. Thesis, Department of Material Science and Engineering, MIT, 1987, p. 192.
B.J. Keene “Review of Data for the Surface Tension of Pure Metals”, International Materials Reviews 38-4, (1993), pp 157-192
J. J. Brennan, J. A. Pask, “Effect of Nature of Surfaces on wetting of Sapphire by Liquid Aliminum”, J. of The Americal Ceramic Society 51-10, (1968), pp 569-573
S. Bao, K. Tang, A. Kvithyld, T. Engh, and M. Tangstad: “Wetting of Pure aluminum on Graphite, SiC and Al2O3 in Aluminum Filtration”, Trans. Nonferrous Met. Soc. China 22 (2012), pp 1930-1938
Acknowledgments
The authors acknowledge financial support from the ExoMet Project (co-funded by the European Commission (contract FP7-NMP3-LA-2012-280421), by the European Space Agency and by the individual partner organizations).
Author information
Authors and Affiliations
Corresponding author
Additional information
Manuscript submitted November 18, 2014.
Rights and permissions
About this article
Cite this article
Manoylov, A., Bojarevics, V. & Pericleous, K. Modeling the Break-up of Nano-particle Clusters in Aluminum- and Magnesium-Based Metal Matrix Nano-composites. Metall Mater Trans A 46, 2893–2907 (2015). https://doi.org/10.1007/s11661-015-2934-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11661-015-2934-0




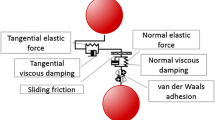

 indicates zone where elastic tangential force is applicable,
indicates zone where elastic tangential force is applicable,  indicates the microslip area
indicates the microslip area




















