Weibull Analysis of Mechanical Data for Castings: A Guide to the Interpretation of Probability Plots

Abstract

The Weibull statistics used in the analysis of mechanical data from castings are reviewed. The insight that can be gained from the three-parameter analysis is introduced, and in particular, the meaning of the threshold value in the three-parameter Weibull distribution from a casting process standpoint is discussed. Weibull mixtures, which are necessary when different defect populations are present in castings, are discussed in detail. Data sets from the literature are reinterpreted for demonstration of the guidelines. Step-by-step procedures are outlined for analysis of Weibull mixtures and for fatigue life data sets with run-outs. The results indicate that knowledge of the casting process is necessary for the accurate interpretation of Weibull probability plots. Because the filling systems of most castings currently are designed poorly, a mixture of Weibull distributions can be expected to be the norm rather than the exception. A single Weibull distribution can be expected only in castings whose filling systems were designed so that no new damage to liquid metal takes place during filling.

1 Introduction

All statistical models that address the phenomenon of fracture are built on the concept first introduced by Griffith[1] that the difference between the ideal and actual performances is attributable directly to the presence of defects (flaws) weakening the structure. Hence, the statistical distributions of fracture-related mechanical properties, i.e., fracture stress, elongation, fracture toughness, fatigue life, etc., can be linked to the defect distribution. Statistically, this implies that the worst (largest) defect is the one that determines the fracture-related mechanical properties,[2] which constitutes the “weakest link,” based on the theory developed by Pierce.[3] The “weakest link” theory applies in situations that are analogous to the failure of a chain when one of its links has failed.[4] Based on the “weakest link” theory, Wallodi Weibull[5–7] introduced an empirical distribution that has since been applied widely to ceramics and metals. The cumulative probability function of the Weibull distribution is expressed as follows:

$$ P = 1 - \exp \left[ { - \left( {{\frac{{\sigma - \sigma_{\text{T}} }}{{\sigma_{0} }}}} \right)^{m} } \right] $$

(1)

where P is the probability of failure at a given stress (strain, fatigue life, etc.) σ or lower. The threshold value σ_T is the value below which no specimen is expected to fail. The term σ₀ is the scale parameter, and m is the shape parameter, which is referred to alternatively as the Weibull modulus.

One of the most commonly used methods of presenting the Weibull fits to data is the Weibull probability plot. After rearranging, Eq. [1] can be written as

$$ \ln \left[ { - \ln \left( {1 - P} \right)} \right] = m\ln (\sigma - \sigma_{\text{T}} ) - m\ln (\sigma_{0} ) $$

(2)

Note that Eq. [2] has a linear form when the left-hand side of the equation is plotted vs ln(σ–σ _T) with a slope of m and an intercept of –m ln(σ ₀). Alternatively, the Weibull probability plot can be obtained when the left-hand side of the equation is plotted vs ln(σ). This method of presentation gives a straight line relationship only when σ _T = 0. This is demonstrated in Figure 1, in which three Weibull distributions are plotted. Note that the trend of the curve at low values of ln(σ) is influenced by the value of the threshold σ _T; a positive threshold results in higher slope at low values of ln(σ). When the threshold is negative, however, the slope decreases with decreasing ln(σ). An example for each type is presented in Figure 2, which shows the elongation (e _F) of sand cast 319,[8] permanent mold- and ablation cast A356.[9] The Weibull parameters for the three data sets were estimated by using the maximum likelihood (ML) method, the details of which are provided in Appendix 1. Note that all estimates in this study were made using the ML method except in Appendix 2. Probability was assigned to each data point by using the following plotting position formula:

$$ P = {\frac{i - 0.5}{n}} $$

(3)

where i is the rank in ascending order and n is the sample size. In Figure 2, the elongation of sand-cast 319 is lower than the other two data sets and the data indicate a straight line. The ablation cast A356 data have the highest elongation and indicate the presence of a positive threshold, meaning that no elongation results lower than 5.1 pct are predicted. In contrast, the elongation of A356 castings poured into a permanent mold has a negative threshold, indicating that elongations down to zero are possible.

Fig. 1

The probability plot for three Weibull distributions showing the effect of the threshold value

Fig. 2

The Weibull probability plot for the elongation of three aluminum casting data sets: sand cast 319 (Δ)[8] as well as A356 cast in permanent molds (_*) and by the ablation process (O).[9]

A detail that may be useful to acknowledge at this early stage is that the weakest link is not necessarily the largest defect, because the macro- and micro-location may have an important influence on its effectiveness. Nevertheless, in this account, the usual identification of the weakest link with the largest defect will be assumed for convenience. This assumption will be made for strength and ductility, for which there is ample evidence for the double effect of either largest defect or volume fraction of defects.[10]

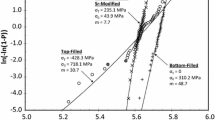
Green and Campbell[11] showed that the tensile strength (S _T) of A356 castings alloys follows a Weibull distribution and that the filling system design has a strong effect on the Weibull modulus (assuming σ _t = 0). Their results for turbulently (top-filled [TF]) and quiescently filled (bottom-filled [BF]) castings are presented in Figure 3. The Weibull parameters are also indicated with threshold taken as zero for both data sets. The fit for the BF castings is good, whereas the one for TF castings, the difference between the data and fit is noteworthy, mainly because a different slope indicated by the lowest points. Consequently, the two-parameter Weibull fit to this data set can be rejected when formal goodness-of-fit tests are used.[12] Since the Weibull analysis presented by Green and Campbell was published, the two-parameter Weibull modulus has been used extensively to characterize the tensile properties, especially tensile strength. According to Campbell,[13] m is often between 1 and 10 for pressure die castings, and between 10 and 30 for many gravity-filled castings. For good quality aerospace castings, m is expected to be between 50 and 100. It is necessary to note that these data refer to an analysis by the two-parameter Weibull statistics.

Fig. 3

Weibull probability plot for the tensile strength of Al-7 pct Si-Mg alloy castings filled turbulently (TF) and quiescently (BF), as reported by Green and Campbell.[11]

Since the results of Green and Campbell[11] were published, the two-parameter Weibull distribution has been used extensively in the casting literature to characterize fracture-related mechanical properties such as tensile strength (S _T),[14] elongation and fatigue life (N _f),[15–17] without determining whether σ _T is indeed zero. Some issues need to be addressed concerning this approach. Many data sets presented in the literature show the tendency for the two-parameter plots to steepen in slope at lower values, providing strong evidence of a threshold value above zero and therefore suggesting that a three-parameter Weibull analysis would be more appropriate. Conversely, in some data sets, the slope of the relationship implied by the data decreases at low values, as evidenced by the permanent mold castings in Figure 2 as well as the TF castings in Figure 3. Hence some guidelines for Weibull analysis of mechanical data for castings will be beneficial encouraging the reanalysis and reinterpretation of some data sets. This article is intended to provide guidance on the interpretation of Weibull probability plots for mechanical properties of castings.

2 The Effect of Threshold

2.1 Positive Threshold

The first known fits of the three-parameter Weibull distribution to mechanical data were given by Weibull[5] to the tensile strength (S _T) data for aluminum die castings.[18] The Weibull probability plot for the tensile strength of aluminum die castings is presented in Figure 4. The fit obtained by the ML method as well as the one originally reported by Weibull[5] are given. Weibull suggested that σ _T be varied iteratively until the linear form given in Eq. [2] is obtained. The two methods give very similar fits, especially at high values of S _T.

Fig. 4

Weibull probability plot for the tensile strength data of aluminum die castings reported by Shewhart.[18] The fit obtained by the ML method (solid curve) and that obtained originally by Weibull[5] by changing the threshold value systematically (dashed curve) are also indicated

For Weibull probability plots to be interpreted correctly, a relationship between maximum defect size and mechanical property is necessary to link the distributions of defect size and the mechanical property of interest. A relationship between fracture stress, σ _F, and maximum defect size a was suggested by Gruenberg et al.[19] based on elastoplastic and linear elastic fracture mechanics, and was applied successfully[20] to A356 castings. The effect of defect size a distribution on the statistical distribution of fracture stress (σ _F) is shown schematically in Figure 5, with the curve showing the relationship suggested by Gruenberg et al. The threshold value corresponds to the flaw size where the probability of finding a larger flaw is practically zero. For the Weibull distribution to have a positive threshold, this critical flaw size should be relatively small. Hence the mean and the standard deviation of the maximum flaw size distribution should be low as well. These conditions can be met in castings only when (1) the melt quality is high and the damage to liquid metal from ingot and prior processing is low, resulting in low number of small “old” bifilms, and (2) the filling system of the casting is designed such that no additional damage via the formation of “young” bifilms takes place.[21]

Fig. 5

Schematic illustration of the effect of a single defect size distribution on the distribution of fracture stress (σ _F). The threshold value σ _T is also indicated

One fundamental concern regarding the use of the two-parameter Weibull approach that can lead to misleading conclusions has been illustrated recently by the Zahedi et al.[8] When σ _T is assumed to be zero, as in the two-parameter fits, there is a probability that the fracture stress of a metallic specimen will be predicted to be less than the yield stress, even if the specimen has reached and deformed plastically beyond the yield stress. One author showed that in the two-parameter Weibull model, the ratio of the average to the standard deviation is a function only of m.[22] Increases in the average and/or decreases in the standard deviation increase the value of m. Hence, a higher m value does not necessarily mean higher repeatability or reliability. To illustrate this point, a fictitious increase of 50 MPa was introduced by Zahedi et al. to every tensile strength data, and two- and three-parameter Weibull distributions were fitted to the fictitious data. The results are presented in Figure 6. For the two-parameter Weibull case, shown in Figure 6(a), the stress σ ₀ increases by 50 MPa and m increases from 46.5 to 56.6. In the three-parameter case in Figure 6(b), σ ₀ and m remain constant, but σ _T increases 50 MPa. Hence, what should cause a true shift in only threshold stress (in the three-parameter case) changes, misleadingly, both the scale parameter and the Weibull modulus of the three-parameter fit. It was shown by Fok et al.[23] that the Weibull modulus obtained from a two-parameter fit to data coming from a three-parameter distribution is affected strongly by the threshold stress and can be two orders of magnitude higher than the true m derived from a three-parameter analysis.

Fig. 6

The tensile strength of 319 alloy castings and the fictitious 50 MPa increase.[8] The three-parameter (a) and two-parameter Weibull fits are also indicated

2.2 No Threshold

Holland and Zaretsky[24] investigated the fracture stress of A357-T6 castings with large sample sizes (up to n = 388) and found that the threshold can be taken as zero. This finding lends support to the assumption made in the casting literature that there is no threshold. From a statistical point of view, σ _T can be taken zero when (1) the Newton-Raphson method does not converge on a solution for Eqs. [A.1] through [A.3] in Appendix 1, or (2) when the estimated threshold value is close to zero. From a casting process point of view, the absence of a threshold indicates that the upper tail of the defect distribution is at relatively high values. Two such distributions are shown schematically in Figure 7. In both cases, the resultant fracture stress distribution has a low or no threshold. For illustration, the K _Ic data for A357-T6 castings as reported by Zinkham[25] are analyzed for both two- and three-parameter Weibull distributions in Figure 8. Note that both fits represent the distribution equally well. The threshold of 11.3 MPa.m^1/2 is significantly lower than the minimum value in the data set (18.7 MPa.m^1/2). It should be noted that the yield strength of all specimens is around 300 MPa and the maximum value in this data set is 23.8 MPa.m^1/2. Tiryakioğlu[26] showed that the plane strain fracture toughness of cast Al-7 pct Si-Mg alloys without structural defects, K_Ic(int) (in MPa.m^1/2) can be estimated by

$$ K_{\text{Ic(int)}} = 50.0 - 0.073\,\sigma_{Y} $$

(4)

Equation 4 estimates a fracture toughness of 28.1 MPa.m^1/2 for Al-7 pct Si-Mg castings without casting defects when σ _Y  = 300 MPa. Therefore, it can be concluded that the maximum defect size distribution in the castings studied by Zinkham was similar to the one drawn with solid line in Figure 8. Similarly, the elongation values for 319 presented in Figure 2 are significantly lower than those for A356, which indicates larger defect sizes and/or higher volume fraction of defects.

Fig. 7

Schematic illustration of two defect size distributions and the resultant distributions of fracture stress with no threshold value

Fig. 8

Weibull probability plot analysis for K_Ic of A357-T6 castings as reported by Zinkham.[25] Two- and three-parameter Weibull fits are equally adequate, although it should be noted that the fitted parameters are significantly different

Deciding whether to use a two- or three-parameter Weibull distribution is an important step. When both types represent the data equally well, it is desirable to use the two-parameter version because it is easier to estimate the parameters. However, it is recommended that both versions be considered and even small details should receive attention, especially when the threshold is not too far away from zero.[27] The benefit of having a positive threshold is great, and one may lose valuable information when the threshold is assumed to be zero. It is probably this reason that the use of a threshold value is required in statistical analysis of tensile data for the development of design values (allowables) for metallic materials in standards such as the Military Handbook 5.[28] Zahedi et al.[8] fitted two- and three-parameter Weibull distributions to the tensile strength of 319 alloy castings with four different melt treatments. Zahedi et al. followed the procedure outlined in Military Handbook 5 to calculate A-design allowables for aerospace castings. “A” allowables represent the values for which at least 99 pct of the population are expected to be equal or exceed with a confidence of 95 pct. Zahedi et al. demonstrated that “A” allowables for three-parameter fits are consistently higher than those for two-parameter fits. The differences ranged between 7.7 pct and 14.9 pct. If these were true allowables, these differences would represent valuable weight savings that could be realized by simply using the right statistical approach.

2.3 Negative Threshold

A negative threshold indicates that the slope of the curve decreases at low values of σ. For mechanical properties, a negative threshold is, of course, meaningless. A negative threshold is indicative of the presence of a second defect distribution, which impairs the properties to a greater extent than the one for higher values of σ. The treatment of these multiple defect distributions, however, is complicated and will be discussed in detail in Section II–D.

2.4 Weibull Mixtures

Weibull[5] analyzed the tensile strength of malleable cast iron reported by Pearson[29] after noticing that 15 of the 75 castings were poured at a different location. The Weibull probability plot for the data of Pearson is presented in Figure 9. For the mixture of distributions, Weibull[6] suggested the following form of the probability P of failure:

$$ P = pP_{1} + \left( {1 - p} \right)P_{2} $$

(5)

where p is fraction of the Weibull distribution number 1 in the mixture and subscripts 1 and 2 refer to the two Weibull distributions. The value of p as well as the parameter estimates for the two Weibull distributions are given in Figure 9.

Fig. 9

Reanalysis of the tensile strength of malleable iron castings as reported by Pearson.[29]

The Weibull mixture, which is referred alternatively to as bi-Weibull, in castings is usually a result of multiple defect distributions being present in the structure, impairing properties at different levels, as shown for fatigue life of aluminum castings.[30–32] This process is shown schematically in Figure 10. Evidence for the presence of a Weibull mixture is that the slope in a probability plot (1) decreases significantly as observed for the top-filled castings in Figure 3 or (2) approaches zero and then increases again,[33] like an inflection point. When these clues are taken into account, it can be observed that Weibull mixtures are not uncommon in castings. Cox et al.[34] investigated the effect of top and bottom filling in investment castings with different alloys. For the hot isostatically pressed (HIP) Ni alloy IN939, the authors observed that tensile strength data below 1100 MPa had a much lower slope in the Weibull probability plot than those above 1100 MPa. Consequently, the authors fitted different lines to the two regions.

Fig. 10

Schematic illustration of how two different defect size distributions present simultaneously in castings affect the fracture stress distribution

Turning our attention back to the elongation of A356 presented in Figure 2, the data for permanent mold castings have a lower slope and low values of elongation. Moreover, both permanent mold and ablation cast specimens show an inflection point. Hence, it can be reasonably assumed that both data come from Weibull mixtures. Because the types of defects have not been investigated on the fracture surfaces, we can use Eq. [5] for Weibull mixtures (this point is discussed in detail below). The revised analysis of the A356 elongation data in Figure 2 is presented in Figure 11. Note that the Weibull mixture represents the data well. The ablation cast result is largely unchanged with a threshold minimum elongation revised from 5.1 pct to 6.2 pct; the permanent molded material is now interpreted as no longer having a negative threshold but a positive value at 1.4 pct elongation.

Fig. 11

Reinterpretation of the A356 data sets from Fig. 2

From a process viewpoint, most Weibull plots for mechanical data for castings can be expected to reveal two populations of defects: the original rather fine scattering of defects remaining in suspension in the original poured liquid (prior damage), and the large new bifilms (new damage) that would have been produced during the pour if the filling system was not designed properly. Because the filling systems of many castings are designed poorly, the bi-Weibull can be expected to be the norm rather than the exception. A single Weibull distribution normally can be expected in castings whose filling systems were designed so that no new damage to liquid metal takes place during filling. Therefore, one should take certain process information, such as melt quality and the design of the filling system into account during the Weibull analysis of casting data.

Prior studies[30,31,35,36] have shown that there are multiple defect distributions in castings, including bifilms (both thick and coarse “old,” and thin and fine “young” films) and pores. The treatment of the link between defect size distributions and the resultant Weibull mixture was discussed in detail by Johnson.[37] The three types indicated by Johnson[37] are summarized in Table I (after adapting to three-parameter Weibull), with the mixture methods described by Tarum.[38] According to Johnson,[37] to determine which kind of Weibull mixture is appropriate, (1) the types of defects causing the premature fracture have to be identified on the fracture surfaces, and (2) it should be determined whether the two defect distributions are competing with each other.

Table I Weibull Mixtures for Various Types of Defect Distributions*

Nyahumwa et al.[30] investigated the fatigue life (N _f) variability in Al-7 pct Si-Mg castings and identified the fatigue crack initiator for each specimen. Fatigue failures were attributed to “old” and “young” bifilms; pores and facets were interpreted as slip planes. Consequently, they used the partially concurrent version of Weibull mixtures listed in Table I and attributed the lower distribution to the old bifilms and the upper distribution to slip planes. The results are summarized in Figure 12. Note that the specimens in which failure was attributed to slip planes are now marked as internal defects. These facets are usually associated with defects such as pores,[39] sand inclusions,[40] and inclusions[31,39,41] associated with entrainment of surface of the liquid metal.[42] Critically, Cox et al.[34] and Campbell[43] observed only facets on the fracture surfaces of Ni-base superalloys that had been cast turbulently. Those that had been cast with carefully designed filling systems that avoided the entrainment of the oxide from the liquid surface were free from facets.

Fig. 12

Reinterpretation of the fatigue life data by Nyahumwa et al.[35] Both the “mutually exclusive” and “partially concurrent” versions of Weibull mixtures yield the same fit

Turning our attention back to Figure 12, it is obvious that the two distributions are not overlapping. Hence, there is no competition between the internal defects and the old bifilms on or near the surface of the specimen: The old, coarse bifilms degrade the fatigue life to a greater extent so that when one is present on or near the surface of the specimen, the old oxide bifilm “wins” over internal defects, which is consistent with the results reported.[41,44]

Similar results were reported by Staley et al.[32] who investigated the effect of HIP on the fatigue life of A206-T71 specimens excised from ingots. Staley et al. identified the defects resulting in fatigue failure to be either “old” spinel (MgAl₂O₄) or “young” alumina (Al₂O₃) bifilms. The Weibull analysis of the fatigue life data is presented in Figure 13. Note that the two Weibull distributions are distinctly separate from each other, as in Figure 12. When there is a spinel bifilm in the specimen, there is no competition, and spinel “wins” all the time over alumina. The dominance of spinel bifilms can be attributed to the partial healing of defects associated with young alumina bifilms during the HIP cycle. Because alumina was found to be present in all specimens, the defect distributions are partially concurrent. The fits by the partially concurrent version in Table I are shown in Figures 12 and 13. However, because in both cases the distributions are not overlapping and there is no competition (old films win all the time), the mutually exclusive version in Table I (Eq. [4]) gave identical fit to those indicated in Figures 12 and 13 with the same estimated parameters. Therefore, the mutually exclusive version can be used when there is no overlapping of the two distributions although the defects are partially concurrent in the specimens.

Fig. 13

Weibull probability plot for the fatigue life data for hot isostatically pressed A206-T71 castings.[32] The presence of two defect distributions necessitates the use of the Weibull mixtures approach

When multiple defect populations are clearly noncompetitive as in Figures 12 and 13, the recommended procedure is as follows:

• 1. Group the specimens by the same defect population,

• 2. Fit Weibull distributions to each group,

• 3. Combine the two fits into a single fit by using the same estimated parameters from step 2. If Eq. [5] is used, then adjust only p to obtain the best fit. For “concurrent” version (Table I), there is no need for further adjustment.

Figures 9 and 11 through 13 were obtained according to the previous procedure.

Another statistical issue that needs to be addressed is the presence of run-outs in the fatigue life data sets. For instance, Figure 13 shows two run-outs in which fatigue failure could not be obtained after 10⁷ cycles and the tests were terminated. Consequently, those points in Figure 13 do not represent fracture, and therefore, they need to be treated differently. In statistical terms, those data sets are censored, and their proper treatment is complex. A more statistically inclined reader is advised to the classic papers[45–47] in the literature. However, it is usually sufficient to follow the regression method outlined in Appendix 2. The run-outs should never be disregarded for analytical convenience because extreme points usually provide valuable information. They may indicate the true fatigue potential of the castings.

3 Conclusions

• 1. Deciding whether to use two- or three-parameter Weibull distribution is an important decision. When both types represent the data equally well, it is desirable to use the two-parameter version because it is easier to estimate the parameters. However, it is recommended that both versions be considered, and even small details should receive attention, especially when the threshold is not too far away from zero.

• 2. One should not assume that the threshold is zero. There is valuable insight into the defect distributions in castings that can be obtained from the correct interpretation of Weibull probability plots.

• 3. A negative threshold is indicative of the presence of a second defect distribution, which impairs the properties to a greater extent than the distribution for higher values.

• 4. From a process viewpoint, most Weibull plots for mechanical data for castings can be expected to reveal two populations of defects: the original rather fine scattering of defects remaining in suspension in the original poured liquid (prior damage), and the large new bifilms (new damage) that would have been produced during the pour if the filling system was not designed properly.

• 5. Because the filling systems of most castings currently are designed poorly, the bi-Weibull can be expected to be the norm, rather than the exception. A single Weibull distribution can be expected only in castings whose filling systems were designed so that no new damage to liquid metal takes place during filling. Therefore, one should take process information, such as melt quality and the design of the filling system, into account during the Weibull analysis of casting data.

• 6. The mutually exclusive and partially concurrent versions of Weibull mixtures yield identical fits with the same estimated parameters when the two distributions are distinctly separate and one of the defects always “wins” in initiating failure.

• 7. Run-outs in fatigue life data should be treated differently and should never be discarded for analytical convenience. A simple method to estimate Weibull parameters in data sets with run-outs was demonstrated.

Appendices

Appendix 1. Maximum Likelihood Method to Estimate Weibull Parameters

The ML estimates for the three parameters of the Weibull distribution are obtained by the following equations:

$$ - (m - 1)\sum\limits_{i = 1}^{n} {\left( {\sigma_{i} - \sigma_{\text{T}} } \right)}^{ - 1} + {\frac{m}{{\sigma_{0} }}}\sum\limits_{i = 1}^{n} {\left( {{\frac{{\sigma_{i} - \sigma_{\text{T}} }}{{\sigma_{0} }}}} \right)^{m - 1} } = 0 $$

(A.1)

$$ - {\frac{nm}{{\sigma_{0} }}} + {\frac{m}{{\sigma_{0} }}}\sum\limits_{i = 1}^{n} {\left( {{\frac{{\sigma_{i} - \sigma_{\text{T}} }}{{\sigma_{0} }}}} \right)^{m} } = 0 $$

(A.2)

$$ \frac{n}{m} - n\,\ln (\sigma_{0} )\sum\limits_{i = 1}^{n} {\ln \left( {\sigma_{i} - \sigma_{\text{T}} } \right)} - \sum\limits_{i = 1}^{n} {\left( {{\frac{{\sigma_{i} - \sigma_{\text{T}} }}{{\sigma_{0} }}}} \right)^{m} } \ln \left( {{\frac{{\sigma_{i} - \sigma_{\text{T}} }}{{\sigma_{0} }}}} \right) = 0 $$

(A.3)

These equations are solved simultaneously with an iterative procedure such as the Newton-Raphson method. When the threshold is taken as zero (two-parameter Weibull distribution), the ML estimate for shape parameter m is obtained by solving the following equation:

$$ \sum\limits_{i = 1}^{n} {\ln (\sigma_{i} } ) - n\left( {{\frac{{\sum\limits_{i = 1}^{n} {\ln (\sigma_{i} } )\sigma_{i}^{m} }}{{\sum\limits_{i = 1}^{n} {\sigma_{i}^{m} } }}}} \right) + \frac{n}{m} = 0 $$

(A.4)

The scale parameter can then be estimated by

$$ \sigma_{0} = \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {\sigma_{i}^{m} } } \right)^{{\frac{1}{m}}} $$

(A.5)

Appendix 2. Simple Linear Regression Method for Fitting to Fatigue Data with Run-Outs

Because fatigue testing is interrupted at a predetermined cycle (typically 10⁷), data from any specimen in which fracture has not taken place then (run-out) cannot be treated as fatigue life. Although run-outs may not be included as fatigue data, they represent “survival,” and therefore, their presence can be accounted for in probability of failure. Twenty fictitious results from fatigue tests are given in Table II, including two run-outs at 10⁷ cycles. The data, including the two run-outs, are ranked in ascending order and assigned probabilities by using Eq. [3]. The Weibull probability plot is presented in Figure 14. The best fit is obtained by adjusting σ_T iteratively until the linear form given in Eq. [2] is obtained, as initially recommended by Weibull.[5] This technique was used to determine the best fit to the first eighteen data points, excluding the two run-outs. This way, the presence of the run-outs is accounted for, but the cycle at which fatigue life was interrupted (10⁷) is not taken as fatigue life data.

Table II Data That Include Two Run-Outs for the Demonstration of How Weibull Parameters Can be Estimated in Censored Fatigue Life Samples

Fig. 14

Weibull probability plot for the (censored) fatigue life data in Appendix 2