1 Introduction

1.1 Objective and Previous Work

The microstructure of heat-treatable aluminum alloys developed for aerospace applications is reviewed by Staley[4] and by Tiryakioglu.[5] For the purpose of the present work on 7085-T7X, these structural elements are divided into two groups: microscale and nanoscale. The nanoscale features, such as solutes and strengthening precipitates, interact with dislocations, which are nanoscale defects underlying plastic flow. The present work does not include models at the nanoscale. However the stress-strain relations at macroscale, resulting from structural evolution at the nanoscale, are well characterized by tensile tests conducted on 7085-T7X.

In a toughness test, microscale features such as constituent particles, dispersoids, and grain boundary precipitates[6] act mainly to produce microscale damage during plastic flow. Hahn and Rosenfield[7] pointed out that the reduction of the volume fraction of coarse particles (over 1 μm diameter) drastically improves plane strain fracture toughness. In uniaxial tension, voids nucleate at these particles at very small strains of the order of a few percents.[8,9] Considering the high stress triaxiality at a crack tip compared to uniaxial tension, Hahn and Rosenfield speculated that virtually all the coarse particles engulfed in the plastic zone are damaged. Cracking of smaller dispersoid particles (of the order of 0.1 μm) is nearly concurrent with the crack advance.[10] Rupture at these smaller particles seems to occur during the void link up stage after localization of the strain.

For 7085-T7X, it is therefore assumed that damage nucleates almost immediately after the initiation of plastic deformation, mainly by cracking or by debonding of coarse constituent particles from the matrix. The voids associated with these coarse particles are therefore assumed to contribute to the bulk of the void volume fraction (VVF) increase during plastic deformation. Such damage evolution can be modeled using continuum mechanics.

In the first part of this work,[11] data on plane strain fracture toughness, yield strength, and strain hardening were presented. These were for samples of multiple orientations and locations in aluminum alloy 7085 plates of multiple gages, aged past peak strength with various 2nd step aging times (T7X). These data were fit to an expression adapted from Hahn and Rosenfield.[12] In this model, the influence of the microstructure on toughness was lumped into a single parameter, the critical strain ε c . The influence of the nanostructure was indirectly accounted for by the stress-strain coefficients. The expression gives plane strain toughness K Ic as a function of this strain ε c , the elastic modulus E, yield strength σ y , and a measure of strain hardening. The inferred values of critical strain ε c showed no trend of ε c with aging time, consistent with the assumption that the microstructure does not change with aging time in this case. Dependence of critical strain on test orientation and on through-thickness position was interpreted from available microstructural and fractographic information. Although the formula shows toughness increasing with strength, the change of strain hardening with aging time dominates the change of strength, so there is negative correlation of strength and toughness.

The current article aims to develop a micromechanical foundation for the results in the preceding article.[11] Three requirements were set for this work.

  1. (1)

    The plastic fields near the crack tip are to be calculated by a finite element (FE) model incorporating the actual geometry of the compact tension (CT) test specimen.

  2. (2)

    The microstructure is to be represented by a single parameter, which is independent of aging time.

  3. (3)

    A constitutive model and a toughness criterion are needed, and both must be found consistent with the observed covariance of toughness, strength, and strain hardening with aging time.

1.2 Modeling of Crack Tip and Toughness

1.2.1 Analytical modeling

The stresses and strains at a plane strain crack tip can be approximated using the slip-line field solution for a parallel-sided crack of finite tip radius. Thomason[13] assumed that the material contains microvoids forming at coarse constituent particles. Based on the VVF and the stress triaxiality, he derived a fracture strain profile ahead of the crack tip. When loading is gradually applied, the strains calculated from the slip-line analysis increase and reach the fracture limit. From this analysis, Thomason was able to calculate the distance from the tip at which fracture initiates and the corresponding crack tip opening displacement (CTOD). Then this author obtained the expression for K Ic as

$$ K_{{Ic}} = {\sqrt {r{\left\{ {\frac{{4.62E\sigma _{y} {\left( {\exp \varepsilon _{I} - 1} \right)}}} {{1 - \nu ^{2} }} + 8.81\sigma ^{2}_{y} \tan {\left[ {\frac{\pi } {2}{\left( {1 - \frac{f} {{0.09}}} \right)}} \right]}} \right\}}} } $$
(1)

Here, r is the radius of the crack tip, ε I is the plane strain instability limit (ε I  = n for a power law material), and f is the void volume fraction. Equation [1] is valid for volume fractions between 2 and 9 pct. An important result of this model is that fracture initiates ahead of the crack tip at a distance that depends on the VVF f. This is consistent with experimental observations,[10] as discussed in the preceding article.[11] Fracture will initiate at the tip for void volume fractions equal to 9 pct and higher in Eq. [1].

Unlike other models for the prediction of K Ic (Reference 11), Eq. [1] includes the crack tip radius. Because of blunting the crack tip has a finite radius, which might depend on the flow properties and microstructure of the material. For crack paths which are partially intergranular, the crack tip radius is likely to be influenced by the grain shape and size.

1.2.2 FE modeling

A number of publications[14–18] have reviewed computational aspects of a crack behavior with material descriptions expressed at different length scales, i.e., from continuum to discrete dislocation scales. The FE approaches used to predict K Ic were reviewed by Pardoen and Hutchinson.[19]

The FE modeling of the material behavior at a crack tip and calculation of the plane strain fracture toughness K Ic is a very complex boundary value problem (e.g., References 20 through 22). In principle, it involves a detailed knowledge of the material microstructure and its distribution in the three-dimensional physical space. For instance, FE modeling of fracture involving intergranular separation due to void growth at grain boundary precipitates was performed by Becker et al.[23] and Pardoen et al.[24] However, due to this complexity, a number of simplifications are made leading to three main approaches as reviewed in Pardoen and Hutchinson.[19] These approaches are all based on material damage that leads to softening in the plastic zone at the crack tip. They (1) explicitly account for a few voids near the crack tip, (2) account for the VVF through a continuum potential, and (3) use a cohesive zone model where damage is replaced by a critical stress and work for a crack to propagate. All these models contain a length scale.

For ductile materials, damage is the process of microvoid nucleation, growth, and coalescence. In the materials studied in this work, these voids occur around coarse particles, both constituents and boundary precipitates. As mentioned previously, the debonding is believed to occur at very low strains for the coarsest particles in the plastic zone. An appropriate single parameter to represent the microstructure would be the initial value of VVF, after nucleation and before growth.

Two main factors, plastic strain and stress triaxiality, have long been recognized as influencing at least growth and coalescence.[25,26] The triaxiality is defined as the ratio of the mean stress to the effective stress. Numerical simulations have shown the importance of these parameters on the crack tip behavior (e.g., References 27 through 30). In particular, hydrostatic tension is high near the tip of a crack deformed in plane strain conditions, thus enhancing void growth. Therefore, damage and stress triaxiality are essential parameters to consider for the numerical modeling of plane strain toughness. These parameters are taken into account most effectively with the use of a Gurson-type plastic potential,[1] which corresponds to approach (2) in Pardoen and Hutchinson.[19]

The influence of strain hardening on void growth was investigated analytically by Tracey[31] and Perrin et al.[32] and numerically by Becker,[33] Tvergaard,[34] Faleskog and Shih,[35] and Li et al.[36] One of the landmark studies was carried out by Koplik and Needleman.[37] Based on FE modeling of a cylindrical unit cell containing a spherical void, these authors showed that the VVF increase was hindered by a higher strain-hardening rate. Leblond et al.[3] showed that the VVF increase, as predicted with the Gurson[1]–Tvergaard[2] model (GT model), was independent of strain hardening, in contradiction with the simulation results of Koplik and Needleman. Leblond et al. proposed a modification of the GT model to account for strain-hardening-dependent void growth.

1.3 Article Outline

Section II describes the constitutive modeling of the material samples studied in this work. A few results of Koplik and Needleman[37] on the growth of a void in a unit cell are reproduced to highlight features of relevance to the present work. Then specific plastic potentials that account for VVF are discussed, i.e., the classical flow potential GT model as well as a simplified version of the Leblond et al.[3] model (LPDs).

In Section II, a phenomenological strain-hardening law is also developed to account for the specific behavior of the materials investigated in this work. Finally, the arguments and methods used to identify particular constitutive parameters are explained.

In Section III, the deformation of a CT specimen is simulated using the FE method in order to predict plane strain toughness K Ic . In addition to the geometry, mesh, and boundary conditions, the multiaxial constitutive model developed in Section II is an important input to the FE model. In this work, some of the parameters in the plastic flow potentials were estimated from unit cell computations.

In general, fracture toughness cannot be determined numerically without a fracture criterion. However, the simulations of a deforming CT specimen with a constitutive model that accounts for damage suggest that K Ic corresponds to the actual loading when a plastic flow localization phenomenon initiates near the crack tip. Based on this assumption, plane strain fracture toughness values are computed using strain-hardening data from simple tensile tests in conjunction with the flow potentials.

2 Constitutive modeling

2.1 Unit Cell Modeling

In order to assess the influence of strain hardening on the growth of a void embedded in an elastoplastic matrix, an FE model of a unit cell was investigated. This model, which duplicates the work of Koplik and Needleman,[37] is depicted in Figure 1. A spherical void is located at the centroid of a cylinder. The radius (R) and half-length (L) of the cylinder are unity. The radius (r) of the spherical void is varied to produce the desired level of initial VVF f 0. Values of \( r \mathord{\left/ {\vphantom {r R}} \right. \kern-\nulldelimiterspace} R \) equal to \( 1 \mathord{\left/ {\vphantom {1 8}} \right. \kern-\nulldelimiterspace} 8 \) and \( 1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-\nulldelimiterspace} 4 \) produce f 0 values of 0.0013 and 0.0104, respectively. The model is comprised of 480 4-node full-integration (CAX4) elements (ABAQUS).[38] This provides the same level of discretization that was used initially by Koplik and Needleman. For this particular problem, ABAQUS uses the Cauchy stress, the Jaumann stress rate, and a logarithimic strain. All the necessary rotations are handled by ABAQUS outside of the user subroutine.

Fig. 1
figure 1

FE model for a spherical void in an elastoplastic matrix[37]

Full size image

Axisymmetry and axial symmetry (L direction) were assumed. The loading consisted of uniaxial tension superimposed with hydrostatic tension, which was characterized by the stress triaxiality factor T defined as

$$ T = \frac{{\Sigma _{{kk}} }} {{3\Sigma _{e} }} $$
(2)

where \( \Sigma _{e} = {\sqrt {\frac{3} {2}S_{{ij}} S_{{ij}} } } \) is the average von Mises effective stress of the damaged material (unit cell) and Σ ij and S ij are the average Cauchy and deviatoric stress components applied to the unit cell, respectively. Typically T = 0, 1/3, and \( 2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3 \) for simple shear, uniaxial tension, and balanced biaxial tension, respectively. Near the tip of a crack deforming under plane strain conditions, the stress triaxiality T is roughly between 2 and 3.

In order to understand the sensitivity of the unit cell model, several cases were run with material having hypothetical properties. A Swift-type strain-hardening law was used

$$ \ifmmode\expandafter\bar\else\expandafter\=\fi{\sigma } = C{\left( {\varepsilon _{0} + \ifmmode\expandafter\bar\else\expandafter\=\fi{\varepsilon }} \right)}^{n} $$
(3)

where C, ε 0, and n are constant coefficients and \( \ifmmode\expandafter\bar\else\expandafter\=\fi{\sigma } \) and \( \ifmmode\expandafter\bar\else\expandafter\=\fi{\varepsilon } \) are the effective stress and strain, respectively, of the matrix, which was assumed to behave as a von Mises material. In these examples, the strain hardening varied from none (n = 0) to a significant amount. A typical value of the plastic strain offset ε 0 = 0.01 was selected. The strength coefficient C was adjusted to produce given values of the yield stress.

Figure 2(a) shows the VVF growth from its initial value f 0 = 0.13 pct as a function of the equivalent strain. The VVF is defined as the ratio of the volume of the void to the volume of the cell. The results corresponding to three levels of stress triaxiality T (1, 2, and 3) and two values of strain hardening n (0 and 0.1) are shown in this figure. The yield stress of the matrix is assumed to be equal to 199 MPa. This figure shows the classical result of increasing VVF as strain increases and the strong influence of stress triaxiality. Moreover, it shows that, for a given value of T, the VVF increases more as the strain-hardening exponent decreases.

Fig. 2
figure 2

VVF growth as a function of equivalent strain for three levels of stress triaxiality T (1, 2, and 3) and two values of strain hardening n (0 and 0.1). (a) FE unit cell model (Fig. 1), (b) original LPD model, and (c) simplified model (LPDs)

Full size image

2.2 Flow Potential for Damaged Materials

In order to model the behavior of a damaged material, Gurson[1] proposed a model further generalized by Tvergaard,[2] denoted as the GT model, to describe the plastic behavior of materials containing microvoids

$$ \Phi {\left( {\Sigma_{e}, \Sigma_{m}, f, {\Sigma_0 }} \right)} = {\left( {\frac{{\Sigma _{e} }} {{\Sigma _{0} }}} \right)}^{2} + 2qf\cos h {\left( {\frac{{3\Sigma _{m} }} {{2\Sigma _{0} }}} \right)} - 1 - ({qf})^{2} = 0 $$
(4)

where f and \( \Sigma_{m}\,{\text{=}}\,{\Sigma _{{kk}} } \mathord{\left/ {\vphantom {{\Sigma _{{kk}} } 3}} \right. \kern-\nulldelimiterspace} 3 \) represent the VVF and the mean hydrostatic tension, respectively, Σ e is the equivalent stress of the damaged material, and Σ0 is the yield stress for a perfectly plastic matrix (no hardening) since the model was developed under this assumption. The constant coefficient q accounts for the effects of void interaction. Without any specific information, the recommended value for q is 1.5.[2] Note that when the initial value of f is equal to zero, this plastic potential reduces to that of von Mises.

In order to generalize the GT model to hardening materials, many authors substitute the effective stress of the matrix \( \ifmmode\expandafter\bar\else\expandafter\=\fi{\Sigma } \) for the yield stress Σ0. However, according to Leblond et al.,[3] this generalization leads to a model that cannot describe the influence of strain hardening on VVF growth as predicted with the FE unit cell simulations (Figure 2(a)). Therefore, these authors (see also Leblond[39]) proposed the following modification of the GT model

$$ \Phi {\left( {\Sigma _{e} ,\Sigma _{m} ,f,\Sigma _{1} ,\Sigma _{2} } \right)} = {\left( {\frac{{\Sigma _{e} }} {{\Sigma _{1} }}} \right)}^{2} + 2qf\cos h {\left( {\frac{{3\Sigma _{m} }} {{2\Sigma _{2} }}} \right)} - 1 - ({qf})^{2} = 0 $$
(5)

where Σ1 and Σ2 are now two independent state variables. This model is denoted LPD. Leblond et al.[3] showed that, under high stress triaxiality (for example, pure hydrostatic tension for the sake of simplicity), the plastic strain around a void in a unit cell is very high, which is a hurdle to its growth. These authors showed that Σ2 increases at a faster rate than Σ1. They proposed evolution equations that depend on the plastic strain gradient around a cavity. Since the implementation of these original (LPD) equations in an FE code is not straightforward, Eq. [5] was used in conjunction with a simplified evolution equation for Σ1 and Σ2, i.e., \( \Sigma _{1} = \ifmmode\expandafter\bar\else\expandafter\=\fi{\Sigma }{\left( {\ifmmode\expandafter\bar\else\expandafter\=\fi{E}_{1} } \right)} \) and \( \Sigma_{2}\,{\text{=}}\,\ifmmode\expandafter\bar\else\expandafter\=\fi{\Sigma }{\left( {\ifmmode\expandafter\bar\else\expandafter\=\fi{E}_{2} } \right)} \) (both Σ1 and Σ2 use the same Swift hardening law), where

$$ \begin{gathered} \dot{\overline{E}} _{1} = \dot{\overline{E}} {\left( {1 - 1 \mathord{\left/ {\vphantom {1 {\xi _{1} }}} \right. \kern-\nulldelimiterspace} {\xi _{1} }} \right)} \hfill \\ \dot{\overline{E}} _{2} = \dot{\overline{E}} {\left( {1 - 1 \mathord{\left/ {\vphantom {1 {\xi _{2} }}} \right. \kern-\nulldelimiterspace} {\xi _{2} }} \right)} \hfill \\ \end{gathered} $$
(6)

Here, \( \ifmmode\expandafter\bar\else\expandafter\=\fi{E} \) is the effective strain of the matrix while ξ 1 and ξ 2 are two constant coefficients. Although phenomenological, these evolution equations keep the spirit of the modification proposed by Leblond et al.,[3] which was based on micromechanical considerations. The complete model (Eqs. [5] and [6]) is denoted LPDs, as a simplification of the original LPD model. It was implemented in ABAQUS though the user-defined material subroutine.

Figures 2(b) and (c) show the VVF growth as a function of the equivalent strain of the damaged material for both models (LPD and LPDs), with the set of parameter levels investigated in Figure 2(a). In the original LPD model, the parameter q is equal to 1, while in the simplified model (LPDs) q is set to 1.5. The parameters ξ 1 and ξ 2 are set to 1 and 2, respectively. This identification is not made rigorously nor is the set of parameters unique. The VVF evolutions calculated with these plastic potentials (LPD and LPDs) and with the FE unit cell model can be compared. The evolutions are not in perfect coincidence because these approaches are totally different. The rate of strain hardening seems to increase faster at larger strain with the unit cell model, which might reflect the interaction of the void with the outside boundary of the cell. However, this example shows that both LPD and LPDs model can reproduce some of the features obtained from the FE unit cell simulations. In particular, the VVF growth is higher when the strain-hardening exponent is lower. If \( \ifmmode\expandafter\bar\else\expandafter\=\fi{\Sigma } \) is substituted for the yield stress Σ0 in the original GT model, the VVF growth curves would not depend on strain hardening in this case. In fact, the GT model predictions correspond to the solid lines in Figure 2b, irrespective of the strain-hardening exponent.

2.3 Representation of Strain Hardening

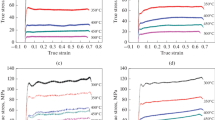
Figures 3(a) and (b) represent the experimental hardening behavior of a 7085-T7X plate, 165.1-mm thick, measured in uniaxial tension in the rolling direction. The derivative of the stress-strain curve \( {d\sigma } \mathord{\left/ {\vphantom {{d\sigma } {d\varepsilon }}} \right. \kern-\nulldelimiterspace} {d\varepsilon } \) was numerically determined based on local approximation by quadratic polynomial. These figures show the same features reported for the 76.2-mm plate in the previous article.[11] For most of the aging times, the rate of strain hardening (Figure 3(b)) exhibits a local maximum at a strain of about 2 pct. This peak reaches higher values of hardening rates as the aging time increases. Strain hardening of this type cannot be approximated by a simple power law such as given by Eq. [3]. Therefore, a phenomenological strain-hardening law was developed specifically for these materials.

Fig. 3
figure 3

Experimental strain-hardening curves in L direction, 7085–T7X plate, 165.1-mm thick. (a) True stress vs true plastic strain. (b) True stress derivative vs true plastic strain

Full size image

The Voce (saturation-type) rate of strain hardening, which usually describes the behavior of aluminum alloys well, is defined as

$$ \frac{{d\ifmmode\expandafter\bar\else\expandafter\=\fi{\sigma }}} {{d\ifmmode\expandafter\bar\else\expandafter\=\fi{\varepsilon }}} = BC\exp {\left( { - C\ifmmode\expandafter\bar\else\expandafter\=\fi{\varepsilon }} \right)} $$
(7)

where B and C are two constant coefficients. In this work, the coefficient B is assumed to be a Gaussian-type function of the strain as schematically represented in Figure 4 and the rate of strain hardening is defined by Eq. [7] with

$$ B = b_{0} {\left\{ {1 - b_{1} \exp {\left[ { - b_{2} {\left( {\ifmmode\expandafter\bar\else\expandafter\=\fi{\varepsilon } - b_{3} } \right)}^{2} } \right]}} \right\}} $$
(8)

where the b k are constants. Therefore, five coefficients (b k ,C) are available to describe the rate of strain hardening. These coefficients are obtained using the least-squares method from the experimental rate of strain-hardening data of Figure 3(b). The whole stress-strain curve is completely defined with an integration constant, which is conveniently taken as the yield stress.

Fig. 4
figure 4

Modified Voce model of strain hardening. (a) Voce model, Eq. [7] and Gaussian, Eq. [8]. (b) Combined hardening rate

Full size image

Table I provides the coefficients for all the stress-strain curves of Figures 3(a) and (b). Figure 5 shows the hardening rate approximations for the 7085-T7X samples with different aging times measured at quarter thickness (t/4) of the 165.1-mm-thick plate. For the sake of clarity, the experimental data is not shown in this figure but comparison with Figure 3(b) shows that they are well approximated by the model. Note that because the behavior after 6 to 7 pct strain is not known, it is assumed that the rate of strain hardening is the same after this amount of strain for all aging times and set equal to the behavior of the sample aged for time τ = 7.5τ PA hours (where τ PA is the peak-aged time). Since the purpose of this work is to show that the hardening difference observed between 0 and 6 pct in these materials has an influence of plane strain toughness, the veracity of the stress-strain extrapolation is not relevant here. Nevertheless, the rate of strain hardening is small for this type of materials and thus, the departure between the extrapolation and the real behavior is not expected to be large. The rate of hardening Eq. [7] was implemented in ABAQUS for use in the unit cell problem.

Table I Coefficients for Modified Voce Strain-Hardening Law for 7085-T7X
Full size table
Fig. 5
figure 5

Hardening rate from coefficients in Table I

Full size image

2.4 Application to 7085-T7X

The FE unit cell model was run for several of the strain-hardening behaviors defined previously. Figure 6 shows the results for two cases, corresponding to relative aging times \( \tau \mathord{\left/ {\vphantom {\tau {\tau _{{PA}} }}} \right. \kern-\nulldelimiterspace} {\tau _{{PA}} } \) of 1 and 5.5. The VVF growth is represented as a function of the equivalent strain for two initial void shapes, a sphere and a prolate ellipsoid (2:1 axis aspect ratio) for the initial VVF f 0 = 0.13 pct and a triaxiality of T = 2.5. For the prolate ellipsoid, the long axis was aligned with the tensile axis because only longitudinal-long transverse (L-T) plane strain toughness is considered in this article. This figure shows that the VVF growth does depend on the initial void shape and on the hardening rate.

Fig. 6
figure 6

VVF as a function of equivalent strain for two initial void shapes, sphere and prolate ellipsoid (2:1 axis aspect ratio), and two relative aging times (\( \tau \mathord{\left/ {\vphantom {\tau {\tau _{{PA}} }}} \right. \kern-\nulldelimiterspace} {\tau _{{PA}} } = 1 \) and 5.5). (a) FE unit cell model and (b) LPDs model

Full size image

The LPDs flow potential was run for the same triaxiality and initial VVF used in the FE unit cell model. The LPDs potential is a continuum description of damaged material and does not explicitly account for a single void or void shapes. It addresses the behavior of a sufficiently large continuum containing numerous voids represented by a VVF. In this work, the parameters of the potential were set in order to match in an approximate manner the results of the FE unit cell model. For the sake of clarity, the results of the LPDs model are reported in Figure 6 for comparison with the prolate ellipsoid only. For this case, which describes the VVF evolution in the toughness simulations (Section III), the coefficients were set to q = 2, ξ 1 = 1, and \( \xi _{2}\,{\text{=}}\,1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3 \). This choice is arbitrary but it is motivated by the existence of microstructural fibering inherently present in this type of material whether in the form of void shape or cluster of voids. Although the absolute VVF growths obtained with the unit cell and LPDs models are not the same, these parameters were set such that the difference in VVF growth for the two aging times was approximately the same in each of the two models (for instance, a 0.4 pct growth difference between the two materials at a strain of 0.09 is indicated in Figure 6).

Although the choices and assumptions made in this section to develop a constitutive description for the 7085-T7X plates can be disputed, the material model is well defined. The stress-strain behavior takes into account the local maximum of the strain-hardening rate observed at about 2 pct strain for these materials. The plastic potential LPDs, with parameters set once for all the plate samples to the values given in the previous paragraph, is able to account for the influence of hardening on VVF growth, unlike the GT model.

3 FE Modeling of plane strain fracture toughness

3.1 CT Specimen Modeling

The deformation of a CT specimen used in Reference 11 was analyzed. The FE code ABAQUS[38] was used to perform the numerical modeling. The mesh for a standard 76.2-mm-thick CT specimen is shown in Figure 7. The distance from the load line to the crack tip is 76.2 mm. The crack tip (Figure 7) is modeled as a blunted surface with a constant radius. The radius is varied between 2.54 and 25.4 μm. For finite strain crack problems ABAQUS[38] recommends a crack tip radius on the order of 10−3 r p , where r p is the size of the plastic zone. For the problems considered here, the plastic zone size at a load corresponding to K Ic is of the order of 2 mm. Hence, the crack tip radii used are slightly larger than the recommended value. The size of the elements comprising the notch should be roughly 1/10 of the notch tip radius, which is approximately the element size used in these analyses. The elements around the notch are skewed in the radial direction because with loading, the crack tip blunts driving the aspect ratio of these elements closer to unity. Plane strain conditions are assumed. Single-point reduced integration elements are used (CPE4R). Symmetry is assumed about the crack plane. Loading is applied through concentrated forces on one node in the pin hole in the vertical direction. The constitutive model developed in Section II is implemented in ABAQUS as a user subroutine. The plastic potential LPDs reduces to the GT potential with an appropriate choice of the coefficients ξ 1, ξ 2, and obviously to von Mises when the initial VVF (f 0) is set to zero.

Fig. 7
figure 7

FE mesh for a standard 76.2-mm-thick CT specimen

Full size image

To validate the model it was first used with the von Mises potential. Figure 8 shows the effective strain profile at the tip of a crack for different levels of loading defined by the normalized value \( {K_{I} } \mathord{\left/ {\vphantom {{K_{I} } {K^{{\exp }}_{{Ic}} }}} \right. \kern-\nulldelimiterspace} {K^{{\exp }}_{{Ic}} } \), where \( K^{{\exp }}_{{Ic}} \) is the experimental value, ranging from 0 to 2. These curves correspond to 7085-T7X aged to peak conditions (artificial relative aging time \( \tau \mathord{\left/ {\vphantom {\tau {\tau _{{PA}} }}} \right. \kern-\nulldelimiterspace} {\tau _{{PA}} }\,{\text{=}}\,1 \)). The crack tip radius is 6.4 μm. As expected, the strain decreases monotonically as the distance from the crack tip increases.

Fig. 8
figure 8

Effective strain profile at the tip of a crack for different levels of loading (normalized to the experimental value) with a von Mises potential

Full size image

3.2 Plane Strain Toughness Criterion

The model was then applied to the same material but with the GT model with an initial VVF of f 0 = 0.2 pct and the parameter q = 1.5. The equivalent strain distribution ahead of the crack tip is shown in Figure 9(a). In this case, the strain decreases monotonically as the distance from the crack tip decreases. However, after a certain level of \( {K_{I} } \mathord{\left/ {\vphantom {{K_{I} } {K^{{\exp }}_{{Ic}} }}} \right. \kern-\nulldelimiterspace} {K^{{\exp }}_{{Ic}} } \) a local maximum develops at a distance from the crack tip (about 0.03 mm from the tip in this figure). It was observed that this strain peak develops very rapidly over several elements of the mesh. Many simulations were carried out with a power law as the constitutive description of hardening and with other values of the crack tip radius, namely, 2.54 and 25.4 μm. The presence of a peak or at least localization of the strain ahead of the crack tip was always observed, although the values of the load at which this instability developed were different in each case. Therefore, this behavior is not due to numerical artifacts. The exact location of the peak with respect to the crack tip varies also but is approximately 0.03 mm.

Fig. 9
figure 9

Deformation ahead of crack tip with the GT model. (a) Effective strain profile (compare Fig. 8), (b) VVF evolution, and (c) maximum principal stress (normalized to yield)

Full size image

Figures 9(b) and (c) show the VVF evolution as well as the maximum principal stress ahead of the crack tip corresponding to the case in Figure 9(a). A peak of VVF is observed as well near the crack tip at the same location as the peak of strain. The major stress increases as the distance from the crack tip increases up to a maximum value and then decreases slowly. This effect is due to the stress triaxiality effect. It has been well documented in the literature that stress triaxiality takes values of 2 to 3 (e.g., 2.4 in a slip line field approach by Hancock and Cowling)[40] at a plane strain crack tip. It should be noted that in cases where the VVF is zero (von Mises), no peak or localization takes place for all applied K I values up to nearly twice K Ic as seen in Figure 8. This is true for all crack tip radii and both the GT and LPDs constitutive models.

The developing peak of VVF can be interpreted physically as a result of two competing contributing factors, the effective strain and the stress triaxiality (Figure 2). The VVF grows first at the crack tip since a necessary condition for growth is plastic strain, which occurs first at the tip. As loading increases, the plastic zone spreads and more regions experience growth in VVF. At a latter stage, on the one hand, the strain is high at the crack tip but the stress triaxiality is low because of the free surface. On the other hand, well away from the tip but in the plastic zone, the stress triaxiality is high but plastic strain is very low. In between, there exists a location where both strain and stress triaxiality are high enough to trigger void growth at a higher rate than in the surrounding areas. In turn, this higher VVF growth rate leads to plastic flow localization. This behavior is similar to that observed in the analytical model of Thomason[13] reviewed in Section I–B1, which shows that, except for very high levels of VVF, fracture does not initiate directly at the crack tip.

In this work, K Ic was not defined using a traditional formula for CT specimen cracks. Since the plane strain instability is likely to produce unstable crack growth, the value of K I at which the peak VVF starts to develop is defined as K Ic . More precisely, the value of K I at which d(VVF)/dx ≥ 0 for any point x in the crack plane near the crack tip, where x is the distance measured from the crack tip, is defined as K Ic The advantage of such definition is that K Ic does not depend on an arbitrary critical value of strain, stress, or VVF. It results directly from plastic flow localization in nonuniform stress and strain fields. The disadvantage of this definition is that it depends on the crack tip radius. Thus, it cannot provide an absolute value of K Ic , but if used consistently it can provide a good basis for the comparison of K Ic when the features of material samples are the same (for instance, different aging time in 7085-T7X as studied in this work).

3.3 Toughness Results and Discussion

In this section, the model is applied to the predictions of K Ic for the L-T CT specimens whose stress-strain curves are given in Figures 3(a) and (b). The FE model described is used with two material descriptions, the GT and LPDs model. The value of q in the GT model is 1.43. This value is close to the recommended value of 1.5 and makes the VVF growth of the GT model in reasonable agreement with that of the FE unit cell model. The LPDs model is used with q = 2, ξ 1 = 1 and \( \xi _{2}\,{\text{=}}\,1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3 \), as explained in Section II–B. The strain-hardening evolution described by Eqs. [7] and [8] is the same for both the GT and LPDs models, and K Ic is the result of the simulation as defined and explained in Section III–B.

The initial value of the VVF variable f 0 is used as a calibration factor for only one value of K Ic , namely, for the sample aged for 5.5τ PA , where τ PA is the peak-aged time. This is carried out for different crack tip radii to show the effect of mesh size interaction. The VVF is adjusted to match the measured K Ic for a single aging time. In essence, this shows the numerical relationship between the modeled crack tip radius and the assumed initial void volume fraction. In any case, the values of these parameters were found to be physically acceptable as discussed subsequently. Figure 10 shows the result of this calibration with the LPDs model. The value of f 0 to match the observed toughness depends on the assumed crack tip radius 0.11, 0.19, and 0.37 pct for radii of 2.5, 6.4, and 25 μm, respectively. This is a physically reasonable range of dimensions, since the order of magnitude of f 0 corresponds to the amount of constituents and large boundary precipitates (Table IV in Reference 11), while the tip radius is on the order of a subgrain/grain dimension. Further computations use the middle of this range, namely, 0.19 pct and 6.4 μm. The dashed lines indicate the sensitivity of this calibration to variability in the toughness value.

Fig. 10
figure 10

Calibration of initial VVF with crack tip radius for a single value of K Ic

Full size image

Figure 11 shows the predicted and experimental values of L-T K Ic for the 7085-T7X plate at the \( t \mathord{\left/ {\vphantom {t 4}} \right. \kern-\nulldelimiterspace} 4 \) location as a function of aging time. The predicted values use a crack tip radius of 6.4 μm. As explained previously, all the plane strain toughness values are identical for the material aged for the relative aging time \( \tau \mathord{\left/ {\vphantom {\tau {\tau _{{PA}} }}} \right. \kern-\nulldelimiterspace} {\tau _{{PA}} }\,{\text{=}}\,5.5 \). For the samples aged to the other aging times, the only changes made between the different simulations are the strain-hardening coefficients. Using the GT model, the predicted K Ic for peak-aged time (\( \tau \mathord{\left/ {\vphantom {\tau {\tau _{{PA}} }}} \right. \kern-\nulldelimiterspace} {\tau _{{PA}} }\,{\text{=}}\,1 \)) is almost the same as that of the sample aged at the relative time \( \tau \mathord{\left/ {\vphantom {\tau {\tau _{{PA}} }}} \right. \kern-\nulldelimiterspace} {\tau _{{PA}} }\,{\text{=}}\,5.5 \). However, with the LPDs model the predicted K Ic significantly decreases as aging time decreases, in agreement with the experiments. The trend is the same for the LPDs model using crack tip radii of 2.5 and 25 μm with the appropriate values of initial VVF (f 0), as explained in the previous paragraph.

Fig. 11
figure 11

Predicted and experimental values of L-T K Ic for the 7085-T7X plate at the \( t \mathord{\left/ {\vphantom {t 4}} \right. \kern-\nulldelimiterspace} 4 \) location as a function of aging time

Full size image

The results of Figure 11 show that strain hardening can account for the differences in plane strain fracture toughness for the material investigated in this article. However, strain hardening differences by themselves are not sufficient since the GT model does not lead to any substantial K Ic changes. A plastic potential, such as LPDs, which accounts for strain-hardening-dependent VVF growth is also an essential element to the success of these simulations. It is also interesting to note that the material description mimics the observed stress-strain behavior as well as micromechanics calculations of K Ic reasonably well with parametric values that have the correct order of magnitude.

Figure 12 represents the theoretical value of K Ic as a function of the different hypothetical initial VVF for the material aged for \( \tau \mathord{\left/ {\vphantom {\tau {\tau _{{PA}} }}} \right. \kern-\nulldelimiterspace} {\tau _{{PA}} }\,{\text{=}}\,5.5 \). Results from both the GT and LPDs models are given for a crack tip radius of 6.4 μm. It shows that for about 1 pct initial VVF, the value of K Ic would drop from a value of 44 to about \( 23\,{\text{Mpa}}{\sqrt {\text{m}} } \). This is consistent with the general observation that alloys containing more constituent particles, and consequently more microvoids, exhibit lower fracture toughness.[7,41]

Fig. 12
figure 12

K Ic as a function of the different hypothetical initial VVF for the material aged for relative aging time of \( \tau \mathord{\left/ {\vphantom {\tau {\tau _{{PA}} }}} \right. \kern-\nulldelimiterspace} {\tau _{{PA}} }\,{\text{=}}\,5.5 \)

Full size image

4 Summary and conclusions

This is the companion article to Reference 11 for predicting plane strain fracture toughness in overaged aluminum aerospace alloy 7085-T7X. The first article dealt with experimental work and analytical fracture toughness modeling. The results from this first article showed the importance of using an accurate strain hardening description to analyze fracture toughness.

In order to understand in more depth the role of strain hardening, this current article used a numerical approach to predict plane strain toughness. K Ic was computed for samples machined out of a given 165.1-mm-thick 7085-T7X plate, and exposed to different overaging times. For these samples, the stress-strain curves, which are a signature of the nanostructure, were different but the microstructure, which includes the coarse particles nucleating void at very low plastic strain, was similar.

Constitutive models consisting of a strain-hardening law and plastic potentials that account for damage and its evolution were selected. The strain-hardening law was developed in order to capture the specific behavior observed in these alloys, i.e., nonmonotonically decreasing rate of hardening as a function of plastic strain.

The LPD potential for damaged materials proposed by Leblond et al.[3] was used and simplified for convenient implementation in the FE code ABAQUS. Unlike the GT model, this potential (original, LPD, and simplified LPDs) differentiates the void growth in materials with different amounts of strain hardening.

The growth of a void embedded in a cylindrical unit cell was investigated using FE simulations. The results of these simulations were used to calibrate constitutive coefficients in the plastic potentials.

The deformation of a CT specimen was simulated with ABAQUS and the constitutive models described previously. With these constitutive models containing void growth, unlike with von Mises, a plastic instability located a short distance from the crack tip developed. As an engineering approach to plane strain toughness, K Ic was defined as the stress intensity factor corresponding to the onset of this plastic flow localization. With this definition, it is not necessary to introduce a critical value of the stress, strain, or state variables, or a fracture criterion.

The FE model was calibrated by selecting an initial VVF such that the resulting K Ic corresponds to one of the 2nd step aging time toughness values (\( \tau \mathord{\left/ {\vphantom {\tau {\tau _{{PA}} }}} \right. \kern-\nulldelimiterspace} {\tau _{{PA}} }\,{\text{=}}\,5.5 \)). Maintaining this initial VVF and varying only the stress-strain curve coefficients, toughness predictions were made for the remaining 7085-T7X plate samples subjected to different second step aging times. Toughness predictions were in good agreement with experimental results.

To achieve these results, it was essential to provide an accurate description of the stress-strain behavior and to use a suitable potential that accounts for damage. In particular, the Leblond et al.[3] potential was able to capture the trend in toughness vs aging time because of its inherent strain-hardening dependent void growth. The GT model, with its lack of sensitivity to strain hardening, does not. Both models have similar trends when the strain hardening is fixed and the initial VVF is varied, i.e., a decrease of K Ic with an increase of f 0.

Both this article and its companion[11] illustrate the importance of the stress-strain curve description on plane strain fracture toughness predictions. For materials with different microstructures, the prediction of K Ic becomes a more complicated task. However, even in this case, it is likely that an accurate description of the stress-strain behavior is necessary.