1 Introduction

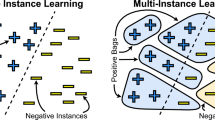
Multiple Instance Learning (MIL) [20] deals with classification of point sets: such sets are named bags and the corresponding points inside the bags are called instances. The main peculiarity of a MIL problem, with respect to the classical supervised classification, resides in the fact that only the labels of each overall bag give a contribution to the learning phase, since the labels of the instances belonging to the bags are unknown.

The first MIL problem proposed in the literature is a drug design problem [12], aimed at discriminating between active and non-active molecules (bags) on the basis of the possible three-dimensional conformations (instances) they can assume. MIL applications can be found in various fields: text categorization, image recognition, medical diagnosis, bankruptcy prediction and so on.

In this work we focus on binary MIL problems, whose aim is to discriminate between positive and negative bags. For such problems a crucial question, related to the number of classes of instances, is what we mean by a positive bag in contraposition to a negative one. In the case of two classes of instances, a very common assumption in the literature is the so-called standard MIL assumption, stating that a bag is positive if and only if it contains at least a positive instance. A typical application is in medical diagnosis by means of images [22]: a patient is considered positive if and only if his/her medical scan (bag) is characterized by at least an abnormal subregion (instance) and is negative if and only if all the subregions of his/her medical scan are normal.

For solving a MIL problem, in the literature there exist various approaches [1, 9], depending on the space where the classification process is performed. In particular, in the instance-space approaches the classification is carried out at the instance level and the class label of each bag is obtained as aggregation of the information coming from the labels of the corresponding instances. On the other hand, if the classification process is performed at the global level, i.e. considering each overall bag as a global entity, we say that the corresponding approach is of the bag-space type. A compromise between the instance-space and the bag-space approaches is given by the so-called embedding-space approaches, where each bag is represented by a specific instance and only such representative instances will successively contribute to the classification process. Some instance-space approaches are mi-SVM [2], MICA [21], MIC\(^{bundle}\) [8] and, more recently, MIL-RL [5] and mi-SPSVM [7]. An embedding-space approach is MI-SVM [2], while some bag-space techniques can be found in [19, 26, 27]. Finally, very recently, a semi-embedding-space technique (Algorithm MI-MSph) has been designed in [3], where the positive bags are represented by the respective barycenters, maintaining the representation of the negative bags in terms of their original instances.

In this paper we propose a kernel version of the recent MIL semiproximal Support Vector Machine approach presented in [7] and based on the combination of two different philosophies designed for supervised classification: the well-established Support Vector Machine (SVM) technique, characterized by a good generalization capability (see for example [10]), and the Proximal Support Vector Machine (PSVM) approach, which has exhibited a reasonable compromise between efficiency and accuracy (see [17]).

The kernel trick is a well-known technique providing nonlinear separation surfaces in the SVM framework (see for example [23]). If, on one hand, using kernel functions substantially improves the final accuracy of the classifier, on the other hand the kernel techniques in general exhibit higher computational times, which could limit their use in solving large scale problems. Despite of that, our semiproximal kernel-based approach exhibits quite comparable CPU times and significantly better accuracy with respect to the linear version of the algorithm, whose computational efficiency has been amply shown in [7] by means of extensive numerical experiments.

The paper is organized in the following way. In the next section we formalize the binary MIL problem and we recall the mi-SPSVM algorithm presented in [7]. In Sect. 3 we present the corresponding kernelized version of mi-SPSVM and in Sect. 4 some numerical experiments are proposed on a set of benchmark MIL problems. Finally in Sect. 5 some conclusions are drawn.

Throughout the paper we indicate by \(\Vert x\Vert\) the Euclidean norm of the vector x and by \(x^Ty\) the scalar product between the vectors x and y.

2 The semiproximal SVM approach for MIL

Given m positive bags \(\mathcal{X}_i^+\), \(i=1,\ldots ,m\), and k negative ones \(\mathcal{X}_i^-\), \(i=1,\ldots ,k\), let \(J^+_i\) and \(J_i^-\) be the corresponding index sets such that

$$\begin{aligned} \mathcal{X}_i^+=\{x_j\in \mathbb {R}^n {~} | {~} j \in J_i^+\} \quad i=1,\ldots ,m \end{aligned}$$

and

$$\begin{aligned} \mathcal{X}_i^-=\{x_j\in \mathbb {R}^n {~} | {~} j \in J_i^-\} \quad i=1,\ldots ,k, \end{aligned}$$

with \(x_j\in \mathbb {R}^n\) being a generic instance.

Under the standard MIL assumption, the objective is to find a separation surface S such that all the instances of the negative bags lie on one side with respect to S and, for each positive bag, at least an instance lies on the other side (see Fig. 1, with four bags: two positive and two negative).

Fig. 1
figure 1

A surface S separating two positive bags (continuous polygons) and two negative ones (dashed polygons). The circles inside the bags are the instances

Full size image

The semiproximal SVM technique (Algorithm mi-SPSVM in [7]) is an instance-space approach which generates a separation hyperplane

$$\begin{aligned} H(w,b) {\mathop {=}\limits ^{\triangle }}\{x\in \mathbb {R}^n {~} | {~} w^{T}x + b = 0\}, \end{aligned}$$

by exploiting the nice properties exhibited by both the SVM (good accuracy) and PSVM (good efficiency) techniques for supervised classification. In particular, given two finite sets of points (instances) \(\mathcal X^+\) and \(\mathcal X^-\), indexed respectively by \(J^+\) and \(J^-\), in the standard SVM approach the quadratic programming problem

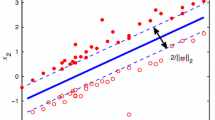
$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \min _{w,b,\xi } &{} \displaystyle \frac{1}{2}\Vert w\Vert ^2+C \displaystyle \sum _{j\in J^+} \xi _j + C \displaystyle \sum _{j\in J^-} \xi _j\\ \\ &{} \xi _j \ge 1-(w^T x_j+b) \quad j\in J^+ \\ &{} \xi _j \ge 1+(w^T x_j+b) \quad j\in J^- \\ &{} \xi _j \ge 0 \quad j\in J^+\cup J^- \\ \end{array}\right. \end{aligned}$$
(1)

is solved, providing a separation hyperplane placed in the middle between the two supporting hyperplanes (see Fig. 2):

$$\begin{aligned} H^+(w,b) {\mathop {=}\limits ^{\triangle }}\{x\in \mathbb {R}^n {~} | {~} w^{T}x + b = 1\} \end{aligned}$$

and

$$\begin{aligned} H^-(w,b) {\mathop {=}\limits ^{\triangle }}\{x\in \mathbb {R}^n {~} | {~} w^{T}x + b = -1\}. \end{aligned}$$
Fig. 2
figure 2

A separating hyperplane H provided by the SVM approach for supervised classification. \(H^+\) and \(H^-\) are the supporting hyperplanes

Full size image

In problem (1), variables \(\xi _j\)s represent a measure of the misclassification error of the instances \(x_j\)s, while the positive constant C tunes the trade-off between the maximization of the margin (the area comprised between \(H^+\) and \(H^-\)), obtained by minimizing the Euclidean norm of w, and the minimization of the misclassification error.

On the other hand the PSVM technique [17], for \(C>0\), solves the optimization problem

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \min _{w,b,\xi } &{} \displaystyle \frac{1}{2}\left\| \begin{array}{c}w \\ b \end{array}\right\| ^2+\displaystyle \frac{C}{2} \displaystyle \sum _{j \in J^+} \xi _j^2+\displaystyle \frac{C}{2} \displaystyle \sum _{j \in J^-} \xi _j^2 \\ \\ &{} \xi _j = 1-(w^T x_j+b) \quad j\in J^+ \\ &{} \xi _j = 1+(w^T x_j+b) \quad j\in J^-, \end{array}\right. \end{aligned}$$
(2)

providing a separation hyperplane placed in the middle between two proximal hyperplanes, \(H^+\) and \(H^-\), which cluster the points of \(\mathcal X^+\) and \(\mathcal X^-\), respectively (see Fig. 3).

Fig. 3
figure 3

A separating hyperplane H provided by the PSVM approach for supervised classification. \(H^+\) and \(H^-\) are the proximal (clustering) hyperplanes

Full size image

Differently from problem (1), problem (2) is stricly convex with respect to both w and b and it can be solved in a closed form, improving significantly the efficiency with respect to the classical SVM technique.

Coming back to the solution of the MIL problem introduced at the beginning of this section, the main idea characterizing the semiproximal approach (Algorithm mi-SPSVM in [7]) takes into account the different roles played by the positive and the negative bags. In fact, considering the standard MIL assumption, a correct classification of the negative bags requires more effort with respect to the classification of the positive ones, the former needing the correct classification of all the instances and the latter of at least one. In other words, classifying correctly the positive bags is indeed easier than classifying the negative ones, allowing \(H^+\) to possibly be a proximal (clustering, instead of supporting) hyperplane for the instances of the positive bags.

In particular, indicating by \(J^+\) the index set of all the instances of the positive bags and by \(J^-\) the index set of all the instances of the negative bags, the mi-SPSVM algorithm initially solves the quadratic program

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \min _{w,b,\xi } &{} \displaystyle \frac{1}{2}\left\| \begin{array}{c}w \\ b \end{array}\right\| ^2+\displaystyle \frac{C}{2} \displaystyle \sum _{j \in J^+} \xi _j^2 + C \displaystyle \sum _{j\in J^-} \xi _j\\ \\ &{} \xi _j = 1-(w^T x_j+b) \quad j\in J^+ \\ &{} \xi _j \ge 1+(w^T x_j+b) \quad j\in J^- \\ &{} \xi _j \ge 0 \quad j\in J^-, \end{array}\right. \end{aligned}$$
(3)

providing a separation hyperplane located in the middle between a supporting hyperplane \(H^-\) for the instances of the negative bags and a proximal hyperplane \(H^+\) which clusters the instances of the positive bags (see Fig. 4).

Fig. 4
figure 4

The semiproximal SVM hyperplane H separating two positive bags (continuous polygons) and two negative ones (dashed polygons). The circles inside the bags are the instances

Full size image

The algorithm, named mi-SPSVM and described in Algorithm 1, proceeds by repeatedly solving problem (3) for different configurations of the sets \(J^+\) and \(J^-\), in order to compute the current separation hyperplane \(H(\bar{w}, \bar{b})\). In particular, the core of the procedure is constituted by steps 6-11, aimed at determining the sets \(J^*\) and \(\bar{J}\) needed to update \(J^+\) and \(J^-\) at steps 13-14. While the satisfaction of the standard MIL assumption is guaranteed by means of the set \(J^*\) whose indexes remain in \(J^+\), at each iteration the cardinality of \(J^-\) is increased by adding the indexes of the set \(\bar{J}\): such indexes indeed correspond to the current positive instances which lie in the negative side with respect to the current hyperplane.

In [7] the finite termination of the algorithm has been shown, proving also that the sequence of the optimal objective function values of problem (3), generated by varying \(J^+\) and \(J^-\) at each iteration according to steps 13-14, is monotonically nonincreasing. Finally, the numerical experiments therein presented, in comparison with some other reimplemented approaches drawn from the literature, have proved a very good performance of mi-SPSVM, not only in terms of accuracy but also in terms of CPU time.

3 Embedding kernel transformations into the semiproximal approach

Kernel transformations constitute a very powerful trick useful to construct nonlinear classifiers, starting from a linear separation surface (hyperplane) obtained in a higher dimensional space.

figure a

In particular, let I be the input space, such that \(x_j\in I\subseteq \mathbb {R}^n\), for any \(j\in J^+_i\), \(i=1,\ldots ,m\), and for any \(j\in J_i^-\), \(i=1,\ldots ,k\), and let \(F\subseteq \mathbb {R}^N\) be the feature space such that \(N>n\). Given a map

$$\begin{aligned} \phi :I \mapsto F, \end{aligned}$$

the kernel function \(\mathcal K\) is defined as:

$$\begin{aligned} \mathcal K: I \times I \mapsto \mathbb {R}\end{aligned}$$

such that

$$\begin{aligned} \mathcal{K}(x,y) = \phi (x)^T \phi (y). \end{aligned}$$

Analogously to the standard SVM, embedding the kernel functions into Algorithm mi-SPSVM is related to the optimal solution to the Wolfe dual of problem (3):

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \min _{\lambda ,\mu } &{}\displaystyle \frac{1}{2}\lambda ^T X^+ X^{+T} \lambda + \displaystyle \frac{1}{2}\mu ^T X^- X^{-T} \mu - \lambda ^T X^+ X^{-T}\mu \\ \\ &{}+\displaystyle \frac{1}{2} (e^T \lambda - e^T \mu )^2 +\displaystyle \frac{\Vert \lambda \Vert ^2}{2C}-\lambda ^Te-\mu ^Te\\ \\ &{} 0\le \mu \le Ce,\end{array}\right. \end{aligned}$$
(4)

where \(\lambda\) is the vector containing the Lagrangian multipliers introduced in correspondence to the constraints

$$\begin{aligned} \xi _j = 1-(w^T x_j+b),\quad j\in J^+, \end{aligned}$$

\(\mu\) is the vector containing the Lagrangian multipliers defined in correspondence to the constraints

$$\begin{aligned} \xi _j \ge 1+(w^T x_j+b),\quad j \in J^-, \end{aligned}$$

e is the vector of ones of appropriate dimension, \(X^+\) is the matrix whose jth row is the vector \(x_j\), \(j\in J^+\), and \(X^-\) is the matrix whose jth row is the vector \(x_j\), \(j\in J^-\).

From the primal-dual relationships, the optimal solution \((w^*,b^*)\) obtained by solving problem (3) is also computable by means of the following formulae:

$$\begin{aligned} w^* = X^{+T} \lambda ^* - X^{-T} \mu ^*\end{aligned}$$
(5)

and

$$\begin{aligned} b^* = e^T \lambda ^* - e^T \mu ^*,\end{aligned}$$
(6)

where (\(\lambda ^*,\mu ^*\)) is the optimal solution to problem (4). Note that, differently from the classical SVM model, the optimal value of the bias \(b^*\) is uniquely determined by (6), due to the strict convexity of the primal problem (3) with respect to w and b.

It is easy to show that rewriting the Wolfe dual problem (4) in terms of the kernel function \(\mathcal K\) gives:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \min _{\lambda ,\mu } &{}\displaystyle \frac{1}{2}\lambda ^T K^{++} \lambda + \displaystyle \frac{1}{2}\mu ^T K^{--} \mu - \lambda ^T K^{+-}\mu \\ \\ &{}+\displaystyle \frac{1}{2} (e^T \lambda - e^T \mu )^2 +\displaystyle \frac{\Vert \lambda \Vert ^2}{2C}-\lambda ^Te-\mu ^Te\\ \\ &{} 0\le \mu \le Ce,\end{array}\right. \end{aligned}$$
(7)

where the generic elements of the matrices \(K^{++}\), \(K^{--}\) and \(K^{+-}\) are of the type:

$$\begin{aligned}{} & {} K_{pq}^{++}=\mathcal{K}(x_p,x_q), \quad \text{ with } p,q \in J^+, \\{} & {} K_{pq}^{--}=\mathcal{K}(x_p,x_q), \quad \text{ with } p,q \in J^-, \end{aligned}$$

and

$$\begin{aligned} K_{pq}^{+-}=\mathcal{K}(x_p,x_q), \quad \text{ with } p\in J^+,{~} q\in J^-. \end{aligned}$$

Note that, in order to tackle the above problem (7), it is enough to know only the analytical form of the kernel function \(\mathcal K\), without needing explicitly the map \(\phi\) (this is the reason of the expression “the kernel trick”, very common in the literature). Moreover, problem (7) coincides exactly with problem (4) in case the linear kernel function \(\mathcal{K} (x,y) = x^T y\) is adopted.

We conclude this section by observing that using the kernel trick into Algorithm mi-SPSVM involves also steps 8 and 11, where, in order to compute the sets \(J^*\) and \(\bar{J}\), the quantity \(\bar{w}^T\phi (x_j) + \bar{b}\) should be evaluated for \(j\in J^+\). Taking into account formulae (5) and (6), with \(x_j\) substituted by \(\phi (x_j)\) for any \(j\in J^+\cup J^-\), it is easy to see that also in this case there is no need to know explicitly the map \(\phi\), since such evaluation corresponds to calculating the following vector:

$$\begin{aligned} K^{++}\lambda ^*-K^{+-}\mu ^*+e^T\lambda ^* - e^T \mu ^*, \end{aligned}$$

where (\(\lambda ^*,\mu ^*\)) is the optimal solution to problem (7).

4 Computational study of the semiproximal kernelized version

The kernelized version of Algorithm mi-SPSVM, named mi-KSPSVM, has been implemented in Matlab (version R2019b) and run on a Windows 10 system, characterized by 16 GB of RAM and a 2.30 GHz Intel Core i7 processor. About the choice of the kernel function, we have used the RBF (Radial Basis Function) kernel [25]

$$\begin{aligned} \mathcal{K} (x,y) = \exp \left( -\frac{\Vert x-y\Vert ^2}{2 \sigma ^2}\right) , \end{aligned}$$
(8)

which is the most common one adopted in the literature.

The code has been tested on the twelve most commonly used (in the literature) benchmark MIL problems [2], listed in Table 1: the first three data sets are image recognition problems, the TST ones are text categorization problems, while the last two ones are drug design problems.

Table 1 Data sets
Full size table

A crucial issue regards the choice of the hyperparameters C and \(\sigma\): the former adjusts the trade-off between the maximization of the margin and the minimization of the misclassification error, while the latter tunes the kernel function values in formula (8).

We have adopted the following strategies. About the choice of C we have used a bi-level cross validation approach [4] of the same type adopted in [7], using the same grid of values \(2^{i}\), with \(i=-7,\ldots ,7\), as in [21]. As for \(\sigma\), we have preliminarily investigated on some potential values taken inside the grid \(2^{i}\), with \(i=-4,\ldots ,7\), noting that the best testing accuracies are obtained in correspondence to the values of i belonging to the set \(\{-3,-2,2,3,4\}\). Then, in order to automate the choice, we have embedded the computation of \(\sigma\) into the bi-level cross validation using the grid \(2^{i}\), with \(i=-3,-2,2,3,4\).

In Table 2 we report the results in terms of average training correctness, average testing correctness (accuracy) and average CPU time, compared with the linear kernel semiproximal version mi-SPSVM [7] run on the same machine as mi-KSPSVM. Highlighting in bold the best correctness value for each data set, it appears clear that, while in terms of computational times the two algorithms are quite comparable, on the other hand mi-KSPSVM significantly overcomes mi-SPSVM not only in terms of accuracy, but also in terms of average training correctness.

Table 2 mi-KSPSVM vs mi-SPSVM [7]: average training correctness, average testing correctness (accuracy) and average CPU time
Full size table

For the sake of completeness, in Table 3 we report the average testing results of mi-KSPSVM and mi-SPSVM, expressed in terms of sensitivity, specificity and F-score. While the sensitivity and the specificity express the capability of the classifier to correctly identify the positive bags (sensitivity) and the negative ones (specificity), the F-score is the harmonic mean of sensitivity and precision, the latter expressing the percentage of the true positive bags among all the bags classified as positive. From Table 3 (where, for each data set and for each evaluation metric, the best value is highlighted in bold), mi-KSPSVM appears to be the best performant also in terms of specificity and F-score. We recall that, in case the accuracy is not equal to 100%, low values of sensitivity [resp. specificity] are generally a consequence of high values of specificity [resp. sensitivity].

Table 3 mi-KSPSVM vs mi-SPSVM [7]: average testing results in terms of sensitivity, specificity and F-score
Full size table

In order to investigate the behaviour of the code with respect to the literature, in Table 4 we also present the comparison of our accuracy results with those ones obtained by the following approaches, for which we have reported the best published values obtained using indifferently the linear or the nonlinear kernel:

  • mi-SVM [2]: it is an instace-space approach based on solving heuristically a SVM type mixed integer program, by means of a BCD (Block Coordinate Descent) method [24].

  • MI-SVM [2]: it is an embedding-space approach, where each positive bag is represented by a single feature vector, the instance furthest from the current hyperplane.

  • MICA: [21]: it is an instance-space approach, where each positive bag is represented by the convex combination of its instances.

  • MIC\(^{bundle}\) [8]: it is an instace-space approach, solving a nonsmooth nonconvex optimization problem by means of bundle methods [14,15,16].

  • MI-Kernel [19]: it is a bag-space kernel-based approach, where the similarities between the bags are measured by set kernels.

For each data set, the best value is in bold and the character “−” means that the corresponding result is not available. Looking at Table 4, we observe that our approach is the best on six data sets (Fox, TST1, TST3, TST7, TST9, TST10) out of 12, and it appears quite comparable on Elephant, Tiger and Musk-1.

Table 4 mi-KSPSVM vs mi-SVM [2], MI-SVM [2], MICA [21], MIC\(^{bundle}\) [8] and MI-Kernel [19]: average testing correctness (accuracy)
Full size table

To better analyze the accuracy and the CPU time results, we have also performed the nonparametric statistical Friedman test [13], used to compare different classifiers (see [11, 18]) and furnished by the Statistics and Machine Learning Toolbox of Matlab. Such test is based on providing, for each data set, any classifier with a rank, computed on the basis of its performance with respect to the other approaches. For example, on Elephant, mi-SVM is the winner and then it has rank 1, MI-SVM has rank 2, mi-KSPSVM has rank 3, while both MICA and MIC\(^{bundle}\), which present the same performance, have rank 4. The Friedman test provides in output the so-called p-value, which, in case it assumes small values (generally less than or equal to 0.05), suggests to reject the null hypothesis, implying that there is a significant difference among the algorithms.

We have applied the Friedman test to the following comparisons, on the basis of the accuracy and the CPU time results reported in Tables 2 and 4:

  • The comparison of mi-SPSVM against mi-KSPSVM in terms of average testing correctness and average CPU time has provided p-values equal to 0.0005 and 0.5637, respectively.

  • The comparison among mi-KSPSVM, mi-SVM, MI-SVM, MICA and MIC\(^{bundle}\) on the image recognition problems (Elephant, Fox and Tiger) has furnished a p-value equal to 0.2069.

  • The comparison among mi-KSPSVM, mi-SVM, MI-SVM and MICA on the TST problems has given a p-value equal to 0.0370.

  • The comparison among all the algorithms (mi-KSPSVM, mi-SVM, MI-SVM, MICA, MIC\(^{bundle}\) and MI-Kernel) on the two musk problems has output a p-value equal to 0.7220.

The above p-values confirm the following observations:

  • The linear and the nonlinear versions of the semiproximal SVM approach are comparable in terms of CPU time, but not in terms of accuracy (in fact mi-KSPSVM always significantly overcomes mi-SPSVM).

  • On the image recognition problems all the approaches present a comparable behaviour.

  • On the TST problems, there is a significant difference among the classifiers (in fact mi-KSPSVM wins on 5 data sets out of 7).

  • All the classifiers are comparable on the two musk data sets.

We conclude the section by highlighting that the numerical results presented in [7] have already shown that the main advantage of the semiproximal technique resides in the computational efficiency of the approach, without sacrificing the accuracy performance. Here we have shown that the kernelized version improves significantly the average testing correctness with respect to the linear one, maintaining the same computational advantage in terms of CPU time.

5 Conclusions

In this paper we have presented the kernelized version of the semipromixal SVM technique proposed in [7]. The numerical results, performed on a set of benchmark problems and supported by the statistical Friedman test, have shown that embedding the kernel trick into the semiproximal framework greatly improves the accuracy of the classifier, still preserving the good performance in term of computational effort.

Future research could be devoted to extend the kernel trick to other types of MIL classifiers, such as to the spherical separation approach adopted in [3], as done in [6] for the supervised case.