1 Introduction and problem statement

In discrete location one has a set \(J=\{1,\ldots ,n\}\) of clients, a set \(I=\{1,\ldots ,m\}\) of potential sites, and the location of the facilities is sought so that a certain performance measure is optimized. In the \(p\)-median problem, first introduced in [25, 26], the number of facilities to locate is fixed (to \(p\)), and the goal is to minimize the overall total transportation cost. This is done by solving the following combinatorial optimization problem:

$$\begin{aligned} \min _{N\subseteq I}\Bigl \{\sum _{j\in J}\omega _j \min _{i\in N}d_{ij}:\ |N|=p\Bigr \}, \end{aligned}$$
(1)

where \(d_{ij}\) is the cost of satisfying one unit of demand of client \(j \in J\) from the facility located at site \(i\in I\), and \(\omega _j\) is the demand of client \(j\).

The \(p\)-median problem is a famous fundamental problem in discrete location theory known to be NP-hard [30]. There are plenty of exact and heuristic methods proposed for solving the problem [1–3, 17, 45, 48]. Problem (1) is easily formulated as an integer program, as we recall now. For each \(i\in I\) let \(y_i\) be a binary variable which takes the value \(1\) if the facility at site \(i\) is open, and \(0\) otherwise, and for each pair \(i\in I\), \(j\in J\) let \(x_{ij}\) be the binary variable, which is equal to \(1\) if client \(j\) is served by facility at \(i\), and \(0\) otherwise. With this notation, the \(p\)-median problem is written as follows [49]

$$\begin{aligned} \min _{(x,y)}&\sum _{i\in I}\sum _{j\in J}\omega _j d_{ij}x_{ij}\end{aligned}$$
(2)
$$\begin{aligned}&\sum _{i\in I}x_{ij}=1\qquad&\qquad&j\in J\end{aligned}$$
(3)
$$\begin{aligned}&x_{ij}\le y_i&\qquad&i\in I, j\in J\end{aligned}$$
(4)
$$\begin{aligned}&\sum _{i\in I}y_i=p\end{aligned}$$
(5)
$$\begin{aligned}&y_i\in \{0,1\}&\qquad&i\in I \end{aligned}$$
(6)
$$\begin{aligned}&x_{ij}\in \{0,1\}&\qquad&i\in I, j\in J \end{aligned}$$
(7)

Constraints (3) ensure that each client \(j\) is served by exactly one facility. Constraints (4) impose that a client can only be served by open facilities. Constraint (5) enforces the number of facilities to be \(p\). We denote the feasible set of the \(p\)-median problem as \(X_{pM} = \{(x,y)\): satisfying (3)–(7)}.

In the Uncapacitated Facility Location Problem (UFLP) [37], the number of plants to be opened is not fixed in advance. Instead, one minimizes the total cost, which is assumed to be given by the total transportation cost plus a cost associated with the plants to be opened. This leads to the following combinatorial problem:

$$\begin{aligned} \min _{N\subseteq I}\left\{ \sum _{j\in J}\omega _j \min _{i\in N}d_{ij} + \sum _{i \in N} f_i\right\} , \end{aligned}$$
(8)

where, as for the \(p\)-median, \(d_{ij}\) is the cost of satisfying one unit of demand of client \(j \in J\) from the facility located at site \(i \in I\), \(\omega _j\) is the demand of client \(j\), and now we have an operating cost \(f_i\) associated with facility at \(i\in I.\) The UFLP is easily formulated as a linear integer program, similar to (2)–(7), but the feasible region \(X_{UFLP}\) is defined now by constraints (3), (4), (6), (6), and in the objective (2) the term \(\sum _{i \in I} f_i y_i\) is added. For extensive reviews of the Uncapacitated Facility Location Problem and methods of solving it, see e.g. [8, 12, 33–36, 54].

In the formulations above it is assumed that the parameters \(\omega _j\) are known, which may be rather unrealistic in practice (for review, see [15, 24, 28, 51] and references therein). When the parameters are not known precisely, and some estimates \(\widehat{\omega }_j\) are given instead, as opposed to classic robust discrete optimization theory [6, 7], one may consider a robust version based on a threshold model. It was introduced in [11] and is specifically useful when there is no fully reliable information about possible demand changes (see also [10, 13]). Such situation may arise when locating facilities to serve clients during a long period of time, within which neither demand changes nor their probability distribution are known. For other robust optimization approaches the reader is also referred to [4, 5, 46].

In the threshold model, a threshold value \(\tau >0\) is introduced, to be interpreted as the highest admissible total cost (or budget) of satisfying the demands of all clients, and the robustness \(\rho (S)\) of a solution \(S\subseteq I\) is defined as the smallest error in the estimates \(\widehat{\omega }_j\) which makes the total cost exceed the threshold \(\tau .\) For the \(p\)-median, the robustness \(\rho _{pM}(S)\) of a solution \(S\) is then

$$\begin{aligned} \rho _{pM}(S) = \min _{\omega \in \mathbb R_+^n} \Bigl \{\Vert \omega - \widehat{\omega }\Vert : \, \sum _{j\in J}\omega _j \min _{i\in S}d_{ij} > \tau \Bigr \}, \end{aligned}$$
(9)

where \(\Vert \cdot \Vert \) is a norm. If we write the solutions \(S \subseteq I \) in terms of the variables \((x,y)\), we obtain the robustness \(\rho _{pM}(x,y)\) of a solution \((x,y) \in X_{pM}\) as

$$\begin{aligned} \rho _{pM}(x,y) = \min _{\omega \in \mathbb R_+^n} \Bigl \{\Vert \omega - \widehat{\omega }\Vert : \, \sum _{i \in I} \sum _{j \in J} \omega _j d_{ij}x_{ij} > \tau \Bigr \}. \end{aligned}$$

In [11] it was proven that the robustness of a solution can explicitly be computed when the objective function is linear in \(\widehat{\omega }\). Applied to the \(p\)-median problem this yields

$$\begin{aligned} \rho _{pM}(x,y) = \max \left\{ 0, \frac{\tau - \sum _{i \in I} \sum _{j \in J} \widehat{\omega }_j d_{ij}x_{ij}}{\Vert \left( \sum _{i \in I} d_{ij}x_{ij}\right) _{j \in J}\Vert ^\circ }\right\} , \end{aligned}$$
(10)

where \(\Vert \cdot \Vert ^\circ \) denotes the dual norm of \(\Vert \cdot \Vert \).

If, instead of considering the \(p\)-median problem, the UFLP is addressed, the robustness function \(\rho _{UFLP}\) takes the form

$$\begin{aligned} \rho _{UFLP}(x,y) = \max \left\{ 0, \frac{\tau -\sum _{i \in I} f_i y_i - \sum _{i \in I} \sum _{j \in J} \widehat{\omega }_j d_{ij}x_{ij}}{\Vert (\sum _{i \in I} d_{ij}x_{ij})_{j \in J}\Vert ^\circ }\right\} , \end{aligned}$$
(11)

For the two models under consideration, maximizing the robustness and minimizing the estimated total cost are different objectives. In this paper we address the bi-objective problem in which both are considered as separate criteria, yielding, for the case of the \(p\)-median, the following bi-criteria nonlinear integer programming problem

and, for the case of the UFLP,

The location problems with multiple criteria have intensively been studied in the literature since 1970th. The first reviews of such problems are supposed to be [14, 27]. Excellent reviews on this topic can also be find in very recent paper [22] and in [19]. The reader is also referred to [29, 32] for the review and some solution methods for multicriteria location problems on networks.

The remainder of the paper is organized as follows. Section 2 describes an effective procedure for finding an approximation to the Pareto optimal set of the two bi-objective problems above, namely, the so-called \(\varepsilon \)-constraint method. The effectiveness of such approach is illustrated with computational experiments on a wide range of problem instances taken from the literature, as presented in Sect. 3. The paper concludes in Sect. 4 with some final remarks and possible lines of future research.

2 Algorithm for finding a dominating set

Different solution concepts can be applied to finding solutions to bi-criteria integer programming problems such as \((BpM)\) or \((BUFLP)\), [18, 20]. Since the analysis is identical for both problems, let us focus on the bi-objective version \((BpM)\) of the \(p\)-median problem. The set of Pareto optimal solutions of \((BpM)\) is the set of solutions \((x^*,y^*) \in X_{pM}\) such that no \((x,y) \in X_{pM}\) exists satisfying

$$\begin{aligned} \begin{array}{rcl} \sum _{i\in I}\sum _{j\in J}\widehat{\omega }_j d_{ij}x_{ij} &{} \le &{} \sum _{i\in I}\sum _{j\in J}\widehat{\omega }_j d_{ij}x^*_{ij} \\ \rho _{pM}(x,y) &{} \ge &{} \rho _{pM}(x^*,y^*), \end{array} \end{aligned}$$
(12)

with at least one inequality strict. Similarly, the set of weakly Pareto optimal solutions of \((BpM)\) is the set of of solutions \((x^*,y^*) \in X_{pM}\) such that no \((x,y)\) exists satisfying (12) with both inequalities strict.

In this paper we will construct an approximation to the Pareto set of \((BpM)\), namely, a \(\varvec{\delta } = (\delta _1,\delta _2)\)-dominating set for \((BpM),\) [9, 23, 50]. We recall that a set \(X^* \subset X_{pM}\) is a \(\varvec{\delta }\)-dominating set for \((BpM)\) if, for any \((x,y) \in X_{pM}\) there exists \((x^*,y^*) \in X^*\) such that

$$\begin{aligned} \begin{array}{rcl} \sum _{i\in I}\sum _{j\in J}\widehat{\omega }_j d_{ij}x^*_{ij} &{} \le &{} \sum _{i\in I}\sum _{j\in J}\widehat{\omega }_j d_{ij}x_{ij} + \delta _1\\ \rho _{pM}(x^*,y^*) &{} \ge &{} \rho _{pM}(x,y) - \delta _2 . \end{array} \end{aligned}$$
(13)

A \(\varvec{\delta }\)-dominating set for \((BpM)\) is obtained by implementing the well-known \(\varepsilon \)-constraint method, which has been successfully used, among others, for solving the set partitioning problem [21], the traveling salesman problem [41], a bi-objective stochastic covering tour problem [53], a semiobnoxious location problem [9, 50], the assignment problem and the spanning tree problem [40, 42, 43]. Note that there was also proposed an augmented modification of \(\varepsilon \)-constraint method allowing one to avoid some drawbacks of the original method, e.g. providing weak Pareto optimal solutions or problems with method efficiency for the case of multiple criteria [38]. Such approach was proved to be effective for multi-objective combinatorial optimization problems [39] including reliability and uncertainty issues [47].

When applied to bi-criteria problems like \((BpM)\), the main idea of the method is to optimize an objective function, considering the other as constraint, bounded by some parameter \(\varepsilon \ge 0\). Varying then the parameter in its full range and solving exactly a series of corresponding subproblems allows one to obtain the whole weak Pareto optimal set, or, under some assumptions of uniqueness, the Pareto optimal set. If instead of solving the problems exactly, a given tolerance is allowed, then a \(\varvec{\delta }\)-dominating set is obtained.

Here we address the problem of minimizing, with an accuracy \(\delta _1,\) the estimated transportation cost, while the robustness is not smaller than \(\varepsilon > 0\!:\)

$$\begin{aligned} \min _{(x,y)}&\sum _{i\in I}\sum _{j\in J}\widehat{\omega }_j d_{ij}x_{ij}\nonumber \\ \text{ s.t. }&\rho _{pM}(x,y) \ge \varepsilon \nonumber \\&(x,y)\in X_{pM}. \end{aligned}$$
(14)

The parameter \(\varepsilon \ge 0\) is varied in a fine grid to assure that a \(\mathbf {\delta }\)-dominating set is obtained, [52]. For a given \(\varepsilon ,\) such subproblem has a linear objective, the linear constraints defining \(X_{pM}\), and one non-linear constraint, since \(\rho _{pM}\) is, in general, non-linear. However for the most natural choice of the norm \(\Vert \cdot \Vert \) defining the error in estimates, namely, the \(\ell _{\infty }\) norm, yielding the highest individual deviation in the demands estimates, subproblem (14) can be reduced to a linear \(p\)-median type problem of the form (2)–(7) with one extra linear constraint. Indeed, in such case \(\Vert \cdot \Vert ^\circ \) is the \(\ell _1\) norm, and (14) takes the following linear form

Note that such a reduction is correct only under the additional obvious assumption that the chosen threshold value is always strictly greater than the optimal value of the \(p\)-median problem. Under this assumption, made in what follows, we have that, for \(\varepsilon =0,\) the constraint is redundant and thus \((P_0)\) is just the \(p\)-median problem.

For any problem \((P_\varepsilon ),\) let \(X_{pM}(\varepsilon )\) and \(Sol_{pM}(\varepsilon ,\delta _1)\) be respectively the feasible set and the set of its \(\delta _1\)-optimal solutions. The following algorithm provides a sequence of points yielding a \(\varvec{\delta }=(\delta _1,\delta _2)\)-dominating set for \((BpM)\). We start by solving the \(p\)-median problem, i.e., solving \((P_0),\) and taking as first value of \(\varepsilon \) the robustness of an optimal solution \((x^0,y^0)\) to the \(p\)-median problem. Then, at each iteration the parameter \(\varepsilon \) is updated to the robustness of the optimal solution found, increased by a small positive quantity \(\delta _2\).

  1. 0.

    Initialization: Find \((x^0,y^0)\in Sol_{pM}(0,\delta _1)\), set \(\varepsilon _0 :=\dfrac{\tau - \sum _{i\in I}\sum _{j\in J}\widehat{\omega }_jd_{ij}x^0_{ij}}{\sum _{i\in I}\sum _{j\in J}d_{ij}x^0_{ij}}\), \(k:=0\);

  2. 1.

    Set \(\bar{\varepsilon }_k:= \varepsilon _k + \delta _2\);

  3. 2.

    Solve the problem \((P_{\bar{\varepsilon }_k})\) with a precision \(\delta _1\);

  4. 3.

    If \(X_{pM}(\bar{\varepsilon }_k)=\varnothing \), then stop, otherwise set

    $$\begin{aligned} (x^{k+1},y^{k+1})\in Sol_{pM}(\bar{\varepsilon }_k,\delta _1); \end{aligned}$$
  5. 4.

    Set \(\varepsilon _{k+1} := \dfrac{\tau - \sum _{i\in I}\sum _{j\in J}\widehat{\omega }_jd_{ij}x^{k+1}_{ij}}{\sum _{i\in I}\sum _{j\in J}d_{ij}x^{k+1}_{ij}}\), \(k:=k+1\) and go to step 1.

As stopping criterion of the algorithm we use the condition of the feasible set of the problem \((P_{\bar{\varepsilon }_k})\) for some \(\bar{\varepsilon }_k\) being empty. The validity of this condition follows from the following

Proposition 1

If \(\varepsilon \ge \varepsilon ^*,\) then \(X_{pM}(\varepsilon ^*) \subseteq X_{pM}(\varepsilon ).\) In particular, if \(X_{pM}(\varepsilon ) = \varnothing \), then \(\not \exists (x',y')\in X_{pM}:\) \(\rho _{pM}(x',y')>\varepsilon \).

The finiteness of the procedure follows from the finiteness of the feasible set \(X_{pM}\) and the monotonicity of the sequence \(\varepsilon _k.\) This way a finite set of points \(\{(x^0,y^0), (x^1,y^1), \ldots , (x^k,y^k)\}\) is returned by the algorithm. Such points satisfy the following

Proposition 2

The set \(\{(x^0,y^0), (x^1,y^1), \ldots , (x^k,y^k)\}\) returned by the algorithm is a \(\varvec{\delta }\)-dominating set for \((BpM).\) For \(\delta _1=0,\) i.e., if the subproblems are solved to optimality, then each \((x^j,y^j)\) is weakly efficient solution to \((BpM),\) and, moreover, if \(Sol_{pM}(\bar{\varepsilon }_j, \delta _1)\) is a singleton, then \((x^{j+1},y^{j+1})\) is also efficient to \((BpM).\)

Identical results can be derived for the biobjective version of the UFLP in the same way.

3 Computational results

The described scheme of the \(\varepsilon \)-constraint method has been implemented in C++. Experiments have been carried out on a PC with Pentium \(4\) CPU \(3.2\) GHz and \(1.5\) GB of RAM. The commercial IP solver used to solve subproblems \((P_{\varepsilon })\) was CPLEX Optimizer 12.1.0.Footnote 1 Our test bed consists of instances taken from two different sources: all metric instances from the TSP library with a number of potential sites for locating facilities and clients from \(50\) to \(500\) (overall \(37\) problems), and also the test instances from the benchmark library “Discrete Location problems”Footnote 2 [31] (DLP) of classes \(Euclidean\), \(Uniform\), \(PCodes\), \(Chess\) and \(FPP\) for which \(|I|=|J|=100\). Each of these classes contains \(30\) instances. For \((BpM)\), the computational results for the TSP instances are obtained for different numbers \(p\) of facilities to be opened which vary from \(5\) to \(50\) depending on the problem size. For both the \(p\)-median problem and the UFLP, three different values are taken for the budget \(\tau \), namely, \(\tau = 1.05Z\), \(\tau = 1.1Z\), \(\tau = 1.3Z\), where \(Z\) is the optimal cost of the corresponding \(p\)-median or uncapacitated facility location problem. Clients’ demand estimates \(\widehat{\omega }_j\) are randomly chosen with uniform distribution in the interval [1000, 10,000]. The stepsize \(\delta _2\) is assumed to be \(0.01\), and \(\delta _1=0.\)

For each instance, a \(\varvec{\delta }\)-dominating set is built. If we represent such a set in the objective space, we obtain plots like Fig. 1, which corresponds to \((BpM)\) for the problem instance KroA200.tsp and the choices \(p=50\) and \(\tau = 1.3Z,\) or Fig. 2, in which an approximation to the Pareto set of \((BUFLP)\) is obtained for the problem instance 411Eucl from the class Euclidean of DLP with the same value of budget \(\tau \). An interesting feature of those two plots, repeatedly found in our experiments, is that the robustness does not vary much with respect to the variation in total cost, suggesting that, in order to increase significantly the robustness, solutions of higher estimated cost may be needed.

Fig. 1
figure 1

\(\varvec{\delta }\)-dominating set for \((BpM)\) in KroA200.tsp

Full size image
Fig. 2
figure 2

\(\varvec{\delta }\)-dominating set for \((PUFLP)\) in 411Eucl

Full size image

Let us analyze in what follows how the cardinality of the \(\varvec{\delta }\)-dominating set is affected by the parameters of the problems, discussing first the results obtained for \((BpM)\). Computational results for the \(37\) instances of the TSP library are reported in Tables 1 and 2, where column \(p\) represents the number of open facilities, ranging from \(p=5\) to \(p=50,\) columns \(1\), \(2,\ldots \) under the common banner \(|S|\) contain the number of instances for which \(1\), \(2\), etc. different points have been found with a certain budget \(\tau \). For example, for \(\tau =1.05Z\) and \(p=5,\) \(32\) out of the \(37\) instances yielded just one point in the \(\varvec{\delta }\)-dominating set. Results for only \(31\) problems are presented when the number of medians is greater than or equal to \(30\): in these cases the problems in which the number of potential sites for locating facilities and clients is less than \(100\) are excluded from consideration.

Table 1 Cardinality of the approximate solution set to \((BpM)\)
Full size table
Table 2 Cardinality of the approximate solution set to \((BpM)\)
Full size table

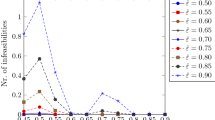
The distribution of the cardinality of the \(\varvec{\delta }\)-dominating set for the three budgets and \(7\) values of \(p\) considered is represented in the boxplot of Fig. 3.

Fig. 3
figure 3

Cardinality of the approximate solution set to \((BpM)\). TSP instances

Full size image

Results for the instances from the library DLP are presented in Table 3, where the first column represents the class of instances, and other notations are the same as for the case of TSP. The distribution of the cardinality of the \(\varvec{\delta }\)-dominating set for the three budgets and the \(5\) classes of instances considered is represented in the boxplot of Fig. 4.

Analyzing the obtained results one can note that, for overwhelming majority of the problem instances from the test library DLP, the \(\varvec{\delta }\)-dominating set contains only one single solution. This is particularly remarkable for small budgets (\(1.05Z\) and \(1.1Z\)), i.e. greater than the minimal one for \(5\) and \(10\,\%\) respectively. The maximum cardinality found never exceeds \(3\), and is obtained for only one instance of the Euclidean class with \(\tau =1.1Z\). Increasing the budget results in the growth in the number of instances in which the \(\varvec{\delta }\)-dominating set contains \(2\) and \(3\) points. So the maximum cardinality found for the largest budget \(\tau = 1.3\) is equal to \(6\) and obtained in only one problem instance. The correlation between cardinality of the solution set and the budget \(\tau \) can especially be observed for the TSP problem instances.

Table 3 Results on DLP instances
Full size table
Fig. 4
figure 4

Cardinality of the approximate solution set to \((BpM)\). DLP instances

Full size image

The computational results for the UFLP are very similar and not fully reproduced here. As for the \(p\)-median, in most cases for both classes of instances the \(\varvec{\delta }\)-dominating set contains only \(1\) or \(2\) solutions when the budget is relatively small, e.g. \(1.05Z\). When the budget is increased, however, there is a little growth in the number of problem instances for which more than one point is obtained.

Let us provide an example of how the optimal value of the location objective and the robustness criterion changes from the first \(\delta \)-efficient solution, being the optimal value of the corresponding problem, to the last found solution. In Tables 4, 5, 6, and 7, 8, 9 we present the results for the UFLP and the \(p\)-median problem obtained for all of \(30\) Euclidean class instances. In the first two columns we give the problem name and the number of facilities opened. Columns \(Obj.\) and \(Obj.\ rob.\) present the optimal value and its robustness (first \(\delta \)-efficient solution) respectively. The next two columns, \(Max.\ obj. (\%)\) and \(Max.\ rob. (\%)\), indicate the increase (in percent points) of the value of the location criterion and the robustness of the last \(\delta \)-efficient solution with respect to the first one. In columns \(N_{\delta }\) and \(Time\,(s)\) one can find the cardinality of the approximate solution set and the computational time in seconds. Note that due to the big number of the problems in which only one \(\delta \)-efficient solution has been found, we omit them from Tables 7, 8, and 9.

Table 4 Results on Euclidean class instances for the UFLP ant \(\tau =1.05Z\) instances
Full size table
Table 5 Results on Euclidean class instances for the UFLP ant \(\tau =1.1Z\) instances
Full size table
Table 6 Results on Euclidean class instances for the UFLP ant \(\tau =1.3Z\) instances
Full size table
Table 7 Results on Euclidean class instances for the \(p\)-median ant \(\tau =1.05Z\) instances
Full size table
Table 8 Results on Euclidean class instances for the \(p\)-median ant \(\tau =1.1Z\) instances
Full size table
Table 9 Results on Euclidean class instances for the \(p\)-median ant \(\tau =1.3Z\) instances
Full size table

From the computational results for the UFLP one can see that when the budget is relatively small, i.e. \(\tau = 1.05Z\) or \(\tau = 1.10Z\) the difference between the values of location objective for the first and last \(\delta \)-efficient solutions lies within \(1\) % for all cases, while the robustness changes by more than \(10\) % (problem \(2611\) in Table 5). The same can be seen in the case when \(\tau = 1.3\) (Table 6). Here the maximum growth of robustness is more than \(25\) % for problem \(2611\), while the value of the UFLP objective for this problem only changes up to \(3\) %. The same observations can also be made on the results for the \(p\)-median problem, though the difference in the values of both criteria is not as big as for the UFLP.

Based on these results one can conclude that when the robustness is of primary importance for the decision-maker, it may make sense to choose more robust solutions enjoying less effective location positions. In this case the loss of the optimal value of transportation costs for serving the demand of all customers will be only of a small percentage, while the growth of the robustness value might be significant. One can also note that the cardinality of the approximate solution set, especially in the case of the \(p\)-median, is rather small even when the budget is relatively big. Therefore there are not so many options for the decision-maker to vary the efficiency of serving the demand of customers during some long period of time, and the optimal \(p\)-median solution, having its own significant robustness value, may be preferred.

4 Concluding remarks

In facility location problems, using cost minimization as unique criterion may not be a good idea when demands are uncertain; however, for small changes in the budget, in our computational experience it is not rare to find that the efficient set is approximated by a very small set of solutions, and the robustness presents very small variations as compared with the solution costs. In this paper, a robustness criterion, namely, the threshold robustness, is suggested to be used in combination with the cost minimization objective. Finding an approximation to the set of Pareto optimal solutions is reduced to solving a finite set of linear integer programs. Our numerical experience with relatively small data sets for the \(p\)-median and the UFLP shows that the so-obtained approximation has a very low cardinality, which is very appealing from a practical perspective.

There are two challenges that may be future lines of research. The first one is to face problems of much larger size, because commercial solvers are not always efficient for big problem instances and may take a long time to solve one particular problem. This would probably call for the use of multiple-objective combinatorial optimization heuristics. The second one is to be able to find a full description of the Pareto-optimal set. While, in theory, this can be done, again, by the \(\varepsilon \)-constraint method (under the mild assumption of integrality in the distances and estimated demands), its cardinality may be too large to be of practical interest. These issues deserve further study.