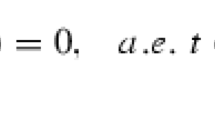Existence results for perturbed boundary value problem with fractional order

Abstract

In this work, we deal with the following class of fractional differential equations with fractional derivative boundary conditions:

$$\begin{aligned} {\left\{ \begin{array}{ll} -D^{\alpha } u(t)+a(t) u(t)=w(t)f(t,u(t)), \ \ \ \ \ t \in (0,1),\\ u^{(j)}(0)=0, \ \ 0 \le j \le n-2, \ \ [D^{\beta } u(t)]_{t=1}=0, \end{array}\right. } \end{aligned}$$

where $n\ge 3$, $n-1< \alpha < n$, $1 \le \beta \le n-2$, $D^{\alpha }$ and $D^{\beta }$ are the standard Riemann-Liouville fractional derivatives and a is a continuous function on [0, 1]. The associated Green’s function is derived in term of a series of functions by the perturbed approach. Sharp estimates on it are established. We give sufficient conditions for existence results by the means of Schauder’s fixed point theorem. Some examples are given to illustrate our results.

1 Introduction

In this paper, we study the following problem for the Riemann-Liouville fractional differential equation with fractional derivative boundary conditions

$$\begin{aligned} {\left\{ \begin{array}{ll} -D^{\alpha } u(t)+a(t) u(t)=w(t)f(t,u(t)), \ \ \ \ \ t \in (0,1),\\ u^{(j)}(0)=0, \ \ 0 \le j \le n-2, \ \ [D^{\beta } u(t)]_{t=1}=0, \end{array}\right. } \end{aligned}$$

(1)

where $n-1< \alpha < n$, $n>2$, $1 \le \beta \le n-2$. $a: [0,1]\longrightarrow {\mathbb {R}}$ be a continuous function. f and w are appropriate functions to be specified later. $D^{\alpha }$ is the $\alpha$-th left Riemann-Liouville fractional derivative. Fractional calculus has been used to model physical and engineering processes, which are found to be best described by fractional differential equations. It is worth noting that the standard mathematical models of integer-order derivatives, including nonlinear models, do not work adequately in many cases. In the recent years, fractional calculus has been applied in various fields such as mechanics, electricity, chemistry, biology, economics. For more details, see [1, 14, 15].

The Green’s function is a fundamental tool for studying the existence of solutions of BVPs of fractional order. By using the theory of the fixed point on cones, the existence of solutions can be shown based on the construction of the mentioned function and its main properties. More precisely, in the literature, the Green’s functions are derived by considering of a linear equation with one term

$$\begin{aligned} D^{\alpha }u(t)=0, \ \ 0<t<1, \end{aligned}$$

subject to certain boundary conditions and convert it to an integral equation, which is the aim of many papers; see for example, [2,3,4,5,6, 8, 12]. However, this method is not applicable in the presence of a perturbed term

$$\begin{aligned} -D^{\alpha } u(t)+a(t) u(t)=0, \ \ 0<t<1, \end{aligned}$$

(2)

and also it is not possible to show the positivity of the associated Green’s function. To overcome this difficulty, Graef et al., [7, 9,10,11] proposed new techniques for the construction of the related Green’s function of (2) with various kinds of boundary conditions. By using spectral theory, they obtained the Green’s function as a series of functions.

In [7], Graef et al. considered the boundary value problem consisting of the fractional differential equation

$$\begin{aligned} -D^{\alpha } u(t)+a(t) u(t)=w(t)f(u), \ \ t \in (0,1), \end{aligned}$$

and subject to boundary conditions

$$\begin{aligned} u(0)=u^{'}(0)=u^{'}(1)=0, \end{aligned}$$

where $2< \alpha < 3$, $a \in {\mathcal {C}}([0,1])$, $w \in {\mathcal {C}}([0,1])$ satisfies $w(t) \ge 0$ a.e. on [0, 1] and $f\in {\mathcal {C}}({\mathbb {R}},{\mathbb {R}})$. The authors obtained the Green’s function associated to the problem as a series of functions and showed its positivity. And then by deriving certain property of the series, they established the existence and the uniqueness of solutions of the above problem.

Recently, Zou [18] studied the following problem

$$\begin{aligned} -D^{\alpha } u(t)+a(t) u(t)=f(t,u(t)), \ \ t \in (0,1), \ u(0)=u^{'}(0)=u^{'}(1)=0, \end{aligned}$$

where $2< \alpha < 3$, $a \in {\mathcal {C}}[0,1]$, and $f\in {\mathcal {C}}([0,1]\times [0,\infty ) ,{\mathbb {R}})$. The author derived new properties of the associated Green’s function than ones given in [7], to obtain the existence of positive solutions.

On the other hand, in [17], Zhen and Wang considered the following fractional differential equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} -D^{\alpha } u(t)+a(t) u(t)=w(t)f(u,t), \ \ t \in (0,1), \ \alpha >2 \\ u^{(k)}(0)=0, \ \ k=0,1,..., [ \alpha ], \ \ u(1)=\int _{0}^{1} u(s) dA(s), \end{array}\right. } \end{aligned}$$

where $a \in {\mathcal {C}}([0,1])$, $w\in L^1[0,1]$ with $w(t) \ne 0$ a.e on [0, 1] and $f \in {\mathcal {C}}({\mathbb {R}}\times [0,1],{\mathbb {R}})$. The authors used the perturbation approach for deriving the associated Green’s function. And so, the existence of solutions is established by the fixed point theorem.

Motivated by the cited papers, in this work, we first improve main properties on the Green’s function $G_{0}(t,s)$ associated to the following linear BVP

$$\begin{aligned} -D^{\alpha } u(t)=h(t), \ \ \ u^{(j)}(0)=0, \ \ 0 \le j \le n-2, \ \ [D^{\beta } u(t)]_{t=1}=0. \end{aligned}$$

(3)

Next, by applying the spectral theory, we derive the Green’s function associated to problem (1) and we establish some estimates. Moreover, we show its positivity which is the main tool to ensure our main result. Finally, we give sufficient conditions on the nonlinearity to obtain the existence of solutions of problem (1).

The paper is developed as follows: In the next section, we get suitable properties on the Green’s function $G_{0}(t,s)$. After that, we construct the Green’s function G(t, s) as a series of functions and we prove some new estimates on it. Section 3 is devoted to show the existence of nontrivial and positive solutions of problem (1). In the last section, two examples are given to illustrate our results.

2 Preliminaries

In this section, we firstly present some necessary definitions and properties about fractional calculus theory. We refer the reader to [14, 15] for more details.

Definition 1

[14] The Riemann-Liouville fractional integral of order

$\alpha >0\$for a measurable function $f:(0,+\infty )\rightarrow {\mathbb {R}}$ is defined as

$$\begin{aligned} I^{\alpha }f(t)=\frac{1}{\Gamma (\alpha )}\int _{0}^{t}(t-s)^{\alpha -1}f(s)ds,\ t>0, \end{aligned}$$

where $\Gamma$ is the Euler Gamma function, provided that the right-hand side is pointwise defined on$(0,+\infty ).$

Definition 2

[14] The Riemann-Liouville fractional derivative of order $\alpha >0\$ for a measurable function $f:(0,+\infty )\rightarrow {\mathbb {R}}$ is defined as

$$\begin{aligned} D^{\alpha }f(t)=\dfrac{1}{\Gamma (n-\alpha )}(\frac{d}{dt} )^{n}\int _{0}^{t}(t-s)^{n-\alpha -1}f(s)ds=(\frac{d}{dt})^{n}I^{n-\alpha }f(t),\ \end{aligned}$$

provided that the right-hand side is pointwise defined on ${\mathbb {R}} ^{+}$.

Here $n=[\alpha ]+1$, $[\alpha ]$ denotes the integer part of the real number $\alpha$

Lemma 3

[14] Let $\alpha >0$. Let $u\in {\mathcal {C}} (0,1)\cap L^{1}(0,1).$ Then

• (i) $D^{\alpha }I^{\alpha }u=u.$

• (ii) For $\delta >\alpha -1,$ $D^{\alpha }t^{\delta }=\dfrac{\Gamma (\delta +1)}{\Gamma (\delta -\alpha +1)}t^{\delta -\alpha }.$ Moreover, we have $D^{\alpha }t^{\alpha -i}=0,\ i=1,2,\ldots ,n.$

• (iii) $D^{\alpha }u(t)=0$ if and only if $u(t)=c_{1}t^{\alpha -1}+c_{2}t^{\alpha -2}+\cdots +c_{n}t^{\alpha -n},$ $c_{i}\in {\mathbb {R}},\ \mathrm {i=1,2,\ldots ,n.}$

• (iv) Assume that $D^{\alpha }u\in {\mathcal {C}} (0,1)\cap L^{1}(0,1),$ then we have

  $$\begin{aligned} I^{\alpha }D^{\alpha }u(t)=u(t)+c_{1}t^{\alpha -1}+c_{2}t^{\alpha -2}+\cdots +c_{n}t^{\alpha -n}, c_{i}\in {\mathbb {R}} ,\ i=1,2,\ldots ,n. \end{aligned}$$

Lemma 4

• (i) Let $\sigma , \lambda \in (0, \infty )$, $c, x \in [0,1]$. Then

  $$\begin{aligned} \min ( 1, \frac{\sigma }{\lambda }) (1-c x^{\sigma }) \le (1-c x^{\sigma }) \le \max (1, \frac{\sigma }{\lambda }) (1-c x^{\sigma }). \end{aligned}$$

• (ii) For $x,t \in [0,1]$, we have $xt\le \min (x,t) \le t$.

3 Estimates on the Green’s function

In this section, we shall construct the explicit expression of the Green’s function associated to the following BVP

$$\begin{aligned} {\left\{ \begin{array}{ll} -D^{\alpha } u(t)+a(t) u(t)=0, \ \ \ \ \ t \in (0,1),\\ u^{(j)}(0)=0, \ \ 0\le j \le n-2, \ \ {[D^{\beta } u(t)]}_{t=1}=0. \end{array}\right. } \end{aligned}$$

(4)

First, we give the expression of the Green’s function related to problem (3). The proof of the following lemma is essentially given in [13, Theorem 3.1].

Lemma 5

Let $h \in {\mathcal {C}}([0,1])$, then the fractional boundary value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} {-}D^{\alpha } u(t)=h(t), \, \, \, \, \, t \in (0,1),\\ u^{(j)}(0)=0, \, \, 0\le j \le n-2, \\ {[D^{\beta } u(t)]}_{t=1}=0, \end{array}\right. } \end{aligned}$$

(5)

has a unique solution

$$\begin{aligned} u(t)=\int _{0}^{1} G_{0}(t,s)h(s)ds, \end{aligned}$$

(6)

where for $t,s \in [0,1]$,

$$\begin{aligned} \mathrm {\ }G_{0}(t,s)=\frac{t^{\alpha -1}(1-s)^{\alpha -\beta -1}-((t-s)^{+})^{\alpha -1}}{ \Gamma (\alpha )}. \end{aligned}$$

(7)

Here, for $x \in {\mathbb {R}}$, $x^{+} = max(x,0)$.

Proof

From Lemma 3, the solution of problem (5) satisfy

$$\begin{aligned} u(t)=c_1t^{\alpha -1}+c_2t^{\alpha -2}+\cdots +c_nt^{\alpha -n}-I^{\alpha }h(t) \end{aligned}$$

(8)

Since $u^{(j)}(0)=0, \ \ 0\le j \le n-2$, it is clear that $c_2=c_3=\cdots =c_n=0$.

Now, we take the R.L fractional derivative of order $\beta$ of (8) for $t>0$ we obtain

$$\begin{aligned} D^{\beta } u(t)= & {} c_1D^{\beta }\big (t^{\alpha -1}\big )-\frac{1}{\Gamma (\alpha -\beta )}\int _{0}^{t} (t-s)^{\alpha -\beta -1}h(s)ds\\= & {} c_1\frac{\Gamma (\alpha )}{\Gamma (\alpha -\beta )}(t)^{\alpha -\beta -1}-\frac{1}{\Gamma (\alpha -\beta )}\int _{0}^{t} (t-s)^{\alpha -\beta -1}h(s)ds \end{aligned}$$

Then the condition $[D^{\beta } u(t)]_{t=1}=0$ implies that

$$\begin{aligned} 0=c_1\frac{\Gamma (\alpha )}{\Gamma (\alpha -\beta )}(1)^{\alpha -\beta -1}-\frac{1}{\Gamma (\alpha -\beta )}\int _{0}^{1} (1-s)^{\alpha -\beta -1}h(s)ds, \end{aligned}$$

and so,

$$\begin{aligned} c_1= \frac{1}{\Gamma (\alpha )}\int _{0}^{1} (1-s)^{\alpha -\beta -1}h(s)ds. \end{aligned}$$

(9)

As a consequence, the unique solution u of problem (5) is given by

$$\begin{aligned} u(t)= & {} \frac{t^{\alpha -1}}{\Gamma (\alpha )}\int _{0}^{1} (1-s)^{\alpha -\beta -1}h(s)ds-\frac{1}{\Gamma (\alpha )}\int _{0}^{t} (t-s)^{\alpha -1}h(s)ds\\= & {} \int _{0}^{1} G_0(t,s)h(s)ds. \end{aligned}$$

$\square$

Next, we give some properties of the Green’s function $G_{0}$, stated in [13, Theorem 3.2].

Proposition 6

The function $G_{0}(t,s)$ has the following properties:

• (i) $G_{0}$ is continuous on $[0,1]\times [0,1]$.

• (ii) $G_{0}(t,s)\ge 0$ for $t,s \in [0,1]$.

• (iii) $\max _{t \in [0,1]} G_{0}(t,s)=G_{0}(1,s)$ for $s \in [0,1].$

Proof

It is obvious to see that $G_{0}(t,s)$ is continuous on $[0,1]\times [0,1]$. Hence, (i) holds.

Let’s prove (iii). If $0 \le t \le s \le 1$, then we obtain

$$\begin{aligned} \frac{\partial G_0(t,s)}{\partial t}=\frac{(\alpha -1)t^{\alpha -2}(1-s)^{\alpha -\beta -1}}{\Gamma (\alpha )}\ge 0. \end{aligned}$$

Thus, $G_0(t,s)$ is increasing with respect to t. As a direct consequence, we deduce that,

$$\begin{aligned} G_0(t,s) \le G_0(1,s), \ \ \text {for all} \ s\in [0,1] \end{aligned}$$

Now, if $0 \le s \le t \le 1$, then we get

$$\begin{aligned} \frac{\partial G_0(t,s)}{\partial t}= & {} \frac{(\alpha -1)t^{\alpha -2}(1-s)^{\alpha -\beta -1}-(\alpha -1)(t-s)^{\alpha -2}}{\Gamma (\alpha )}\\= & {} \frac{(\alpha -1)}{\Gamma (\alpha )}\Big (t^{\alpha -2}(1-s)^{\alpha -\beta -1}-(t-s)^{\alpha -2}\Big )\\= & {} \frac{(\alpha -1)t^{\alpha -2}}{\Gamma (\alpha )}\Big ((1-s)^{\alpha -\beta -1}-(1-\frac{s}{t})^{\alpha -2}\Big ). \end{aligned}$$

So, to show that $\frac{\partial G_0(t,s)}{\partial t} \ge 0$, we must prove that

$$\begin{aligned} \Big ((1-s)^{\alpha -\beta -1}-(1-\frac{s}{t})^{\alpha -2}\Big ) \ge 0. \end{aligned}$$

Using the fact that $\alpha -\beta -1 < \alpha -2$, we have

$$\begin{aligned} \Big ((1-s)^{\alpha -\beta -1}-(1-\frac{s}{t})^{\alpha -2}\Big ) \ge \Big ((1-s)^{\alpha -\beta -1}-(1-s)^{\alpha -2}\Big )\ge 0 . \end{aligned}$$

Which implies that $\frac{\partial G_0(t,s)}{\partial t} \ge 0$. As a result, we get that is increasing with respect

$$\begin{aligned} G_0(t,s) \le G_0(1,s), \ \ \text {for all} \ s\in [0,1]. \end{aligned}$$

Hence, it follows that

$$\begin{aligned} \max _{t \in [0,1]} G_{0}(t,s)=G_{0}(1,s) \ \text {for all} \ s \in [0,1]. \end{aligned}$$

To show (ii), let fix $s \in [0,1]$, we have that $G_0(0,s)=0.$ And, from (iii), $G_0(t,s)$ is increasing in t for each $s \in [0,1]$, we get that $G_0(t,s) \ge 0$ for each $(t,s) \in [0,1]\times [0,1]$. Therefore, (ii) holds and the proof is complete. $\square$

Now, we state new sharp estimates on $G_{0}$ that will be used later.

Lemma 7

• (i) Let $n\in {\mathbb {N}}$, $n-1< \alpha <n$ and $1\le \beta \le n-2$. Define the function H(t, s) on $[0,1]\times [0,1]$ by

  $$\begin{aligned} H(t,s)= \frac{1}{\Gamma (\alpha )} t ^{\alpha -2} (1-s)^{\alpha -\beta -1} \min (t,s). \end{aligned}$$

  (10)

  Then $G_{0}$ has the following property

  $$\begin{aligned} H(t,s) \le G_{0}(t,s) \le (\alpha -1)\beta H(t,s). \end{aligned}$$

  (11)

• (ii) For $t,s\in [0,1]$, we have

  $$\begin{aligned} t^{\alpha -1}\frac{s(1-s)^{\alpha -\beta -1}}{\Gamma (\alpha )} \le G_{0}(t,s) \le (\alpha -1)\beta t^{\alpha -2} \frac{s(1-s)^{\alpha -\beta -1}}{\Gamma (\alpha )} . \end{aligned}$$

  (12)

Proof

• (i) For $t\in (0,1]$ and $s \in [0,1)$, we have

  $$\begin{aligned} \Gamma (\alpha ) G_{0}(t,s)= t^{\alpha -1}(1-s)^{\alpha -\beta -1} [1- \frac{((t-s)^+)^{\alpha -1}}{t^{\alpha -1}(1-s)^{\alpha -\beta -1}}] \end{aligned}$$

  From Lemma 4, for $\lambda =1$, $\sigma =\alpha -1$, $c=(1-s)^{\alpha }$ and $x=\frac{(t-s)^+}{t(1-s)}$, we obtain

  $$\begin{aligned}&t^{\alpha -1}(1-s)^{\alpha -\beta -1} (1-(1-s)^{\beta } \frac{(t-s)^+}{t(1-s)}) \\&\quad \le \Gamma (\alpha ) G_{0}(t,s) \le (\alpha -1) t^{\alpha -1}(1-s)^{\alpha -\beta -1} (1-(1-s)^{\beta } \frac{(t-s)^+}{t(1-s)}). \end{aligned}$$

  Applying again Lemma 4, for $\lambda =1$, $\sigma =\beta \ge 1$, $x =(1-s)$ and $c=\frac{(t-s)^+}{t(1-s)}$, we get

  $$\begin{aligned}&t^{\alpha -1}(1-s)^{\alpha -\beta -1}(1-\frac{(t-s)^+}{t}) \le \Gamma (\alpha ) G_{0}(t,s) \\&\quad \le (\alpha -1) t^{\alpha -1}(1-s)^{\alpha -\beta -1} \beta (1-\frac{(t-s)^+}{t}). \end{aligned}$$

  By using the fact that $(1-\frac{(t-s)^+}{t})=\frac{1}{t} \min (t,s)$, we conclude that

  $$\begin{aligned} H(t,s) \le G_{0}(t,s) \le (\alpha -1) \beta H(t,s). \end{aligned}$$

• (ii) From Lemma 4, (ii), formula (12) holds.

The proof is completed. $\square$

In the next lemma, we derive an important property of Green’s function $G_{0}$.

Lemma 8

For $t,\tau ,s \in (0,1)$, we have

$$\begin{aligned} \frac{G_{0}(t,\tau )G_{0}(\tau ,s)}{G_{0}(t,s)}\le \frac{((\alpha -1) \beta )^2}{\Gamma (\alpha )} \tau ^{\alpha -1}(1-\tau )^{\alpha -\beta -1}. \end{aligned}$$

(13)

Proof

By Lemma 7 (i), for $t,\tau ,s \in (0,1)$, we obtain

$$\begin{aligned} \frac{G_{0}(t,\tau )G_{0}(\tau ,s)}{G_{0}(t,s)}\le \frac{((\alpha -1)\beta )^2}{\Gamma (\alpha )} \tau ^{\alpha -2}(1-\tau )^{\alpha -\beta -1} \frac{\min (t,\tau )\min (\tau ,s)}{\min (t,s)}. \end{aligned}$$

If $t\le s$. Then

$$\begin{aligned} \frac{\min (t,\tau )\min (\tau ,s)}{\min (t,s)} \le \frac{t\min (\tau ,s)}{t}\le \tau . \end{aligned}$$

On the other hand, if $s\le t$ we have

$$\begin{aligned} \frac{\min (t,\tau )\min (\tau ,s)}{\min (t,s)} \le \frac{s\min (t,\tau )}{s}\le \tau , \end{aligned}$$

which completes the proof. $\square$

Now, let $G: [0,1]\times [0,1] \longrightarrow {\mathbb {R}}$ be defined by

$$\begin{aligned} G(t,s)= \sum _{k=0}^{\infty } (-1)^k G_{k}(t,s), \end{aligned}$$

(14)

where $G_{0}$ is given by (7) and $G_{k}: [0,1]\times [0,1] \longrightarrow {\mathbb {R}}$,

$$\begin{aligned} G_{k}(t,s) = \int _{0}^{1} a(\tau ) G_{0}(t,\tau ) G_{k-1}(\tau ,s)d\tau ,\ \ a \in {\mathcal {C}}[0,1],\ k \ge 1. \end{aligned}$$

(15)

In order to express the Green’s function associated with the linear problem (4), we shall use the spectral theory in Banach spaces. To this end, we require the following lemma.

Lemma 9

[16] Let X be a Banach space and ${\mathcal {A}}:X \longrightarrow X$ be a linear operator with the operator norm $\Vert {\mathcal {A}}\Vert$ and spectral radius $r( {\mathcal {A}})$ of ${\mathcal {A}}$. Then

• (i) $r( {\mathcal {A}}) \le \Vert {\mathcal {A}} \Vert$;

• (ii) if $r( {\mathcal {A}}) < 1$, then $( {\mathcal {I}}- {\mathcal {A}})^{-1}$ exists and $( {\mathcal {I}}- {\mathcal {A}})^{-1}=\sum \nolimits _{n=0}^{\infty } {\mathcal {A}}^n$, where ${\mathcal {I}}$ stands for the identity operator.

Let X denotes the Banach space $({\mathcal {C}}([0,1]), \Vert . \Vert )$ where $\left\| u \right\| =\max \nolimits _{0\le t\le 1}\left| u(t)\right|$, and let

$$\begin{aligned} \sigma = \frac{(\alpha -1)\beta }{\Gamma (\alpha )(\alpha -\beta )(\alpha -\beta +1)}. \end{aligned}$$

(16)

The next theorem, which is our main contribution in this paper, presents a careful analysis of Green’s function which allows us to deduce the existence results of our problem (1).

Theorem 10

Let ${\overline{a}}=\max _{t\in [0,1]} \vert a(t) \vert < \frac{1}{\sigma }$. Then, G, defined by (14) as a series of functions, is uniformly convergent for $(t,s) \in [0,1]\times [0,1]$ and continuous on $[0,1]\times [0,1]$. Furthermore, G is the Green’s function for the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -D^{\alpha } u(t)+a(t) u(t)=0, \ \ \ \ \ t \in (0,1),\\ u^{(j)}(0)=0, \ \ 0\le j \le n-2, \ \ [D^{\beta } u(t)]_{t=1}=0. \end{array}\right. } \end{aligned}$$

(17)

Moreover, we get

$$\begin{aligned} \vert G(t,s) \vert \le \frac{\sigma }{1-\sigma {\overline{a}}} s(1-s)^{\alpha -\beta -1} \ \ on \ [0,1]\times [0,1], \end{aligned}$$

(18)

Proof

Let $y \in X$, assume that u is the solution of problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -D^{\alpha } u(t)+a(t) u(t)=y(t), \ \ \ \ \ t \in (0,1),\\ u^{(j)}(0)=0, \ \ 0\le j \le n-2, \ \ [D^{\beta } u(t)]_{t=1}=0. \end{array}\right. } \end{aligned}$$

(19)

Then, u satisfies

$$\begin{aligned} u(t)= \int _{0}^{1} G_{0}(t,s)[y(s)-a(s)u(s)]ds, \end{aligned}$$

which implies

$$\begin{aligned} u(t)+\int _{0}^{1} a(s)G_{0}(t,s)u(s)ds=\int _{0}^{1} G_{0}(t,s)y(s)ds. \end{aligned}$$

(20)

Define ${\mathcal {A}}$ and ${\mathcal {B}}: X \longrightarrow X$ by

$$\begin{aligned}&({\mathcal {A}}y)(t)= \int _{0}^{1} G_{0}(t,s)y(s)ds, \ t\in [0,1], \end{aligned}$$

(21)

$$\begin{aligned}&({\mathcal {B}}u)(t)= \int _{0}^{1} a(s)G_{0}(t,s)u(s)ds, \ t \in [0,1]. \end{aligned}$$

(22)

Then, equation (20) becomes

$$\begin{aligned} ({\mathcal {I}}+{\mathcal {B}})u={\mathcal {A}}y. \end{aligned}$$

(23)

We divide the proof into several steps:

Step 1: Let us verify that $\Vert {\mathcal {B}} \Vert <1$. For any $u \in X$ with $\Vert u \Vert =1$ and $t\in [0,1]$, by (12), we have

$$\begin{aligned} \vert {\mathcal {B}}u(t) \vert = \vert \int _{0}^{1} G_{0}(t,s)a(s)u(s)ds \vert \le \frac{(\alpha -1)\beta }{\Gamma (\alpha )} {\overline{a}} \int _{0}^{1}s (1-s)^{\alpha -\beta -1}ds\Vert u \Vert \le \sigma {\overline{a}}. \end{aligned}$$

Thus, since ${\overline{a}} < \frac{1}{\sigma }$, we have $\Vert {\mathcal {B}} \Vert <1.$ And by Lemma 9, we deduce that

$$\begin{aligned} u= ({\mathcal {I}}+{\mathcal {B}})^{-1} {\mathcal {A}}y=\sum _{k=0}^{\infty }(-{\mathcal {B}})^{k}{\mathcal {A}}y. \end{aligned}$$

(24)

Step 2: We shall prove that

$$\begin{aligned} (-{\mathcal {B}})^{k} {\mathcal {A}} y(t) = \int _{0}^{1} (-1)^{k} G_{k}(t,s)y(s)ds, \ \ \ k=0,1,2,... \end{aligned}$$

(25)

It is clear that, for $k=0$, (25) holds. Assume that (25) holds for $k=m-1$. Then, by (15), (21), (22), (25) and Fubini’s Theorem, we have

$$\begin{aligned} (-{\mathcal {B}})^{m} {\mathcal {A}} y(t)= & {} (-{\mathcal {B}}(-{\mathcal {B}})^{m-1} {\mathcal {A}} y)(t)\\= & {} \int _{0}^{1} - a(\tau ) G_{0}(t,\tau ) \int _{0}^{1} (-1)^{m-1} G_{m-1}(\tau ,s)y(s)ds d\tau \\= & {} \int _{0}^{1} (-1)^{m} y(s)\int _{0}^{1} a(\tau ) G_{0}(t,\tau ) G_{m-1}(\tau ,s) d\tau ds \\= & {} \int _{0}^{1} (-1)^{m} G_{m}(t,s) y(s) ds. \end{aligned}$$

Thus, (25) holds for $k=m$. And so, (25) holds for any $k=0,1,2,...$

Step 3: We show that for $k=0,1,2,...$

$$\begin{aligned} \vert (-1)^{k} G_{k}(t,s) \vert \le \sigma ^{k+1} {\overline{a}}^{k} s (1-s)^{\alpha -\beta -1}. \end{aligned}$$

(26)

For $k=0$, (26) holds. Assume that (26) holds for $k=m \ge 0$. Then, for $t,s\in [0,1]$, we have

$$\begin{aligned} \vert (-1)^{m+1} G_{m+1}(t,s) \vert= & {} \Big \vert \int _{0}^{1} (-1)^{m+1} G_{0}(t,\tau ) G_{m}(\tau ,s) d\tau \Big \vert \\\le & {} \sigma ^{m+1} {\overline{a}}^{m}\Big (\int _{0}^{1} \vert a(\tau ) \vert G_{0}(t,\tau ) d\tau \Big ) s (1-s)^{\alpha -\beta -1}\\= & {} \sigma ^{m+2} {\overline{a}}^{m+1} s (1-s)^{\alpha -\beta -1}. \end{aligned}$$

So, (26) holds for $k=m+1$. Then, by induction, for any $k=0,1,2,...$, we have that (26) holds.

Since $\sigma {\overline{a}}<1$, then, for $(t,s) \in [0,1]\times [0,1]$, we obtain

$$\begin{aligned} \vert G(t,s) \vert= & {} \Big \vert \sum _{k=0}^{\infty } (-1)^{k} G_{k}(t,s) \Big \vert \\\le & {} \sum _{k=0}^{\infty } \sigma ^{k+1} {\overline{a}}^{k} s (1-s)^{\alpha -\beta -1} < \infty . \end{aligned}$$

Thus, G is uniformly convergent on $[0,1]\times [0,1]$, and G satisfies (18).

In addition, from (14), (24) and (25), we get

$$\begin{aligned} u(t)= \sum _{k=0}^{\infty } (-1)^{k}\int _{0}^{1} G_{k}(t,s) y(s)ds= \int _{0}^{1} G(t,s) y(s)ds,\ \ t \in [0,1]. \end{aligned}$$

(27)

Step 4: We shall verify that u, defined by (27), is a solution of problem (19). From (14), (21) and (22), we deduce that u satisfies (24). Moreover, by (21) and (22), u satisfies (20).

Therefore, u is a solution of problem (19) and so G is the Green’s function of problem (4). $\square$

The following result ensures the positivity of the related Green’s function.

Proposition 11

Let $\gamma =\frac{((\alpha -1)\beta )^2}{\Gamma (\alpha )}\int _{0}^{1} \tau ^{\alpha -1}(1-\tau )^{\alpha -\beta -1}d\tau .$ Assume that $\gamma {\overline{a}} < \frac{1}{2}$. Then for $(t,s)\in [0,1]\times [0,1]$, we have

$$\begin{aligned} (1-\frac{\gamma {\overline{a}}}{1-\gamma {\overline{a}}})G_{0}(t,s) \le G(t,s) \le G_{0}(t,s). \end{aligned}$$

(28)

Proof

Since $\gamma {\overline{a}} < \frac{1}{2}$. Then by Lemma 8, we obtain

$$\begin{aligned} \vert G(t,s) \vert \le \sum _{k=0}^{\infty } \vert (-1)^k G_{k}(t,s) \vert \le \frac{1}{1-\gamma {\overline{a}}} G_{0}(t,s). \end{aligned}$$

(29)

And, from the expression of G given by (14), we get

$$\begin{aligned} G(t,s)= & {} G_{0}(t,s)+ \sum _{k=1}^{\infty } (-1)^k G_{k}(t,s) \\= & {} G_{0}(t,s)- \sum _{k=0}^{\infty } (-1)^k G_{k+1}(t,s)\\= & {} G_{0}(t,s)- \sum _{k=0}^{\infty } (-1)^k \int _{0}^{1}a(\tau )G_{0}(t,\tau ) G_{k}(\tau ,s)d\tau \\= & {} G_{0}(t,s)-\int _{0}^{1}a(\tau )G_{0}(t,\tau ) (\sum _{k=0}^{\infty } (-1)^k G_{k}(\tau ,s))d\tau \\= & {} G_{0}(t,s)-\int _{0}^{1}a(\tau )G_{0}(t,\tau ) G(\tau ,s)d\tau . \end{aligned}$$

By (13) and (29), we have

$$\begin{aligned} \int _{0}^{1}a(\tau )G_{0}(t,\tau ) G(\tau ,s)d\tau\le & {} \frac{1}{1-\gamma {\overline{a}}} \int _{0}^{1}a(\tau ) \frac{G_{0}(t,\tau ) G_{0}(\tau ,s)}{G_{0}(t,s)}d\tau \ G_{0}(t,s)\\\le & {} \frac{{\overline{a}}}{1-\gamma {\overline{a}}} \frac{((\alpha -1)\beta )^2}{\Gamma (\alpha )} \int _{0}^{1}\tau ^{\alpha -1}(1-\tau )^{\alpha -\beta -1} d\tau \ G_{0}(t,s)\\= & {} \frac{\gamma {\overline{a}}}{1-\gamma {\overline{a}}} G_{0}(t,s). \end{aligned}$$

This implies that

$$\begin{aligned} G(t,s)\ge & {} G_{0}(t,s) - \frac{\gamma {\overline{a}}}{1-\gamma \phi {\overline{a}}} G_{0}(t,s)=\frac{1-2\gamma {\overline{a}}}{1-\gamma {\overline{a}}} G_{0}(t,s) \ge 0. \end{aligned}$$

So, it follows that $0 \le G(t,s) \le G_{0}(t,s)$. This completes the proof. $\square$

An immediate consequence of Proposition 11 and Lemma 7 (ii) is the following result.

Corollary 12

For $(t,s)\in [0,1]\times [0,1]$, we have

$$\begin{aligned} (1-\frac{\gamma {\overline{a}}}{1-\gamma {\overline{a}}})\frac{t^{\alpha -1}}{\Gamma (\alpha )}s(1-s)^{\alpha -\beta -1} \le G(t,s) \le \frac{(\alpha -1) \beta }{\Gamma (\alpha )} s(1-s)^{\alpha -\beta -1}. \end{aligned}$$

(30)

4 Existence results

In this section, using the estimates of G(t, s) derived above, sufficient conditions on the non-linearity f are discussed to guarantee the existence of solutions of problem (1).

Hereinafter, we suppose the following assumption:

• (H) $w: (0,1) \rightarrow {\mathbb {R}}$ such that $w(t) \not \equiv 0$ a.e on (0, 1) and $0<\sigma _{w}=\int _{0}^{1} s (1-s)^{\alpha -\beta -1} w(s) ds < \infty .$

Theorem 13

Assume that (H) holds. In addition if the following conditions hold:

(C$_{1}$):

$f: [0,1] \times {\mathbb {R}} \longrightarrow {\mathbb {R}}$ is a continuous function.

(C$_{2}$):

$f(t,0) \not \equiv 0$ on [0, 1] and

$$\begin{aligned} \lim \limits _{\vert u \vert \rightarrow \infty } \max \limits _{t \in [0,1]} \frac{\vert f(t, u )\vert }{\vert u \vert }=0. \end{aligned}$$

Then Problem (1) has at least one nontrivial solution.

Proof

From (C$_{2}$), for $\varepsilon = \left( \frac{(\alpha -1)\beta }{\Gamma (\alpha )} \sigma _{w} \right) ^{-1} >0$, there exists $B>0$ such that for each $t \in [0,1]$ and $\vert u \vert \ge B$, we have $\vert f(t, u )\vert \le \varepsilon \vert u \vert .$

Moreover, by (C$_{1}$), there exists $M>0$ such that

$$\begin{aligned} \vert f(t, u )\vert \le M \ \ on \ \ [0,1]\times [-B,B]. \end{aligned}$$

Let $R= \max \lbrace B, \frac{M}{\varepsilon } \rbrace$. Then

$$\begin{aligned} \vert f(t, u )\vert \le \varepsilon R \ \ on \ \ [0,1]\times [-R,R]. \end{aligned}$$

(31)

Let

$$\begin{aligned} \Omega = \lbrace u \in X: \Vert u \Vert \le R \rbrace . \end{aligned}$$

It is clear that $\Omega$ is a non-empty, convex and closed set.

Define the operator $T: \Omega \longrightarrow X$ by

$$\begin{aligned} Tu(t)= \int _{0}^{1} G(t,s) w(s) f(s,u(s))ds, \ \ t\in [0,1], \end{aligned}$$

(32)

where G(t, s) is defined by (14). Obviously, u is a solution of problem (1) if and only if u is a fixed point of T.

Step 1: Let us prove that $T(\Omega ) \subset \Omega$.

By (C$_{1}$) and Theorem 10, we get that $T: \Omega \longrightarrow X$ is continuous.

Let $u \in \Omega$, then by Corollary 12 and (31), we have for $t \in [0,1]$,

$$\begin{aligned} \vert Tu(t) \vert\le & {} \int _{0}^{1} G(t,s) w(s) \vert f(s,u(s)) \vert ds \\\le & {} \frac{(\alpha -1)\beta }{\Gamma (\alpha )} \int _{0}^{1} s(1-s)^{\alpha -\beta -1} w(s) \vert f(s,u(s)) \vert ds \\\le & {} \varepsilon R \frac{(\alpha -1)\beta }{\Gamma (\alpha )} \sigma _{w} \le R. \end{aligned}$$

Thus, $\Vert T u \Vert \le R$. And so, $T(\Omega ) \subset \Omega$.

Step 2: We shall show that T is uniformly bounded.

Let S be bounded set of $\Omega$, then there exists a positive constant N such that $\Vert u \Vert = N$, for all $u \in S$.

Let $N_{1}=1+ \max \nolimits _{t\in [0,1], u \in [-N,N]} \vert f(t,u)\vert$. Then, by (H), (C$_{1}$) and Corollary 12, we obtain for all $u \in S$ and $t\in [0,1]$

$$\begin{aligned} \vert Tu(t) \vert\le & {} \frac{(\alpha -1)\beta }{\Gamma (\alpha )}\int _{0}^{1}s(1-s)^{\alpha -\beta -1} w(s) \vert f(s,u)\vert ds\\\le & {} \frac{(\alpha -1)\beta N_{1}}{\Gamma (\alpha )}\sigma _{w} < \infty . \end{aligned}$$

Hence, T(S) is uniformly bounded.

Step 3: Let us prove that T(S) is equicontinuous on [0, 1].

Using Theorem 10, we obtain that G is uniformly continuous on $[0,1]\times [0,1]$. Then for $t_{1}, t_{2} \in [0, 1]$ such that $t_{1}\le t_{2}$ and for each $s \in [0, 1]$, we obtain $\vert G(t_{2},s)-G(t_{1},s)\vert \rightarrow 0$ as $t_{2} \longrightarrow t_{1}$ and

$$\begin{aligned} \int _{0}^{1}\vert G(t_{2},s)-G(t_{1},s)\vert \vert w(s) f(s,u(s))\vert ds\le & {} \frac{2 (\alpha -1)\beta }{\Gamma (\alpha )}M_{1} \int _{0}^{1}s(1-s)^{\alpha -\beta -1} w(s)ds \\= & {} \frac{2 (\alpha -1)\beta }{\Gamma (\alpha )}M_{1} \sigma < \infty . \end{aligned}$$

The Lebesgue control convergence guarantee that T(S) is equicontinuous. Consequently by Ascoli’s theorem, we conclude that T(S) is relatively compact. Therefore, by Schauder fixed point theorem, T has at least one fixed point in $\Omega$. Hence, problem (1) has a solution u in $\Omega$. It is clear that $u(t) \equiv 0$ is not a solution of (1). $\square$

Now, we will be concerned with the existence of positive solution to the problem (1) under the following conditions:

(C$_{1}^{\prime }$):

$f: [0,1] \times [0,\infty ) \longrightarrow {\mathbb {R}}$ is a continuous function.

(C$_{3}$):

There exist $d_{2}>d_{1}>0$ such that

$$\begin{aligned} \inf _{u \in P} \int _{0}^{1}s(1-s)^{\alpha -\beta -1} w(s)f(s,u(s)) ds \ge d_{1} \Gamma (\alpha ) \left( 1-\frac{\gamma {\overline{a}}}{1-\gamma {\overline{a}}} \right) ^{-1} \end{aligned}$$

(33)

and

$$\begin{aligned} \sup _{u\in P} \int _{0}^{1}s(1-s)^{\alpha -\beta -1} w(s)f(s,u(s)) ds \le d_{2} \frac{\Gamma (\alpha )}{(\alpha -1)\beta }, \end{aligned}$$

(34)

where

$$\begin{aligned} P= \lbrace u \in X: t^{\alpha -1} d_{1} \le u \le d_{2} \rbrace . \end{aligned}$$

(35)

Theorem 14

Under assumptions (H), (C$_{1}^{\ \prime }$) and (C$_{3}$) Problem (1) has at least one positive solution in P.

Proof

Define the operator $T: P\rightarrow X$ by

$$\begin{aligned} Tu(t)= \int _{0}^{1} G(t,s) w(s) f(s,u(s))ds. \end{aligned}$$

It is clear that u is a fixed point of T if and only if u is a solution of problem (1).

Let us prove that $T(P) \subset P$. Let $t \in [0,1]$ and $u \in P$. Then, by Corollary 12, (C$_{1}^{\ \prime }$) and (C$_{3}$), we have

$$\begin{aligned} Tu(t) \ge \left( 1-\frac{\gamma {\overline{a}}}{1-\gamma {\overline{a}}} \right) \frac{t^{\alpha -1}}{\Gamma (\alpha )}\inf _{u \in P}\int _{0}^{1}s(1-s)^{\alpha -\beta -1} w(s)f(s,u(s)) ds \ge d_{1} t^{\alpha -1} \end{aligned}$$

and

$$\begin{aligned} Tu(t)\le \frac{(\alpha -1)\beta }{\Gamma (\alpha )} \sup _{u \in P}\int _{0}^{1}s(1-s)^{\alpha -\beta -1} w(s)f(s,u(s)) ds \le d_{2}. \end{aligned}$$

Thus, $T(P) \subset P$. Using standard arguments, we conclude, by Schauder fixed point theorem, that T has at least one fixed point $u \in P$. Since $u(t)>0$, $t\in [0,1]$, this implies the existence of a positive solution of problem (1) in P. $\square$

As a consequence of Theorem 14, we deduce the following corollaries.

Corollary 15

Assume that (H) holds. Moreover, if there exist $d_{2}>d_{1}>0$ such that for $t\in [0,1]$, f(t, .) is non-decreasing on $[0,d_{2}]$, satisfying

$$\begin{aligned} \int _{0}^{1}s(1-s)^{\alpha -\beta -1} w(s)f(s,s^{\alpha -1}d_{1}) ds \ge d_{1} \Gamma (\alpha ) \left( 1-\frac{\gamma {\overline{a}}}{1-\gamma {\overline{a}}} \right) ^{-1} \end{aligned}$$

and

$$\begin{aligned} \int _{0}^{1}s(1-s)^{\alpha -\beta -1} w(s)f(s,d_{2}) ds \le d_{2} \frac{\Gamma (\alpha )}{(\alpha -1)\beta }. \end{aligned}$$

Then problem (1) has at least one positive solution in P.

Corollary 16

Assume that (H) holds. In addition, if there exist $d_{2}>d_{1}>0$ such that for $t\in [0,1]$, f(t, .) is non-increasing on $[0,d_{2}]$, satisfying

$$\begin{aligned} \int _{0}^{1}s(1-s)^{\alpha -\beta -1} w(s)f(s,d_{2}) ds \ge d_{1} \Gamma (\alpha ) \left( 1-\frac{\gamma {\overline{a}}}{1-\gamma {\overline{a}}} \right) ^{-1} \end{aligned}$$

and

$$\begin{aligned} \int _{0}^{1}s(1-s)^{\alpha -\beta -1} w(s)f(s,s^{\alpha -1} d_{1}) ds \le d_{2} \frac{\Gamma (\alpha )}{(\alpha -1)\beta }. \end{aligned}$$

Then problem (1) has at least one positive solution in P.

5 Examples

In this section, we give two examples to illustrate the applicability of the obtained results.

Example 17

Consider the following problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -D^{\frac{9}{2}} u(t)+a(t) u(t)=w(t)f(t,u(t)), \ \ \ t \in (0,1),\\ u(0)=u^{\prime }(0)=u^{\prime \prime }(0)=u^{\prime \prime \prime }(0)=0, \ \ [D^{\frac{5}{2}} u(t)]_{t=1}=0. \end{array}\right. } \end{aligned}$$

(36)

Set $a(t)= \frac{-e^{t}}{3}$, $w(t)=\frac{1}{1-t}$ and $f(t,u)=\ln (t+2) (u+1) e^{-u}$. It is not difficult to verify that (C$_{1}$) and (C$_{2}$) are satisfied. By direct calculation, we obtain ${\overline{a}} \simeq 0.906093$, $\sigma \simeq 0.10746118$, $\sigma _{w}= \frac{1}{2}$ and $\gamma \simeq 0.265947$.

Hence, $\gamma {\overline{a}} \simeq 0.240972 < \frac{1}{2}$ and ${\overline{a}} \sigma \simeq 0.0973698 <1$. From Theorem 13, problem (36) has at least one nontrivial solution.

Example 18

Consider the following problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -D^{\frac{7}{2}} u(t)+a(t) u(t)=w(t)f(t,u(t)), \ \ \ t \in (0,1),\\ u(0)=u^{\prime }(0)=u^{\prime \prime }(0)=0, \ \ [D^{\frac{3}{2}} u(t)]_{t=1}=0, \end{array}\right. } \end{aligned}$$

(37)

where $a(t)=-\frac{t^2}{2}$, $w(t)=\frac{1}{t}$ and $f(t,u)=\ln (\frac{1}{2}+t)\cos (\sqrt{u})$. A simple calculation yields to ${\overline{a}} = \frac{1}{2}$, $\sigma _{w}=\frac{1}{2}$, $\sigma \simeq 0.188063$ and $\gamma \simeq 0.2686619$. So, assumptions (H) and (C$_{1}^{\ \prime }$) are satisfied. In addition, ${\overline{a}} < \frac{1}{\sigma } \simeq 5.31735$ and $\gamma {\overline{a}} \simeq 0.134331 < \frac{1}{2}$.

Thus, for $d_{1}$ small enough and $d_{2}$ large enough, hypothesis (C$_{3}$) holds and so, by Theorem 14, the problem (37) has at least one positive solution.