Estimation on diffusion coefficient of lithium ions at the interface of LiNi_0.5Mn_1.5O₄/electrolyte in Li-ion battery

Abstract

This research tried to estimate diffusion coefficient for lithium ions through the surface of the spinel LiNi_0.5Mn_1.5O₄ by spin-polarized total energy calculation. In addition, calculated result by this ab initio model was compared with a semi-empirical model. Both of these models predicted diffusion coefficient for lithium ions at the interface of the spinel LiNi_0.5Mn_1.5O₄/electrolyte as 10⁻⁸ cm² s⁻¹ which is 3 orders of magnitude higher than the diffusion coefficient of lithium ions in LiNi_0.5Mn_1.5O₄. Details of these two models have been explained in this paper along with calculated results for surface diffusion coefficient of LiNi_0.5Mn_1.5O₄ cathode material.

Introduction

Manipulating active materials for Li-ion battery technology is still a challenging issue on developing the overall performance of battery. Therefore, any attempt of disclosing mechanism of atomic evolution and movement in active materials would be a necessary foundation of further researches on designing more efficient active materials during charging/discharging. Such kinds of attempts would be well-organized if computational approaches work closely with experimental techniques. In general, physical concept computational models of Li-ion batteries are engaged in multiscale [1]. These kinds of multiscale models are efficient in modeling the overall performance of battery but less efficient in studying the physical mechanism in comparison to first principle simulations. It is not inequitable to claim that first principle simulations are more efficient to evaluate governing physical mechanisms than the other computational methods at higher length scales. But first principle simulations are limited to small atomic systems. Nevertheless, performing simulation at any desired length scale would be helpful to predict and discover governing physical mechanisms. There are some coarse grain thermodynamic models to simulate charging and discharging of Li-ion battery [2–7]. In addition, there are extensive first principle simulations particularly on designing active materials by considering a small part of them [8–13]. In most cases that experimental techniques are expensive or hard to establish, first principle simulations could be used efficiently as they are well-developed in material science and engineering physics.

Any first principle simulation is started from Schrodinger equation (SE). SE governs the dynamics of the probability distribution of electrons [14]. SE is an equation which is derived from the minimization of the total energy of the atomic system. The total energy can be written in the quantum state by Eq. 1:

$$ \mathrm{Totalenergy}={\varphi}_i^{*}\left({\displaystyle \sum_i\left(\frac{-{\hslash}^2}{2{m}_{\mathrm{e}}}{\nabla}^2\right)+{V}_{\mathrm{pp}}(r)}\right){\varphi}_i+{E}_{\mathrm{XC}}+{E}_{\mathrm{e}\mathrm{e}}+{E}_{\mathrm{ii}} $$

(1)

In the minimum formalism of total energy, we have the following (Eqs. 2, 3, and 4):

Time independent:

$$ {E}_{\mathrm{n}}{\varphi}_n(r)=\left[-\frac{\hslash^2}{2 m}{\nabla}^2+ V(r)\right]{\varphi}_n(r) $$

(2)

Time dependent:

$$ ih\frac{\partial }{\partial t}\psi \left( r, t\right)=\left[-\frac{\hslash^2}{2 m}{\nabla}^2+ V(r)\right]\psi \left( r, t\right) $$

(3)

$$ \psi \left( r, t\right)={\displaystyle \sum_{n=\mathrm{o}}^{\infty }{a}_n{\varphi}_n}(r){e}^{- i{E}_{\mathrm{n}} t} $$

(4)

In first principle simulation or total energy first principle simulation, SE was used to calculate the ground state wave function, and then according to Eq. 1, overall total energy could be calculated. This calculated total energy could be used for estimating activation energy of atomic diffusion, elastic constant, chemical potential, and other physical quantities. In the case of Li-ion battery, total energy first principle simulation is very successful to estimate voltage and atomic diffusion constant.

Besides, there are more approaches in studying Li-ion battery. One of them is a very old one, that is, Fickian approach. Fickian transport approach is probably the oldest phenomenological description of diffusion [15]. This approach can be applied to every scale according to the used scale for parameters, namely, diffusion constant. In general, there is no explicit dependency of the results to the atomic arrangement and its defects in the Fickian approach. But a statistical approach could be used to modify the concept of the Fick’s equation to shift the resolution of the results to the atomic scale, e.g., the Einstein’s relation or Einstein–Smoluchowski relation to assess the diffusion coefficient (Eq. 5) [15].

$$ {D}_x=\frac{\left\langle {X}^2\right\rangle }{2\tau},{D}_y=\frac{\left\langle {Y}^2\right\rangle }{2\tau},{D}_z=\frac{\left\langle {Z}^2\right\rangle }{2\tau}\overset{\mathrm{yields}}{\to }{D}_R=\frac{\left\langle {R}^2\right\rangle }{6\tau} $$

(5)

More general expression could be written for diffusion coefficient according to the statistical approach to consider the length of arbitrary particle jumps and diffusion memory (correlation) effect [16]. In statistical approach, path memory (correlation) of atomic diffusion could be easily formulated by Eq. 6. If the atomic jumps are mediated by the atomic defects, correlation effects always arise [15]. Thereby, according to Eq. 6, the presence of atomic defects could be implicitly defined.

$$ \left\langle {X}^2\right\rangle ={\displaystyle \sum_{i=0}^n\left\langle {x}_i^2\right\rangle +2\begin{array}{c}\hfill {\displaystyle \sum_{i=1}^{n=1}{\displaystyle \sum_{j= i+1}^n\left\langle {x}_i{x}_j\right\rangle }}\hfill \\ {}\hfill \underset{\mathrm{Correlation}\ \mathrm{term}}{\leftrightarrow}\hfill \end{array}} $$

(6)

In more developed mathematical formulation, phase field (PF) model could be used to go beyond the Fickian approach. Some researchers have gone beyond the Fickian transport description by PF continuous approach to study the intercalation of lithium ions in active materials [17, 18]. More reliable results were claimed by this approach in comparison with the Fickian one. But mathematical handling of the Fickian approach is simpler than the PF technique.

In addition, if a model uses a Fickian approach to assess a physical description for lithium ions de/intercalation in active materials, a drift in chemical potential caused by the presence of an external force must be applied to that common form of Fick’s formula. Also, the term of friction force caused by viscosity of liquid is needed to model lithium ion diffusion in electrolyte [19]. According to the Stokes’s theorem, the friction term is neglected if viscosity is lower than 0.05.

In the present research, our published semi-empirical model on estimating the diffusion coefficient of lithium ions at interface of active material and electrolyte would be explained in more details considering its physical concepts. Our calculated results on mentioned diffusion coefficient at interface were published before [20] with lack of description of physical details of model. In addition, a spin-polarized total energy calculation was used to study more on diffusion coefficient at surface of active material and its calculated results were compared to the result of mentioned semi-empirical model. Activation energy of diffusion could also estimate directly with this spin-polarized total energy calculation.

Experimental

Fabrication of LiNi_0.5Mn_1.5O₄

LiNi_0.5Mn_1.5O₄ powders were synthesized via a solid state method. Appropriate amounts of MnO₂, Ni₂O₃, and Li₂CO₃ powders were mixed in ball milling for 10 h. This planetary ball milling facility was used to activate powders. Subsequently, the mixed precursor powders were calcined in an electric furnace at 800 °C for 5 h in air.

Characterization of active material

X-ray diffraction (XRD) using CuK_α radiation with a wave length of 0.154 nm, Fourier transform infra-red spectroscopy (FTIR), and scanning electron microscope (SEM) were used to characterize and assess the synthesized active material. Electrochemical impedance spectroscopy (EIS) tests were implemented on Autolab PGSTAT 302N. Cyclic voltammogram (CV) test was also performed on Autolab PGSTAT30 to determine the diffusion coefficient of lithium ion in active materials during deintercalation (charging). A three-electrode setup was used for CV with a 100-mV scan rate. The two separated pure lithium were used as the counter and the reference electrodes, and cathode was connected to the working electrode.

Assembly of battery

To study the lithium ion transportation in active material experimentally, 0.02 g of active material (LiNi_0.5Mn_1.5O₄) in powder form without conductive material (i.e., carbon black) was poured in a small Al cap (current collector) as a cathode. And pure lithium was used as the anode. As the electrolyte, 1 M LiClO₄ in EC/DMC (1:1) was used. Figure 1 shows the used Li-ion cell. The assembly of this cell was performed under a controlled Ar atmosphere in a container.

Fig. 1

Used Li-ion cell (102 × 89 mm (150 × 150 DPI))

Chronoamperometry

Autolab PGSTAT30 was used to measure the current versus time at constant voltage (chronoamperometry) in active materials during charging/discharging (a two-electrode setup was used). The pure graphite was used as the reference electrode and cathode was connected to a working electrode.

Description of simulation techniques

Ab initio model

Spin-polarized total energy calculation was performed with QUMEC ab initio simulation package (www.qumec.org). Ab initio calculation in this package used spin polarization calculation and generalized gradient approach (GGA) [21]. The general algorithm of this ab initio package has been explained before [20]. The overall algorithm of this spin polarization total energy calculation has been shown in Fig. 2.

Fig. 2

The overall algorithm of used spin polarization total energy calculation for estimating diffusion constant (258 × 157 mm (126 × 130 DPI))

Semi-empirical model

The overall framework of model (algorithm and numerical method) has been explained in [19]. Here, we tried to explain the physical concepts of the model. This model actually has three joint physical sections, namely, diffusion in a particle of active material, diffusion in electrolyte, and decision on how lithium ions cross across the interface between active material and electrolyte. The diffusion of lithium ions within the bulk of active materials was modeled simply by applying the Fickian approach. But to calculate the flux of lithium ions in electrolyte in the presence of external electrical potential (Nernst-Planck Equation), the electrical potential in electrolyte must be calculated by Poisson’s equation. This calculated potential is an additional term to the conventional Fickian formula to find out the flux of lithium in electrolyte. In addition, a stochastic boundary condition was introduced to connect the two mentioned kinetic formulas in active material and electrolyte.

Physical concepts of the model

Applying external potential introduces charges at the surface of active material. According to the sign of the charge, ions may attract to or repel from the surface of active material in electrolyte. In general, the layer of charged surface and counter ions is called “electric double layer” [22]. In the simplest model of an electric double layer, the counter ions bind directly to the surface and neutralize the surface charges much like in a plate capacitor. During charging in the present model, the charge surface of active materials is positive due to the extraction of electrons by applying external potential and the counter ions is ClO₄ ⁻. Consequently, every lithium ions exclude to reside as near as several nanometers at the surface of active material and this was applied to the lithium ions in electrolyte near the surface of cathode. This model is a simple one to handle the physics of atoms at the surface of active material and electrolyte but efficient. Other used physical concepts are explained in following titles.

Potential in electrolyte and active material

Potential in active material was assumed/considered constant which is identical to the applied external voltage during charging. To take into account the potential around the surface of active material in the electrolyte, a diffuse layer was assumed according the Gouy–Chapman technique [22]. Then, the Poisson’s equation was solved numerically by finite difference method (FDM). This equation and its discretized form are as follow (Eqs. 7 and 8):

$$ \frac{\partial^2\psi}{\partial {x}^2}+\frac{\partial^2\psi}{\partial {y}^2}+\frac{\partial^2\psi}{\partial {z}^2}=\frac{\rho_o}{\varepsilon {\varepsilon}_o} $$

(7)

$$ \frac{\psi_{i-1, j, k}-2{\psi}_{i, j, k}+{\psi}_{i+1, j, k}}{\varDelta {x}^2}+\frac{\psi_{i, j-1, k}-2{\psi}_{i, j, k}+{\psi}_{i, j+1, k}}{\varDelta {y}^2}+\frac{\psi_{i, j, k-1}-2{\psi}_{i, j, k}+{\psi}_{i, j, k+1}}{\varDelta {z}^2}=\frac{\rho_o}{\varepsilon {\varepsilon}_o} $$

(8)

Due to the dependence of ρ _o on ψ, this equation was solved iteratively by first guess on ψ.

Diffusion of lithium in electrolyte

Diffusion of lithium ions in electrolyte was calculated according to the Fickian approach with consideration to account the presence of potential in electrolyte which is introduced by external applied voltage during charging [23]. This mentioned modified Fickian formula is as follow (Eq. 9):

$$ j=- D\nabla C-\frac{F}{RT} DzC\nabla \varphi; \frac{\partial C}{\partial t}=-\nabla \cdotp j\to \frac{\partial C}{\partial t}=\nabla \cdotp \left( D\nabla C+\frac{F}{RT} DzC\nabla \varphi \right) $$

(9)

Diffusion of lithium in active material

Conventional Fickian approach was used and solved numerically by FDM (Eq. 10) [15].

$$ j=- D\nabla C;\frac{\partial C}{\partial t}=-\nabla \cdotp j\to \frac{\partial C}{\partial t}=\nabla \cdotp D\nabla C $$

(10)

Used stochastic boundary condition

Interfacial boundary condition at the interface of active material and electrolyte was stochastically defined according to the thermodynamic principles. The decision on passing lithium ions through this interface was set by the difference of electrochemical potential in the electrolyte (final state) and active material (initial state). The mentioned procedure was used to make a decision on thermodynamic, but the kinetics of the diffusion process through the interface is still debating. The kinetics of the diffusion clarifies the needed time to pass a lithium ion through the interface if thermodynamically feasible, that is, to find the time scale of the stochastic boundary condition.

The thermodynamics of diffusion was analytically introduced, but the time scale of the stochastic boundary condition was determined by regulating the simulated results to the chronoamperometry experimental results.

In the case of diffusion’s thermodynamics, as electrochemical potential is related to the chemical potential and according to the dependency of chemical potential to activity of lithium ions, the proposed boundary condition is straight forward related to the local concentration of lithium ions. Before performing any calculation, activity of lithium ions in active material and electrolyte must be determined according to the local concentration of lithium ions analytically. Electrolyte was defined as a Henry solution with activity coefficient according to the Eq. 11 (Debye–Hückel equation).

$$ Ln\left({\gamma}_i\right)=-\frac{z_i^2{q}^3{N}_A^{0.5}}{4\pi {\left({\varepsilon}_r{\varepsilon}_o{k}_B T\right)}^{1.5}}\sqrt{\frac{I}{2}} $$

(11)

According to formula 8, activity coefficient of lithium in electrolyte was calculated at 0.00061.

Identical to the previous, a Henry solution was again used for calculating the activity of lithium ion in active materials. Activity coefficient was defined according to the graph in Fig. 3 [24].

Fig. 3

Activity coefficient of lithium ion in LiNi_0.5Mn_1.5O₄ particle (159 × 94 mm (104 × 104 DPI))

After calculating the activity both in active material and electrolyte, the following set of equations (Eqs. 12, 13, 14, and 15) were used to calculate the related probability of lithium ions to pass across the interface/boundary of active material and electrolyte:

$$ \mu \mathrm{Li} inE={\mu}_{\mathrm{Li} inE}^o+ RTLn\left({a}_{\mathrm{Li} inE}\right)+ F{\varphi}_E $$

(12)

$$ \mu \mathrm{Li} inA={\mu}_{\mathrm{Li} inA}^o+ RTLn\left({a}_{\mathrm{Li} inA}\right)+ F{\varphi}_A $$

(13)

$$ {E}_{\mathrm{Li} inE}-{E}_{\mathrm{Li} inA}=\frac{\mu_{\mathrm{Li} inE}-{\mu}_{\mathrm{Li} inA}}{F} $$

(14)

$$ {P}_{\mathrm{Li}\ \mathrm{from}\ A\ \mathrm{to}\ E}= \exp \left(\frac{-\left({E}_{LiinE}-{E}_{LiinA}\right)}{RT}\right) $$

(15)

This stochastic boundary condition contains the two important physical properties, namely, potential in active material and activity of lithium ions depending on local lithium concentration at interface of active material and electrolyte. The benefit of this introduced stochastic boundary condition is its explicit using of physical meaning, and there is no coefficient with no or less physical meaning to fit the results.

It is important to mention that the calculated probability of lithium ions to pass across the interface/boundary of active material and electrolyte according to Eq. 15 just makes a decision on initial and final states without any discussion on transition state energy. This simplification was used due to the lack of information on transition state energy (energy of lithium ion in active material exactly at the surface). Actually, this assumption is not wrong. To interpret the physical meaning of this, two points of view could be considered. First, in the case with negligible transition state energy due to the open structure at the surface in comparison with bulk of active material and the case two if the transition state energy is not small enough to be negligible. In this last case, the calculated probability is a fraction of the probability of passing a lithium ion from initial to final state to the probability of passing a lithium ion from final to initial state. So, for both cases, this used probability is relevant but it works better for case one.

Results and discussion

Figure 4 shows SEM image of LiNi_0.5Mn_1.5O₄ powders and their particles size distribution. XRD and FTIR results confirmed the spinel LiNi_0.5Mn_1.5O₄ (Fig. 5).

Fig. 4

a Image of LiNi_0.5Mn_1.5O₄ powders and b their particles size distribution (127 × 163 mm (150 × 125 DPI))

Fig. 5

XRD and FTIR results confirmed the spinel LiNi_0.5Mn_1.5O₄ (159 × 144 mm (150 × 150 DPI))

Positions of picks in XRD result are well-adapted to the LiNi_0.5Mn_1.5O₄ spinel. The LiNi_0.5Mn_1.5O₄ spinel, depending on Ni ordering in the lattice, shows two different space groups, Fd3m or P4₃32 [25]. Although it is hard to detect these two space groups from each other by conventional XRD method, it was confirmed by the X-ray diffraction (XRD) data that face-centered spinel (Fd3m) transforms into primitive simple cubic (P4₃32) structure by an annealing process at 700 °C [26]. Hence, according to the used calcination temperature at 800 °C and fast cooling in air (no annealing), synthesized powders would be face-centered spinel (Fd3m) structure. In addition, FTIR result in Fig. 5a confirmed Fd3m space group for synthesized LiNi_0.5Mn_1.5O₄ powders. The FTIR peaks are related to bands in Fd3m space group, and 650 and 428 cm⁻¹ peaks which are related to bands in P4₃32 space group were absent and could not specify.

By these synthesized powders, a cell was assembled like what is shown in Fig. 1 and it was charged at the constant voltage (4.9 V). Figure 6 shows cyclic voltammetry of synthesized LiNi_0.5Mn_1.5O₄ powders. According to this figure, the diffusion coefficient of lithium ions in LiNi_0.5Mn_1.5O₄ would be 3 × 10⁻¹¹ cm² s⁻¹ at 4.5 V. This diffusion coefficient was used straightforward in the model for estimating ionic diffusion in cathode’s bulk by the Fickian approach. In addition, the used diffusion coefficient of lithium ions in electrolyte was 10⁻⁷ cm² s⁻¹ [27].

Fig. 6

Cyclic voltammetry of synthesized LiNi_0.5Mn_1.5O₄ powders. Presence of Mn³⁺/Mn⁴⁺ is related to the presence of oxygen vacancy in final crystal structure of cathode material (159 × 88 mm (150 × 150 DPI))

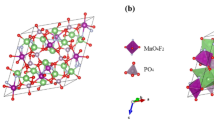
The diffusion coefficient of lithium ion through mentioned interface was estimated at 10⁻⁸ cm² s⁻¹ by this multiscale model and published before [20]. It is obvious that this estimated diffusion coefficient of mentioned interfacial is about 3 orders of magnitude higher than bulk and 1 order of magnitude lower than electrolyte. Our proposed semi-empirical model is an indirect estimation on lithium ion diffusion coefficient at the surface of active material. On the other hand, this model estimates the diffusion coefficient in the last layer of active materials in contact with electrolyte. First principle computing would be helpful to estimate this diffusion coefficient straightforwardly. So, spin-polarized total energy calculation was used to simulate the diffusion coefficient of lithium ions through the last layers of tetrahedral and octahedral oxygen site at the surface of active materials (directions 1→2 and 1→3 or from 8a to 16c according to Wyckoff positions in Fig. 7a). Figure 7b shows better spatial view of direction 1→2. The benefit of this spin-polarized total energy calculation in comparison to semi-empirical model is straightforward estimation of activation energy of lithium ions diffusion through the surface of active material as well.

Fig. 7

a Diffusion direction of lithium ions through the last layers of tetrahedral (8a according to Wyckoff position) and octahedral oxygen site (16c according to Wyckoff position) at the surface of active materials; b better spatial view of direction 1→2 or 8a to 16c (173 × 91 mm (150 × 150 DPI))

Although the formation of solid electrolyte interface is important in the case of LiNi_0.5Mn_1.5O₄ [27–29], it would be reasonable to neglect solid electrolyte interface formation to simplify a calculation in spin-polarized total energy calculation and semi-empirical model because these two models assess the diffusion coefficient at the early stage of charging/discharging. For this reason, spin-polarized total energy calculation was applied to perfect (not affected by electrolyte) surface of active material. For the same reason (as simulation was performed for early stage of charging/discharging), more simplification could be applied, i.e., considering no change in crystal structure of LiNi_0.5Mn_1.5O₄ by the level of applied voltage [26] and neglecting the diffusion coefficient dependency on lithium content [24, 30].

Calculated total energies were well converged to 0.09 eV accuracy for a supper lattice of LiNi_0.5Mn_1.5O₄. Then, activation energy through direction 1→2 (from tetrahedral site to square octahedral site or from 8a to 16c according to Wyckoff positions) in Fig. 7 was calculated at 0.24 eV; that is to say, the diffusion coefficient became 1.4 × 10⁻⁸ cm² s⁻¹ according to Arrhenius equation with inserting relevant parameters [20].

Both spin-polarized total energy calculation and semi-empirical model [20] confirm the same level of diffusion coefficient (10⁻⁸ cm² s⁻¹) at interface of LiNi_0.5Mn_1.5O₄ and electrolyte. For more description, alternating current (AC) impedance spectroscopy was performed to check this calculated diffusion coefficient at mentioned interface and estimate it experimentally. AC or electrochemical impedance spectroscopy (EIS) result of LiNi_0.5Mn_1.5O₄ cathode material has been shown in Fig. 8. According to fitted circle to experimental EIS result, charge transfer resistance (R _C) was estimated at 776 Ω. Then, exchange current was calculated at 3.3 × 10⁻⁵ A according to Eq. 16 and by assuming small overpotential.

Fig. 8

EIS result of LiNi_0.5Mn_1.5O₄ cathode material (anode: pure graphite and electrolyte: 1 M LiClO₄ in EC/DMC (1:1)) at 5 V (171 × 125 mm (150 × 150 DPI))

$$ {R}_{\mathrm{C}}=\frac{ R T}{nF{ i}_0} $$

(16)

Also, final current could be calculated according to Butler–Volmer equation (Eq. 17).

$$ i={i}_0\left( \exp \left(\alpha \frac{nF}{RT}\eta \right)- \exp \left(-\left(1-\alpha \right)\frac{nF}{RT}\eta \right)\right) $$

(17)

Although Eq. 17 is applicable when polarization just depends on charge transfer not diffusion, this equation could even be used for mass transfer, then for low overpotential and assuming α = 1, Eq. 17 could be simplified to Eq. 18:

$$ i={i}_0\left( \exp \left(\frac{nF}{RT}\eta \right)\right) $$

(18)

Consequently, final current would be calculated at 0.0016 A. According to Eq. 19 and this calculated current, diffusion coefficient of lithium ions at surface of active material and electrolyte could be estimated.

$$ i=\frac{nFD}{\delta} C $$

(19)

The thickness of diffusion layer at surface of active materials in electrolyte (δ) would be at level of micrometer (according to the estimated local concentration of lithium ions in electrolyte [20]). Then, diffusion coefficient in mass control case would be 10⁻⁸ cm² s⁻¹ for diffusion layer higher than 6 μm, and for lower than 6 μm, it would be 10⁻⁹ cm² s⁻¹. So, estimated diffusion constant at surface of active materials by AC impedance spectroscopy shows good consistency with simulated results.

This level of diffusion coefficient at surface of LiNi_0.5Mn_1.5O₄ cathode material is very high and this would have more contribution to facilitate the overall intercalation process by reducing the powder size of LiNi_0.5Mn_1.5O₄. Decreasing powder size would lead to increase the cathode surface and this would be helpful for any high-rate application. It was confirmed that the nano LiNi_0.5Mn_1.5O₄ active material has less reduction in final capacity by increasing rate of charging and discharging (c-rate) in comparison with micron size one at high rate of charging and discharging [31]. In addition, it would be important to save this high level of diffusion coefficient at the surface of LiNi_0.5Mn_1.5O₄ cathode material for high-rate applications. So, developing relevant electrolyte for reducing or maybe preventing the chemical attack of electrolyte seems important if any high-rate application of LiNi_0.5Mn_1.5O₄ cathode material is the main concern. As a last application, further research on increasing of bulk lithium ion diffusion constant in LiNi_0.5Mn_1.5O₄ cathode material seems necessary to shift it closer to diffusion constant through the surface of this cathode material. This would be helpful to use all potentials of LiNi_0.5Mn_1.5O₄ cathode material during intercalation process.

Conclusions

Calculated results of a semi-empirical model and a spin-polarized total energy calculation were used to estimate lithium ions transport at interface of LiNi_0.5Mn_1.5O₄ cathode and electrolyte. Then, activation energy of lithium ion diffusion through the surface of active material was estimated at 0.24 eV by spin-polarized total energy calculation. According to this calculated activation energy, diffusion coefficient becomes 10⁻⁸ cm² s⁻¹. This value of diffusion coefficient was confirmed by semi-empirical model. This level of diffusion coefficient is 3 orders of magnitude higher than bulk diffusion constant of LiNi_0.5Mn_1.5O₄ (estimated experimental bulk diffusion constant of lithium ions in LiNi_0.5Mn_1.5O₄ is 10⁻¹¹ cm² s⁻¹).

Appendix A: Nomenclature

• a: Activity

• C: Atomic/ionic concentration

• D _i : Diffusion coefficient in i direction

• E: Electrochemical potential

• E _n: Corresponding energy to wavefunction

• m _e: Mass of electron

• V _pp: Pseudopotential

• E _xc: Exchange correlation energy

• E _ee: Electron–electron interaction energy

• E _ii: Madelung energy

• F: Faraday’s constant

• I: Ionic strength of the solution, defined below

• i: Current

• i ₀: Exchange current

• j: Atomic flux

• k _B: Boltzmann’s constant

• n: Number of involved electrons (oxidation state)

• N _A: Avogadro’s number

• P: Probability

• R: Universal gas constant

• R _C: Charge transfer resistance

• T: Temperature

• W: The numbers of nearest octahedral sites to a tetrahedral site

• Z or Z _i : The charge number of ion species i

• α: Reaction order

• β: The distance between the two nearest lattice sites

• γ _i : Coefficient of activity

• δ: Thickness of diffusion layer

• ε or ε _r: Relative permittivity of the solvent

• ε _o: Permittivity of free space

• η: Overpotential

• ρ _o: Charge distribution

• μ ^o: Standard chemical potential

• μ: Chemical potential

• τ: Inverse of atomic frequency

• Γ: Atomic jumps (times per second)

• ψ or φ: Local electrostatic potential

• φ _i : Wave function

• φ _i ^*: Complex conjugate of wave function

• Ψ: Quantum mechanical wavefunction

• ‹R ²›: Mean displacement