A note on utility-based pricing in models with transaction costs

Abstract

This paper considers the utility-based and indifference pricing in a market with transaction costs. The utility maximization problem, including contingent claims in the market with transaction costs, has been widely researched. In this paper, closely following the results of Bouchard (Financ Stoch 6:495–516, 2002), we consider the market equilibrium of contingent claims. This is done by specifying the utility function as exponential utility and, thus, determining equilibrium in the market with transaction costs. Unlike Davis and Yoshikawa (Math Finan Econ, 2015), we use the strong assumption to deduce the equilibrium at which trade does not occur (zero trade equilibrium). It implicitly shows that transaction costs may generate a non-zero trade equilibrium under a weaker assumption.

1 Introduction

Friction caused by transaction costs is one of the most significant problems in market analysis, because such friction is difficult to handle. However, as summarized in [13], there is currently an abundance of studies in this field as many researchers have worked on the development of a theoretical basis for a market with transaction costs. Similarly to [13], we believe that the main topics for the theory of a market with transaction costs are approximative hedging, arbitrage theory, and consumption–investment problems. If we consider contingent claims in a market with transaction costs (this problem might be categorized as a consumption–investment problem), the major issue is tackling the super hedging and utility maximization problems. This paper addresses the utility maximization problem of wealth including contingent claims. More precisely, our purpose is to embed wealth with transaction costs into the utility indifference framework and the framework of utility-based pricing, as well as to deduce the market equilibrium with transaction costs. The utility maximization problem in a market with transaction costs has developed in several ways. However, every study has derived from the standard framework formulated by [12]. Following this framework, the papers of Bouchard (e.g., [2, 4], and [3]) provided significant results on utility maximization including contingent claims, particularly the ‘liquidation function’, a tool to express total wealth in a market with transaction costs. This concept is effective for deducing a solution for the utility maximization problem. Since then, further studies have been conducted to overcome problems related to Kabanov and Bouchard’s models; e.g., introducing a bid-ask process, which was defined stochastically to represent a generalized concept of a transaction matrix ([16]); expansion of a utility function from a one-dimensional to a multi-dimensional function; or considering a more expanded setting of a utility function, such as [5, 14], or [1].

Our research is based on [3] because he proved the existence of a solution to the utility maximization problem, including contingent claims. Our purpose is not to tackle the utility maximization problem in a general or abstract setting but to deduce the equilibrium in a market with transaction costs. Fortunately, [5], and [1] proved the existence of a solution to the utility maximization problem using a multivariate utility function with transaction costs described by the general bid-ask processes. We believe that our method to deduce the equilibrium will be applicable in a more general setting because the form of the solution to the utility maximization of [5] and [1] is essentially the same as the one presented by [3]. Our method of deducing the equilibrium is as follows. First, by specifying the utility function as an exponential function, we deduce a clear relationship between the amount of the contingent claim and the corresponding utility. Our most important result was that the utility indifference price and utility-based price at the point at which the amount is zero are given independently of the risk aversion of each investor. Using this result, we easily deduce the equilibrium in a market with transaction costs.

The remainder of this paper is divided into three parts. The first part, Sect. 2, sets up the model for a market with transaction costs and provides an overview of the result of [3]. The next section deduces the equilibrium in a market with transaction costs within a framework of indifference pricing and utility-based pricing. The last section comprises concluding remarks.

2 Model, overviews, and setting up the problem of a market with transaction costs

This section sets up the model and summarizes the utility maximization problem in models with transaction costs as per the preceding studies. Following [12], for initial capital $x \in {\mathbb {R}}^d$, strategy $L$ which is right continuous non-decreasing process, and continuous semimartingale $S^i$, we define the portfolio holdings $X=X^{x,L} \in {\mathbb {R}}_+^d$ using the dynamics:

$$\begin{aligned} \begin{array}{cc} X_t^i = x^i + \hat{X}_-^i \cdot S_t^i + \sum _{j=1}^d \left( L_t^{ji} - \left( 1+\lambda ^{ij}\right) L_t^{ij}\right) ,&\qquad i,j=1,\ldots ,d, \end{array} \end{aligned}$$

where $X^i$ is the $i$-th factor of $X$ with $\hat{X}^i:=X^i / S^i$, and $\hat{X}_-^i \cdot S_t^i$ is the stochastic integral of $\hat{X}_-^i$ with respect to $S^i$. Additionally $L_t^{ij}$ is the cumulative net amount of funds transferred from asset $i$ to asset $j$ up to date $t$ with $L_{0-} = 0$, and the matrix $(\lambda ^{ij}) \in {\mathbb {M}}^{d}$, where ${\mathbb {M}}^{d}$ is the set of square matrices with $d$-lines and non-negative entries, represents the constant proportional costs with zero diagonal that satisfies:

$$\begin{aligned} \begin{array}{cc} \left( 1+\lambda ^{ij}\right) \le \left( 1+\lambda ^{ik}\right) \left( 1+\lambda ^{kj}\right)&\qquad \forall i,j,k \in \{1,\ldots ,d\} . \end{array} \end{aligned}$$

We define the solvency region (see, e.g., [11]),

$$\begin{aligned} K:=\Bigg \{x \in {\mathbb {R}}^{d}; \exists a \in {\mathbb {M}}^{d}, x^i + \sum _{j=1}^d \bigg (a^{ji} - \big (1+ \lambda ^{ij}\big )a^{ij}\bigg ) \ge 0; \quad i=1,\ldots ,d\Bigg \}, \end{aligned}$$

For this closed convex cone, we define a partial ordering on ${\mathbb {R}}^d$ such that

$$\begin{aligned} x_1 \succeq x_2 \text{ if } \text{ and } \text{ only } \text{ if } x_1 - x_2 \in K. \end{aligned}$$

A trading strategy $L$ is said to be $\kappa$-admissible for initial holdings $x \in K$ if, for a constant $\kappa \ge 0$, the no-bankruptcy condition holds:

$$\begin{aligned} X_t^{x,L} \succeq - \kappa S_t. \end{aligned}$$

We denote by ${\mathcal {A}}_\kappa (x)$ the set of all $\kappa$-admissible trading strategies for initial holdings $x\in K$ and we introduce the set

$$\begin{aligned} {\mathcal {X}}(x) :=\bigg \{X \in L^0\big ({\mathbb {R}}^{d},{\mathcal {F}}_T\big ): X=X_T^{x,L} \,\text{ for } \text{ some } L \in \cup _{\kappa \ge 0} {\mathcal {A}}_\kappa (x)\bigg \}, \end{aligned}$$

where $T$ is fixed as a finite time horizon. This set implicitly denotes that $X \in {\mathcal {X}}(x)$ is uniformly bounded from below.

We formulate indifference pricing in a market with transaction costs, which is based on the utility maximization for $X_T^{x,L}$. To evaluate the expected utility for $X_T^{x,L}$, we define the liquidation value and the utility function. Let ${\mathbf {1}}_1:=(1,0,\ldots ,0)$, ${\mathbf {1}}:=(1,\ldots ,1)$, and

$$\begin{aligned} l(x) := \sup \big \{r \in {\mathbb {R}}: x \succeq r {\mathbf {1}}_1\big \}, \end{aligned}$$

which is the liquidation function.

We define the utility function $U: {\mathbb {R}} \rightarrow {\mathbb {R}}$ as a $C^1$-strictly increasing, strictly concave function that satisfies the following conditions:

$$\begin{aligned} \lim _{r \uparrow \infty }U'(r) = 0,\ \lim _{r \downarrow -\infty }U'(r) = \infty . \end{aligned}$$

We fix a contingent claim $B$, which is a bounded $d$-dimensional ${\mathcal {F}}_T$-measurable random variable, assuming that $B \succeq -c S_T$ for some $c \in {\mathbb {R}}$.

Using the liquidation function, we construct the utility indifference framework as below:

$$\begin{aligned}&\sup _{X^{x,L} \in {\mathcal {X}}(x)} {\mathbb {E}}U\left[ l\big (X^{x,L}\big )\right] \nonumber \\&\quad = \sup _{X^{x+p(B;x,q) q,L} \in {\mathcal {X}}\big (x+q p(B;x,q) {\mathbf {1}}_1\big )} {\mathbb {E}}U\left[ l\big (X^{x + q p(B;x,q) {\mathbf {1}}_1,L} - q B\big )\right] , \end{aligned}$$

(1)

where $p(B;x,q)$ is the utility indifference price (note that [3, 4], and [8] call this price the reservation price), and $q$ is the amount of the contingent claim $B$. Theorem 7 of [3] proves the existence of a solution to the right-hand side of the previous equation.¹ As we can easily deduce that the existence theorem holds in the case of $q=0$ by carefully reading the proof of the aforementioned theorem, the existence of a solution to the left-hand side holds, although the existence was independently proven by [6].

Furthermore, Theorem 7 of [3] characterizes the solution to the problem $\sup _{X^{x,L} \in {\mathcal {X}}(x)} {\mathbb {E}}U[l(X^{x,L} - B q)]$ by using the dual problem. To set up the dual problem, we need to define the positive polar of $K$ such that,

$$\begin{aligned} K^*:=\left\{ y \in {\mathbb {R}}^d: x^\top y \ge 0, \quad \forall x \in K \right\} . \end{aligned}$$

Hereafter, we assume $\text{ Int }(K^*) \ne \emptyset$. We need to define the subset of ${\mathcal {X}}(x)$ such that,

$$\begin{aligned} {\mathcal {X}}_+(x) :=\left\{ X_T^{x,L}: L \in {\mathcal {A}}_0(x),\quad t\le T\right\} . \end{aligned}$$

Based on this subset, we define three convex cones as follows:

$$\begin{aligned} {\mathbf {Y}}_+&:= \bigg \{(y, Y) \in K^*\times L^0\big ({\mathcal {F}}_T; K^*\big ): {\mathbb {E}}[YX] \le yx,\ \forall x \in K,\ X \in {\mathcal {X}}_+(x)\bigg \},\\ {\mathbf {Y}}_+^V&:= \bigg \{(y, Y) \in {\mathbf {Y}}_+: {\mathbb {E}}[Y^1] = y^1,\ V\big (Y^1\big ) \in L^1 \bigg \},\\ {\mathbf {Y}}_{++}^V&:= \bigg \{(y, Y) \in {\mathbf {Y}}_+^V: P\big (Y^1=0\big ) = 0 \bigg \}, \end{aligned}$$

where $V(\cdot )$ is a dual function of $U(\cdot )$.

For the dual problem

$$\begin{aligned} w^q(x) := \inf _{(y,Y) \in {\mathbf {Y}}_+^V} {\mathbb {E}}\bigg [V\big (Y^1\big ) + y^\top x - q Y^\top B\bigg ], \end{aligned}$$

(2)

Theorem 7 of Bouchard [3] shows that there exists a solution $(\hat{y}_{x,q}, \hat{Y}_{x,q}) \in {\mathbf {Y}}_{++}^V$ such that, $w^q(x) = {\mathbb {E}}[V(\hat{Y}^1_{x,q}) + \hat{y}_{x,q}^\top x - q \hat{Y}_{x,q}^\top B],$ where $\hat{Y}^1_{x,q}$ is the first factor of $\hat{Y}_{x,q}$. Using this result, Theorem 7 of Bouchard [3] deduces the solution to $u^q(x)=\sup _{X^{x, L} \in {\mathcal {X}}(x)} {\mathbb {E}}U[l(X^{x,L} - B q )]$, which is given by

$$\begin{aligned} \hat{X}_{x,q}= I\left( \hat{Y}^1_{x,q}\right) {\mathbf {1}}_1 + q B \in {\mathcal {X}}(x), \end{aligned}$$

where $I:=(U')^{-1}$.

Example 1

The model with transaction costs has wide applicability but it looks cumbersome to get model implication. Then, we give an example. Let $d=3$. Without loss of generality, we can assume $S^1\equiv 1$, which implies that $S^1$ is cash account of the domestic currency. We can also assume that $S^2, S^3$ are risky assets described by some SDE, such as $dS_t^i = \sigma _i dW_t^i$ for $i=2,3$, where $\sigma _i$ are constants and $W^i$ are Brownian motions. By definition of liquidation function, the agent liquidates her(his) position of risky assets to cash account at maturity. To consider an example of contingent claim on these assets gives clearer implication. In fact, we consider a contingent claim $B$, for example, given such that,

$$\begin{aligned} B := \Big (K 1_{S^2_T \le K}+K' 1_{S^3_T \ge K'}, -S^2_T 1_{S^2_T \le K}, -S^3_T 1_{S^3_T \ge K'}\Big ), \end{aligned}$$

where $K,\,K'\ge 0$ are constants. In this case, after simply liquidating risky assets to cash account, the payoff at maturity is

$$\begin{aligned} \Big (K-{1 \over 1+\lambda ^{21}}S_T^2\Big )1_{S_T^2\le K} - \Big ({1 \over 1+\lambda ^{31}}S_T^3-K'\Big )1_{S_T^3\ge K'}. \end{aligned}$$

This payoff implies that the contingent claim $B$ is like put and call option with strike price $\big (1+\lambda ^{21}\big )K,\ \big (1+\lambda ^{31}\big )K'$ and satisfies the condition $B \succeq -cS_T$ by setting $c \ge 1$.

3 Equilibrium in a market with transaction costs

We specify the utility function as $U(r) := - e^{-\gamma r}$, which implies that $V(r') = {r' \over \gamma } \ln \left( {r' \over \gamma } \right) - {r' \over \gamma }$. From the property of the Legendre–Fenchel transform, the domain of $V(r')$ is given by $r' \ge 0$. Then, (2) is rewritten as follows,

$$\begin{aligned} w^q(x)&= \inf _{(y,Y) \in {\mathbf {Y}}_+^V} {\mathbb {E}}\Bigg [{Y^1 \over \gamma } \ln \bigg ({Y^1 \over \gamma } \bigg ) - {Y^1 \over \gamma } + y^\top x - q Y^\top B \Bigg ]. \end{aligned}$$

Let ${\mathcal {M}}_{{\mathcal {X}}_+(x)}$ be the set of super martingale measures for $X \in {\mathcal {X}}_+(x)$. For all $Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}$, the relative entropy $H\big [Q|P\big ] < \infty$, which implies that $V\big (Y^1\big ) \in L^1$. By definition of ${\mathbf {Y}}_+$, for a super martingale measure $Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}$, we write $Y = {dQ \over dP} y \in L^0\big ({\mathcal {F}}_T;K^*\big )$. Then,

$$\begin{aligned} w^q(x)&= \inf _{y \in K^*, Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}} {\mathbb {E}}\left[ {y^1 \over \gamma } {dQ \over dP} \ln \left( {y^1 \over \gamma } {dQ \over dP} \right) - {y^1 \over \gamma } {dQ \over dP} + {dQ \over dP} y^\top (x - q B) \right] \\&= \inf _{y \in K^*, Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}} {\mathbb {E}}\biggl [{y^1 \over \gamma } {dQ \over dP} \ln \left( {dQ \over dP} \right) + {y^1 \over \gamma } {dQ \over dP} \ln \left( {y^1 \over \gamma } \right) - {y^1 \over \gamma } {dQ \over dP}\\&\quad +\, {dQ \over dP} y^\top (x - q B) \biggr ]\\&= \inf _{y \in K^*, Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}} \biggl \{y^\top \bigg ({1 \over \gamma } {\mathbb {E}}\left[ {dQ \over dP} \ln \left( {dQ \over dP} \right) \right] {\mathbf {1}}_1 + {\mathbb {E}}\left[ {dQ \over dP} (x - q B) \right] \bigg )\\&\quad + \,{y^1 \over \gamma } \ln \left( {y^1 \over \gamma } \right) - {y^1 \over \gamma } \biggr \}\\&= \inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}}\biggl \{\inf _{\!y \in K^*}\biggl \{y^\top \bigg ({1 \over \gamma } {\mathbb {E}}\left[ {dQ \over dP} \ln \left( {dQ \over dP} \right) \right] {\mathbf {1}}_1 + {\mathbb {E}}\left[ {dQ \over dP} (x - q B) \right] \bigg ) \\&\quad +\, {y^1 \over \gamma } \ln \left( {y^1 \over \gamma } \right) - {y^1 \over \gamma } \biggr \}\biggr \}. \end{aligned}$$

Let $y_{-1}:=y/y^1$. Because $y^1 >0$, if $y \in K^*$, then $y_{-1} \in K^*$. Therefore, we calculate $w^q(x)$ as follow:

$$\begin{aligned} w^q(x)&= \inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}} \biggl \{\inf _{y^1 \in {\mathbb {R}}_+}\biggl \{y^1\inf _{y_{-1} \in K^*}\Bigg \{y_{-1}^\top \bigg ({1 \over \gamma } {\mathbb {E}}\left[ {dQ \over dP} \ln \left( {dQ \over dP} \right) \right] {\mathbf {1}}_1 \\&\quad +\, {\mathbb {E}}\left[ {dQ \over dP} (x - q B) \right] \bigg )\Biggr \} + {y^1 \over \gamma } \ln \left( {y^1 \over \gamma } \right) - {y^1 \over \gamma } \biggr \}\biggr \}\\&= \inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}} \biggl \{\inf _{y^1 \in {\mathbb {R}}_+}\biggl \{y^1l\left( {1 \over \gamma } {\mathbb {E}}\left[ {dQ \over dP} \ln \left( {dQ \over dP} \right) \right] {\mathbf {1}}_1 + {\mathbb {E}}\left[ {dQ \over dP} (x - q B) \right] \right) \\&\quad +\, {y^1 \over \gamma } \ln \left( {y^1 \over \gamma } \right) - {y^1 \over \gamma } \biggr \}\biggr \}\\&= \inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}} \left\{ \inf _{y^1 \in {\mathbb {R}}_+}\left\{ y^1\left[ {1 \over \gamma } H\big [Q|P\big ] + l\left( x + {\mathbb {E}}^Q\left[ - q B \right] \right) \right] + {y^1 \over \gamma } \ln \left( {y^1 \over \gamma } \right) - {y^1 \over \gamma } \right\} \right\} \\&= \inf _{y^1 \in {\mathbb {R}}_+} \left\{ y^1\inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}}\left\{ {1 \over \gamma } H\big [Q|P\big ] + l\left( x + {\mathbb {E}}^Q\left[ - q B \right] \right) \right\} + {y^1 \over \gamma } \ln \left( {y^1 \over \gamma } \right) - {y^1 \over \gamma } \right\} . \end{aligned}$$

On line 2, we use the property of the liquidation function; $l(x) = \inf \big \{yx : y \in K^* \text{ with } y^1 = 1\big \}$ for $x \in {\mathbb {R}}^d$ (c.f. Proposition 1(i) of [3]). On line 3, we use the fact that, for a constant $c$, $l\left( x + c {\mathbf {1}}_1\right) = l(x) + c$ (see, e.g., Proposition 1(iii) of [3], Proposition 2.1(iii) of [4], and Proposition 2.1(iii) of [2]). The optimal $y^1$ is given by,

$$\begin{aligned} \hat{y}_{x,q}^1&= \gamma e^{-\gamma \inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}}\bigg \{{1 \over \gamma } H\big [Q|P\big ] + l\big (x + {\mathbb {E}}^Q[- q B]\big )\bigg \} }. \end{aligned}$$

Hereafter, we denote the solution of $\inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}}\left\{ {1 \over \gamma } H\big [Q|P\big ] + l\left( x + {\mathbb {E}}^Q\left[ - q B \right] \right) \right\}$ by $Q^{x,q}$.

By definition of $I(\cdot )$, we have $I(x) = -{1 \over \gamma } \ln \left( {x \over \gamma }\right)$. Therefore,

$$\begin{aligned} \hat{X}_{x,q}&= -{1 \over \gamma } \ln \left( {\hat{y}_{x,q}^1 \over \gamma }{dQ^{x,q} \over dP} \right) {\mathbf {1}}_1 + q B. \end{aligned}$$

Note Remark 9 of [3]. Then, because ${\mathcal {X}}\big (x + q p(B;x,q) {\mathbf {1}}_1\big ) = {\mathcal {X}}(x) + q p(B;x,q) {\mathbf {1}}_1$, for $X^{x + q p(B;x,q) {\mathbf {1}}_1,L} \in {\mathcal {X}}\big (x + q p(B;x,q){\mathbf {1}}_1\big )$,

$$\begin{aligned}&\sup _{X^{x + q p(B;x,q) {\mathbf {1}}_1,L} \in {\mathcal {X}}\big (x + q p(B;x,q) {\mathbf {1}}_1\big )} {\mathbb {E}}U\left[ l\big (X^{x + q p(B;x,q) {\mathbf {1}}_1,L} - q B \big )\right] \\&\quad = e^{-\gamma q p(B;x,q)} \sup _{X^{x,L} \in {\mathcal {X}}(x)} {\mathbb {E}}U\left[ l\big (X^{x,L} - q B\big )\right] . \end{aligned}$$

The utility indifference framework is rewritten as,

$$\begin{aligned} \sup _{X^{x,L} \in {\mathcal {X}}(x)}{\mathbb {E}}U\left[ l\big (X^{x,L}\big )\right]&= e^{-\gamma q p(B;x,q)} \sup _{X^{x,L} \in {\mathcal {X}}(x)} {\mathbb {E}}U\left[ l\big (X^{x,L} - q B\big )\right] . \end{aligned}$$

Equivalently, we can write this framework as follows:

$$\begin{aligned} {\mathbb {E}}U\left[ l\left( \hat{X}_{x,0}\right) \right] = e^{-\gamma q p(B;x,q)} {\mathbb {E}}U\left[ l\left( \hat{X}_{x,q} - q B\right) \right] , \end{aligned}$$

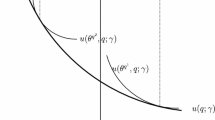
We define $u(X^{x,L},q;\gamma ) := \ln \bigg (\!\!-{\mathbb {E}}{U}\big [l(X^{x,L}-q B)\big ]\bigg )$ and, $u(q;x,\gamma ) := u\big (\hat{X}_{x,q},q;\gamma \big )$; then the indifference framework is

$$\begin{aligned} u(0;x,\gamma )&= -\gamma p(B;x,q) q + u(q;x,\gamma ) \nonumber \\ \leftrightarrow u(q;x,\gamma )&= u(0;x,\gamma ) + \gamma p(B;x,q) q \end{aligned}$$

(3)

Analyzing $u\big (X^{x,L},q;\gamma \big )$, we characterize the indifference framework in a market with transaction costs. By definition, $u\big (\hat{X}_{x,q},q;\gamma \big ) \le u\big (X^{x,L},q;\gamma \big )$. For optimal $\hat{X}_{x,\tilde{q}}$, which is the solution for the amount $\tilde{q}$, we need the following:

$$\begin{aligned} u\big (\hat{X}_{x,\tilde{q}},q;\gamma \big )&= \ln \bigg (-{\mathbb {E}}{U}\big [l(\hat{X}_{x,\tilde{q}}- qB)\big ]\bigg ) \nonumber \\&= \ln \left( -{\mathbb {E}}{U}\left[ l\left( -{1 \over \gamma } \ln \left( {\hat{y}_{x,\tilde{q}}^1 \over \gamma }{dQ^{x,\tilde{q}} \over dP} \right) {\mathbf {1}}_1 + \tilde{q} B - q B \right) \right] \right) \nonumber \\&= \ln \left( -{\mathbb {E}}{U}\left[ -{1 \over \gamma } \ln \left( {\hat{y}_{x,\tilde{q}}^1 \over \gamma }{dQ^{x,\tilde{q}} \over dP} \right) + l\left( (\tilde{q} - q)B\right) \right] \right) \nonumber \\&= \ln \left( {\mathbb {E}}\left[ {\hat{y}_{x,\tilde{q}}^1 \over \gamma }{dQ^{x,\tilde{q}} \over dP} e^{-\gamma l\left( (\tilde{q}-q)B\right) }\right] \right) = \ln \left( {\hat{y}_{x,\tilde{q}}^1 \over \gamma } {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ e^{-\gamma l\left( (\tilde{q}-q)B\right) }\right] \right) \nonumber \\&= \ln {\hat{y}_{x,\tilde{q}}^1 \over \gamma } + \left\{ \begin{array}{l@{\quad }l} \ln {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ e^{-\gamma (\tilde{q}-q) l\left( B\right) }\right] &{} \tilde{q} \ge q\\ \ln {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ e^{\gamma (\tilde{q}-q) l\left( -B\right) }\right] &{} \tilde{q} < q \end{array}\right. \end{aligned}$$

(4)

where on line 3, we use the fact $l(x + c {\mathbf {1}}_1) = l(x) + c$ and on line 5, we use the fact $l(cx) = c l(x)$ for $c \ge 0$ (see Proposition 2.1(c) of [4]).

Lemma 1

$u\big (\hat{X}_{x,\tilde{q}},q;\gamma \big )$ is a convex function about $q$.

Proof

For $q,q' \in {\mathbb {R}}$ and $0 \le t \le 1$,

$$\begin{aligned}&u\left( \hat{X}_{x,\tilde{q}},t q + (1-t)q';\gamma \right) \\&\quad = \ln {\hat{y}_{x,\tilde{q}}^1 \over \gamma } + \ln \Bigg ({\mathbb {E}}^{Q^{x,\tilde{q}}}\bigg [e^{-\gamma l\big ((t q + (1-t)q'- \tilde{q})B\big )}\bigg ]\Bigg )\\&\quad = \ln {\hat{y}_{x,\tilde{q}}^1 \over \gamma } + \ln \Bigg ({\mathbb {E}}^{Q^{x,\tilde{q}}}\bigg [e^{-\gamma l\big ((t (q-\tilde{q}) + (1-t)(q'- \tilde{q}))B\big )}\bigg ]\Bigg )\\&\quad \le \ln {\hat{y}_{x,\tilde{q}}^1 \over \gamma } + \ln \Bigg ({\mathbb {E}}^{Q^{x,\tilde{q}}}\bigg [e^{-\gamma l\big (t (q-\tilde{q})B\big ) - \gamma l\big ( (1-t)(q'- \tilde{q})B\big )}\bigg ]\Bigg )\\&\quad = \ln {\hat{y}_{x,\tilde{q}}^1 \over \gamma } + \ln \Bigg ({\mathbb {E}}^{Q^{x,\tilde{q}}}\bigg [e^{-\gamma t l\big ((q-\tilde{q})B\big )}e^{- \gamma (1-t) l\big ((q'- \tilde{q})B\big )}\bigg ]\Bigg )\\&\quad \le \ln {\hat{y}_{x,\tilde{q}}^1 \over \gamma } + \ln \Bigg ({\mathbb {E}}^{Q^{x,\tilde{q}}}\bigg [e^{-\gamma l\big ((q-\tilde{q})B\big )}\bigg ]^t{\mathbb {E}}^{Q^{x,\tilde{q}}}\bigg [e^{- \gamma l\big ((q'- \tilde{q})B\big )}\bigg ]^{ (1-t) }\Bigg )\\&\quad = t u\Big (\hat{X}_{x,\tilde{q}},q;\gamma \Big ) + (1-t) u\Big (\hat{X}_{x,\tilde{q}},q';\gamma \Big ) \end{aligned}$$

On line 3, we use $l(x + y) \ge l(x) + l(y)$ for $x,y \in {\mathbb {R}}$ (see Proposition 2.1(b) of [4]). We use Hölder’s inequality on line 5. $\square$

Lemma 2

For a fixed $\tilde{q}$, the function $u(\hat{X}_{x,\tilde{q}},q;\gamma )$ has a kink point at $q = \tilde{q}$. Furthermore, $u\big (\hat{X}_{x,\tilde{q}},q;\gamma \big )$ is differentiable at $q = \tilde{q}$ if and only if $l(B) = -l(-B)$.

Proof

When $\tilde{q} \ne q$, the continuity of $u\big (\hat{X}_{x,\tilde{q}},q;\gamma \big )$ is clear; i.e., $\lim _{\varDelta q \downarrow 0} u\big (\hat{X}_{x,\tilde{q}},q + \varDelta q;\gamma \big )=\lim _{\varDelta q \downarrow 0} u\big (\hat{X}_{x,\tilde{q}},q-\varDelta q;\gamma \big )$ for $\varDelta q \ge 0$ which is given independently of $\tilde{q}$. When $\tilde{q} = q$, $u\big (\hat{X}_{x,\tilde{q}},q;\gamma \big )$ is continuous because $\lim _{q \uparrow \tilde{q}} \ln {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ e^{-\gamma (\tilde{q}-q) l\left( B\right) }\right] =\lim _{q \downarrow \tilde{q}} \ln {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ e^{\gamma (\tilde{q}-q) l\left( -B\right) }\right] =0$.

Consider the slope of $u\big (\hat{X}_{x,\tilde{q}},q;\gamma \big )$. For $q > \tilde{q}$,

$$\begin{aligned}&{{u\left( \hat{X}_{x,\tilde{q}},q + \varDelta q;\gamma \right) - u\left( \hat{X}_{x,\tilde{q}},q;\gamma \right) \over \varDelta q}}\\&\quad ={1 \over \varDelta q}\ln {{\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ e^{\gamma (\tilde{q} - q - \varDelta q) l\left( -B\right) }\right] \over {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ e^{\gamma (\tilde{q} - q) l\left( -B\right) }\right] }={1 \over \varDelta q}\ln {\mathbb {E}}^{Q^{x,\tilde{q},q}}\left[ e^{-\gamma \varDelta q l\left( -B\right) }\right] \\&\quad \ge {1 \over \varDelta q} {\mathbb {E}}^{Q^{x,\tilde{q},q}}\left[ -\gamma \varDelta q l\left( -B\right) \right] ={\mathbb {E}}^{Q^{x,\tilde{q},q}}\left[ -\gamma l\left( -B\right) \right] , \end{aligned}$$

where we used a Radon–Nikodym derivative defined such that $d Q^{x,\tilde{q},q} / dQ^{x,\tilde{q}} := e^{\gamma (\tilde{q} - q) l\left( -B\right) } / {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ e^{\gamma (\tilde{q} - q) l\left( -B\right) }\right]$ as well as Jensen’s inequality.

Using the same logic, for sufficiently small $\varDelta q$ such that $q-\varDelta q > \tilde{q}$, it holds that ${u\big (\hat{X}_{x,\tilde{q}},q;\gamma \big ) - u\big (\hat{X}_{x,\tilde{q}},q - \varDelta q;\gamma \big ) \over \varDelta q} \le {\mathbb {E}}^{Q^{x,\tilde{q},q}}\left[ -\gamma l\left( -B\right) \right] .$ That is, when $q \ge \tilde{q}$, the following holds,

$$\begin{aligned} -{{\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ \gamma l\left( -B\right) e^{\gamma (\tilde{q} - q) l\left( -B\right) } \right] \over {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ e^{\gamma (\tilde{q} - q) l\left( -B\right) }\right] } \in \partial u\left( \hat{X}_{x,\tilde{q}},q;\gamma \right) \end{aligned}$$

where $\partial u\big (\hat{X}_{x,\tilde{q}},q;\gamma \big )$ is a subdifferential of $u\big (\hat{X}_{x,\tilde{q}},q;\gamma \big )$ at $q$. The same method can be applied to $q \le \tilde{q}$; therefore,

$$\begin{aligned} {{\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ \gamma l\left( B\right) e^{-\gamma (\tilde{q} - q) l\left( -B\right) } \right] \over {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ e^{-\gamma (\tilde{q} - q) l\left( B\right) }\right] } \in \partial u\left( \hat{X}_{x,\tilde{q}},q;\gamma \right) \end{aligned}$$

Hence,

$$\begin{aligned} \lim _{q \downarrow \tilde{q}} {u\left( \hat{X}_{x,\tilde{q}},q;\gamma \right) - u\left( \hat{X}_{x,\tilde{q}},\tilde{q};\gamma \right) \over q - \tilde{q}}&\ge \lim _{q \downarrow \tilde{q}} -{{\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ \gamma l\left( -B\right) e^{\gamma (\tilde{q} - q) l\left( -B\right) } \right] \over {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ e^{\gamma (\tilde{q} - q) l\left( -B\right) }\right] }\\&= {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ -\gamma l(-B)\right] ,\\ \lim _{q \uparrow \tilde{q}} {u\left( \hat{X}_{x,\tilde{q}},q;\gamma \right) - u\left( \hat{X}_{x,\tilde{q}},\tilde{q};\gamma \right) \over q - \tilde{q}}&\le \lim _{q \uparrow \tilde{q}} {{\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ \gamma l\left( B\right) e^{-\gamma (\tilde{q} - q) l\left( -B\right) } \right] \over {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ e^{-\gamma (\tilde{q} - q) l\left( B\right) }\right] }\\&= {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ \gamma l(B)\right] . \end{aligned}$$

Let $\bar{0}$ be the $d$-dimensional zero vector; then, $l(\bar{0}) = 0$. As $0=l(\bar{0}) = l(B-B) \ge l(B) + l(-B)$ (see Proposition 2.1(b) of [4]), $-l(-B) \ge l(B)$. Therefore,

$$\begin{aligned} -{\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ \gamma l(-B)\right] \ge {\mathbb {E}}^{Q^{x,\tilde{q}}}\left[ \gamma l(B)\right] , \end{aligned}$$

(5)

implying that $u\big (\hat{X}_{x,\tilde{q}},q;\gamma \big )$ is non-differentiable at $q = \tilde{q}$. $\square$

Lemma 3

$u(q;x,\gamma )$ is a convex function of $q$.

Proof

For $0 \le t \le 1$ and $q,q' \in {\mathbb {R}}$,

$$\begin{aligned} t u(q;x,\gamma ) + (1-t) u(q';x,\gamma )&= t u\left( \hat{X}_{x,q},q;\gamma \right) + (1-t) u\left( \hat{X}_{x,q'},q';\gamma \right) \\&= t \ln \bigg ({\mathbb {E}}e^{-\gamma l\big (\hat{X}_{x,q}-q B\big )}\bigg ) + (1 - t) \ln \bigg ({\mathbb {E}}e^{-\gamma l\big (\hat{X}_{x,q'}-q' B\big )}\bigg )\\&= \ln \bigg ({\mathbb {E}}e^{-\gamma l\big (\hat{X}_{x,q}-q B\big )}\bigg )^t \ln \bigg ({\mathbb {E}}e^{-\gamma l\big (\hat{X}_{x,q'}-q' B\big )}\bigg )^{1 - t}\\&\ge \ln \bigg ({\mathbb {E}}e^{-\gamma t l\big (\hat{X}_{x,q}-q B\big ) -\gamma (1-t) l\left( \hat{X}_{x,q'}-q' B\right) }\bigg )\\&= \ln \bigg ({\mathbb {E}}e^{-\gamma l\big (t\hat{X}_{x,q}- t q B\big ) + l\big ((1-t)\hat{X}_{x,q'}-(1-t) q' B\big )}\bigg )\\&\ge \ln \Bigg ({\mathbb {E}}e^{-\gamma l\big (t\hat{X}_{x,q} + (1-t)\hat{X}_{x,q'} - \big (t q + (1-t) q'\big ) B\big )}\Bigg )\\&\ge \ln \Bigg ({\mathbb {E}}e^{-\gamma l\big (\hat{X}_{x,t q + (1-t) q'} - \big (t q + (1-t) q'\big ) B\big )}\Bigg )\\&= u\bigg (t q + (1-t) q'; x, \gamma \bigg ) \end{aligned}$$

On line 4, we use Hölder’s inequality, and we use the convexity of function $I(\cdot )$ which is included in the definition of $\hat{X}_{x,q}$. $\square$

By (3), the utility indifference price is given by

$$\begin{aligned} p(B;x,q) = {1 \over \gamma }{u(q;x,\gamma ) - u(0;x,\gamma ) \over q}. \end{aligned}$$

The initial endowment $x$ and risk-aversion $\gamma$ depend on each investor’s personal situation. Therefore, the utility indifference price $p(B;x,q)$ are different from each other. Hereafter, we consider the feature of the utility indifference price around $q=0$.

To deduce the utility indifference price at $q=0$, we need to calculate,

$$\begin{aligned} p(B;x,0)&= \lim _{q \rightarrow 0} p(B;x,q)\\&= {1 \over \gamma }\lim _{q \rightarrow 0} {u(q;x,\gamma ) - u(0;x,\gamma ) \over q} \end{aligned}$$

However, the following Lemma and Proposition show that the utility indifference price $p(B;x,0)$ cannot be uniquely defined.

Lemma 4

When $q \rightarrow 0$, the measure $Q^{x,q}$ converges to $Q^{x,0}$.

Proof

By Theorem 7 of [3], $H\big [Q^{x,q}|P\big ]$ exists. Since $\bar{0} \in B$, there also exists $H\big [Q^{x,0}|P\big ]$, where $\bar{0}$ is the $d$-dimensional zero vector. Let $q_n$ be a series converging to zero, when $n\rightarrow \infty$. By definition of $H\big [Q^{x,0}|P\big ]$, it holds that $H\big [Q^{x,0}|P\big ] \le H\big [Q^{x,q_n}|P\big ]$ for all $q_n\in {\mathbb {R}}$. Then,

$$\begin{aligned} H\big [Q^{x,0}|P\big ] \le \liminf _{n\rightarrow \infty } H\big [Q^{x,q_n}|P\big ]. \end{aligned}$$

(6)

We show the opposite inequality. Since $Q^{x,0}$ is not the optimizer of $\inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}} \Big \{{1 \over \gamma }H\big [Q|P\big ] + l\big (x + {\mathbb {E}}^Q[-q_n B]\big ) \Big \}$, it holds that

$$\begin{aligned}&{1 \over \gamma }H\big [Q^{x,q_n}|P\big ] + l\left( x + {\mathbb {E}}^{Q^{x,q_n}}[-q_n B]\right) \\&\quad = \inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}} \left\{ {1 \over \gamma }H\big [Q|P\big ] + l\left( x + {\mathbb {E}}^Q[-q_n B]\right) \right\} \\&\quad \le {1 \over \gamma }H\big [Q^{x,0}|P\big ] + l\left( x + {\mathbb {E}}^{Q^{x,0}}[-q_n B]\right) . \end{aligned}$$

By boundedness of $B$, some constant $K>0$ exists such that

$$\begin{aligned} -q_n K{\mathbf {1}}_1 \preceq -q_n {\mathbb {E}}^{Q^{x,q_n}}[B]. \end{aligned}$$

Therefore,

$$\begin{aligned} {1 \over \gamma }H\big [Q^{x,q_n}|P\big ] + l(x) -q_n K \le {1 \over \gamma }H\big [Q^{x,q_n}|P\big ] + l\left( x + {\mathbb {E}}^{Q^{x,q_n}}[-q_n B]\right) , \end{aligned}$$

which we use for $x,x' \in {\mathbb {R}}^d$, $x \succeq x' \rightarrow l(x) \ge l(x')$ (c.f. Proposition 1(iv) of [3]). From above inequalities, it holds that ${1 \over \gamma }H\big [Q^{x,q_n}|P\big ] + l(x) -q_n K \le {1 \over \gamma }H\big [Q^{x,0}|P\big ] + l\left( x + {\mathbb {E}}^{Q^{x,0}}[-q_n B]\right)$. Taking limit superior to both side, we attain

$$\begin{aligned} \limsup _{n\rightarrow \infty } H\big [Q^{x,q_n}|P\big ] \le H\big [Q^{x,0}|P\big ]. \end{aligned}$$

(7)

By (6) and (7), $\limsup _{n\rightarrow \infty } H\big [Q^{x,q_n}|P\big ] \le H\big [Q^{x,0}|P\big ] \le \liminf _{n\rightarrow \infty } H\big [Q^{x,q_n}|P\big ]$. However, by definition of limit superior and inferior, $\liminf _{n\rightarrow \infty } H\big [Q^{x,q_n}|P\big ] \le \limsup _{n\rightarrow \infty } H\big [Q^{x,q_n}|P\big ]$. Therefore, it holds that $H\big [Q^{x,0}|P\big ]= \liminf _{n\rightarrow \infty } H\big [Q^{x,q_n}|P\big ] = \limsup _{n\rightarrow \infty } H\big [Q^{x,q_n}|P\big ] = \lim _{q\rightarrow 0}H\big [Q^{x,q}|P\big ]$. From non-negativity and convexity of relative entropy (c.f. Theorems 1.4.1., 1.5.1. of [10]), $Q^{x,q}$ converges to $Q^{x,0}$, when $q\rightarrow 0$.

$\square$

Proposition 1

On the utility indifference price $p(B;x,q)$, when $q=0$, there exists a utility indifference price in the range such that,

$$\begin{aligned} p(B;x,0) \in \Bigg (l\big ({\mathbb {E}}^{Q^{x,0}}\left[ B\right] \big ), -l\big (-{\mathbb {E}}^{Q^{x,0}}\left[ B\right] \big ) \Bigg ). \end{aligned}$$

Proof

From (4), $u\big (\hat{X}_{x,\tilde{q}},\tilde{q};\gamma \big ) =\ln {\hat{y}_{x,\tilde{q}}^1 \over \gamma }$. Furthermore, by definition, $u(q;x,\gamma ) = u\big (\hat{X}_{x,q}, q;\gamma \big )$ $= \ln {\hat{y}_{x,q}^1 \over \gamma }$. Therefore,

$$\begin{aligned} u(q;x,\gamma ) = -\gamma \inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}}\left\{ {1 \over \gamma } H\big [Q|P\big ] + l\left( x + {\mathbb {E}}^Q\left[ - q B \right] \right) \right\} . \end{aligned}$$

It also holds that,

$$\begin{aligned}&\lim _{q \downarrow 0} p(B;x,q) = {1 \over \gamma }\lim _{q \downarrow 0} {u(q;x,\gamma ) - u(0;x,\gamma ) \over q} \nonumber \\&\quad = -\lim _{q \downarrow 0} {\inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}}\Bigg \{{1 \over \gamma } H\big [Q|P\big ] + l\bigg (x + {\mathbb {E}}^Q\left[ - q B \right] \bigg )\Bigg \} - \inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}}\left\{ {1 \over \gamma } H\big [Q|P\big ]\right\} - l(x)\over q} \nonumber \\&\quad = -\lim _{q \downarrow 0} {\inf _{Q \in {\mathcal {M}}_{{\mathcal {X}}_+(x)}}\Bigg \{{1 \over \gamma } H\big [Q|P\big ] + l\bigg (x + {\mathbb {E}}^Q\left[ - q B \right] \bigg )\Bigg \} - {1 \over \gamma } H\big [Q^{x,0}|P\big ] - l(x)\over q} \end{aligned}$$

(8)

For positive and negative $q$, by definition $H\big [Q^{x,q}|P\big ] \ge H\big [Q^{x,0}|P\big ]$ and by Lemma 4, $H\big [Q^{x,q}|P\big ] \rightarrow H\big [Q^{x,0}|P\big ]$ when $q \rightarrow 0$. Therefore, using the non-negativity of relative entropy, $\lim _{q \rightarrow 0} {H\big [Q^{x,q}|P\big ] - H\big [Q^{x,0}|P\big ] \over \gamma q} = 0$. Using this fact, we continue the calculation as follows:

$$\begin{aligned} (8)&= -\lim _{q \downarrow 0} {{1 \over \gamma } H\big [Q^{x,q}|P\big ] + l\bigg (x + {\mathbb {E}}^{Q^{x,q}}\left[ - q B \right] \bigg ) - {1 \over \gamma } H\big [Q^{x,0}|P\big ] - l(x)\over q} \\&= -\lim _{q \downarrow 0} \Bigg ({H\big [Q^{x,q}|P\big ] - H\big [Q^{x,0}|P\big ] \over \gamma q} + {l\bigg (x + {\mathbb {E}}^{Q^{x,q}}\left[ - q B \right] \bigg ) - l(x) \over q} \Bigg ) \\&= -\lim _{q \downarrow 0} {l\bigg (x + {\mathbb {E}}^{Q^{x,q}}\left[ - q B \right] \bigg ) - l(x) \over q}\\&\le -\lim _{q \downarrow 0} {l(x) + l\bigg ({\mathbb {E}}^{Q^{x,q}}\left[ - q B \right] \bigg ) - l(x) \over q} \\&= -\lim _{q \downarrow 0} {l\bigg ({\mathbb {E}}^{Q^{x,q}}\left[ - q B \right] \bigg )\over q} = -\lim _{q \downarrow 0} {q l\bigg ({\mathbb {E}}^{Q^{x,q}}\left[ - B \right] \bigg )\over q} = -\lim _{q \downarrow 0} l\bigg ({\mathbb {E}}^{Q^{x,q}}\left[ - B \right] \bigg )\\&= -l\bigg ({\mathbb {E}}^{Q^{x,0}}\left[ - B \right] \bigg ) \end{aligned}$$

Likewise, we calculate $\lim _{q \uparrow 0} p(B;x,q)$, as follows:

$$\begin{aligned} \lim _{q \uparrow 0} p(B;x,q)&= {1 \over \gamma }\lim _{q \uparrow 0} {u(q;x,\gamma ) - u(0;x,\gamma ) \over q} \\&= -\lim _{q \uparrow 0} {l\left( x + {\mathbb {E}}^{Q^{x,q}}\left[ - q B \right] \right) - l(x) \over q} \ge l\left( {\mathbb {E}}^{Q^{x,0}}\left[ B \right] \right) , \end{aligned}$$

where we use $q < 0$. $\square$

By Proposition 1, the utility indifference price at $q = 0$ is given independently of risk-aversion. Thus, we attain the market equilibrium. Before this, we provide the following definition of market equilibrium.

Definition 1

Let an economy specify on investor’s preferences, which are described by the utility function $U :=\big \{U_i(\cdot ); U_i(x) := -e^{-\gamma _i x},\ i=1,\ldots , n\big \}$. Each investor’s wealth is defined by his or her portfolio holdings $X=X^{x,L} \in {\mathbb {R}}_+^d$ and a contingent claim $B$ through the liquidation function. An allocation $q^*:= \big \{q^*_i, i=1,\ldots , n,\ q^*_i \in {\mathbb {R}}\big \}$ and a price $p$ of the contingent claim $B$ constitutes a price equilibrium if an assignment exists such that the following conditions hold:

• (1) For any investor with utility function $\{U_i, \ i=1,\ldots ,n\}$, when the investor holds $q_i^*$-units of the contingent claim, $(p,q_i^*)$ is preferred to all other allocations $(p,q'_i)$; that is, an expected utility corresponding to the allocation $(p,q^*_i)$ is larger than another expected utility corresponding to the allocation $(p,q'_i)$.

• (2) $\sum _{i=1}^n q_i^*= 0$.

Theorem 1

In a market with transaction costs, let every investor with different risk-aversions construct his or her strategies according to utility indifference pricing. Furthermore, let initial endowments $x$ be common for all investors; then, equilibrium will be zero trade. The equilibrium price is given by $p(B;0)$, which exists in the range as follows:

$$\begin{aligned} p(B;0) \in \Bigg (l\big ({\mathbb {E}}^{Q^{x, 0}}\left[ B\right] \big ), -l\big (-{\mathbb {E}}^{Q^{x, 0}}\left[ B\right] \big ) \Bigg ). \end{aligned}$$

Proof

The case of $q > 0$ indicates that an investor’s strategy is to sell the contingent claim $B$. For $q > q' >0$,

$$\begin{aligned}&{\gamma \big (p(B;x,q) - p(B;x,q')\big )}\nonumber \\&\quad = {u(q;x,\gamma ) - u(0;x,\gamma ) \over q} - {u(q';x,\gamma ) - u(0;x,\gamma ) \over q' } \nonumber \\&\quad = {q' u(q;x,\gamma ) - q' u(0;x,\gamma ) - q u(q';x,\gamma ) + q u(0;x,\gamma ) \over q q'} \end{aligned}$$

(9)

$$\begin{aligned}&\quad = {q' u(q;x,\gamma ) + (q - q') u(0;x,\gamma ) - q u(q';x,\gamma ) \over q q'} \nonumber \\&\quad = {q \left( {q' \over q} u(q;x,\gamma ) + {(q - q') \over q} u(0;x,\gamma )\right) - q u(q';x,\gamma ) \over q q'} \nonumber \\&\quad \ge {q u\big ({q' \over q} q + {(q - q') \over q} 0;x,\gamma \big ) - q u(q';x,\gamma ) \over q q'} = 0. \end{aligned}$$

(10)

Therefore, $p(B;x,q) > p(B;x,q')$. In contrast, for $q<q'<0$, it holds that $p(B;x,q) < p(B;x,q')$. That is, the utility indifference price is non decreasing if the investor is in sell side and the utility indifference price is non-increasing if the investor is on the buy-side. It is well known that the utility indifference price is the threshold price. That is, from the sell-side of contingent claims, the utility indifference price is a minimum price, and from the buy-side of contingent claims, the utility indifference price is a maximum price.

Since the utility indifference price at $q = 0$ is independent of risk-aversion, if initial endowments are common for all investors, the utility indifference price $p(B;x, 0)$ is also common for all investors. Therefore, utility indifference sell prices for any investor are more expensive than utility indifference buy prices for all investors. Therefore, the equilibrium is zero trade and the equilibrium price is given by $p(B;x,0)$. $\square$

Remark 1

In the previous theorem, initial endowments are assumed to be common for all investors. However, if initial endowments are different for each investor, utility indifference prices at $q=0$ might be different from each other because they exist in a range that depends on the initial endowment.

More precisely, we consider $n$-investors with initial endowment $\big \{x_i;\ i=1,\ldots , n\big \}$. Each utility indifference price $p(B;x_i,0)$ is within a certain range as $p(B;x_i,0) \in \left( l\big ({\mathbb {E}}^{Q^{x_i,0}}\left[ B\right] \big ), -l\big (-{\mathbb {E}}^{Q^{x_i,0}}\left[ B\right] \big ) \right)$. Choose $x^*$ from $\big \{x_i;\ i=1,\ldots ,n\big \}$ and assume that for all $i \in [1, n]$,

$$\begin{aligned} -l\big (-{\mathbb {E}}^{Q^{x^*,0}}\left[ B\right] \big ) \ge -l\big (-{\mathbb {E}}^{Q^{x_i,0}}\left[ B\right] \big ). \end{aligned}$$

Likewise, choose $x_*$ and assume that for all $i \in [1,n]$,

$$\begin{aligned} l\big ({\mathbb {E}}^{Q^{x_*,0}}\left[ B\right] \big ) \le l\big ({\mathbb {E}}^{Q^{x_i,0}}\left[ B\right] \big ). \end{aligned}$$

Then, for initial endowments $x^i \ne x^j$, utility indifference prices $p\big (B;x^i,0\big )$ and $p\big (B;x^j,0\big )$ exists in the range $\left( l\big ({\mathbb {E}}^{Q^{x_*, 0}}\left[ B\right] \big ), -l\big (-{\mathbb {E}}^{Q^{x^*, 0}}\left[ B\right] \big )\right)$. However, the utility indifference price $p\big (B;x^i,0\big )$ can be different from $p\big (B;x^j,0\big )$, because $Q^{x_i,0}$ might be different from $Q^{x_j,0}$; that is, price ranges $\left( l\big ({\mathbb {E}}^{Q^{x_i,0}}\left[ B\right] \big ), -l\big (-{\mathbb {E}}^{Q^{x_i,0}}\left[ B\right] \big ) \right)$ and $\left( l\big ({\mathbb {E}}^{Q^{x_j,0}}\left[ B\right] \big ), -l\big (-{\mathbb {E}}^{Q^{x_j,0}}\left[ B\right] \big ) \right)$ might be different from each other, implying that an equilibrium price $p^*(B) \in \left( l\big ({\mathbb {E}}^{Q^{x_*, 0}}\left[ B\right] \big ), -l\big (-{\mathbb {E}}^{Q^{x^*, 0}}\left[ B\right] \big )\right)$ exists such that $p(B;x,0) = p\big (B;x^i,q\big ) = p\big (B;x^j;-q\big )$ for a quantity $q$. In this case, the equilibrium is not zero trade. $\square$

Theorem 1 is obtained through the framework of indifference pricing. Hereafter, we consider the case of utility-based prices. Following [9], we define the utility-based price for $B$ as the value $p^{HK}(B;x)$ such that the agent’s holdings $q$ in the claims are optimal in the model where the claims can be traded at time 0 at price $p^{HK}(B;x)$. That is, we need to consider the problem $\sup _{X^{x + p^{HK}(B;x) q,L} \in {\mathcal {X}}\big (x + q p^{HK}(B;x) {\mathbf {1}}_1\big ). q \in {\mathbb {R}}} {\mathbb {E}}U\left[ l\big (X^{x + q p^{HK}(B;x) {\mathbf {1}}_1,L} - q B\big )\right]$.

$$\begin{aligned}&{\sup _{X^{x + q p^{HK}(B;x) {\mathbf {1}}_1,L} \in {\mathcal {X}}\big (x + q p^{HK}(B;x) {\mathbf {1}}_1\big ), q \in {\mathbb {R}}} {\mathbb {E}}U\bigg [l\big (X^{x + q p^{HK}(B;x) {\mathbf {1}}_1,L} - q B \big )\bigg ]}\\&\quad = \sup _{q \in {\mathbb {R}}} \left\{ e^{-\gamma q p^{HK}(B;x)} \sup _{X^{x,L} \in {\mathcal {X}}(x)} {\mathbb {E}}U\bigg [l\big (X^{x,L} - q B\big )\bigg ] \right\} \\&\quad = \sup _{q \in {\mathbb {R}}} \left\{ e^{-\gamma q p^{HK}(B;x)} \sup _{X^{x,L} \in {\mathcal {X}}(x)} \left( -e^{u\big (X^{x,L},q;\gamma \big )}\right) \right\} \\&\quad = \sup _{q \in {\mathbb {R}}} \left\{ -e^{-\gamma q p^{HK}(B;x)} \inf _{X^{x,L} \in {\mathcal {X}}(x)} e^{u\big (X^{x,L},q;\gamma \big )}\right\} \\&\quad = \sup _{q \in {\mathbb {R}}} \left\{ -e^{-\gamma q p^{HK}(B;x)} e^{\inf _{X^{x,L} \in {\mathcal {X}}(x)} u(X^{x,L},q;\gamma )}\right\} \\&\quad = \sup _{q \in {\mathbb {R}}} \left\{ -e^{-\gamma q p^{HK}(B;x) + u\big (q;x, \gamma \big )}\right\} \\&\quad = -e^{\inf _{q \in {\mathbb {R}}} \left\{ -\gamma q p^{HK}(B;x) + u(q;x, \gamma )\right\} }. \end{aligned}$$

Therefore, considering $\inf _{q \in {\mathbb {R}}} \left\{ -\gamma q p^{HK}(B;x) + u(q;x, \gamma )\right\}$ is sufficient. As $u(q;x, \gamma )$ is a proper convex function [that is, $u(q;x,\gamma ) < \infty$ for at least one $q$ and $u(q;x,\gamma ) > -\infty$ for every $q$], if $-\gamma p^{HK}(B;x) \in \partial u\big (q^*;x, \gamma \big )$, then $-\gamma q p^{HK}(B;x) + u(q;x, \gamma )$ achieves its infimum at $q = q^*$ from Theorem 23.5 of [15]. Using this principle, we obtain equilibrium.

Theorem 2

In a market with transaction costs, let every investor with different risk-aversions construct his or her strategies according to utility-based pricing. Furthermore, an initial endowment $x$ is common for all investors. Then, the equilibrium is zero trade and the equilibrium price is given by $p^*(B)$, which exists in the range given by

$$\begin{aligned} p^*(B) \in \left( l\big ({\mathbb {E}}^{Q^{\tilde{x}, 0}}\left[ B\right] \big ), -l\big (-{\mathbb {E}}^{Q^{\bar{x}, 0}}\left[ B\right] \big ) \right) . \end{aligned}$$

Proof

By definition of subdifferential, any $\alpha _q \in \partial u(q;x,\gamma )$ satisfies ${u(q_0;x, \gamma ) - u(q;x, \gamma ) \over q_0 - q} \le \alpha _q$ for $q_0 \in (0, q)$ [if $q_0 > q$, ${u(q_0;x, \gamma ) - u(q;x, \gamma ) \over q_0 - q} \ge \alpha _q$] and any $\alpha _0 \in \partial u(0;x,\gamma )$ satisfies ${u(q_0;x, \gamma ) - u(0;x, \gamma ) \over q_0 - 0} \ge \alpha _0$. That is, if ${u(q_0;x, \gamma ) - u(q;x, \gamma ) \over q_0 - q} > {u(q_0;x, \gamma ) - u(0;x, \gamma ) \over q_0 - 0}$, then $\partial u(q;x,\gamma ) \cap \partial u(0;x,\gamma ) = \emptyset$.

Consider the case of $q > 0$. For $q_0 \in (0,q)$,

$$\begin{aligned}&{{u(q_0;x,\gamma ) - u(q;x,\gamma ) \over q_0 - q} - {u(q;x,\gamma ) - u(0;x,\gamma ) \over q - 0}}\\&\quad = {q u(q_0;x,\gamma ) - q u(q;x,\gamma ) - (q_0 - q) u(q;x,\gamma ) + (q_0 - q) u(0;x,\gamma ) \over q(q_0 - q)}\\&\quad = {-q_0 u(q;x,\gamma ) + (q_0 - q) u(0;x,\gamma ) + q u(q_0;x,\gamma ) \over q(q_0 - q)}\\&\quad = {-q \left( {q_0 \over q} u(q;x,\gamma ) + {q - q_0 \over q} u(0;x,\gamma )\right) + q u(q_0;x,\gamma ) \over q(q_0 - q)}\\&\quad \ge {-q u\left( {q_0 \over q} q + {q - q_0 \over q} 0 ;x,\gamma \right) + q u(q_0;x,\gamma ) \over q(q_0 - q)} = 0. \end{aligned}$$

From (10), for $q_0 \in (0,q)$, ${u(q;x,\gamma ) - u(0;x,\gamma ) \over q - 0} \ge {u(q_0;x,\gamma ) - u(0;x,\gamma ) \over q_0 - 0}$. Therefore, for $q_0 \in (0,q)$, it holds that

$$\begin{aligned} {u(q_0;x,\gamma ) - u(q;x,\gamma ) \over q_0 - q} \ge {u(q_0;x,\gamma ) - u(0;x,\gamma ) \over q_0 - 0}. \end{aligned}$$

Hence, even if $\partial u(q;x,\gamma ) \cap \partial u(0;x,\gamma ) \ne \emptyset$, the utility-based price at $q >0$ is not smaller than the utility-based price at $q=0$. The same logic is valid for the case $q < 0$. Therefore, the utility-based prices for the sell-side ($q>0$) and the utility-based price for the buy-side ($q<0$) are separated for all investors.

However, from the proof of Proposition 1, we have $\partial u(0;x,\gamma ) \in (\gamma l\big ({\mathbb {E}}^{Q^{x,0}}\left[ B\right] \big ), -\gamma l\big (-{\mathbb {E}}^{Q^{x,0}}\left[ B\right] \big ))$, which implies that an equilibrium price exists in this range. Therefore, as with Theorem 1, if initial endowments $x$ are common for all investors, the equilibrium is given by zero trade because the utility-based price given by $\partial u(0;x,\gamma )$ is common for all investors. $\square$

Remark 2

One of the most natural expansions of the previous model with transaction costs is to include randomness and time into the transaction matrix $\big (\lambda ^{ij}\big )$; that is, to consider $\big (\lambda ^{ij}(t, \omega )\big )$. In [11], this expansion was indirectly introduced as bid-ask processes $\big (\pi _t^{ij}\big )\in \varPi _t$, as formulated by [16]. It is also possible to consider the model in which asset processes are not necessarily continuous. In relation to such a model, the utility maximization problem has been considered by [5] and [1]. Fortunately, the utility maximization problem in the [5] and [1] model has a solution, and the form of the solution is essentially the same as the form of the solution of [3]. This result implies that our equilibrium approach can be applied to the model formulated by [5, 16], and [1]. Our approach to deducing the equilibrium in the generalized model will be explored in future research, as it is beyond the scope of this paper, which focuses on using a simple method to deduce equilibrium features.

4 Concluding remarks

[7] showed that, if no friction exists through transaction costs, the equilibrium will be zero trade in the utility indifference framework and the utility-based framework. Theorems 1 and 2 show that the equilibrium is zero trade even in a market with transaction costs. However, these results are under the assumption that initial endowments are common for all investors. If we abandon this strong assumption, non zero-trade equilibrium might appear. Transaction costs are usually regarded as obstacles to market liquidity. However, we find that transaction costs can generate the non zero-trade equilibrium, implying that transaction costs are not necessarily obstacles for making liquidity in a market. In this sense, such a scenario may have interesting implications.