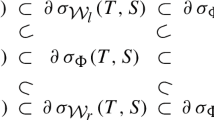On the analysis of some perturbed Browder’s operators

Abstract

In this paper, we are interested with a new class of perturbation named the $\Phi$-perturbation function which allowing us to derive some advances on the semi-Browder and Browder operators theory acting in Banach spaces. More precisely, sufficient conditions are investigated to reach the stability analysis of perturbed semi-Browder and Browder operators via such approach of perturbation. Our mainly results are subsequently used to develop a new characterization of Browder’s spectra of linear operators on the $\Phi$-perturbation function based approach. Furthermore, illustrative examples are presented to enrich the validity of our theoretical results.

1 Introduction

The study of stability problem of perturbed linear operators is one of the most attractive topics in the operators theory or functional differential equations due to their applicability in various areas of physical sciences, mathematical biology and control theory. Mainly, in recent years the theory of Fredholm operators and their derivative sets are vital importance in the Fredholm theory of integral equations. Under this investigation, the redundancy and flexibility offered by Fredholm theory have spurred their applications in a variety of areas like: the investigation of various classes of integral equations, stability problem of essential spectra, the theory of block operators matrices,...An interested reader can found some basic information in this prospect in some works of following references [1, 2, 5, 6, 9, 13, 17, 18, 24, 33, 34, 36].

More than the general class of Fredholm operators is the class of Browder operators and their derivative sets. So, the spectral analysis problem around the theory of stability of Browder and semi-Browder perturbed operators has been developed very intensively and the focus of many studies. Although there exists a wide literature on this topic, we would like to mention some of them [1, 2, 5, 8, 10,11,12, 16, 21, 23, 25, 26]. Especially, Gabiner [12] focused on the perturbation theory of semi-Browder bounded linear operators under commuting compact operators on Banach space. In fact, the author in [12, Theorem 2], was proved for bounded commuting linear operators T and V under compactness criterion of the operator $K :=T-V\in \mathcal {K}(X)$, that:

$$\begin{aligned}&T\in \Phi _-(X) \, \, (\text{ resp. } T\in \Phi _+(X))\, \, \, \\&\hbox {implies}\ \, \\&desc(V)<\infty \, \, \, (\text{ resp. } asc(V)<\infty )\ \, \, \ \hbox { if and only if }\ \, \, desc(T)<\infty \\&\quad (\text{ resp. } asc(T)<\infty ). \end{aligned}$$

Later, Rakočević extend the above descriptive result to more general classes of perturbation. Precisely, in [27, 28], he shows for linear bounded commuting operators T and K, the following items:

$$\begin{aligned}&\mathbf{(i)}\, \, T\in \Phi _-(X) \ \hbox { with }\ desc(T)<\infty , \, K \in P(\Phi _-(X))\,\\&\qquad \hbox {implies}\, \\&\qquad T+K\in \Phi _-(X)\ \hbox { with }\ desc(T+K)<\infty \end{aligned}$$

and

$$\begin{aligned}&\mathbf{(ii)} \, \, T\in \Phi _+(X) \ \text{ with } \ asc(T)<\infty , \, K \in P(\Phi _+(X)) \, \\&\qquad \hbox {implies}\, \\&\qquad T+K\in \Phi _+(X) \text{ with } asc(T+K)<\infty , \end{aligned}$$

where $P(\Phi _*(X)) := \{T \in \mathcal {L}(X): T+K\in \Phi _*(X),\, \, \forall K \in \Phi _*(X)\},$ for $\Phi _*(X)\in \{\Phi _-(X), \Phi _+(X)\}.$ So, the above mentioned stability analysis of perturbed bounded semi Browder operators under some criterions of perturbations are frequently uses to give a fairly comprehensive description of some Browder’s essential spectra of linear operators under commuting arguments of some classes of perturbations. Based upon, many mathematicians tackled the problem of the stability of some sets of Browder’s essential spectra of linear operators involving some criterions of perturbations. A positive answer of such proposed analysis problem have been developed by many authors, see [1, 5, 10, 11, 17, 23, 25,26,27,28, 39, 40]. In this prospect, we mention the stability results of Browder’ s essential defect and approximate point spectrum of perturbed linear bounded operator invested by Rakočević and proved in [28] as:

$$\begin{aligned} \sigma _{eb}^-(T)=\sigma _{eb}^-(T+K)\quad \hbox {and}\quad \sigma _{eb}^+(T) = \sigma _{eb}^+(T+K). \end{aligned}$$

On the other hand, since 2004, important progress has been made in the spectral theory originated by Mebekhta in his pioneering paper [20] to offer to the reader a new class of perturbations coined by the notion of $\Phi$-perturbation function, denoted by $\mathcal {F}_{\Vert .\Vert }(.)$. The specificity of the invention introduced by Mebekhta [20] around this class of perturbation appears that it contains the class of compact operators as well as other classes of non ideal of the set of linear bounded operators likewise the classes of measures: particularly, the measure of non strict singularity also non strict cosingularity perturbations intensely studied in the literature [22, 31, 35].

As far as we know, in most published papers, the analysis of perturbed Browder and semi-Browder operators has been treated with some statements involving many important classes of operators on two closed sided ideal of the set of bounded operators [5, 25, 26, 30] or which class isn’t belongs to two closed sided ideal of the set of bounded operators [1, 3, 4, 22]. Therefore, motivated by the notion of $\Phi$-perturbation function, it is important and challenging to enlarge the above descriptive and mentioned results in order to ameliorate and enrich the theory of Browder’s operators by means of new concept of perturbation. Therefore, our contribution in this paper is to investigate some elementary properties of perturbed linear bounded operators by means of the $\Phi$-perturbation function which severely affected our ability in studying the spectral analysis problem of semi-Browder operators of linear bounded operators. Precisely, we begin to develop under weaker criterions via the $\Phi$-perturbation function of two commuting bounded operators T and K the following equivalence:

$$\begin{aligned}&\, \, asc(T)<\infty \,\, \text{ if } \text{ and } \text{ only } \text{ if } \,\, asc(T+K)<\infty .\\&\, \, desc(T)<\infty \,\, \text{ if } \text{ and } \text{ only } \text{ if } \,\, desc(T+K)<\infty . \end{aligned}$$

These key results permit to derive consequently in other part of this work, our interest about semi-Browder and Browder analysis of perturbed Browder’s operators. More precisely, for two commuting bounded operators T and K, we show under the hypothesis:

$$\begin{aligned} \mathcal {F}_{\Vert .\Vert }(K^n)<\varphi (T^n),\quad \hbox {for some}\quad n\ge 1, \end{aligned}$$

that:

$$\begin{aligned} T\in \mathcal {B_*}(X)\quad \text{ if } \text{ and } \text{ only } \text{ if }\quad T+K\in \mathcal {B_*}(X), \end{aligned}$$

for $\mathcal {B_*}(X) \in \{\mathcal {B_+}(X), \mathcal {B_-}(X), \mathcal {B}(X)\}$ (see Sects. 2 and 3 for the definitions of $\mathcal {F}_{\Vert .\Vert }$ and $\varphi$).

Consequently, the topic of our analysis of perturbed results of Browder’s operators via the notion of the $\Phi$-perturbation function described in the above results permits to derive some localization informations about their corresponding essential spectra as follows:

$$\begin{aligned} \sigma _{eb}^*(T+K)\subset \sigma _{eb}^*(T)\cup \{\nu :\, \, \mathbf{d}(\nu , \sigma _{eb}^*(T))\le \eta \} , \end{aligned}$$

where $\Bigl (\sigma _{eb}^*(.), \mathbf{d}(\nu , \sigma _{eb}^*(.))\Bigl ) \in \left\{ \Bigl (\sigma _{eb}^+(.), \mathbf{d}(\nu , \sigma _{eb}^+(.))\Bigl ), \Bigl (\sigma _{eb}^-(.), \mathbf{d}(\nu , \sigma _{eb}^-(.))\Bigl )\right\}$ and $\mathbf{d}(\nu , \sigma _{eb}^*(.))$ denotes the distance of $\nu$ from $\sigma _{eb}^*(.)$.

At the end of this paper, motivated by the concept of $\Phi$-perturbation function, we find a new chap of the characterization problem of the Browder’s essential spectra of linear bounded operator. By this ways, such contribution generalizes the ones existing in the literature, we refer the reader to [25,26,27,28]. Our new invested Browder’s characterization provide an improvements and an amelioration of some earlier works [5, 10, 11, 17, 18, 22, 25, 26].

Our paper is organized as follows:

In Sect. 2, we introduce some definitions, notations and properties of linear operators. In particular, we introduce en detail the notion of $\Phi$-perturbation function and their property.

The purpose of Sect. 3 is dedicated to develop some advances on spectral theory of semi-Browder and Browder operators involving this notion. The obtained results are applied to improve a refinement description of Bowder’s essential approximate point and Browder’s essential defect spectra. Finally, we close this work by introducing some necessary criterions via $\Phi$-perturbation function that are essential to characterize the Browder’s essential spectra of linear bounded operators.

2 General definitions and tools

In this section, we recall some definitions preliminary results relevant to linear bounded operators.

Firstly, we will use the following notations throughout this paper:

• X be a Banach space,

• $\mathcal {L}(X):$ denotes the set of all bounded linear operators on X,

• $\mathcal {K}(X):$ denotes the subspace of all compact operators of $\mathcal {L}(X),$

• $\mathcal{SS}\mathcal{}(X):$ denotes the set of strictly singular operators on X,

• $\mathcal{SC}\mathcal{}(X):$ denotes the set of strictly cosingular operators on X,

• $\mathcal{WC}\mathcal{}(X):$ denotes the set of weakly compacts operators on X.

For $T \in \mathcal {L}(X)$, we write:

• $\mathcal { N}(T) :=\{ x \in X: \ Tx=0 \} \subset X$: for the null space of T,

• $\mathcal {R}(T) \subset X$: for the range of T, 

• $\alpha (T):$ as the nullity of T, it is defined as the dimension of $\mathcal {N} (T)$,

• $\beta (T):$ as the deficiency of T, it is defined as the codimension of $\mathcal {R}(T)$ in X.

Definition 2.1

Let $T\in \mathcal {L}(X),$ we define:

(i) the approximate point spectrum of T, $\sigma _{ap}(T)$, by:

$$\begin{aligned} \sigma _{ap}(T):=\left\{ \nu \in \mathbb {C}:\,\displaystyle \inf _{\Vert x\Vert =1,x\in \mathcal {D}(T)} \Vert (\nu I-T)x\Vert =0\right\} :=\mathbb {C}\backslash \rho _{ap}(T) \end{aligned}$$

(ii) the defect spectrum of T,  $\sigma _{\delta }(T),$ by:

$$\begin{aligned} \sigma _{\delta }(T):=\{\nu \in \mathbb {C}:\,\nu I-T\,\text{ is } \text{ not } \text{ surjective }\} :=\mathbb {C}\backslash \rho _{\delta }(T). \end{aligned}$$

(iii) the spectrum of T, $\sigma (T)$, by:

$$\begin{aligned} \sigma (T) := \mathbb {C}\backslash \rho (T), \end{aligned}$$

where the resolvent set of T,  $\rho (T),$ defined by:

$$\begin{aligned} \rho (T):=\{\nu \in \mathbb {C}:\,\nu I-T\,\text{ has } \text{ a } \text{ bounded } \text{ inverse }\}. \end{aligned}$$

$\diamondsuit$

A useful classes of linear operators which have extensive application in spectral theory are those of:

Definition 2.2

(i) Set of upper semi-Fredholm operators on X is defined by:

$$\begin{aligned} \Phi _+(X):=\{T\in \mathcal {L}(X):\,\,\alpha (T)<\infty \text{ and } R(T) \text{ is } \text{ closed }\}. \end{aligned}$$

(ii) Set of lower semi-Fredholm operators on X is defined by:

$$\begin{aligned} \Phi _-(X) :=\{T\in \mathcal {L}(X):\,\,\beta (T)<\infty \text{ and } R(T) \text{ is } \text{ closed }\}. \end{aligned}$$

(iii) Set of Fredholm operator on X is defined as:

$$\begin{aligned} \Phi (X) := \Phi _-(X) \cap \Phi _+(X). \end{aligned}$$

$\diamondsuit$

Set of Fredholm operator with index i(T) null defines the set of Weyl operators as:

$$\begin{aligned} \mathcal {W}(X):= \{T\in \mathcal {L}(X):\,T\in \Phi (X)\,\text{ and }\,i(T)=0\}, \end{aligned}$$

where the index i(T), of T is defined by the quantities $i(T)=\alpha (T)-\beta (T)$.

Definition 2.3

Let $T\in \mathcal {L}(X)$. We define:

(i) the ascent of T by:

$$\begin{aligned} \,asc(T):=\min \{n\in \mathbb {N}: \, \mathcal {N}(T^{n})=\mathcal {N}(T^{n+1}) \}, \end{aligned}$$

whenever these minimum exist. If no such numbers exist the ascent of T is defined to be $\infty$.

(ii) the descent of T by:

$$\begin{aligned} desc(T) :=\min \{n\in \mathbb {N}: \mathcal {R}(T^{n})=\mathcal {R}(T^{n+1})\}, \end{aligned}$$

the infinimum over the empty set is taken to be $\infty$. $\diamondsuit$

For other sets of linear operators, we introduce the set of upper (resp. lower) semi-Browder operators on X as follows:

Definition 2.4

(i) Set of upper semi-Browder operators on X is defined as:

$$\begin{aligned} \mathcal {B}_+(X):=\{T\in \mathcal {L}(X): \, T\in \Phi _+(X) \text{ with } asc(T)<\infty \}. \end{aligned}$$

(ii) Set of lower semi-Browder operators on X is defined as:

$$\begin{aligned} \mathcal {B}_-(X):=\{T\in \mathcal {L}(X): \, T\in \Phi _-(X) \text{ with } desc(T)<\infty \}. \end{aligned}$$

(iii) Set of Browder operators on X is defined by:

$$\begin{aligned} \mathcal {B}(X) := \mathcal {B}_-(X)\cap \mathcal {B}_+(X). \end{aligned}$$

$\diamondsuit$

Remark 2.1

Due to the results developed by V. Muller in [23, Chapter 3, Corollary 11], the following implication holds:

$$\begin{aligned}&T\in \Phi _+(X)\, (\hbox {resp}.\, T\in \Phi _-(X))\, \hbox {with}\ \, asc(T)<+\infty \, (\hbox {resp}. \, desc(T)<\infty )\,\\&\quad \Longrightarrow \, \\&\quad i(T )\le 0\, \, (\hbox {resp}.\, i(T)\ge 0). \end{aligned}$$

$\diamondsuit$

Before moving to describe the stability analysis of perturbed semi Browder’s and Browder operators and the characterization of their corresponding essential spectra, the following definition will be required.

Definition 2.5

Let $T \in \mathcal {L}(X)$. Then, we define:

$\mathbf{(i)}$ the Browder’s essential approximate point spectrum of T, $\sigma _{eb}^{+}(T)$, as:

$$\begin{aligned} \sigma _{eb}^{+}(T) := \{\nu \in \mathbb {C}: \, \nu I-T\notin \mathcal {B}_{+}(X)\}. \end{aligned}$$

$\mathbf{(ii)}$ the Browder’s essential defect spectrum of T, denoted by $\sigma _{eb}^{-}(T)$, as:

$$\begin{aligned} \sigma _{eb}^{-}(T) := \{\nu \in \mathbb {C}: \, \nu I-T\notin \mathcal {B}_{-}(X)\}. \end{aligned}$$

$\mathbf{(iii)}$ the Browder’s essential spectrum of T, denoted by $\sigma _{eb}(T)$, as:

$$\begin{aligned} \sigma _{eb}(T) := \{\nu \in \mathbb {C}: \, \nu I-T\notin \mathcal {B}(X)\}. \end{aligned}$$

$\diamondsuit$

Remark 2.2

As far as we known, for each Banach space X,  the above various notion of essential spectra remains not equal in general but satisfies only the direct inclusion as:

$$\begin{aligned} \sigma _{ef}^{+}(T) \subset \sigma _{ew}(T)\subset \sigma _{eb}(T):=\sigma _{eb}^+(T)\cup \sigma _{eb}^-(T) \end{aligned}$$

and

$$\begin{aligned} \sigma _{ef}^{-}(T) \subset \sigma _{ew}(T)\subset \sigma _{eb}(T), \end{aligned}$$

where the upper (resp. lower and Weyl) Fredholm essential spectrum of T denoted by $\sigma _{ef}^{+}(T)$ $(\text{ resp. } \sigma _{ef}^{-}(T), \,$ $\sigma _{ew}(T))$ and defined as the complemented in $\mathbb {C}$ of $\Phi _{+,T}(X)$ $(\text{ resp. } \Phi _{-,T}(X),$ $\mathcal {W}_{T}(X) )$, (see [17] for more detail).

Therefore, to appreciate this statement, let us introduce the following example originating from V. Rako$\check{\text {c}}$evi$\acute{\text {c}}$ in [25] and Salinas [29] as follows:

Consider T be the right shift operator on a separable Hilbert space H and $K\in \mathcal {L}(X)$ be quasinilpotent. Assume that $V= T\oplus T^* \oplus K.$ Then, due to the work developed in [29], we obtain that:

$$\begin{aligned} \sigma _{eb}(V)= \mathcal {U} \, \, \text{ and }\ \, \, \sigma _{eb}^+(V)= \sigma _{eb}^-(V) =\mathcal {U},\, \, (\mathcal {U} \ \hbox { denotes the closed unit ball}) \end{aligned}$$

by virtue of the paper of V. Rakočević [25]. But, we derive from [29] that:

$$\begin{aligned} \sigma _{ef}^{+}(T)= \sigma _{ef}^{-}(T)= \sigma _{ew}(V)= d\mathcal {U} \cup \{0\}. \end{aligned}$$

Whence,

$$\begin{aligned} \sigma _{ew}(T)\ne \sigma _{eb}(T). \end{aligned}$$

Consequently, from the above argument the study of problems via Weyl essential and Browder’s essential spectra may be regards as an important study in the theory of Fredholm operators. $\diamondsuit$

An important notion of Fredholm perturbations emerged in 2004 as the most famous generalization of other classes of non ideal of $\mathcal {L}(X)$ who named the theory of $\Phi$-perturbation function and was introduced in the pioneer paper of Mebekhta [20] to offer to the reader a frequency of spectral analysis via this kind of perturbation.

Definition 2.6

Let X be a normed space. A map:

$$\begin{aligned} \mathcal {F}_{\Vert .\Vert }: \mathcal {L}(X)\longrightarrow & {} [0, +\infty ) \\ T\longmapsto & {} \mathcal {F}_{\Vert .\Vert }(T) \end{aligned}$$

is called a $\Phi$-perturbation function on X, if it satisfies the following properties:

• $\mathbf{(i)}$ $\mathcal {F}_{\Vert .\Vert }(T+K)=\mathcal {F}_{\Vert .\Vert }(T),$ for all $K\in \mathcal {K}(X),$

• $\mathbf{(ii)}$ $\mathcal {F}_{\Vert .\Vert }(I)=1,$

• $\mathbf{(iii)}$ $\min \{\mathcal {F}_{\Vert .\Vert }(ST),\mathcal {F}_{\Vert .\Vert }(TS)\}\le \Vert S\Vert \mathcal {F}_{\Vert .\Vert }(T),$ for all $T, S\in \mathcal {L}(X),$

• $\mathbf{(iv)}$ if $\mathcal {F}_{\Vert .\Vert }(T)<|\nu |,$ then $\nu I-T$ is a Fredholm operator on X, for $\nu \in {\mathbb {C}}^*.$ $\diamondsuit$

Before proceeding to illustrate the validity of our abstract theoretical results, we must appreciate to the readers some examples of $\Phi$-perturbation function.

$$\begin{aligned} {\textbf {Examples of }}\Phi -{\textbf {perturbation function:}} \end{aligned}$$

Let X be a Banach space and $T\in \mathcal {L}(X).$

Example

${\textbf {(1)}}$: The essential norm of T defined by:

$$\begin{aligned} \Vert T\Vert _e:=\inf \{\Vert T+K\Vert ,\,K\in \mathcal {K}(X)\}. \end{aligned}$$

is a $\Phi$-perturbation function.

Indeed,

• $\mathbf{(a)}$ Let $T \in \mathcal {L}(X)$ and $K\in \mathcal {K}(X)$. Then, we get:

  $$\begin{aligned} \Vert T+K\Vert _e= & {} \inf \{\Vert T+K+K'\Vert ,\, K'\in \mathcal {K}(X)\} \\= & {} \inf \{\Vert T+K''\Vert ,\, K''=K+K'\in \mathcal {K}(X)\} \\= & {} \Vert T\Vert _e. \end{aligned}$$

• $\mathbf{(b)}$ Following item $\mathbf{(a)}$, one has $\Vert I\Vert _e = \Vert I-K\Vert _e$, for $K \in \mathcal {K}(X),$ we conclude that:

  $$\begin{aligned} \Vert I\Vert _e = \Vert I-K\Vert _e \le \Vert I-K + K'\Vert \le \Vert I\Vert =1, \text{ for } K' \in \mathcal {K}(X). \end{aligned}$$

On the other side, while

$$\begin{aligned} \Vert I\Vert = \Vert I-K+K\Vert \le \Vert I+K\Vert , \text{ for } K \in \mathcal {K}(X) \end{aligned}$$

we infer that $1 \le \Vert I\Vert _e.$ Thus, the result of the item $\mathbf{(ii)}$ of Definition 2.6 is obvious.

• $\mathbf{(c)}$ Let T and S be two bounded operators on X. Since $\mathcal {K}(X)$ is a closed two-sided ideal of $\mathcal {L}(X),$ then we have:

  $$\begin{aligned} \Vert ST\Vert _e= & {} \inf \{\Vert ST+SK\Vert ,\, K\in \mathcal {K}(X)\} \\\le & {} \Vert ST+SK\Vert ,\, \, K\in \mathcal {K}(X) \\\le & {} \Vert S\Vert \Vert T+K\Vert ,\, \, K\in \mathcal {K}(X). \end{aligned}$$

So, we deduce that $\Vert ST\Vert _e\le \Vert S\Vert \Vert T\Vert _e.$ Therefore, the assertion $\mathbf{(iii)}$ of Definition 2.6 may be checked.

• $\mathbf{(d)}$ Suppose that $\nu I-T\notin \Phi (X),$ for such $\nu \in \mathbb {C}.$ That is, $\nu I-T\notin \Phi _+(X),$ then the use of Lemma 4.3 in [19] asserts that there exists an infinite dimensional subspace M of X such that the restriction of $\nu I-T$ to M, denoted by $(\nu I-T)/_{M}$ is compact. Thus, we have:

  $$\begin{aligned} \Vert \nu I/_{M}\Vert _e = \Vert (\nu I-T)/_{M}+T/_{M}\Vert _e = \Vert T/_{M}\Vert _e \le \Vert T\Vert _e <|\nu |, \end{aligned}$$

which contradict the fact that $\Vert \nu I/_{M}\Vert _e=|\nu |,$ since M is an infinite dimensional subspace.

Consequently, the result of the item $\mathbf{(ii)}$ of Definition 2.6 is obvious.

Example

${\textbf {(2):}}$ The measure of non strict singularity is a $\Phi$-perturbation function.

In fact, let X be a Banach space and $T\in \mathcal {L}(X)$, the notion of measure of non strict singularity of T is defined by:

$$\begin{aligned} \Delta (T):=\sup _{M}\inf _{N\subset M}\gamma (T/_{ N}), \end{aligned}$$

where M and N represent infinite dimensional subspaces of X,  $T/_{ M}$ denotes the restriction of T to the subspace N and $\gamma (.)$ express the Hausdorff measure of non compactness.

It is obvious to see that the measure of non strict singularity, $\Delta (T),$ is a $\Phi$-perturbation function. To proof it, we will provide separately the assertions of Definition 2.6.

• $\mathbf{(a)}$ Let $K \in \mathcal {K}(X)$. Thus, one has $K \in \mathcal {K}(X)\subset \mathcal{SS}\mathcal{}(X)$, we derive easily from Corollary 3.4 in [31] that:

  $$\begin{aligned} \Delta (T+K)=\Delta (T). \end{aligned}$$

  (2.1)

Hence, the result of this item is required.

• $\mathbf{(b)}$ Clearly, $\Delta (I)=1$, thus the item $\mathbf{(ii)}$ of Definition 2.6 may be checked.

• $\mathbf{(c)}$ The desired result of item $\mathbf{(iii)}$ of Definition 2.6 may be obvious while $\Delta (T)\le \Vert T\Vert$, for all linear operator T and from the use of Corollary 2.5 in [31].

• $\mathbf{(d)}$ Assume that $|\nu |>\Delta (T),$ for all $\nu \in {\mathbb {C}}^*$ and proving that $\nu I-T \in \Phi (X).$

Obviously, the use of the properties of the notion of the measure of non strict singularity in [31] revels that for all closed infinite dimensional subspace M of X and $\xi \in [0, 1]$ that:

$$\begin{aligned} \gamma ( \nu I)= & {} \gamma ( (\nu I - \xi T) +\xi T) \\\le & {} \gamma (\nu I - \xi T)+ \Delta ( \xi T) \\\le & {} \gamma (\nu I - \xi T)+ \xi \Delta ( T). \end{aligned}$$

Thus, asserts that:

$$\begin{aligned} \gamma (\nu I - \xi T)\ge & {} \gamma ( \nu I) -\Delta (T) = \vert \nu \vert -\Delta (T) \, \, > 0,\, \,\forall \xi \in [0.1]. \end{aligned}$$

Consequently, we deduce from Theorem 2.11 in [31], that $\nu I - \xi T\in \Phi _+(X),$ for all $\xi \in [0.1]$. According with the local constancy of the index, we obtain:

$$\begin{aligned} i(\nu I - \xi T)= i(\nu I - T) = i(\nu I )=0, \, \, \forall \xi \in [0, 1]. \end{aligned}$$

So, $\alpha (\nu I - T)=\beta (\nu I - T)<+\infty$ which imply that $\nu I - T\in \Phi (X).$

Remark 2.3

As property of $\Phi$-perturbation function of a bounded linear operator T on X, M. Mbekhta in [20] has introduced:

$$\begin{aligned} \mathcal {F}_{\Vert .\Vert }(T)\le \Vert T\Vert \, \, \, \hbox {and}\ \, \, \, \mathcal {F}_{\Vert .\Vert }(T)=0,\, \hbox {for all }\ T\in \mathcal {K}(X). \end{aligned}$$

$\diamondsuit$

In the following, we recall some basic properties of $\Phi$-perturbation function those are used to state our main results.

Lemma 2.1

[7, Lemma 2.1] Let $T\in \mathcal {L}(X).$ Then, we get:

(i) $\mathcal {F}_{\Vert .\Vert }(\nu T)=|\nu |\mathcal {F}_{\Vert .\Vert }(T),$ for all $\nu \in \mathbb {C}^*.$

(ii) If $\mathcal {F}_{\Vert .\Vert }(T)<|\nu |,$ for each scalar $\nu$, then we get: $\nu I-T\in \mathcal {W}(X).$ $\diamondsuit$

3 Stability results of semi-Browder and Browder operators via $\Phi$-perturbation function

To study some stability results of classes of semi-Browder and Browder operators in view of $\Phi$-perturbation function, the following definition will be considered as:

Definition 3.1

We define a $\varphi$ function as:

$$\begin{aligned} \varphi :\mathcal {L}(X)\longrightarrow & {} [0,+\infty ), \end{aligned}$$

such that:

(i) $\varphi (T)>0\, \,$ if and only if $\, \, T\in \Phi _*(X),$   for $\Phi _*(X)\in \{\Phi _+(X),\Phi _-(X)\}.$

(ii) $\varphi (T+K)\le \varphi (T)+\mathcal {F}_{\Vert .\Vert }(K), \, \text{ for } \text{ all } \text{ bounded } \text{ operators } T \text{ and } K.$ $\diamondsuit$

As a preparation to introduce our aim, we begin by proving some important results of perturbed operator via the $\Phi$-perturbation function.

Lemma 3.1

Let T and K be two commuting bounded operators on X.

Assume that $\mathcal {F}_{\Vert .\Vert }(K^n)<\varphi (T^n),$ for some $n\ge 1.$ Thus, we get:

$$\begin{aligned}&\mathbf{(i)} \, \, asc(T)<\infty \,\, \text{ if } \text{ and } \text{ only } \text{ if } \,\, asc(T+K)<\infty .\\&\mathbf{(ii)}\, \, \, desc(T)<\infty \,\, \text{ if } \text{ and } \text{ only } \text{ if } \,\, desc(T+K)<\infty . \end{aligned}$$

$\diamondsuit$

Proof

Let consider the commuting bounded operators T and K such that $\mathcal {F}_{\Vert .\Vert }(K^n)<\varphi (T^n),$ for some $n\ge 1.$

$\mathbf{(i)}$ Suppose that $asc(T)<\infty .$ Then, according to Proposition 1.6 in [37], we infer that:

$$\begin{aligned} \overline{N^\infty (T)}\cap R^\infty (T)={N^\infty (T)}\cap R^\infty (T)=\{0\}. \end{aligned}$$

So, to reach the desired result, we will apply again Proposition 1.6 in [37] for a constrictive perturbed operator $T_\xi$ for considered $\xi \in [0,1].$

To do this, consider $\xi \in [0,1].$ Then, for some $n\ge 1,$ we have:

$$\begin{aligned} \mathcal {F}_{\Vert .\Vert }((\xi K)^n) = \xi ^n\mathcal {F}_{\Vert .\Vert }(K^n) < \varphi (T^n). \end{aligned}$$

Thus, the use of Lemma 5.1 in [7], reveals that:

$$\begin{aligned} T_\xi := T+ \xi K\in \Phi _+(X). \end{aligned}$$

Since $TK=KT$, then according with Theorem 3 in [14, 15], for all $\xi \in [0,1],$ there exists $r(\xi )>0$ such that for all $\nu$ in the open disc $\mathbb {D}(\xi , r(\xi )),$

$$\begin{aligned} \overline{N^\infty (T_\xi )}\cap R^\infty (T_\xi ) =\overline{N^\infty (T_\nu )}\cap R^\infty (T_\nu ). \end{aligned}$$

Hence, $\overline{N^\infty (T_\xi )}\cap R^\infty (T_\xi )$ is locally constant function of $\xi$ on the interval [0, 1].

On the other hand, while every locally constant function on a connected set [0, 1] is constant, then we obtain:

$$\begin{aligned} \overline{N^\infty (T_\xi )}\cap R^\infty (T_\xi )= & {} \overline{N^\infty (T+K)}\cap R^\infty (T+ K) \nonumber \\= & {} \overline{N^\infty (T)}\cap R^\infty (T),\,\,\forall \xi \in [0, 1]. \end{aligned}$$

(3.1)

Thus, following Eq. (3.1), one has

$$\begin{aligned} \overline{N^\infty (T+K)}\cap R^\infty (T+ K)=\{0\}. \end{aligned}$$

Consequently, the use of Proposition 1.6 in [37], asserts that $asc(T+K)<\infty .$

Conversely, we will proof the following implication.

In fact, consider the perturbed operator $T_{1+\xi }$, for $\xi \in [-1,0],$ defined as:

$$\begin{aligned} T_{1+\xi } := T +(1+\xi ) K. \end{aligned}$$

The use of Proposition 1.6 in [37] in view of the assumption that $asc(T+K)< +\infty$, implies that:

$$\begin{aligned} \overline{N^{\infty }(T+K)}\cap R^{\infty }(T+K)=\{0\}. \end{aligned}$$

One has

$$\begin{aligned} \mathcal {F}_{\Vert .\Vert }(((1+\xi ) K)^n) = |1+\xi |^n\mathcal {F}_{\Vert .\Vert }(K^n)\le \mathcal {F}_{\Vert .\Vert }(K^n) < \varphi (T^n), \text{ for } \text{ some } n\ge 1, \end{aligned}$$

we infer from [7, Lemma 5.1] that:

$$\begin{aligned} T_{1+\xi }\in \Phi _+(X),\, \, \hbox { for }\ \, \xi \in [-1,0]. \end{aligned}$$

Now, while $T+K$ and T are two commuting operators, we will adopt the same reasoning as the direct implication mentioned above to check the aim. Precisely, it is sufficient to replace the perturbed operator $T_\xi ,$ for $\xi \in [0, 1]$ by $T_{1+\xi },$ for $\xi \in [-1, 0].$

$\mathbf{(ii)}$ We adopt the same reasoning as the statement $\mathbf{(i)}$ to conclude that $T+\xi K\in \Phi _-(X),$ for all $\xi \in [0,1].$ From Theorem 1.2.3 and Proposition 1.2.7 in [9], it is easy to see in view of the fact that $R(T+\xi K)$ is a closed subspace of X that $R((T+\xi K)^*)$ is a closed subspace of $X^*$ with $\alpha ((T+\xi K)^*) = \beta (T+\xi K)<\infty .$ Therefore, the perturbed operator $T_{\xi }$ satisfied the following form:

$$\begin{aligned} T_{\xi }^*:= (T+ \xi K)^*:= T^*+ \xi K^*\in \Phi _+(X^*), \forall \xi \in [0,1]. \end{aligned}$$

Next, as the previous item $\mathbf{(i)}$ explanation, we deduce that:

$$\begin{aligned} asc((T+K)^*)=asc(T^*+K^*)=desc(T+K)<\infty , \end{aligned}$$

for the two commuting operators $T^*$ and $K^*$.

For the reverse implication, let $\xi \in [-1,0].$ Thus, we obtain:

$$\begin{aligned} \mathcal {F}_{\Vert .\Vert }(((1+\xi )K)^n) = |1+\xi | \mathcal {F}_{\Vert .\Vert }(K^n)\le \mathcal {F}_{\Vert .\Vert }(K^n) < \varphi (T^n),\,\, \text{ for } \text{ some } n\ge 1 . \end{aligned}$$

The use of Lemma 5.1 in [7], asserts that:

$$\begin{aligned} T+(1+\xi )K\in \Phi _-(X),\quad \hbox {for}\quad \xi \in [-1,0]. \end{aligned}$$

Hence, we consider the perturbed operator $(T+K)_{1+\xi }^*$ defined by:

$$\begin{aligned} (T+K)_{1+\xi }^*:= (T+(1+\xi ) K)^*:= T^*+(1+\xi ) K^*,\quad \xi \in [-1,0], \end{aligned}$$

which uses to reach the desired result in an analogous way as the second implication in item $\mathbf{(i)}.$ $\square$

Remark 3.1

The result of Lemma 3.1 is an amelioration and an improvement of the results of S. Grabiner [12] to the case of $\Phi$-perturbation function, while for $K\in \mathcal {K}(X)$ (resp. $K \in \mathcal{WC}\mathcal{}(X)$, for X be a Banach space which satisfies the Dunford–Pettis property) which commutes with bounded operator T, we infer that $K^n \in \mathcal {K}(X)$, for some $n \in \mathbb {N}^*$ (resp. $K^2 \in \mathcal {K}(X)$). Thus asserts that $\mathcal {F}_{\Vert .\Vert }(K^n)=0$ (resp. $\mathcal {F}_{\Vert .\Vert }(K^2)=0$) and therefore, $\mathcal {F}_{\Vert .\Vert }(K^n) < \varphi (T^n)=\varphi ((T+K)^n)$ (resp. $\mathcal {F}_{\Vert .\Vert }(K^2) < \varphi (T^2)=\varphi ((T+K)^2)$). Consequently, the use of Lemma 3.1 reveals that:

$$\begin{aligned}&asc(T)<+\infty ~\hbox {if and only if}~ asc(T+K)<+\infty \nonumber \\&desc(T)<+\infty ~ \hbox {if and only if}~ desc(T+K)<+\infty . \end{aligned}$$

$\diamondsuit$

An outstanding tool of the concept of $\Phi$-perturbation function, in the theory of perturbed semi Browder operators is presented in the following theorem.

Theorem 3.1

Let T and K be two commuting bounded operators on X.

Assume that $\mathcal {F}_{\Vert .\Vert }(K^n)<\varphi (T^n),$ for some $n\ge 1.$ Then, we get:

$$\begin{aligned} T\in \mathcal {B}_*(X)\,\,\mathrm{if\; and \;only\; if }\,\,T+K\in \mathcal {B}_*(X), \end{aligned}$$

for $\mathcal {B}_*(X)\in \{\mathcal {B}_+(X),\mathcal {B}_-(X)\}.$ $\diamondsuit$

Proof

The results proved in Lemma 3.1 and [7, Lemma 5.1] allowing us to formulate our desired results. $\square$

Now, we analyze some examples to show how the previous theorem can be implemented. But before, let us mention some fact, for $T\in \mathcal {L}(X)$, as:

$$\begin{aligned} \inf _{N\subset M}\gamma (T/_{ N})>0 \, \,\Longleftrightarrow & {} \, \, T\in \Phi _+(X)\nonumber \\ \inf _{N\supset M}\Vert Q_N T \Vert >0\, \,\Longleftrightarrow & {} \, \, T\in \Phi _-(X)\nonumber \\ \Delta (T)=0\, \,\Longleftrightarrow & {} \, \, T\in \mathcal{SS}\mathcal{}(X)\nonumber \\ \nabla (T)=0 \, \,\Longleftrightarrow & {} \, \, T\in \mathcal{SC}\mathcal{}(X), \end{aligned}$$

where $Q_N$ denotes the quotient map from X onto $X\vert _{N}$, M and N are two infinite codimensional subspaces of X and $\nabla (T) := \displaystyle \sup _{M} \inf _{N\supset M}\Vert Q_N T \Vert$ represents a measure of non strict cosingularity of T (see [7, 20, 40] for more information).

So, the following items illustrate the applicability of the results of Theorem 3.1:

(i) the stability result of upper semi-Browder operator developed in Theorem 3.1 remains true for $X= L_1(\Omega , d\lambda )$, where $(\Omega , \Sigma , \lambda )$ is a positive measure space, $K\in \mathcal{SS}\mathcal{}(L_1(\Omega , d\lambda ))$, T be the identity operator in $L_1(\Omega , d\lambda )$, the $\Phi$-perturbation function $\mathcal {F}_{\Vert .\Vert }$ is nothing else that the measure of non strict singularity $\Delta$ and the $\varphi$ function of T considered as the quantity $\inf _{N\subset M}\gamma (T/_{ N})$, for infinite codimensional subspaces N and M of $L_1(\Omega , d\lambda )$.

In fact, if we take, for a positive measure space $(\Omega , \Sigma , \lambda )$, that $K\in \mathcal{SS}\mathcal{}(L_1(\Omega , d\lambda ))$, $T=I \in \mathcal {B}_+(L_1(\Omega , d\lambda ))$, we get from what proceed that:

$$\begin{aligned} \mathcal {F}_{\Vert .\Vert }(K) = \Delta (K)=0 < \varphi (I) = \inf _{N\subset M}\gamma (I/_{ N})=1. \end{aligned}$$

Therefore, in such descriptive situation, we illustrate the validity of our investigation given in Theorem 3.1 which reproof that $I+K\in \mathcal {B}_+(L_1(\Omega , d\lambda ))$.

(ii) We omit the stability result of lower semi-Browder operator invested in Theorem 3.1 for superprojective space $X= l_p (1<p< \infty )$ or $X= L_p(\Omega , d\lambda ) (1<p \le 2)$ and $(\Omega , \Sigma , \lambda )$ is a positive measure space, introduced in [38], $K\in \mathcal{SS}\mathcal{}(l_p), (1<p< \infty )$ or $K\in \mathcal{SS}\mathcal{}(L_p(\Omega , d\lambda )), (1<p \le 2)$, T be the identity operator in $l_p, (1<p< \infty )$ or $L_p(\Omega , d\lambda ), (1<p \le 2)$, the measure of non strict cosingularity $\nabla$ is considered as an example of the $\Phi$-perturbation function $\mathcal {F}_{\Vert .\Vert }$ and the quantity $\displaystyle \inf _{N\supset M}\Vert Q_N T \Vert$ is nothing else as the $\varphi$ function of T. More precisely, in what follows the stability criterion of lower semi-Browder operator is satisfied in such case as:

$$\begin{aligned} \mathcal {F}_{\Vert .\Vert }(K) = \nabla (K)=0 < \varphi (I) = \inf _{N\supset M}\Vert Q_N I \Vert =1, \end{aligned}$$

while $\mathcal{SS}\mathcal{}(l_p) \subset \mathcal{SC}\mathcal{}(l_p), (1<p< \infty )$ or $\mathcal{SS}\mathcal{}(L_p(\Omega , d\lambda )) \subset \mathcal{SC}\mathcal{}(L_p), (1<p \le 2).$ Hence, we have reproved that $I+K\in \mathcal {B}_-(l_p), (1<p< \infty )$ or $I+K\in \mathcal {B}_-(L_p(\Omega , d\lambda )), (1<p \le 2)$.

Based upon the results of Theorem 3.1, some Browder essential spectra of linear bounded operators may be derived as follows:

Theorem 3.2

Let T and K be two commuting bounded linear operators. For some $n\ge 1,$ we assume that the following assertions hold:

$\mathbf{(i)}$ If there exists $\eta \ge 1$ such that $\mathcal {F}_{\Vert .\Vert }(K^n)<\varphi ((\nu I-T)^n),$ for all $\nu \in \rho _*(T)$ with $\mathbf{d}(\nu , \sigma _{eb}^*(T))> \eta$. Then, we get:

$$\begin{aligned} \sigma _{eb}^*(T+K)\subset \sigma _{eb}^*(T)\cup \{\nu :\, \, \mathbf{d}(\nu , \sigma _{eb}^*(T))\le \eta \} . \end{aligned}$$

$\mathbf{(ii)}$ If there exists $\eta \ge 1$ such that $\mathcal {F}_{\Vert .\Vert }(K^n)<\varphi ((\nu I-T-K)^n),$ for all $\nu \in \rho _*(T+K)$ with $\mathbf{d}(\nu , \sigma _{eb}^*(T+K))> \eta$. Then, we get:

$$\begin{aligned} \sigma _{eb}^*(T)\subset \sigma _{eb}^*(T+K)\cup \{\nu :\, \, \mathbf{d}(\nu , \sigma _{eb}^*(T+K))\le \eta \} , \end{aligned}$$

where $(\rho _*(.), \sigma _{eb}^*(.)) \in \{(\rho _{ap}(.), \sigma _{eb}^+(.)),\, (\rho _{\delta }(.), \sigma _{eb}^-(.)) \}$. $\diamondsuit$

Proof

$\mathbf{(i)}$ Let $\xi \notin \sigma _{eb}^*(T)\cup \{\nu :\, \mathbf{d}(\nu , \sigma _{eb}^*(T))\le \eta \}.$ Then, there exists $\eta \ge 0$ such that for such $\xi \in \rho _*(T),$ we have $\mathbf{d}(\xi , \sigma _{eb}^*(T))>\eta$ and $\xi I-T\in \mathcal {B}_*(X).$ According with the assumption for such $\xi \in \rho _*(T),$ that:

$$\begin{aligned} \mathcal {F}_{\Vert .\Vert }(K^n)<\varphi ((\xi I-T)^n), \end{aligned}$$

we conclude from Theorem 3.1, that:

$$\begin{aligned} \xi I-T-K\in \mathcal {B}_*(X), \end{aligned}$$

for $(\rho _*(.), \sigma _{eb}^*(.), \mathcal {B}_*(X))\in \{(\rho _{ap}(.), \sigma _{eb}^+(.), \mathcal {B}_+(X)), (\rho _{\delta }(.), \sigma _{eb}^-(.), \mathcal {B}_-(X))\}.$

$\mathbf{(ii)}$ This assertion can be proved in the same ways as the first item. $\square$

As an immediate consequence of Theorem 3.1, we derive the stability result for the Browder operator via $\Phi$-perturbation function.

Corollary 3.1

Let T and K be two commuting bounded operators on X. Assume that:

$$\begin{aligned} \mathcal {F}_{\Vert .\Vert }(K^n)<\varphi (T^n),\mathrm{for\; some\; } n\ge 1. \end{aligned}$$

Then, we have:

$$\begin{aligned} T\in \mathcal {B}(X)\,\,\mathrm{if \;and\; only\; if }\,\,T+K\in \mathcal {B}(X). \qquad \qquad \qquad \qquad \qquad \qquad \diamondsuit \end{aligned}$$

Remark 3.2

It should be noted that all the results of the present paper remain valid in view of the concept of measures of non strict singularity or non strict cosingularity. $\diamondsuit$

Let $T\in \mathcal {L}(X).$ We define:

$$\begin{aligned} r_e(T) := \displaystyle \lim _{n \longrightarrow +\infty }( \mathcal {F}_{\Vert .\Vert }(T^n))^{\frac{1}{n}} \end{aligned}$$

and

$$\begin{aligned} r_{\varphi }(T) := \displaystyle \lim _{n \longrightarrow +\infty }\varphi (T^n)^{\frac{1}{n}},\quad \hbox {for}\quad 0\notin \{\sigma _{ef}^+(T), \sigma _{ef}^-(T)\}, \end{aligned}$$

where:

• the existence of those limits are referred to Theorem 2.17 in [20] and Lemma 1.21 in [23],

• the complemented in $\mathbb {C}$ of $\Phi _{T}(X)$ defines the essential spectrum of T, denoted by $\sigma _{ef}(T)$,

• $r_e(T)$ express the radius of the essential spectrum $\sigma _{ef}(T)$ as:

  $$\begin{aligned} r_e(T) := \sup \{ \vert \xi \vert , \, \, \xi \in \sigma _{ef}(T)\}. \end{aligned}$$

We point out that the above quantity are extremely useful to locate the eigenvalues of the Browder essential spectrum as follows.

Lemma 3.2

Let T be a bounded operator on X such that $0\notin \{\sigma _{ef}^+(T), \sigma _{ef}^-(T)\}.$ Then, we obtain:

$$\begin{aligned} r_e(T) < r_{\varphi }(T)\Longrightarrow \sigma _{eb}(T)\subseteq \overline{\mathbb {D}}\Bigl (0, r_{\varphi }(T)^{-1}r_e(T)\Bigl ). \end{aligned}$$

$\diamondsuit$

Proof

Assume that $r_e(T) < r_{\varphi }(T)$ and consider $\xi \notin \overline{\mathbb {D}}\Bigl (0, r_{\varphi }(T)^{-1}r_e(T)\Bigl )$. Thus, one has $|\xi | > r_{\varphi }(T)^{-1}r_e(T),$ we infer that there exists $n\in \mathbb {N}^*$ for which $|\xi |>(\varphi (I)^{-\frac{1}{n}})(\mathcal {F}_{\Vert .\Vert }(T^n))^{\frac{1}{n}}.$ This means that there exists $n\in \mathbb {N}^*$ such that $\varphi (I)>\mathcal {F}_{\Vert .\Vert }((\frac{T}{\xi })^n).$ Keeping into account from Corollary 3.1, we conclude that:

$$\begin{aligned} \xi I-T := \xi (I-\frac{T}{\xi }) \in \mathcal {B}(X). \end{aligned}$$

Therefore, we prove the requested analysis of the Browder essential spectrum of the operator T. $\square$

4 Characterization of Browder’s essential spectra via $\Phi$-perturbation function

The goal of this section is to describe the Browder’s essential approximate point spectrum, the Browder’s essential defect spectrum and the Browder’s essential spectrum of linear bounded operator involving the concept of $\Phi$-perturbation function as generalization of some works provided in the literature.

Theorem 4.1

Let $T\in \mathcal {L}(X)$ and $n\in \mathbb {N}^*$. Then:

$\mathbf{(i)}$ $\sigma _{eb}^+(T)\subset \displaystyle \bigcap _{K\in \mathcal {E}^n(X),\,KT=TK}\sigma _{ap}(T+K),$

where, the subset $\mathcal {E}^n(X)$ is defined as:

$$\begin{aligned} \mathcal {E}^n(X):= \left\{ \begin{array}{l} K\in \mathcal {L}(X): \hbox { there exists}\ \eta \ge 0 \, \hbox {such that:}\ \\ \mathbf{d}(\nu , \sigma _{eb}^+(T+K))>\eta \ \hbox {and}\ \, \mathcal {F}_{\Vert .\Vert }(K^n)< \varphi ((\nu I -T-K)^n) ,\\ \quad \forall \nu \in \rho _{ap}(T+K). \end{array}\right. \end{aligned}$$

$\mathbf{(ii)}$ $\sigma _{eb}^-(T)\subset \displaystyle \bigcap _{K\in \widetilde{\mathcal {E}}^n(X),\,KT=TK}\sigma _{\delta }(T+K),$

where the subset $\widetilde{\mathcal {E}}^n(X)$ is defined as:

$$\begin{aligned} \widetilde{\mathcal {E}}^n(X):= \left\{ \begin{array}{l} K\in \mathcal {L}(X): \hbox { there exists}\ \eta \ge 0 \, \hbox {such that:}\ \\ \mathbf{d}(\nu , \sigma _{eb}^-(T+K))> \eta \ \hbox {and}\ \, \mathcal {F}_{\Vert .\Vert }(K^n)< \varphi ((\nu I -T-K)^n),\\ \quad ~\forall \nu \in \rho _{\delta }(T+K). \end{array}\right. \qquad \qquad \, \diamondsuit \end{aligned}$$

Proof

$\mathbf{(i)}$ Let $\xi \notin \bigcap \{\sigma _{ap}(T+K),\,\, K\in \mathcal {E}^n(X),\, \, KT=TK\},$ then there exists $K\in \mathcal {E}^n(X)$ which commuting with T and satisfy:

$$\begin{aligned} \inf _{\Vert x\Vert =1,x\in \mathcal {D}(T)}\Vert (\xi I-T-K)x\Vert >0. \end{aligned}$$

Thus, according to Theorem 2.1 in [25], we get $\xi I-T-K\in \Phi _+(X)$ with $i(\xi I-T-K)\le 0$ and $asc(\xi I-T-K)<\infty .$ While $\mathcal {F}_{\Vert .\Vert }(K^n)<\varphi ((\mu I-T-K)^n),$ for such $\xi \in \rho _{ap}(T+K)$ and $K\in \mathcal {E}^n(X),$ the use of Theorem 3.1 asserts that $\xi I-T-K+K=\xi I-T\in \mathcal {B}_+(X).$

$\mathbf{(ii)}$ Let $\xi \notin \bigcap \left\{ \sigma _\delta (T+K),\,\, K\in \widetilde{\mathcal {E}}^n(X),\, \, KT=TK\right\} ,$ then there exists $\widetilde{K}\in \widetilde{\mathcal {E}}^n(X)$ such that $T\widetilde{K}=\widetilde{K}T$ and $\xi I-T-\widetilde{K}$ is surjective. Hence, we obtain that $\xi I-T-\widetilde{K}\in \Phi _-(X)$ with $i(\xi I-T-\widetilde{K})=\alpha (\xi I-T-\widetilde{K})\ge 0$ and $desc(\xi I-T-\widetilde{K})=0.$ Therefore, we deduce from Theorem 3.1 with the fact that $\widetilde{K}\in \widetilde{\mathcal {E}}^n(X),$ that $\xi I-T\in \mathcal {B}_-(X),$ for $\xi \in \rho _{\delta }(T+\widetilde{K}).$ $\square$

To state the characterization of the Browder’s essential spectrum involving the concept of $\Phi$-perturbation function, we will proceed firstly to show the link between a $\Phi$-perturbation function and Browder’s operators.

Proposition 4.1

Let T be an invertible operator on X and K is bounded linear operator on X, such that:

(i) $TK=KT$,

(ii) $\mathcal {F}_{\Vert .\Vert }(KT^{-1})<\varphi (I)$. Then, we get:

$$\begin{aligned} T+K\in \mathcal {B}_*(X),\ \hbox { where }\ \, \mathcal {B}_*(X) \in \{ \mathcal {B}_+(X), \mathcal {B}_-(X), \mathcal {B}(X)\}. \qquad \qquad \qquad \qquad \qquad \qquad \diamondsuit \end{aligned}$$

Proof

The proof is based on the following expression of the operator $T+K$, while $0\in \rho (T)$:

$$\begin{aligned} T+K = (I+KT^{-1})T. \end{aligned}$$

(4.1)

By virtue $\mathcal {F}_{\Vert .\Vert }(KT^{-1})<\varphi (I)$ for commuting operators T and K, we conclude thanks to Theorem 3.1, that:

$$\begin{aligned} I+KT^{-1} \in \mathcal {B}_*(X), \, \, \hbox {for }\ \, \, \mathcal {B}_*(X)\in \{\mathcal {B}_+(X), \mathcal {B}_-(X)\}. \end{aligned}$$

That is $I+KT^{-1} \in \Phi (X)$ with $i(I+KT^{-1})=0.$

Therefore, one has $T\in \Phi _*(X)$, the use of Theorems 16.5 and 16.12 in [23] and Eq. (4.1), implies that:

$$\begin{aligned} T+K \in \Phi _*(X)\ \,\hbox { with }\ \, i( T+K )= & {} i(I+KT^{-1}) + i(T)\\= & {} 0,\ \hbox {for}\ \Phi _*(X) \in \{\Phi _+(X), \Phi _-(X)\}. \end{aligned}$$

Consequently,

$$\begin{aligned} T+K \in \Phi _*(X)\ \, \, \hbox { with }\ \, \, \alpha ( T+K ) = \beta (T+K)<\infty . \end{aligned}$$

(4.2)

Thus, to reach the result for the semi-Browder operators, it remains to show further that:

$$\begin{aligned} asc(T+K)< \infty \ \, \, \ \hbox {and}\ \, \, desc(T+K)<\infty . \end{aligned}$$

In fact, for every $n \in \mathbb {N}$, we have:

$$\begin{aligned} (T+K)^n= & {} (I+KT^{-1})^nT^n \\= & {} T^n(I+KT^{-1})^n. \end{aligned}$$

As $T^n$ is one to one, for every $n \in \mathbb {N}$, we infer that:

$$\begin{aligned} \mathcal {N}((T+K)^n)\subset \mathcal {N}((I+KT^{-1})^n). \end{aligned}$$

Thus,

$$\begin{aligned} \alpha ((T+K)^n) \le \alpha ((I+KT^{-1})^n). \end{aligned}$$

Taking into account from Lemma 1 in [8] and Theorem 3.1, we infer that:

$$\begin{aligned} \alpha ((T+K)^n) \le asc(I+KT^{-1})\alpha (I+KT^{-1})<\infty ,\ \, \hbox { for every }\ n\in \mathbb {N}. \end{aligned}$$

Hence, we obtain $asc(T+K)< \infty$, which yields $T+K\in \mathcal {B}_+(X).$

Therefore, $desc(T+K)<\infty$, by virtue of Theorem 4.5-(c) in [32] and Eq. (4.2).

Consequently, the desired result for Browder’s operator follows immediately. $\square$

Before moving to the characterization of the Browder spectrum, the following key notations will be required:

$$\begin{aligned} \Theta (X):= & {} \left\{ K\in \mathcal {L}(X): KT=TK,\, \, \mathcal {F}_{\Vert .\Vert }(K(\nu I-T-K)^{-1})< \varphi (I),\, \, \, \forall \nu \in \rho (T+K) \right\} \\ \text{ and } \\ \widetilde{\Theta }(X):= & {} \left\{ K\in \mathcal {L}(X): KT=TK,\, \, \mathcal {F}_{\Vert .\Vert }((\nu I-T-K)^{-1}K) < \varphi (I),\, \, \, \forall \nu \in \rho (T+K) \right\} . \end{aligned}$$

Theorem 4.2

Let $T\in \mathcal {L}(X).$ Then, we get:

$$\begin{aligned} \sigma _{eb}(T):= & {} \displaystyle \bigcap \left\{ \sigma (T+K),\, K\in \Theta (X) \right\} \\:= & {} \displaystyle \bigcap \left\{ \sigma (T+K),\, K\in \widetilde{\Theta }(X) \right\} . \end{aligned}$$

$\diamondsuit$

Proof

The direct inclusion may be obvious since all compact operator K which commutes with T stills an operator of the subset $\Theta (X)\,(\text{ resp. }\ \widetilde{\Theta }(X))$. For this argument, we may easily observe that:

$$\begin{aligned}&\displaystyle \bigcap \{\sigma (T+K), \, {K\in \Theta (X)}\} \subset \displaystyle \bigcap \{\sigma (T+K),\, \, K \in \mathcal {K}(X) \ \hbox {with}\ KT=TK\} =\sigma _{eb}(T) \\&\quad (\text{ resp. } \ \displaystyle \bigcap \{\sigma (T+K), \, {K\in \widetilde{\Theta }(X)}\} \subset \sigma _{eb}(T)). \end{aligned}$$

For the reverse inclusion, assume that $\xi \notin \displaystyle \bigcap \{\sigma (T+K), K\in \Theta (X)\}\,(\text{ resp. } \ \displaystyle \bigcap \{\sigma (T+K), K\in \widetilde{\Theta }(X) \}).$ Then, there exists $K\in \Theta (X)\,(\text{ resp. } \ \widetilde{\Theta }(X))$ such that $\xi \in \rho (T+K).$

Thus, for such $\xi \in \rho (T+K)$, we have:

$$\begin{aligned} \mathcal {F}_{\Vert .\Vert }(K(\xi I-T-K)^{-1})< \varphi (I)\,\,\,(\text{ resp. } \ \mathcal {F}_{\Vert .\Vert }((\xi I-T-K)^{-1}K) < \varphi (I)). \end{aligned}$$

On the other hand, we infer from the fact $KT=TK$ that K commutes with $\xi I-T-K$. Therefore, Proposition 4.1 asserts that:

$$\begin{aligned} \xi I-T-K+K=\xi I-T\in \mathcal {B}(X), \end{aligned}$$

so, $\xi \notin \sigma _{eb}(T)$ and the required statement follows. $\square$

Remark 4.1

$\mathbf{(i)}$ Theorem 4.1 and 4.2 may be regarded as an improvement and generalization of the results of V. Rako$\check{\text {c}}$evi$\acute{\text {c}}$ in [25, 26] to the concept of $\Phi$-perturbation function.

$\mathbf{(ii)}$ It should be noted that the result of Theorem 4.2 covered the characterization of the Weyl spectrum of T. Also, the class of compact (resp. weakly compact) operators remains as an illustrative example of this kind of Browder’s essential spectra characterization of linear bounded operator. $\diamondsuit$

Conclusion: The main focus of this work is based on the notion of $\Phi$-perturbation function. Such concept of perturbation has played a central role throughout the history of modern spectral theory. Particularly, this notion of perturbation appears as a new line in the spectral analysis problems likewise: in the study of the stability analysis of perturbed linear operators and the characterization problem of linear bounded operators. More precisely, the main objective of this paper is to exhibit the importance of the use of the notion of $\Phi$-perturbation function to outline a new approach in the analysis of the stability problems of lower (resp. upper)-semi Browder and Browder operators. Therefore, the obtained stability results of some sets of Browder operators play a significant role in the spectral description of some corresponding sets of essential spectra. So, our invested analysis appears to achieve some progress in the theory of Browder operators and fulfill a substantial contribution to earlier works.