Real-time detection of lines using parallel coordinates and CUDA

Abstract

The Hough transform is a well-known and popular algorithm for detecting lines in raster images. The standard Hough transform is rather slow to be usable in real time, so different accelerated and approximated algorithms exist. This study proposes a modified accumulation scheme for the Hough transform, using a new parameterization of lines “PClines”. This algorithm is suitable for computer systems with a small but fast read-write memory, such as today’s graphics processors. The algorithm requires no floating-point computations or goniometric functions. This makes it suitable for special and low-power processors and special-purpose chips. The proposed algorithm is evaluated both on synthetic binary images and on complex real-world photos of high resolutions. The results show that using today’s commodity graphics chips, the Hough transform can be computed at interactive frame rates, even with a high resolution of the Hough space and with the Hough transform fully computed.

1 Introduction

The Hough transform is a well-known tool for detecting shapes and objects in raster images. Originally, Hough [11] defined the transformation for detecting lines; later it was extended for more complex shapes, such as circles, ellipses, etc., and even generalized for arbitrary patterns [2].

When used for detecting lines in 2D raster images, the Hough transform is defined by a parameterization of lines: each line is described by two parameters. The input image is preprocessed and for each pixel which is likely to belong to a line, voting accumulators corresponding to lines which could be coincident with the pixel are increased. Next, the accumulators in the parameter space are searched for local maxima above a given threshold; such accumulators correspond to likely lines in the original image. The Hough transform was formalized by Princen et al. [20] and described as an hypothesis testing process.

The following section reviews existing parameterizations of lines suitable for a fast and/or precise detection of lines. Also, different acceleration approaches are mentioned as the background of the work to be presented here.

The classical Hough transform (based on any parameterization) has some advantages over the accelerated and approximated methods (it does not introduce any further detection error and it has a low number of parameters and, therefore, usually requires less detailed application-specific fine-tuning). This makes the real-time implementation of the Hough transform desirable. This study presents an algorithm for real-time detection of lines based on the PClines parameterization of lines.

The algorithm proposed in this study uses a modified strategy for accumulating the votes in the array of accumulators in the Hough space. The strategy was designed to meet the nature of today’s graphics chips (GPUs) and other special-purpose computational platforms. The implementation achieves real-time performance at executing the “full” Hough transform on the GPU.

The PClines parameterization is reviewed in Sect. 3. The modified HT accumulation algorithm is presented in Sect. 4 of the paper. Section 5 presents the experiments comparing the commonly used variant of the Hough transform with the implementation of the algorithm run on a GPU. The results show that the GPU implementation based on PClines achieves such a performance which allows running the Hough transform with a high-resolution accumulator space in real time. Section 6 concludes the study and proposes directions for future work.

2 Background

Hough [11] parameterized the lines by their slope and y-axis intercept. Using this parameterization, the Hough space must be infinite and the same is true for any point-to-line mapping (PTLM) where a point in the source image corresponds to a line in the Hough space, and a point in the Hough space represents a line in the x–y image space [3]. However, for any PTLM, a complementary PTLM can be found so that the two mappings define two finite Hough spaces containing all lines possible in the x–y image space. Some naturally bounded parameterizations exist, such as the very popular $\theta{-}\varrho$ parameterization introduced by Duda and Hart [7], which is based on the line equation in the normal form. Other bounded parameterizations were introduced by Wallace [26], Natterer [15], Eckhardt and Maderlechner [8]. As the line’s parameters, intersections with a bounding rectangle or circle were used, together with angles defined by these intersections and the input point.

The majority of currently used implementations seem to be using the $\theta{-}\varrho$ parameterization [7]—for example, the well-known OpenCV library¹ implements several variants of line detectors based on the $\theta{-}\varrho$ parameterization and none other. In this parameterization, for each input pixel, a sinusoid curve must be rasterized which makes this method very computationally complex and not suitable for GPU implementation (especially without GP-GPU capabilities such as CUDA or OpenCL). That is why several research groups invested great effort to deal with these undesirable properties. Different methods focus on special data structures, non-uniform resolution of the accumulation array or special rules for picking points from the input image.

O’Rourke and Sloan [18] developed two special data structures: dynamically quantized spaces (DQS) [17] and dynamically quantized pyramid (DQP) [17]. Both these methods use splitting and merging cells of the space represented as a binary tree, or possibly a quadtree. After processing the whole image, each cell contains approximately the same number of votes; this leads to a higher resolution of the Hough space of accumulators at locations around the peaks.

A typical method using special picking rules is the Randomized Hough Transform (RHT) [27]. This method is based on the idea that each point in an n-dimensional Hough space of parameters can be exactly defined by an n-tuple of points from the input raster image. Instead of accumulation of a hypersurface in the Hough space for each point, n points are randomly picked and the corresponding accumulator in the parameter space is increased. The advantages of this approach are mostly its rapid speedup and small storage. Unfortunately, when detecting lines in a noisy input image, the probability of picking two points from the same line is small, decreasing the probability of finding the true line.

Another approach based on repartitioning the Hough space is represented by the Fast Hough Transform (FHT) [14]. The algorithm assumes that each edge point in the input image defines a hyperplane in the parameter space. These hyperplanes recursively divide the space into hypercubes and perform the Hough transform only on the hypercubes with votes exceeding a selected threshold. This approach reduces both the computational load and the storage requirements.

Using principal axis analysis for line detection was discussed by Rau and Chen [21]. Using this method for line detection, the parameters are first transferred to a one-dimensional angle-count histogram. After transformation, the dominant distribution of image features is analyzed, with searching priority in peak detection set according to the principal axis.

The Hough transform also provides space for parallel implementations using special hardware such as a distributed memory multiprocessor [25], graphics hardware [24], pyramid multiprocessors [1] or reconfigurable architectures [19].

Recently, Dubská et al. [6] presented PClines—a new parameterization of lines based on parallel coordinates. Since this parameterization and the parallel coordinates are not common knowledge, we will give a detailed description of that parameterization (which is fundamental for the algorithm presented in this study) in the following section.

3 PClines: line detection using parallel coordinates

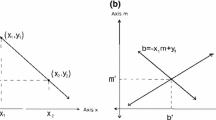
Parallel coordinates (PC) were invented in 1885 by d'Ocagne [4] and they were further studied and popularized by Inselberg [12]. The coordinate system used for representing geometric primitives in parallel coordinates is defined by mutually parallel axes. Each N-dimensional vector is represented by (N − 1) lines connecting the axes (see Fig. 1). In this text, we will be using an Euclidean plane with a u–v Cartesian coordinate system to define positions of points in the space of parallel coordinates. For defining these points, a notation ${(u,v,w)_{\mathbb{P}^2}}$ will be used for homogeneous coordinates in the projective space ${\mathbb{P}^2}$ and ${(u,v)_{\mathbb{E}^2}}$ will be used for Cartesian coordinates in the Euclidean space ${\mathbb{E}^2. }$

Fig. 1

Representation of a 5-dimensional vector in parallel coordinates. The vector is represented by its coordinates C ₁,..., C ₅ on axes x ^′₁ ,..., x ^′₅ , connected by a complete polyline (composed of 4 infinite lines)

In the two-dimensional case, points in the x–y space are represented as lines in the space of parallel coordinates. Representations of collinear points intersect at one point—the representation of a line (see Fig. 2).

Fig. 2

Three collinear points in parallel coordinates: (left) Cartesian space and (right) space of parallel coordinates. Line ℓ is represented by point $\overline{\ell}$ in parallel coordinates

Based on this relationship, it is possible to define a point-to-line mapping between the original x–y space and the space of parallel coordinates. For some cases, such as line $\ell:y=x,$ the corresponding point $\overline{\ell}$ in the parallel coordinates lies in infinity (it is an ideal point) and the points on this line are represented by the parallel horizontal lines. Projective space ${\mathbb{P}^2}$ (contrary to the Euclidean ${\mathbb{E}^2}$ space) provides coordinates for these special cases. A relationship between line $\ell: ax+by+c=0$ (denoted as [a, b, c]) in cartesian coordinates and its representing point $\overline{\ell}$ in parallel coordinates can be defined by mapping:

$$ \ell: [a, b, c] \to \overline{\ell}:(db,-c,a+b)_{{\mathbb{P}}^2}, $$

(1)

where d is the distance between parallel axes x′ and y′.

3.1 Parameterization “PClines” for line detection

This section gives an overview of the “PClines” parameterization introduced by Dubská et al. [6]. The text is kept very concise; for more information, the original paper should be consulted. In the following text, we will use the intuitive slope–intercept line equation $\ell: y = mx + b,$ where m defines the slope of the line and b the y-coordinate of an intersection between the line and y-axis. Using this parameterization, the corresponding point $\overline{\ell}$ in the parallel space has coordinates ${( d ,b,1-m)_{\mathbb{P}^2}. }$ The line’s representation $\overline{\ell}$ is between the axes x′ and y′ if and only if the slope is negative, i.e., $-\infty<m<0.$ For $m = 1, \overline{\ell}$ is an ideal point (a point in infinity). For horizontal lines (m = 0), $\overline{\ell}$ lies on the y′-axis, and for vertical lines ($m=\pm\infty$), $\overline{\ell}$ lies on the x′-axis. The system defined by parallel axes x′, y′ is further referred as straight ($\mathcal{S}$) space.

The representations of the lines with a positive slope lie in an infinite area outside the space between axes x′, y′. To enclose also these representations to a finite part, we propose a twisted ($\mathcal{T}$) system x′,  −y′, which is identical to the straight space, except that the y′-axis is inverted. In the twisted space, $\overline{\ell}$ is between the axes x′ and −y′ if and only if $0<m<\infty.$ By combining the straight and twisted spaces, the whole $\mathcal{TS}$ plane can be constructed, as shown in Fig. 3.

Fig. 3

Left Original x–y space and right its PClines representation, the corresponding $\mathcal{TS}$ space. Another example of the $\mathcal{TS}$ space can be found in Fig. 14

Figure 3 (left view) shows the original x–y image with three points A, B, and C and three lines $\ell_1, \ell_2,$ and $\ell_3$ coincident with the points. The origin of x–y is placed into the middle of the image for the convenience of the figures and the right view depicts the corresponding $\mathcal{TS}$ space. It should be noted that a finite part of the u–v plane sufficient for representing all possible lines in the bordered input image is defined as follows:

$$ \begin{aligned} -d \leq u \leq& d ,\\ -{\rm max}\left(\frac{W}{2}, \frac{H}{2}\right) &\leq v \leq& {\rm max}\left(\frac{W}{2}, \frac{H}{2}\right) , \end{aligned} $$

(2)

where W and H are the width and height of the input raster image, respectively.

Any line $\ell:y=mx+b$ is now represented either by point ${\overline{\ell}_{\mathcal{S}}}$ in the straight space or by ${\overline{\ell}_{\mathcal{T}}}$ in the twisted space of the u–v plane:

$$ \begin{aligned} \overline{\ell}_{{\mathcal{S}}} &=&(d,b,1-m)_{{\mathbb{P}}^2},\quad-\infty \leq m \leq 0, \\ \overline{\ell}_{{\mathcal{T}}} &=& (-d,-b,1+m)_{{\mathbb{P}}^2},\quad 0 \leq m \leq \infty . \end{aligned} $$

(3)

Consequently, any line $\ell$ has exactly one image $\overline{\ell}$ in the $\mathcal{TS}$ space; except for cases that m = 0 and $m=\pm\infty,$ when $\overline{\ell}$ lies in both spaces either on y′- or x′-axis. That allows the $\mathcal{T}$ and $\mathcal{S}$ spaces to be “attached” one to another. Figure 3 illustrates the spaces attached along the x′-axis. Attaching also the y′- and −y′-axes results in an enclosed Mobius strip.

Equation (3) defines line-to-point mapping which can be used as a parameterization for the Hough transform. In this case, the $\mathcal{TS}$ space is used as an accumulator space, as depicted in Algorithm 1.

The space $\mathcal{TS}$ is discretized directly according to Eq.(2); other discretizations—denser or sparser—would be possible by just linearly mapping the u and v coordinates used in the algorithm. The condition used in step 3 is application specific and it typically involves an edge detection operator and thresholding. The lines rasterized in steps 4 and 5, in fact, constitute a two-segment polyline defined by three points: $(-d,-y), (0,x), (d,y),$ where $(-d,-y)$ and (0, x) are vertices of the line accumulated in the $\mathcal{T}$ half and (0, x) and (d,  y) are vertices of the line accumulated in the $\mathcal{S}$ half. Step 8 scans the space of accumulators S for local maxima above a given threshold—this is a standard Hough transform step. The line’s parameters m–b are computed by the functions m(u) and b(u, v) based on the u and v coordinates of the point in the $\mathcal{TS}$ space using Eq. (1); any other parameterization of lines can be the output of the algorithm.

Step 8 of the pseudocode looks for local maxima above a given threshold in the $\mathcal{TS}$ space. Usually, a small neighborhood ($3\times3, 5\times5$ or $7\times7$ in cases of high resolution of the Hough space) is used for detecting the local maxima. The accumulator value must be above a given threshold to be considered for a “high local maxima”. The threshold is another input parameter of the algorithm, but since it does not influence the algorithm’s structure, it is used silently by step 8 for simplicity of the algorithmic notation.

4 Real-time line detection algorithm using PClines and CUDA

The key characteristic of Algorithm 1 in the previous section is that steps 4 and 5 must rasterize the lines in the $\mathcal{T}$ and $\mathcal{S}$ spaces (or the half-period of the sinus curve in the case of the $\theta{-}\varrho$ parameterization) and increment the corresponding accumulators in the Hough space. In some systems, such a large random-access read-write memory might be expensive or even not available at all.

This section presents an algorithm that overcomes this limitation and which is suitable for graphics processors and other special-purpose or embedded systems. It builds upon an algorithm recently published by the authors of this article [13]. The principle of these algorithms can work with other line parameterizations as well.

4.1 Hough transform on a small read-write memory of accumulators

The classical Hough transform accesses sparsely a relatively large amount of memory. This behavior can diminish the effect of caching. On CUDA and similar architectures, this effect is even more significant, as the global memory is not cached. To achieve real-time performance, the memory requirements must be limited to the shared memory of a multiprocessor (typically 16 kB).

Algorithm 2 shows the modified Hough transform accumulation procedure. The key difference from Algorithm 1 is the actual size of the Hough space actively used at a time. The new algorithm stores only $n \times (v_{\rm max}-v_{\rm min})$ accumulators, where n is the neighborhood size required for the maxima detection. Values $v_{min}$ and $v_{max}$ define the discretization of the Hough space (or more precisely $\mathcal{TS}$ space) in the vertical v dimension (2); $v_{max} - v_{min}$ is the resolution in this dimension. The borders in the horizontal dimension u are 1 and u _max.

First, the detected edges are stored in a set P (line 1). Then, first n columns of the Hough space are computed by lines 2–7. The memory necessary for containing the n columns is all the read-write random-access memory required by the algorithm, and even for high resolutions of the Hough space, the buffer of n columns fits easily in the shared memory of the GPU multiprocessors.

S(u, v) is the discretized accumulator space – a buffer which is zeroed (lines 2 and 14), incremented (lines 5 and 16) and searched for maxima (line 10). Function v(u, x, y) computes the v coordinate based on the u coordinate and the point to be accumulated (x, y):

$$ \begin{aligned} u \in {\mathcal{T}}, v(u,x,y) = \frac{(x - y)u}{u_{\rm max}/2} + y ,\\ u \in {\mathcal{S}}, v(u,x,y) = \frac{(y - x)u}{u_{\rm max}/2} + x , \end{aligned} $$

(4)

In the main loop (lines 9–18), for every column of the Hough space, the maxima are detected (line 10), the accumulated neighborhood is shifted by one column (lines 11–13), and a new column is accumulated (lines 14–17); please refer to Fig. 4 for an illustration of the algorithm. Thus, only the buffer of n columns is being reused. The memory shift can be implemented using a circular buffer of lines to avoid data copying. Also, in the actual implementation, pixels of one column follow each other in the memory; this can be viewed as if the image was transposed.

Fig. 4

Illustration of Algorithm 2. The gray rectangle represents the buffer of n columns. For column 4, the above-threshold maxima are detected in each step within the buffer. Then, the column 7 values are accumulated into the buffer, using the space of column 2, which will not be needed in future processing

In the pseudocode, maxima are not detected at the edges of the Hough space (i.e., when $u\in\{1,\dots,{\lceil\frac{n}{2}\rceil}\}\cup\{u_{\rm max} -{\lceil\frac{n}{2}\rceil},\ldots,u_{\rm max}\}$). Eventual handling of the maxima detection at the edge of the Hough space does not change the algorithm structure, but it would unnecessarily complicate the pseudocode. Two solutions exist—either copying the border data or rasterizing necessary parts of the lines outside the Hough space. Both approaches perform similarly and their implementation is straightforward.

On CUDA, the threads in a block can be used for processing the set of edges P (lines 15–17 and 4–6) in parallel, using an atomic increment of the shared memory so as to avoid read-write collisions. To use all the multiprocessors of the GPU, the loop on line 9 is broken to a number (e.g., 90 is suitable for current NVIDIA GeForce graphics chips) of sub-loops processed by individual blocks of threads.

The algorithm as described above uses exactly $n \times (v_{\rm max}-v_{\rm min})$ memory cells, typically 16-bit integer values. In cases where the runtime system has a higher amount of fast random-access read-write memory, this memory can be used fully; instead of accumulating one column of the Hough space (lines 15–17 of the algorithm), several columns are processed at a time, and more than one column is searched for maxima by line 10. This leads to a further speedup by reducing the number of steps carried out by the loop over u (line 9).

4.2 Harnessing the edge orientation

O’Gorman and Clowes [16] came up with the idea not to accumulate values for each $\theta,$ but just one value instead. The appropriate $\theta$ for a point can be obtained from the gradient of the detected edge which contains this point [22]. The u position of the corresponding place in the $\mathcal{TS}$ space, where d is distance between axes y and x (−y and x), is linked with $\theta:$

$$ u = \frac{d}{-\ {\rm sgn}\,(\pi/2 - \theta) - {\rm arctan}\,(\theta)} $$

(5)

so an identical approach can be taken in the case of the PClines parameterization.

One common way to calculate the local gradient direction of the image intensity is using the Sobel operator. Sobel kernels for convolution are as follows: $S_x = [1,2,1]^T \cdot [1, 0, -1]$ and $S_y = [1, 0, -1]^T \cdot [1, 2, 1].$ Using these convolution kernels, two gradient values G _x and G _y can be obtained for any discrete location in the input image. Based on these, the gradient’s direction is $\theta = {\rm arctan}\,(G_y/G_x).$ The line’s inclination in the slope–intercept parameterization m–b is related to $\theta:$

$$ m = -\tan\frac{1}{\theta}. $$

(6)

The slope m of line $\ell$ defines the u coordinate of the line’s image $\overline{\ell}$ in the $\mathcal{TS}$ space: $u = d/(1-m)$ for $\mathcal{S}$ space and $u = -d/(1+m)$ for $\mathcal{T}$ space. When $\overline{\ell}$ is in the $\mathcal{S}$ space,

$$ u_{{\mathcal{S}}} = d\frac{1}{1-m} = d\frac{1}{1 + \tan\theta^{-1}} = d\frac{G_y}{G_y + G_x} $$

(7)

and similarly in the $\mathcal{T}$ space

$$ u_{{\mathcal{T}}} = d\frac{G_y}{-G_y + G_x}. $$

(8)

The u coordinate can be expressed independently of the location of $\overline{\ell}$ as

$$u=d\frac{G_{y}}{({\hbox{sgn}\,G_{y}})\,( {\hbox{sgn}\;G_{x} })G_{y}+G_{x}}.$$

(9)

It should be noted that contrary to the “standard” $\theta{-}\varrho$ parameterization, no goniometric operation is needed to compute the horizontal position of the ideal gradient in the accumulator space. To avoid errors caused by noise and the discrete nature of the input image, accumulators within a suitable interval $\langle u-r,\,u+r\rangle$ around the calculated angle (or more precisely u position) are also incremented. This unfortunately introduces a new parameter of the method—radius r. However, experiments show that neither the robustness nor the speed is affected notably by the selection of r.

The dependency of u on $\theta$ is not linear and thus the radius width should vary for different u. However, the sensitivity of the algorithm to the radius is very low and the dependency is “close to linear” (see Fig. 5), so in practice, we set a constant “radius” in the u coordinate in the same way it is set for $\theta$—experiments show that this does not cause any measurable error.

Fig. 5

Dependency of u on θ: non-linear, but close to linear, so the error in the “radius” is small and acceptable

This approach for utilizing the detected gradient can be incorporated into the new accumulation scheme presented in the previous section. When extracting the “edge points” for which the two lines are accumulated in the $\mathcal{TS}$ space (line 1 in Algorithm 2), the edge inclination is also extracted: Then, instead of accumulating all points from set P (lines 4–6), only those points which fall into the interval with radius w around currently processed $\theta$ are processed and accumulated into the buffer of n lines:

and similarly for lines 15–17.

It should be noted that the edge extraction phase (line 1) can sort the detected edges by their gradient inclination $\alpha,$ so that loops on lines 15–17 and 4–6 do not visit all edges, but only edges potentially accumulated, based on the current u (line 9 of Algorithm 2). For (partial) sorting the edges on GPU, an efficient prefix sum can be used [10].

5 Experimental results

This section presents the experimental evaluation of the proposed algorithm. Section 5.1 briefly describes a PClines-based algorithm for OpenGL which is used as a reference in the measurements. Section 5.2 contains the results achieved by a CUDA implementation of the PClines-based algorithm presented in this study compared to other implementations/algorithms.

The following hardware was used for testing (in bold face is the identifier used later on in this text):

GTX 480: NVIDIA GTX 480 in a computer with Intel Core i7-920, 6 GB $3\times$DDR3-1066 (533 MHz) RAM;

GTX 280: NVIDIA GTX 280 in a computer with Intel Core i7-920, 6 GB $3\times$DDR3-1066 (533 MHz) RAM;

HD 5970-1: AMD Radeon HD5970 (single core used) in a computer with Intel Core i5-660, 4 GB $3\times$DDR3-1066 (533 MHz) RAM;

HD 5970-2: AMD Radeon HD5970 (both cores used) in a computer with Intel Core i5-660, 4 GB $3\times$DDR3-1066 (533 MHz) RAM; and

i7-920: Intel Core i7-920, 6 GB $3\times$DDR3-1066 (533 MHz) RAM—the same computer is used for testing the GTX 480 and GTX 280.

An evaluation of the accuracy of the PClines line parameterization can be found in a recent paper where the PClines parameterization was introduced [6]. The measurements report that PClines are equal or more accurate than the “standard” $\theta{-}\varrho$ parameterization.

5.1 OpenGL implementation of PClines as a reference

Contrary to the “standard” $\theta{-}\varrho$ parameterization where sinusoids need to be rasterized into the accumulator space, in the case of PClines, for each edge point detected in the input image, two-line segments are rasterized. Rasterization of line segments (and blending the rasterized pixels into a frame buffer) is a natural task for the graphics chips. Recently, we published a paper about an OpenGL implementation of the PClines [5]. The whole process is done by the graphics chip, programmed in OpenGL and GLSL:

Edges are extracted by a geometry shader which accesses a texture with the input image and, for each pixel in the input image, it emits zero, two, or three endpoints of a polyline to be rasterized into the $\mathcal{TS}$ space.

Line segments are rasterized by OpenGL and blended into the frame buffer.

The $\mathcal{TS}$ space is searched by another geometry shader which emits the parameters of detected lines.

This implementation using OpenGL and GLSL will be used as a reference and referred to as “PClinesGL” in the charts. For more information on the algorithm and its implementation, please refer to the original paper [5].

5.2 Performance evaluation on real-life images

Two datasets were used for measuring the performance of different algorithms. The first one was a set of real photographs with different amounts of edge points and different dimensions (see Fig. 6).

Fig. 6

Images used in the test. The number in the top-left corner of each thumbnail image is the image ID used on the horizontal axis in Figs. 7 and 8. The bottom-left corner of each thumbnail image states the number of edge points and pixel resolution of the tested image

The images are sorted according to the number of edge points detected by the Sobel filter. Only this limited set of images is selected for the graphs to be readable. The images were selected randomly from a large set of images and they well represent the behavior of the algorithms for all images we have observed.

The presented algorithm (referred to below as PClines–CUDA) was compared to different alternatives:

• A software implementation of the PClines based on a Hough transform implementation taken from the OpenCV library² and parallelized by OpenMP and slightly optimized.

• A CUDA implementation of the standard $\theta{-}\varrho$ parameterization (ThetaRho-CUDA). The arrangement of the algorithm is very similar to the presented PClines-based one.

• The OpenGL implementation of PClines (PClines-OpenGL) as described in Sect. 5.1.

The results are shown in Fig. 7. The measurements verify that the computational complexity is linearly proportional to the number of edge points extracted from the input image and the edge-detection phase is linearly proportional to the image resolution. The GPU-accelerated implementations are notably faster than the software implementation. A detailed comparison of the GPU-accelerated implementations is shown in Fig. 8.

Fig. 7

Performance evaluation on real-world images (see Fig.6) using the Sobel operator and only accumulating an interval on the u-axis (Sect. 4.2)

Fig. 8

Performance evaluation on real-world images (see Fig.6) using the Sobel operator and only accumulating an interval on the u-axis (Sect. 5.2). Only the hardware-accelerated methods are shown here for better clarity

5.3 Performance evaluation on synthetic binary images

The second dataset consisted of automatically generated black-and-white images. The generator randomly places L white lines in an originally black image and then inverts pixels on P random positions in the image. The evaluation is done on 36 images (resolution $1,600\times1,200$): images 1–6, 7–12, 13–18, 19–24, 25–30, 31–36 are generated with $L=1, 30, 60, 90, 120, 150$, respectively, with increasing $P=1,\,3{,}000,\,6{,}000,\,9{,}000,\,12{,}000$ for each L. The suitable parameters for images of these properties were H _ϱ = 960 and H _θ = 1170 (resolution of the Hough space) and the threshold for accumulators in the Hough space was 400. The purpose of this test was to accurately observe the dependency of processing time on the number of lines in the image and on the number of pixels processed as edges. These two quantities determine the number of repetitions in critical parts of the algorithm.

Figure 9 shows the results of the four implementations; Fig. 10 contains a selection of the graphs—only the hardware-accelerated methods. Once again, it should be noted that all the accelerated versions are several times faster than the commonly used OpenCV implementation and achieve real-time or near real-time speeds even for high-resolution inputs.

Fig. 9

Performance evaluation on generated data

Fig. 10

Performance evaluation on generated data. Only the hardware-accelerated methods are shown here for better clarity

On current graphics chips, the algorithm presented here (PClines–CUDA) and the previously published algorithm (ThetaRho-CUDA) perform equally fast (it should be noted that, in Figs. 8 and  10, their curves totally overlap). On special, embedded, and low-power architectures, the PClines-based version may perform much better or can be the only feasible one, because it requires no floating-point computations and no goniometric functions (which are cheaply available on the GPUs). The only advantages of the PClines-based algorithm on GPU is, therefore, its better accuracy [6] and its ability to directly detect parallel lines and sets of lines coincident with one point.

Figures 8 and  10 show that, on the pre-Fermi NVIDIA card (GTX280), the OpenGL version of the PClines-based Hough transform performs better than CUDA. That is because the atomic increment operation ( atomicInc ) in the shared memory is not optimized on this generation of the graphics chips. Very good results also come from recent Radeon graphics chips (with the OpenGL version). Figures 8 and  10 also show that the OpenGL algorithm by Dubská et al. [5] scales well on the dual-core graphics card Radeon HD5970. When executed on both the cores, the speed is almost doubled compared to the single-core version. A comparable scaling is achieved also on the CUDA version of the algorithm. However, on CUDA, the problem must be “manually” divided into an appropriate number of blocks within the kernel. Such a division is discussed in Sect. 4.1.

5.4 Discussion

The Fermi architecture (compared to the previous generation) speeded up the algorithm in the OpenGL version just the amount which can be expected from the increase in the number of the streaming multiprocessors. However, the CUDA version presented in this study speeded up notably more (about 4 times) on the Fermi architecture. This can be explained by the improved atomic operations in the shared memory, involving the new design of the L2 cache on the GTX480 [see Fermi White Paper (2009)]. Attribution of the performance boost between the GTX280 and GTX480 to the atomic instructions was verified by running the algorithm with the non-atomic equivalents of the increment/add instructions (Fig. 11). For weaker graphics chips (low-power, mobile, etc.), the OpenGL ersion of the PClines-based algorithm might be the right choice.

Fig. 11

Comparison of the speed on graphics cards of two different generations: GTX480 and GTX280. In the case of GTX480, execution without atomic instructions (atomic add and inc were replaced by non-atomic equivalents) is about three times faster (blue, red). However, in the case of GTX280 (magenta, green), the performance when using atomic instructions is about 25× slower. It should be noted that this includes only the edge-detection part of the algorithm. This part is the most time-consuming one and more importantly it is much more prone to the speed of atomic instructions. The rest of the algorithm is severely affected by the incorrect results produced by non-atomic operations and thus their timing was omitted

We evaluated several different configurations of the shared memory as it is used by the algorithm. Namely, different number of columns can be allocated for the circular buffer of columns, as noted in the last paragraph of Sect. 4.1. We allocated varying numbers of these columns and observed the results in Fig. 12. Different configurations of the shared memory also illustrate the performance of the algorithm in terms of being computation/memory bound. We measured instructions per cycle (1/CPI) and the effective bandwidth in Fig. 13. These measurements indicate that the algorithm is mostly computation bound and using the whole shared memory helps in accessing the global memory more efficiently. This behavior reflects the nature of the algorithm which was designed to be using memory efficiently by processing the data in stripes. This access strategy helps serialize and minimize the accesses to the global memory.

Fig. 12

Time performance for several selected images from Fig. 6 for different configurations of the shared memory usage (i.e., number of spare columns used by the algorithm). Note that as expected in the algorithm design, using the whole shared memory for the accumulation buffer indeed speeds the computation up. However, for high number of blocks within the kernel, the impact of this improvement is diminished and also, very large shared memory would not help notably anymore (as illustrated in Figure 13). Time performance for several selected images from Fig. 6 for different configurations of the shared memory usage (i.e., number of spare columns used by the algorithm). Note that as expected in the algorithm design, using the whole shared memory for the accumulation buffer indeed speeds the computation up. However, for high number of blocks within the kernel, the impact of this improvement is diminished and also very large shared memory would not help notably anymore (as illustrated in Fig. 13)

Fig. 13

Usage of the graphics chip in terms of memory and computation percentual load compared to theoretical limits. Green boxes represent percentual usage of the computational power of the graphics board (CPI/theoretical maximum). Red boxes reflect the usage of the theoretical memory bandwidth (effective bandwidth/theoretical max). The graph shows five series of measurements on five different images (select ed from Fig 6); a single measurement within the series represents one shared memory configuration, equally as in Fig. 12

Fig. 14

Original x–y space (left) and its PClines representation the corresponding $\mathcal{TS}$ space (right)

6 Conclusions

This study presents an algorithm based on the PClines parameterization for real-time detection of lines. The algorithm is suitable for platforms featuring a small but fast internal memory, while the external memory is relatively slow and prefers sequential access. This describes many recent acceleration platforms, DSPs, embedded devices, but most importantly current graphics chips. The main contribution of the study is the accumulation strategy suitable for such architectures. It is shown that this algorithm allows for real-time computation of the “full” Hough transform on high-resolution images.

The measurements show that the GPU-accelerated algorithm achieves interactive (or faster) detection times even for images of really high resolutions. For images with smaller resolutions, this algorithm can be used in low-power and embedded devices; the algorithm should be also usable for designing specialized circuitry (e.g., FPGA) because it requires no floating-point calculation or goniometric functions.

Since the PClines parameterization is a point-to-line mapping, it can be used efficiently for detecting lines that are mutually parallel or that are coincident with one vanishing point. We intend to exploit this feature for rapid (real-time) detection of parallel lines, chessboard patterns, and similar structures. In the near future, we also intend to explore possibilities for implementing the algorithm in the programmable circuitry (FPGA).