Introduction

Electromagnetic surface waves (ESW) are a fascinating phenomenon at the interface of different media with unique properties and potential applications that have gained significant attention across various fields [1, 2]. ESW has characteristics like confinement to the surface and sensitivity to the interface, and they propagate along the surface of a conductor or dielectric, whereas bulk waves travel in the medium. The concept of ESW was first presented in the early twentieth century by Sommerfeld and Zenneck, who reported the propagation of surface plasmon polaritons (SPP) along a metal-dielectric interface [3]. After this groundbreaking work, the developments in the optics sector have gained considerable interest in this field, which has resulted in the discovery of new types of ESW. Despite tremendous advancement and progress in this field, there are many areas of ESW that can be explored which will be a step forward in this enchanting field. The interaction of light with complex media, propagation control, and integration of complex media into sophisticated practical devices are some of the common challenges present in this field [4,5,6]. Addressing these challenges will be helpful to provide a cornerstone to the next-generation technologies that leverage the unique properties of ESW. Studying the behavior of ESW and how they interact with various materials will be useful in designing novel systems and devices. Depending on the characteristics of propagation, type of interface, and geometry of media, ESW can be divided into several types [7]. The simplest type of ESW is surface plasmon polaritons (SPP) that is an electromagnetic surface wave whose amplitude exponentially decays with increasing distance from the interface [8]. Metals have a negative dielectric constant below plasma frequency, resulting in a free electron response similar to plasma. The colors that metal displays are caused by the resonant coupling of the electromagnetic field and oscillation of free charges on the metal surface. The resonance frequency of SPP is influenced by the surrounding material as well as the size, shape, and composition of the materials. Due to these characteristics, SPP are extremely important in devices that are very sensitive to applied signal and have high efficiency. From the optical to the terahertz (THz) frequency range, SPP can be excited at a variety of frequencies [9,10,11,12,13,14,15]. Thus, SPP offers a variety of applications including telecommunications [16, 17], imaging [18], optical sensing [19], chemical and biological sensors [20, 21], integrated photonics [22, 23], and spectroscopy [24, 25].

Chiral materials are distinguished by the absence of mirror symmetry, which means that the chiral material structure cannot be superimposed on its mirror image. Because of this characteristic, they exhibit distinctive optical behaviors, especially when interacting with light [26]. A subclass of chiral materials known as UACM is distinguished by their unusual combination of chirality and anisotropy. UACM have different refractive index and chirality on the longitudinal axis (axis parallel to the optical axis) and perpendicular axis [27]. Therefore, this intrinsic anisotropy is coupled with the chirality of the material, which means that the structure of the material lacks mirror symmetry and exhibits different interactions with left circularly polarized (LCP) and right circularly polarized (RCP) light [28]. Coupling between the electric and magnetic fields due to chirality causes hybrid modes in UACM that have combined characteristics of transverse magnetic (TM) and transverse electric (TE) waves [29]. This coupling may lead to strong confinement and long propagation length which is not possible in achiral anisotropic materials. These characteristics make it possible to precisely control how SPP propagates and polarizes, which enables scientists and engineers to design and finely tune the advanced nanophotonic devices that are very useful in the era of modern science and technology. Since waveguides effectively direct light from one place to another and play a crucial role in many advanced applications, the performance of the waveguide can be greatly improved by incorporating UACM. Waveguides that have UACM can support more modes as compared to ordinary waveguides, therefore providing greater design flexibility when designing modern plasmonic devices.

Graphene, a genuinely two-dimensional material made of honeycomb carbon atoms, has gained a lot of interest due to its unique and astonishing properties. It has exceptional mechanical strength, lightweight, and flexibility; therefore, it has great importance and a number of uses in composite materials and flexible electronic devices. Despite it having only one atom thickness, it is nearly transparent and absorbs about 2.3% of incident light. The free electrons in graphene exhibit a linear dispersion between their momentum and energy close to the Dirac point, behaving like massless fermions. This phenomenon gives rise to several intriguing characteristics of graphene, such as its exceptionally high charge mobility and unique conductivity, that is the algebraic sum of its interband and intraband conductivity [30]. Light-matter interactions at the nanoscale can be enhanced by graphene’s ability to confine electromagnetic waves to dimensions much smaller than the wavelength of light [31]. This characteristic is crucial for reducing the size of photonic devices and integrating them into compact circuits. Due to the gapless linear dispersion of Dirac fermions, its optical properties can be tuned by chemical doping or applying an external electric field, which is not possible in traditional materials. Owing to its distinct composition and structure, it possesses exceptional properties that make it a highly attractive material across various fields, including nanotechnology, optoelectronics, and plasmonics [32].

The efficiency and performance of optical devices can be increased by using waveguides that confine propagation, which is a useful factor to minimize the losses in EM signals. In order to investigate the characteristics of SPP, we will examine a graphene-filled waveguide surrounded by UACM. The very strong interaction of graphene with light makes it suitable for replacing the conventional material used in waveguides. Graphene-based waveguides integrated with UACM have many unique advantages such as an extra degree of freedom in fabrication, tuning, flexibility, and supporting a wide range of frequencies with minimized losses. In this manuscript, to study the behavior of the normalized propagation constant, we derived the characteristic equation by applying impedance boundary conditions at the interface. The effects of different parameters of graphene and UACM are investigated.

Mathematical Formulation

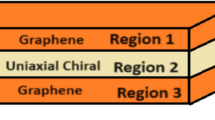
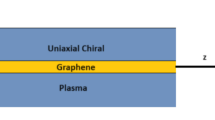
The proposed waveguide having graphene as the core and UACM as the substrate and cladding is illustrated in Fig. 1. Homogenization of a waveguide structure typically involves the effective parameters (defining geometry, mathematical modeling, etc.) that describe the macroscopic behavior of the waveguide based on its microscopic structure. Therefore, it is important to mention that this theoretical model is homogenous and has graphene as the core and UACM as cladding and substrate with chirality on the z-axis.

Fig. 1
figure 1

Illustration of UACM-graphene-UACM waveguide

Full size image

Consider an electromagnetic wave that attenuates along the x-axis as a function of time and propagates along the z-axis as a function of time with angular frequency ω where time dependence \({e}^{\text{i}\omega \text{t}}\) is implicit. To study SPP in the proposed waveguide, we start from the constitutive relations of UACM.

$$D=\left[{\varepsilon }_{\text{t}}{\overline{\overline{I}}}_{\text{t}}+{\varepsilon }_{\text{z}}{\widehat{e}}_{\text{z}}{\widehat{e}}_{\text{z}} \right].E-i \kappa \sqrt{{\mu }_{0}{\varepsilon }_{0}}{\widehat{e}}_{\text{z}}{\widehat{e}}_{\text{z}}.H$$
(1)
$$B=\left[{\mu }_{\text{t}}{\overline{\overline{I}}}_{\text{t}}+{\mu }_{\text{z}}{\widehat{e}}_{\text{z}}{\widehat{e}}_{\text{z}} \right].H-i \kappa \sqrt{{\mu }_{0}{\varepsilon }_{0}}{\widehat{e}}_{\text{z}}{\widehat{e}}_{\text{z}}.E$$
(2)

Here, mutually perpendicular unit vectors are defined as \({\widehat{e}}_{\text{x}}\),\({\widehat{e}}_{\text{y}}\), and \({\widehat{e}}_{\text{z}}\). The constitutive relation described in the above equations is defined by a dyadic vector \({\overline{\overline{I}}}_{\text{t}}={\widehat{e}}_{\text{x}}{\widehat{e}}_{\text{x}}+{\widehat{e}}_{\text{z}}{\widehat{e}}_{\text{z}}\); permeability and permittivity of free space are denoted by \({\mu }_{0}\) and \({\varepsilon }_{0}\), respectively. \({\varepsilon }_{\text{t}}\),\({\mu }_{\text{t}}\) and \({\varepsilon }_{\text{z}}\), \({\mu }_{\text{z}}\) are transverse and longitudinal components of permittivity and permeability, and \(\kappa\) is the chirality parameter. The field components of a wave propagating in cladding that has UACM are defined as

$${E}_{\text{z}1}={(A}_{1} {e}^{{-\gamma }_{R1}x}+{A}_{2} {e}^{{-\gamma }_{L1}x}) {e}^{-i\beta z}$$
(3)
$${H}_{\text{z}1}=[\frac{i {\alpha }_{1}}{{\eta }_{t}}{(A}_{1} {e}^{{-\gamma }_{R1}x})+\frac{i {\alpha }_{2}}{{\eta }_{t}}( {A}_{2} {e}^{{-\gamma }_{L1}x})] {e}^{-i\beta z}$$
(4)

whereas longitudinal field components in a substrate are given as

$${E}_{\text{z}2}={(A}_{3} {e}^{{\gamma }_{R2}x}+{A}_{4} {e}^{{\gamma }_{L2}x}) {e}^{-i\beta z}$$
(5)
$${H}_{\text{z}1}=[\frac{i {\alpha }_{1}}{{\eta }_{t}}{(A}_{3} {e}^{{\gamma }_{R2}x})+\frac{i {\alpha }_{2}}{{\eta }_{t}}( {A}_{4} {e}^{{\gamma }_{L2}x})] {e}^{-i\beta z}$$
(6)

Here, \({A}_{1}\), \({A}_{2}\), \({A}_{3},\) and \({A}_{4}\) are unknown coefficients that are associated with the amplitudes of EM fields and can be found by applying boundary conditions at the interface where

$${\gamma }_{\text{R}1}={\gamma }_{\text{R}2}=\sqrt{{\beta }^{2}-{q}_{1}^{2}}$$
(7)
$${\gamma }_{\text{L}1}={\gamma }_{\text{L}2}=\sqrt{{\beta }^{2}-{q}_{2}^{2}}$$
(8)

The relation between electric and magnetic fields is

$$\left({E}_{\text{z}} , {H}_{\text{z}}\right)=\left({E}_{\text{z}} ,\frac{i{\alpha }_{1, 2}}{{\eta }_{t}} {E}_{\text{z}}\right)$$
(9)

Here, \({\alpha }_{1}=\left(\frac{{q}_{1}^{2}}{{\lambda }^{2}}-\frac{{\varepsilon }_{z}}{{\varepsilon }_{t}}\right) \frac{\sqrt{{{\mu }_{t}\varepsilon }_{t}}}{\gamma \sqrt{{{\mu }_{z}\varepsilon }_{z}}}\), \({\alpha }_{2}=\left(\frac{{q}_{2}^{2}}{{\lambda }^{2}}-\frac{{\varepsilon }_{z}}{{\varepsilon }_{t}}\right)\frac{\sqrt{{{\mu }_{t}\varepsilon }_{t}}}{\gamma \sqrt{{{\mu }_{z}\varepsilon }_{z}}}\), \({q}_{t}=\omega \sqrt{{\varepsilon }_{t}{\mu }_{0}}\), and \({\eta }_{t}=\sqrt{{\varepsilon }_{t}/{\mu }_{t}}\)

The transverse field components of cladding and substrate consisting of UACM can be derived from [33]. Fields propagating in UACM are characterized by two different wavenumbers which are defined as

$${q}_{1}^{2}=\frac{{\lambda }^{2}}{2}\left[\frac{{\mu }_{\text{z}}}{{\mu }_{\text{t}}}+\frac{{\varepsilon }_{\text{z}}}{{\varepsilon }_{\text{t}}}+\sqrt{{\left(\frac{{\mu }_{\text{z}}}{{\mu }_{\text{t}}}-\frac{{\varepsilon }_{\text{z}}}{{\varepsilon }_{\text{t}}}\right)}^{2}+\frac{4{\gamma }^{2}{\mu }_{\text{z}}{\varepsilon }_{\text{z}}}{{\mu }_{\text{t}}{\varepsilon }_{\text{t}}}}\right]$$
(10)
$${q}_{2}^{2}=\frac{{\lambda }^{2}}{2}\left[\frac{{\mu }_{\text{z}}}{{\mu }_{\text{t}}}+\frac{{\varepsilon }_{\text{z}}}{{\varepsilon }_{\text{t}}}-\sqrt{{\left(\frac{{\mu }_{\text{z}}}{{\mu }_{\text{t}}}-\frac{{\varepsilon }_{\text{z}}}{{\varepsilon }_{\text{t}}}\right)}^{2}+\frac{4{\gamma }^{2}{\mu }_{\text{z}}{\varepsilon }_{\text{z}}}{{\mu }_{\text{t}}{\varepsilon }_{\text{t}}}}\right]$$
(11)

Here

$${\lambda }^{2}={\beta }^{2}-{{q}_{\text{t}}}^{2}$$
(12)

Core of the waveguide is a graphene sheet that is deposited on a dielectric having a negligible thickness. Its conductivity is modeled with the help of the well-known Kubo formalism. Its conductivity is the combination of inter-band and intra-band conductivities. There is a significant effect of chemical potential, relaxation time, temperature, and incident wave frequency on the conductivity of graphene [34]. Therefore, its optical conductivity is the source of most of its photonic properties. The mathematical relation for graphene conductivity is

$$\sigma g={\sigma }_{\text{intra}}+{\sigma }_{\text{inter}}$$
(13)
$$\sigma g=\frac{i{e}^{2}{K}_{\text{B}}T}{\pi {\hslash }^{2}\left(\omega +\frac{i}{\tau }\right)}\left(\frac{{\mu }_{\text{c}}}{{K}_{\text{B}}T}+2\mathit{Log}[{e}^{-\frac{{\mu }_{\text{c}}}{{K}_{\text{B}}T}}+1]\right)+\frac{i{e}^{2}}{4\pi \hslash }Log\left(\frac{2\left|{\mu }_{\text{c}}\right|-\hslash \left(\omega +\frac{i}{\tau }\right)}{2\left|{\mu }_{\text{c}}\right|+\hslash \left(\omega +\frac{i}{\tau }\right)}\right)$$
(14)

In the above relation, e is the charge of an electron, \({K}_{\text{B}}\) is the Boltzmann constant, and \(\hslash\) is the reduced Planks constant having numerical values of \(1.6\times {10}^{-19}\text{c}, 1.38\times {10}^{-23}\) J/C, and \(1.05\times {10}^{-34}\) Js, respectively. For our calculation, we have taken temperature T = 300 K.

The boundary conditions in general form for graphene sandwiched between UACM can be expressed as

$${\widehat{e}}_{\text{x}}\times \left({E}_{1}-{E}_{2}\right)=0$$
(15)
$${\widehat{e}}_{\text{x}}\times \left({H}_{1}-{H}_{2}\right)=\sigma g E$$
(16)

Boundary conditions given above are applied at the interface of graphene and UACM that gives us the characteristic equation.

$${q}_{\text{t}}{ \alpha }_{1}{({\alpha }_{1}-{\alpha }_{2})}^{2} {\alpha }_{2}\left({\gamma }_{\text{L}1}+{\gamma }_{\text{L}2}\right)\left( {\gamma }_{\text{R}1}+{\gamma }_{\text{R}2}\right)-{q}_{\text{t}}\left({\alpha }_{1}{\gamma }_{\text{L}1}-{\alpha }_{2}{\gamma }_{\text{R}1}\right)\left({\alpha }_{1}{\gamma }_{\text{L}2}-{\alpha }_{2}{\gamma }_{\text{R}2}\right){{\eta }_{\text{t}}}^{2}\sigma g+i \left({\alpha }_{1}-{\alpha }_{2}\right)\left(-{\alpha }_{2}\left({\gamma }_{\text{L}1}+{\gamma }_{\text{L}2}\right){\gamma }_{\text{R}1}{\gamma }_{\text{R}2}+{\alpha }_{1}{\gamma }_{\text{L}1}{\gamma }_{\text{L}2}\left( {\gamma }_{\text{R}1}+{\gamma }_{\text{R}2}\right)+{{q}_{\text{t}}}^{2}{\alpha }_{1}{\alpha }_{2}\left({\alpha }_{1}\left({\gamma }_{\text{L}1}+{\gamma }_{\text{L}2}\right)-{\alpha }_{2}\left( {\gamma }_{\text{R}1}+{\gamma }_{\text{R}2}\right)\right)\right){q}_{\text{t}}\sigma g=0$$
(17)

With the help of the above characteristic equation, we are now able to analyze and investigate our analytical results.

Results and Discussion

In this section, the generated numerical results are elucidated to study the behavior of SPP at the UAC-G-UAC planar waveguide. Wolfram Mathematica software is used to compute numerical results. We have theoretically investigated the characteristics of SPP in UACM-graphene-UACM waveguides using the characteristic Eq. 17. Based on numerical results, the influence of parameters such as chemical potential, relaxation time, number of graphene layers, and chirality parameter on the normalized propagation constant has been explored. As part of this paper, we present three different cases: case I, \({\varepsilon }_{\text{t}}\) > 0,\({\varepsilon }_{\text{z}}\)> 0; case II, \({\varepsilon }_{\text{t}}\) < 0, \({\varepsilon }_{\text{z}}>\) 0, and case III, \({\varepsilon }_{\text{t}}\) < 0, \({\varepsilon }_{\text{z}}\) < 0 of UACM that provide an extra degree of freedom to design and tune the waveguide. In our calculation, we have assumed that the transverse and longitudinal components of permeability are the same, i.e., \({\mu }_{\text{z}}={\mu }_{\text{t}}={\mu }_{0}=4 \pi \times {10}^{-7} H/m\).

Case I: \({\varepsilon }_{\text{t}}\) > 0, \({\varepsilon }_{\text{z}}\)> 0

In this case, the normalized propagation constant is analyzed by choosing parameters i.e., \({\varepsilon }_{\text{t}}={1.5 \varepsilon }_{0}\) and \({\varepsilon }_{\text{z}}={\varepsilon }_{0}\). The impact of chemical potential, relaxation time, number of graphene layers, and chirality parameter on normalized propagation constant are presented. In Fig. 2a, we demonstrate the impact of varying chemical potentials on the normalized propagation constant. Chemical potential can be tuned through doping or external fields. The frequency range extends from 0 to 2 terahertz. It is observed that by increasing chemical potential, the normalized propagation constant and cutoff frequency decreases. In this respect, it can be said that the smallest chemical potentials, such as 0.1 eV, have the highest cutoff frequency and normalized propagation constants, while large chemical potentials (0.7 eV) have the lowest cutoff frequency and normalized propagation constants. The conductivity of graphene is greatly influenced by its relaxation time, which also affects its optical properties. In Fig. 2b, we illustrate the influence of relaxation time on the normalized propagation constant with respect to frequency. Relaxation time increases from \(\tau =1\times {10}^{-12}\) s to \(\tau =1.9\times {10}^{-12}\) s. It is evident from the characteristics curves that the normalized propagation constant is inversely related to relaxation time. Based on this analysis, it appears that lower values of relaxation time have a more significant effect on the normalized propagation constant. Consequently, SPP can be controlled by adjusting the relaxation time within a particular frequency range. The impact of the number of graphene layers on the normalized propagation constant with respect to frequency is discussed in Fig. 2c. The cutoff frequency and normalized propagation constant decrease with the increasing number of graphene layers. The analysis clearly indicates that single-layer graphene (N = 1) exhibits lower energy losses than multilayer graphene. Figure 2d illustrates the impact of chirality on the normalized propagation constant versus frequency. Chirality parameters increase, i.e., from \(\kappa =0.40 {\Omega }^{-1}\) to \(\kappa =0.55 {\Omega }^{-1}\). The findings reveal that increasing the chirality leads to an increase in the propagation of SPP; hence, normalized propagation increases with the increase of chirality. The results demonstrate that increasing the chirality causes the normalized propagation constant peaks to shift towards the lower frequency region and shrink the gap between them which means as we increase the chirality, its impact decreases gradually. It is worth to mention that the cutoff frequency is the same for all chirality parameters that can be very helpful in the waveguide community.

Fig. 2
figure 2

Impact of different parameters on normalized propagation constant: a chemical potential, b relaxation time, c number of graphene layers, and d chirality

Full size image

A waveguide may experience losses due to a variety of physical factors. The signal transmission efficiency through the waveguide is decreased by these losses. These losses mostly stem from several physical mechanisms, such as interband transitions, radiative damping, and scattering losses. The impact of chemical potential and chirality on propagation losses is analyzed in Fig. 3. From Fig. 3a, it is observed that attenuation increases with the increase of chemical potential. Furthermore, this trend is more dominant at lower frequency; as the frequency increases, the impact of chemical potential on attenuation decreases significantly. Figure 3b represents the impact of chirality on attenuation. The graph suggests that smaller values of chirality have smaller attenuation (propagation losses). As the chirality of UACM increases, the attenuation of the signal through the waveguide also increases. The effect of chirality is smaller at lower frequency and becomes more prominent at higher frequency.

Fig. 3
figure 3

Impact of different parameters on attenuation: a chemical potential and b chirality

Full size image

Case II: \({\varepsilon }_{\text{t}}\) < 0, \({\varepsilon }_{\text{z}}>\) 0

In this case, calculation and analysis are made by setting the transverse component negative and the longitudinal component positive; therefore, we set \({\varepsilon }_{\text{t}}={-0.2 \varepsilon }_{0}\) and \({\varepsilon }_{\text{z}}={\varepsilon }_{0}\). Figure 4a depicts the influence of chemical potential on normalized propagation constant as a function of frequency. It is noted that when the chemical potential is 0.1 eV, the normalized propagation constant is high, and the cutoff frequency is 3 THz. It is found that with a chemical potential of 0.3 eV, the normalized propagation is decreased, but the cutoff frequency is 5.5 GHz. Similarly, at 0.5 and 0.7 eV, the normalized propagation constant reduced but the cutoff frequency increased, reaching 7.5 and 8.9 THz, respectively. This trend suggests that as chemical potential increases, the normalized propagation constant decreases as well. It is worth mentioning that in this case, the frequency range extends up to 14 THz. In addition, the proposed frequency range significantly affects the characteristics curves. The chemical potential becomes insignificant after 14 THz. The variation in normalized propagation constant under the different values is illustrated in Fig. 4b. It is observed that the normalized propagation constant increases with relaxation time, while the cutoff frequency decreases. Furthermore, after 4 THz, characteristic curves exhibit an unphysical region. Figure 4c shows the impact of graphene layers on the normalized propagation constant. Single-layer graphene exhibits the highest normalized propagation constant and the lowest cutoff frequency. Furthermore, characteristic curves exhibit an unphysical region after 11 THz. Figure 4d demonstrates the impact of chirality on the relationship between the normalized propagation constant and the frequency. It is found that the chirality parameter does not have a significant effect on normalized propagation constants in the lower frequency region. However, chirality plays a significant role in the propagation of SPP at high frequencies. Based on these findings, it has been demonstrated that the propagation is decreased as chirality increases. Hence,\(\kappa =0.40 {\Omega }^{-1}\) exhibits the highest propagation constant, while \(\kappa =0.55 {\Omega }^{-1}\) has the lowest propagation constant. Additionally, the characteristic curves shrink with increasing chirality value.

Fig. 4
figure 4

Impact of different parameters on normalized propagation constant: a chemical potential, b relaxation time, c number of graphene layers, and d chirality

Full size image

Figure 5a, b represents the impact of chemical potential and chirality on the attenuation of the waveguide for the case when the transverse component of permittivity is negative and the longitudinal component is positive (\({\varepsilon }_{\text{t}}={-0.2 \varepsilon }_{0}\) and \({\varepsilon }_{\text{z}}={\varepsilon }_{0}\)). An increase in chemical potential increases the propagation losses. From Fig. 5a, it is clear that chemical potential has a significant effect on attenuation; therefore, the proper choice of chemical potential of graphene can reduce the signal loss in the waveguide. In Fig. 5b, the impact of chirality on attenuation is depicted. In this case, attenuation decreases with the increase of the chirality of the waveguide.

Fig. 5
figure 5

Impact of different parameters on attenuation: a chemical potential and b chirality

Full size image

Case III: \({\varepsilon }_{\text{t}}\) < 0, \({\varepsilon }_{\text{z}}\) < 0

In this case, the longitudinal and transverse permittivity components are considered negative, i.e., \({\varepsilon }_{t}={-0.2 \varepsilon }_{0}\) and\({\varepsilon }_{\text{z}}=-0.5 {\varepsilon }_{0}\). The effect of chemical potential on the normalized propagation constant is analyzed in Fig. 6a. When chemical potential is 0.1 eV then the cutoff frequency is 6 THz and the highest normalized propagation constant. An increase in chemical potential, i.e., 0.3 eV, 0.5 eV, and 0.7 eV increases the cutoff frequency after 10 THz, 13 THz, and 15.5 THz, respectively. With increasing chemical potential, although the cutoff frequency increases, the normalized propagation constant decreases. The effect of relaxation time on the normalized propagation constant is illustrated in Fig. 6b. It is observed that the normalized propagation increases with relaxation time, while the cutoff frequency decreases. It is of peculiar interest to note that until 7 THz, this trend appears more prominent, and after this frequency, relaxation time has no effect on normalized propagation constants. The influence of graphene layers on the normalized propagation constant is depicted in Fig. 6c. Graphene monolayers show a cutoff frequency of 6 THz and a normalized propagation constant with the maximum value. It is necessary to note that for two, three, and four layers of graphene, the cutoff frequency is 8 THz, 10 THz, and 12 THz, respectively. Figure 6d shows the relationship between chirality and normalized propagation constants. The chirality parameter having different values (\(\kappa =0.40 {\Omega }^{-1}\), \(\kappa=0.45\Omega^{\left(-1\right)}\), \(\kappa=0.50\Omega^{-1}\), and \(\kappa =0.55 {\Omega }^{-1}\) is analyzed. At \(\kappa =0.40 {\Omega }^{-1}\), normalized propagation constant has a maximum value, whereas \(\kappa =0.55 {\Omega }^{-1}\) have a minimum value of the normalized propagation constant. This case shows that chirality has little effect on the cutoff frequency, while it has a significant effect on the normalized propagation constant. In addition, the dispersion curves in the graph expand as we move towards higher frequency regions, indicating that chirality has a small impact at lower frequencies, and its effect is more significant at higher frequencies.

Fig. 6
figure 6

Impact of different parameters on normalized propagation constant: a chemical potential, b relaxation time, c number of graphene layers, and d chirality

Full size image

The impact of chemical potential and chirality on attenuation for \({\varepsilon }_{\text{t}}={-0.2 \varepsilon }_{0}\) and \({\varepsilon }_{\text{z}}=-0.5 {\varepsilon }_{0}\) is elaborated in Fig. 7. Different values of the chemical potential of graphene on attenuation are illustrated in Fig. 7a. According to the figure, chemical potential has a direct relationship with attenuation, i.e., propagation losses increase with the increase of chemical potential. It is important to mention here that this chemical potential has the highest impact on the attenuation of the waveguide. Figure 7b describes the impact of chirality on attenuation. The figure indicates that an increase in chirality increases the attenuation of the waveguide; however, this impact of chirality decreases as the frequency increases and becomes insignificant after 0.2 THz. The curves converge after this frequency, indicating a saturation point where further increases in chirality do not significantly impact the attenuation of this type of waveguide.

Fig. 7
figure 7

Impact of different parameters on attenuation: a chemical potential and b chirality

Full size image

Fields distribution for \({E}_{\text{z}}\) component of uniaxial chiral medium is presented in Fig. 8a, and \({H}_{\text{z}}\) component is depicted in Fig. 8b. According to Fig. 5, the SPP of the dispersion curves of the proposed waveguide displays an exponential decay, thereby validating the existence of SPP.

Fig. 8
figure 8

Field distribution of uniaxial chiral material: a \({E}_{\text{z}}\) component and b \({H}_{\text{Z}}\) component

Full size image

Conclusion

We have developed a model of SPP at UACM-graphene-UACM waveguides to explore the characteristics of SPP. The characteristic equation for the proposed model is derived by applying boundary conditions. Numerical analysis of the normalized propagation constant of the proposed structure under the different parameters like chemical potential, relaxation time, number of graphene layers, and chirality parameter of UACM gives comprehensive insight. Three different types of UACM are characterized by their longitudinal and transverse permittivity as case I: \({\varepsilon }_{t}\) > 0, \({\varepsilon }_{z}\) > 0, case II: \({\varepsilon }_{t}\) < 0, \({\varepsilon }_{z}>\) 0, and case III: \({\varepsilon }_{t}\) < 0, \({\varepsilon }_{z}\) < 0. Based on numerical analysis, we find that waveguides of type case I are suitable for frequencies of 6 THz, waveguides of type case II can be used for frequencies of up to 14 THz, and waveguides of type case III can be used for frequencies of up to 30 THz. It is concluded that the normalized propagation constant can be tuned by tuning graphene features such as chemical potential, number of graphene layers, and relaxation time. Moreover, the chirality parameter is also very sensitive to the normalized propagation constant for the proposed waveguide. This model provides a wide range of possibilities and an additional degree of freedom to fabricate waveguides according to the specifications of specific applications. There are several areas of research associated with plasmonics, including real-time chiroptical sensing, surface-enhanced spectroscopy, biosensing, ultrafast optical switching, modulators, and the development of compact and efficient multipurpose waveguide devices.