Introduction

In the recent past, the study of metal and dielectric interface has led to a new concept of surface plasmon polaritons (SPP) called SPP waves. The collective oscillation of delocalized electrons at the surface of a metal and electromagnetic waves generated in dielectric medium are called surface plasmon polaritons. A fundamental property of SPP waves is their localization to the interface. Hence, SSP waves propagate along the interface and attenuate as they move away from it [1]. If dielectric medium is isotropic and homogeneous, then excited waves are p polarized SPP waves and exhibit similar properties in all directions along the interface plane. However, if isotropic dielectric medium is replaced by anisotropic dielectric medium, it allows for the excitation of SSP waves with different polarizations or varying properties along different directions [2,3,4] which enables us to have better control on SPP waves. It has eye-catching applications in subwavelength scale imaging [5,6,7,8], chemical and biosensing [9,10,11,12], solar cells [1], photonic data storage [13], nanophotonics [14,15,16], plasmonics color filter [17], near-field optics [18], surface-enhanced Raman spectroscopy [19, 20], and near field optics [21].

The study of electromagnetic radiations at terahertz (THz) frequency region has been an active area of research in the past few decades. Development in this regard are efficient detectors, high-power sources, and low-loss waveguides for THz applications are worth to mention. It is challenging but interesting to efficiently couple THz radiation to low-loss waveguides. In this frequency regime, metals behave like perfect electric conductors (PEC), leading to loosely confined SSP and an increase in the loss of the electromagnetic signal [22]. Recently, a variety of mechanisms and materials have been investigated to explore the properties of SPPs. By incorporating anisotropic semiconductor sheets into the structure, the anisotropic effect of conventional nanostructured metamaterial was enhanced. SPPs at the interface of a metal-free metamaterial with anisotropic inclusions and acoustic metamaterials were studied [23, 24]. In addition to many other advantages of graphene over metal, the conductivity of graphene can be adjusted by the Fermi energy or chemical potential [25,26,27]. To realize surface plasmon polaritons (SPP) in the THz frequency region, instead of using metal, we will focus on the use of graphene, a honeycomb of carbon atoms. It is a two-dimensional material with remarkable properties that enhance light-matter interaction. It is an intriguing substance that has attracted significant interest from scientists because of its extraordinary properties and Promising applications. Due to its remarkable properties, such as its zero bandgap, remarkable electron mobility at room temperature, high thermal conductivity, large surface area, and impermeability to gases [28]. With a single atom’s thickness, it is among the thinnest materials ever discovered having a hexagonal lattice structure and it is frequently termed as a “wonder material.” Graphene can be bent or stretched without losing its structural integrity because it is incredibly strong and flexible despite its extreme thinness. More than 97% of light can pass through because it is almost transparent [29]. Its fine-structure constant, which is independent of incident frequency over a broad range, defines its dynamic conductivity and remarkable photonic properties. It is a fascinating material for many potential applications, including optoelectronics, sensors, and communication systems. To fulfill the requirements in practical applications, graphene is frequently chemically modified. Due to its diverse and extraordinary properties, graphene emerges as a potential candidate for next-generation electronics, including faster transistors, flexible displays, and high-performance sensors, as well as applications in plasmonics, optoelectronics, and energy-related systems.

Chirality refers to the property of an object or material that is not superimposable onto its mirror image. Chiral materials exhibit handedness or a lack of symmetry, and their optical and chemical properties can differ based on the orientation of the chirality present in these materials [30, 31]. Uniaxial chiral (UAC) materials are a specific type of anisotropic chiral materials that exhibit uniaxial symmetry. Uniaxial symmetry means material possesses symmetry along a single axis of preferred orientation or alignment. In UAC materials, the optical and physical properties depend on the direction parallel to this preferred axis [32]. This implies that the material’s properties differ along this axis compared to the other planes. UAC materials can exhibit interesting optical phenomena, including circular dichroism and circular birefringence. These phenomena are associated with the differential absorption and phase shift of left-handed and right-handed circularly polarized light, respectively. They are of particular interest in the development of advanced optical devices, including chiral liquid crystal displays, chiral metamaterials, and optical elements for controlling the polarization and propagation of light. UAC materials can find applications in slab waveguides [33], which are planar structures that guide and confine light within a thin layer or slab of material.

These unique characteristics of UAC and graphene encouraged us to study SPP waves at the planar interface. In this work, we have examined the interaction of EM waves at uniaxial chiral-graphene planar structure to explore the SPPs which have not been previously studied according to the best of our knowledge. UAC media can support a greater variety of SPP modes compared to isotropic chiral media, left-handed materials, or other optical materials. This enhanced capability arises from the unique characteristics of UAC media, which is defined by both longitudinal and transverse permittivity. In contrast to other conventional optical materials, UAC materials are characterized by more constitutive parameters as described in Eq. (1), which provide an extra degree of freedom to control the EM waves. Furthermore, UAC media may simultaneously exhibit positive and negative permittivity. These novel properties of UAC media are very beneficial in the plasmonics community. In this manuscript, the dispersion relation is obtained by applying boundary conditions and used to analyze the effective mode index for different parameters such as chemical potential, relaxation time, number of graphene layers, and chirality parameters. Field distribution for uniaxial chiral medium is also presented to confirm the existence of SPP for the proposed structure. Present work may have groundbreaking applications in the plasmonic community to fabricate high-density nanophotonic chips at the THz frequency regime.

Mathematical Formulation

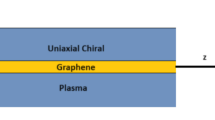
Schematic illustration of the proposed model comprising uniaxial chiral material and graphene is shown in Fig. 1. The electromagnetic wave is propagating along z-axis and attenuates along x-axis. Here, time dependence \({e}^{j\omega t}\) is implicit, with ω being the incident frequency. The constitutive relations for UAC material are expressed as [34].

Fig.1
figure 1

Schematic illustration of uniaxial chiral and graphene interface

Full size image
$$\genfrac{}{}{0pt}{}{{\varvec{D}}=\left[{\varepsilon }_{t}{\overline{\overline{I}}}_{t}+{\varepsilon }_{z}{\widehat{e}}_{z}{\widehat{e}}_{z} \right].{\varvec{E}}-j\gamma \sqrt{{\mu }_{0}{\varepsilon }_{0}}{\widehat{e}}_{z}{\widehat{e}}_{z}.{\varvec{H}}}{{\varvec{B}}=\left[{\mu }_{t}{\overline{\overline{I}}}_{t}+{\mu }_{z}{\widehat{e}}_{z}{\widehat{e}}_{z} \right].{\varvec{H}}-j\gamma \sqrt{{\mu }_{0}{\varepsilon }_{0}}{\widehat{e}}_{z}{\widehat{e}}_{z}.{\varvec{E}}}$$
(1)

The nomenclature of the above relation is described as: \({\overline{\overline{{\text{I}}}}}_{{\text{t}}}={\widehat{{\text{e}}}}_{{\text{x}}}{\widehat{{\text{e}}}}_{{\text{x}}}+{\widehat{{\text{e}}}}_{{\text{z}}}{\widehat{{\text{e}}}}_{{\text{z}}}\) is a dyadic vector,\(\gamma\) is the chirality parameter which is responsible for electromagnetic coupling and chirality in the media. \({\mu }_{0}\) and \({\varepsilon }_{0}\) are permeability and permittivity of free space.\({\varepsilon }_{t}\),\({\mu }_{t}\) and \({\varepsilon }_{z}\), \({\mu }_{z}\) are transverse and longitudinal components of permittivity and permeability of the medium, respectively. \({\widehat{e}}_{x}\),\({\widehat{e}}_{y}\) and \({\widehat{e}}_{z}\) are mutually perpendicular unit vectors in a Cartesian coordinate system.

Since each field excited in UAC propagates in two components, these components are characterized by two different wavenumbers which are given and defined as.

$${k}_{1}^{2}=\frac{{\lambda }^{2}}{2}\left[\frac{{\mu }_{z}}{{\mu }_{t}}+\frac{{\varepsilon }_{z}}{{\varepsilon }_{t}}+\sqrt{{\left(\frac{{\mu }_{z}}{{\mu }_{t}}-\frac{{\varepsilon }_{z}}{{\varepsilon }_{t}}\right)}^{2}+\frac{4{\gamma }^{2}{\mu }_{z}{\varepsilon }_{z}}{{\mu }_{t}{\varepsilon }_{t}}}\right]$$
(2)
$${k}_{2}^{2}=\frac{{\lambda }^{2}}{2}\left[\frac{{\mu }_{z}}{{\mu }_{t}}+\frac{{\varepsilon }_{z}}{{\varepsilon }_{t}}-\sqrt{{\left(\frac{{\mu }_{z}}{{\mu }_{t}}-\frac{{\varepsilon }_{z}}{{\varepsilon }_{t}}\right)}^{2}+\frac{4{\gamma }^{2}{\mu }_{z}{\varepsilon }_{z}}{{\mu }_{t}{\varepsilon }_{t}}}\right]$$
(3)

Here, \({\lambda }^{2}={\beta }^{2}-{{k}_{t}}^{2}\)

Leading to the wave equation:

$$\frac{{\partial }^{2}{E}_{z}}{\partial {x}^{2}}+{{k}^{2} E}_{z}=0$$
(4)

and solution of the wave equation is

$${{\text{E}}}_{{\text{z}}}={(B}_{1} {e}^{-{k}_{1}x}+{B}_{2} {e}^{-{k}_{2}x}) {e}^{-i\beta z}$$
(5)
$${{\text{H}}}_{{\text{z}}}=\frac{i}{{\eta }_{t}}\left({B}_{1}{\alpha }_{1} {e}^{-{k}_{1}x}+{B}_{2}{\alpha }_{2} {e}^{-{k}_{2}x}\right) {e}^{-i\beta z}$$
(6)

Here, \({{\text{B}}}_{1}\) and \({{\text{B}}}_{2}\) are unknown coefficients called amplitudes of fields and are calculated by applying boundary conditions. The remaining electric and magnetic field components can be derived from [34].

$$\left({{\text{E}}}_{{\text{z}}} , {{\text{H}}}_{{\text{z}}}\right)=\left({{\text{E}}}_{{\text{z}}} ,\frac{i{\alpha }_{1, 2}}{{\eta }_{t}} {{\text{E}}}_{{\text{z}}}\right)$$
(7)

Here, \({\alpha }_{1}=\left(\frac{{k}_{1}^{2}}{{\lambda }^{2}}-\frac{{\varepsilon }_{z}}{{\varepsilon }_{t}}\right) \frac{\sqrt{{{\mu }_{t}\varepsilon }_{t}}}{\gamma \sqrt{{{\mu }_{z}\varepsilon }_{z}}}\), \({\alpha }_{2}=\left(\frac{{k}_{2}^{2}}{{\lambda }^{2}}-\frac{{\varepsilon }_{z}}{{\varepsilon }_{t}}\right)\frac{\sqrt{{{\mu }_{t}\varepsilon }_{t}}}{\gamma \sqrt{{{\mu }_{z}\varepsilon }_{z}}}\), \({k}_{t}=\omega \sqrt{{\varepsilon }_{t}{\mu }_{0}}\), and \({\eta }_{t}=\sqrt{{\varepsilon }_{t}/{\mu }_{t}}\)

At x < 0 EM field components for the graphene medium are given below:

$${{\text{E}}}_{{\text{z}}}={B}_{3} {e}^{qx}{e}^{-i\beta z}$$
(8)
$${{\text{H}}}_{{\text{z}}}={B}_{4} {e}^{qx}{e}^{-i\beta z}$$
(9)

Here, \({B}_{3}\) and \({B}_{4}\) are amplitudes of electric and magnetic fields, where \(q=\sqrt{{\beta }^{2}-{k}_{0}^{2}}\) and \({k}_{0}=\omega \sqrt{{\mu }_{0}{\varepsilon }_{0}}\). Other EM field components can be derived from [35].

Kubo formulism is utilized for the modelling of monolayer graphene conductivity. Its conductivity is very sensitive to incident wave frequency (\(\omega )\), scattering rate (\(\uptau )\), temperature (T), and chemical potential (\({\mu }_{c})\). The intraband and interband conductivities of graphene are given as

$$\sigma ={\sigma }_{{\text{intra}}}+{\sigma }_{{\text{inter}}}$$
(10)
$$\begin{aligned}\sigma =&\;\frac{i{e}^{2}{K}_{B}T}{\pi {\mathrm{\hslash }}^{2}\left(\omega +\frac{i}{\tau }\right)}\left(\frac{{\mu }_{c}}{{K}_{B}T}+2\mathit{log}[{e}^{-\frac{{\mu }_{c}}{{K}_{B}T}}+1]\right)\\&+\frac{j{e}^{2}}{4\pi \mathrm{\hslash }}\left(\frac{2\left|{\mu }_{c}\right|-\mathrm{\hslash }\left(\omega +\frac{i}{\tau }\right)}{2\left|{\mu }_{c}\right|+\mathrm{\hslash }\left(\omega +\frac{i}{\tau }\right)}\right)\end{aligned}$$
(11)

The first part represents the intraband conductivity while the latter one represents the interband conductivity of graphene. Here, e =\(1.6\times {10}^{-19}c\) is a charge on the electron, \({K}_{B}=1.38\times {10}^{-23}\) J/C is the Boltzmann constant,\(\hslash =1.05\times {10}^{-34}\) Js is the reduced Planks constant, T is the temperature (we have taken 300 K), and \(\omega\) is the incident frequency.

$${\widehat{{\text{e}}}}_{{\text{x}}}\times \left({E}_{1}-{E}_{2}\right)=0$$
(12)
$${\widehat{{\text{e}}}}_{{\text{x}}}\times \left({H}_{1}-{H}_{2}\right)=\sigma E$$
(13)

By applying boundary conditions described in 12 and 13, we get the following dispersion relation:

$$\begin{aligned}&-{k}_{1}{k}_{2}\left({\alpha }_{1}-{\alpha }_{2}\right){\eta }_{t}{\mu }_{0}\omega \left(q\sigma +i{\varepsilon }_{0}\omega \right)\\&-i{{k}_{t}}^{2}{\alpha }_{1}\left({\alpha }_{1}-{\alpha }_{2}\right){\alpha }_{2}q{\eta }_{t}\left(q-i{\mu }_{0}\sigma \omega \right)\\&+{k}_{t}\left({k}_{2}{\alpha }_{1}-{k}_{1}{\alpha }_{2}\right)\left({q}^{2}{{\eta }_{t}}^{2}\sigma +iq\left({\alpha }_{1}{\alpha }_{2}{\mu }_{0}\right.\right.\\&\left.\left.+{{\eta }_{t}}^{2}\left({\varepsilon }_{0}-{\mu }_{0}{\sigma }^{2}\right)\right)\omega +{\varepsilon }_{0}{{\eta }_{t}}^{2}{\mu }_{0}\sigma {\omega }^{2}\right)=0\end{aligned}$$
(14)

Results and Discussion

In this section, the characteristics of SPPs at the UAC-graphene planar interface have been investigated theoretically with the help of dispersion relation. The variation in effective mode index under the different parameters such as chemical potential, relaxation time, number of graphene layers, and chirality parameters versus incident wave frequency are analyzed. For the sake of easy realization of the UAC, we consistently presume:\({\mu }_{t}={\mu }_{z}={\mu }_{0}=4 \pi \times {10}^{-7} H/m\). The permittivity of the UAC might be partially negative; therefore, our study focuses on the plane wave properties in three types of UAC material. Three types of uniaxial chiral media, i.e., \({\varepsilon }_{t}\) > 0,\({\varepsilon }_{z}\)> 0, \({\varepsilon }_{t}\) < 0, \({\varepsilon }_{z}\) < 0 and \({\varepsilon }_{t}\) > 0, \({\varepsilon }_{z}\) < 0 are analyzed to explore the properties of SPPs for the proposed structure. The effective mode index is calculated by dividing the real part of the propagation constant \((\beta )\) by the wave number in a vacuum (\({k}_{0}\)). Mathematically\({N}_{eff}= Re(\frac{ \beta }{{k}_{0}})\).

Case 1: \({{\varvec{\varepsilon}}}_{{\varvec{t}}}>0\), \({{\varvec{\varepsilon}}}_{{\varvec{z}}}>0\)

In this case, the effective mode index is calculated by adjusting \({\varepsilon }_{t}=1.5{\varepsilon }_{0}\) and \({\varepsilon }_{z}={\varepsilon }_{0}\). Static electric field could be used to vary the chemical potential, which is the key parameter to tune the conductivity of graphene. We present a scenario in which the proper choice of chemical potential provides exciting possibilities for tailoring and manipulating SPPs. The chemical potential of graphene is controlled by the carrier concentration or doping level and biasing as reported in [36]. The effect of chemical potential on effective mode index versus incident wave frequency is revealed in Fig. 2(a). Chemical potential varies from \({\mu }_{c}=0.2\) to 0.4 eV. The effective mode index is observed to decrease with an increase in chemical potential. It is evident that manipulating the chemical potential of graphene can either increase or decrease the effective mode index. The influence of relaxation time on the effective mode index is investigated in Fig. 2(b). Since relaxation time depends upon the scattering rate and quality of graphene as presented in [37]. The results suggest that there is an inverse relationship between the effective mode index and relaxation time. The findings suggest that manipulating the relaxation time enables control over the graphene conductivity and, consequently, the effective mode index of the SPP of the proposed structure. The effect of number of graphene layers (N) on the effective mode index versus incident frequency is discussed in Fig. 2(c). It can be noted that by increasing the number of graphene layers effective mode index significantly decreases. This phenomenon can be explained by considering the unique properties of graphene. In pristine, defect-free single-layer graphene, the conductivity is exceptionally high due to the absence of scattering processes. However, when multiple layers of graphene are stacked, the electronic properties are significantly altered. The electrical conductivity of multilayer graphene decreases compared to that of a single layer as reported in [38]. This decrease in conductivity leads decreasing effective mode index as compared to the single-layer counterpart. In order to investigate the chiral strength (i.e., \(\gamma =0.05 {\Omega }^{-1}\), \(\gamma =0.10 {\Omega }^{-1}\), and \(\gamma =0.15 {\Omega }^{-1}\)) on effective mode index is elaborated in Fig. 2(d). The increase in chirality decreases the effective mode index. The chirality parameter \(\gamma\) had significant effect on effective mode index at lower frequencies, diminishing as the frequency increases and become non-significant at 1.5 THz.

Fig. 2
figure 2

Variation of effective mode index with respect to incident frequency with permittivity \({\varepsilon }_{t}=1.5{\varepsilon }_{0}\) and \({\varepsilon }_{z}={\varepsilon }_{0}\): influence of chemical potential (a), relaxation time (b), number of graphene layers (c), chirality (d)

Full size image

Case II \({{\varvec{\varepsilon}}}_{{\varvec{t}}}\) < 0, \({{\varvec{\varepsilon}}}_{{\varvec{z}}}\) < 0

In this case, the numerical analysis of the effective mode index is carried out by choosing \({\varepsilon }_{t}=- 3{\varepsilon }_{0}\) and \({\varepsilon }_{z}=- {0.4 \varepsilon }_{0}\). It is explicitly shown in Fig. 3(a) that chemical potential (\({\mu }_{c}\)) has a significant effect on the effective mode index of SPPs. The relative contribution of the intraband and interband conductivities varies with chemical potential, as explained by Eq. (11); hence, adjusting the suitable value of chemical potential provides some control over SPP. In Fig. 3(a), an increase in chemical potential decreases the effective mode index as reported in [39]. Moreover, as we increase the value of chemical potential (\({\mu }_{c}\)), the curves come closer to each other. This suggests that lower chemical potential have higher impact as compared to higher value of chemical potential. Since graphene possesses a metallic surface character in the terahertz frequency range, it allows to generate the surface plasmon polaritons. By employing chemical potential or electrostatic manipulation, it becomes feasible to finely adjust the Fermi level of graphene [40]. This, in turn, alters its surface conductivity, which serves as a crucial characteristic in Plasmonics and gives an extra degree of freedom while fabricating the waveguides. The effect of relaxation time on the effective mode index is deliberated in Fig. 3(b). Relaxation time extends from \(\uptau =1\times {10}^{-13}\) s to \(\uptau =1.6\times {10}^{-13}\) s. It can be seen that an increase in relaxation time decreases the effective mode index. Figure 3(c) describes the impact of number of graphene layers on effective mode index versus incident wave frequency. An increase in the number of graphene layers causes to decrease in the effective mode index, and this trend is more dominant as compared to case I. Figure 3(d) illustrates the impact of chirality (γ) on the relationship between the effective mode index and incident frequency of propagating SPPs. The effects of different values of chirality, i.e., γ = 0.1 \({\Omega }^{-1}\), γ = 0.3 \({\Omega }^{-1}\), and γ = 0.5 \({\Omega }^{-1}\) are examined. The findings reveal that an increase in chirality leads to an increase in the effective mode index [41]. It is necessary to mention that the curves become squeezing at higher values of chirality. This observation suggests that higher values of chirality have a small impact on the effective mode index, despite the uniform change in chirality. This phenomenon highlights the significant influence of smaller chirality on the effective mode index of SPPs.

Fig. 3
figure 3

Variation of effective mode index with respect to incident frequency with permittivity \({\varepsilon }_{t}=- 3{\varepsilon }_{0}\) and \({\varepsilon }_{z}=- {0.4 \varepsilon }_{0}\): influence of chemical potential (a), relaxation time (b), number of graphene layers (c), chirality (d)

Full size image

Case III \({{\varvec{\varepsilon}}}_{{\varvec{t}}}\) > 0, \({{\varvec{\varepsilon}}}_{{\varvec{z}}}\) < 0

In this case, we have computed our result by considering the transverse and longitudinal components of permittivity as \({\varepsilon }_{t}=0.5{\varepsilon }_{0}\) and \({\varepsilon }_{z}=-0.5{\varepsilon }_{0}\). It is important to note that both components exhibit opposite signs of permittivity. Consequently, the effective mode index is very sensitive, and even slight changes in parameters have a substantial impact on it. The influence of chemical potential (\({\mu }_{c}\)) on the effective mode index is illustrated in Fig. 4(a).Specifically, curves in black, blue, and red represent the chemical potential of 0.2 eV, 0.3 eV, and 0.4 eV, respectively. It can be seen that an increase in chemical potential (\({\mu }_{c}\)) decreases the effective mode index as reported in [42]. The effect of relaxation time on the effective mode index is comprehended in Fig. 4(b). The relaxation time (τ) is an indispensable parameter that significantly influences the conductivity of graphene and has a fundamental impact on the optical properties of the material. It is inferred that an increase in relaxation time decreases the effective mode index as reported in [43]. It is interesting to note that the specific value of relaxation time (\(\uptau\)) has a significant impact on the resonant behavior of graphene and its bandwidth. The impact of the number of graphene layers on the effective mode index is elucidated in Fig. 4(c). The proximity of the blue and red lines is observed to be closer compared to the black and blue lines. This suggests that the effective mode index is more sensitive to single and double layers as compared to double and three layers of graphene. The effect of chirality parameter \(\gamma =0.05 {\Omega }^{-1}\), \(\gamma =0.10 {\Omega }^{-1}\), and \(\gamma =0.15 {\Omega }^{-1}\) on effective mode index is investigated in Fig. 4(d). It is worth mentioned to note that effective mode index starts decreasing by increasing chirality parameter as reported in [44]. Additionally, the graphical representation illustrates that the influence of chirality is not significant at lower frequencies. However, as we move to the higher frequency region, a substantial effect on the effective mode index is exhibited.

Fig. 4
figure 4

Variation of effective mode index with respect to incident frequency with permittivity \({\varepsilon }_{t}=0.5{\varepsilon }_{0}\) and \({\varepsilon }_{z}=-0.5{\varepsilon }_{0}\): influence of chemical potential (a), relaxation time (b), number of graphene layers (c), chirality (d)

Full size image

Normalized field distribution of \({E}_{z}\) and \({H}_{z}\) for uniaxial chiral medium are presented in Fig. 5. The amplitude of surface plasmon polaritons exponentially decays while moving along the interface of two dissimilar media. From the figure, it is clear that the field exponentially decays while propagating hence this behavior confirms the existence of SPPs in uniaxial chiral graphene medium [44].

Fig. 5
figure 5

Normalized field distribution of uniaxial chiral material (\({E}_{Z})\) component (a) and (\({H}_{Z})\) component (b)

Full size image

Conclusion

We have analyzed the excitation of SPP waves at the UAC-graphene planar interface. The dispersion relation for the proposed model is derived analytically. We have examined the variation of the effective mode index versus incident wave frequency under different parameters, including chemical potential, relaxation time, the number of graphene layers, and chirality parameters. Three different types of uniaxial chiral material are characterized by their permittivity as follows: Case I: \({\varepsilon }_{t}\) > 0, \({\varepsilon }_{z}\) < 0, Case II \({\varepsilon }_{t}\) < 0, \({\varepsilon }_{z}\) < 0 and Case III \({\varepsilon }_{t}\) > 0, \({\varepsilon }_{z}\) < 0. It is noteworthy that the effective mode index has a small magnitude in the first case as compared to other two cases. Our results suggest that case III is very sensitive to the effect mode index. Numerical findings suggest that the effective mode index is notably influenced by graphene and UAC features. Normalized field profile of \({E}_{z}\) and \({H}_{z}\) components of UAC confirm the existence of SPPs. The present work may have enchanting applications in optical and chiral sensing, as well as plasmonics and nanophotonics community for the fabrication of high-density nanophotonic chips at the THz frequency range.