Introduction

Surface plasmons polaritons (SPPs) are quantum oscillations of electromagnetic waves that propagate on a metal–dielectric interface with extraordinary properties and promises many potential applications in every aspect of human life such as communication system, biochemical sensing, high resolution imaging system, modulators, and shifters. SPPs have also been suggested as one of the most interesting tools for the development of the upcoming ultracompact-integrated nanophotonic chips. The tunability of SPPs at nanophotonic chips is very crucial for realizing functional SPPs nanophotonic circuits. Numerous planar waveguide structure has been studied by researchers such as metal sandwiched between dielectric layers, dielectric sandwiched between metal layers and other waveguide structure by using plasmonic material and dielectric interface to fabricate ultra-high integrated photonic chips at subwavelength scale. Additionally, dielectric constant has played vital role to tailor the SPPs attributes. Though, in most waveguide structures, only isotropic materials are being used. By leading the anisotropic material into nano-plasmonic structures provide additional degree of freedom to control SPPs as summarized in [1,2,3,4]. It was studied that both transverse electric and transverse magnetic surface waves modes coexist in anisotropic medium. Furthermore, by introducing anisotropy, electromagnetic surface wave attributes can be modified to fabricate nanophotonics chips as presented in [5]. Numerous experimental researches have been carried out to verify the anisotropic propagation of SPPs in nanophotonic circuits [4, 6, 7]. Experimental evidence of the SPPs’ anisotropic propagation in the presence of a weak dielectric anisotropy is in good agreement with the numerical characteristic equation [4]. It was demonstrated that in dielectric-metal-dielectric structure, if top isotropic material is substituted with anisotropic material, the decay length of SPPs waves could be enhanced more than 50% as reported in [8].

Electromagnetic wave propagation in plasma medium attracted much attention in the last few decades due to its unique and extraordinary properties in communication system, biomedical sensing, and air chemistry. Numerous researchers have carried out extensive study on reflection as well transmission properties of plasma [9,10,11,12,13]. Isotropic plasma and anisotropic plasma are two classes of plasma categorized by researchers. Anisotropic plasma medium has attribute over other conventional dielectric materials because electrons density can be tailored by its tensorial permittivity and easy control of EM surface waves due to the presence of external magnetic field [14].

Graphene, a purely two-dimensional version of graphite, with honeycomb structure has attracted tremendous research attention due to its ground-breaking applications in field of scientific community such as electronic and optical properties. Among its exceptional properties, zero bandgap structure distinguishes it from other naturally accruing material because the graphene’s electrons behave like massless fermions, that is very emerging for the fabrication of compact nanophotonic devices. Furthermore, the surface conductivity of graphene can be controlled by adjusting the chemical potential, relaxation time, and EM wave frequency. These parameters play a crucial role in determining the electrical properties of graphene, making it a versatile material with various applications in electronics and optoelectronics. as reported in [15, 16]. Recent advancement in graphene-based plasmonics devices and revolutionized in optical community by its ultra-fast response, photodetectors, terahertz lenses, and modulators [17]. Stronger mode of confinement, high bandwidth, high propagation length, and low attenuation are current challenges in the plasmonics waveguide community [18]. To overcome these bottle-neck problems, graphene hailed all issues due to extra degree of freedom compared to conventional plasmonic material. These unexceptional EM characteristics motivate us to study anisotropic plasma-graphene-anisotropic plasma waveguide structure which has not been presented formerly.

The presented manuscript deals with plasmon modes in graphene medium surrounded by anisotropic plasma layers in THz frequency range. Numerical problems are solved by applying boundary condition and Maxwell’s equation in differential from are used to find electric and magnetic field components. Normalized phase constant and phase velocity for different values of chemical potential or Fermi level of graphene, relaxation time, number of graphene layer electron plasma frequency and cyclotron frequency are analyzed. Field profile for anisotropic plasma medium is also studied.

Methodology

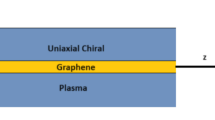
The geometry for anisotropic plasma-graphene- anisotropic plasma is shown in Fig. 1. SPPs waves are propagating along z axis. Graphene is sandwiched between the anisotropic plasma layers.

Fig. 1
figure 1

Three-layer geometry of anisotropic plasma-graphene-anisotropic plasma parallel plate waveguide structure (PPWG)

Full size image

The constitutive relations for anisotropic plasma are given below:

$$D={\varepsilon }_{0}\overline{\overline{\varepsilon }}.E$$
(1)
$$H=1/{\mu }_{0}B$$
(2)

where \({\mu }_{0}\) and \({\varepsilon }_{0}\) permeability of free space and permittivity of free space respectively, and \(\overline{\overline{\upvarepsilon }}\) as follow.

$$[\overline{\overline{\varepsilon }}]=\left[\begin{array}{ccc}{\varepsilon }_{1}& -j{\varepsilon }_{2}& 0\\ j{\varepsilon }_{2}& {\varepsilon }_{1}& 0\\ 0& 0& {\varepsilon }_{3}\end{array}\right]$$
(3)

\({\varepsilon }_{1}\), \({\varepsilon }_{2}\), and \({\varepsilon }_{3}\) are reported in [19]. The wave equation for \({\mathrm{H}}_{\mathrm{z}}\) and \({\mathrm{E}}_{\mathrm{z}}\) in the anisotropic plasma can be written as follows [20]. The time dependency \({e}^{j\omega t}\) is taken.

$$\left[\begin{array}{c}{\nabla }^{2}{E}_{z}\\ {\nabla }^{2}{H}_{z}\end{array}\right]+\left[\begin{array}{cc}{g}_{1}& {jg}_{2}\\ {jg}_{3}& {g}_{4}\end{array}\right]\left[\begin{array}{c}{E}_{z}\\ {H}_{z}\end{array}\right]=0,$$
(4)

where

$$\nabla ={\widehat{e}}_{x}\frac{\partial }{\partial x}+{\widehat{e}}_{y}\frac{\partial }{\partial y}$$
(5 )
$${g}_{1}=-(\frac{{\beta }^{2}{\varepsilon }_{3}}{ {\varepsilon }_{1}}-{\omega }^{2}{\mu }_{0}{\varepsilon }_{3})$$
(6)
$${g}_{2}=\frac{\omega {\mu }_{0}\beta {\varepsilon }_{2}}{{\varepsilon }_{1}}$$
(7)
$${g}_{3}=-\beta \omega {\varepsilon }_{3}\frac{{\varepsilon }_{3}}{{\varepsilon }_{1}}$$
(8)
$${g}_{4}=\frac{{\omega }^{2}{\mu }_{0}{\varepsilon }_{1}^{2}-{{\omega }^{2}{\mu }_{0}\varepsilon }_{2}^{2})}{{\varepsilon }_{1}}-{\beta }^{2}$$
(9)

The eigenvalues are denoted as follows:

$${{q}_{1}}^{2}=\frac{1}{2}\left\{{g}_{1}+{g}_{4 }+\sqrt{{{(g}_{1}+{g}_{4})}^{2}-4\left({g}_{1}{g}_{4}-{g}_{2}{g}_{3}\right)}\right\}$$
(10)
$${{q}_{2}}^{2}=\frac{1}{2}\{{g}_{1}+{g}_{4 }-\sqrt{{{(g}_{1}+{g}_{4})}^{2}-4\left({g}_{1}{g}_{4}-{g}_{2}{g}_{3}\right)}\}$$
(11)

Electromagnetic field components of the anisotropic plasma mediums are given below:

$${E}_{z1}={c}_{1}{e}^{-{q}_{1}x}+{c}_{2}{e}^{-{q}_{2}x}$$
(12)
$${H}_{z1}={j(c}_{1}{\alpha }_{1}{e}^{-{q}_{1}x}+{c}_{2}{\alpha }_{2}{e}^{-{q}_{2}x})$$
(13)
$${E}_{z2}={c}_{3}{e}^{{q}_{1}x}+{c}_{4}{e}^{{q}_{2}x}$$
(14)
$${H}_{z2}={j(c}_{3}{\alpha }_{1}{e}^{-{q}_{1}x}+{c}_{4}{\alpha }_{2}{e}^{-{q}_{2}x})$$
(15)

Remaining field components are derived from [21]. Following boundary conditions are used to obtain characteristic equation:

$$\widehat{x}\times \left[{H}_{1}-{H}_{2}\right]=\sigma E$$
(16)
$$\widehat{x}\times \left[{E}_{1}-{E}_{2}\right]=0$$
(17)

The above boundary conditions are employed to obtain characteristic equation. \(\sigma\) is graphene conductivity follow as:

$$\sigma \left(\mu ,\tau ,\mathrm{T}\right)=\frac{j{e}^{2}\left(\omega -j{\tau }^{-1}\right)}{\pi {h}^{2}}\times \left[\frac{1}{{\left(\omega -j{\tau }^{-1}\right)}^{2}}{\int }_{0}^{\infty }\times \xi \left(\frac{\sigma {f}_{d}\left(\xi ,\mu ,T\right)}{\sigma \xi }-\frac{\sigma {f}_{d}\left(-\xi ,\mu ,T\right)}{\sigma \xi }\right)d\xi -{\int }_{0}^{\infty }\times \frac{{f}_{d}\left(-\xi ,\mu ,T\right)-{f}_{d}\left(\xi ,\mu ,T\right)}{{\left(\omega -j{\tau }^{-1}\right)}^{2}-4{\left({}^{\xi }/_{{\hslash}}\right)}^{2}}d\xi \right]$$
(18)

where \(\mu ,\tau ,\mathrm{T},\) \(e,\) \({f}_{d},\) \(\omega ,\) \(\xi ,\) and \(\hslash\) represent chemical potential, relaxation time, temperature, electron charge, Fermi–Dirac distribution, angular frequency, energy, and reduced Plank’s constant, respectively [22]. By applying boundary conditions 16 and 17, the following characteristic equation is obtained:

$$\mathrm{i}\sigma {q}_{1}(b-d{\alpha }_{1})+{q}_{2}(-\mathrm{i}b\sigma +{\alpha }_{2}(\mathrm{i}d\sigma +2({b}^{2}+df){q}_{1})-2({b}^{2}+df){q}_{1}{\alpha }_{1})= 0$$
(19)

Results

In this part, numerical simulation results are presented to explore the properties of SPPs modes at anisotropic plasma-graphene-anisotropic plasma waveguide structure. Normalized phase constant, as well as group velocity for different values of Fermi level or chemical potential, relaxation time, number of graphene layers, electron plasma frequency, and cyclotron frequency, is studied. Field profile for anisotropic plasma medium is also presented for the verification of EM surface waves. Graphene is emerging plasmonic material with fascinating and extraordinary properties to control nanophotonic devices by tailoring chemical potential and gate voltage. The complex surface conductivity of single-layer graphene is modeled by Kubo formulism. Kubo formula is the function of incident frequency, relaxation time, chemical potential, and temperature. In all the graphs, T = 300 K is considered. To study the higher and lower SPPs for proposed structure between incident wave frequency and normalized phase constant in Fig. 2(a and b). Incident wave frequency band extends from \(0\) to \(62\) THz frequency range. Normalized phase constant \(Re(\frac{\beta }{{k}_{0}})\), \(\beta\) is propagation constant and \({k}_{0}\) is the wavenumber in free space. To study the impact of chemical potential on normalized phase constant versus incident frequency in THz frequency range is depicted in Fig. 2a. Chemical potential or Fermi level of graphene is the following: \(\mu =h{v}_{F}\sqrt{\pi {n}_{2D}}\). \({v}_{F}\) denoted electrons Fermi velocity. Additionally, by tailoring gate voltage one can easily tailored carrier density \({n}_{2D}\) as reported in [23]. Higher and lower plasmon modes for proposed waveguide structure are strongly influenced by chemical potential. As chemical potential or Fermi level of graphene increases from 0.2 to 0.5 eV, higher mode dispersion curves are shifted toward high-frequency region in contrast to lower mode and frequency band broadened for both modes. By increasing chemical potential normalized phase constant decreases for higher mode as reported in [23,24,25,26]. When the chemical potential is increased, the SPPs’ absorption and dampening properties can be enhanced. Because of the increased scattering and collision processes that are caused by higher charge carrier densities, the coherent propagation of surface plasmons is reduced due to the higher scattering and collision processes. But in the case of higher mode normalized phase constant starts increasing at higher chemical potential. It is possible to achieve rapid and efficient control of light propagation by dynamically changing the graphene’s chemical potential, which is crucial for high-speed signal processing. Figure 2b depicts the impact of relaxation time on normalized phase constant versus incident frequency. Relaxation time increases from \(0.1\times {10}^{-13}s\) to \(5\times {10}^{-13}s\) shown by blue, red, black, and orange thin peaks. Both lower mode as well as higher mode are strongly influenced by relaxation time. Normalized phase constant gets reduced at higher relaxation time for higher mode as reported in [24]. In the case of lower mode higher normalized phase constant shown at higher relaxation time. By increasing relaxation time, higher mode dispersion peaks are forward at low-frequency region and lower mode dispersion peaks are forward toward high-frequency region. Moreover, as relaxation time increases higher mode peaks starts squeezing and low mode peaks broadened. Lower mode curves show overlapping at 60 THz, but higher mode curves overlap at higher incident frequencies. The former tunability trait suggests that SPPs modes can be engineered by graphene conductivity features such as chemical potential as well as relaxation time. To demonstrate the variation on normalized phase constant under different numbers of graphene layers for lower and higher is presented in Fig. 3a. Since single layer of graphene absorbed 2.3% of incident light as summarized in [27]. Normalized phase constant starts decreasing for greater number of graphene layers as reported in [23, 24]. Normalized phase constant starts increasing for greater number of graphene layers. Dispersion peaks broadening occur in higher mode but remains same lower mode for different graphene layers. Figure 3b presents the impact of plasma frequency on normalized phase constant. At higher plasma frequency both modes dispersion curves are shifted toward high-frequency region as reported in [12, 28, 29].

Fig. 2
figure 2

Effect on normalized phase constant under different values of chemical potential and relaxation time in Fig. 2a and b respectively

Full size image
Fig. 3
figure 3

Effect on normalized phase constant under different graphene layers and plasma frequency in Fig. 3a and b respectively

Full size image

Dispersion peaks start squeezing for higher as well as lower mode at higher plasma frequency. So, it is of significant interest to mention that permittivity tensor tunes both modes of proposed waveguide structure. Figure 4a depicts the influence of cyclotron frequency on normalized phase constant versus incident wave frequency. Cyclotron frequency can tailor both modes according to desired application for nanophotonic circuits. In contrast to lower mode, by increasing cyclotron frequency higher mode dispersion curves are shifted toward low-frequency region. Figure 4b depicts the influence of chemical potential on phase velocity. It can be noted that phase velocity of proposed structure can be tuned by tunning chemical potential of graphene material. Variation in phase velocity under the different graphene layers and plasma frequency are revealed in Figs. 5a and b respectively. For the case of lower mode, in Fig. 5a, phase velocity starts decreasing for greater number of graphene layers in contrast to higher mode. In Fig. 5b, the higher mode of phase velocity is strongly affected by plasma frequency of electrons compared to lower mode. Additionally, phase velocity strongly depends upon plasma frequency for both modes. Since EM surface wave has two conditions: it propagate between two dissimilar media and show attenuation as its propagate away from the interface [24]. To verify EM surface waves, normalized field distribution for anisotropic plasma medium is presented in Fig. 6. It can be noted that from blue and black peaks with increasing distances from interface, field profiles decrease exponentially. The exponential decrease in field profiles has important implications in various applications. For instance, in signal processing, it is crucial to account for this behavior when designing communication systems. By understanding the rate of decrease, engineers can optimize the transmission of signals over long distances.

Fig. 4
figure 4

Effect on normalized phase constant under different values of cyclotron frequency in Fig. 4a and effect on phase velocity under different values of chemical potential

Full size image
Fig. 5
figure 5

Effect on phase velocity under different graphene layers and plasma frequency in Figs. 5a and 5b respectively

Full size image
Fig. 6
figure 6

Normalized field distribution of anisotropic plasma medium at \({\omega }_{p}=2\times {10}^{14}Hz\), \({\omega }_{c}=40\times {10}^{10}Hz\), \(\mu =0.2 eV\), and \(\tau =5\times {10}^{-13}s\)

Full size image

Conclusion

A theoretical model is developed at anisotropic plasma-graphene-anisotropic plasma waveguide structure. Normalized phase constant and phase velocity as the function of incident wave frequency in THz regime were studied for different values chemical potential or Fermi energy of graphene, relaxation time, number of graphene layers, plasma frequency, and cyclotron frequency. Compared to lower mode, higher mode strongly depends upon graphene as well as anisotropic plasma parameters. Normalized field distribution for anisotropic plasma was also studied to confirm EM surface waves condition. The presented results may be helpful to increase the efficiency of nanophotonic devices due to the extra degree of graphene over other plasmonic materials.