Introduction

Discussion on invisibility cloaks and other devices which are designed based on the theory of transformation optics (TO) [1–6] has been increasing during the last years. All these devices including interior invisibility cloak [1, 2], exterior invisibility cloak [3], concentrator [4, 5] rotator [6], etc. are designed and solved by the TO theory. Different shapes of these devices such as square shape [4] and elliptical [7] interior cloak are also studied. Some development to the above devices are also reported such as twin interior [8] and exterior [9] cloak. A cloak using non-Euclidean geometry in order to remove some singularities in the structure of the Euclidean interior cloak is also reported [10].

Solving Maxwell’s wave equation analytically using the result of TO theory for some of these devices are also reported. Cylindrical [11–14], spherical [13–17] and elliptical [18], interior invisibility cloak, a cone-shape interior cloak [19], spherical concentrator [20] and superscatterer [21] can be exemplified. Analytical solution for a cylindrical cloak with reduced material parameter is expressed in [22, 23].

In this paper, we first solve the Maxwell’s wave equation and applying boundary conditions for a TO device with a general form of transformation function in a 2D cylindrical coordinate, then we illustrate some simulations based on the result of analytical solution for some of the above devices to show the performance of the device. We especially emphasize on the solution of the wave equation in an external invisibility cloak with polynomial transformation function of different order and also an exponential transformation function which were not considered before. We also compare the simulations with the simulations of a finite element software (COMSOL Multiphysics).

The paper is organized as follows: in “Maxwell’s Wave Equation in a General Cylindrical TO Medium”, Maxwell’s wave equation is solved in a general transformation media with a general form of transformation relation. In “Two Neighbouring Cylindrical TO Media”, we design our desired TO device using two different transformation media of “Maxwell’s Wave Equation in a General Cylindrical TO Medium” in touch to each other and solve the wave equation for it by satisfying the boundary conditions. In “Numerical Simulations”, we explain some examples and provide some numerical simulations using two different methods. We consider some examples for transformation function and provide some simulations according to the numerical results obtain for these functions in order to compare those with the corresponding field distributions extracted from the analytical solutions. Finally, the concluding remark will be presented in “Conclusion”.

Fig. 1
figure 1

The structure of a general TO device. This device depending on the transformation function f(r) and g(r) can be interior or exterior invisibility cloak, concentrator, etc.

Full size image

Maxwell’s Wave Equation in a General Cylindrical TO Medium

If we consider a coordinate transformation function

$$\begin{array}{@{}rcl@{}} r^{\prime}=\mathcal{F}(r),\qquad \theta^{\prime}=\theta, \qquad z^{\prime}=z; \end{array} $$
(1)

in a cylindrical coordinate system which relates virtual space (primed coordinate) to physical space (unprimed coordinate) and wherein \(\mathcal {F}(r)\) is an arbitrary function, then according to the TO theory, dielectric properties of a general TO device (cloak, concentrator, etc.) with above transformation relation is a diagonal matrix

$$\begin{array}{@{}rcl@{}} \boldsymbol{\epsilon}=\left(\begin{array}{ccc} \epsilon_{r}&0&0\\ 0&\epsilon_{\theta}&0\\ 0&0&\epsilon_{z} \end{array}\right) \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} \boldsymbol{\mu}=\left(\begin{array}{ccc} \mu_{r}&0&0\\ 0&\mu_{\theta}&0\\ 0&0&\mu_{z} \end{array}\right) \end{array} $$
(3)

where in 𝜖 and μ are relative permittivity and permeability tensor of the device, respectively, and the diagonal elements are given by [1, 2, 14]

$$\begin{array}{@{}rcl@{}} \epsilon_{r}=\mu_{r}&=&\frac{\mathcal{F}(r)}{r\mathcal{F}^{\prime}(r)},\qquad \epsilon_{\theta}=\mu_{\theta}=\frac{r\mathcal{F}^{\prime}(r)}{\mathcal{F}(r)},\\ &&\epsilon_{z}=\mu_{z} =\frac{\mathcal{F}(r)\mathcal{F}^{\prime}(r)}{r}. \end{array} $$
(4)

and we have assumed the virtual space to be the empty space 𝜖 ′ = μ ′ = 1.

If we choose TE mode (electric field along the z direction) for solving the wave equation, therefore, only 𝜖 z , μ r and μ 𝜃 are relevant and the wave equation in this general cylindrical TO device take the form of [12]

$$\begin{array}{@{}rcl@{}} \frac{1}{\epsilon_{z} r}\frac{\partial}{\partial r} \left(\frac{r}{\mu_{\theta}}\frac{\partial E_{z}}{\partial r}\right)+\frac{1}{\epsilon_{z} r^{2}}\frac{\partial}{\partial \theta}\left(\frac{1}{\mu_{r}}\frac{\partial E_{z}}{\partial \theta}\right)+{k_{0}^{2}}E_{z}=0;\\ \end{array} $$
(5)

where k 0 is the wave vector of light in vacuum. By substituting (4) into Eq. 5 and after separation of variables E z (r, 𝜃) = ψ(r)P(𝜃) and introduction of a constant l, the radial and polar differential equations will have the following form, respectively,

$$\begin{array}{@{}rcl@{}} &&\frac{\mathcal{F}}{\mathcal{F}^{\prime}}\frac{d}{d r}\left(\frac{\mathcal{F}}{\mathcal{F}^{\prime}}\frac{d\psi(r)}{dr}\right)+\left({k_{0}^{2}}\mathcal{F}^{2}-l^{2}\right)\psi(r)=0, \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} &&\frac{d^{2}P(\theta)}{d\theta^{2}}+l^{2}=0. \end{array} $$
(7)

The general solution for polar differential equation (7) is e ±il𝜃, and l, due to the rotational boundary condition, is an integer number. For finding the solution of radial differential equation, a change of variable of the form \(x=\mathcal {F}(r)\) is needed, so that after applying this procedure, Eq. 6 becomes

$$\begin{array}{@{}rcl@{}} x^{2}\frac{d^{2}\psi}{dx^{2}}+x\frac{d\psi}{dx}+({k_{0}^{2}}x^{2}-l^{2})\psi=0. \end{array} $$
(8)

Equation 8 is a Bessel differential equation with variable x. Thus, the solution for radial differential equation is

$$\begin{array}{@{}rcl@{}} \psi_{l}(r)=AJ_{l}\left(k_{0}f(r)\right)+BH_{l}^{(1)}\left(k_{0}f(r)\right), \end{array} $$
(9)

where J l (.) and \(H_{l}^{(1)}(.)\) are l-order Bessel and Hankel functions of the first kind. Therefore, a simple set of solutions of the form ψ l (r)e il𝜃 exist for E z in the general transformation medium.

Two Neighbouring Cylindrical TO Media

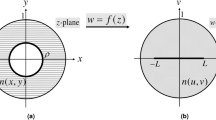
Suppose our device is a coaxial infinite cylinder with inner (outer) radius a(b), so this device has three regions including core(r < a), shell (a < r < b) and outside (r>b). We also suppose that this device is surrounded by vacuum, i.e. 𝜖 o = μ o = 1. We set the transformation function for the core material to be g(r) and for the shell to be f(r). Figure 1 is depicted to show the structure of our general device.

If f(a) = 0,f(b) = b, regardless of the g(r), this device would be an interior invisibility cloak and if f(a) = c, f(b) = b and g(0) = 0,g(a) = c, the resulting device would be an external invisibility cloak for a < b < c and concentrator for a < c < b.

The electric fields for a general device depicted in Fig. 1, in three regions are as follows:

$$\begin{array}{@{}rcl@{}} E_{z}(r>b)&=& \sum\limits_{l=-\infty}^{+\infty} \alpha^{in}_{l} J_{l}(k_{0}r)e^{il\theta}\\ &+&\sum\limits_{l=-\infty}^{+\infty} \alpha_{l}^{sc}H_{l}(k_{0}r)e^{il\theta} \\ E_{z}(a<r<b)&=&\sum\limits_{l=-\infty}^{+\infty} \alpha^{(1)}_{l} J_{l}(k_{0}f(r))e^{il\theta}\\ &+&\sum\limits_{l=-\infty}^{+\infty} \alpha_{l}^{(2)}H_{l}(k_{0}f(r))e^{il\theta}\\ E_{z}(r<a)&=&\sum\limits_{l=-\infty}^{+\infty} \alpha^{(3)}_{l} J_{l}(k_{0}g(r))e^{il\theta} \end{array} $$
(10)

where \({\alpha _{l}^{i}}\)(i = 1,2,3,i n, s c) are the expansion coefficients for the fields in the relevant regions.

Boundary conditions for the problem at hand are continuity of tangential component of electric field (E z ) and magnetic field (H 𝜃 ), at r = a and r = b. Therefore, using the orthogonality of e il𝜃 at r = b, we have

$$\begin{array}{@{}rcl@{}} \alpha_{l}^{in}J_{l}(k_{0}b)&+&\alpha_{l}^{sc}H_{l}(k_{0}b)=\\ &&\alpha_{l}^{(1)}J_{l}(k_{0}f(b))+\alpha_{l}^{(2)}H_{l}(k_{0}f(b)) \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} \alpha_{l}^{in}J^{\prime}_{l}(k_{0}b)&+&\alpha_{l}^{sc}H^{\prime}_{l}(k_{0}b)=\\ &&\frac{f(b)}{b}\left[\alpha_{l}^{(1)}J^{\prime}_{l}(k_{0}f(b))+ \alpha_{l}^{(2)}H^{\prime}_{l}(k_{0}f(b))\right] \end{array} $$
(12)

and for interface at r = a, we obtain

$$\begin{array}{@{}rcl@{}} \alpha_{l}^{(3)}{}&&J_{l}(k_{0}g(a+\delta))=\\ &&\alpha_{l}^{(1)}J_{l}(k_{0}f(a+\delta))+\alpha_{l}^{(2)}H_{l}(k_{0}f(a+\delta)) \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} \alpha_{l}^{(3)}{}&&J^{\prime}_{l}(k_{0}g(a+\delta))=\\ &&\frac{f(a+\delta)}{g(a+\delta)}\left[\alpha_{l}^{(1)}J^{\prime}_{l}(k_{0}f(a+\delta))+\alpha_{l}^{(2)}H^{\prime}_{l}(k_{0}f(a+\delta))\right]. \end{array} $$
(14)

In Eqs. 13 and 14, the parameter δ ≠ 0,δ≪1 is applied for interior cloak because of the reason expressed in [12], and δ = 0 is applied for other TO devices such as external cloak and concentrator.

For the case δ = 0, the above relations take the simple forms of

$$\begin{array}{@{}rcl@{}} (\alpha_{l}^{in}-\alpha_{l}^{(1)})J_{l}(k_{0}b)+(\alpha_{l}^{sc}-\alpha_{l}^{(2)})H_{l}(k_{0}b)=0, \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}} (\alpha_{l}^{in}-\alpha_{l}^{(1)})J^{\prime}_{l}(k_{0}b)+(\alpha_{l}^{sc}-\alpha_{l}^{(2)})H^{\prime}_{l}(k_{0}b)=0, \end{array} $$
(16)

in r = b and

$$\begin{array}{@{}rcl@{}} (\alpha_{l}^{(3)}-\alpha_{l}^{(1)})J_{l}(k_{0}c)-\alpha_{l}^{(2)}H_{l}(k_{0}c)=0, \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} (\alpha_{l}^{(3)}-\alpha_{l}^{(1)})J^{\prime}_{l}(k_{0}c)-\alpha_{l}^{(2)}H^{\prime}_{l}(k_{0}c)=0, \end{array} $$
(18)

in r = a, respectively. In Eqs. 15–18, we have used the fact that f(b) = b and f(a) = c.

Since b and c are arbitrary and Bessel functions are not always zero, so, as a direct result, we have

$$\begin{array}{@{}rcl@{}} \alpha_{l}^{(1)}=\alpha_{l}^{(3)}=\alpha_{l}^{in},\qquad\alpha_{l}^{(2)}=\alpha_{l}^{sc}=0. \end{array} $$
(19)

For the case δ ≠ 0 (interior cloak) with respect to the fact that f(a) = 0 and f(a+δ)≃0 with the same reasoning expressed in [12], we obtain that

$$\begin{array}{@{}rcl@{}} \alpha_{l}^{(1)}=\alpha_{l}^{in},\qquad \alpha_{l}^{sc}=\alpha_{l}^{(2)}=0, \qquad\alpha_{l}^{(3)}=0. \end{array} $$
(20)

The above results are obtained for any form of incident field which shows that the TO device work properly and perfectly for any kind of incident field. For numerical simulation of the electric fields in all regions, we have to specify the incident field. The expansion of the electric field for plane wave and for a line source in term of Bessel function is brought here to use in numerical simulations in the next section.

The expansion for the z-component of a TE mode plane wave in term of Bessel function is given by [24]

$$\begin{array}{@{}rcl@{}} E_{z}(r,\theta)=E_{0}\sum\limits_{l=-\infty}^{+\infty}i^{-l}J_{l}(k_{0}r)e^{il(\theta-\theta_{0})}, \end{array} $$
(21)

where 𝜃 0 is incident angle and for the line source is [24]

$$\begin{array}{@{}rcl@{}} E_{z}= E_{0}\left\lbrace \begin{array}{ccc} {\sum}_{l=-\infty}^{+\infty} J_{l}(k_{0}r)H_{l}(k_{0}r^{\prime})e^{il(\theta-\theta^{\prime})}&r<r^{\prime}\\\\ {\sum}_{l=-\infty}^{+\infty} J_{l}(k_{0}r^{\prime})H_{l}(k_{0}r)e^{il(\theta-\theta^{\prime})}&r>r^{\prime} \end{array}\right., \end{array} $$
(22)

where r ′ and 𝜃 ′ show the position of the point source in cylindrical polar coordinate. E 0 in both cases is the amplitude of the electric field.

Numerical Simulations

In this section, we do some simulations for some examples of different TO devices. The simulations are done with two methods: the first one is based on the above theoretical approach using Mathematica software and the other method using a finite element software (COMSOL Multiphysics). Finally, we compare the results for the electric field distributions which are obtained from the two methods.

Interior Invisibility Cloak

Since the case of linear transformation function was analysed by many researchers like in [11, 12], here, we consider a second-order transformation function, so that for this kind of cloak, we choose (only) f(r) to be

$$\begin{array}{@{}rcl@{}} f(r)=b\left(\frac{r-a}{b-a}\right)^{n}, \end{array} $$
(23)

with n = 2, where f(a) = 0 and f(b) = b as we expected. Figure 2 shows the diagram for transformation function and Fig. 3 shows the numerical simulation of the scattering pattern from our TO device by using the electric field of a TE mode cylindrical line (point) source located at r ′ = 2 and 𝜃 ′ = π/3 (see (22)). It should be noted that in employing (21) and (22) by Mathematica, we have truncated the summation over l to a finite number. Thus, hereafter in all examples, we have chosen −40 ≤ l ≤ 40. Figure 4 is the numerical simulation for an interior invisibility cloak with a second-order transformation function prepared with finite element method using COMSOL Multiphysics software. The parameters which we applied to do the simulations in the two methods are 2a = b = 2λ = 1 unit. According to Figs. 3 and 4, one can see that the two methods have a very good agreement with each other.

Fig. 2
figure 2

Second-order transformation function for an interior cloak, n = 2

Full size image
Fig. 3
figure 3

Numerical simulation of z-component electric field from a cylindrical interior cloak with a second-order transformation function illuminated by a point source located at \(r^{\prime }=2, \theta ^{\prime }=\pi /3\). This distribution is obtained by analytical solution of the wave equation and then diagramed by Mathematica software

Full size image
Fig. 4
figure 4

The same situation as in Fig. 3, but the electric field distribution is obtained by using finite element method in COMSOL Multiphysics for the considered TO device

Full size image

According to the analytical solution for the case of interior invisibility cloak, Eq. 20, \(\alpha _{l}^{(3)}=0\), which means that no wave penetrate into the core of the device. The simulations in both approaches also approve this result. Therefore, each object which is placed inside the core cavity of the device will be hidden from the outside observer. Figure 5 is brought to show this hiding effect. In this figure, an arbitrary object is placed inside the cavity of the cloak of Fig. 4. The scattering pattern in both figures are exactly the same and are similar to the scattering pattern of empty space which prove that the object as well as the cloak itself are hidden.

Fig. 5
figure 5

An arbitrary object (here star shape) is hidden from the observer by an internal cloak with a second-order transformation function n = 2. The simulation parameters are exactly the same as the parameters in Fig. 4. The similarity of the scattering pattern here with the one in Fig. 4 approves the hiding effect for the object

Full size image

In order to construct interior invisibility cloak experimentally, due to some singularities in the material parameters of the cloak, 𝜖 𝜃 and μ 𝜃 , at inner radius r = a, some reduced cloaks with different orders of polynomial transformation function are proposed. Effective medium theory is applied to design proper metamaterials at an operating frequency which due to reduction in material properties lead to imperfect cloaks [25, 26].

Concentrator

We consider the following general form of transformation function for a concentrator in cylindrical polar coordinate

$$\begin{array}{@{}rcl@{}} f(r)=(c-b)\left(\frac{r-b}{a-b}\right)^{n}+b, \end{array} $$
(24)

and

$$\begin{array}{@{}rcl@{}} g(r)=c(r/a)^{m}, \end{array} $$
(25)

with a < c < b, so that the conditions f(a) = c, f(b) = b and g(0)=0,g(a) = c are satisfied. So the simulation result for a concentrator with m = n = 3 illuminated by a TE plane wave from the left using the Mathematica software (−40≤l≤40) is illustrated in Fig. 7. The corresponding diagram for transformation function is plotted in Fig. 6. Figure 8 shows the same situation as in Fig. 7, but using COMSOL Multiphysics software. The parameters which we used in the two methods are 2a = b = 2λ = 1 unit and c = 0.75 unit. The similarity of the two simulations in Figs. 7 and 8 is clear.

Fig. 6
figure 6

Transformation function for a concentrator with m = n = 3

Full size image
Fig. 7
figure 7

Numerical simulation of electric field for a cylindrical concentrator with a third-order transformation function in core and shell, m = n = 3 illuminated by a TE plane wave from the left using Mathematica software. Normal incidence is considered 𝜃 0 = 0 (see (21))

Full size image
Fig. 8
figure 8

The same situation as in Fig. 7, but using finite element method in COMSOL Multiphysics

Full size image

Some concentrators are also designed and constructed experimentally using metamaterials created based on effective medium theory. See for instance references [27] and [28].

Exterior Invisibility Cloak

The transformation relations (24) and (25) are still valid for the case of external cloak. The only change which we should apply here is that a < b < c. In the following, we exemplify three different situations for the transformation function of the core and shell.

For the first example, we consider the most simple case m = n = 1. The diagram for transformation function is brought in Fig. 9, and Figs. 10 and 11 are the simulation results elicited from the Mathematica (−40≤l≤40) and COMSOL software, respectively. It should be noted that we set the parameters in all the examples for external cloak to be 2a = b = c/2=2λ = 1 unit. We also mention that the aforementioned example with m = n = 1 is exactly the same as the one in [3] which was done by Lai et al. using finite element approach. One can see that the result of the analytical solution with Mathematica software (Fig. 10) is matched with the result of finite element approach (Fig. 11 here and Fig. 2a in [3]) (Fig. 12).

Fig. 9
figure 9

Polynomial first-order transformation function in core and shell for an exterior cloak, m = n = 1

Full size image
Fig. 10
figure 10

Numerical simulation of electric field for an external cloak with linear transformation function in core and shell, m = n = 1, illuminated by a TE plane wave from the left using Mathematica software. Normal incidence is considered 𝜃 0 = 0

Full size image
Fig. 11
figure 11

The same situation as in Fig. 10, but using finite element method in COMSOL Multiphysics

Full size image
Fig. 12
figure 12

Second-order transformation function in core and shell for an external cloak, m = n = 2

Full size image

External cloak with a second-order transformation function in its core and shell is analysed in Figs. 13 and 14. Figure 13 shows the simulation result obtained by solving wave equation analytically using Mathematica software with m = n = 2. Figure 14 shows the full wave simulation result of a z-component electric field using finite element software (COMSOL) for the same external cloak. In these figures, the cloak is illuminated by a point (line) source located at r ′ = 2, 𝜃 ′ = π/3. The results of the two methods have a very good coincidence with each other. The corresponding diagram for transformation function is plotted in Fig. 12.

Fig. 13
figure 13

Scattering pattern of electric field z-component for an external cloak with a second order-transformation function in core and shell, m = n = 2, illuminated by a point source located at \(r^{\prime }=2,\theta ^{\prime }=\pi /3\) using calculation with Mathematica software

Full size image
Fig. 14
figure 14

The same situation as in Fig. 13, but using finite element method in COMSOL Multiphysics

Full size image

In the last example for the external cloak with polynomial transformation function, we prefer to choose different orders for transformation functions in core and shell. So, we choose linear transformation function for the shell and a third-order transformation function for the core, i.e. m = 3,n = 1. Figure 15 is the diagram for transformation function and Figs. 16 and 17 are the simulations for this case by theoretical solution and finite element method, respectively. According to these figures, also in this case, one can see the same field distributions inside and outside of the external cloak device for the normal incident of a TE plane wave.

Fig. 15
figure 15

Transformation function for an external cloak, third order in core and first order in shell, m = 3,n = 1

Full size image
Fig. 16
figure 16

Scattering pattern of electric field z-component for an external cloak with different orders of transformation function in core and shell. The order for core transformation function was set to be m = 3, and the order of the shell transformation function is n = 1; (−40≤l≤40)

Full size image
Fig. 17
figure 17

The same situation as in Fig. 16, but using finite element method in COMSOL Multiphysics

Full size image

Exponential Transformation Function

It should be notice that the transformation functions which we applied so far in all the examples were polynomials in different orders. But the theory allows us to study other kinds of transformation function (e.g. logarithmic, exponential, trigonometric, Gaussian, etc.). So, for the last example, we choose exponential transformation function. Therefore, we choose f(r) to be of the form

$$\begin{array}{@{}rcl@{}} f(r) = b \mathrm{e}^{\alpha(r-b)}, \end{array} $$
(26)

where \(\alpha =\frac {\ln (c/b)}{a-b}<0\). Again, we remind that the conditions f(a) = c, f(b) = b are still satisfied.

The above exponential form for transformation function, Eq. 26, according to the relation (4), will lead to the following constitutive parameter for the shell in our TO device

$$\begin{array}{@{}rcl@{}} \epsilon_{r}&=&\mu_{r}=\frac{1}{\alpha r},\qquad \epsilon_{\theta}=\mu_{\theta}=\alpha r,\\\\\epsilon_{z} &=&\mu_{z}=\alpha b^{2}\frac{\mathrm{e}^{2\alpha(r-b)}}{r}; \end{array} $$
(27)

which we think may be easier to constructed experimentally using metamaterials due to its simple form of 𝜖 r and 𝜖 𝜃 .

For the core material, we easily choose linear transformation function, so we choose (25) with m = 1 for g(r). Thus, the form of the core constitutive parameter would be

$$\begin{array}{@{}rcl@{}} \epsilon_{r}=\mu_{r} =1 \qquad \epsilon_{\theta}=\mu_{\theta}=1, \qquad\epsilon_{z}=\mu_{z}=(c/a)^{2} \end{array} $$
(28)

which is very simple to construct experimentally. The diagram for transformation function in this case is shown in Fig. 18.

Fig. 18
figure 18

Transformation function for an external cloak, exponential form in shell and linear polynomial form in core

Full size image

The corresponding numerical simulations for an external cloak with foregoing transformation functions are shown in Figs. 19 and 20. The former, Fig. 19, is the numerical simulation results extracted from analytical solution method and the latter, Fig. 20, is the simulation obtained from finite element method. The required parameters to do the simulations are given by 2a = b = c/2=2λ = 1 unit. A TE plane wave is incident on the external cloak at an angle 𝜃 0 = 45 degree.

Fig. 19
figure 19

Scattering pattern of electric field z-component for an external cloak with exponential transformation function in shell and linear transformation function for the core. The relation for the shell transformation function is expressed by Eq. 26 and the relation for the core transformation function is expressed by Eq. 25 with m = 1. (−40≤l≤40) and 𝜃 0 = 45

Full size image
Fig. 20
figure 20

The same situation as in Fig. 19, but using finite element method in COMSOL Multiphysics

Full size image

For hiding an object with an external cloak according to the approach expressed in [3], the object should be inserted beside the cloak (b < r ′<c) and the corresponding antiobject have to be placed in the negative shell of the cloak (a < r < b). All the geometric and dielectric properties of the object and its corresponding antiobject are related to each other according to transformation relation and TO theory. In Fig. 21, we have used of the external cloak structure which is shown in Fig. 20 to hide a curved-sheet object with relative constitutive parameters 𝜖 ′ = 2μ ′ = 2 in the bottom of the cloak. So, the constitutive parameters for the antiobject according to Eq. 27 have to be equal to

$$\begin{array}{@{}rcl@{}} \boldsymbol{\epsilon}=2\boldsymbol{\mu}=2\left(\begin{array}{ccc} \frac{1}{\alpha r}&0&0\\ 0&\alpha r&0\\ 0&0&\alpha b^{2}\frac{\mathrm{e}^{2\alpha(r-b)}}{r} \end{array}\right). \end{array} $$
(29)
Fig. 21
figure 21

An object with \(\epsilon ^{\prime }=2\mu ^{\prime }=2\) is hidden by using the desired antiobject embedded in the negative shell of an external cloak. The simulation parameters are exactly the same as in Fig. 20. The structure is illuminated by a plane wave with incident angle 𝜃 0 = 0 from the left. The wave front of the wave is unaffected by the object and the cloak

Full size image

The antiobject is a curved-sheet with inner and outer radius r = 0.7 and r = 0.9 unit, respectively. The inner/outer radius of the object can be easily calculated with respect to the transformation relation (26).

Experimental verification of an external cloak, due to having negative refractive index in its structure, is not an easy task. We could find only one paper in this subject in [29] wherein illusion optics effect is created using external cloak. The cloak including positive and negative index part is constructed using a periodic L-C network at the frequency of 51 MHz.

We are trying to design a structure for an external cloak using effective medium theory so that its material parameters would be relatively matched to the theoretical ones at our desired frequency. We will introduce the result in our next paper.

It is also possible to generalize the solution in this paper for very long cylinder with more than one-layer coverage of transformation media. The theory is also capable to use for non-cylindrical transformation media.

Conclusion

In this paper, we presented a solution to the Maxwell’s wave equation in a 2D cylindrical transformation medium. Our considered sample or device is created with putting in touch two transformation media with different transformation functions. We chose a general form of radial transformation functions for each of the two media in the device. Propagation of the wave in the interior/exterior invisibility cloak and concentrator was solved as an example of our device. The concentration was on external invisibility cloak, but the interior cloak and concentrator was also considered in a higher-order transformation function. We confirmed the results of the analytical solution by comparing the simulations obtained based on this method, with the simulations prepared by finite element method.