Experimental study on swelling and intrusive behavior of bentonite under various solutions and its simple model construction

Abstract

Understanding the amount of bentonite intrusion into rock cracks is necessary to evaluate the performance of natural barrier materials for geological disposal. In this study, assuming a possible chemical action in geological disposals, bentonite was immersed in various solutions to accelerate the chemical action, and a half-year swelling and intrusion experiment was conducted. The experimental results showed that the swelling pressure and intrusion distance of bentonite in a solution environment differed depending on the solution type and that both were smaller than those in a purified water environment. The swelling pressure of bentonite in the environments of the KOH, NaOH, MgCl₂, and NaCl solutions decreased significantly, and it did not significantly enter into the gaps in these systems. This is undesired in situations where gaps such as the cracks of rock must be filled. Furthermore, a numerical analysis model was constructed that can simply represent the complex intrusion behavior of bentonite in cracks considering the balance of three forces acting on bentonite. The analysis results confirmed that under conditions where the external swelling pressure fluctuates over time, the intruding fluid fills the cracks more slowly than under conditions where the external swelling pressure is constant. It was also confirmed that under conditions where the viscosity of the intruding fluid decreases over time, the intruding fluid fills the cracks faster than under conditions where the upper limit viscosity is constant. The numerical results clarified that the governing equation for bentonite intrusion into closed cracks may express the long-term intrusive behavior of bentonite into cracks during geological disposal.

1 Introduction

Geological disposal confines high-level radioactive wastes to stable bedrock deeper than 300 m underground and isolates them from human inhabited environment for a long period [2]. The safety of geological disposal is ensured by a multi-barrier system (Fig. 1) consisting of engineered barriers (vitrified waste, overpack, and buffer material) and a natural barrier (host rock).

Fig. 1

Multi-barrier system for geological disposal (concepted by Nuclear Waste Management Organization of Japan (NUMO))

The swelling and gap filling of the buffer material (bentonite) caused by groundwater infiltration are anticipated to fill and seal cracks in the excavation-damaged zone after the closure of an underground facility for geological disposal [2, 18]. However, the performance of the cushioning material may deteriorate with the swelling performance deterioration of bentonite owing to chemical action [e.g., 11, 16, 30–32]. Depending on the type of chemical components in groundwater that reacts with bentonite, the degree of crack clogging in rocks may also differ, and the physical properties of the rocks, such as permeability, are expected to vary extensively. However, no studies have clarified the relationship between bentonite performance deterioration owing to chemical action and rock crack closure. Therefore, evaluating the degree of deterioration and rock crack closure, focusing on the boundary region between the engineered and natural barrier materials, is necessary because of the difference in the chemical composition of groundwater received by bentonite. In this study, swelling and intrusion experiments on bentonite samples were performed under various solution environments to evaluate their properties, and an attempt was made to analytically predict the amount of bentonite intrusion into cracks. The amount of bentonite intrusion can be easily predicted if a simple analytical model that considers the dominant factors of bentonite intrusion into cracks could possibly be constructed. Over the last 30 years, the efforts of several researchers and engineers have resulted in a huge amount of research result accumulation, including experiments and numerical simulations on the swelling [e.g., 7–9, 22, 25], permeability [e.g., 6, 7, 22, 25], and self-sealing [e.g., 10, 26] properties of engineered barrier materials (bentonite-based). Conversely, although experimental and theoretical/analytical studies on the properties of bentonite intrusion into cracks exist [e.g., 1, 3–5, 12, 20, 21], the results are limited compared to the amount of the aforementioned research results. Experimental studies have examined the properties of bentonite intrusion into simulated cracks using transparent acrylic containers [5, 12, 20]. Xu et al. [28, 29] conducted similar experiments using bentonite-based materials comprising bentonite mixed with sand. Existing studies have used distilled and deionized water, and the effects of other solution environments have rarely been investigated. Among the existing theoretical and analytical studies [1, 3, 4, 20, 21, 28, 29], those cited in numerous studies are summarized as follows. Kanno and Matsumoto [5] and Matsumoto and Tanai [12,13,14] reported that the intrusion distance of a bentonite specimen entering a simulated crack tends to be proportional to the square root of the intrusion time, and bentonite intrusion into cracks was experimentally proven to have no directional dependence. Thus, the results suggested that the bentonite that intrudes into cracks behaves as a viscous fluid in a two-dimensional channel. Kanno and Iwata [3, 4] applied a solid-phase diffusion model, combining solid-phase diffusion theory with a viscous fluid model, to study bentonite intrusion phenomena. The solid-phase diffusion theory was based on the mass transfer theory [15], which describes the infiltration behavior of water into bentonite and the swelling behavior of the bentonite accompanying infiltration of water. The solid-phase diffusion model considered the movement of water and soil particles in bentonite. For water to infiltrate, the cracks were to be filled with bentonite (solid phase), which is an infiltration medium. In addition, when the tip of the rock crack was closed, the pressure of the fluid trapped in the crack was assumed to act on the solid–liquid interface of bentonite that intruded the crack. However, considering the effect of the trapped fluid pressure in a solid-phase diffusion model that does not consider the solid–liquid interface in cracks was challenging.

Thus, in this study, swelling and intrusion experiments were conducted on bentonite immersed in various solutions to expedite potential chemical reactions relevant to geological disposal. This approach facilitated an analysis of the swelling and intrusion properties of bentonite in various solution environments. Furthermore, a simple analytical model was constructed, assuming bentonite to be a highly viscous fluid, for understanding the behavior of a fluid entering a closed-tip crack. Assuming a high-humidity environment throughout crack, the swelling of bentonite intruding into a crack was considered to be an absorption/diffusion phenomenon of the trapped fluid in the solid phase owing to the fluid in that environmental zone and was incorporated into the analytical model.

In this study, we focus on the boundary area between artificial and natural barrier materials. Few studies have evaluated the degree of deterioration of bentonite-based materials due to the presence of different chemical components in groundwater and the degree of crack closure in rocks present in these systems using experiments and simple models. Therefore, this study will provide valuable knowledge for achieving ultra-long-term safety in artificial and natural barrier materials during the geological disposal of radioactive waste.

2 Swelling and intrusion experiments on bentonite in various solutions

2.1 Experimental method

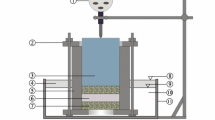
Figure 2a, b shows a schematic and photograph of the bentonite swelling and intrusion experimental equipment. The experiments were conducted in a temperature-controlled room (22 ± 1 °C). The equipment was capable of simultaneously measuring the swelling pressure P_s of bentonite and its intrusion distance δ_e into the crack by fixing the cylindrical bentonite specimen using a transparent acrylic jig. Two simulated cracks were created on the upper and lower sides by placing thin spacers between the upper, middle, and lower acrylic plates. In addition, the intrusion distance of bentonite was observed by using transparent acrylic upper and middle plates.

Fig. 2

Schematic (a) and photograph (b) of the experimental setup for the swelling and intrusion experiments of bentonite under various solutions, definition of intrusion distance (c)

As shown in Fig. 3a, c, δ_e of the bentonite intruding into the crack was the distance from the side of the bentonite specimen. The specimen was immersed in purified water (AS ONE, A300) and various other solutions while restraining volume change. The intrusion distance of the bentonite packed in the circumferential direction was measured for 180 days by taking photographs from above. Measurements were taken at approximate intervals of one week and at one-day intervals for approximately two weeks, immediately after the start of the experiment. In addition, the load F generated in the vertical direction was measured at 1-min intervals using a compact compression load cell (Unipulse, UNLS-5KN) and a data logger (Tokyo Measuring Instruments Laboratory, TDS-303), and the swelling pressure P_s was calculated using Eq. (1).

$$P_{{\text{s}}} = \frac{F}{A}$$

(1)

where A denotes the cross-sectional area of the specimen. Water was supplied at regular intervals such that the water level was maintained and the liquid level was at the center of the middle plate. The liquid was supplied from the lower simulated crack.

Fig. 3

Unoriented X-ray powder diffraction patterns of Kunigel-V1

2.2 Preparation method of bentonite specimen

In this study, Na-type bentonite (Kunimine Industries, Kunigel-V1; particle density = 2.715 Mg/m³, liquid limit = 470.71%, plastic limit = 34.40%, plastic index = 436.31, swelling index = 17 mL/2g) from Tsukinuno Mine, Japan, was used. The swelling index was evaluated based on JBAS104:77 (Japan Bentonite Manufacturers Association Standard). To calculate this index, 2 g of dried bentonite powder was added in 10 portions to a graduated cylinder containing 100 mL of distilled water, and the volume of the sample in the cylinder was measured after 24 h. As shown by the X-ray diffraction pattern (Fig. 3), Kunigel-V1 is mainly composed of montmorillonite and quartz with traces of feldspars, calcite, and clinoptilolite. The specimens were statically compacted to a specified dry density (Fig. 4) and were cylindrical with a diameter and height of 50 and 27 mm, respectively.

Fig. 4

Preparation method of bentonite specimen

2.3 Experimental conditions

The main purpose of this study was to clarify the relationship between the performance deterioration of bentonite and the degree of crack closure owing to the action of chemical components in groundwater. Thus, this study focused on the boundary region of the buffer material (bentonite) and the natural barrier (bedrock). The inflow of groundwater from the outside was considered a phenomenon that significantly affected various bentonite properties, especially the properties of swelling and intrusion into cracks. Therefore, this study excluded the influence of iron ions from overpack corrosion, as well as the reaction of oxygen introduced from the ground during excavation for facility construction with iron in steel shoring materials and rock masses. After the closure of the geological repository, the following five solutions were considered as substitutes for groundwater, KOH, Ca(OH)₂, and NaOH solutions, assuming highly alkaline pore water generated by the reaction of cementitious materials with groundwater; MgCl₂ and NaCl solutions, assuming seawater in the groundwater of coastal areas. All solutions had concentrations of 1 mol/L expect the Ca(OH)₂ solution (poorly soluble; 0.017 mol/L). The concentration of some solutions is higher than in typical groundwater. In this study, to observe the effects of different types of solutions on the swelling properties of bentonite, the concentrations of all solutions were identical except for the Ca(OH)₂ solution. The compacted (dry) densities of the specimens were 1.8 Mg/m³ and 1.5 Mg/m³, and the initial water content was 0% (oven-dried at 40 °C for 24 h before the test). In addition, preliminary experiments confirmed that drying at 40 °C can remove the moisture from bentonite as well as can be achieved when drying at 105 °C. Therefore, drying at 40 °C is the same as drying at 105 °C, and the water content is 0%. The crack widths in the swelling and intrusion experiments were 0.5, 1.0, and 1.5 mm.

2.4 Experimental results and discussions

Table 1 summarizes the values (ρ_d: dry density, a: crack widths, P_s,init: magnitude of the initial swelling pressure peak, t_init: elapsed time of the initial swelling pressure peak occurrence, P_s,max: maximum swelling pressure, P_s: equilibrium swelling pressure, δ_e: intrusion distance, ρ_δ: dry density of intruded bentonite, A: constant of proportionality) obtained from the swelling and intrusion experiments.

Table 1 Quantities obtained from the swelling and intrusion experiments

Figure 5 shows the time variation of the swelling pressure obtained from the swelling and intrusion experiments in the solution environment. From the initial behavior of the swelling pressure of each sample, a swelling pressure peak was observed within a few days, which gradually decreased. The initial peak of the swelling pressure was observed approximately one week after the test started for bentonite (dry density ρ_d = 1.8 Mg/m³) immersed in purified water and after approximately four days for bentonite (ρ_d = 1.5 Mg/m³) immersed in purified water and Ca(OH)₂ solution. Comparing the specimens investigated under purified water conditions, a higher compaction density resulted in a slower appearance of the initial peak of the swelling pressure. In the other samples, the peak appeared after approximately one day. However, the peak also appeared earlier depending on the immersion solution. The increase in the distance between the unit layers was assumed to have caused the swelling pressure of bentonite owing to water immersion that leads to the absorption of a large amount of water between the layers of montmorillonite. This is well known in the literature.

Fig. 5

Swelling pressure of bentonite under various solutions in the swelling and intrusion experiments

After 180 days since the experiment started, the swelling pressures of bentonite immersed in purified water ranged approximately 0.36–0.42 MPa (ρ_d = 1.8 Mg/m³) and 0.16–0.19 MPa (ρ_d = 1.5 Mg/m³). Therefore, a difference in the swelling pressure due to difference in the compaction density was confirmed. In addition, for specimens with ρ_d = 1.8 Mg/m³, the swelling pressure at a crack width of 1.5 mm was approximately 10% lower than that at crack widths of 0.5 and 1.0 mm. The swelling pressure of bentonite was small compared to that in a previous study (P_s = 0.48 MPa, specimen dimensions (diameter 50 mm, height 10 mm), purified water, ρ_d = 1.4 Mg/m³) [6], although the conditions were slightly different. This may have been due to a decrease in the specimen density owing to crack filling, details discussed later. However, the swelling pressure of bentonite immersed in the Ca(OH)₂ solution was approximately P_s = 0.20 MPa, which was similar to that of bentonite immersed in purified water. For KOH, NaOH and MgCl₂, and NaCl solutions, approximately P_s = 0.03, 0.08, and 0.09 MPa were observed, respectively. Their swelling pressures were less than half of that in purified water. Therefore, the magnitude of the bentonite swelling pressure differed depending on the type of immersing solution used. The cation exchange between the montmorillonite layers may have led to the difference. The original interlayer cations (Na⁺) were not electrically strongly bonded and were easily exchanged with other cations. The ion selectivity (exchange penetration power) was greater for other cations, such as K⁺, Ca²⁺, and Mg²⁺, than for Na⁺. Therefore, the exchange of Na⁺ with other cations restricted intercalation and caused a decrease in the swelling pressure. Conversely, by supplying a solution containing a large number of ions, the difference in the ion concentration levels between the interlayer water of montmorillonite in bentonite and the solution decreased, which reduced the swelling pressure. It was also noted that the concentration of Ca(OH)₂ solution was 0.017 mol/L (saturated) and its aqueous solution was poorly soluble. Therefore, the concentration of the Ca(OH)₂ solution was lower than the other solutions (1 mol/L) and close to that of purified water. Thus, the swelling pressure of bentonite immersed in the Ca(OH)₂ solution was similar to that of bentonite immersed in purified water, and the swelling pressure of this system was greater than that of bentonite immersed in other solutions, such as the NaOH solution. When the Na⁺ in the interlayers of montmorillonite hydrates, it absorbs water and bentonite swells. When immersed in a NaCl solution, the Na⁺ in the NaCl solution is also hydrated, and therefore, some of the H₂O that tries to enter between the layers of montmorillonite is removed, causing the interlayers to contract and reducing the swelling pressure. As a result, the intrusion distance may have become smaller because the swelling pressure, which is the driving force, is small during the intrusive behavior described below. It is very important to clarify the influence of seawater-type groundwater in coastal areas. In the future, experiments with various solution concentrations will be conducted to quantitatively clarify the effects of NaCl solutions on the swelling properties and intrusive behavior of bentonite. Regarding the swelling behavior of bentonite, it is well known that after the start of water immersion, the swelling pressure either monotonically increases over time or increases and then decreases [23]. Attempts have also been made to experimentally clarify the details of bentonite swelling behavior in distilled water environments [24]. However, in this study, we conducted experiments using various solutions while considering the intrusion of bentonite into cracks. Therefore, to compare the swelling behavior of this system over time with the results of previous studies in distilled water environments [e.g., 23, 24], we believe that it will be necessary to collect data under additional experimental conditions in the future.

Figures 6 and 7 show photographs of the bentonite intrusion and the intrusion distance measurements from the swelling and intrusion experiments in the solution environment, respectively. As shown in Fig. 6, the intrusion of bentonite spread almost concentrically in all cases. The intrusion distance of bentonite differed depending on the solution type used for immersion. Particularly, the intrusion distance of bentonite immersed in solutions other than the Ca(OH)₂ solution was much smaller than that of bentonite in purified water. In addition, on observing the intrusion state of bentonite in the Ca(OH)₂ solution, cracks were observed at the tip of the intruding bentonite. This tendency was not observed in the other solutions, and the cause is a subject for future investigation.

Fig. 6

Examples of bentonite intrusion under various solutions (a–f purified water; g KOH, h Ca(OH)₂, i NaOH, j MgCl₂, and k NaCl solutions) in the swelling and intrusion experiments (e.g., a–c dry density ρ_d = 1.8 Mg/m³, d–k ρ_d = 1.5 Mg/m³; a and d crack widths a = 0.5 mm, b and e a = 1.0 mm, c, f–k a = 1.5 mm)

Fig. 7

Relationship between elapsed time and intrusion distance of bentonite under various solutions in the swelling and intrusion experiments

From the results of the intrusion distance measurement, shown in Fig. 7, all samples were observed to reach an equilibrium state after a certain number of days. The bentonite immersed in purified water (ρ_d = 1.8 Mg/m³, a = 1.5 mm) reached equilibrium in approximately 150 days, while those immersed in purified water (other than the aforementioned) and Ca(OH)₂ solution reached equilibrium in approximately 100 days. The bentonite immersed in the NaCl solution reached equilibrium after approximately 40 days, while the other samples attained equilibrium after approximately 10 days. However, the bentonite immersed in the MgCl₂ solution extended the intrusion distance and reached an equilibrium state after approximately 60 days. Hence, bentonite in a solution environment reached equilibrium within a shorter period than that in a purified water environment. By focusing on the difference in compaction density of the specimens, a direct correlation between higher compaction densities and increased intrusion distances was observed, independent of the crack width. If the swelling pressure was the driving force that contributed significantly to crack filling, it can be reasonably concluded that samples exhibiting higher compaction densities and greater swelling pressures demonstrated extended intrusion distances. By focusing on the difference in crack width, it was revealed that the crack width was positively correlated with the intrusion distance across all compaction densities. This result was consistent with a previous report [14]. By focusing on the difference in solution type, the intrusion distance of bentonite immersed in solution was found to be shorter than that immersed in purified water. Particularly, bentonite barely intruded the cracks in the other solution environments, except for the Ca(OH)₂ solution. This result had a negative effect in situations where the effect of filling gaps such as cracks was expected.

Based on previous reports [5, 12,13,14], the intrusion distance δ_e (At^1/2) of bentonite was determined using the square root of the elapsed time t; using this relationship, a constant of proportionality A (dependent on the crack opening width and material) was obtained (Fig. 8 and Table 1).

Fig. 8

Relationship between square root of elapsed time and intrusion distance of bentonite under various solutions in the swelling and intrusion experiments

Figure 8 shows only the approximation line for the condition of crack width a = 1.5 mm. The results confirmed that the larger the intrusion distance, the larger the constant of proportionality A, which was consistent with the results of previous reports [5, 12,13,14]. The constants of proportionality A for bentonite (Kunigel-V1, specimen dimensions: diameter 50 mm, height 50 mm, purified water, ρ_d = 1.8 Mg/m³, initial water content 10%) in previous reports [5, 12,13,14] were 0.34 (a = 0.5 mm), 0.98 (a = 0.5 mm), and 1.30 (a = 0.5 mm). Since the dimensions and initial water content of the specimens in this study were different, comparisons were challenging. However, the resultant values were almost similar and the magnitude relationship of the constant of proportionality A was the same due to the difference in crack width.

Figure 9 shows an example of the strong correlation between the results obtained from the swelling and intrusion experiments. A very high correlation (correlation coefficient 0.94–0.99) among the equilibrium swelling pressure P_s, intrusion distance δ_e, and constant of proportionality A was observed.

Fig. 9

Examples of correlations between various quantities

Measurements were obtained to determine the density of bentonite that intruded into the cracks (Fig. 10). Previous studies reported a decrease in the dry density of the intruding bentonite with an increase in the intrusion distance [12,13,14]. In this study, the dry density distribution of bentonite was measured based on the intrusion distance. However, measurements were difficult under wet and dry conditions due to the adhesion of intruders to jigs and the cracks formed by drying shrinkage, respectively. Therefore, the relationship between the intrusion distance and the dry density of the intruder, as shown in Fig. 10, represented the average dry density of the intruder. For the bentonite immersed KOH and NaOH solutions, where the intrusion distance was very short, measuring the intrusive mass was challenging. Therefore, the samples under these solution conditions were not shown in Fig. 10. The dry densities of the intrusions ranged from 0.24 to 0.53 Mg/m³. By focusing on the bentonite immersed in purified water, a decrease in the dry density values with increase in crack widths and intrusion distances was observed. However, the difference in dry density owing to the difference in the solution species could not be confirmed.

Fig. 10

Relationship between intrusion distance and dry density of bentonite under various solutions in the swelling and intrusion experiments

3 Simplified model for intrusion behavior of bentonite

3.1 Construction of analytical model for intrusion behavior of bentonite

A governing equation was formulated for bentonite intrusion (referred to as the intruding fluid) into a closed-tip (closed channel) crack, followed by the derivation of a numerical solution for this equation. Cracks in the network structure of a rock mass were of importance in the radionuclide migration assessment. However, the intrusive behavior of bentonite in network cracks was complex. Therefore, this study aimed to identify the dominant factor influencing bentonite intrusion and simply analyzed the bentonite intrusion behavior in a single crack. In addition, this study posited that bentonite swelling, attributed to groundwater in the cracks, resulted from its absorption and diffusion into the groundwater. When constructing the governing equation for bentonite intrusion into cracks, the relationship between groundwater compression and absorption/diffusion phenomena due to bentonite intrusion was required. Therefore, this study assumed the groundwater within the crack to be water vapor (gas) and analyzed the intrusion of bentonite into the crack with a tip-closed model to limit the groundwater mass. Figure 11 shows an overview of fluid intrusion into closed channels, where δ_n is the intrusion distance of the intruding fluid, a is the channel width (crack width), B is the channel depth (crack depth), and L is the crack length. The analytical area targeted in this study ranged from the channel inlet to the crack tip. The force exerted by the swelling pressure of bentonite outside the channel acted as the driving force, causing bentonite intrusion into the channel. In addition, because the interior of the flow channel was assumed to be a high-humidity environment, the sealed fluid contained moisture. This water was assumed to cause swelling of the bentonite by volumetric expansion. Thus, the bentonite intrusion into the closed channel was considered to depend on the swelling pressure of the bentonite outside the channel and the volumetric expansion of the bentonite owing to moisture in the trapped fluid. Therefore, a simplified governing equation was developed to characterize the intrusion behavior of bentonite in closed cracks based on the balance of forces acting on the intruding fluid in the closed channel. Therefore, in this study, a numerical analysis model was proposed that can simply represent the complex intrusion behavior of bentonite in cracks based on the balance of three forces acting on bentonite. Furthermore, the proposed numerical analysis model focuses on the diffusion coefficient, swelling pressure, and viscosity of bentonite, and considers changes in the intrusion behavior of bentonite due to changes in these physical properties. In the following sections, the volumetric expansion of bentonite was defined by the acting force, moisture content of the trapped fluid, and formulation of the governing equations.

Fig. 11

Overview and analytical area of bentonite intrusion into closed crack

3.1.1 Definition of forces acting on intrusion fluids

As shown in Fig. 11, three main forces acted on the fluid entering the closed channel. Force F_s caused by the swelling pressure of the bentonite outside the channel acted as a drive force on the fluid entering the closed channel. In addition, because bentonite was assumed to be a highly viscous fluid, frictional drag was generated on the intruding fluid of the channel inner wall, and the viscous drag force F_v acted. Owing to the moisture in the trapped fluid, the force F_p caused by the volumetric expansion of bentonite acted on the intruding fluid. F_p is the force caused by the compression of the trapped fluid due to the swelling and intrusion of bentonite into a crack and is defined as the resistance force acting on the intruding bentonite. In this study, all pressures acting on a fluid entering a closed channel, except the atmospheric pressure, were defined as gauge pressures. Since this study dealt with the intrusion of a highly viscosity fluid into a closed channel, the intrusion velocity of the fluid in the channel was considered extremely low. In this case, the viscous drag caused by the frictional drag on the inner wall of the channel was dominant. Thus, the influence of the inertial force could be ignored. Therefore, the balance of the forces acting on the intruding fluid was given by Eq. (2).

$$F_{{\text{s}}} = F_{{\text{v}}} + F_{{\text{p}}}$$

(2)

The definitions of the force F_s caused by the external swelling pressure, viscous drag force F_v, and force F_p caused by the volumetric expansion of the bentonite owing to the moisture in the trapped fluid are given in the following sections.

3.1.2 Definition of variable external swelling pressure and viscosity

From the relationship between the swelling pressure of bentonite obtained from the swelling and intrusion experiments at an elapsed time, the results confirmed that the swelling pressure fractured over time (Fig. 5). Simultaneous swelling and intrusion experiments confirmed that the solution eroded the bentonite near the interface between the bentonite and the solution in the crack, thereby reducing the density of the bentonite (Fig. 10). From the relationship between fluid density ρ and viscosity μ (μ = ρν), where ν is the kinematic viscosity, the apparent viscosity of bentonite was observed to decrease near the interface between the bentonite and the solution in the cracks. Since the erosion range of bentonite was assumed to increase with time, its viscosity was assumed to depend on time and decrease with it.

Thus, the external swelling pressure and viscosity of the intruding fluid were considered to depend on time. Therefore, the time-varying external swelling pressure and viscosity of the intruding fluid were defined as the external swelling pressure and viscosity variables, respectively. By considering the variable external swelling pressure P(t) to increase or decrease exponentially with time (Fig. 12a), a dimensionless function X(t), which was dependent on time, was applied and expressed by Eq. (3).

$$P\left( t \right) = P_{{\text{s}}} \cdot X\left( t \right)$$

(3)

where P_s is the maximum swelling pressure of the bentonite outside the channel and t is the intrusion time. When the external swelling pressure increases exponentially with time and converges to the upper limit of the swelling pressure P_s, the dimensionless function X(t) for the variable external swelling pressure can be given by Eq. (4).

$$X\left( t \right) = 1 - \left( {1 - \frac{{P_{0} }}{{P_{{\text{s}}} }}} \right) \cdot e^{ - \gamma t}$$

(4)

where P₀ is the lower-limit swelling pressure of bentonite outside the channel and γ is a constant related to the swelling velocity. In contrast, when the external swelling pressure decreased exponentially with time and converged to the lower-limit swelling pressure P₀, the dimensionless function X(t) for the fluctuating external swelling pressure was given by Eq. (5).

$$X\left( t \right) = \frac{{P_{0} }}{{P_{{\text{s}}} }} + \left( {1 - \frac{{P_{0} }}{{P_{{\text{s}}} }}} \right) \cdot e^{ - \lambda t}$$

(5)

where λ is a constant related to the swelling velocity. By considering that the variable viscosity μ(t) decreases exponentially with time (Fig. 12b), a dimensionless time-dependent function Y(t) was applied and expressed as Eq. (6).

$$\mu \left( t \right) = \mu_{{\text{s}}} \cdot Y\left( t \right)$$

(6)

where μ_s is the upper limit of the intruding fluid viscosity. The viscosity of bentonite depending on its water content is thought to change as the water content varies over time. When the intruding fluid viscosity decreases exponentially over time and converges to its lower limit μ₀, the dimensionless function Y(t) for the variable viscosity can be expressed by Eq. (7).

$$Y\left( t \right) = \frac{{\mu_{0} }}{{\mu_{{\text{s}}} }} + \left( {1 - \frac{{\mu_{0} }}{{\mu_{{\text{s}}} }}} \right) \cdot e^{ - \eta t}$$

(7)

where η is a constant related to the rate of viscosity decrease.

Fig. 12

Modeling of variable external swelling pressure and viscosity

Since the external swelling pressure and viscosity of the intruding fluid was dependent on time, the force F_s caused by the external swelling pressure and the viscous drag force F_v acting on the intruding fluid was also dependent on time. Therefore, from Eq. (3), force F_s caused by the external swelling pressure can be expressed by Eq. (8).

$$F_{\text{s}} = P_{\text{s}} \cdot X\left( t \right) \cdot aB$$

(8)

where the time-dependent dimensionless function X(t) is given by Eqs. (4) or (5), depending on the increase or decrease in the external swelling pressure, respectively. Additionally, when the cross section of the channel was extremely large compared to the channel width a (a <  < B), the viscous flow in the channel was regarded as a two-dimensional flow. Therefore, the average flow velocity dδ_n/dt on the intruding fluid in a planar Poiseuille flow [27] was determined using Eq. (9) when applying the variable viscosity expressed in Eq. (6):

$$\frac{{{\text{d}}\delta_{\text{n}} }}{{{\text{d}}t}} = \frac{{a^{2} }}{{12\mu_{\text{s}} \cdot Y\left( t \right)}} \cdot \frac{\Delta P}{{\delta_{\text{n}} }}$$

(9)

where ΔP is the pressure difference acting at the crack inlet and the intrusion front (ΔP > 0) and δ_n is the intrusion distance of the intruding fluid from the crack inlet to the intrusion front of the intruding fluid. Note that the maximum value of δ_n is equal to the crack length L because the intrusion of fluid stops at the tip of the crack. From Eq. (9), the viscous drag force F_v (= ΔP·aB) acting on the intruding fluid is given by Eq. (10):

$$\begin{aligned}\Delta P \cdot aB = \frac{{12\mu_{\text{s}} \cdot Y\left( t \right)}}{{a^{2} }} \cdot \delta_{\text{n}} \frac{{{\text{d}}\delta_{\text{n}} }}{{{\text{d}}t}} \cdot aB \\ F_{\text{v}} = \frac{{12\mu_{\text{s}} \cdot Y\left( t \right)B}}{a} \cdot \delta_{\text{n}} \frac{{{\text{d}}\delta_{\text{n}} }}{{{\text{d}}t}}\end{aligned}$$

(10)

where the time-dependent dimensionless function Y(t) is given by Eq. (7).

3.1.3 Absorption and diffusion phenomenon of trapped fluid on bentonite

This study considered the absorption of trapped fluid containing water by bentonite that intruded into the cracks and the diffusion of the trapped fluid into bentonite, which caused a volumetric expansion of the bentonite. Considering the absorption/diffusion of the trapped fluid in the bentonite, the volume of the trapped fluid decreased with time, as shown in Fig. 13. Assuming that the total of the intruding (bentonite) and trapped fluid volumes was constant in the system, the volume of the intruding fluid V_B increased as the volume of the trapped fluid V_F decreased (Fig. 13).

Fig. 13

Overview of absorption/diffusion of trapped fluid

This increase in the intruding fluid volume was considered to be the apparent volumetric expansion of the bentonite caused by the absorption of the trapped fluid containing moisture and the diffusion of the trapped fluid into the bentonite. Furthermore, it was assumed that the absorption of trapped fluid molecules (water molecules) into bentonite follows Henry’s law and that the diffusion of trapped fluid molecules in bentonite follows Fick’s first law. Henry’s law describes the dissolution of gases in liquids, whereas Fick’s first law describes the diffusion of matter. Bentonite was modeled as a highly viscous liquid, while the trapped fluid that contained water was considered to be water vapor (gas). Therefore, Henry’s law can be applied in this study. In addition, assuming that the trapped fluid molecules absorbed in bentonite diffused according to the concentration gradient, Fick’s first law can be applied. Phan et al. [19] proposed an analytical model for liquid intrusion into a closed channel by considering a phenomenon in which a trapped gas dissolves and diffuses into an intruding liquid. The analytical model proposed by Phan et al. [19] was applied to the absorption/diffusion theory for bentonite–trapped fluids. The concentration C of the encapsulated fluid molecules at the solid–gas interface was given by Eq. (11) using Henry’s law.

$$P_{{\text{g}}} = K_{{\text{H}}} \cdot C$$

(11)

where P_g is the compressive pressure of the trapped fluid and K_H is Henry’s constant, which represents the absorption rate of the trapped fluid molecules into the bentonite. In addition, the concentration C₀ of the trapped fluid molecules immediately before the bentonite crack intrusion can be expressed by Eq. (12).

$$P_{{\text{a}}} = K_{{\text{H}}} \cdot C_{0}$$

(12)

where P_a is the atmospheric pressure. Immediately before the bentonite entered the crack, the crack was filled with trapped fluid molecules having a concentration of C₀; therefore, the concentration of the trapped fluid molecules at the inlet of the channel was C₀. The mass diffusion flux (mass passing per unit time and unit area) Φ_m of the trapped fluid molecules in the bentonite can be expressed as Eq. (13) using Fick’s first law.

$$\begin{aligned} {\Phi }_{{\text{m}}} & = \frac{1}{aB} \cdot \frac{{{\text{d}}m}}{{{\text{d}}t}} \\ & = - \frac{{D_{{\text{d}}} M\left( {C - C_{0} } \right)}}{{\delta_{{\text{n}}} }} \\ \end{aligned}$$

(13)

where m is the mass of the trapped fluid, D_d is the diffusion coefficient of the trapped fluid molecules in bentonite, and M is the molar mass of the trapped fluid. Φ_m of the trapped fluid molecules in bentonite was linearly related to the gradient between concentrations of the trapped fluid molecules at the bentonite intrusion front position (C) and that at the channel inlet (C₀), as expressed by Eq. (13). Assuming the trapped fluid to be an ideal gas and applying its equation of state, the compression pressure P_g of the trapped fluid was given by Eq. (14).

$$P_{{\text{g}}} = \frac{mRT}{{MaB\left( {L - \delta_{{\text{n}}} } \right)}}$$

(14)

where R is the gas constant, T is the absolute temperature. The initial mass m₀ of the trapped fluid can be obtained from Eq. (15), by applying Eq. (14).

$$m_{0} = \frac{{P_{{\text{a}}} MaBL}}{RT}$$

(15)

From Eq. (15), the atmospheric pressure P_a was given by Eq. (16).

$$P_{{\text{a}}} = \frac{{m_{0} RT}}{MaBL}$$

(16)

In this study, the force caused by the compressive pressure (P_g−P_a), as the gauge pressure based on atmospheric pressure, was defined as the force F_p caused by the volumetric expansion of bentonite owing to the moisture in the trapped fluid. F_p was calculated from Eqs. (14) and (16), and was expressed by Eq. (17).

$$\begin{aligned} F_{{\text{p}}} & = aB\left( {P_{{\text{g}}} - P_{{\text{a}}} } \right) \\ & = \frac{RT}{M} \cdot \left( {\frac{m}{{L - \delta_{{\text{n}}} }} - \frac{{m_{0} }}{L}} \right) \\ \end{aligned}$$

(17)

When a crack is filled with water, the relationship between the solid–liquid phases is established; therefore, the theory of absorption/diffusion of the trapped fluid (gas) into the bentonite proposed in this study was not applicable. Alternatively, the theory was modified such that it could be applied. In this case, bentonite was unable to enter the crack because the water trapped in the crack was an incompressible fluid. Alternatively, bentonite was assumed to gradually intrude the cracks owing to its swelling caused by water absorption.

3.1.4 Formulation of governing equations and derivation of numerical solutions

A governing equation was formulated for fluid intrusion in a closed channel considering the absorption/diffusion of the trapped fluid into bentonite. Substituting Eqs. (8), (10), and (17) into Eq. (2), the governing equation for the intruding fluid intrusion distance was given by Eq. (18).

$$\frac{{{\text{d}}\delta_{\text{n}} }}{{{\text{d}}t}} = \frac{{a^{2} }}{{12\mu_{\text{s}} \delta_{\text{n}} \cdot Y\left( t \right)}}\left\{ {P_{\text{s}} \cdot X\left( t \right) - \frac{RT}{{MaB}}\left( {\frac{m}{{L - \delta_{\text{n}} }} - \frac{{m_{0} }}{L}} \right)} \right\}$$

(18)

Substituting Eqs. (11), (12), (14), and (16) into Eq. (13) yielded Eq. (19) as the governing equation for the mass-change rate of the trapped fluid.

$$\frac{{{\text{d}}m}}{{{\text{d}}t}} = - \frac{{D_{\text{d}} RT}}{{K_{\text{H}} }} \cdot \frac{{mL - m_{0} \left( {L - \delta_{\text{n}} } \right)}}{{\delta_{\text{n}} L\left( {L - \delta_{\text{n}} } \right)}}$$

(19)

where the intrusion distance of the intruding fluid and mass of the trapped fluid were normalized, and their respective physical quantities were represented by δ_n^* (= δ_n/L) and m* (= m/m₀). By applying the normalized physical quantities (δ_n^* and m^*) and normalizing Eqs. (18) and (19), Eqs. (20) and (21) were yielded, respectively.

$$\frac{{{\text{d}}\delta_{\text{n}}^{*} }}{{{\text{d}}t}} = \frac{\varepsilon }{{\delta_{\text{n}}^{*} \cdot Y\left( t \right)}}\left\{ {X\left( t \right) - \alpha \cdot \left( {\frac{{m^{*} }}{{1 - \delta_{\text{n}}^{*} }} - 1} \right)} \right\}$$

(20)

$$\frac{{{\text{d}}m^{*} }}{{{\text{d}}t}} = \beta \cdot \frac{{1 - m^{*} - \delta_{\text{n}}^{*} }}{{\delta_{\text{n}}^{*} \left( {1 - \delta_{\text{n}}^{*} } \right)}}$$

(21)

where α is the ratio of atmospheric pressure to external swelling pressure, β is the ratio of the absorption/diffusion rate of the trapped flu to the intrusion rate of the intruding fluid, and ε is a physical constant related to the intruding fluid, and are represented by Eqs. (22), (23), and (24), respectively.

$$\alpha = \frac{{P_{{\text{a}}} }}{{P_{{\text{s}}} }}$$

(22)

$$\beta = \frac{{D_{{\text{d}}} RT}}{{K_{{\text{H}}} L^{2} }}$$

(23)

$$\varepsilon = \frac{{P_{{\text{s}}} }}{{12\mu_{{\text{s}}} }} \cdot \left( \frac{a}{L} \right)^{2}$$

(24)

Immediately before bentonite crack intrusion (t = 0), the intrusion distance was zero (δ_n = 0) and the mass of the trapped fluid was equal to the initial mass (m = m₀). Therefore, the initial conditions are expressed in Eq. (25).

$$\delta_{{\text{n}}}^{*} = 0\quad {\text{and}}\quad m^{*} = 1\quad {\text{and}}\quad t = 0$$

(25)

The simultaneous ordinary differential equations, given in Eqs. (20) and (21), are the equations of motion for a fluid entering a closed channel. By applying the initial conditions (Eq. (25)) and numerically integrating the system of ordinary differential equations, numerical solutions (δ_n^* and m^*) were derived. The numerical solution δ_n^* derived herein was the intrusion distance of bentonite into a closed crack in a high-humidity environment. When X(t) = 1 and Y(t) = 1, Eq. (20) was taken as the governing equation for the intrusion distance of the intruding fluid, considering a constant external swelling pressure and viscosity.

3.2 Numerical results on intrusion behavior of bentonite

By applying the numerical solution derived using the numerical integration of the governing equations (Eqs. 20 and 21) formulated in this study, the variation in the distance of the bentonite intrusion into the cracks over time was analyzed. First, to investigate the effects of the absorption/diffusion phenomena of the trapped fluid on the intrusive behavior of bentonite, an analytical study on the time variation of obtaining intrusion distance for the intruding fluid considering constant external swelling pressure and viscosity was conducted. Second, to investigate the effect of the time dependence of the external swelling pressure and intruding fluid viscosity on the intrusive behavior of bentonite, an analytical study on the time variation of obtaining intrusion distance for the intruding fluid considering variable external swelling pressures and viscosities was conducted.

3.2.1 Setting analytical parameters

The analytical parameters set for analyzing the time variation of obtaining intrusion distance for the intruding fluid, considering a constant external swelling pressure and viscosity, are shown in Table 2.

Table 2 Analytical conditions (constant external swelling pressure and constant viscosity)

The crack into which the bentonite intruded was a closed channel with a rectangular cross section. The channel has a length L of 0.5 m, channel depth B of unit depth 1.0 m, and channel width a of 0.5, 1.0, and 1.5 mm. The viscous drag acting on the fluid entering the channel was considered to depend on the size and shape of the channel cross section. Three channel widths were used to confirm this effect. The analysis conducted in this study aims to clarify the influence of changes in the physical properties of bentonite (viscosity, etc.) on the intruding behavior of bentonite. Therefore, the physical property values of bentonite were arbitrarily set considering the measurement data reported by existing studies for the numerical analysis. A detailed examination of the validity of the physical properties of bentonite that were applied in this analysis will be considered in future studies. The bentonite that intruded into the crack was a viscous fluid with a constant viscosity μ_s of 1.0 × 10⁸ Pa·s. External swelling pressures P_s of 0.1, 0.2, and 0.4 MPa were assumed to act on the intruding fluid at the channel inlet. The viscosity of bentonite was set with reference to viscosity estimates obtained from previous studies [3, 4]. In addition, the external swelling pressure was considered to change under the influence of various factors such as differences in the compaction density of bentonite [2] and solution species [7]. Considering this effect, three cases of external swelling pressures were considered in this study. Water vapor was the fluid trapped in the closed crack. The gas constant R was 8.3145 N·m/(mol·K), the absolute temperature T was 298.15 K (25 °C), and the molar mass M was 18.02 × 10^–3 kg/mol. The atmospheric pressure P_a was 1.01 × 10⁵ Pa. The water vapor absorption rate (Henry’s constant) K_H for bentonite was set to 1.0 × 10⁴ Pa·m³/mol. The diffusion coefficients D_d of the water molecules in bentonite were set to 1.0 × 10⁻⁸, 1.0 × 10⁻¹⁰, and 1.0 × 10⁻¹² m²/s. Since the diffusion coefficient was considered to change depending on the difference in the solution type, three cases were considered in this study. Henry’s constant was set with reference to Henry’s constant for gaseous water [17]. The order of the diffusion coefficients was set with reference to the estimated values of the solid-phase diffusion coefficients obtained in previous studies [3, 4].

Table 3 lists the analytical parameters set for analyzing the time variation of obtaining the intrusion distance for the intruding fluid, considering the variable external swelling pressure and viscosity.

Table 3 Analytical conditions (variable external swelling pressure and variable viscosity)

The crack into which bentonite intruded was a closed channel with a rectangular cross section, a channel length L of 0.5 m, depth B of unit depth (B = 1.0 m), and width a of 1.0 mm. The bentonite that intruded into the cracks was considered to be a viscous fluid with variable viscosity (upper and lower limits of viscosity were set to μ_s = 1.0 × 10⁸ Pa·s and μ₀ = 0.1 × 10⁸ Pa·s, respectively). External swelling pressure variations on the intruding fluid at the channel inlet were observed, which when increased: the lower and upper limits of swelling pressure were P₀ = 0 MPa and P_s = 0.4 MPa, respectively, and when decreased: the upper and lower limits of swelling pressure were P_s = 0.4 MPa and P₀ = 0.04 MPa. The constant γ related to the swelling velocity was set to 1.0 × 10⁻³, 1.0 × 10⁻⁴, and 1.0 × 10⁻⁵ h⁻¹ under the condition that the external swelling pressure increased. As γ increased, the maximum swelling pressure P_s was achieved earlier. The constant λ for the swelling velocity was set to 1.0 × 10⁻², 1.0 × 10⁻³, and 1.0 × 10⁻⁴ h⁻¹ under the condition that the external swelling pressure decreased. The larger the value of λ, the earlier the lower-limit swelling pressure P₀ was achieved. Conversely, the constant η related to the rate of viscosity decrease was set to 1.0 × 10⁻³, 1.0 × 10⁻⁴, and 1.0 × 10⁻⁵ h⁻¹ under the conditions of viscosity decrease. The larger the value of η, the earlier the intruding fluid reached the lower viscosity limit μ₀. For the analytical parameters (R, T, M, P_a, K_H) related to the trapped fluid in the closed crack, the numerical values set in the aforementioned analysis (analysis of time interval for intruding length of the intruding fluid considering constant external swelling pressure and viscosity) were applied. The diffusion coefficient D_d of the water molecules in bentonite was set to 1.0 × 10⁻¹⁰ m²/s. The Runge–Kutta method was applied for numerical integration of the system of ordinary differential equations.

3.2.2 Numerical results and discussions

The intrusion characteristics of bentonite in cracks were investigated based on the results of numerical solution for fluid intrusion in closed channels derived in this study. Figure 14 shows the numerical results of the time variation of the intrusion distance for the intruding fluid, considering a constant external swelling pressure and viscosity. The vertical axis in Fig. 14 represents the normalized intrusion length δ_n^*, while the horizontal axis represents the square root of the intrusion time t^1/2. δ_n^* = 1 indicates that the intruding fluid completely filled the closed channel.

Fig. 14

Time variation of intrusion distance of intruding fluid considering constant external swelling pressure and constant viscosity. a a = 1.0 mm, D_d = 1.0 × 10⁻¹⁰ m²/s, b P_s = 0.2 MPa, D_d = 1.0 × 10⁻¹⁰ m²/s, c P_s = 0.2 MPa, a = 1.0 mm

Figure 14a shows the variation in the intrusive behavior of the intruding fluid owing to the variation in the external swelling pressure. As shown in Fig. 14a, the intrusion velocity of the intruding fluid increased under a high external swelling pressure. This was assumed to have occurred because the higher the external swelling pressure, the greater the driving force for the intruding fluid into the channel; thus, the intrusion velocity of the intruding fluid increased. Figure 14b shows the variation in the intrusive behavior of the intruding fluid due to the change in the channel width. As shown in Fig. 14b, the intruding fluid intrusion velocity decreased when the channel width was small. A smaller channel width was assumed to exert a larger viscous frictional resistance on the intruding fluid, resulting in a lower intrusion velocity. Furthermore, it was confirmed that at the initial stage, the intrusion distance is proportional to the square root of the intrusion time. This implies that fluid intrusion during the initial stage was a viscous fluid flow. Figure 14c shows the variations in the intrusive behavior of the intruding fluid due to the variation in the diffusion coefficient of the trapped fluid. As shown in Fig. 14c, the intruding fluid quickly filled the channel when the diffusion coefficient of the trapped fluid was high. It was posited that an increase in the diffusion coefficient of the trapped fluid correlates with a higher rate of the trapped fluid molecules being absorbed by the intruding fluid. By this effect, the apparent volumetric expansion of the intruding fluid due to the absorption/diffusion of the trapped fluid was accelerated; therefore, the intruding fluid was assumed to fill the channel early. In addition, the study examined how variation in the diffusion coefficient of the trapped fluid affect the intrusive behavior of the intruding fluid. In contrast, the absorption rate of the trapped fluid to the intruding fluid was considered to increase as the value of Henry’s constant decreased. Therefore, the smaller the value of Henry’s constant, the faster the intrusion velocity owing to the apparent volumetric expansion of the intruding fluid, and the faster the intruding fluid fills the channel. In addition, Fig. 14c shows that the intrusion distance tends to be proportional to the square root of the intrusion time at the initial stage of the intruding fluid. In contrast, the results indicated that a higher diffusion coefficient led to the intruding fluid reaching the crack tip more promptly after sufficient time had elapsed. This indicated that the intruding fluid at the initial stage was dependent on the external swelling pressure and viscous resistance force, and after a sufficient time had passed, the intruding fluid was dominant owing to absorption/diffusion of the trapped fluid.

Figures 15 and 16 show the numerical results of the time variation of the intrusion distance for the intruding fluid, considering variable external swelling pressure and viscosity. In the numerical results shown in Fig. 15, to examine the effects of time-dependent variations in the external swelling pressure on the intrusion behavior of the intruding fluid, analyses were performed under a constant viscosity (Y(t) = 1). Red line in Fig. 15a, b shows the intrusion behavior of the intruding fluid when the external swelling pressure increased exponentially with time and converged to the upper swelling pressure P_s. The results shown in Fig. 15a, b (red line) confirmed that the intrusion velocity of the intruding fluid decreased when the constant γ related to the swelling velocity was low during the initial stage. When γ was small, time was required to reach the upper swelling pressure limit P_s. Therefore, the intrusion velocity of the intruding fluid decreased compared to the condition in which the maximum swelling pressure was reached early (large γ condition). In addition, after a sufficient time had passed since the experiment started, the external swelling pressure reached the maximum P_s under all conditions related to γ. Therefore, as shown in Fig. 15a, b, after a sufficient period of time had elapsed, the time evolutions of the intruding fluid under all conditions regarding γ tended to be identical. Blue line in Fig. 15c, d shows the intrusive behavior of the intruding fluid when the external swelling pressure decreased exponentially with time and converged to a lower swelling pressure P₀. The results shown in Fig. 15c, d (blue line) confirmed that the intrusion velocity of the intruding fluid increased when the constant λ related to the swelling velocity was low during the initial stage. Time was required to reach the lower-limit swelling pressure P₀ when λ was small. Therefore, the intrusion velocity of the intruding fluid was considered to have increased compared to the condition in which the lower limit of the swelling pressure was reached earlier (condition with a large λ). In addition, after a sufficient amount of time had passed since the experiment started, the external swelling pressure reached the lower limit P₀ under all conditions related to λ. Therefore, as shown in Fig. 15c, d, after a sufficient period of time had elapsed, the time evolutions of the intruding fluid under all conditions regarding λ tended to be identical.

Fig. 15

Time variation of crack intrusion distance of bentonite under constant or variable (increasing or decreasing) external swelling pressure

Fig. 16

Time evolution of crack intrusion distance of bentonite with constant or variable (decreasing) viscosity

Dashed black line in Fig. 15 shows the intrusive behavior of the intruding fluid when considering constant external swelling pressure. The constants γ and λ related to the swelling velocity were set to 1.0 × 10⁻⁵ and 1.0 × 10⁻⁴ h⁻¹, respectively. Under a constant external swelling pressure, X(t) = 1 and Y(t) = 1 in Eq. (20). From the results shown in Fig. 15, it was observed that fluctuations in the external swelling pressure over time resulted in a slower crack-filling rate by the intruding fluid compared to a constant external swelling pressure scenario.

In the numerical results shown in Fig. 16, to study the influence of intruding fluid viscosity variations over time on the intrusive behavior of the intruding fluid, the analysis was performed under the condition of a constant external swelling pressure (X(t) = 1). Green line in Fig. 16 shows the intrusive behavior of the intruding fluid when its viscosity decreased exponentially with time and converged to the minimum viscosity μ₀ of the intrusive fluid. From the results shown in Fig. 16 (green line), it was confirmed that a smaller initial value of the constant η, associated with lower viscosity, resulted in a reduced intrusion velocity of the intruding fluid. When η was small, time was required to reach the minimum viscosity μ₀ of the intruding fluid. Therefore, the intrusion velocity of the intruding fluid decreased compared to the condition where the lower viscosity limit was reached early (large η). In addition, after a sufficient amount of time had passed since the experiment started, the viscosity of the intruding fluid reached a minimum of μ₀ under all conditions related to η. Therefore, as shown in Fig. 16, after a sufficient period of time has elapsed, the time evolutions of the intruding fluid under all conditions regarding η tended to be identical.

Dashed black line in Fig. 16 shows the intrusive behavior of the intruding fluid when considering constant and variable viscosities. The constant η related to the rate of viscosity decrease was set to 1.0 × 10^–4 h⁻¹, under the condition of constant viscosity, X(t) = 1 and Y(t) = 1 in Eq. (20). The results shown in Fig. 16 confirmed that when the viscosity of the intruding fluid decreased over time, the intruding fluid filled the cracks earlier than when the viscosity was constant at the maximum viscosity μ_s.

For the geological disposal of high-level radioactive waste, considering the ultra-long-term intrusion behavior of bentonite into cracks (thousands to tens of thousands of years) is necessary. From the findings of this study, it can be concluded that ultra-long-term bentonite intrusion resulted from the absorption/diffusion of the enclosing fluid of bentonite within cracks. Thus, the governing equation for fluid intrusion in a closed channel developed in this study is expected to express the ultra-long-term intrusive behavior of bentonite in cracks during geological disposal.

4 Conclusions

In this study, swelling pressure and intrusion experiments were performed using bentonite soaked in various solutions to promote chemical action, assuming the possible chemical actions during geological disposal. The experiments demonstrated the effect of chemical action on the amount of intruding bentonite. Additionally, a simple model was developed to analyze the intrusion behavior of bentonite in closed cracks with swelling. The results are summarized below.

In the bentonite swelling and intrusion experiments, the swelling pressure and intrusion distance of the bentonite differed depending on the type of immersion solution. The swelling pressure and intrusion distance of the bentonite immersed in solutions were smaller than those of the bentonite immersed in purified water. Particularly, in KOH, NaOH, MgCl₂, and NaCl solutions, the swelling pressure was significantly reduced, and bentonite hardly intruded into the cracks. From these experimental results, it was observed that the crack-sealing property may not be influenced by variations in the groundwater composition, which occur after the closure of an underground facility for geological disposal. Conversely, a detrimental impact was observed in this scenario in which the effect of closing cracks in the excavation-damaged zone after closure was identified in some groundwater conditions.

While modeling the rock crack-filling properties of bentonite samples, after analyzing the differences from previous research reports, bentonite was assumed to be a highly viscous fluid. An analytical model was constructed for analyzing the behavior of the fluid entering a crack with a closed tip. In addition, a high-humidity environment within the entire crack was assumed, and the swelling of bentonite at the gas–solid interface was considered to occur via the absorption of the trapped fluid into the solid phase. This phenomenon was subsequently integrated into the analytical model. Furthermore, efforts were made to integrate the time-dependent variations in the external swelling pressure and viscosity of bentonite into the governing equation used to predict the intrusion distance. The exponential increase or decrease in distance over time was considered and subsequently formulated. Using the constructed analytical model, several cases were analyzed to ascertain the trends in the experimental values and identify the dominant factor influencing the intrusion behavior of bentonite. The analysis results confirmed that under conditions where the external swelling pressure fluctuates over time, the intruding fluid fills the cracks more slowly than under conditions where the external swelling pressure is constant. It was also confirmed that under conditions where the viscosity of the intruding fluid decreases over time, the intruding fluid fills the cracks faster than under conditions where the upper limit viscosity is constant. From the numerical results, it was determined that the long-term bentonite intrusion behavior in the geological disposal site resulted from the absorption/diffusion of the trapped fluid in the bentonite that was present in the crack. The established governing equation for fluid intrusion in a closed channel may be used to express the ultra-long-term intrusive behavior of bentonite in cracks during geological disposal.