Numerical investigation of debris flow–structure interactions in the Yarlung Zangbo River valley, north Himalaya, with a novel integrated approach considering structural damage

Abstract

In the Yarlung Zangbo River valley in north Himalaya, many high-frequency debris flows develop, with large amounts of run-out debris materials. To reduce the hazard scale of the debris flow, check dams are frequently used to mitigate and prevent debris flow movement, and many check dams are damaged under the impact of debris flows. This paper proposed a novel integrated three-dimensional numerical approach to quantitatively assess the dynamic process of a debris flow and its interaction with a check dam considering check dam damage. The numerical approach is based on the SPH-FDEM method, which uses the SPH of Bingham fluid to simulate debris flows while using the FDEM to simulate structural check dams composed of rock blocks. A test of granular flow impact measurement in an inclined flume was used to validate the rheological characteristics of the debris flow and its interaction with the structure. The debris flow in the G62 gully, which is near NR 318 and has the potential to destroy the road, is used as a case for numerical simulation. Several different engineering conditions, including without a check dam, with an undamaged check dam and with a damaged check dam, were considered. The simulation results show that the debris flow scale without considering the check dam is consistent with the field investigation. The run-out speed, viscous dissipation energy, and frictional energy of the debris flow with time can be quantitatively acquired. When a check dam is considered, the processes of the dam undergoing debris impact, fracture generation and evolution, the separation of broken blocks from the main check dam body, and the transport of these blocks by the debris flow can be clearly observed. The stress, damage area, damage extent, damage mode, fracture energy, and fracture area of the check dam can be quantitatively acquired from the model, which greatly expands the applicability of debris flow numerical models.

1 Introduction

The Qinghai–Tibet Plateau, which is also called the third pole of the world, has an average elevation of over 4000 m [7]. Due to violent plate movement and strong extrusion, steep mountains and deeply cut valleys are developed on the south boundary of the Qinghai–Tibet Plateau, which provide topographic conditions and geological conditions for debris flows [18, 46, 51]. Many debris flow valleys with basin areas ranging from several square kilometers to hundreds of square kilometers exist in mountainous areas, many of them threatening property and lives [34, 52, 53]. Structures such as check dams established in gullies have become a common way to mitigate debris flows [39, 42]. However, check dams are frequently damaged under the impact of debris flows, and the dynamic process of debris flow–structure interactions considering check dam damage is not well understood. Knowing the dynamic process of debris flow–structure interactions is very important and has become a hot topic of study [14, 21, 24, 33, 40, 41].

Numerical simulation can reflect the dynamic process of a specific disaster that considers the complex topographical condition and real-time flow process and can provide a considerable amount of quantitative information for debris flow prevention and mitigation [2, 16, 52]. Thus, it gradually became a popular way to study the debris flow–structure interaction process. Several numerical methods have been applied to simulate flow–structure interactions, including the discrete element method (DEM) [23, 49, 54], DEM coupling [26, 28], the coupled Eulerian–Lagrangian method (CEL) [9, 22], the arbitrary Lagrangian–Eulerian method (ALE) [25], smoothed particle hydrodynamics (SPH) [3, 11, 16, 44, 45, 47, 48], and the depth-integrated shallow water method (DISWM) [35]. Among the different types of numerical models, the way to simulate the debris flow and the structure varies. In a DEM model, the way to simulate flows is using solid discrete elements (particles) to simulate flow while using rigid wall elements to simulate check dams. However, the purely DEM is more suitable for dry granular simulation and fluid is difficult to be considered in the model. To overcome this shortcoming, Li et al. [26] developed a coupled computational fluid dynamic (CFD)–DEM) model for two-phrase debris flow simulation and applied it to study the impacts on flexible barriers. Liu et al. [28] developed a coupled SPH-DEM-FEM model for fluid–particle–structure interactions and applied it to the Wenjia gully debris flow. The DEM-CFD or DEM-SPH coupling can well simulate debris flow behavior, but the large computational requirements from two-phase coupling restrict its application to practical problems. The CEL is a coupling technique that has gradually become popular in geological disaster simulation. In the CEL, debris flows can be simulated by the Eulerian material which can deform freely based on the fixed Eulerian meshes, while check dams can be simulated by conventional finite elements, making it suitable for fluid–structure coupling. However, the Eulerian domain must include the irregular potential debris flow, wasting extra computational resources and making it difficult to be applied in a real debris flow simulation [9]. The ALE is another kind of method combining the characteristics of Eulerian and Lagrangian methods. In the ALE, the debris flow is simulated by a Lagrangian finite element-based material. The finite element simulated debris flows are not a priori fixed in space or attached to a material and can move arbitrarily to optimize the shapes of elements, allowing the simulation of highly linear large-deformation behavior and avoiding wasting extra computational resources. However, the Lagrangian finite element limits simulating the separation and splashing of fluids. In the SPH model, flow can be represented by a continuum of smoothed particles, while the check dam can be represented by deformable finite elements [3] or smoothed particles [16]. The continuum characteristics of SPH make it suitable for debris flow simulation. In the DISWM model, the flow can be simulated by depth-integrated flow, while the check dam can be simulated by revising terrain data on the check dam position [5]. The DISWM is very suitable for simulating debris flows because it can easily consider the hydrological process of debris flows [5, 12, 15, 52]. Most of the debris flows are initialized by rainfall, and the formed flood wash-out loose material to generate debris flow, so the volume of debris flow will increase with rainfall. In the abovementioned three-dimension numerical models of the DEM-CFD/SPH, the ALE and the CEL, source materials frequently have certain volumes at the initial time of the simulation and keep the same in the whole process, indicating the hydrological processes are not considered. Considering hydrological processes of debris flows can make the simulation more realistic. As for the DISWM, although it is efficient and can consider hydrological process, it is not a three-dimensional model, so the stress and strain interactions between the debris flow and check dam cannot be acquired, and the deformation and damage information of the check dam cannot be reflected with the model.

In this paper, the authors propose a new type of debris flow–structure numerical model based on SPH and the coupled finite-discrete element method (FDEM) (SPH–FDEM) in Abaqus software. The debris flow is simulated by the Bingham SPH model, while the structure is simulated by the FDEM, which can consider the structure, deformation and damage of the material at the same time. Compared to the abovementioned types of flow–structure numerical models, this type of model has some advantages: (1) The model is a three-dimensional model with high computationally efficient, making it can be applied to a real debris flow simulation. (2) Debris flow run-out process can depend on hydrology, leading to a realer run-out simulation. (3) The structural characteristics of the check dam can be considered, and the check dam can present deformable or damage characteristics under different impact forces of debris flows. The authors apply this model to a typical north Himalayan debris gully and analyzed its dynamic process to show its characteristics. The debris flow conditions without a check dam with a check dam that remained undamaged and with a check dam that was damaged are carefully simulated and analyzed.

2 Background

2.1 Study area

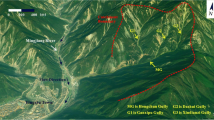
The study area is in the upstream area of the Yarlung Zangbo River, south of the Qinghai–Tibet Plateau (Fig. 1a). The Yarlung Zangbo River flows through the area from west to the east across the plateau surface, and many tributaries of the Yarlung Zangbo River have developed. The landform of the study area is composed of high mountains, wide valleys, and lake basins, with an average altitude of over 4000 m.

Fig. 1

Location and topography of the study area: a Location of the study area based on the contour map of elevation; b well-developed debris flows in the study area

The study area is near the plate suture associated with the Indo-Asian collision, making the geological structure and stratigraphic lithology very complex. This is the Yarlung Zangbo suture zone, which lies at the northern boundary of the Tethys-Himalaya zone and collides with the Asian plate directly. The Tethys-Himalaya belongs to a stage of relative subsidence, and the rock layers are mostly derived from marine sedimentary deposits after the demise of the Tethys Ocean: mainly sandstone, sand mudstone, dolomite, limestone, and shale. Tectonics in the Tethys-Himalaya are very active, and most of the earthquakes in the Tethys-Himalaya correspond to normal faults, followed by strike-slip faults.

Around these tributaries, many gullies have formed due to the existence of faults and strong erosion. Due to active tectonics, rocks in the Tethys-Himalaya zone are very fragmented, providing a large amount of source material. The study area has a cold semiarid plateau climate. The average precipitation is 433 mm/year, and the average evaporation is 2250 mm/year. Rainfall in the study area is very concentrated, and approximately 70% of the annual rainfall is concentrated between July and August. Due to the topographical and climatic conditions, many gullies have formed debris flows and formed typical debris flow gullies (Fig. 1b). Compared to the large debris gullies, such as the Xulong gulley and Waka gulley, that the authors previously investigated in the upstream deep river valleys of the Jinsha River, eastern margin of the Qinghai–Tibet Plateau [46], the smaller watershed debris flow gullies in the study area usually have a larger amount of debris flow materials (Fig. 2a). These gullies are mainly high-frequency debris flow gullies according to field investigations and remote sensing analyses. At the mouths of debris flow gullies near roads and villages, check dams are frequently built to prevent and mitigate debris flows, and many dams have been backfilled with debris flow material (Fig. 2b). In addition, under the impact of high-frequency debris flows, these check dams are usually locally damaged (Fig. 2c) or severely damaged (Fig. 2d). Providing a dynamic model to investigate whether debris flows will destroy dams is important and essential.

Fig. 2

Debris flow and check dam in the study area: a debris flow in the small watershed gully; b check dam in the gully and large amount of debris material; c local damage of the dam; d residual check dam severely destroyed by debris flow

2.2 G62 debris flow gully

In this section, the authors introduce a typical debris flow gully, the G62 debris flow gully, for dynamic process assessment. The G62 debris flow gully is near national road 318 (NR 318), with a gully mouth location of 29° 4′ 4″ N, 87° 33′ 9″ E at an elevation of 4246 m (Fig. 3a). It is a typical rainfall-induced debris flow gully. The basin area of the debris gully is 1.1 km², and it is 1.51 km long, with a channel gradient of 340‰. Because of rapid downward erosion, the gully presents a V-shape, and the inclined angle of the gully slope is approximately 30°. The bedrock of the gully is slate and covered with low vegetation. On the right bank of the debris flow gully, the rock is a steeply inclined away from the dip and bends toward the free surface under gravity, generating fragmental rocks. Under the effect of weathering, tectonics and erosion, the surface of the bedrock becomes fragmented and generates eluvium with thicknesses from 0.2 to 1 m. In addition, talus, whose thickness ranges from 2 to 10 m, accumulates on the toe of the slope. All of the fragmental rocks, eluvium, and talus provide enough source material for debris flows (Fig. 3b).

Fig. 3

Engineering geology conditions of the G62 debris flow gully: a overall view of gully; b source material condition of debris flow; c location relationships between debris flow fans and river

Multistage debris flow fans exist at the gully mouth. There are at least three stages of debris flow fans at the gully mouth, and the newer debris flow fans have obvious cutting and erosion effects on the older fans, forming multilevel terraces (Fig. 3c). The phenomenon also indicates that the debris flow gully is a high-frequency debris flow gully. The newest debris flow fan has been investigated in detail, which showed that the diameter of the debris flow fan is 136 m and that the length of the fan is 358 m. The average thickness of the newest debris flow fan is 4 m, and the diffusion angle is 150°. The debris flow fan is mainly composed of gravels with sand and soil, indicating that the debris flow is a diluted debris flow. Field measurements have shown that the debris flow density was approximately 1600 kg/m³. On the surface of the debris flow fan, boulders exist, and the largest boulder is 0.5 m in diameter, indicating that the debris flow had a large carrying capacity and impact during run-out.

A small river exists in front of the debris flow fan, and the debris flow fan has strongly squeezed the river due to the geometries of the debris flow fan and river. The front of the debris flow fan has an obvious cutting phenomenon (Fig. 3c), which indicates that the debris flow once blocked the river and then the river water eroded the debris flow fan to form a new river channel. In front of the river is NR 318, which is the most important road in Tibet. There was no structure in the gully to prevent and mitigate debris flow damage during the authors’ investigation in 2021. Considering that debris flows in the G62 gully can have large volumes and have the potential to reach and destroy the road, the authors choose this gully to estimate the potential dynamic process of a debris flow. To prevent a debris flow from reaching the road, a check dam is used to simulate the interception of the debris flow.

3 Methodology

In this paper, the debris flow in the numerical model is represented by continuous pseudoparticles via SPH, and the check dam is represented by a FDEM based on a type of cohesive interface element (CIE). The authors introduce SPH and FDEM and how their elements interact as follows:

3.1 Configuration of SPH

SPH is a type of continuum method and is developed on the Lagrangian modeling scheme but has mesh-free characteristics, unlike the traditional Lagrangian finite element method (FEM). A collection of pseudoparticles is used instead of nodes and elements in conventional finite elements, so SPH can be used to simulate large-deformation problems without the limitation of element distortion (Fig. 4a). By directly interpolating properties on a discrete set of points distributed over the solution domain, the prescribed set of continuum equations is discretized. In the computational domain, each particle behavior is approximated by a variable field, which is further affected by the accumulated contributions from neighboring particles (Fig. 4b). The kernel function $W$, which is expressed as Eq. 1, is frequently used to describe the contribution of a particle from neighboring particles:

$${\varvec{f}}\left( {\mathbf{x}} \right) \simeq \mathop \sum \limits_{j} \frac{{m_{j} }}{{\rho_{j} }}f_{j} W\left( {\left| {{\text{x}} - {\text{x}}_{j} } \right|, h} \right)$$

(1)

where ${\varvec{f}}\left( {\mathbf{x}} \right)$ is a function of the particle position vector, $j$ denotes neighboring particles that can contribute, $h$ is the smoothing length that determines how many particles affect interpolation for a particular particle, and $m$ is the mass of the particle.

Fig. 4

Sketch of SPH: a conventional finite element mesh and SPH particles; b kernel function

The continuity equation of material can be replaced by the interpolant as follows:

$$\rho \left( {\text{x}} \right) = \mathop \sum \limits_{j} m_{j} \left( {\left| {{\text{x}} - {\text{x}}_{j} } \right|, h} \right)$$

(2)

where $\rho \left( {\text{x}} \right)$ is the material density everywhere, x is the spatial location.

The movement of each particle follows Newton’s law, which can be expressed per unit volume as Eq. 3.

$$\rho {\varvec{a}} = {\varvec{F}}$$

(3)

where $\rho$ is the density of the particle, ${\varvec{a}}$ is the accelerated velocity of the particle, and ${\varvec{F}}$ denotes the resultant force.

Equation 3 can be further expanded into Eq. 4.

$${\varvec{F}} = \rho {\varvec{g}} - \nabla {\varvec{p}} + \mu \nabla^{2} {\varvec{u}}$$

(4)

In Eq. 4, the first term on the right side of the equal sign is gravity, the second term is the force generated by the pressure difference, and the third term is the shear force generated by the velocity difference.

Based on Eq. 4, the accelerated velocity of a particle $i$ in space can be expressed as Eq. 5.

$${\varvec{a}}_{{\varvec{i}}} = {\varvec{g}} - \frac{{\nabla {\varvec{p}}_{{\varvec{i}}} }}{{\rho_{i} }} + \frac{{\mu \nabla^{2} {\varvec{u}}_{{\varvec{i}}} }}{{\rho_{i} }}$$

(5)

As for the moving speed as well as moving distance of the particle, they can be expressed as follows:

$${\varvec{a}}_{{\varvec{t}}} = \frac{{{\text{d}}{\varvec{v}}_{{\varvec{t}}} }}{{{\text{d}}{\varvec{t}}}}$$

(6)

$${\varvec{v}}_{{\varvec{t}}} = \frac{{{\text{d}}{\mathbf{x}}_{{\varvec{t}}} }}{{{\text{d}}{\varvec{t}}}}$$

(7)

where ${\varvec{v}}$ is the velocity.

Pseudoparticles in SPH correspond to a type of continuous node element in continuum particle elements (PC3D), and the interaction between the SPH pseudoparticles and Lagrangian finite elements depends on node-based surface in node-to-surface contact technique (Fig. 5a). Node-based surfaces are defined on nodes and it assumes that the node has a nonzero contact thickness surface. The contact thickness for particles is the same value specified as the characteristic length. The node-based surface can only be treated as a slave surface when contacting with finite element surface (master surface), indicating the finite element surface can penetrate the node-based surface but the node-based surface can’t penetrate the finite element surface. When a pseudoparticle will encounter a finite element-meshed object, the surfaces of finite elements are discretized using nodes that allow slight interpenetration of the particle and finite element surface nodes to calculate the contact force. Whether a pseudoparticle contacts with the finite element-meshed object is determined by the relative positions of nodes at different steps. In a step, once the particle is penetrated by the finite element surface, a contact force is generated. The normal contact force is perpendicular to the finite element surface, and the magnitude is determined by the penetration depth of nodes which can be calculated by Eq. 8.

$${\varvec{F}}_{{\varvec{n}}} = k_{p} {\varvec{d}}_{{\varvec{p}}}$$

(8)

where ${\varvec{F}}_{{\varvec{n}}}$ is the normal component of the contact force, $k_{p}$ depends on the material properties of the interactive elements, and ${\varvec{d}}_{{\varvec{p}}}$ is the penetration distance between the master surface and the node.

Fig. 5

Sketch of node-to-surface contact and surface-to-surface contact

If a pseudoparticle has relative tangential movement or trend with finite element surface, a tangential contact force is generated. The tangential contact force is perpendicular to the normal contact force. If relative tangential movement trend exists without relative tangential movement, the tangential contact force is equal to the sliding force. Otherwise, the tangential contact force is equal to the dynamic friction force. Whether relative tangential movement occurs is determined by the relative magnitude of the maximum static friction force and sliding force. The maximum static friction force is assumed equal to the dynamic friction force and can be calculated as Eq. 9.

$${\varvec{F}}_{{\varvec{t}}} = \mu {\varvec{F}}_{{\varvec{n}}}$$

(9)

where ${\varvec{F}}_{{\varvec{t}}}$ is the dynamic friction force and $\mu$ is the Coulomb friction coefficient.

The behavior of debris flows has frequently been described by Bingham fluids in previous literature [27, 36, 55]. A Bingham fluid is a type of non-Newtonian fluid that begins to flow when the yield stress of the material is greater than a certain value, and its fluidity is linear. As a type of flow, its basic rheological behavior must obey mass conservation (Eq. 10), momentum conservation (Eq. 11) [19], and the energy conservation of the equation of state (EOS) (Eqs. 12–20) [1, 17, 19, 27].

The mass conservation equation on a particle can be expressed as:

$$\frac{{{\text{d}}\rho }}{{{\text{d}}t}}\left( {{\text{x}}_{i} } \right) = \mathop \sum \limits_{j = 1}^{N} m_{j} \left( {{\varvec{v}}\left( {{\text{x}}_{j} } \right) - {\varvec{v}}\left( {{\text{x}}_{i} } \right)} \right)A_{ij}$$

(10)

The momentum conservation equation on a particle can be expressed as:

$$\frac{{{\text{d}}{\varvec{v}}}}{{{\text{d}}t}}\left( {{\text{x}}_{i} } \right) = \mathop \sum \limits_{j = 1}^{N} m_{j} \left( {\frac{{{\varvec{\sigma}}\left( {{\text{x}}_{j} } \right)}}{{\rho_{i}^{2} }}\frac{{{\text{x}}_{i} - {\text{x}}_{j} }}{{r_{ij} }}\frac{{\partial W_{ij} }}{{\partial r_{ij} }} - \frac{{{\varvec{\sigma}}\left( {{\text{x}}_{i} } \right)}}{{\rho_{j}^{2} }}\frac{{{\text{x}}_{j} - {\text{x}}_{i} }}{{r_{ji} }}\frac{{\partial W_{ji} }}{{\partial r_{ji} }}} \right)$$

(11)

where ${\varvec{\sigma}}$ is the total stress, $r$ is the distance from two particles.

The energy conservation equation on a particle can be expressed as:

$$\frac{{{\text{d}}E}}{{{\text{d}}t}}\left( {{\text{x}}_{i} } \right) = \frac{{P_{i} }}{{\rho_{i}^{2} }}\mathop \sum \limits_{j = 1}^{N} m_{j} \left( {{\varvec{v}}\left( {{\text{x}}_{j} } \right) - {\varvec{v}}\left( {{\text{x}}_{i} } \right)} \right)\frac{{{\text{x}}_{i} - {\text{x}}_{j} }}{{r_{ij} }}\frac{{\partial W_{ij} }}{{\partial r_{ij} }}$$

(12)

where $E$ is internal energy.

The EOS is assumed for the pressure as a function of the current density and the internal energy per unit mass, which can be expressed as follows:

$$p = f\left( {\rho , E_{m} } \right)$$

(13)

where $p$ is the pressure stress defined as positive in compression,

One of the most common types of liquid simulation is the U_s–U_p Mie–Grüneisen EOS, which is linear for energy and can be expressed as follows:

$$p - p_{H} = {\Gamma }\rho \left( {E_{m} - E_{H} } \right)$$

(14)

where $p_{H}$ is the Hugoniot pressure which only relies on density, $E_{m}$ is the internal energy per unit mass, $E_{H}$ is the specific energy (per unit mass) which only relies on density, and Γ is the Grüneisen ratio defined as:

$${\Gamma } = {\Gamma }_{0} \frac{{\rho_{0} }}{\rho }$$

(15)

where, ${\Gamma }_{0}$ is the material constant and $\rho_{0}$ is the reference density.

The Hugoniot energy ($E_{H}$) is related to the Hugoniot pressure with:

$$E_{H} = \frac{{p_{H} \eta }}{{2\rho_{0} }}$$

(16)

where, $\eta$ = 1 − $\rho_{0}$/$\rho$ is the nominal volumetric compressive strain, and above equations can be converted into the following equation.

$$p = p_{H} \left( {1 - \frac{{{\Gamma }_{0} \eta }}{2}} \right) + {\Gamma }_{0} \rho_{0} E_{m}$$

(17)

A common fit to the Hugoniot data can be expressed as follows:

$$p_{H} = \frac{{\rho_{0} c_{0}^{2} \eta }}{{\left( {1 - s\eta } \right)^{2} }}$$

(18)

where $c_{0}$ is the reference sound speed, $s$ is the slope of U_s–U_p curve, $c_{0}$ and $s$ are the linear relationship between the shock velocity (U_s) and particle velocity (U_p) and can be expressed as follows:

$$U_{s} = c_{0} + sU_{p}$$

(19)

With the above assumptions, the linear U_s–U_p Hugoniot form can be written as follows:

$$p = \frac{{\rho_{0} c_{0}^{2} \eta_{s} }}{{\left( {1 - s\eta_{s} } \right)^{2} }}\left( {1 - \frac{{{\Gamma }_{0} \eta_{s} }}{2}} \right) + {\Gamma }_{0} \rho_{0} E_{m}$$

(20)

The flow behavior of debris flows is frequently described by the Bingham fluid model [36, 37]. The Bingham model is a kind of non-Newtonian fluid, which will not flow until the material reaches a critical value of minimum layer shear stress, the yield shear stress ($\tau_{0}$). After reaching the yield shear stress, the material will flow like the Newtonian fluid, whose layer shear stress is proportional to strain rate, and the proportional coefficient is fluid viscosity. Shear behavior of a Bingham fluid can be described by Eq. 21 [9]:

$$\eta_{t} = \left\{ {\begin{array}{*{20}l} {\eta_{0} } \hfill & {{\text{if}}\;\tau < \tau_{0} } \hfill \\ {\frac{1}{{\dot{\gamma }}}\left( {\tau_{0} + k\left( {\dot{\gamma } - \frac{{\tau_{0} }}{{\eta_{0} }}} \right)} \right)} \hfill & {{\text{if}}\;\tau \ge \tau_{0} } \hfill \\ \end{array} } \right.$$

(21)

where $\eta_{t}$ is the dynamic viscosity, $\tau$ is the shear stress, $\dot{\gamma }$ is the shear strain rate, $\eta_{0}$ is the shear viscosity at low shear rates, $\tau_{0}$ is the yield shear stress, and k is the flow consistency index.

3.2 Configuration of FDEM

FDEM is a type of method combining the characteristics of FEM and DEM [32]. The FDEM can solve deformation, fracturing and movement problems simultaneously, expanding the application scope of both methods. The principle of the FDEM is the insertion CIEs into the boundaries of finite element meshes (Fig. 6). The CIEs and finite element meshes share nodes to transmit force and displacement.

Fig. 6

Sketch of FDEM

The CIEs can deform and fracture based on the traction–separation constitutive response with a stress–displacement law (Fig. 7). Damage to CIEs can occur in the opening mode (mode I, tension damage), sliding mode (mode II, shear damage), and mixed mode of opening and sliding. A linear relationship between the stress and displacement of the CIE can be expressed as follows:

$${\varvec{t}} = \left\{ {\begin{array}{*{20}l} {k\delta } \hfill & {\delta < \delta^{0} } \hfill \\ {\left( {1 - D} \right)k\delta } \hfill & {\delta \ge \delta^{0} } \hfill \\ \end{array} } \right.$$

(22)

where ${\varvec{t}}$ is the traction stress vector, $k$ is the CIE contact stiffness coefficient, ${\varvec{\delta}}$ is the traction displacement vector, D is the damage variable.

Fig. 7

Linear-form constitutive response of cohesive elements: a Stress–displacement in the normal direction; b stress–displacement in the tangential direction; c the mixed mode

D can be further expressed as:

$$D = \left\{ {\begin{array}{*{20}l} {\frac{{{\varvec{\delta}}^{{\varvec{t}}} \left( {{\varvec{\delta}}_{{{\varvec{max}}}} - {\varvec{\delta}}^{0} } \right)}}{{{\varvec{\delta}}_{{{\varvec{max}}}} \left( {{\varvec{\delta}}^{{\varvec{t}}} - {\varvec{\delta}}^{0} } \right)}}} \hfill & \\ {{\text{For}}\;{\text{pure}}\;{\text{single}}\;{\text{fracture}}\;{\text{mode}}} \hfill \\ {\max \left\{ {d_{{{\text{mult}}}} ,\max \left( {d_{n} , d_{s} , d_{t} } \right)} \right\}} \hfill &\\ {{\text{For}}\;{\text{mixed}}\;{\text{fracutre}}\;{\text{mode}}} \hfill \\ \end{array} } \right.$$

(23)

$${\varvec{\delta}}^{{\varvec{t}}} = \frac{{2G^{c} }}{{{\varvec{T}}_{{{\varvec{eff}}}}^{{\varvec{o}}} }}$$

(24)

$$d_{{{\text{mult}}}} = 1 - \left( {1 - d_{n} } \right)\left( {1 - d_{s} } \right)\left( {1 - d_{t} } \right)$$

(25)

where ${\varvec{\delta}}^{0}$ is the displacement corresponding to the peak stress value, ${\varvec{\delta}}_{{{\varvec{max}}}}$ is the maximum displacement during the loading history, and ${\varvec{\delta}}^{{\varvec{t}}}$ is the failure displacement when the stress decreases to the minimum value, $G^{c}$ is the fracture energy, ${\varvec{T}}_{{{\varvec{eff}}}}^{{\varvec{o}}}$ is the effective traction stress at damage initiation, $d_{n}$, $d_{s}$, and $d_{t}$ represent the damage variables in normal and two tangential directions, respectively.

In the opening mode and sliding mode, after the CIE reaches the peak traction stress, damage is initiated, and the traction stress decreases. Finally, when the traction stress decreases to the minimum value, the CIE is completely fractured. For the mixed mode of opening and sliding, a QUADS damage failure criterion can be used to determine the initial damage of CIEs [30] (Eq. 26).

$$\left\{ {\frac{{\left\langle {{\varvec{t}}_{{\varvec{n}}} } \right\rangle }}{{t_{n}^{o} }}} \right\}^{2} + \left\{ {\frac{{{\varvec{t}}_{{\varvec{s}}} }}{{t_{s}^{o} }}} \right\}^{2} + \left\{ {\frac{{{\varvec{t}}_{{\varvec{t}}} }}{{t_{t}^{o} }}} \right\}^{2} = 1$$

(26)

where ${\varvec{t}}_{{\varvec{n}}}$, ${\varvec{t}}_{{\varvec{s}}}$, and ${\varvec{t}}_{{\varvec{t}}}$ are the normal component and tangential components to the cracked surface, respectively; $t_{n}^{o}$, $t_{s}^{o}$, and $t_{t}^{o}$ represent the peak values of the nominal stress in the three directions; $< >$ is the symbol that signifies that a purely compressive stress state does not initiate damage.

The quadratic power law based on fracture energy can be used to determine the complete fracturing of CIEs (Eq. 27), which can be expressed as follows:

$$\left\{ {\frac{{G_{n} }}{{G_{n}^{C} }}} \right\}^{2} + \left\{ {\frac{{G_{s} }}{{G_{s}^{C} }}} \right\}^{2} + \left\{ {\frac{{G_{t} }}{{G_{t}^{C} }}} \right\}^{2} = 1$$

(27)

where $G_{n}^{C}$ $G_{s}^{C}$ and $G_{t}^{C}$ represent the fracture energy corresponding to completely fracturing in normal and two tangential directions, respectively; $G_{n}$ $G_{s}$ and $G_{t}$ are the actual fracture energy in normal and two tangential directions, respectively.

After the CIE is completely fractured, the separate finite elements can contact each other. The interaction between two discrete elements is based on element-based surface contact, which discretizes the element surfaces using nodes and allows for slight interpenetration of different surfaces. Whether two objects contact with each other is determined by the relative positions of nodes at different steps. The surface-to-surface contact, point-to-surface contact and edge-to-edge contact can be detected. For the most common of surface-to-surface contact, a master surface and a slave surface are defined, and their roles are exchanged every two steps. If the nodes of the master surface penetrate the slave surface is checked, a normal contact force is generated (Fig. 5b). The normal contact force on nodes is generated by contact surface rebound in physical mechanism and is perpendicular to the finite element surface. The normal contact force can also by calculated by Eq. 8. When the finite element surface has trend or moves relative to another finite element surface, a tangential contact force is generated. The tangential contact force is perpendicular to the normal contact force and the magnitude is equal to the sliding force without relative movement or equal to the dynamic friction force with relative movement. The maximum static friction force is assumed equal to the dynamic friction force and can be calculated as Eq. 9. As for the edge-to-edge contact, it is based on the contact normal direction on the cross product between the two respective edges considered for contact. A feature angle which is the angle formed between the normals of the two facets connected to an edge need to be specified to activate feature and perimeter edges to participate in edge-to-edge contact. In this manuscript, a feature angle value of 1° was set to accurately detect the edge-to-edge contact.

The movement of the object is based on an explicit central-difference time integration rule and it performs a large number of small time increments efficiently. If the system meets the dynamic balance conditions, that the resultant force on the node is equal to the node mass matrix M multiplied by the node acceleration $\ddot{\varvec{u}}$:

$$M\ddot{\varvec{u}} = {\varvec{P}} - {\varvec{I}}$$

(28)

And the accelerations at the increment are computed by:

$$\ddot{\varvec{u}}_{{\left( {\varvec{t}} \right)}} = \left( {\varvec{M}} \right)^{ - 1} \left( {{\varvec{P}} - {\varvec{I}}} \right)_{t}$$

(29)

where M is the mass matrix, ${\varvec{P}}$ is the applied load vector, and $\varvec{ I}$ is the internal force vector.

The equations of motion for the body are integrated using the explicit central-difference integration rule which is expressed as follows:

$$\dot{\varvec{u}}_{{\left( {{\varvec{i}} + \frac{1}{2}} \right)}}^{{\varvec{N}}} = \dot{\varvec{u}}_{{\left( {{\varvec{i}} - \frac{1}{2}} \right)}}^{{\varvec{N}}} + \frac{{\Delta t_{{\left( {i + 1} \right)}} + \Delta t_{\left( i \right)} }}{2}\dot{\varvec{u}}_{{\left( {\varvec{i}} \right)}}^{{\varvec{N}}}$$

(30)

$$\dot{\varvec{u}}_{{\left( {{\varvec{i}} + 1} \right)}}^{{\varvec{N}}} = \dot{\varvec{u}}_{{\left( {\varvec{i}} \right)}}^{{\varvec{N}}} + \Delta t_{{\left( {i + 1} \right)}} \ddot{\varvec{u}}_{{\left( {{\varvec{i}} + \frac{1}{2}} \right)}}^{{\varvec{N}}}$$

(31)

where ${ }{\varvec{u}}^{{\varvec{N}}}$ is a degree of freedom (a displacement or rotation component) and the subscript $i$ refers to the increment number in an explicit dynamics step. The central-difference integration operator is explicit in the sense that the kinematic state is advanced using known values of $\dot{\varvec{u}}_{{\left( {{\varvec{i}} - \frac{1}{2}} \right)}}^{{\varvec{N}}}$ and $\ddot{\varvec{u}}_{{\left( {\varvec{i}} \right)}}^{{\varvec{N}}}$ from the previous increment.

The time increment based on the stability estimate can be rewritten in the form:

$$\Delta t \le {\text{min}}\left( {L_{e} \sqrt {\frac{\rho }{{\hat{\lambda } + 2\hat{\mu }}}} } \right)$$

(32)

where $L_{e}$ is a characteristic length, $\hat{\lambda }$ and $\hat{\mu }$ are the effective Lamé’s constants for the material.

The FDEM model proposed in this manuscript has been validated by the authors’ previous literature of a rock slide simulation [4, 8].

3.3 Model validation

Here, the authors validated the dynamic process of the debris flow and its interaction between rigid structures based on the above methodology in our numerical model, and the granular flow test conducted by Moriguchi et al. [31] is used. The reason why the authors chose granular flow test to validate debris flow is that both of the macroscopic fluidities of the debris flow and granular flow can be described by Bingham fluid model when the debris flow is treated as a single-phase material [16, 31, 36]. In his test, a flume, sand box and impact force measuring instrument are included in the model, whose schematic view is shown in Fig. 8a. The flume has an inclined angle of 45°, and the granular flow will move along the flume after the box door is rapidly removed. The dynamic process and shape of the granular flow are recorded by a high-speed camera. When the granular flow moves at the bottom and collides with the impact force measuring instrument, the time histories of the impact force will be recorded. The authors construct a numerical model based on the SPH-FEM to simulate the test using the number of 2880 SPH pseudoparticles to simulate granular flow while using finite elements to simulate the flume and measuring instrument (Fig. 8b). The smoothing length is automatically calculated such that the average number of particles associated with an element is roughly between 30 and 50. The characteristic length of SPH particles is 0.025 m. Because the Bingham model has been recognized as one of the most versatile models for simulating granular flow behavior and has been used in many occasions to model lava flow, snow avalanche, rock avalanche, and flow of fresh concrete [31], the behavior of the granular model is controlled by the above Bingham fluid constitutive model, while the measuring instrument is simplified to an elastic material. In the numerical model, parameters from the studies of Moriguchi [31], Dai [16] and Lin [27] are adopted, and detailed parameters are shown in Table 1.

Fig. 8

Sand flow model test: a schematic of the sand flow model; b numerical model

Table 1 Parameters used in the SPH simulation of granular flow

Figure 9 shows the evolution of granular flow moving along the flume and colliding with the impact force measuring instrument under the conditions that the inclined angle equals 45° and that the frictional angle equals 35°. The comparison of the free surface configurations between the two-dimensional Eulerian model of Moriguchi [31] and the three-dimensional CEL model of Lin [27] is carried out. It can be observed that granular material collapses after the box door is rapidly removed. Then, the granular material flows along the flume and constantly accelerates, and the maximum speed of the particles can reach 3 m/s. After the granular material collides with the measuring instrument, the head of the granular material quickly stops, and subsequent particles decelerate constantly, finally accumulating. To quantitatively assess the reliability of the SPH-FEM model, the authors further compared the impact force of the measurement in the laboratory experiment [31], several other numerical models [16, 27] and the SPH-FEM model, and corresponding results are shown in Fig. 9b. Laboratory experiment result shows that the average impact force originally formed at 0.75 s and obviously increased until 1.2 s, and then almost keeps the peak value of 192 N. As for the other three numerical results, although they don’t completely agree with the laboratory experiment, they generally have similar variation trend and close value with the laboratory experiment. Impact force originally formed at 0.8 s and the peak impact force value was 234 N in the SPH-FEM model. In the laboratory experiment, five groups of tests with flume inclination 45° were carried out, and the peak impact forces was from 168.9 to 212.7 N. The error of peak impact force is within 20% for the SPH-FEM model, so the simulation result of SPH-FEM model is considered acceptable. In addition, simulation conditions of SPH-FEM model were almost the same as Lin’s CEL model, and their simulation results are very close, again indicating the simulation result of SPH-FEM model is reasonable. Above all, it is reasonable to consider SPH-FEM model used in this study can effectively describe the behavior of a debris flow and its interaction with a rigid structure.

Fig. 9

Results comparison between the model test, CEL model and FEM-SPH model. a Left column: the laboratory experimental results [31]; middle column: FEM-SPH model results obtained in Lin’s study [27]; right column: FEM-SPH model results obtained in this study; b impact force of the measuring instrument when flume inclination equaling 45°

4 Numerical simulation

4.1 Model inputs

In this section, the SPH-FDEM method is used to simulate debris flows in the G62 gully. Although parameters in the laboratory test can’t be directly used in a full-scale landslide simulation due to scaling effect, SPH approach based on the Bingham fluid model can be used to simulate the debris flow and study its interaction with structure according to the Model validation section. Before the simulation, digital elevation data with an accuracy of 5 m are used to construct the terrain model of the G62 debris flow gully. The terrain model of the gully is set composed of nondeformable finite shell elements, and the model has fixed displacements in all directions. The debris flow is simulated by SPH pseudoparticles based on the Bingham model. Pellegrino systematically introduced the empirical values of Bingham fluid debris flows [36]. In most cases in Pellegrino’s study, the value of the yield shear stress $\tau_{0}$ mainly ranges from several Pa to hundreds of Pa, $\eta_{0}$ mainly ranges from a few tenths to several Pa^.s, and k mainly ranges from 0 to several tens. The solid volumetric concentration affects the rheological parameters, and $\tau_{0}$ and $\eta_{0}$ increase with increasing solid volumetric concentration. In the studies by Pellegrino et al. [36], the best-fitting Bingham parameters are $\tau_{0}$ = 144 Pa and $\eta_{0}$ = 1.8 Pa s when the solid volumetric concentration is 42%. In the G62 debris flow gully, the debris flow density is 1600 kg/m³; therefore, the solid volumetric concentration is 40% when the sediment mixture density is assumed to be 2500 kg/m³ [6]. The rheological parameters adopted for the debris flow should be lower. In the simulation, the value of the debris flow parameter $\tau_{0}$ is set to 120 Pa, $\eta_{0}$ is set to 1.5 Pa^.s, and k is set to 4 according to the solid volumetric concentration from rheological parameters presented in previous literature [15, 37]. For the friction coefficient between the debris flow and ground surface, an empirical value of 0.3 is given when relatively poor vegetation covers the surface from previous literature [6]. The smoothing length is still automatically calculated to affect 30 to 50 surrounding particles, while the characteristic length of SPH particles is 0.6 m. The parameters used in the debris flow simulation are shown in Table 2.

Table 2 Parameters used in the debris flow–structure interaction

An inflow point that represents the position at which the debris flow starts is set. The inflow point is usually set at the boundary of the catchment area and drainage channel because the catchment area is the main formation area of the debris flow. Field investigation and remote sensing show that the average debris flow width in the gully is approximately 10 m; therefore, the outflow width of the debris flow in the simulation is also set to 10 m. The occurrence of debris flows is usually accompanied by rainstorms and floods, indicating that the run-out process of debris flows depends on the rainfall intensity and duration. The debris flow hydrography is frequently used for the debris flow run-out simulation and simulation results show using hydrography to determine debris flow run-out process is reasonable [12, 13]. The hydrography’s abscissa is the duration and the ordinate is discharge while the surrounding area is the total volume of debris flow. The debris flow hydrography is obtained from the flood hydrography, and the debris flow discharge is the product of flood discharge and bulking factor, which is corresponding to solid volumetric concentration [6]. The flood hydrography is frequently calculated based on the hydrological data of basin and empirical formulas in the technical standards. Due to the lack of hydrological data in the study area, back analysis, which is the most important way to calibrate a simulation result [7, 29, 43], is applied for the simulation. From the investigation, the average cross-sectional area of the debris flow sediment is 20 m², while the length of debris flow sediment is 800 m. Because the solid volumetric concentration is 40%, the total volume of the newest debris flow is 4 × 10⁴ m³. In the back analysis, the hydrograph that determines the process of the debris flow is simplified as a triangle type [5, 13]. According to the watershed area and with reference to the many debris flow flows that the authors have investigated [5, 6], the duration of the debris flow is assumed to be 120 s according to the Basin area. The numerical model and hydrology graph are shown in Fig. 10.

Fig. 10

Debris flow model of the G62 gully with hydrology graph

4.2 Results and discussion

4.2.1 Typical process of a debris flow without a check dam

A typical dynamic process of a debris flow is shown in Fig. 10. After the debris flow started, the debris material flowed from the inflow point and along the bottom of the gully (Fig. 11a). The debris flow continued to accelerate in the straight, steep terrain of the upstream valley within the first 40 s. In this acceleration period, the front part of the debris flow had a higher speed than the back part of the debris flow. The local maximum speed of the debris flow could reach 32 m/s (Fig. 11b). After 40 s, since there were some bends in the middle-downstream valley, the debris flow decelerated due to collision at the bends. For this reason, the debris flow no longer accelerated stably. Different acceleration characteristics existed between different parts of the debris flow in the middle-downstream valley (Fig. 11c). When the debris flow reached the downstream area near the gully mouth, the debris flow slowed significantly because the terrain became gentle (Fig. 11d). Finally, the debris flow quickly dissipated energy due to the friction effect after running out of the debris flow gully, running into the broad river valley, and accumulating along the river valley, forming a debris flow fan (Fig. 11e). Comparing the numerical results and field investigation (Fig. 11f), the debris flow scale in the numerical simulation fits the real debris flow scale well, indicating that the numerical results are reasonable and acceptable. In addition to the speed of the debris flow, some other quantitative information could be acquired from the model, such as the accumulated viscous dissipation energy (E_V) and accumulated frictional energy (E_f) (Fig. 12). Both E_V and E_f increased with time. Within the initial 40 s of the debris flow, the values of E_V and E_f were very small because the run-out volume of the debris flow was very small and the speed of the debris flow was small. With the run-out volume as well as the movement speed (distance) of the debris flow rapidly increasing, the growth rates of E_V and E_f also increased_, leading to rapid increases in E_V and E_f at the same time.

Fig. 11

Typical dynamic process of the debris flow

Fig. 12

Variation of different physical parameters of the debris flow a accumulated viscous dissipation energy; b accumulated frictional energy

4.2.2 Typical process of a debris flow with a check dam

Debris flows in the G62 gully have the potential to threaten NR 318. To mitigate the debris flow scale, the check dam is considered in the prevention condition. During the site investigation, the authors found that most of the check dams was composed of polygonal rock blocks with concrete bonded (Fig. 2). The structure of check dams is similar to the masonry structures and this kind of material composed of blocks bonded together is very suitable to be simulated by FDEM. In previous literature, FDEM has been applied to study the mechanical behavior of masonry structures, a kind of heterogeneous anisotropic material composed of units (e.g., bricks, stones, blocks, etc.) bonded together with or without mortar. The quadratic nominal stress criterion (QUADS) damage failure criterion, was defined in Eq. 22, fits the fracture behavior of masonry [2]. To address the structural features of the check dam, the Voronoi diagram of FDEM was used to simulate polygonal rock blocks in the check dams. CIEs were inserted into the boundaries of Voronoi polygons to simulate concrete interface and previous literature has proven that using CIEs to simulate mortar/concrete interface between blocks can get good simulation results [10, 20, 38, 50]. Therefore, the Voronoi FDEM provides a reasonable approach for the simulation of check dams in the study area. The numerical check dam model is constructed with following processes. First, Voronoi polygons were used to divide the geometry of the check dam, and each polygon represents a rock block, while the boundary geometry between polygons represents the mortar layer (Fig. 13a). Then, the check dam was meshed (Fig. 13b). The rock blocks were meshed by finite elements with an elastic constitutive model (Fig. 13c), while the boundaries of polygons were inserted into CIEs (Fig. 13d). Rock blocks were assigned the following parameters: a density of 2500 kg/m³, Poisson’s ratio of 0.25 and Young's modulus of 38 GPa. For the CIE parameters of concrete, the authors adopted the parameters presented in Sherzer’s study, which are shown in Table 2 [38]. After constructing the rectangular check dam, Boolean operations were used to modify the shape of the check dam to make it fit the complex terrain. The bottom of the check dam was fixed to the ground surface. The maximum height of the check dam was 20 m, while the maximum length was 150 m with a thickness of 4 m.

Fig. 13

Check wall simulated by the Voronoi FDEM

Figure 14 shows the dynamic process of the debris flow interacting with the check dam. The scenes of debris flow speed and stress were recorded. To determine whether the check dam was damaged, the contour map of the overall scalar stiffness degradation (SDEG), which represents damage variable D in Eq. 23, was also recorded. The variable D represents the damage extent of the CIE: When the CIE is in the elastic deformation period and does not damage, the variable D is 0. When the CIE is in the damage period, the variable D is on the scale of 0 to 1. If the CIE is completely damaged, the variable D is 1, and the corresponding CIE is deleted from the numerical scenario. The debris flow reached the check dam at 60 s. After the debris flow collided with the check dam, the front part rapidly decelerated and stopped. The part of the check dam that was impacted by the debris flow presented an obvious stress concentration phenomenon (Fig. 14a). Because the check dam bottom was fixed on the ground surface, the bottom part of the check dam would also present a stress concentration phenomenon under the impact of the debris flow. The maximum stress in the stress concentration area could reach 2.4 × 10⁶ Pa. With the run-out process, debris flow material was constantly deposited in front of the check dam (Fig. 14b–d). During this period, the stress concentration area of the check dam increases with the contact area between the debris flow and check dam. The maximum stress of the check dam at the left top corner constantly increases from 2.3 × 10⁷ Pa (T = 63 s) to 2 × 10⁸ Pa (T = 120 s). The authors think there are two reasons why the maximum stress of the left top corner rapidly increased. One of the reasons is that the corner on the edge was prone to stress concentration. The other reason is that the left top corner was very close to the debris flow. This is why the stress in the right top corner also increased but was not as noticeable in the left top corner because the right top corner was too far from the debris flow body. In addition, the impact force of the check dam can be acquired quantitatively (Fig. 14e). The check dam was suffered from the initial debris flow impact at 60 s, and then the impact force constantly increased with time in general. During 60–90 s, slope of the curve within unit time is increasing, indicating the impact force increment is increasing with time. The reason for this phenomenon is that the run-out debris flow volume increases linearly within unit time in the first 30 s. During 90–110 s, the increasing rate of the impact force slows down, and the impact force reached the peak value of 1.84 × 10⁸ N at 110 s. After 110 s, the impact force decreased and finally stabilized at 1.75 × 10⁸ N. Notably, the SDEG of check dam CIEs was 0 in the whole debris flow run-out process, indicating that the check dam only deformed elastically without damage.

Fig. 14

Interaction with stress, velocity, damage extent and impact force information between the debris flow and check dam at different times on the condition that the check dam is undamaged

The strength of a check dam will decrease when the dam is in nature for a long time and suffers from various external loads and erosion, such as tectonics and weathering. Thus, the check dam might be intensely destroyed when suffering the impact of a debris flow. To investigate the damage process of a check dam under the impact of a debris flow, another group of weaker parameters of CIEs were set to simulate a weaker check dam. Under this condition, $t_{n}$ and $t_{s}$ were set to 1.5 MPa and 5 MPa, respectively, while the values of $G_{{\text{I}}}^{C}$ and $G_{{{\text{II}}}}^{C}$ were set to 15 N/m and 120 N/m, respectively. The scenes of the debris flow impacting the check dam at 63 s, 75 s, 90 s, and 120 s were recorded.

Figure 15 shows the process of the debris flow impacting the check dam. After the debris flow impacts the dam, stress will concentrate and increase at the contact area (Fig. 15a). After the concentration stress exceeds the peak strength of the CIEs, fractures are generated, and the dam is finally destroyed by the debris with increasing impact force (Fig. 15b). At the moment when the dam is destroyed, the damaged part will explode due to the sudden release of accumulated elastic energy, generating broken blocks. The movement of broken blocks also obeys the movement Eqs.28 to 31. The maximum speed of the exploded broken block can reach 6 m/s. Then, the separated broken blocks will be carried by the debris material and continue to move. With the continuous impact of the debris flow, the destroyed cavity area generated by the debris flow impact will continue to increase. The number of broken blocks will also continue to increase and be carried by the debris flow to move a long distance (Fig. 15c, d). An advantage of the SPH-FDEM model to simulate a debris flow destroying a check dam is that the movement of broken blocks can be considered in the model, unlike in Liu’s SPH-DEM-FEM model [28] based on the element deletion technique. In Liu’s model, when the dam is destroyed by the impact of the debris flow, the stiffness of the completely damaged finite elements will drop to zero, being deleted and excluded from the subsequent computation. This will lead to the loss of material mass and an incomplete description of the subsequent dynamic process.

Fig. 15

Interaction between the debris flow and check dam based on the stress contour map on the condition that the check dam is destroyed by debris

To clearly show the fragmentation of the check dam, the contour maps of the SDEG and model mix ratio during damage evolution (MMIXDME) are also shown (Fig. 16). MMIXDME is a parameter representing the ratio of the fracture energy consumed during the sliding mode to the fracture energy consumed during the opening mode in a mixed mode of opening and sliding, which is defined as follows:

$${\text{MMIXDME}} = {1} - \frac{{G_{n} }}{{G_{T} }}$$

(33)

where $G_{n}$ is the fracture energy consumed by the opening mode and $G_{T}$ is the fracture energy consumed by all fracture modes. The value of MMIXDME equaling 0 represents when the CIE completely undergoes opening mode damage. The value of MMIXDME equaling 1 is when the CIE completely undergoes sliding mode damage. A value of − 1 indicates that the CIE is intact. When MMIXDME ranges between 0.0 and 0.5, the CIE is predominantly exhibiting opening mode damage. When MMIXDME ranges between 0.5 and 1, the CIE is predominantly exhibiting sliding mode damage. Figure 16a shows that the scale of the damaged CIEs increased with time. In addition, the damage extent of the CIEs around the completely destroyed part decreased with increasing distance from the boundary of the destroyed part. Figure 15b shows that the MMIXDME of damaged CIEs dominated from 0 to 0.5, indicating that fractures presented in the dam were mainly tension fractures. From the field investigation, fractures in the dam have relatively large openings, and most of the fractures extend along the weak segments and present stepped shapes, indicating that the fractures are mainly tension fractures (Fig. 2). In terms of fracture properties, the simulation results are consistent with the real conditions.

Fig. 16

The damage condition of the CIEs during the process of a debris flow impacting a check dam. (In the contour map of SDEG, higher the value means higher the damage extent of CIE. The CIE is intact when the value is 0, and the CIE is completely damaged when the value is 1; In the contour map of MMIXDME, CIE is predominantly exhibiting opening mode damage when the value is between 0 to 0.5, and CIE is predominantly exhibiting sliding mode damage when the value is between 0.5 to 1. CIE is intact when the value is − 1.)

In addition to the fracture extent and mode of the check dam, the number of completely damaged CIEs, the area of completely damaged CIEs, the accumulated fracture energy, and the percentage of CIEs dominated by the opening mode were recorded during the whole impact process (Fig. 17). For the number of completely damaged CIEs, there is no damaged CIE before 62 s because the debris flow has not yet collided with the check dam (Fig. 17a). After 62 s, the completely damaged CIE starts to generate under the impact of the debris flow. In the initial 2 s after the collision, from 62 to 64 s, the number of completely damaged CIEs sharply rises to 120, forming a large cavity at the bottom of the dam. After 64 s, the number of completely damaged CIEs increases in a stepped shape. Each time the number of completely damaged CIEs increases, meaning that a block has fallen off the dam body due to complete loss of cohesion, the cavity formed by the impact of debris flow will become larger. This phenomenon also indicates that the subsequent erosion effect of the debris flow on the dam is inhomogeneous during the whole interaction period. At the end of the simulation, the number of completely damaged CIEs is 423. The completely damaged CIE area is almost linearly related to the number of completely CIEs because the length and width of each CIE are almost the same (Fig. 17b). The final accumulated completely damaged area formed in the check dam is 1463 m². The fracture energy sharply increases after the debris flow impacts the check dam (Fig. 17c). In addition to the completely damaged CIEs, many partially damaged CIEs are generated after the debris flow impacts the dam. Therefore, the fracture energy reaches 250,000 J during the initial 2 s after collision. Then, the fracture energy continues to increase due to the fracture process of undamaged and partially damaged CIEs. The fracture energy also increases in a stepped shape after 64 s, which also proves that the erosion effect of the debris flow on the dam is inhomogeneous throughout the whole process. During the whole simulation process, the fracture energy of the check dam is approximately 400,000 J. The percentage of CIEs dominated by the opening mode during the whole process can also be quantitatively acquired (Fig. 17d). From 62 to 64 s, which are the initial 2 s of the dam being hit by the debris flow, the check dam experiences an impact force perpendicular to the check dam within a very short time. During this time, the rock block inside the check dam easily slides along the mortar layer and separates from the main body after the frontal impact force. Therefore, the fractures generated by debris impact in this period are mainly sliding mode fractures, accounting for 65% of all these fractures, while opening mode fractures account for 35%. After the dam body is impacted by the debris flow to generate a cavity, the debris flows along the cavity, and the dam body is mainly affected by lateral erosion. The dam body at the edge of the cavity experiences a tension force under the effect of the debris flow lateral frictional force. The percentage of opening mode fractures rapidly increases to 57% at 74 s and gradually increases to 72% at the end of the simulation. The fracture types formed by direct impact and lateral erosion are very different.

Fig. 17

Variation in different physical parameters of the CIEs with time: a number of completely damaged CIEs; b completely damaged CIE area; c accumulated fracture energy; d percentage of CIEs

5 Conclusions

Aiming to quantitatively assess the dynamic process of a debris flow and its interaction with a check dam considering check dam damage in the Yarlung Zangbo River valley, this paper addresses a novel numerical approach to simulate the above process based on the SPH-FDEM. A case from the G62 gully, which potentially threatens NR 318, was adopted for the three-dimensional numerical simulation. The debris flow simulated by calibrated Bingham fluid based on SPH has a deposit scale similar to that of the debris flow investigated in the field investigation, proving that the SPH model proposed in this study can effectively solve the three-dimensional debris flow simulation problem. The run-out speed, viscous dissipation energy, and frictional energy can be directly acquired. The SPH method can be coupled with FDEM, and the method using Voronoi polygons to divide the geometry of the check dam can effectively reflect the structural characteristics of mortar-bonded check dams. The interaction between the SPH debris flow and FDEM check dam also can be effectively simulated, and the stress, damage area, damage extent, damage mode, fracture energy, and fracture area can be quantitatively acquired. Compared to the existing debris flow numerical models, the SPH-FDEM model proposed in this study greatly expands the applicability of debris flow numerical models and has the following characteristics:

• (1) Previous models frequently consider check dams as rigid bodies and do not consider the damage process when simulating debris flows impacting check dams. The proposed model can consider the damage process of the check dam and can further consider the structural characteristics of the check dam, which allows more information to be acquired from the debris flow simulation.

• (2) The hydrological process is frequently not considered in the existing three-dimensional numerical models, making the debris flow volume fixed, not even changing with rainfall or flooding. The SPH-FDEM is a three-dimensional model with the potential to consider the real hydrological process of debris flows, making the simulation of the debris flow run-out process more realistic.