Study on the freezing temperature of saline soil

Abstract

Freezing temperature is an important parameter in studying the freezing mechanism of saline soil. An equation for calculating the freezing temperature is proposed based on the phase transition theory in porous medium, including two main influencing factors, the water activity and pore size. In this equation, the effect of the water activity on the freezing temperature of soil is calculated by Pitzer model, while the impact of pore size is replaced by water content. Through comparing the calculated results with the published experimental data, the equation is proved to be competent in predicting the freezing temperature for the saline soil with sodium chloride or calcium chloride. For the saline soil with sodium carbonate, the effect of salt hydrate crystallization should be taken into consideration. With respect to the saline soil with sodium sulfate, it is difficult to determine the freezing temperature, since there is uncertainty of the resultant when freezing (that is, heptahydrate or decahydrate). In addition, the effects of pore size and multi-component solutes on freezing temperature are also discussed. The study would be helpful for revealing the freezing mechanism and also providing a useful theoretical method for engineering design of saline soil in cold regions.

1 Introduction

Saline soil is widely distributed in seasonally frozen soil regions or permafrost regions in northwest China [18, 19]. In recent years, various engineering constructions have been increasingly built in these saline frozen regions [15, 17]. To date, however, very limited research has been conducted on the physical properties of saline soils due to their complexities. Freezing temperature is one of the most important soil properties since it determines the state of soils, frozen, or thawed. There are many factors that affect the freezing temperature, among which water and salt content are the two main influencing factors [2]. Therefore, it is of great importance to further investigate the influences of these two factors on freezing temperatures in those saline frozen regions.

In the previous literature, freezing temperatures of saline soils were obtained by indoor experiments [2], and regress methods were then used to obtain the relationship between the freezing temperatures and water/salt contents. Since different kinds of salts were frequently contained in the soils, the statistical functions became very complicated and limited in use practically. Wan et al. [16] studied the freezing temperature of Qinghai–Tibet silty clay on the basis of Pitzer model, but it is only applicable for the soils with water content of 18%. Therefore, an improved theory is urgently needed to predict the freezing temperatures of soils with different water and salt contents.

Before investigating the freezing temperatures of saline soils, it is worth mentioning phase diagram in water–salt system, which aims at determining the phase transition direction and limit when the external conditions change. The freezing temperatures of solution under different concentrations can be obtained from phase diagram. Previously, phase diagram data are obtained by experiment. In last decades, some different models have been put forward to describe the nature of solution. The first model is well known as Debye–Hukel (DH) model [10], but it is not applicable for the solution with high concentrations. Pitzer [13] proposed a semiempirical model that can overcome the defect of DH model, and it can also be extended to the solution with multi-component solutes. After that, many other models were proposed to describe the nature of solution, such as Lin and Lee (LL) model [11, 12] and Khoshkbarchi and Vera (KV) model [8, 9]. Currently, it is relatively mature to describe the nature of solution in physical chemistry study, so the freezing temperature of general solution can be easily obtained based on physical chemistry method. From this perspective, if the existing solution theory is applied to the study of frozen saline soil, not only the nature of salt can be better understood by civil engineers, but also some novel ideas can be developed in the following study.

In this paper, a formula for calculating the freezing temperatures of saline soils is derived based on the phase transition theory in porous media [3, 5], which includes two parts, the water activity and pore size. The proposed formula is proved to be reliable by comparing the calculated results with the phase diagram data. To further verify the reasonableness of this formula, based on the previous experimental data, the influencing factors of freezing temperature are extensively analyzed including water content, salt content, crystallization, compactness, and multi-component solutes. The study would be helpful for revealing the freezing mechanism of saline soil and also providing a theoretical basis for numerical simulation of saline soil engineering in cold regions afterward.

2 Theoretical Analyses

2.1 Freezing temperature of saline solution in pore medium

In thermodynamics [1], an equilibrium state between water and ice will be reached when their chemical potentials are equal, i.e.,

$$\mu_{\text{w}} \left( {p_{\text{l}} ,T,a_{\text{w}} } \right) = \mu_{\text{i}} \left( {p_{\text{i}} ,T} \right)$$

(1)

where $\mu_{\text{w}} (p_{\text{l}} ,T,a_{\text{w}} )$ and $\mu_{\text{i}} (p_{\text{i}} ,T)$ are the chemical potential of solvent (water) and ice, respectively. T is the current temperature (in K), and p _l and p _i are the pressure of liquid solution and ice (in Pa), respectively. The chemical potential of water and ice can be expressed as follows:

$$\mu_{\text{w}} \left( {p_{\text{l}} ,T,a_{\text{w}} } \right) = \mu_{\text{w}}^{*} \left( {p_{0} ,T_{0} } \right) + \int_{{p_{0} }}^{{p_{l} }} {V_{\text{w}} {\text{d}}p} - \int_{{T_{0} }}^{T} {S_{\text{w}} {\text{d}}T} + RT\ln a_{\text{w}}$$

(2)

$$\mu_{\text{i}} \left( {p_{\text{i}} ,T} \right) = \mu_{\text{i}}^{*} \left( {p_{0} ,T_{0} } \right) + \int_{{p_{0} }}^{{p_{\text{i}} }} {V_{\text{i}} {\text{d}}p} - \int_{{T_{0} }}^{T} {S_{\text{i}} {\text{d}}T}$$

(3)

where $\mu_{\text{w}}^{*} (p_{0} ,T_{0} )$ and $\mu_{\text{i}}^{*} (p_{0} ,T_{0} )$ are the chemical potential of pure water and ice at pressure p ₀ and temperature T ₀, respectively. V _w and V _i are molar volume of liquid water and ice crystals (in m³ mol⁻¹). R is the ideal gas constant (in J mol⁻¹ K⁻¹). a _w is the water activity in solution. S _w and S _i are molar entropy of liquid water and ice crystals (in J mol⁻¹ K⁻¹), respectively. When the two phases are in equilibrium state at pressure p ₀ and temperature T ₀, the following equation can be obtained:

$$\mu_{\text{w}}^{*} \left( {p_{0} ,T_{0} } \right) = \mu_{\text{i}}^{*} \left( {p_{0} ,T_{0} } \right)$$

(4)

where p ₀ is the atmospheric pressure. T ₀ is the freezing temperature of pure water (T ₀ = 273.15 K). Substituting Eqs. (2)–(4) into Eq. (1), we can obtain

$$\int_{{T_{0} }}^{T} {\frac{{S_{\text{w}} - S_{\text{i}} }}{{V_{\text{i}} }}{\text{d}}T} - \frac{{RT\ln a_{\text{w}} }}{{V_{\text{i}} }} + \left( {p_{\text{i}} - \frac{{V_{\text{w}} }}{{V_{\text{i}} }}p_{\text{l}} } \right) + \left( {\frac{{V_{\text{w}} }}{{V_{\text{i}} }} - 1} \right)p_{0} = 0$$

(5)

In Eq. (5), the second item represents the effect of concentration on freezing temperature, and the third one represents the pressure difference between ice and water. The fourth one represents the effect of volume change due to phase change. And Eq. (5) can be expressed as:

$$\int_{{T_{0} }}^{T} {\frac{{S_{\text{w}} - S_{\text{i}} }}{{V_{\text{i}} }}{\text{d}}T} - \frac{{RT\ln a_{\text{w}} }}{{V_{\text{i}} }} + \left( {p_{\text{i}} - p_{\text{l}} } \right) - \left( {\frac{{V_{\text{w}} }}{{V_{\text{i}} }} - 1} \right)\left( {p_{\text{l}} - p_{0} } \right) = 0$$

(6)

where $\Delta S_{\text{m}} = \frac{{\left( {S_{\text{w}} - S_{\text{i}} } \right)}}{{V_{\text{i}} }}$ is denoted as the entropy of per molar volume during phase change (in Pa K⁻¹). When the reference state of the liquid solution is at atmospheric pressure, we have $p_{\text{l}} = p_{0}$ [4, 20] in Eq. (6), and the fourth item of Eq. (6) can be eliminated. Because the difference between T ₀ and T is small in Kelvin temperature [1, 5]; for simplicity, the change of temperature is ignored in the second item; then, we can obtain

$$T - T_{0} = \frac{{RT_{0} \ln a_{\text{w}} }}{{\Delta S_{\text{m}} V_{\text{i}} }} - \frac{{p_{\text{i}} - p_{\text{l}} }}{{\Delta S_{\text{m}} }}$$

(7)

Based on Young–Laplace equation [3, 5, 14], the following equation can be obtained:

$$p_{\text{i}} - p_{\text{l}} = - \frac{{2\gamma_{\text{il}} \cos \theta }}{r}$$

(8)

where $\gamma_{\text{il}}$ denotes the surface energy of ice/liquid solution interface (in J m⁻²), while r is its current mean curvature radius, and θ is the contact angle. Substituting Eq. (8) into Eq. (7), we can obtain

$$\Delta T = T - T_{0} = \frac{{RT_{0} \ln a_{\text{w}} }}{{V_{\text{i}} \Delta S_{\text{m}} }} + \frac{{2\gamma_{\text{il}} \cos \theta }}{{r\Delta S_{\text{m}} }}$$

(9)

Equation (9) indicates that the freezing temperature is determined by two aspects. The first one is water activity which is influenced by the salt concentration. The higher the concentration is, the smaller the water activity is. The freezing temperature will decrease more obviously. The second one is the effect of pore size. The smaller the pore size is, the lower the freezing temperature is.

The freezing temperatures of saline solution in pore medium are also influenced by surcharge load; however, large pressure is needed for the freezing temperature depression of soils [14, 22]. As for the soil with low surcharge load, the effect of load is ignored and the effect of saline content on freezing temperature is mainly investigated in this paper.

2.2 The effect of salt concentration on freezing temperature

For free solution, the pore radius r → ∞, then the effect of the pore size can be neglected [1], and the freezing temperature of solution is mainly determined by the water activity of the solution; then, Eq. (9) can be simplified as

$$\Delta T = T - T_{0} = \frac{{RT_{0} \ln a_{\text{w}} }}{{V_{\text{i}} \Delta S_{\text{m}} }}$$

(10)

Equation (10) is a formula for calculating the freezing temperature of the solution. In Pitzer model [10, 13], the water activity a _w is defined as

$$\ln a_{\text{w}} = - \phi \sum {m_{\text{i}} M_{\text{w}} }$$

(11)

where ϕ is the osmotic coefficient, m _i is the molar concentration (in mol kg⁻¹), and M _w is the relative molecular mass of water (in kg mol⁻¹). The osmotic coefficient ϕ is expressed as

$$\phi - 1 = \left| {Z_{\text{C}} Z_{\text{A}} } \right|f^{\phi } + \frac{{2\nu_{\text{C}} \nu_{\text{A}} }}{\nu }mB_{\text{CA}}^{\phi } + \frac{{2\left( {\nu_{\text{C}} \nu_{\text{A}} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}{\nu }m^{2} C_{\text{CA}}^{\phi }$$

(12)

where C and A represent cation and anion, respectively. Z _C and Z _A are the charge numbers of the cations and anions, respectively. $\nu_{\text{C}}$ and $\nu_{\text{A}}$ are the numbers of the cations and anions in solution, respectively. m is the molar concentration of salt (in mol kg⁻¹). $C_{\text{CA}}^{\phi }$ is parameter of salt (in kg² mol⁻²). $f^{\phi }$ and $B_{\text{CA}}^{\phi }$ are the two functions depended on ionic strength, which are defined as follows:

$$f^{\phi } = - A^{\phi } \frac{{I^{1/2} }}{{1 + bI^{1/2} }}$$

(13)

$$B_{\text{CA}}^{\phi } = \beta_{\text{CA}}^{\left( 0 \right)} + \beta_{\text{CA}}^{\left( 1 \right)} \exp \left( { - \alpha_{1} I^{1/2} } \right) + \beta_{\text{CA}}^{\left( 2 \right)} \exp \left( { - \alpha_{2} I^{1/2} } \right)$$

(14)

where I is ionic strength of the solution (in mol kg⁻¹), defined as $I = \frac{1}{2}\sum {m_{i} } Z_{i}^{2}$. b is the empirical parameter (in kg^0.5 mol^−0.5), generally b = 1.2 kg^0.5 mol^−0.5. $A^{\phi }$ is the Debye–Hukel parameter (in kg^0.5 mol^−0.5) for osmotic coefficient ϕ, which is determined by the solute type and environmental temperature, defined as:

$$A^{\phi } = \frac{1}{3}(2\pi N_{0} \rho_{\text{w}} )^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left( {\frac{{e^{2} }}{DkT}} \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}}$$

(15)

where N ₀ is the Avogadro constant (in mol⁻¹), ρ _w is the density of water (in kg m⁻³) at temperature T, e is the elementary charge (in C), and D is the dielectric constant of water (in F m⁻¹). k is the Boltzmann constant (in J K⁻¹). $A^{\phi }$ is equal to 0.3920 kg^0.5 mol^−0.5 when water temperature is 25 °C, while $A^{\phi }$ equals 0.3437 kg^0.5 mol^−0.5 when water temperature keeps at 0 °C.

To illustrate the calculation accuracy of Pitzer model, four kinds of salts are selected as objectives including sodium chloride, calcium chloride, sodium sulfate, and sodium carbonate. The related parameters are given in Table 1.

Table 1 Parameters of electrolyte solution [10]

The freezing temperatures of the solutions with these four salts are calculated by Pitzer model, as shown in Fig. 1. The red triangles represent the freezing temperatures obtained from the phase diagram [10], while the black lines represent the calculated results by Pitzer model. It can be seen that the agreement between the phase diagram results and the calculated results is very good.

Fig. 1

Freezing temperature of solution (a sodium chloride, b calcium chloride, c sodium sulfate, d sodium carbonate)

Pitzer model can be extended to the case of multi-components. Havie and Wear [6, 7] rearranged Pitzer model and presented the more convenient formula of osmotic coefficient of mixed electrolyte theory, namely HW formula.

$$\begin{aligned} \phi - 1 & = \left( {\sum\limits_{i} {m_{i} } } \right)^{{ - 1}} \left\{ {2\left[ {\frac{{ - A^{\phi } I^{{3/2}} }}{{1 + 1.2I^{{1/2}} }} + \sum\limits_{{i_{{\text{C}}} = 1}}^{{N_{{\text{C}}} }} {\sum\limits_{{i_{{\text{A}}} = 1}}^{{N_{{\text{A}}} }} {m_{{\text{C}}} m_{{\text{A}}} \left( {B_{{{\text{CA}}}}^{\phi } + ZC_{{{\text{CA}}}} } \right) + \sum\limits_{{i_{{\text{C}}} = 1}}^{{N_{{\text{C}}} - 1}} {\sum\limits_{{j_{{{\text{C}}^{\prime } }} = i_{{\text{C}}} + 1}}^{{N_{{\text{C}}} }} {m_{{\text{C}}} m_{{{\text{C}}^{\prime } }} \left( {\Phi _{{{\text{CC}}^{\prime } }}^{\Phi } + \sum\limits_{{i_{{\text{A}}} = 1}}^{{N_{{\text{A}}} }} {m_{{\text{A}}} \Psi _{{{\text{CC}}^{\prime } {\text{A}}}} } } \right)} } } } } \right.} \right. \\ & \quad + \left. {\left. {\sum\limits_{{i_{{\text{A}}} = 1}}^{{N_{{\text{A}}} - 1}} {\sum\limits_{{J_{{{\text{A}}^{\prime } }} = i_{{\text{A}}} + 1}}^{{N_{{\text{A}}} }} {m_{{\text{A}}} m_{{{\text{A}}^{\prime } }} \left( {\Phi _{{{\text{AA}}^{\prime } }}^{\Phi } + \sum\limits_{{i_{{\text{C}}} = 1}}^{{N_{{\text{C}}} }} {m_{{\text{C}}} \Psi _{{{\text{AA}}^{\prime } {\text{C}}}} } + \sum\limits_{{i_{{\text{N}}} = 1}}^{{N_{{\text{N}}} - 1}} {\sum\limits_{{i_{{\text{A}}} = 1}}^{{N_{{\text{A}}} }} {m_{{\text{N}}} m_{{\text{A}}} \lambda _{{{\text{NA}}}} + } \sum\limits_{{i_{{\text{N}}} = 1}}^{{N_{{\text{N}}} - 1}} {\sum\limits_{{i_{{\text{C}}} = 1}}^{{N_{{\text{C}}} }} {m_{{\text{N}}} m_{{\text{C}}} \lambda _{{{\text{NC}}}} } } } } \right)} } } \right]} \right\} \\ \end{aligned}$$

(16)

where C and C′ are cations. A and A′ are anions. m _C and Z _C are molar concentration and charge number of the cation, respectively. N _C is the number of cationic species. The similar definitions hold for anion A and neutral molecule N. C, A, and N represent cation, anion, and neutral molecules, respectively. $\varPsi_{ijk}$ are the third virial coefficients, which are independent of ionic strength (in kg² mol⁻²). The second virial coefficients $\lambda_{Ni}$ represent the interactions between ions and neutral species (in kg mol⁻¹). There are the following equations:

$$C_{\text{CA}} = \frac{{C_{\text{CA}}^{\phi } }}{{2\left| {Z_{\text{C}} Z_{\text{A}} } \right|^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}$$

(17)

$$Z = \sum\limits_{\text{i}} {\left| {Z_{\text{i}} } \right|} m_{\text{i}}$$

(18)

$$B_{\text{CA}}^{\phi } = \beta_{\text{CA}}^{(0)} + \beta_{\text{CA}}^{(1)} \exp \left( { - \alpha_{1} I^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) + \beta_{\text{CA}}^{(2)} \exp \left( { - \alpha_{2} I^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)$$

(19)

$$B_{\text{CA}}^{\phi } = \beta_{\text{CA}}^{(0)} + \beta_{\text{CA}}^{(1)} g\left( {\alpha_{1} I^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) + \beta_{\text{CA}}^{(2)} g\left( {\alpha_{2} I^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)$$

(20)

$$B_{\text{CA}}^{'} = {{\left[ {\beta_{\text{CA}}^{(1)} g'\left( {\alpha_{1} I^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) + \beta_{\text{CA}}^{(2)} g'\left( {\alpha_{2} I^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\beta_{\text{CA}}^{(1)} g'\left( {\alpha_{1} I^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) + \beta_{\text{CA}}^{(2)} g'\left( {\alpha_{2} I^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right)} \right]} I}} \right. \kern-0pt} I}$$

(21)

where g and g′ are expressed as:

$$g\left( x \right) = 2{{\left[ {1 - (1 + x)exp( - x)} \right]} \mathord{\left/ {\vphantom {{\left[ {1 - (1 + x)exp( - x)} \right]} {x^{2} }}} \right. \kern-0pt} {x^{2} }}$$

(22)

$$g^{\prime}\left( x \right) = 2{{[1 - (1 + x + \frac{{x^{2} }}{2})exp( - x)]} \mathord{\left/ {\vphantom {{[1 - (1 + x + \frac{{x^{2} }}{2})exp( - x)]} {x^{2} }}} \right. \kern-0pt} {x^{2} }}$$

(23)

where $\beta_{\text{CA}}^{(0)} ,\beta_{\text{CA}}^{(1)}$ and $\beta_{\text{CA}}^{(2)}$ are the characteristic parameters of CA electrolyte (in kg mol⁻¹). Because of strong electrostatic association tendency of high valence electrolyte, β ⁽²⁾ is important in the case of 2–2 salts (e.g., MgSO₄) or in the higher cases, which can be ignored for other cases. For the cases of 1–1, 1–2, or 2–1 valence pairs salts (e.g., NaCl, Na₂SO₄, CaCl₂). $\alpha_{1} = 2.0 \,{\text{kg}}^{0.5} \,{\text{mol}}^{ - 0.5}$, $\alpha_{2} = 0\, {\text{k}}g^{0.5} \,{\text{mol}}^{ - 0.5}$.

$\varPhi_{ij}^{\varPhi } ,\varPhi_{ij} ,\varPhi_{ij}^{'}$ are the second virial coefficients in the ion interaction approach (in kg mol⁻¹), which depend on ionic strength, and are given as follows:

$$\varPhi_{ij}^{\varPhi } = \theta_{ij} + {}^{E}\theta_{ij} + I{}^{E}\theta_{ij}^{'}$$

(24)

$$\varPhi_{ij} = \theta_{ij} + {}^{E}\theta_{ij}$$

(25)

$$\varPhi_{ij}^{'} = {}^{E}\theta_{ij}^{'}$$

(26)

where θ is the interaction parameter between two types of co-ions. ${}^{E}\theta_{ij}$ and ${}^{E}\theta^{\prime}_{ij}$ are the charges of ions i and j. They are the functions of ionic strength and can be obtained by taking a classic asymmetric mixed effect into consideration. When the charges of the ions i and j are equal, both ${}^{E}\theta_{ij}$ and ${}^{E}\theta^{\prime}_{ij}$ equal zero. Their equations are defined as follows:

$${}^{E}\theta_{ij} = \frac{{Z_{i} Z_{j} }}{4I}\left[ {J\left( {x_{ij} } \right) - \frac{{J\left( {x_{ii} } \right)}}{2} - \frac{{J\left( {x_{jj} } \right)}}{2}} \right]$$

(27)

$${}^{E}\theta_{ij}^{'} = - \frac{{{}^{E}\theta_{ij} }}{I} + \frac{{Z_{i} Z_{j} }}{{8I^{2} }}\left[ {x_{ij} J'\left( {x_{ij} } \right) - \frac{{x_{ii} J'\left( {x_{ii} } \right)}}{2} - \frac{{x_{jj} J'\left( {x_{jj} } \right)}}{2}} \right]$$

(28)

$$x_{jj} = 6Z_{i} Z_{j} A^{\phi } I^{1/2}$$

(29)

where J(x) is integral of short-range interaction potential energy, and $J^{\prime}(x)$ is the first derivative of J(x). For precise calculation, J(x) can be expressed as:

$$J\left( x \right) = x\left[ {4 + C_{1} x^{{ - C_{2} }} \exp ( - C_{3} x^{{C_{4} }} )} \right]^{ - 1}$$

(30)

$$J'\left( x \right) = x[4 + C_{1} x^{{ - C_{2} }} \exp ( - C_{3} x^{{C_{4} }} )]^{ - 1} + [4 + C_{1} x^{{ - C_{2} }} \exp ( - C_{3} x^{{C_{4} }} )]^{ - 2}\times \left[ \begin{aligned} C_{1} x^{{ - C_{2} }} \exp \left( { - C_{3} x^{{C_{4} }} } \right) \hfill \\ \left( {C_{2} x^{{ - C_{2} - 1}} + C_{3} C_{4} x^{{C_{4} - 1}} x^{{ - C_{2} }} } \right) \hfill \\ \end{aligned} \right]$$

(31)

where

$$C_{1} = 4.581,\quad C_{2} = 0.7237,\quad C_{3} = 0.012,\quad C_{4} = 0.528.$$

2.3 The effect of pore size on freezing temperature

If the concentration of pore solution is equal to zero, namely a _w = 1, Eq. (9) can be simplified as

$$\Delta T = T - T_{0} = \frac{{2\gamma_{\text{il}} \cos \theta }}{{r\Delta S_{\text{m}} }}$$

(32)

Equation (32) indicates that the freezing temperature of pore water decreases with the decrease in pore radius. The interfacial energy [20] between ice and liquid solution can be expressed as:

$$\gamma_{\text{il}} = 0.0409 + 3.9 \times 10^{ - 4} \,{\text{T}}$$

(33)

In the cooling process, θ > 90° [14], then cosθ < 0, and the maximum freezing temperature depression occurs in case when θ = 180°. In order to obtain the relationship between freezing temperatures of soil and pore radius, θ = 180° and $\Delta S_{m} = 1.2\,{\text{MPa}}\,{\text{K}}^{ - 1}$ [14] are used in the calculating process. Then, the freezing temperature variation as a function of the pore radius is shown in Fig. 2.

Fig. 2

The relationship of freezing temperature with pore diameters

It can be seen that the pore radius has no effect on the freezing temperature when the pore diameters are larger than 1 μm, indicating that the interfacial energy can be ignored. On the other hand, when the pore diameters are below 1 μm, the freezing temperature of pore solution reduces rapidly with the decrease in pore radius, that is, the interfacial energy cannot be ignored. Under this circumstance, the changes in interfacial energy would have a great influence on freezing temperature.

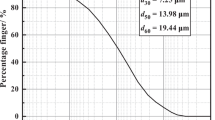
Soil particles provide a type of pore structure. Because of the difference in size distribution, the distribution of pore size varies under different compaction degrees and water contents. Some types of pore size distribution are presented in Fig. 3 (measured by mercury porosimetry). It can be seen that the pore size varies in different types of soils. The majority of pore size in silty clay is below 1 μm, whereas large pores (larger than 1 μm) prefer to distribute in sand soil.

Fig. 3

Pore size distribution curve of silty clay and sand soil

Assuming that conical pore is presented in soil structure (Fig. 4), dotted line AB is the boundary between large pores and small pores. The left zone and the right one represent relative large pores and small pores, respectively. When the soil is saturated, pores are fully filled with solution (Fig. 4a). In this case, the freezing temperature of soil is determined by the large pore solution. Salt type and concentration would be two main influencing factors. Because small pores retain water more easily than large pores [3–5], with the increase in unsaturation, concentration of pore solution gradually increases, and only pore solution of small pores is left (Fig. 4b). At this time, the effect of pore radius on freezing temperature comes to the fore.

Fig. 4

Sketch of pore water state in soil (a saturated state, b unsaturated state)

3 Theoretical verification and discussions

Bing and Ma [2] experimentally obtained the freezing temperatures of Lanzhou loess and Qinghai–Tibet silty clay. The results showed that the freezing temperature reduced with the decrease in soil water content or the increase in salt content. In order to verify the theory mentioned above, these experimental data are employed.

3.1 Soil freezing temperatures at different water contents

Based on the theory mentioned above (Fig. 4), different pore radii correspond with different water contents, so the effect of pore radius can be converted into the effect of water contents. From the experimental results, the freezing temperature depression of Qinghai–Tibet silty clay and Lanzhou loess can be determined by

$$\Delta T = \frac{{A_{1} - A_{2} }}{{1 + \left( {{w \mathord{\left/ {\vphantom {w {A_{3} }}} \right. \kern-0pt} {A_{3} }}} \right)^{\text{p}} }} + A_{2}$$

(34)

The parameters in Eq. (34) are given in Table 2.

Table 2 Parameters of curve fitting

From Fig. 5, it can be seen that the results calculated by Eq. (34) have a good agreement with the experimental data. With a certain salt content, the salt concentration increases with the decrease in soil water, leading to a relative low freezing temperature. Moreover, the effect of pore radius on freezing temperature becomes larger with the decrease in soil water. For this case, the freezing temperature of pore solution is mainly influenced by water and salt contents. From the above analysis, the calculated freezing temperatures of silty clay and Lanzhou loess under different salt contents and different water contents are presented in Fig. 6.

Fig. 5

The relationship between freezing temperature and water content in soils (a Qinghai–Tibet silty clay, b Lanzhou loess)

Fig. 6

Freezing temperatures of soils under different water contents (a sodium chloride silty clay, b calcium chloride silty clay, c sodium chloride loess)

During the calculating process, the used parameters of sodium chloride and calcium chloride are listed in Table 1. It can be seen that the calculated results generally agree well with the experimental results. However, there are some deviations between them. There are two possible reasons: (1) errors may take place when using statistical regression methods to obtain the relationships between water contents and freezing temperatures; (2) errors may appear when experimentally preparing soil samples with different water contents.

3.2 Soil freezing temperatures at different salt contents

When the water contents keep constant, the effect of interfacial energy would be the same. Then, the freezing temperature is only related to the concentration and property of salt. The calculated freezing temperatures for silty clay and Lanzhou loess with the same water content and different salt contents are shown in Fig. 7. The parameters of sodium chloride and calcium chloride are listed in Table 1 in the calculating process. From Fig. 7, it can be seen from these figures that the proposed method can predict the freezing temperature well.

Fig. 7

Freezing temperatures of soils under different salt contents (a sodium chloride silty clay, b calcium chloride silty clay, c sodium chloride loess)

3.3 Effect of salt crystallization on soil freezing temperature

From aqueous phase diagram [10], it can be seen that the freezing temperature would not keep reducing with the decrease in salt content. As for the saturated solution, the freezing temperature would not keep decreasing with the increase in salt content. For sodium chloride and calcium chloride, the solubility is still high when the temperature is negative, so it is difficult to reach saturation in general case. For sodium sulfate and sodium carbonate, however, the solubility is very low in freezing temperature, the solubility of sodium sulfate is 4.25 g/100 g water, and sodium carbonate is 6.04 g/100 g water. Therefore, when the temperature decreases from positive temperature to negative temperature, sodium sulfate and sodium carbonate would probably crystallize with the decrease in ambient temperature. Salt crystallization affects freezing temperature from two aspects:

• (a) Salt hydrate crystallization decreases the liquid water content in soil; when the liquid water content decreases, the effect of interfacial energy on freezing temperature increases.

• (b) Salt hydrate crystallization changes the distribution of pore size in soil, and large pores are converted into small pores. The small pores further decrease the freezing temperature.

The parameters of sodium carbonate in Table 1 are taken in the calculating process, and the change of liquid water content is not taken into consideration in the calculation of Fig. 8. It can be seen that when the solution is unsaturated, there is a good agreement between the calculated and experimental results. However, the deviation appears when the concentration exceeds the solubility at negative temperature. From the theory of phase diagram, the temperature of the eutectic point is the lowest temperature which can be decreased by solute. So the freezing temperature stops decreasing when the concentration of pore solution reaches saturated. Due to the non-uniform distribution of pore sizes ranging from levels of μm to nm, the freezing temperature of soil may be effected by the pore size. It is difficult to consider the effect of pore size on the freezing temperature in the process of salt hydrate crystallization, while the change in liquid water can be obtained easily. The calculated freezing temperatures of Lanzhou loess with sodium carbonate considering the influence of salt crystallization are shown in Fig. 9. From Fig. 9, the agreement between the experimental data and calculated results is seen to be good. It can also be found that the freezing temperatures decrease under the consideration of salt crystallization. Similar results can be found in frozen sodium sulfate soil [16].

Fig. 8

Freezing temperatures of sodium carbonate loess under different salt contents

Fig. 9

Revised freezing temperatures of sodium carbonate loess under different salt contents

3.4 Freezing temperature of silty clay with sodium sulfate

Two types of salt hydrates will crystallize in sodium sulfate solution when temperature decreases, i.e., heptahyrate and decahydrate [10]. They are considered to be metastable and stable products, respectively. Based on Oswald successive segmentation rules, if a material can present in different forms, the unstable state will appear first, then the metastable state, and finally the stable state. Therefore, heptahydrate appears earlier than decahydrate in the process of salt crystallization. From the phase diagram of sodium sulfate solution (Fig. 10), if only decahydrate crystallizes in the cooling process, the lowest freezing temperature is about −1.25 °C. While if only heptahydrate appears in the cooling process, the lowest freezing temperature is about −3.55 °C. Due to the instability of heptahydrate, it easily transforms from metastable to stable state (decahydrate) in the cooling process. It is difficult to distinguish the types of salt hydrate crystals in cooling process; freezing temperature of sodium sulfate soil cannot be predicted well enough.

Fig. 10

Phase diagram of sodium sulfate solution

During the process of calculation, the parameters of sodium sulfate in Table 1 are taken. From Fig. 11, when it is supposed that only decahydrate crystallizes in pore solution, then freezing temperature of sodium sulfate silty clay can be calculated as Calculated (I). It can be seen that it predicts the freezing temperature of stage (1) very well, whereas it cannot predict the freezing temperature of soil in other stages. When only heptahydrate crystallizes in pore solution, freezing temperature can be calculated as Calculated (II). It can be seen that theoretical results are predicted well in stage (3). Due to the unstable state of sodium sulfate heptahydrate, it transforms to decahydrate in the cooling process. Freezing temperature of sodium sulfate soil increases rapidly. After that, the freezing temperature decreases with the increase in salt content, so the soil freezing temperature is mainly influenced by salt hydrate crystallization.

Fig. 11

Freezing temperature of sodium sulfate silty clay

3.5 Effect of compactness

Pore size distributions vary with different dry densities for one certain soil. The pore size distributions of Qinghai–Tibet silty clay with different dry densities are shown in Fig. 12 [21, 23].

Fig. 12

Pore size distributions of silty clay under different dry densities

From Fig. 12, it can be seen that the amount of large pores decreases significantly with the increase in compactness, but large pores still exist in soil. Based on the phase transition theory in porous media, ice firstly crystallizes in the zone, where it is least influenced by pore wall. The freezing temperature is determined by the large pores solution. In saturated or supersaturated soil, the freezing temperature of soil is the same as the solution. The effect of water content on freezing temperature appears only for the unsaturated soils. Because the range of small pores does not increase significantly with the increase in dry density, the effect of small pore change on the freezing temperature of soil can be ignored in the process of compaction.

3.6 Effect of multi-component solutes on soil freezing temperature

The influence of multi-component solutes on the freezing temperature of soil can be calculated by the extended Pitzer model, namely HW formula [6, 7]. Taking the mixed solution of sodium sulfate and sodium chloride [16] as an example, the freezing temperature decreases with sodium chloride increase under the unchanged concentration of sodium sulfate condition. The calculated results are shown in Fig. 13. The values of $\theta_{{{\text{Cl}}^{ - 1} ,{\text{SO}}_{4}^{ - 2} }}$ and $\varPsi_{{{\text{Cl}}^{ - 1} ,{\text{SO}}_{4}^{ - 2} ,{\text{Na}}^{ + } }}$ are 0.02 kg mol⁻¹ and 0.0014 kg² mol⁻² during the calculating process [10], respectively.

Fig. 13

Freezing temperature of the mixed solution of sodium sulfate and sodium chloride

From Fig. 13, it can be seen that the agreement between the calculated results and the test results is good. Based on the above theory, the freezing temperatures of soils with multi-component solutes can be obtained by considering the effect of water content. From phase diagram theory, it can be found that solubility of sodium sulfate decreases when sodium chloride is added to the solution, which is called as “common ion effect.” Because this effect on freezing temperature is difficult to be considered, it is neglected in the process of calculation. In addition, some uncertainty occurs because of the salt hydrate crystallization. Therefore, the freezing temperatures of saline soils with multi-component solutes should be studied further.

4 Conclusions

In order to reveal the freezing mechanism of saline soils, a formula for calculating freezing temperatures is proposed. The proposed formula is proved to be reliable by comparing the calculated results with the previous experimental data. Meanwhile, the influence factors of freezing temperature are extensively analyzed. The major conclusions may be summarized as follows:

• 1. If the relationship between freezing temperature and water content is given, the freezing temperatures of saline soils can be easily obtained according to the proposed theory. This method is also applicable for different types of saline soils. Because Pitzer model can be extended to the saline soils with multi-component solutes, it is possible for predicting the freezing temperatures of saline frozen soils under different conditions.

• 2. The freezing temperature of pore solution is closely related to the solubility of salt. For general solution, the temperature of eutectic point is the lowest temperature which can be decreased by salt, the concentration of eutectic point is the maximum concentration of solution at negative temperature state. For the pore solution, if the concentration is lower than that of the eutectic point, the freezing temperatures of soil under different water contents and different salt contents can be easily calculated (e.g., sodium chloride soil and calcium chloride soil). If the concentration exceeds that of eutectic point, salt hydrate crystallization in the cooling progress would lower the freezing temperatures further.

• 3. If ice crystal appears ahead of salt hydrate, the difference between pore solution and general solution is determined by water content. The lower the soil water content is, the larger the deviation between them will be. If salt hydrate crystal appears before ice, which would not only lead to liquid water content increasing, but also change the pore structure of soils, then the freezing temperatures of soils deviate further from those of general solutions.