1 Introduction

It is well known that surface geometry of a rock fracture has a significant impact on both its hydraulic and shear strength behavior. Although we can readily measure the topography of a fracture surface very accurately and at very high resolution for small samples in laboratory [15], when we try to do the same in the field, we face technical limitations caused by a decrease in measurement system accuracy and a reduced point density which is reflected in smoothing of the surface and in roughness reduction [16]. Additionally, methodologies that allow down- or upscaling can also be beneficial when two fracture surface measured at different resolutions need to be quantitatively compared. Several attempts have been made in the past using standard geostatistical methodologies relying heavily on semivariograms to characterize the surface roughness and to reproduce the surface topography [10, 11]. However, semivariogram, which is simply two-point statistics, is not appropriate to quantify surface roughness, as roughness usually requires assessment of surface topography in all directions simultaneously. Recently, a multiple-point geostatistics [14] has received more and more attention especially when reproducing continuous features, such as channeling in geological structures, since it overcomes some weaknesses of standard geostatistics that relies solely on two-point statistics. The idea of multiple-point geostatistics, therefore, may be applied to characterize local roughness as well.

In this study, we proposed a novel approach to account for the local roughness using a so-called roughness pattern, which characterizes how the topography behaves locally. The local roughness pattern is summarized by a probability distribution of occurrence of each roughness pattern. Depending upon how the pattern is defined, the number of the outcome varies. We implemented the reproduction of the probability distribution of the roughness pattern as one of the components in the objective function of a standard geostatistical simulated annealing (SASIM) methodology. A subset of the studied surface, measured at a higher resolution, was used as a reference to calculate the target local roughness pattern. Conditioning data were later sampled from the reference topography on much coarser grid nodes. The proposed approach (SASIM) was also compared against two traditional geostatistical approaches, ordinary kriging (OK) and sequential Gaussian simulation (SGSIM), in downscaling the surface topography into a scale of interest. For comparison, the roughness of simulated topography data was then characterized by a quantitative methodology for roughness evaluation based on the distribution of the apparent dip angles over the surface [7, 8, 15].

2 Geostatistical theories

Geostatistics provides a general set of statistical tools for incorporating the spatial and temporal coordinates of observations in data processing. Geostatistics can be used to analyze, not only sparsely sampled observations, but also exhaustively available spatial information, such as remotely sensed information (e.g., [13]). More recently, geostatistics was also used to increase the spatial resolution of satellite images [12].

2.1 Geostatistical estimation

Geostatistical estimation considers the problem of quantifying the value of an attribute z (e.g., height) at an unsampled grid node u, where u is a vector of spatial coordinates. The information available consists of values of the variable z at N grid nodes u i , i = 1, 2,…, N discretizing the image. Ordinary kriging (OK) provides a model of the unsampled value z(u) as a linear combination of neighboring observations:

$$ z_{OK}^{*} ({\mathbf{u}}) = \sum\limits_{\alpha = 1}^{{n({\mathbf{u}})}} {\lambda_{\alpha } ({\mathbf{u}})z({\mathbf{u}}_{\alpha } )} $$
(1)

where λ α (u) is the ordinary kriging weight assigned to datum z(u α ), and the weights are computed using the following system of (n(u) + 1) linear equations (i.e., ordinary kriging system):

$$ \left\{ {\begin{array}{*{20}c} {\sum\limits_{\beta = 1}^{{n({\mathbf{u}})}} {\lambda_{\beta } ({\mathbf{u}})\gamma ({\mathbf{u}}_{\alpha } - {\mathbf{u}}_{\beta } ) + \mu_{OK} ({\mathbf{u}}) = \gamma ({\mathbf{u}}_{\alpha } - {\mathbf{u}})\alpha = 1, \ldots ,n({\mathbf{u}})} } \hfill \\ {\sum\limits_{\beta = 1}^{{n({\mathbf{u}})}} {\lambda_{\beta } ({\mathbf{u}}) = 1} } \hfill \\ \end{array} } \right. $$
(2)

where μ OK(u) is the Lagrange parameter, γ(u α –u β ) is the data-to-data semivariogram, and γ(u α –u) is the data-to-estimation point semivariogram. The kriging weights are chosen so as to minimize the error variance under the constraint of unbiasedness. The semivariogram, a measure of the variability of the attribute values obtained at two locations as a function of the separation vector between those two locations, is computed as half the average squared difference between the values of data pairs,

$$ \hat{\gamma }({\mathbf{h}}) = {\frac{1}{{2N({\mathbf{h}})}}}\sum\limits_{\alpha = 1}^{{N({\mathbf{h}})}} {\left[ {z\left( {{\mathbf{u}}_{\alpha } } \right) - z\left( {{\mathbf{u}}_{\alpha } + {\mathbf{h}}} \right)} \right]^{2} } $$
(3)

where N(h) is the number of data pairs for a given separation vector h, and z is the attribute. A model is then fit to the experimental semivariogram, so that semivariogram values across a continuous range of separation distances can be derived. The choice of the model is limited to functions that ensure a positive definite covariance function matrix of the left-hand side of the kriging system (Eq. 2). Often, the spatial correlation varies with direction, and such a case requires one to compute semivariograms in different orientations and fit anisotropic semivariogram models. Details of model fitting can be found in Deutsch and Journel [3] and Goovaerts [4].

2.2 Geostatistical simulation

Unlike estimation, geostatistical stochastic simulation does not aim to minimize a local error variance but focuses on reproduction of statistics, such as the sample histogram or the semivariogram model in addition to honor sample data values. Among many available simulation techniques, sequential Gaussian simulation (SGSIM) is one of the most commonly used techniques because of its flexibility and ease in generating conditional realizations.

Geostatistical simulation considers the simulation of the continuous attribute z at N grid nodes conditional to the dataset {z(u α ), α = 1,…,n}. Sequential simulation enables one to model first the conditional cumulative distribution function (ccdf) as:

$$ F\left( {\user2{u}_{j}^{\prime } ;z|(n)} \right) = {\text{Prob}}\left\{ {Z\left( {\user2{u}_{j}^{\prime } } \right) \le z|(n)} \right\} $$
(4)

then to sample it at each of the grid nodes visited along a random path sequentially. In Eq. 4, the notation “|(n)” expresses conditioning to n neighboring data z(u α). To ensure reproduction of the z-semivariogram model, each conditional cumulative distribution function is made conditional not only to the original n data but also to all values simulated at previously visited locations. Other equiprobable realizations \( \left\{ {z^{(l^\prime )} ({\mathbf{u}}_{j}^{\prime } ),j = 1, \ldots ,N} \right\}, \) l ≠ l’, are obtained by repeating the entire sequential drawing process along with different random paths.

In sequential Gaussian simulation, the series of conditional cumulative distribution functions are determined using the multi-Gaussian formalism. Sequential Gaussian simulation typically involves a prior transform of the z-data into y-data with a standard normal histogram, which is referred to as a normal score transform. The simulation is then performed in the normal space, and the simulated normal scores are back-transformed in order to identify the original z-histogram.

2.3 Objective functions in simulated annealing

Simulated annealing (SA), developed as an optimization algorithm, is another technique to generate conditional stochastic realizations (e.g., [3]). The optimization process aims to systematically perturb an initial realization along a random path so as to decrease the value of the objective function. Most commonly used components in the objective function are the reproduction of the sample histogram and the semivariogram models (see Deutsch and Journel [3] or Goovaerts [4] for details).

In addition, Goovaerts [5] showed that the geostatistical estimation process can be formulated as an optimization problem, in which an objective function is minimized. As a result, the estimation criterion has been incorporated into simulated annealing. In the least-squares criterion, the value of z at u j is estimated by minimizing the quadratic function of the estimation error [e(u j )]2, referred to as a loss [4], where the estimation error e(u j ) = z(u j)−z *(u j ) and z *(u j ) is the estimate. Because actual value z(u j ) is unknown, the actual loss cannot be computed. However, the model of uncertainty at the location u j (i.e., conditional cumulative distribution function) allows one to calculate the expected loss as

$$ \varphi \left( {z^{*} \left( {{\mathbf{u}}_{j} } \right)|\left( n \right)} \right) = E\left\{ {\left[ {Z\left( {{\mathbf{u}}_{j} } \right) - z^{*} \left( {{\mathbf{u}}_{j} } \right)} \right]^{2} |\left( n \right)} \right\} $$
(5)

This expected loss is minimal if z *(u j ) is the expected value (i.e., mean or E-type estimate) of the conditional cumulative distribution function at u j . The expected loss corresponding to the E-type estimate is then the variance σ 2(u j ) of the conditional cumulative distribution function. The set of N optimal estimates at N grid nodes u j is the E-type estimate. The corresponding global expected loss, which is the sum of the N local expected losses, is minimal and equal to the sum of the variance of the N conditional cumulative distribution functions. Therefore, the objective function O e to be minimized in this process can be formulated as

$$ O_{e} = \sum\limits_{j = 1}^{N} {\left| {\varphi \left( {z^{*} \left( {{\mathbf{u}}_{j} } \right)|\left( n \right)} \right) - \sigma^{2} \left( {{\mathbf{u}}_{j} } \right)} \right|} $$
(6)

and is equal to zero for the optimal estimation. If this optimal criterion is the only component in the objective function, the simulated annealing algorithm may find the global minimum of the objective function, which leads to the sole optimal realization. In that case, SASIM cannot generate multiple realizations. However, because of the flexibility in formulating the objective function, SASIM can generate multiple conditional realizations with the optimal estimation criterion by combining with different components in the objective function [6]. In this study, the optimal estimation criterion is combined with reproduction of the target statistics to generate multiple realizations.

2.4 Implementation of simulated annealing

Although there are many possible implementations of SA [2], in this paper, the procedure commonly taken was used as follows (e.g., [4]):

(1) Create an initial realization by freezing data values at their locations and assigning to each unsampled grid node a z-value drawn at random from the corresponding marginal cumulative distribution function model.

(2) Compute the initial value of the objective function, O(i = 0) with M components, corresponding to that initial realization

$$ O\left( {i = 0} \right) = \sum\limits_{m = 1}^{M} {\lambda_{m} {\frac{{O_{m} \left( {i = 0} \right)}}{{O_{m} \left( 0 \right)}}}} $$
(7)

where

$$ \sum\limits_{m = 1}^{M} {\lambda_{m} = 1} $$
(8)

Each component O m is standardized by its initial value O m (0). The relative importance of each component is controlled by the weights λ m that sum to unity.

(3) Perturb the realization by selecting randomly a location u j and replacing the current value by a new value randomly drawn from the cumulative distribution function conditioned to n observations.

(4) Assess the impact of the perturbation on the reproduction of target statistics by recomputing the objective function, O new (i), accounting for the modification of the initial realization.

(5) Accept all perturbations that lower the objective function. Unfavorable perturbations are accepted according to the value of a negative exponential probability distribution

$$ \begin{gathered} {\text{Prob}}\left\{ {{\text{Accept}}\;i{\text{th}}\;{\text{pert}} .} \right\} \hfill \\ = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if}}\;O_{new} (i) \le O(i)} \\ {\exp \left( {{{{\left[ {O(i) - O_{new} (i)} \right]}}/{t(i)}}} \right)} & {\text{otherwise}} \\ \end{array} } \right. \hfill \\ \end{gathered} $$
(9)

where t(i) is the “temperature” at the i-th perturbation. The idea is to start with an initially high “temperature” t(0), which allows a large proportion of unfavorable perturbation to be accepted at the beginning of the simulation. As the simulation proceeds, the “temperature” is gradually lowered so as to limit discontinuous modification of the stochastic image. Two important issues are the timing and magnitude of the “temperature” reduction, which defines the annealing schedule. In this study, following Goovaerts [6], a fast annealing schedule was used (e.g., [2]). In the fast schedule, the initial temperature, t(0) = 1, was lowered by a reduction factor 0.05 whenever enough perturbations (5 × N) have been accepted or too many (50 × N) have been attempted.

(6) If the perturbation is accepted, update the i-th realization into a new image (i + 1-th realization) with the objective function value O(i + 1) = O new (i).

(7) Repeat steps from 3 to 6 until either the change in the objective function ΔO becomes the target low value (e.g., ΔO = O(i)–O(i + 1) = 0.001) or the maximum number of attempts at the same “temperature” has been reached three times.

Other realizations, l′ ≠ l, are generated by repeating the whole process starting from different initial realizations. The flow chart of the procedure with the number corresponding to the number used above is depicted in Fig. 1.

Fig. 1
figure 1

Flow chart of the annealing procedure employed in this study

Full size image

3 Fracture surface topography

The present study is the first attempt to take the roughness pattern into account in one of the target statistics that is going to be reproduced during the SASIM optimization process. As it will be shown in Sect. 3.3, the roughness distribution is the frequency distribution F(p i) and is similar to the histogram. However, unlike the histogram, the roughness distribution has a fixed number of bins that corresponds to the number of possible roughness patterns or roughness pattern groups. The objective function O p corresponding to the reproduction of the roughness distribution is, then, formulated as

$$ O_{p} = \sum\limits_{i = 1}^{I} {\left[ {F\left( {p_{i} } \right) - \hat{F}\left( {p_{i} } \right)} \right]^{2} } $$
(10)

where \( \hat{F}\left( {p_{i} } \right)\; \) is the cumulative frequency distribution of the roughness pattern calculated from the realization.

3.1 Topography data

The surface topography used in this study is extracted from surface data that have been acquired on a 0.05-m resolution grid using terrestrial photogrammetry (Fig. 2). The surface morphology is characterized by high elevation areas oriented slightly off from vertical at the left bottom corner of the surface, while the right-hand side of the surface has lower elevation areas (Fig. 2). The direction of the trend is, in general, vertical but slightly off to clockwise. To mimic the fact of having high resolution data into the laboratory and coarser data in the field, we have divided the whole surface data into smaller partitions that were used to extract the proper scale objective function. To demonstrate the proposed methodology, a topography image in a coarser resolution of the entire surface was created simply by sampling the reference topography (Fig. 3). Downscaling methodologies were then applied to reconstruct the topography in the same resolution as the reference topography. In this study, we proposed an approach to characterize the roughness of the fracture surface topography, so-called roughness distribution and local roughness pattern, definitions of which are later explained in this chapter. It is important to note that to properly reproduce the process followed in the practice, where only part of the entire surface is sampled at high resolution, just one of the surface subsets discussed above (Subarea 4) was used to produce the target “roughness distribution”.

Fig. 2
figure 2

Reference fracture surface topography (m) in a 0.05-m resolution. In order to study the sensitivity of the proposed approach to the size of the measured area, the entire area has been subdivided in 4 subareas

Full size image
Fig. 3
figure 3

Conditioning surface topography data (m). The spatial resolution is 0.25 m

Full size image

3.2 Local roughness pattern

Like other digital images, such as remote sensing data, fracture topography data are readily provided as pixel-based images when surveys are conducted by means of a laser scanning or photogrammetric techniques [17]. At any given pixel, therefore, an asperity height z from a reference level is assigned along with x and y coordinates, leading to a 3-dimensional view of the fracture surface. In this study, for any given pixel, the “local” roughness is characterized by comparing the heights of surrounding pixels to the height of that pixel.

Any given pixel at u c (not located along the image edge) is surrounded by 8 adjacent pixels, among which 4 pixels share one of four sides of the pixel, while 4 pixels are located at four corners of the pixel (Fig. 4). The local roughness pattern is then defined as how adjacent pixels behave, or, in more plain words, as a summary of whether or not the heights of adjacent pixels are higher than that of the central pixel. In this study, we do not consider the absolute differences in heights between those pixels. For mathematical convenience, an indicator transform can be defined at any adjacent pixel u i as:

$$ i\left( {{\mathbf{u}}_{i} ;z_{c} } \right) = \left\{ {\begin{array}{*{20}c} {1\quad {\text{if}}\;z\left( {{\mathbf{u}}_{i} } \right) \ge z_{c} } \\ {0\quad {\text{otherwise }}} \\ \end{array} } \right. $$
(11)

where z c is the height of the central pixel u c . In the rest of this paper, for simplicity, only 4 adjacent pixels that share sides of the central pixel are considered (Fig. 4). The concept and methodology shown in this paper can be readily extended to 8 adjacent pixels and further.

Fig. 4
figure 4

A schematic diagram of the central pixel u c and its surrounding adjacent pixels, u 1–u 4

Full size image

As there are two outcomes for each adjacent pixel, either 0 or 1, there are a total of 24 = 16 possible combinations of indicators corresponding to the central pixel u c . To repeat, this combination is referred to as the local roughness pattern. We assigned arbitrary 1 through 16 to the roughness pattern depending upon which adjacent pixels are higher than the central pixel, as summarized in Fig. 5. It must be mentioned that the way we assigned the local roughness pattern numbers does not affect the final result of the study.

Fig. 5
figure 5

16 possible roughness patterns are shown. Gray pixels have higher elevations than the central black pixel, while white pixels are lower than the black one

Full size image

3.3 Roughness distribution

Once the local roughness pattern is defined, the whole image can be searched to obtain the distribution of each roughness pattern. This distribution (or histogram), referred to as “roughness distribution,” is described by a frequency table, which lists the frequency of the occurrence of each roughness pattern. The frequency of occurrence of a given roughness pattern, p i , denoted f(p i ) is then defined as the number of occurrence divided by the total number of pixels (Fig. 6a).

Fig. 6
figure 6

Roughness distribution obtained for the reference topography shown in Fig. 2 is calculated a for the entire area and b for four subareas of the whole surfaces as identified in Fig. 3. The horizontal axis plots the roughness pattern classes which correspond to those indentified in Fig. 6

Full size image

As mentioned before, the roughness pattern is not limited to those in Fig. 4 but can be extended in a very flexible way. For example, instead of using only 4 adjacent pixels, we can use surrounding 8 pixels, which results in a total of 256 possible outcomes. Roughness patterns can also be categorized in much smaller number of groups depending upon their physical similarities and characteristics. For example, the roughness patterns 2 and 12 in Fig. 5 appear when there is a slope from north to south, while the roughness patterns 5 and 15 represent the slope from south to north. Therefore, instead of counting the number of the occurrence of each roughness pattern, a combined number of occurrences for similar patterns, such as 2 and 12, can be recorded as a pattern of a north-to-south slope. By grouping roughness patterns based on its physical attribute, we can readily reduce the possible outcomes of the roughness patterns, especially when more surrounding pixels are taken into account.

3.4 Roughness of reference fracture surface topography

The concept of the local roughness introduced into the previous section is demonstrated using the reference topography data (Fig. 2). Figure 6a shows the probability distribution of the roughness patterns obtained for the reference topography. There are two distinct peaks of the patterns 7 and 10, while the patterns 4 and 13 have the next highest probability values. As can be seen in Fig. 5, the patterns 4, 7, 10, and 13 all have slopes in one of the four diagonal directions. It may not be too surprising that 50% of locations have one of these 4 patterns as they seem occur more naturally compared to patterns such as 1, 6, 11, and 16. It has to be also mentioned, however, that the probability of having the pattern 16 is much greater than the other three patterns. The rest of the patterns have either three white or gray pixels out of four adjacent pixels, which may be generally less common for natural rock surface topography.

To investigate whether this roughness distribution is unique to a given rock type or fracture surface, and consequently whether it is possible to use just a subsection of the entire surface to generate the objective function, we divided the reference surface into quarters (i.e., 2.5 × 2.5 m squares) and computed the roughness distribution for each square. The result (Fig. 6b) indicated that, despite slight differences among four distributions, the roughness distributions are similar among them. Thus, we can assume that the roughness distribution is more-or-less unique to the fracture surface we are considering and the effect of the global trend is minimal. This experimental observation is important since in practice, the target distribution can be readily obtained from the preliminary investigation using small rock joint samples collected at the study site. In the rest of this study, the roughness distribution obtained from Subarea 4 of the reference fracture surface topography was used as the known target distribution.

3.5 Surface topography downscaling

In geostatistical downscaling, asperity heights at finer grid nodes conditioning to coarse resolution topography data are either estimated or simulated. The conditioning initial topography data in a coarser resolution (i.e., 0.25 m) were sampled from the fine resolution (i.e., 0.05 m) reference topography (Fig. 2). Figure 3 shows the conditioning surface topography image. Figure 7 shows standardized experimental semivariograms with an anisotropic model fitted in major (80° counterclockwise from E) and minor (170° counterclockwise from E) directions as they showed clear anisotropy. The major direction agrees well to the vertical trend shown in Fig. 2. The model includes a nugget effect (0.07) and a spherical model with a sill of 0.93, a range of 6 m, and an anisotropy ratio of 0.4. There is a drift effect in the minor direction at the lag distance greater than 2.4 m. It can have a significant effect when estimating a value at the location that is at distance of 2.4 m or more from the closest datum. In this study, however, geostatistical estimation was performed where conditioning data are available at every 0.25 m grid node. Therefore, the drift effect can be ignored.

Fig. 7
figure 7

Directional standardized experimental semivariograms computed in two directions (80o and 170o counterclockwise from E) from conditioning surface topography data with anisotropic spherical semivariogram models fitted

Full size image

In this study, three geostatistical approaches (OK, SGSIM, and SASIM) were used to investigate the effect of taking local roughness on surface topography downscaling. It is worth to remind that the SASIM objective function has two components: (1) the optimal estimation criterion (minimization of the local error variance) described in Sect. 2.3; (2) the reproduction of the roughness distribution (Eq. 10). Another potential advantage of SASIM is the ease to modify the relative weights to components in the objective function. Depending upon weights assigned to each component, the outcome of simulation varies quite obviously [6]. In this study, the same weights were assigned to both components. More research is needed to find optimum weights, but it is beyond the scope of the present study. For SGSIM and SASIM, 50 realizations were generated so that some uncertainty analysis can be conducted.

Downscaled asperity heights were first compared to the reference topography to calculate prediction errors (mean square error and mean absolute error). In this calculation, all 50 realizations were considered for SASIM and SGSIM. The local roughness of the downscaled asperity heights were then assessed in terms of “roughness distribution” and roughness polar distribution [9, 15]. The simulated values and distributions were compared with those obtained from the original reference surface.

4 Results and discussion

4.1 Surface topography downscaling

Figures 8–10 show downscaled (i.e., estimated and simulated) surface topography images obtained using OK, SGSIM, and SASIM, respectively. For SGSIM and SASIM, first three realizations are shown. Asperity heights were predicted at every 0.05-m grid nodes in all three approaches. As expected, OK result reproduces the general (or global) trend quite well (Fig. 8), but the estimated surfaces are much smoother compared to other simulated results because of the smoothing effect inherent to kriging [4]. This smoothing effect may not be desirable since it leads to underestimate the surface roughness that could be reflected in underestimation on the calculations for shear strength of rock joints and fluid flow and transport through the fracture. On the other hand, both simulated results (SGSIM and SASIM) show noisier topographies (Figs. 9, 10), with SGSIM results to be much noisier than SASIM ones. The reason is that SGSIM process focuses on the reproduction of target statistics and not on minimizing local error variances. On the other hand, SASIM reproduces global features much better than SGSIM, because it incorporates the estimation criterion (Eq. 10) in one of the objective function components. As explained in Sect. 2.3, if the estimation criterion is the only component in the objective function, SASIM would result in the optimal realization, and it would be equal to the OK estimate. However, in this study, the estimation criterion is combined with the reproduction of the local roughness distribution, making SASIM able to generate multiple equiprobable realizations (Figs 9, 10). Although different realizations are not exactly the same, all realizations reproduce same global trends, such as higher asperity values in the lower left corner of the surface and lower asperity values in the right-hand side of the surface. It is worth to note that when conditioning data are sparse in space, simulated results can significantly vary among realizations. However, in this study, which is representative for studying rock fracture roughness, conditioning data are available at every 0.25-m grid node, which means no sparse in space.

Fig. 8
figure 8

Estimated fracture surface topography using ordinary kriging

Full size image
Fig. 9
figure 9

First three realizations of fracture surface topography using sequential Gaussian simulation

Full size image
Fig. 10
figure 10

First three realizations of fracture surface topography using sequential Gaussian simulation

Full size image

Differences among three approaches are also assessed using estimation errors. Mean square (MSE), and absolute (MAE) errors are summarized in Table 1. For SGSIM and SASIM, as estimation errors are calculated for all realizations, averaged values with their standard deviations are listed. It is not surprising that OK outperforms other two approaches in terms of prediction errors because it aims to minimize local error variances. What is more important here is that SASIM results in much smaller prediction errors than SGSIM. In addition, the standard deviations for both MAE and MSE are reduced for SASIM. This means that the variations among realizations are much smaller for SASIM than those for SGSIM. This implies that SASIM consistently produces a realization that has a much smaller prediction error than SGSIM. From the analysis of prediction errors, the superiority of the proposed SASIM methodology over SGSIM is demonstrated. It should be mentioned that, for the surface considered in this study, computation time to generate one realization with SASIM was 355 s using a DELL PC with Intel CoreDuo 2.66 GHz, 2.00 GB RAM. This computation time for SASIM was about 33 times greater than that of SGSIM and about 200 times greater than that of OK. Although, this can be a clear disadvantage of SASIM especially when simulated surfaces are getting larger and larger, depending upon the objective of the study, SASIM cannot be omitted just because it is computationally expensive. In addition, given the structure of the SASIM algorithm, it is reasonable to speculate that the computation time could be reduced to a fraction of the time taken by the present serial implementation if the code would be moved to GPUs.

Table 1 Prediction errors with their standard deviations in parenthesis
Full size table

4.2 Roughness of downscaled topography

Using downscaled topography data, roughness distributions were first estimated. Figure 11 shows calculated roughness distributions along with the target distribution obtained from the reference topography. For SASIM and SGSIM, because such distributions were calculated for all realizations, average roughness distributions values across 50 realizations with their standard deviations are plotted. There are some interesting observations to be made:

Fig. 11
figure 11

Pattern distributions calculated from downscaled topography images with the target distribution. Error bars indicate their standard deviations between different realizations

Full size image
  1. 1.

    In general, the roughness distribution calculated from OK estimates follows the trend of the target distribution despite some over-estimation in the patterns 14 and 16. OK performs well in this study partly because of spatially relatively dense, in other words not sparse, conditioning data. Depending upon the difference in the resolution between conditioning data and estimation grid nodes, the performance of OK could vary. In particular, if resolutions are very different, the pattern distribution of OK may be far from the reference distribution.

  2. 2.

    For SGSIM simulations, due to increase of noisiness in the simulated image, the local roughness was basically randomized leading to almost equal probabilities of the occurrences for the patterns 2 through 15. The patterns 1 and 16 that are a tip and a dip have much higher probability values. Error bars are in general very small for all patterns. This is important because this indicates that the pattern distributions among different realizations are quite consistent and do not vary. SGSIM is thus not an appropriate methodology for downscaling of fracture surface topography images in terms of the local roughness reproduction.

  3. 3.

    The average pattern distribution of the SASIM matches well to the target distribution because the reproduction of the target pattern distribution was implemented in the objective function. The standard deviation of each occurrence probability is very small, indicating that the roughness distributions for different realizations are quite consistent. The proposed SASIM approach, therefore, not only can reproduce the global trend but can also replicate the local roughness characteristics. This approach should be desirable because it can generate realizations with less estimation errors and that have the roughness distribution similar to the target pattern distribution.

So far, downscaled topography data have been assessed in terms of the estimation errors and the roughness distribution. In the rest of this paper, they are assessed using different indicators. First, semivariograms in two directions (80° and 170° from E to counterclockwise) for three downscaled data were calculated and compared with the semivariogram calculated using the reference data (Fig. 12). For SGSIM and SASIM, the first realization was used for the calculation of the semivariogram. Figure 12 shows all three standardized semivariograms for downscaled topography data. All three semivariograms reproduce well the general trend of the reference semivariogram. There are, however, some noticeable features to be observed. For example, for OK, because of the well-known smoothing effect, semivariogram values are smaller than the others, especially near the origin when the lag distance is small for both directions. Semivariograms for SGSIM have the largest values except when the lag distance is greater than 2 m in the minor direction (170° from E to counterclockwise). Semivariograms for SASIM lie in general between those of OK and SGSIM. This demonstrates that at the same lag distance, the order of the semivariogram value is OK < SASIM < SGSIM, i.e. the same order when downscaled images are sorted based upon the degree of their noisiness. In general, we notice that all three downscaled topography data reproduce the semivariogram of the conditioning data well. The reason is that, since we are dealing with the case where conditioning data are spatially not sparse (available at every grid node), semivariograms calculated from conditioning data and those with estimated/simulated data are not too different.

Fig. 12
figure 12

Standardized experimental semivariograms computed in two directions (80o and 170o counterclockwise from E) from three downscaled topography data (open symbols) with those computed with conditioning surface topography data (filled symbols)

Full size image

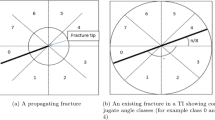
The spatial distributions of roughness for all surfaces obtained with the three geostatistical methodologies discussed herein have been also evaluated using the roughness metric proposed by Grasselli et al. [7], Grasselli [9] and revisited by Tatone and Grasselli [15]. The roughness metric value can be readily obtained using a 3D evaluation methodology where the associated roughness metric is defined in terms of the maximum apparent asperity inclination measured on the surface, θ *max and an empirical fitting parameter C as, θ *max /(C + 1) [15]. It is worth noting that the roughness metric θ *max /(C + 1) can be readily used into shear strength criteria such as the one proposed by Grasselli [9]. Tatone [16] extended the use of this roughness metric suggesting an empirical relationship between the roughness parameter, θ *max /(C + 1) and the well-known joint roughness coefficient (JRC) that enables shear strength to be estimated according to the Barton-Bandis shear strength criterion [1].

In the present study, the polar distributions of the roughness metric values, θ *max /(C + 1), obtained for the simulated surfaces are compared to the one calculated for the reference surface (Fig. 13). OK captures well the anisotropic character of the surface but results in lower roughness values (smaller radius) with respect to those calculated for the reference surface that are direct consequence of the “smoothing” procedure used for the downscaling process. SGSIM roughness distributions are characterized by a higher but more isotropic roughness distribution compare to the reference one. SASIM roughness distributions match well both magnitude and shape of the curve calculated for the original surface used as reference. These results show that surfaces obtained through the SASIM methodology are able not only to correctly reproduce the roughness but also to capture the anisotropic character of the surface. More in general, roughness metric values in Table 2 illustrate that kriging results in a smooth profile (lower roughness metric value compared to the reference surface), while SGSIM generates homogeneous and rough and noisy profiles (higher roughness metric value compared to the reference surface). SASIM is in between being able to capture both the anisotropy in roughens distribution and its magnitude.

Fig. 13
figure 13

Comparison between the polar distributions of the roughness metric values, θ *max /(C + 1), calculated using Grasselli’s approach (2006). SASIM curves are close to the one calculated for the reference surface. OK results in an anisotropic but smoother curve, while the SGSIM curves have higher roughness value

Full size image
Table 2 Prediction errors with their standard deviations in parenthesis
Full size table

5 Summary and conclusions

This study demonstrates an attempt to account for local roughness information in geostatistical simulation of the fracture surface topography. The roughness of the surface topography was characterized by so-called local roughness pattern that summarizes how the topography behaves locally. This pattern has a finite number of outcomes allowing one to calculate the probability of the occurrence of each roughness pattern. This probability distribution is referred to as roughness distribution.

The reproduction of the roughness distribution is one of the objectives in a proposed simulated annealing (SASIM) technique. The objective function also includes the component of optimal estimation criteria which allows to pursue both estimation and simulation characteristics. The proposed SASIM was compared to standard geostatistical methodologies, ordinary kriging and sequential Gaussian simulation, in downscaling of the fracture surface topography. Results show that the proposed SASIM can reproduce both global and local features of the surface topography while keeping estimation errors much smaller than those obtained with one of the standard geostatistical simulation techniques with an expense of the computation time.

One of the downsides of the technique is that one needs to have a target roughness distribution prior to apply the technique. However, we have showed that the target roughness distribution can be easily obtained using high-resolution measurements made on smaller areas, i.e., small fracture samples obtained from a core or fragment of the surface to be analyzed. From the presented results, it seems indeed that the roughness distribution is more-or-less area independent.

Further improvements are needed for a statistically more robust determination of relative weight parameters for the different components in the objective function. We envisage applying the proposed methodology to develop a robust estimation of scale-independent shear strength of rock fractures and to improve our capabilities in predicting water flow and transport phenomena during large-scale numerical simulations.