Liquefaction potential of coastal slopes induced by solitary waves

Abstract

Tsunami runup and drawdown can cause liquefaction failure of coastal fine sand slopes due to the generation of high excess pore pressure and the reduction of the effective over burden pressure during the drawdown. The region immediately seaward of the initial shoreline is the most susceptible to tsunami-induced liquefaction failure because the water level drops significantly below the still water level during the set down phase of the drawdown. The objective of this work is to develop and validate a numerical model to assess the potential for tsunami-induced liquefaction failure of coastal sandy slopes. The transient pressure distribution acting on the slope due to wave runup and drawdown is computed by solving for the hybrid Boussinesq—nonlinear shallow water equations using a finite volume method. The subsurface pore water pressure and deformation fields are solved simultaneously using a finite element method. Two different soil constitutive models have been examined: a linear elastic model and a non-associative Mohr–Coulomb model. The numerical methods are validated by comparing the results with analytical models, and with experimental measurements from a large-scale laboratory study of breaking solitary waves over a planar fine sand beach. Good comparisons were observed from both the analytical and experimental validation studies. Numerical case studies are shown for a full-scale simulation of a 10-m solitary wave over a 1:15 and 1:5 sloped fine sand beach. The results show that the soil near the bed surface, particularly along the seepage face, is at risk to liquefaction failure. The depth of the seepage face increases and the width of the seepage face decreases with increasing bed slope. The rate of bed surface loading and unloading due to wave runup and drawdown, respectively, also increases with increasing bed slope. Consequently, the case with the steeper slope is more susceptible to liquefaction failure due to the higher hydraulic gradient. The analysis also suggests that the results are strongly influenced by the soil permeability and relative compressibility between the pore fluid and solid skeleton, and that a coupled solid/fluid formulation is needed for the soil solver. Finally, the results show the drawdown pore pressure response is strongly influenced by nonlinear material behavior for the full-scale simulation.

1 Introduction

As demonstrated by the 2004 Indian Ocean Tsunami, high intensity wave runup and drawdown can lead to significant loss of lives, as well as costly damages to coastlines and coastal structures. Although there exist many studies of tsunami wave propagation and inundation modeling, few studies considered the effect of the mobile bed, and even fewer studies examined the effect of wave–seabed interactions in the near-shore region. During wave shoaling, breaking and runup processes, excess pore water pressure develops in the nearly saturated phreatic zone (region below the subsurface water table) due to the much faster rise time of the surface water pressure compared to the drainage time of the excess pore pressure. During the tsunami drawdown process, the shallow water tongue rapidly retreats toward the sea, followed by a drop in water level exposing potentially a large portion of beach face that was initially submerged. Consequently, a seepage face is created along the bed surface between the initial shoreline and maximum drawdown location due to inability of the subsurface water table to respond to the rapid surface water changes. In regions where the excess pore water pressure approaches the suddenly reduced effective overburden pressure, the sand will liquefy. If the liquefied layer is confined to a localized, thin layer near the bed surface, there may be enhanced erosion of the beach face caused by the exfiltration and reduction in soil shear strength [27]. However, if the liquefaction zone is deep and broad, it may quickly spread in all directions, leading to a liquefaction flow slide. Hence, the objective of this work is to assess the liquefaction potential of coastal fine sand slopes subject to rapid tsunami runup and drawdown. Tsunamis are characterized by long wavelengths. To simplify the dynamics, we employ the typical approach of modeling a tsunami as a solitary wave, which theoretically has infinite wavelength. The effects of leading depression, wave–wave interactions, wave–bathymetry–structure interactions, and 3D effects are subjects of future research.

1.1 Previous work on wave–seabed interactions

In the past few decades, much work focused on the study of wave–seabed interaction related to short-crested waves over a flat soil bed. An excellent review of work related to seafloor dynamics reported in the past 50 years has been presented in Jeng [16]. A brief summary of the notable field and experimental works given in Jeng [16] and recent experimental studies in this area are highlighted below.

Field measurements of wave induced pore water pressure fluctuations have been conducted for silty clay in the Mississippi Delta [2, 3], for silty sand in Shimizu Harbor, Japan [24–26], and other coastal locations in Japan [20, 52]. They concluded that pore water pressure fluctuations in the seabed due to short period waves are significant and are affected by the soil permeability and deformability, and wave-induced liquefaction is related to the upward seepage flow induced in the sea bed during the passage of wave troughs [16]. To understand the soil behavior in a controlled setting, wave tank experiments [14, 19, 33, 39, 41, 42, 47], compressive tests [12, 51], and centrifugal wave tank studies [29, 30, 32] have also been conducted. Wave tank experiments have the advantage that they can provide the spatial and temporal distribution of the wave-induced pressures at the structure and at the bed surface. Recent large-scale wave tank experiments include the study of tsunami-induced scour around a vertical cylinder by Yeh et al. [47] and Tonkin et al. [39]. Nevertheless, the diffusion time of the soil response in the wave tank cannot be scaled properly due to the Froude scaling for one-gravity acceleration (1g) environments. Compared to wave tank studies, compressibility tests can provide better estimates of the soil characteristics and allow a deeper soil column (e.g., [12]), but they are also limited to the 1g environment, and the setup cannot simulate the dynamic spatial distribution of the wave loads. To overcome the 1g limitation and to provide spatial distribution of the wave loads, Sekiguchi and Phillips [32] and Phillips and Sekiguchi [29] developed a novel setup to conduct wave experiments in a centrifuge. Viscous scaling was used to satisfy the time-scaling laws for fluid wave propagation and the consolidation of the soil [30]. However, the study was limited to short period progressive or standing waves with an equivalent field period of 4.5 s over a flat bottom. The effects of long-period wave runup and drawdown over coastal slopes were not considered.

Under the project LIMAS (Liquefaction around Marine Structures), various experimental and numerical studies have been conducted to study the liquefaction around marine structures, induced by earthquakes or wave loads. Sumer et al. [35] summarized the state-of-the-art of physical and numerical modeling of seismic-induced liquefactions, with special reference to marine structures. De Groot et al. [13] analyzed the possible contributions of liquefaction phenomena on structure failure under regular waves, and they concluded that “liquefaction flow failure” is only possible with the combination of loose soil and poor drainage conditions. Kudella et al. [19] conducted large-scale experiments in a wave flume to study pore pressure generation under a caisson breakwater under pulsating and breaking waves. Even under unfavorable conditions (loose sand and poor drainage conditions), total liquefaction was not observed in the study. However, the residual soil deformation due to pore pressure generation led to the failure of the breakwater. Sumer et al. [34] presented experimental results on liquefaction around a buried pipeline under progressive wave loading. The presence of the pipeline was found to have significant influence on the pore pressure buildup, particularly on the bottom of the pipe. Dunn et al. [15] presented a numerical study on the same process, which answered some questions raised in the physical simulations of Sumer et al. [34]. In summary, recent studies have contributed to advancing the understanding of liquefaction around marine structures, but more research is needed, particularly in the near-shore region, where critical structures and ports are located.

1.2 Research needs and objectives

As summarized above, although much work has been done related to wave-induced liquefaction caused by wind or tidal waves over a flat bed, very little work (if any) has been done related to tsunami-induced liquefaction of coastal slopes. It should be emphasize that tsunamis are very different from wind or tidal waves because:

• 1. Tsunami wave loading is characterized by a single cycle or a few cycles spaced relatively far apart in time. The wave periods are approximately 500–1,000 s for tsunamis compared to 5–10 s for storm waves.

• 2. Tsunami waves are in general higher than storm waves, inducing larger pore pressure changes on the seabed. These differences may produce loading and failure scenarios in the seabed that are fundamentally different from the well-studied phenomena of (wind or tidal) wave-induced pore pressure buildup.

• 3. Tsunami runup can reach miles onshore, where the top soil could be initially unsaturated.

• 4. Tsunami drawdown can cause the water level to drop significantly below the initial water surface, exposing a large portion of the beach face that was previously submerged.

Currently, there are not enough quantitative laboratory or field data to examine the transient response of coastal slopes subject to tsunami runup and drawdown. This is due, in part, to the difficulty in obtaining real-time data on site. On the other hand, it is difficult to distinguish the various modes of soil failure (e.g., erosion, liquefaction, or localization induced slope instability), particularly in situations with multiple wave runups and drawdowns. Moreover, reconnaissance surveys can only provide very limited information about the sequence of events and actual failure mechanisms. Laboratory studies are also difficult to conduct and interpret due to scaling conflicts between the fluid and the porous media. As a result, numerical modeling is a valuable tool to study the response and failure mechanisms of coastal slopes subject to tsunami runup and drawdown.

The objective of this work is to develop and validate a numerical model to assess the potential for tsunami-induced liquefaction failure of coastal sandy slopes.

2 Numerical model

2.1 Surface wave simulator

To model the tsunami runup and drawdown, we solved the depth-averaged nonlinear shallow water equations (SWE) and Boussinesq equations. The nonlinear SWE have been used by many authors [18, 44, 53] to investigate the propagation, runup, and drawdown of long-period waves. Since dispersion effects are believed to be important before the wave breaks, Boussinesq equations are solved during the pre-breaking phase, while the SWEs are solved post breaking. The breaking criterion is defined as when the water surface slope is greater than 20°, or equivalently dη/dx > 0.36 where η is the local wave height [21, 31]. The switch to SWE after wave breaking avoids numerical instabilities caused by the higher order terms in the Boussinesq equations. The governing equations are presented below, formulated after [9]:

$$ \frac{{\partial {\mathbf{U}}^{*} }}{\partial t} + \frac{{\partial {\mathbf{F}}}}{\partial x} = {\mathbf{S}} $$

(1)

where ${\mathbf{U}}^{*}$ is the vector of conservative variable

$$ {\mathbf{U}}^{*} = {\mathbf{U}} + \left\{ {\begin{array}{*{20}c} 0 \\ {\left( {B + \frac{1}{3}} \right)d^{2} (hu)_{xx} + \frac{1}{3}dd_{x} (hu)_{x} } \\ \end{array} } \right\}\quad {\text{and}}\quad {\mathbf{U}} = \left\{ {\begin{array}{*{20}c} h \\ {hu} \\ \end{array} } \right\} $$

(2)

and ${\mathbf{F}}$ is the vector of flux

$$ {\mathbf{F}} = \left\{ {\begin{array}{*{20}c} {uh} \\ {u^{2} h + gh^{2} /2} \\ \end{array} } \right\} $$

(3)

where $h$ is the depth of the water column, $u$ is the depth-averaged velocity, and ${\mathbf{S}}$ is the source term:

$$ {\mathbf{S}} = \left[ {\begin{array}{*{20}c} 0 \\ { - gh\left( {S_{0} + S_{f} } \right) + Bgd^{3} \eta_{xxx} + 2Bgd^{2} \eta_{xx} } \\ \end{array} } \right] $$

(4)

where $S_{0}$ and $S_{f}$ represent the bed slope and friction slope, respectively. η is the wave elevation, and $d = h - \eta$ is the still water level. The coefficient B is a linear dispersion coefficient, and is set to be equal to 1/15 to give the closest fit to exact linear dispersion [21].

The following bed friction relationship is used to close the equations:

$$ S_{f} = \frac{{n^{2} u\left| u \right|}}{{h^{4/3} }} $$

(5)

where $n$ is the Manning’s roughness coefficient, and is taken to be 0.03 to account for the increase in effective roughness caused by the mobile bed.

It should be cautioned that both the nonlinear SWE and the Boussinesq equations are not suitable for modeling wave propagation over very large bottom slopes due to inappropriateness of the depth-averaged approximations and due to numerical difficulties associated with treating the source terms. To accurately model wave propagation over very large bottom slopes, a Reynolds Averaged Navier Stokes solver or Large Eddy Simulation solver with free surface tracking capabilities (e.g., volume of fluid techniques) is needed, which is outside the scope of this paper.

The system of equations is solved by using a Gudunov-type finite volume method (FVM). Specifically, it is solved by total variation diminishing version of the weight averaged flux method, with extended Harten-Leer-Lax Riemann solver [40, 54]. As explained in the references above, the shoreline is captured by solving exact Riemann problem on the dry/wet interface. A threshold value of ε = 0.001 × D (where D is the maximum depth of the still water) is set as the dry bottom limit; for h < ε, the cell is regarded to be dry. To simulate the far-field boundary where the wave is transmitted outside the computation without reflection, an absorption boundary condition is implemented and used in the computation. To ensure stability in a wave-propagation problem, the CFL condition is set to be between 0.7 and 0.9.

The numerical model without the dispersion terms has been validated against benchmark cases ranging from analytical solutions to experimental measurements. The comparison with the analytical solution for the SWE by Carrier and Greenspan [11] is shown in Fig. 1. The water surface profiles predicted by the wave simulator compare well with the analytical solution. The full wave simulator including the dispersion terms was validated against experimental studies obtained by Synolakis [36]. The numerical results produced by the wave simulator agreed well with analytical solutions and with experimental measurements, which confirms the accuracy and reliability of the method.

Fig. 1

Validation against the benchmark case [11]. The computed water surface profiles (symbols) at t = 3π/4, 7π/8, π, 9π/8 and 5π/4 are compared to the analytical solutions (solid lines) at the corresponding time instances. For this comparison, only the nonlinear shallow water equations are solved with dispersion and friction terms turned off

2.2 Subsurface pore water pressure simulator

To investigate the sub-surface response within the bed due to wave loading, we employ a mixed finite element (FE) formulation to simultaneously solve for the solid matrix deformations and pore water pressures. The governing equations for the coupled model consist of balance equations enforcing the conservation of mass and linear momentum for the solid/fluid mixture [4]. In this work, we ignore geometric nonlinearities (small-strain assumption), but retain material nonlinearities in the form of an elastoplastic constitutive model. The governing equations for the transient evolution of the system are given by:

$$ \nabla \cdot \left( {\sigma ^{\prime} - bp_{\text{e}} {\mathbf{1}}} \right) + \rho_{\text{b}} {\mathbf{g}} = {\mathbf{0}} $$

(6)

$$ \nabla \cdot \frac{{\partial {\mathbf{u}}}}{\partial t} + \nabla \cdot {\mathbf{v}} + \frac{n}{K^{\prime} }\frac{{\partial p_{\text{e}} }}{\partial t} = 0 $$

(7)

Here, $\sigma ^{\prime}$ is the effective Cauchy stress, $b$ is Biot’s coefficient, $p_{\text{e}}$ is the excess pore water pressure, $\rho_{\text{b}}$ is the buoyant density of the solid matrix in the saturating fluid, ${\mathbf{u}}$ is the displacement of the solid matrix, ${\mathbf{v}}$ is the Darcy velocity, $n$ is the porosity, and $K^{\prime}$ is the effective bulk modulus of the pore fluid. By working in terms of the excess pressure, we remove the hydrostatic component from the computation and can immediately solve for transient changes in pressure due to the imposed boundary conditions.

Biot’s coefficient can be determined from the bulk modulus of the solid skeleton $K_{\text{sk}}$ and the bulk modulus of the solid constituent $K_{\text{s}}$ as

$$ b = 1 - \frac{{K_{\text{sk}} }}{{K_{\text{s}} }} $$

(8)

In soils the ratio $K_{\text{sk}} /K_{\text{s}}$ is typically very small and is usually ignored. In this work, we follow this approximation and assume throughout that $b = 1.$ The definition of the effective stress then matches that of Terzaghi [38]. See also Borja [5] for an extensive discussion of effective stress definitions for saturated and unsaturated porous media.

If the pore space is absolutely saturated, then the effective bulk modulus of the pore fluid is simply equal to the bulk modulus $K_{\text{w}}$ of pure water (~2.2 GPa). Even a small amount of entrained air (either as free air or dissolved air) can lead to a drastic reduction in the effective modulus, and cause a large increase in the apparent compressibility of the pore fluid. A commonly used relationship for $K^{\prime}$ is [43, 46]:

$$ \frac{1}{{K^{\prime}}} = \frac{1}{{K_{\text{w}} }} + \frac{1 - S}{{p_{0} }} $$

(9)

where $S$ is the degree of saturation and $p_{0}$ is the absolute water pressure.

We supplement the governing balance laws with constitutive relations for the solid and fluid components. For the fluid, we employ Darcy’s Law in the form,

$$ {\mathbf{v}} = - \frac{{\mathbf{k}}}{\mu} \cdot \nabla p_{\text{e}} $$

(10)

where ${\mathbf{k}}$ is a tensor of intrinsic permeabilities (with typical units of m²) and $\mu$ is the dynamic viscosity of the fluid. An isotropic medium can be represented with a single scalar permeability $k$ such that ${\mathbf{k}} = k{\mathbf{1}},$ where ${\mathbf{1}}$ is the second-order unit tensor. In this work we assume that all permeability fields are isotropic.

An elastoplastic constitutive model for the effective stress can be written in general incremental form as,

$$ \Updelta \sigma^{\prime}_{\text{e}} = {\mathbf{C}}^{\text{ep}} :\Updelta \varepsilon,\quad\varepsilon = \frac{1}{2}(\nabla {\mathbf{u}} + \nabla^{t} {\mathbf{u}}) $$

(11)

where ${\mathbf{C}}^{\text{ep}}$ is a non-constant, fourth-order tensor of tangent moduli relating strain increments $(\Updelta \varepsilon )$ to effective stress increments $(\Updelta \sigma^{\prime}_{\text{e}} ).$ This tensor accounts for the drained behavior of the soil skeleton. In the elastic regime, we adopt a linear model for the sand behavior. In this case the tangent moduli are constant and can be defined by any two elastic parameters describing the response of the porous skeleton, e.g., the drained bulk modulus $K_{\text{d}}$ and Poisson ratio $\nu .$ Note that this linear-elastic model is a simplified assumption. In most sands, some degree of pressure-dependence on the bulk and shear moduli is commonly observed.

In order to define the plastic behavior, we adopt a non-associative Mohr–Coulomb (MC) model. Under plane-strain conditions, let the in-plane principal stresses be given by $\sigma^{\prime}_{1}$ and $\sigma^{\prime}_{3} .$ The out-of-plane principal stress $\sigma^{\prime}_{2}$ is assumed to remain intermediate and has no effect on plastic yielding. Using the solid mechanics convention, tensile stresses are positive. Let the mean normal effective stress and mean shear effective stress be given by,

$$ \sigma_{\text{m}} = \frac{{\sigma^{\prime}_{1} + \sigma^{\prime}_{3} }}{2}\quad {\text{and}}\quad \tau_{\text{m}} = \frac{{\sigma^{\prime}_{1} - \sigma^{\prime}_{3} }}{2} $$

(12)

The MC yield surface is implicitly defined as

$$ F = \left| {\tau_{\text{m}} } \right| + \sigma_{\text{m}} \sin (\phi ) - c\cos (\phi ) = 0 $$

(13)

where $\phi$ is the friction angle for the sand, and $c$ is the cohesion. Sands typically display little to no cohesion, and so $c \approx 0.$ The plastic potential is similarly defined as,

$$ G = \left| {\tau_{\text{m}} } \right| + \sigma_{\text{m}} \sin (\psi ) - c\cos (\psi ) $$

(14)

where the friction angle is now replaced with the dilatancy angle $\psi .$ Choosing $\psi = \phi$ results in an associative model, while allowing the dilatancy angle to be less than the friction angle results in a non-associative model. In general, $\psi \le \phi$ is required to ensure non-negative plastic dissipation. Non-associative models are typically preferred for modeling geomaterial behavior, as associative models tend to overpredict plastic volumetric deformations.

The elastoplastic model is implemented using an implicit return-mapping algorithm [8]. From a numerical standpoint, one challenge introduced by the MC surface is that it contains a sharp apex at the intersection with the mean normal stress axis (Fig. 2). As a result, for certain stress paths in the tension region the return mapping to the yield surface may not always be successful, since the stress point needs to be mapped to the apex itself. Special checks must therefore be included to detect and handle this case appropriately. A robust alternative is to replace the non-smooth MC surface with a smooth approximation for which the return-mapping is always well-defined. We employ this second approach, substituting a hyperbolic approximation [1] defined by

Fig. 2

Mohr–Coulomb yield surface and its hyperbolic approximation

$$ \bar{F} = \left[ {\tau_{\text{m}}^{2} + [ac\cos (\phi )]^{2} } \right]^{1/2} + \sigma_{\text{m}} \sin (\phi ) - c\cos (\phi ) = 0 $$

(15)

where $a$ is a shape parameter defining the hyperbolic fit. Choosing $a = 0,$ the original MC surface is recovered, while for $a > 0$ the sharp apex is replaced with a rounded tip. Away from the apex, the hyperbolic approximation quickly approaches the MC surface, with a slope defined by the friction angle $\phi .$ The plastic potential $\bar{G}$ is similarly defined, except using the dilatancy angle $\psi .$ In this work, we set $a = 0.5,$ and included a nominal cohesion value $c = 0.05\;{\text{kPa}}.$ This cohesion is orders of magnitude smaller than the typical loading conditions, and is included merely to define the smooth apex. To a good approximation, the sand behavior can be considered cohesionless.

We note that while the non-associative MC model is widely used in engineering to approximate soil behavior, it is a relatively simple model that is unsuitable for capturing some important features of sand-liquefaction behavior [6, 7]. For example, this model would be inappropriate for modeling loose sand subject to short-period waves for an extended period of time. Under cyclic loading, loose sand tends to contract volumetrically. Over many cycles, this inelastic contraction leads to a gradual increase in residual pore pressures, until finally a liquefied state may be reached—a process typically referred to as cyclic or residual liquefaction. The MC model cannot capture the necessary volumetric compaction in order to model this process. See, for example, Sassa and Sekiguchi [30], Dunn et al. [15], and Ou et al. [28] for the numerical studies of this cyclic liquefaction behavior using more sophisticated elastoplastic models. In the current study, however, the primary liquefaction mechanism is instantaneous rather than cyclic. A sudden drawdown of the water level occurs as the wave retreats from the shoreline, leading to a sudden change in the vertical hydraulic gradient profile. In regions where the excess pore water pressure approaches the suddenly reduced effective overburden pressure, the sand may liquefy. In this case, there is no periodic behavior or cyclic inelastic deformations. For modeling plastic deformation induced by the sudden change in loading, the non-associative MC model was deemed sufficient.

The FE formulation is supplemented with appropriate boundary conditions in the form of prescribed pressures, fluxes, displacements, and tractions (described below). In summary, the key assumptions used in developing the above model are that (1) the system remains isothermal, (2) geometric nonlinearities may be ignored, (3) the compressibility of the solid skeleton is much greater than the intrinsic compressibility of the solid grains, (4) the porosity and permeability remain constant and are strain-independent, and (5) the domain of interest is close to full saturation.

The numerical implementation is based on the discrete variational form of the equations, in which the solid displacements and pore pressures are introduced as primitive variables (${\mathbf{u}}/p$ form). The spatial discretization is based on mixed quadrilateral elements with linear interpolation for both displacements and pressures. In such mixed formulations, the interpolation spaces must be carefully chosen to avoid spurious pressure oscillations and sub-optimal convergence behavior [10]. For example, a Lagrangian bilinear-pressure/bilinear-displacement element is typically unstable and produces poor results. In this work, we employ the procedure described by White and Borja [45] to stabilize this otherwise unstable linear/linear combination. The resulting stabilized formulation has a variety of advantages, particularly in terms of computational efficiency, in comparison to standard stable elements. The time-integration is based on a single-step backward-implicit scheme.

The numerical implementation has been validated against benchmark analytical and experimental solutions for coupled consolidation problems [45]. Figure 3 presents one such study, in which the FE result is compared to the analytical solution for Terzaghi’s 1D consolidation problem [38]. The problem examines a 1-m thick soil layer atop a rigid, impermeable base. At t = 0, the saturated soil layer is suddenly subjected to a uniform strip load of 1 kPa, while the surface pressure is maintained at atmospheric conditions. Figure 3 presents the excess pressure profile with depth at several time instances, illustrating the gradual dissipation of pressure as drainage proceeds.

Fig. 3

Benchmark comparison of analytical (solid line) and finite element (dashed line with open circles) solutions to Terzaghi’s 1D consolidation problem at several time instances

3 Validation studies

3.1 Overview of experimental study

To validate the numerical models, the results are compared with experimental measurements collected from a large-scale laboratory study of tsunami propagation and sediment transport over a fine sand beach. The experiments were conducted at the Tsunami Wave Basin at the Oregon State University O.H. Hinsdale Wave Research Laboratory in 2007 [48–50]. A 2D flume with dimensions 48.8 m × 2.16 m wide × 2.1 m deep was especially built for this experiment inside the 3D tsunami wave basin.

Natural fine sand from Oregon was used to construct the mobile bed for this experiment. The sand had a median diameter D ₅₀ = 0.21 mm, and a uniformity coefficient C _u = D ₅₀/D ₁₀ = 1.67. The particle fall velocity, specific gravity, and porosity of a reconstituted laboratory sample were estimated to be 2.9 cm/s, 2.65, and 0.39, respectively. The fall velocity was estimated according to the method of Jimenez and Madsen [17].

In the experiment, numerous sensors were deployed to measure the water surface elevation, flow velocity, sediment concentration, pore water pressure, and bed profile, along with many above water and underwater video recordings [48–50]. Details about the facilities, instruments, bed configurations, wave conditions, and experimental procedures were presented in Young and Xiao [48, 49] and Young et al. [50].

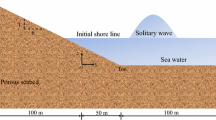
In this paper, we will focus our attention to comparisons with experimental data obtained near the initial shoreline for the case of a 60-cm solitary wave propagating over a fine sand beach with a nominal 1:15 slope. The initial water depth was 1 m. Although numerous sensors were deployed in the experimental study, we will only present the measured time-histories from the wave gauges and pore water pressure sensors at the initial shoreline, x = 27 m. The locations of the sensors where comparisons with numerical predictions are shown in the schematic drawing of the wave flume in Fig. 4. The waves were generated by a piston wave maker at x = 0 m and propagated toward the slope on the right. It should be noted that the region near the coastline is the area of focus because of its importance to coastal structure and coastal ecology, and because that is the region most susceptible to liquefaction failure.

Fig. 4

Elevation view of the experimental setup. The triangular area between 12 and 41.5 m is the mobile (sand) bed, which sits on the concrete bottom of the flume. The circles and squares indicate the locations where the experimental results are compared with numerical predictions

The setup of the numerical models is shown in Fig. 5. As explained in the previous section, the wave simulation is carried out using the FVM described in Sect. 2.1, and the pore water pressure simulation is carried out using the FE analysis described in Sect. 2.2. As shown in Fig. 5, the initial bed profile for the 60 cm solitary waves exhibited a slight S-shape, which is the result of many previous solitary waves of smaller amplitude. The grid used for the FE analysis, and the location of the assumed subsurface water table separating the saturated and unsaturated portions of the sand bed are also depicted in Fig. 5. The FVM model simulated the full cross-shore extent of the flume, from 0 to 41.5 m, to capture the wave runup and drawdown. The FE model only simulated the saturated portion of the sand bed, i.e., the unsaturated portion above the subsurface water table was not modeled. The FVM and FE models are not coupled since the time scale is more than an order of magnitude different between the surface and subsurface hydrodynamics for nearly saturated fine sand beach subject to rapid breaking solitary wave runup and drawdown.

Fig. 5

Schematic of the setup for the numerical model, including the FE mesh configuration used for the subsurface pore water pressure analysis

3.2 Predicted vs. measured wave and pore pressure time histories

Comparison of the predicted and measured surface water elevation at WG1 (x = 10 m) and WG12 (x = 27 m) is shown in Figs. 6 and 7, respectively. Also shown in Fig. 6 is the theoretical profile according to Munk [22], validating the accuracy of the wave maker. For the 60 cm solitary wave, a plunging breaker initiated immediately after x = ~22 m at t ~ 7.5 s, which impinged on the shallow water near the shore at x = ~24 m. The broken wave formed a turbulent bore with a height of ~20 cm at x = ~26 m, which then climbed onshore. The wave reached its maximum runup at x = ~38.5 m at t = ~13 s, followed immediately by wave drawdown. The drawdown wave reached the position of the initial shoreline at around t = ~15 s, leading to a hydraulic jump at x = 24 m due to transition from supercritical to subcritical flow caused by the sudden deceleration as a result of the collision between the rapidly retreating water tongue and the relatively still massive body of water. The drawdown wave continued to travel offshore and reached WG1 at x = 10 m at t ~ 20 s. Considering the complex wave breaking, bore formation and collapse processes, the agreement between the numerical predictions and experimental measurements is satisfactory. It is important to note that at t > 20 s, wave–wave interactions became important, and the flow is complicated by a hydraulic jump and a large re-circulating flow immediately seaward of the hydraulic jump. The depth-averaged model cannot represent these interactions accurately. Therefore, the agreement after t = 20 s begins to deteriorate. However, the overall agreement of the numerical predictions and experimental measurements is relatively good for WG1 and WG12. Similar good comparisons were also observed at the 14 other locations where different wave gauges and ultrasonic sensors were deployed, but they are not shown in this paper due to space limitations.

Fig. 6

Comparison of the theoretical and measured wave elevation time history at x = 10 m

Fig. 7

Comparison of the predicted and measured wave elevation time history at x = 27 m

The hydrostatic pressure distribution at the bed surface is applied as a dynamic boundary condition for the FE analysis of the soil deformation fields and pore pressure distributions. Figure 5 illustrates the geometry and mesh used for this analysis. The water table was assumed to be flat and in line with the still waterline, i.e., at z = 0 m. The assumption of a flat water table seems reasonable in this case given the idealized experimental setup. A preliminary analysis of boundary sensitivities indicated that the vadose zone (the unsaturated portion of beach above the subsurface water table) had only minor influence on the pore pressure distributions on the phreatic zone (the nearly saturated region below the subsurface water table). Therefore, for the purposes of this analysis, only the phreatic zone was modeled. Note, however, that this implies a fixed phreatic surface which does not move with the wave-motion. In reality, water table fluctuations are observed, especially near the intersection of the water table line with the bed boundary. Given that the inundation process is very rapid in comparison to the permeability of the sand, these fluctuations are expected to be quite small and should not change the results significantly. Further exploration of this aspect, however, can be found in Nielsen [23] and Teo et al. [37].

Constitutive parameters used for the FE analysis are given in Table 1. These values are consistent with typical dense fine sand, and were calibrated to provide a good match with the experimental measurements. The permeability field was assumed to be isotropic and homogenous. Also, observations during the wave tank experiments indicated that the sand had not reached complete saturation despite the many days of soaking before the 60 cm wave runs. The effective modulus for the pore fluid was taken to be $K^{\prime} = 4\,{\text{MPa}},$ corresponding to 97% saturation. We hypothesize that the presence of residual air accounts for the apparent increase in compressibility of the pore fluid in comparison to that of pure water.

Table 1 Parameter values used in the subsurface finite element analysis

The lower boundary representing the concrete base was considered a zero-flux, zero-displacement boundary. The right boundary representing the concrete wall was also considered a zero-flux, zero-displacement boundary. The upper boundary is broken into two sections, one representing the exposed bed surface, and one representing the flat water table line. The pressure at the bed surface was assigned based on the excess hydrostatic pressure caused by the wave motion, $\bar{p}_{\text{wave}} .$ The excess pressure on the water table surface was set to 0 (gauge atmospheric). By definition, the traction at these boundaries is given by

$$ {\mathbf{t}} = \sigma \cdot {\mathbf{n}} = \sigma^{\prime} \cdot {\mathbf{n}} - p_{\text{e}} {\mathbf{n}} $$

(16)

where ${\mathbf{n}}$ is the unit normal to the surface. Since the sand bed boundary is in contact with water only, the effective stress should be 0 there. To enforce this condition, it is therefore necessary to apply a traction such that

$$ {\mathbf{t}}_{\text{wave}} = - \bar{p}_{\text{wave}} {\mathbf{n}} $$

(17)

On the water table boundary, the excess pressure is zero, but the effective stress is not zero as a result of two components: the weight of the unsaturated soil above the water table, and the weight of the passing wave. For the wave component we can again use Eq. (17). This implies that the traction given by Eq. (17) should be applied at both the bed surface boundary and the water table boundary, though the resulting effective stress states are quite different.

Figure 8 presents the predicted and measured time histories of the evolution of the change in pore pressure from the initial hydrostatic state at the four pore pressure sensors (PPS5–8) deployed at the initial shoreline (x = 27 m). The location of the pore pressure sensors is shown in Fig. 4. They are spaced 0.15 m apart vertically. PPS8 is on the top, and it is located 0.16 m from the bed surface. The pore pressure distribution at PPS8 corresponded well with the variations in water surface elevations shown in Fig. 7, confirming the validity of the hydrostatic pressure assumption. The simulation was performed using both a linear-elastic model and the elastoplastic model described earlier. Both models produced essentially identical results. Plastic deformations therefore do not play a significant role in this case due to the rapid loading and unloading of the model-scale experiment. The sudden rise in pore pressure at PPS5–7 around the 4 s is attributed to the compression of the solid skeleton due to the arrival of the wave at the bed surface. A pure diffusion model does not capture this sudden rise—a key advantage of the coupled solid/fluid formulation. The first and second peaks observed in PPS5–8 corresponded to the passing of the water column associated with wave runup and drawdown, respectively. In both the experimental measurements and numerical predictions, the diffusive behavior of the pressure waves can be discerned by the increases in time lags in peak arrivals, decreases in peak magnitude, and increases in blurring of the peaks and troughs. As shown in Fig. 8, the agreement between numerical predictions and experimental measurements is quite good for t < 13 s. The agreement begins to deteriorate for t > 13 s due to small errors in the simulated wave profile caused by wave–wave interactions, hydraulic jump, and large re-circulating flow that occurred at the end of the drawdown. It is important that to note that since the pore pressure is governed primarily by diffusion, small changes in the boundary condition (e.g., bed surface pressure distribution) can lead to much larger change in the pore pressure distributions. Nevertheless, considering the complexity of the experiment, and the spatial variation of the porosity, saturation, and grain size caused by repeated wave actions, the overall agreement between the numerical predictions and experimental measurements is satisfactory.

Fig. 8

Comparison of the predicted and measured pore water pressure at x = 27 m. The z-values indicated in the graphs are measured from the bed surface at x = 27 m

4 Results

4.1 Overview of model setup

Numerical case studies are presented for a full-scale problem: a solitary wave with an initial height 10 m propagating over an initial water depth of 20 m. The slope of the fine sand beach is selected to be 1:15 and 1:5 to represent a mild slope and a steep slope beach, respectively. The depth of the sand layer to impervious bedrock is assumed to be 20 m. The properties of the sand are the same as given in Table 1. The top and bottom boundary conditions are the same as those used in Sect. 3. The left (landward) and right (seaward) boundaries are approximated as zero-flux, zero horizontal displacement boundaries. Although some flux is expected across the left and right boundaries as the wave passes, the vertical flux is assumed to dominate. This approximation is used because there is no a priori estimate of the pressure or flux profile with depth. Hence, the left and right boundaries are purposely placed far enough away such that the error introduced by the zero-flux boundary conditions has negligible impact in the region of interest, the near-shore region. The model setup for the 1:5 case is shown in Fig. 9. The water table profile is again assumed to be flat and stationary, though we note that for most natural beaches the water table shows some vertical variation. The wave profiles during the runup and drawdown, as well as the bed responses for the two different slopes are studied and compared.

Fig. 9

Model setup for the numerical simulation of a 10-m solitary wave running onto a 1:5 bed slope

The objectives of the case studies are to assess and compare the time, extent, and location of zones with a high potential for liquefaction. There are a variety of criteria we could use to assess liquefaction potential. In this work, we use one based on the mean normal effective stress $\sigma_{\text{m}} .$ When the normal stress is negative (compression), the sand has some shear capacity and is assumed to be in an unliquefied state. Pore pressure increases, however, can cause the mean normal effective stress to exceed the limited tensile strength of the sand. In the process, the local shear capacity decreases until no residual strength is left. The stress point then lies at the apex of the MC yield surface. Since sands are typically cohesionless, the liquefaction threshold used in this work is simply $\sigma_{\text{m}} = 0.$ We note that in defining the smoothed MC model, we have added a nominal cohesion value (0.05 kPa) that allows the mean normal stress to rise slightly above 0, but this slight cohesion is ignored in assessing liquefaction potential.

Another issue that must be addressed is the time-variation of the liquefied zone. As the wave evolves, the mean normal effective stress at a point in the sand may increase to 0, but then later drop below the liquefaction threshold. In this work we make no attempt to model post-liquefaction or solidification behavior, during which the sand has an entirely different constitutive behavior. In assessing liquefaction potential, our primary concern is whether a point in the soil ever liquefies, and base the liquefaction criterion on the cumulative maximum mean normal stress a point encounters over the course of the wave loading.

4.2 Wave propagation—1:15 slope

The runup and drawdown wave profiles of a 10-m solitary wave over a 1:15 sandy slope is shown in Fig. 10. The wave is centered at x = 340 m at t = 0 s. The wave profiles during the runup and drawdown are shown in the left and the right plots, respectively. The time stamps corresponding to the profiles are indicated in the legend, with units of seconds. The wave shoaling on the slope is discernable by the fact that the wave height at t = 12.79 s is slightly greater than the initial height of 10 m. The wave breaking can be observed from the decrease in wave height between t = 12.79 and t = 19.18 s. The maximum runup occurred at t = 49.4 s with the maximum horizontal excursion at x = −233 m. After which, drawdown begins. The drawdown caused the water level to drop ~4 m below the still waterline, which exposed a 50-m wide by 4 m deep area immediately below the initial shoreline. During the drawdown, a hydraulic jump formed at x = 45 m, which lasted for ~30 s.

Fig. 10

Selected wave profiles for a 10-m solitary wave propagating onto a 1:15 slope. Left wave profiles during runup. Right wave profiles during drawdown. The maximum runup occurred at t = 49.4 s with the maximum horizontal excursion at x = −233 m. The time (t) stamps are in units of seconds

The time-histories of the wave surface profile at x = 0 (shoreline), 25, and 40 m are shown in Fig. 11. Notice that the wave broke more than 50 m offshore, and hence the maximum wave height at x = 40 m is only ~7.5 m. The wave height continues to decrease as it propagates onshore due to energy dissipation via friction. At the shoreline (x = 0 m), the maximum wave height is only slightly higher than 5 m. At x = 40 m, the rate of bed surface pressure drop is approximately 70 kPa in 25 s, which can be considered as sudden since the drainage time of the pore pressure for 20 m of nearly saturated fine sand is estimated to be approximately 1,500 s based on the soil properties assumed in Table 1.

Fig. 11

Time series of wave elevation at three different locations: 40 m offshore, 25 m offshore, and at the shoreline, recorded from the numerical simulation of a 10-m wave running onto a 1:15 slope bed

4.3 Pore pressure responses—1:15 slope

The left plots on Fig. 12 presents the time-histories of the predicted excess pore pressures for the 1:15 bed at x = 40 m during the wave runup and drawdown processes. The results are sampled at six points at increasing depths, in 30 cm increments. The cross-shore location of the sampled section, x = 40 m, is chosen because it is in close proximity to the hydraulic jump that formed during the wave drawdown. At this point, the maximum drop in water level is observed, and this cross-section is thus considered critical in terms of liquefaction potential.

Fig. 12

Time histories of excess pore pressure for the 1:15 slope at x = 40 m (left) and the 1:5 slope at x = 25 m (right). The z locations are measured from the bed surface at the respective locations

The simulation was again performed with two material models, a linear-elastic model and the elastoplastic model. In this case, significant differences are observed in the two models. The time-history of the excess pore pressure at the bed surface, z = 0 m, is equivalent to the transient variations in water surface elevation. During the runup phase, the soil is subject to compression due to increase in bed surface traction caused by the passing of the wave, which leads to buildup of excess pore pressure, particularly in the top soil layer. For soil at or deeper than 60 cm beneath the surface, an instantaneous rise in pore pressures at t = ~18 s can be observed, and it is a result of the immediate compression of the solid skeleton due to the sudden increase in overburden stress caused by arrival of the wave. During the drawdown phase, the soil is subject to decompression. The bed surface pressure drops to the atmospheric pressure as the surface water level drops to 0. However, the excess pore pressure beneath the bed surface cannot dissipate as fast, which leads to negative (upward) vertical pore pressure gradients that may cause liquefaction failure of the soil near the bed surface.

Both the elastic and elastoplastic models are able to capture the classic diffusive nature of the excess pore water pressure, which is evident via the increases in time lag in the arrival of the peaks, the decreases in the magnitude of the peaks, and the blurring of the peaks. The pore pressure responses predicted by the two models are essentially identical during the loading phase. However, significant differences can be observed during the unloading phase; the elastoplastic model predicts significantly larger negative pressures, with much less dissipation with depth than the elastic model. The predominant deformation mechanism in these simulations is volumetric, rather than deviatoric, and hence the loading and unloading is close to the hydrostatic axis. When the soil is subject to compression during the runup, the elastic and MC models should produce identical results. On the other hand, when the soil is subject to decompression during the drawdown, the elastic and MC models should produce different results. The elastic model can maintain large tensile stresses, and therefore accommodate high local pressures (and thus higher local pressure gradients). The MC model deforms plastically under large decompression, and so the pressure difference induced by the wave loading must be accommodated over a much larger depth. As a result, the hydraulic gradient for the elastic model is higher, but penetrates to a shallower depth, than the MC model.

To assess the liquefaction potential, we use the cumulative maximum mean normal effective stress criterion described earlier. If the pore pressure conditions are such that $\sigma_{\text{m}}$ ever equals 0, the sand is assumed to have liquefied. Figure 13 presents a spatial picture of the growth of the liquefaction zone based on the elastoplastic material model. The maximum depth of the liquefaction zone is predicted to be 2.8 m.

Fig. 13

Snapshots of the wave motion and contours of the cumulative maximum mean normal stress (σ _m) in the 1:15 slope at several time instants. The high liquefaction potential zone (σ _m  = 0) corresponds to the black region

4.4 Wave propagation—1:5 slope

The wave profiles for a 10-m solitary wave runup and drawdown over a 1:5 slope is shown in Fig. 14 in the same manner as in the 1:15 slope case above. The time-histories of the predicted wave surface profile at x = 0, 25, and 40 m are shown in Fig. 15. The wave started at x = 200 m at t = 0 s. Compared to the 1:15 case, there was no obvious wave shoaling and breaking due to the steep 1:5 slope, as evident via the wave maintaining its 10-m initial wave height up to the initial shoreline. Another significant difference compared to the 1:15 slope case is that the duration of the runup and drawdown processes is much shorter because of the steeper slope. The maximum runup for the 1:5 slope occurred at t = 24.2 s with the maximum excursion at x = −140 m. After which, drawdown begins. As shown in Fig. 15, the wave height at x = 25 m is negative between 20 s < t < 40 s due to the water level dropping below the initial water line, and hence the pressure difference from the initial hydrostatic pressure is negative. Part of the flow retreated back to the sea prior to the front of the wave reaching the maximum runup point. The wave height increased again at t = ~20 s at x = 40 m due to the formation of a hydraulic jump. The front of the hydraulic jump stationed at x = ~29 m, and it was sustained for approximately 15 s. The drawdown caused the water level to drop ~5 m below the still waterline at 25 m offshore. The extent of the seepage face for the 1:5 slope is approximately 25 m wide by 5 m deep, which is much narrower and but slightly deeper than the 1:15 case. The rate of pressure change is approximately 130 kPa in 20 s at x = 25 m, approximately two times faster than that recorded at x = 40 m in the 1:15 slope case.

Fig. 14

Selected wave profiles for a 10-m solitary wave propagating onto a 1:5 slope. Left wave profile during runup. Right wave profiles during drawdown. The maximum runup occurred at t = 24.2 s with the maximum excursion to x = −139.8 m. The time (t) stamps are in units of seconds

Fig. 15

Time series of wave elevation at three different locations: 40 m offshore, 25 m offshore, and at the shoreline, recorded from the numerical simulation of a 10-m wave running onto a 1:5 slope bed

4.5 Pore pressure responses—1:5 slope

The time-histories of the excess pore pressures for the 1:5 bed at x = 25 m during the wave runup and drawdown processes are shown in the right plots in Fig. 12. The results are samples at the same vertical distances from the bed surface as in the 1:15 bed case. The cross-shore location of the sampled section, x = 25 m, is chosen for this case because it is in close proximity to the hydraulic jump that formed during the wave drawdown, and because this is the point where the maximum negative hydraulic gradient was observed. The shape of the time-history responses of the excess pore pressure is similar to the 1:15 case, but the rate of loading and unloading is approximately two times faster due to the faster runup and drawdown rates caused by the steeper slope. For the 1:5 bed, the wave did not break prior to reaching the shoreline, and as a result the peak positive excess pore pressure is higher than the 1:15 bed case. The peak negative excess pore pressure is also higher for the 1:5 bed case because of the deeper extent of the set down. As shown in Fig. 12, matrix compression begins to dominate at 90 cm beneath the bed surface, as evident via the sharp peak in response to the initial wave arrival. Again, the elastic and elastoplastic solutions produce significantly different results during the drawdown phase, with the elastoplastic solution showing a much deeper pressure penetration.

The snapshots of the high liquefaction potential zone in Fig. 16 indicate that the 1:5 bed slope is more susceptible to liquefaction failure due to the faster rate of unloading during wave drawdown. The zone of high liquefaction potential penetrates much deeper into the slope. The maximum depth of the liquefaction zone is predicted to be 4.4 m for the 1:5 slope, compared to 2.8 m for the 1:15 slope.

Fig. 16

Snapshots of the wave motion and contours of the cumulative maximum mean normal stress in the 1:5 slope at several time instants. The high liquefaction potential zone corresponds to the black region

5 Conclusions

During tsunami runup and drawdown, high excess pore pressures are generated within the nearly saturated portion of the fine sand beach due to the rapid changes in bed surface pressure compared to the slow dissipation of pore pressure. The region immediately seaward of the initial shoreline is the most susceptible to tsunami-induced liquefaction failure because the water level drops significantly below the still water level during the set down phase of the drawdown. Consequently, a seepage face is created along the bed surface between the initial shoreline and maximum drawdown location due to inability of the subsurface water table to respond to the rapid surface water changes. In this region, the excess pore pressure can easily exceed the significantly reduced effective overburden pressure (due to drop in water level), which will cause the sand to liquefy. Although there exist many analytical, numerical, and experimental studies of tsunami wave propagation and inundation modeling, few studies considered the effects of the mobile bed, and even fewer (if any) considered the potential for tsunami induced liquefaction failure of coastal fine sand slopes. Moreover, it is extremely difficult to obtain real-time data on site during an actual tsunami. As a result, the objective of this work is to develop and validate a numerical model to assess the potential for tsunami-induced liquefaction failure of coastal sandy slopes.

The wave propagation, breaking, runup and drawdown, as well as resulting pressure distribution acting on the slope, are computed by solving for the hybrid Boussinesq–nonlinear SWE using a finite volume method. The subsurface excess pore water pressure and deformation fields are solved simultaneously using a FE method. Two different soil constitutive models have been examined: a linear elastic model and a non-associative MC model. The FVM and FE models are not coupled since the time scale is more than an order of magnitude different between the surface and subsurface hydrodynamics for a nearly saturated fine sand beach subject to rapid wave runup and drawdown. Analytical validation studies are shown for both the wave simulation model and the soil pore water pressure model. Experimental validation studies are also shown using results from a large-scale laboratory study of breaking solitary wave runup and drawdown over a fine sand beach. Good comparisons were observed from both the analytical and experimental validation studies.

Numerical case studies are shown for a full-scale simulation of a 10-m solitary wave over a 1:15 and 1:5 sloped fine sand beach. The results show that the soil near the bed surface is subject to liquefaction failure, with the deepest liquefaction zone near the seepage face. The depth of the seepage face increases and the width of the seepage face decreases with increasing bed slope. The rate of loading and unloading also increases with increasing bed slope. Consequently, the hydraulic gradient increases with increasing bed slope. As a result, the case with the steeper slope is more susceptible to liquefaction failure. The results show that the cross-shore extent of the zone of high liquefaction potential is narrower for the 1:5 bed due to the smaller width of the seepage face, but the depth is approximately the same between the two different slopes. The analysis also suggests that the results are highly influenced by the soil permeability and relative compressibility between the pore fluid and solid skeleton, and that a coupled solid/fluid formulation is needed for the soil solver. The results suggest that the influence of nonlinear material behavior is negligible for the model-scale laboratory simulation due to the rapid loading and unloading. However, for the full-scale case studies with 10-m solitary waves, significant differences can be observed between the elastic and elastoplastic models during the drawdown phase. The MC elastoplastic model predicted significantly larger negative pressures, with much less dissipation with depth than the elastic model because the soil behaves plastically under decompression. Consequently, the hydraulic gradient for the elastic model is higher, but penetrates to a shallower depth, than the MC model. Nevertheless, the current MC model is relatively simple, and cannot capture important features such as increase in residual pore pressure due to volumetric compression. Therefore, additional work is needed to investigate the influence of nonlinear material behavior and material instability. Further work is also necessary to determine the effect of wave shape, wave–wave interaction, bathymetry, and soil properties on the bed responses.