1 Introduction

Representativeness of data is crucial in correctly characterizing the environmental performance of a product system in Life Cycle Assessment (LCA). According to ISO14044, representativeness is defined as “qualitative assessment of the degree to which the data set reflects the true population of interest (i.e. geographical coverage, time period and technology coverage)” (ISO 2006). In practice, few data used in LCA are provided with empirically measured statistical distribution information, and LCA practitioners often need to work with anecdotal data points or conflicting information from disparate sources. LCA practitioners use, among others, pedigree framework introduced by Weidema and Wesnæs (1996) for characterizing data quality where representativeness is an important element. The framework has been widely adopted in Life Cycle Inventory (LCI) databases (Ecoinvent 2013; Frischknecht et al. 2004), and it is now an integral part of data exchange formats such as EcoSpold version 2 (Ecoinvent 2013) where data fields from 2,100 to 2,173 correspond to relevant criteria for assessing representativeness.

Maintaining representativeness of data used is a universal challenge in an LCA, and it is further severed in the LCAs assessing new technologies, where information may be either immature or well guarded for business reasons (Gavankar et al. (2013); Heijungs and Huijbregts 2004). The sparse and imprecise data also introduces non-random epistemic uncertainty, which is driven by the lack of information, rather than variability in data (Reap et al. 2008; Couso and Dubois 2009; Dubois and Prade 1980; Dubois 2011; Chevalier and Téno 1996; Benetto et al. 2005; Ardente et al. 2004; Andrae et al. 2004; Heijungs and Huijbregts 2004; Huijbregts et al. 2001). This happens because often when the product is new, the information is gathered from multiple sources, such as patents, literature, and laboratory experiments, in order to have a reasonable estimate for an input (Khanna and Bakshi 2009; Healy et al. 2008; Meyer et al. 2010). Moreover, this information may be in incompatible formats such as point estimates, intervals, approximations or linguistic expressions, and may also be conflicting in nature. It is important then to synthesize this data with minimal loss of information in order to get a good estimate of the variable. Formalized information synthesis rooted in robust theory can help reduce epistemic uncertainty and enhance data quality, thereby increasing the credibility of LCAs.

The acknowledgement of epistemic uncertainty due to imprecise data, the need to separate it from the random variability and inability of probabilistic framework to process such uncertainty led to the application of fuzzy numbers in the LCA literature as early as in 1996 when Chevalier and Téno used intervals and min–max numbers to process the data inputs through LCA (Chevalier and Téno 1996). This was followed by the studies by Weckenmann and Schwan (2001) and González et al. (2002) where the options of performing quick and inexpensive LCAs were explored with the help of fuzzy intervals. Ardente et al. (2004) then introduced fuzzy inference technique in the LCA literature, and von Bahr and Steen (2004) proposed reducing epistemological uncertainty by using fuzzy LCI. The article by Tan (2008) then formalized the processing for fuzzy LCI through the matrix-based LCI model introduced by Heijungs and Suh (2002).

The fuzzy-number-based work in the LCA literature mentioned above can be tied to the theoretical framework of possibility theory, and it is presented as such in the more recent LCA literature addressing epistemic uncertainty (Andrae et al. 2004; Benetto et al. 2005; Clavreul et al. 2013). Andrae et al. (2004) presented an overview of possibility theory in the context of uncertainty propagation in LCA. This discussion is carried forward by Clavreul et al. (2013) by illustrating the fundamental difference between the possibilistic and probabilistic representations of uncertainty and the importance of application of appropriate propagation methodology.

Possibility theory can also be used to model and fuse subjective and conflicting information from multiple sources, and in incompatible formats, in order to obtain a more plausible, representative data point. This approach, though highly useful in enhancing data quality, has not yet been introduced in the LCA context. The Shonan Guidance Principle, which addresses the challenges in collection and management of imprecise raw data, advises the ranking of datapoints according to their quality according to the agreed upon criteria, and then picking the best representative data point (ex., Section 2.2.3) (UNEP 2011). However, the document does not provide guidance when ranking multiple data points to get the best one may not be possible.

The objective of this paper is to introduce and apply possibility theory to fuse multiple raw data that may be in conflict or given only in linguistic descriptions (Benoit and Mazijn 2009). We proceed by first presenting the relevant part of possibility theory behind information fusion in the next section. Then, this framework is applied to the disparate numerical data from literature on the manufacturing energy requirement for semiconductor device fabrication and to a hypothetical example of linguistic data on engineered nanomaterial (ENM) fate and transport behavior under certain conditions. We also recap this procedure in a flowchart at the end of the section. The article concludes with the discussion on where such an exercise will be most useful in enhancing the quality of the LCA results without drastically changing the current preferred practices of conducting the assessment, and the role the LCI databases can play in this endeavor.

2 Fusion of data provided by multiple sources

Much theoretical work on information synthesis is housed in the various branches of mathematics, with its numerous applications already evident in the field of economics and finance (Choobineh and Behrens 1992), engineering (Mourelatos and Zhou 2005), risk management (Baskerville and Portougal 2003). When information comes from multiple sources, the heterogeneity and subjectivity behind the assumptions and presentation of data make the character of information gathered inherently different from that exhibited by the information coming from a single random source if it were to produce this information (Dubois and Prade 1994). The latter represents a situation where the data can be processed statistically and probabilistically. But merging of non-random and subjective information is an exercise in filtering less reliable information and seeking consistency out of imprecise information (Dubois and Prade 1994; Bloch et al. 2001). In practice, processing this type of information has been carried out in LCA by expert judgment. However, this type of synthesis can be performed with possibility theory with the help of appropriate fusion operations (Wolkenhauer 1998; Yager 1983; Tanaka and Guo 1999; Dubois and Prade 1994, 2001; Dubois and Prade 2004). To do so, it is necessary to first model or represent the data appropriately. Accordingly, data modeling is presented ahead of the presentation on formalized information fusion in the following text.

2.1 Data modeling with fuzzy set theory

Fuzzy sets are a generalization of the classical sets to account for the non-crisp information coming from linguistic and vague information (Zadeh 1978). In the classical set theory, it is clearly determined whether an item belongs to the set (e.g., “one” or “true”) or not (e.g., “zero” or “false”). However, in the fuzzy set theory, membership degrees or gradation exist between zero and one, and the members can have different degrees of membership, called “membership function”, μ(x) in the interval [0,1]. Abundant literature and textbooks are available explaining the basics of fuzzy sets (Chaturvedi 2008; Dubois and Prade 1980; Lee 2005).

As illustrated in Fig. 1, μ(x) is bound by 0 and 1, i.e., 0 ≤ μ(x)≤ 1. Also, μ(x) is normal, i.e., at least one element exists for which μ(x)= 1. The membership function μ(x) of a fuzzy variable can be also described in terms of α-cuts at different vertical levels α (Fig. 1). Just like the membership function, the α-cuts are the slices through a fuzzy set producing regular classical (non-fuzzy) sets. In that sense, every fuzzy set is a collection of non-fuzzy or crisp sets at the levels of α.

Fig. 1
figure 1

The α-level presentation in a fuzzy set or number

Full size image

Zadeh (1978) proposed an interpretation of membership functions of fuzzy sets as possibility distributions. It is important to note here that fuzzy and possibility theories appear similar under certain situations, but they are not the same. Fuzzy set theory models a proposition’s membership to the known true value set, whereas possibility theory determines how likely the value is the true value (Dubois et al. 2000; Dubois 2001). Conventions of fuzzy numbers however may be used to represent the data under the discussion of possibility theory, as can be seen from the discussion below.

This approach has already been used in the LCA setup (Ardente et al. 2004; Chevalier and Téno 1996; Tan 2008). Under this interpretation, the possibility of a value to be the true value is estimated by using Eq. (1). This setup is mathematically same as the basic calculation of the membership μ(x) of x when x lies within the interval (a,c) with b as the most likely value. This interpretation will be recalled later in Section 3 for the discussion on the fusion of information presented in intervals:

$$ \alpha =\left\{\begin{array}{ll}\frac{x-a}{b-a},\hfill & a\le x<b\hfill \\ {}\kern2.5em 1,\hfill & x=b\hfill \\ {}\frac{c-x}{c-b},\hfill & b>x\ge c\hfill \\ {}\kern2.12em 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right. $$
(1)

2.2 Data modeling with possibility theory

2.2.1 The basics of possibility theory

Conceptually, possibility is the lower bound of probability, i.e., what is possible, must always be probable (Zadeh 1978). Formalization of possibility theory presented in this section is richly available in the literature (Tanaka and Guo 1999; Yager 1983; Wolkenhauer 1998; Dubois and Prade 1988): If Ω is a frame of discernment (i.e., possibility space) consisting of a set of possible values of ω, then possibility distribution function π (ω), where 0 ≤π (ω)≤ 1, represents the possibility of an element ω from the set Ω. The condition of normalcy, i.e., the condition that at least one value from the set Ω is the true value, is assumed in the framework of possibility theory, and is formally expressed as: support i.e., sup {π (ω): ω ∊ Ω}= 1. Also, a possibility measure Π is different from a possibility distribution π. The former is a supremum, i.e., the least upper bound set of the latter, and is defined as:

$$ \varPi (A)=\mathrm{su}{\mathrm{p}}_{\omega \in A}\ \pi\ \left(\omega \right)= \max \left(\left\{\left.\pi \left(\omega \right)\right|\omega \in A\right\}\right). $$
(2)

This measure of possibility Π has its dual measure; it is called “necessity” N, which is always less than or equal to Π, and represents the absolute certainty of a proposition. It is defined as N(A) = 1 − Π (A c), i.e., the proposition is necessary or certain when the opposite is impossible. Here A c represents the compliment of A.

An important aspect of possibility theory is that it is non-additive in order to account for subjective information which may not always add up. This feature separates it from the subjective branch of probability, such as Bayesian probability, which enforces probabilistic additive nature (Dubois et al. 2000). The non-additivity indicates that the union of two independent propositions is not equivalent to their addition. Rather, the possibilistic union follows the theorem of maxivity: Π (A ⋃ B) = MAX (Π (A),Π (B)). This means that when A and B are considered together, whichever is more easily possible will determine whether A ⋃ B happens or not. Necessity measures satisfy an axiom dual to that of possibility measures, and N (A ⋂ B)=MIN (N(A), N(B)).

2.2.2 Data modeling with possibility theory

When the information is available in form of an interval, it can be refined, for example with the help of expert opinion, in that multiple nested intervals can be obtained from the experts with various levels of possibility. These nested possibilistic intervals may thus look like the fuzzy set in Fig. 1, with various possibilities representing alpha-cuts or membership levels much akin to the α-cuts. The nested nature of information can be more formally captured as follows (Dubois and Prade 1994): Let possibility distribution π (ω) represent a family of nested confidence subsets {A 1, A 2, …, A m } where A i  ⊂ A i  + l, i = 1, m − 1 assuming that the set of possibility values is finite. Now, let λ i be the level of confidence or belief that can be interpreted as the lowermost bound of the probability that the true value is in A i. This makes λ i a degree of necessity N(A i ) of A i . By definition, N(A i ) = 1 − Π(A i C) as indicated above, where Π(A i C) is the maximum degree of possibility that the true value is in A i C. Hence, the possibility distribution applicable to the family {(A 1, λ 1), (A 2, λ 2),…, (A m , λ m )} is defined as the least specific possibility distribution that obeys the constraints λ i  = N(A i ), and reflects the minimum specificity principle as (Dubois and Prade 1994):

$$ \pi \left(\omega \right)=\left\{\begin{array}{ll}1\hfill & \mathrm{if}\ \omega \in {A}_1\hfill \\ {}{ \min}_{i:\omega \notin {A}_i}\left(1-{\lambda}_i\right)\hfill & \mathrm{otherwise}\hfill \end{array}\right. $$
(3)

The principle of minimum specificity states that any hypothesis not known to be impossible cannot be ruled out (Dubois and Prade 1988; Yager 1983). This logic makes the most specific opinion as the most restrictive and informative, and also makes a possibility distribution to be at least as specific as another one if and only if each state is at least as possible according to the latter as to the former (Yager 1983). Hence, for nested intervals, π (ω) = 1 if ω belongs to A 1, with A 1 being the common subset of all the nested intervals by definition. Otherwise, π (ω) is the minimum of all the (1−λ i )s corresponding to the intervals that do not have ω.

This logic of minimum specificity does not change when the information is presented as point values or sets of point values instead of intervals. Accordingly, the least specific possibility distribution compatible with the pairs of the possible values (ω i ) and respective beliefs (λ i ) placed on them is presented as (Benferhat et al. 1997):

$$ \pi \left(\omega \right)=\kern1em \left\{\begin{array}{l}\begin{array}{ll} \min \left\{\left.1-{\lambda}_i\right|\left({A}_i{\lambda}_i\right)\right.\hfill & i\mathrm{f}\ \omega \notin {A}_i\hfill \\ {}=\kern1em 1- \max \left\{\left.{\lambda}_i\right|\left({A}_i{\lambda}_i\right)\right\}\hfill & \kern1em \mathrm{if}\ \omega \notin {A}_i\hfill \end{array}\\ {}\kern2em 1,\kern6.5em \mathrm{Otherwise}\end{array}\right. $$
(4)

2.3 Data fusion with possibility theory

The fusion or merging of possibility distributions (i.e., the distributions that look like Eqs. (3) and (4) above) is based on set theoretic or logical methods of the combination of uncertain information. The main properties of these combination rules—as applicable to possibility theory—described in the literature are closure, commutativity, and adaptiveness (Dubois and Prade 1988). Closure refers to the property whereby the result of combination belongs to the same representation framework of the individual pieces of information. In the context of this article, this property implies that if the individual pieces of information are presented as possibility distribution, then their fusion will also be a possibility distribution. Compliance to commutativity indicates that changing the order of the operands (pieces of information to be fused, in this case) does not change the results. Lastly, the adaptiveness indicates that the amount of overlap between the pieces of information affects the choice of fusion operator.

There are two basic modes of data fusion in possibility theory: the conjunctive mode when all the sources agree and are considered as reliable; and the disjunctive mode when sources disagree and at least one of them is wrong, but it is not known which one (Liu 2007; Dubois and Prade 2001). The choice between conjunction and disjunction is influenced by the degree of closeness in the information and the characteristics of their sources, such as datedness and the reliability (Liu 2007; Dubois and Prade 2001). The next step is to choose the procedure for performing conjunction or disjunction. The context of operation decides which procedure to follow. The main choices for conjunction of a and b are “min” (=min a,b), “product” (= a · b) and “Lukasiewicz t-norm” (=max (0, a + b − 1)). Their corresponding dual operations can be used for disjunctive fusion. They are “max” (=max (a,b)), “probabilistic sum” (=a +b − (a·b)) and “Lukasiewicz t-conorm” (min(1, a + b)).

As explained by Dubois and Prade (2004; 1994, 2001), conjunction can be operationalized as “product” if and only if the sources of information are independent of each other, and that there is no common background or communication between them what so ever. Otherwise unjustified reinforcement of possibility may happen upon multiplication. Similarly, to use the “Lukasiewicz t-norm” one needs to make a drastic assumption that some of the sources are lying; in case of a two source operation, one of them is lying on purpose. On the other hand, the “min” operation corresponds to a purely logical view of the combination process and assumes that the source which assigns the least possibility degree to a given value is the best-informed with respect to this value. No reinforcement effect comes into play due to the idempotence of “min” operations. Considering these conditions, this article will follow the logic behind the “min” (and hence “max”) operation.

Hence, for the purpose of information fusion during data gathering stage of LCA, the possibility distributions (π 1, π 2, π 3,…., π n ) on Ω can be merged either conjunctively (π cm) or disjunctively (π dm) as:

$$ \begin{array}{l}{\pi}_{\mathrm{cm}}\ \left(\omega \right)={ \min}_i{\pi}_i\ \left(\omega \right)\hfill \\ {}{\pi}_{\mathrm{dm}}\ \left(\omega \right)={ \max}_i{\pi}_i\ \left(\omega \right)\hfill \end{array} $$
(5)

Upon conjunctive combination of intervals, the result may become subnormalized, i.e., it may happen that the real value may lie outside the conjunction. This is more likely to happen when the overlap between the intervals is not significant and the sources are in conflict. Normalization of the resulting conjunct interval can be achieved by dividing it by the consistency measure of information, i.e., dividing by the measure of overlap (Dubois and Prade 1994). When the information is available as intervals, it can be presented in triangular form as in Fig. 1, and the measure of consistency is the height of the intersection (h) of the overlap between the two triangles. Thus:

$$ \begin{array}{ll}\forall \omega \in \varOmega, \hfill & \pi\ \left(\omega \right)=\frac{\pi_{cm}\left(\omega \right)}{h\ \left({\pi}_1,{\pi}_2\right)}\hfill \end{array}\kern0.5em $$
(6)

In Eq. (6), “h (π 1, π 2)” is natural measure of overlap between the two possibility distributions. It is called the consistency index. Graphically, it is the height of intersection of π 1 and π 2 as can be seen in Fig. 2

Fig. 2
figure 2

Graphical presentation of possibility distribution of data in Table 1. The stacked columns represent possibility intervals on the Y-axis for their corresponding GW intervals on the X-axis

Full size image
$$ h\left({\pi}_{1,}{\pi}_2\right)={ \sup}_{\omega \in \varOmega }\ \left({\pi}_{cm}\left(\omega \right)\right) $$
(7)

Thus normalization focuses on the agreed upon values. But it is also important to keep track of the conflict. This is done by discounting the conjunctive fusion by the weight of inconsistency, which is defined as 1 − h (π 1, π 2). This represents the degree of possibility that both sources are wrong, and mirrors the argument that both sources are supposed to be right under normalization, i.e., when h (π 1, π 2) = 1. However, the available pieces of information may not be clear candidates for conjunctive or disjunctive fusion. This more general case is formalized by Dubois and Prade (1994) in an adaptive fusion rule (Eq. (8)) where neither conjunction nor disjunction presents a suitable option for information fusion and both need to be cooperationalized in order to retain the consist information while not losing the sight of conflict. Equation (8) presents the adaptive fusion of two possibility distributions (π 1, π 2).

$$ \begin{array}{c}\omega \in \kern0.75em \varOmega, \pi \left(\omega \right)= \max \left(\frac{\left. \min \Big({\pi}_1\left(\omega \right),\kern0.5em {\pi}_2\left(\omega \right)\right)\ }{h\kern0.5em \left({\pi}_1,{\pi}_2\right)}\kern0.5em ,\right.\\ {}\left. \min, \left( \max \left(\right({\pi}_1\left(\omega \right),{\pi}_2\left(\omega \right)\right),,,1,-,h,\left({\pi}_1,{\pi}_2\right),\Big)\right)\end{array} $$
(8)

Dubois and Prade (1994) extend this formalization to the fusion of πi with i = 1,…n. It is represented in Eq. 9 with π cm, π dm following the definition in Eq. (5) and h cm following Eq. (6).

$$ \omega \in \kern0.75em \Omega, \kern1em \pi \left(\omega \right)= \max \left(\frac{\pi_{cm}\left(\omega \right)}{h_{cm}}\kern0.5em ,\kern1em \min \left({\uppi}_{\mathrm{dm}}\left(\upomega \right),1-{h}_{cm}\right)\right) $$
(9)

3 Information fusion in LCAs

In this section, we will illustrate how the theoretical framework presented in earlier section can be applied to an LCA study. Consider an LCA an electronic product with one or more semiconductor devices. Semiconductor industry is one of the largest end users of energy (Gopalakrishnan et al. 2010) and, going by the EPA requirement of semiconductor manufacturers’ mandatory greenhouse gas (GHG) reporting (EPA 2013), their GHG emissions is of concern.

On this background, we will illustrate how using information fusion at data gathering stage can refine the global warming indicator result of a semiconductor CMOS (Complementary metal–oxide–semiconductor) wafer fabrication. By industry convention, the wafer is assumed to be ready with the printed CMOS devices. Hence, this process is also alternatively refereed as CMOS device fabrication. A running example of manufacturing energy requirement is used to show the operations with numerical values. This example however, does not allow the demonstration of fusing linguistic opinion-set information. For this reason, we will resort to a very likely situation faced by a practitioner performing a nano-electronics LCA of estimating nanomaterial’s fate and transport. Here, hypothetical opinion sets on the fate and transport of manufactured nanomaterial will be fused to generate a robust possibility distribution of the material’s fate and transport pathways. The below four subsections represent four most common situations faced at the data gathering stage.

3.1 Case 1—two data-points available

We start with the two extreme CMOS device manufacturing energy requirement data points found in the literature: 0.8 E + 04 kWh/m2 (ITRS 2001–5) and 2.5 E + 04 kWh/m2 (Yao et al. 2004). Without further information, the mid-point, i.e., 1.65 kWh/cm2, can be considered as the most likely value (Tan 2008). Based on Eq. (1), this information can be modeled as the fuzzy triangular set with the α-cuts representing the possibility distribution as:

$$ \alpha =\left\{\begin{array}{cc}\hfill \frac{x-0.8}{1.65-0.8},\hfill & \hfill 0.8\le x<1.65\hfill \\ {}\hfill 1,\hfill & \hfill x=1.65\hfill \\ {}\hfill \frac{2.5-x}{2.5-1.65},\hfill & \hfill 2.5\ge x>1.65\hfill \\ {}\hfill 0,\hfill & \hfill \mathrm{otherwise}\hfill \end{array}\right. $$

The possibility distribution for a given number within the range 0.8 to 2.5 E + 04 kWh/m2 can be calculated from this setup. These numbers and their corresponding global warming (GW) impact using TRACI 2 characterization factors are provided in Table 1. As can be seen from Fig. 2, possibility distribution corresponding to the data in Table 1can be thus visualized as a set of nested intervals.

Table 1 Possibility distribution of GW due to CMOS wafer fabrication based on two data points
Full size table

3.2 Case 2: information available as intervals that are not nested

When the information is available from disparate sources and in multiple intervals, it may not be so nicely nested. For CMOS device fabrication, the literature also provides three intervals: 0.8 to 1.4 E + 04 kWh/m2 (ITRS 2001–5), 1.2 to 1.6 E + 04 kWh/m2 adjusted value based on a 150-mm wafer (Schischke et al. 2001), and 1.4 to 1.6 E + 04 kWh/m2 adjusted value based on a 200-mm (Ciceri et al. 2010). In this group, since the third interval can be viewed as a subset of the second one, it will suffice to fuse information from the first two intervals.

In order to use Eq. 8 for this task, we need to find the values of h, which in fact is the common intersection of the two triangular distributions represented by the two intervals. Setting common point α = h in Eq. (1) for both the intervals, we get h = 0.4, and (1 − h) = 0.6. Graphically, this is the height of the intersection of the two triangular distributions as illustrated in Fig. 2, which also depicts the resulting fused possibility distribution.

Representative calculations behind Fig. 3 can be seen in Table 2. The second-to-the-last column of π(ω) corresponds to the fused distribution, with the last column providing respective GW information.

Fig. 3
figure 3

Fusion of distributions π1 and π2, according to Eq. (8). Calculations in Table 1

Full size image
Table 2 Calculations for fused possibility distribution of energy requirement for CMOS wafer and corresponding GW
Full size table

3.3 Case 3: multiple values available from various sources

Often, the information on inputs and outputs used to connect to LCI may be available as multiple point estimates. In these situations, a possibility estimation π can be assigned to these values by the experts. Since possibilities can be postulated as belief functions or likelihood functions (Shafer 1987; Dubois et al. 1995), they can be synthesized with the help of same set of equations as the previous example.

Continuing with the wafer manufacturing energy example, literature offers some more data points as provided in the three right columns of Table 3. Without loss of generality, we can assume that four experts (E) express their confidence λ i on these numbers being the true value. These numbers are the first four columns in Table 3. As this table indicates, these expert opinions are not nested, nor is there any one row that clearly has λ values higher than the other rows for the corresponding columns. In other words, these beliefs are conflicting. To fuse this information, we need to use Eq. (8). As the first step, using Eqs. (4) and (5), π cm is the minimum of λ i s for a given ω, and π dm is the maximum of λ i s for a given ω. Thus h = 0.8 and (1 − h) = 0.2. Putting these values in the Eq. (8), we get Table 4 of fused possibility distribution.

Table 3 Expert belief λ on the given ω that it represents the true value
Full size table
Table 4 Calculations for possibility distribution for the energy estimate for wafer fabrication based on the fusion three intervals and four point estimates coming from heterogeneous sources
Full size table

The data quality difference between individual point estimates and fused information is reflected in the impact assessment presented in the last row of Table 4. Due to linear relationship, the possibility distribution of energy requirement maps exactly to that of respective GW impact values. Putting these numbers in the context of US annual per capita (Kim et al. 2013), the most and the least possible normalized global warming potential (GWP) will also differ from the most possible range of 0.37–0.44 to the least possible value of 0.84. This may be a big difference depending on the objective of the LCA.

3.4 Case 4: information available as linguistic propositions

The procedure for fusion similar when information is available as sets of linguistic propositions (Dubois and Prade 2004). Consider an LCA on the product enabled by an ENM, such as a T-shirt or a pair of socks with nanosilver or sport equipment with carbon nanotubes. In these assessments, the amount of ENM released at various stages of life cycle, their physicochemical characteristic upon release and their chances of being biologically available are often the questions of interest in order to populate the LCI. Often, some of these conditions either co-exist or contradict, and opinions may differ as to which combination of conditions is likely to occur. Even when numerical data are not available, a situation like this can be formulated qualitatively in the setting of possibility theory. Without loss of generality, consider a few simplistic LCI-relevant propositions on which some expert opinions on fate and transport at manufacturing of the ENM could be gathered:

  1. ω1

    The ENM likely to release to air, quantity likely to be above the safety level

  2. ω2

    The ENM likely to release to water and soil, quantity likely to be above the safety level

  3. ω3

    The ENM likely to release to soil, quantity likely to be below the safety level

  4. ω4

    The ENM likely not to release to air

  5. ω5

    The ENM likely to release to water, quantity below the safety level

  6. ω6

    The ENM likely not to release to soil

There will be numerous subsets from various permutations and combinations of these opinions, and it can be assumed that the experts will be able to put their beliefs on at least some of them. Without loss of generality, it can be assumed that three experts (E) provided their beliefs (λ) on some of the subsets of ω i ’s as below:

  1. E1

    {({ω1, ω5}, 0.3), ({ω1, ω2}, 0.5) ({ω1, ω6, ω5}, 0.6)}

  2. E2

    {({ω4, ω5}, 0.7), ({ω4}, 0.9), ({ω6, ω4}, 0.8), ({ω6, ω4, ω4}, 0.8)}

  3. E3

    {({ω1, ω3}, 0.4), ({ω3, ω4, ω5}, 0.4) ({ω3, ω5}, 0.7)

Possibility distributions can be derived from this information by the minimum specificity principle as represented in Eqs. (3) and (4), and are provided in Table 5. Applying Eqs. (4) and (8) to the above matrix, we get Table 6, with the second-to-the-last row representing the possibility distribution, which in fact can be interpreted as fuzzy membership degrees of the linguistic propositions represented by ω1-ω6.

Table 5 Possibility distributions derived from the expert opinions (beliefs) on various subsets in the ENM example
Full size table
Table 6 Calculation for possibility distribution for fused linguistic propositions represented by ω 1–ω 6
Full size table

4 A recap on information fusion process

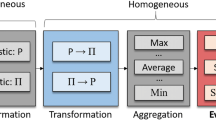
Thus, as the above discussion illustrates, a rather simple procedure can be used to merge the disparate pieces of data in order to produce a more reliable estimate of intermediate input or an elementary LCI. A crisp flowchart of using this approach to various situations is provided in Fig. 4.

Fig. 4
figure 4

A flowchart illustrating which fusion route to use and how and when in merging inadequate information

Full size image

As the flowchart illustrates, the procedure for information fusion will take slightly different routes depending on whether the data is linguistic or numerical, but once the respective route is taken, the flow of logic is similar. When the data is linguistic, the first step is to obtain associated belief values. Then, possibilities can be derived as in Table 5, and fused possibility distribution can be obtained as in Table 6.

As the flowchart further illustrates, when the data is numerical, its merger procedure is determined by whether it is available in intervals or point estimates. When the intervals are nested, the outermost bounds can be taken as minimum and maximum. This setup is similar to that explored in earlier LCA studies with fuzzy data (Ardente et al. 2004; Tan 2008; Tan et al. 2007; Chevalier and Téno 1996). When the intervals are not nested, then they can be merged to get possibility distribution by first capturing the consistency (h), and then getting the values of π cm and π dm to input in Eq. (8). The case of two non-nested intervals can be generalized to accommodate more than two intervals. Lastly, when the estimates are available in data points, the case of two data points follows the path of nested intervals and the case of multiple data points follows the path similar to that followed by linguistic data points once the belief values are obtained. Depending on whether this information is a primary LCI flow or intermediate input, it can be processed further in the LCA framework.

5 Conclusions and discussion

This paper thus demonstrates how conflicting information from multiple sources can be synthesized in LCA using information fusion technique. The technique is demonstrated for a case of electronic product LCA, and the overall procedure and decision points are elaborated using a flowchart.

The question now is when these deliberate efforts—the extra mile—toward data synthesis are justified. The answer lies in the level of representativeness required to meet the goal of the study (Weidema 2000; Frischknecht et al. 2004; Lloyd and Ries 2008; Weidema and Wesnæs 1996; Ciroth et al. 2004; ISO 2006). Two recurring topics from these discussions, namely, the need to account for—and hopefully to enhance—the quality of data used for LCAs, and the need to adherence to the ISO prescribed iteration of LCA exercise upon significant issues identification, are addressed, at least partially, by using the framework described in this article. The framework presented in this paper would be useful especially when significant issues identified are associated with conflicting data from multiple sources. The procedure described in this paper can be followed within the current framework of LCA, without requiring specialized software tool or skills beyond the understanding of basic logic.

For example, an LCA can be conducted by a practitioner in any preferred way. Upon finding a set of the most significant LCI items or intermediate input categories via sensitivity analysis, this type of fusion exercise can be performed to refine the values of the top contributing inputs, which can then be re-assessed for their impacts. Thus, with only a small additional step, the proposed method can be used to enhance the credibility of the key findings of the assessment. Alternatively, this approach can also be applied upfront only to those top intermediate input categories that are of particular interest to the stakeholders and therefore demand more representativeness. Estimation of LCIA ranges with their respective possibility information, akin to the wafer energy-GWP example above, may be highly desirable in the decision making context.

In the interest of collective retention of the individual efforts and progression toward improved data quality, it might be useful for the LCI databases to absorb fused information in a transparent manner. On that front, we hope that the LCI data entry and management software tools, such as ecoEditor, make provisions to incorporate this type of fused data in their databases. Currently, there are limited approaches available to represent merged data in a transparent manner. Such provisions not only improve the representativeness of the data derived from disparate pieces of information, but also allow others to utilize underlying information without having to re-do the exercise. We believe that using fused data, either self generated or taken from established databases, will undoubtedly enhance the representativeness of data used in LCA, thereby aiding LCA’s role as a credible decision informing tool.