Carbon price prediction under output uncertainty

Abstract

Output growth uncertainty is a key issue in climate economics, involving the full range of impacts from emissions, through temperature changes to economic damage. The current study introduces output growth uncertainty into the EZ climate model, in which the predicted global carbon emissions under output growth uncertainty are used as weighted input. The objective of the present study is to calculate the future carbon prices represented by marginal abatement cost (MAC), to maximize social welfare. Moreover, the sensitivity of the two output growth uncertainty parameters, namely population growth rate and per capita output growth rate, is analyzed. Lastly, the significance and influence of output uncertainty for carbon price are also discussed. The results exhibit that (1) the optimal prices of per ton CO₂e emission permits in the years 2020, 2030, 2060, 2080, and 2095 are $294.9, $285.3, $238.0, $143.3, and $15.4, respectively. (2) Population growth rate and per capita output growth rate both positively increase the future carbon prices, while the per capita output growth rate has a greater effect. (3) Compared with the performance under output certainty, carbon prices are estimated to be lower with output uncertainty; the high degree of uncertainty about carbon price is also primarily due to the high degree of output uncertainty. These results highlight the importance of research on output growth uncertainty, thus underpinning the EZ climate model for reducing carbon price and improving policymaking.

Introduction

On October 8, 2018, the Intergovernmental Panel on Climate Change (IPCC) issued the “IPCC Global Warming 1.5 °C Special Report,” which stated that, compared with global warming of 2 °C, a limitation to 1.5 °C is more beneficial for both human and natural ecology. To achieve the goal of controlling global warming within 1.5 °C, many countries have combined “command-and-control” regulation with “economic incentive” measures to demonstrate their determination to control carbon emissions. Among these “economic incentive” measures, carbon pricing is the most important measure. Carbon pricing follows the principle of “who pollutes pays,” by which the companies that have to 26 their emissions of carbon dioxide (CO₂) and other greenhouse gases (GHGs)¹ need to pay for carbon emission permits. There are two main types of carbon pricing: one is a government-mandated strategy, i.e., carbon tax; and the other is a market-based strategy, i.e., a carbon trading market. These two strategies are fundamentally different. Under a carbon tax policy, carbon prices are set by government, and carbon emissions are determined by market forces. Alternatively, under a carbon trading policy, the government determines the carbon emissions, and the market determines carbon prices. In the circumstance of a perfectly competitive market, carbon tax and carbon trading are equivalent, and the private marginal cost of carbon emitters will be equal to the social marginal cost at the final equilibrium state. A carbon price provides not only a benchmark for the initial transaction of a carbon trading market but also a realistic basis for the government to formulate a reasonable carbon tax. No matter which policy is adopted, it will be vitally important to set carbon prices on a scientific basis in the future.

According to marginal cost theory, the optimal carbon price equals the marginal abatement cost (MAC) in a perfectly competitive market (Tang et al. 2020; Ji et al. 2018; Lockwood 2010). Also, MAC refers to the economic cost of reducing one unit of carbon dioxide equivalent (CO₂e) emissions at a certain emission level (Yang et al. 2019). There are three approaches that can be used to evaluate MAC. Firstly, the expert-based evaluation approach is to acquire expert knowledge on abatement costs and the potentials of different technologies across various industries. For example, this approach was used by Jackson (1991), Naucler and Enkvist (2009), Moran et al. (2011), and Vogt-Schilb et al. (2018). Although expert-based evaluations are easy to understand, they have not been widely applied, due to a lack of objectivity. Secondly, MAC is also able to be calculated via a distance function, to estimate past and present values based on historical data (Ma et al. 2019). For example, this approach was used by Hailu and Ma (2017), Ma and Hailu (2016), Wang et al. (2017), and Wu et al. (2019). However, these historical observations do not allow an assessment of future MAC. Thirdly, the “model-derived” approach involves estimating optimal abatement costs in the future via integrated assessment models (IAMs), which integrate energy systems, economic systems, and climate science into a framework to assess the impact of climate policies or climate change (Hare et al. 2018). Typically, IAMs mainly include DICE (dynamic integrated model of climate and the economy) (Nordhaus 2014, 2017), RICE (regional integrated model of climate and the economy) (Nordhaus and Yang 1996), FUND (climate framework for uncertainty, negotiation, and distribution) (Tol 1997), MERGE (model for evaluating regional and global effects of greenhouse gas reduction policies) (Manne and Richels 2005), the EZ climate model (Daniel et al. 2019), CEEPA (China energy and environmental policy analysis) (Tang et al. 2020), EPPA (emissions prediction and policy analysis) (Paltsev et al. 2005), and PAGE (policy analysis of greenhouse effect) (Hope 2011). The interaction between climate change and global economy is highly uncertain, and the quantitative analysis of future optimal MAC under uncertain conditions requires a recursive dynamic programming by IAMs (Traeger 2014). Therefore, this study chooses IAMs to predict future carbon prices given by MACs, via selecting optimal emission reduction rates.

When dealing with global climate change, the existence of uncertainty is vitally important in the decision-making process. These uncertainties could include those related to climate science, social economy, and basic technological driving factors (Berger and Marinacci 2020). There are two major sources of uncertainty, “model uncertainty” and “parameter uncertainty” (Gillingham et al. 2015). Model uncertainty refers to uncertainty regarding the functional form of the equations in the IAMs, as well as which equation can better reflect the underlying mechanism. It mainly includes the uncertainty of the utility function or the climate damage function. The following research summarized the main studies on model uncertainty: Ackerman et al. (2013) used the Epstein-Zin utility function to replace the constant relative risk aversion (CRRA) utility function in the DICE model. The study showed that the social cost of carbon is higher under the Epstein-Zin utility function and that the optimal emission reduction is even higher. Weitzman (2010) analyzed the impact of additive and multiplicative damage functions on economic policies and found that the uncertainty of the damage function form can significantly affect carbon tax. Drouet et al. (2015) summarized available information on the aggregate damage of global warming from the IPCC fifth assessment report. The study used 20 estimates of aggregate economic effects of climate change to fit three different damage functions (i.e., the quadratic, exponential, and sixth damage function). Parameter uncertainty refers to using Monte Carlo simulation to shed light on how uncertainty propagates through a model to output variables of interest. Uncertainty parameters mainly include population growth rate, per capita output growth rate, climate sensitivity, tipping point temperature, and discount rate. Gillingham et al. (2015) explored the uncertainty of three important parameters, namely population growth rate, per capita output growth rate, and equilibrium climate sensitivity, on key output variables of climate change based on six IAMs (i.e., DICE, GCAM, MERGE, FUND, IGSM, and WITCH). Nordhaus (2018) investigated the impact of the uncertainties of five important parameters for climate change (i.e., equilibrium climate sensitivity, productivity growth, coefficients of damage function, coefficients of carbon cycle equation, and the decarbonization rate) on the key output variables (i.e., CO₂ concentrations, temperature increases, damages, and the social cost of carbon) based on the DICE-2016R2 model. Greenstone et al. (2013) evaluated the impacts of two uncertainty parameters, namely equilibrium climate sensitivity and discount rate, on estimating the social cost of carbon using DICE, PAGE, and FUND models. Lemoine and Traeger (2014) integrated tipping point temperature into the DICE-2007 model and showed that it increases the optimal carbon tax. Anderson et al. (2014), guided by the well-known DICE model, evaluated the impact of all uncertain parameters and underscored that discount rate is the most influential parameter. The uncertainty of parameters and models has also been simultaneously considered in some studies. For example, Ackerman and Stanton (2012) used the DICE model to estimate the social cost of carbon from 2010 to 2050, using a combination of climate sensitivity, discount rate, and four damage functions. Berger and Marinacci (2020) analyzed the uncertainty of carbon climate response, connecting carbon emissions to temperature rises. The study also analyzed the uncertainty of the damage function, connecting temperature rises to economic losses.

In summary, existing uncertainty studies have mainly focused on analyzing the uncertainty of models or parameters in the relationship between carbon emissions and temperature rises, as well as temperature rises and economic losses. Only Gillingham et al. (2015) and Nordhaus (2018) considered the impact of output uncertainty. As is well known, output growth uncertainty is a key parameter in climate economics, influencing the whole process of climate change, from emissions to temperature changes to damages (Nordhaus 2008).

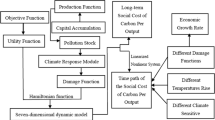
Based on the summaries above, this paper discusses the impact of output growth uncertainty on future carbon prices. Wei et al. (2013) classified IAMs into optimization models, computable general equilibrium models, and simulation models. The optimization models of IAMs mainly use the CRRA utility function, which assumes that intertemporal substitution elasticity and relative risk aversion are reciprocal to each other. However, it is not consistent with empirical rule, but the Epstein-Zin utility function can overcome this defect. Therefore, the current study uses the EZ climate model with Epstein-Zin utility function (Daniel et al. 2019), which focuses on two key output growth parameters: population growth rate and per capita output growth rate. With the goal of maximizing social welfare, the paper emulates carbon price, represented by MAC, based on the future global uncontrolled carbon emission data. Furthermore, we analyze the sensitivity of carbon price for two output uncertainty parameters, namely population growth rate and per capita output growth rate. Lastly, the different impacts between “with output uncertainty” and “without output uncertainty” are compared. The results show that (1) in the base-case calibration, the expected carbon prices of five emission reduction decision time points (2020, 2030, 2060, 2080, and 2095) are $294.9/tCO₂e, $285.3/tCO₂e, $238.0/tCO₂e, $143.3/tCO₂e, and $15.4/tCO₂e, respectively. In parallel, the corresponding average mitigation rates are calculated as 0%, 97%, 122%, 126%, and 116%, respectively. Comparison with the 1.5℃ temperature control policy, carbon prices and average mitigation rates, respectively, are both lower, except in 2095. (2) Both population growth rate and per capita output growth rate will positively increase future carbon prices, while per capita output growth rate has a greater effect. (3) Compared with considering output uncertainty, carbon prices are overestimated in the scenario without output uncertainty; the high carbon price uncertainty is also primarily due to the high output uncertainty. Figure 1 shows a schematic illustration of the EZ climate model under output uncertainty.

Fig. 1

Schematic illustration of the EZ climate model under output uncertainty. Dark yellow = endogenous (determined by the model); black = exogenous (an input to the model); red = control input. The blue arrows correspond to the purely economic component of the model. The yellow arrows illustrate the effect of the climate component. The green and dark green arrows indicate how economy impacts climate and vice versa. The black dotted arrows represent the influence of the control variable in the model

Next, “Theoretical model” section introduces our theoretical model, which includes utility function, global output equation, geophysical equation, abatement cost function, and climate damage function. “Results and discussions” section presents results and discussions, mainly including optimal carbon prices across decades and average mitigation up to a particular time point in the base-case calibration (i.e., optimal economic policy) and 1.5℃ temperature limit policy. We also discuss the impact of population growth rate and per capita output growth rate for carbon prices and compare simulated results of the EZ climate model with and without output uncertainty in this section. “Conclusions” section summarizes the conclusions of this paper.

Theoretical model

The EZ climate model adopts the Epstein-Zin utility function, in which the current utility depends on the indefinite future. Thus, the key outputs of the climate model are represented by a binomial tree structure. Figure 2 shows the model tree structure; the lines connecting “boxes” indicate the paths related to the information of Earth’s fragility, ${\theta }_{t}$. The five “red boxes” in 2100 represent the five states of nature, or nodes. Therefore, the variable ${\theta }_{t}$ also represents all states of nature in period t. The fragility or climate damage of each node in each period is increasing from bottom to top. We divide infinite time into six periods of (2020, 2030), (2030, 2060), (2060, 2080), (2080, 2095), (2095, 2100), and (2100, + ∞) with five-year time steps. Period zero runs from 2020 through 2030. In 2030, the representative agent learns in which state the world is, i.e. state up (“u”) or state down (“d”). Similarly, the representative agent learns whether the world is in state “uu,” “ud” (i.e., “du”), or “dd” in 2060. The beginning of period t, t = 0, 1, 2, 3, 4, corresponds to 2020, 2030, 2060, 2080, and 2095, respectively, i.e., the five emission reduction decision times. At emission reduction decision time t, there are t + 1 nodes. The probability from one node in period t-1 to each of two nodes in period t is 50%. At each node in the binomial tree, more information about ${\theta }_{t}$ and the resulting climate damage is revealed before uncertainty is resolved in 2095. Until 2100 (T = 5), the representative agent no longer mitigates. Therefore, there will be the same number of nodes in 2100 and 2095, and a “2 ^T-1” dimensional optimization problem is created in essence. From 2100 to infinity, gross output continues to grow at the output growth rate of 2100. The EZ climate model makes a tradeoff between current consumption and future damage; thus, the key forecast result is the carbon price under the cost–benefit approach of the optimal economic policy. All prices in this paper are in 2015 international dollars (purchasing power parity corrected).

Fig. 2

Diagram of tree structure used in solving the model for each state of nature across time

Utility function

Assume that, in an economy with a single representative agent, the goal of this representative agent is to maximize social welfare at each time t, $t\epsilon \left[0,T\right]$. The Epstein-Zin utility function is given by: ${U}_{t}={\left[\left(1-\beta \right){C}_{t}^{\rho }+\beta {({E}_{t}\left[{{U}_{t+1}}^{\alpha }\right])}^{\frac{\rho }{\alpha }}\right]}^{\frac{1}{\rho }}$, where ${E}_{t}$ is the predicted value of period t + 1 based on the information of period t, $(1-\beta )/\beta$ is the time preference rate, $1/(1-\rho )$ is the elasticity of intertemporal substitution, and $1-\alpha$ is the relative risk aversion coefficient.

Global output equation

In the EZ climate model, the authors assume no uncertainty about future output growth. Gollier (2021) has shown that the absence of output growth uncertainty leads to a relatively high initial carbon price, with a significantly negative carbon price growth trend. Therefore, in this paper, the authors incorporate realistic output growth uncertainty into the EZ climate model. The gross output in period t is the gross output in period t-1 times the output growth rate in period t: $\bar{{Y }_{t}}={\bar{Y} }_{t-1}(1+{r}_{\bar{{Y }_{t}}})$. Here, the parameter ${r}_{\bar{{Y }_{t}}}$ is the annual output growth rate, which represents the output uncertainty parameter.

The net output is the gross output reduced by both abatement costs and damages:

$$\left.\begin{array}{c}{Y}_{0}={\bar{Y} }_{0}\left[1-{k}_{0}\left({x}_{0}\right)\right]\\ {Y}_{t}=\bar{{Y }_{t}}\left[1-{k}_{t}\left({x}_{t}\right)\right]\left[1-{D}_{t}\left({CRF}_{t},{\theta }_{t}\right)\right], t\epsilon \left[1,T-1\right]\\ {Y}_{T}={\bar{Y} }_{T}\left[1-{D}_{T}\left({CRF}_{T},{\theta }_{T}\right)\right]\end{array}\right\}$$

(1)

In Eq. (1), the abatement cost function ${k}_{t}\left({x}_{t}\right)$ captures the fraction of gross output that is spent to reduce climate impact; ${x}_{t}$ is the CO₂e emissions reduction rate. The climate damage function ${D}_{t}\left({CRF}_{t},{\theta }_{t}\right)$ captures the fraction of gross output that is lost because of the damage caused by climate change. The variable ${CRF}_{t}$ is defined as the cumulative radiative forcing of CO₂e in the atmosphere until time t,² which determines the global temperature increase.

When the economy is at equilibrium, net output equals consumption plus investment: ${Y}_{t}={C}_{t}+{I}_{t}$, where ${I}_{t}=s{Y}_{t}$, s is the saving rate.

Geophysical equation

Actual CO₂e emission is given by ${E}_{t}={\bar{E} }_{t}\left(1-{x}_{t}\right)$. In this specification, ${\bar{E} }_{t}$ is uncontrolled CO₂e emission with ${\bar{E} }_{t}=\frac{{\sigma }_{t}{\bar{Y} }_{t}+{E}_{Lt}}{\bar{X} }$; ${\sigma }_{t}$ is the carbon intensity³ with ${\sigma }_{t}={\sigma }_{0}{(1-{\bar{\delta }}_{1})}^{t}$,${\bar{\delta }}_{1}$ is the annual decline rate of carbon intensity, and ${\sigma }_{t}\bar{{Y }_{t}}$ represents industrial CO₂ emissions. Then, ${E}_{Lt}$ represents land-use CO₂ emissions with ${E}_{Lt}={E}_{L0}{\left(1-{\bar{\delta }}_{2}\right)}^{t}$, and ${\bar{\delta }}_{2}$ is the annual CO₂ emission decline rate caused by land-use changes, and $\bar{X }$ is the share of CO₂ emissions in CO₂e emissions. It is assumed that $\bar{X }$ does not change over time. As every 7.77 GtCO₂e emissions cause CO₂e concentrations in the atmosphere to increase by 1 ppm, emissions are converted into concentrations (Forest 2017).

According to Daniel et al. (2019), average mitigation rate from 0 up to a particular time t is given by ${X}_{t}=\frac{\sum_{s=0}^{t}{{\bar{E} }_{s}x}_{s}}{\sum_{s=0}^{t}{\bar{E} }_{s}}$; carbon sink in a five-year interval is given by $CS={a}_{0}{\left|{CO}_{2}e-\left({a}_{1}+{a}_{2}\times CCS\right)\right|}^{{a}_{3}}$; the relationship between CO₂e concentration and radiative forcing is shown in Eq. (2):

$$RF\left({CO}_{2}e\right)=\frac{\log(\frac{{CO}_{2}e}{ {CO}_{2-pre}})}{log(2)}RF(2{CO}_{2})$$

(2)

where CO₂e represents CO₂e concentration in the atmosphere, $RF\left({CO}_{2}e\right)$ is the change of total radiative forcing of CO₂e since 1750, ${CO}_{2-pre}$ is the atmospheric CO₂ concentration in 1750, and $RF(2{CO}_{2})$ is the radiative forcing of twice-preindustrial CO₂ concentration.

Abatement cost function

Abatement cost in traditional emission reduction technology

When $0<{x}_{t}<{x}_{t}^{0}$, the functional form of MAC, which is used by Daniel et al. (2019), is ${K}_{t}({x}_{t})=314.32{x}_{t}^{2.413}$ in traditional emission reduction technologies. Modifying the formula of the fraction of endowment consumption that is spent to reduce climate impact in the EZ climate model, we recalculated that the fraction of gross output that is spent to reduce climate impact in Eq. (1) is:

$${k}_{t}\left({x}_{t}\right)={\sigma }_{t}\times 92.08{x}_{t}^{3.413}{(1-g)}^{t}$$

(3)

where ${x}_{t}^{0}$ is the maximum emission reduction rate in traditional emission reduction technologies, and g is the decline rate of total abatement cost, i.e., with emission reduction technology change, the abatement cost decreases.

Abatement cost in backstop technology

Backstop technology, which is a general harmless zero-carbon emission energy technology, is introduced into the EZ climate model, examples are solar power generation and carbon-absorbing trees. The existence of backstop technology makes ${x}_{t}>1$ possible. In backstop technology, the marginal cost of the first removed ton of CO₂e from the atmosphere is ${\tau }^{\ast}$, and the marginal cost of removing unlimited CO₂e from the atmosphere is $\tilde{\tau }$, with $\tilde{\tau }\ge {\tau }^{\ast}$. According to Daniel et al. (2019), MAC, under backstop technology, is built in the form of the following equation: ${K}_{t}\left({x}_{t}\right)=\tilde{\tau }-{(\frac{k}{{x}_{t}})}^{\frac{1}{b}}$, where $k={x}_{t}^{0}{(\tilde{\tau }-{\tau }^{\ast})}^{b}$, $b=\frac{\tilde{\tau }-{\tau }^{\ast}}{2.413{\tau }^{\ast}}$.

When ${x}_{t}\ge {x}_{t}^{0}$, the fraction of gross output that is spent to reduce climate impact in Eq. (1) is recalculated. The function form is shown in Eq. (4):

$${k}_{t}\left({x}_{t}\right)={\sigma}_{t}\left\{92.08{\left({x}_{t}^{0}\right)}^{3.413}+\left[\tilde{\tau}\left({x}_{t}-{x}_{t}^{0}\right)-\frac{b{\left(\frac{k}{{x}_{t}}\right)}^{\frac{1}{b}}{x}_{t}}{b-1}+\frac{b{\left(\frac{k}{{x}_{t}^{0}}\right)}^{\frac{1}{b}} {x}_{t}^{0}}{b-1}\right]\right\}{\left(1-g\right)}^{t}$$

(4)

Climate damage function

In this section, the damage in each state of nature in period t, ${D}_{t}\left({CRF}_{t},{\theta }_{t}\right)$, is derived in two steps. Damage depends on the full economic-climate-economic chain, from gross output to emission to concentration to CRF to temperature increase, and finally, from temperature increase to gross output loss through a damage function. Therefore, damage is a function of temperature increase $\Delta {T}_{t}$, which, in turn, is a function of CRF. Climate damage is divided into a non-catastrophic damage component and a catastrophic damage component. Non-catastrophic damage refers to the monetized value of the economic loss from temperature increases that result from CO₂e emission. Catastrophic damage represents the net impact that is irreversible when the temperature increase hits the “tipping point,” which is difficult to monetize.

Climate sensitivity

Climate sensitivity represents the temperature increase caused by the increase of atmospheric CO₂e concentration relative to the pre-industrial level (Weitzman 2009). In 2020, the global CO₂e concentration in the atmosphere reached 500 ppm, which is assumed to be the 100% emission reduction scenario. By 2100, atmospheric CO₂e concentration under output growth uncertainty is regarded as a business as usual (BAU) scenario, and it is similarly assumed that 0% emission reduction leads to a maximum BAU concentration scenario. Mitigation scenarios in any concentrations are calculated through linear interpolation or extrapolation. For example, at a BAU concentration of 1000 ppm, the emission reduction rate of 600 ppm is 80%. Considering three mitigation scenario concentrations at the end of this century—450 ppm, 650 ppm, and BAU concentration—the “median temperature increase” and “chance of > 6 °C” are calculated by linear interpolation or extrapolation, according to Wagner and Weitzman (2015). The BAU concentration is calculated in the “Results and discussions” section, and Table 1 presents the “median temperature increase” and “chance of > 6 °C” under 450 and 650 ppm.

Table 1 Median temperature increase and chance of > 6℃ at a given CO₂e concentration in 2100

Climate sensitivity shows a fat tail distribution, and the gamma distribution reflects fat tail characteristics. Based on the data of “median temperature increase” and “chance of > 6 °C” under 450, 650, and BAU concentrations, the gamma distribution is used to fit the probabilities of temperature change at the end of this century. The parameters, which are given after Monte Carlo simulations, are shown in Table 2. The gamma distribution parameters under BAU concentration are presented in the “Results and discussions” section.

Table 2 Parameters of temperature increase distribution at given CO₂e concentrations in 2100

Through the above analysis, the distribution of temperature increases at three concentration levels at the end of this century is obtained. To obtain the distribution of temperature increase in other periods, the logic of Pindyck (2012) is followed, and the time path of the temperature increase is given by: $\Delta {T}_{t}=2\Delta {T}_{H}(1-{0.5}^{\frac{t}{H}})$, where $\Delta {T}_{H}$ is the temperature increase relative to the pre-industrial-level by the end of this century, and H is a time interval from the beginning of period to the end of this century.

Non-catastrophic damage function

The non-catastrophic damage function relates $\Delta {T}_{t}$ to gross output loss. The exponential-quadratic loss function of Pindyck (2012) is used: $L(\Delta {T}_{t})={e}^{{-\beta (\Delta {T}_{t})}^{2}}$, with L(0) = 1 and L' < 0. This loss function form implies that if the temperature first increases and then decreases, gross output could return to its but-for path without permanent loss. In the absence of global warming, gross output would grow at the rate of ${r}_{\bar{{Y }_{t}}}$, but temperature rise will reduce output growth rate: ${r}_{{Y}_{t}}={r}_{\bar{{Y }_{t}}}-\gamma \Delta {T}_{t}$, according to Pindyck (2012). The parameter $\gamma$ is a key uncertainty parameter that connects $\Delta {T}_{t}$ and economic loss, which is drawn from a displaced gamma distribution with parameters ${\alpha }_{1}$, ${\beta }_{1}$, and ${\theta }_{1}$.

Catastrophic damage function

Catastrophic damage is triggered when a “tipping point” temperature is met. According to the EZ climate model, the probability of hitting a “tipping point” over a given interval of “period” is given by: $P\left(TP\right)=1-{(1-{[\frac{\Delta T\left(t\right)}{\mathrm{max}[\Delta T\left(t\right),peakT]}]}^{2})}^{\frac{period}{30}}$, where the parameter $peakT$ represents the temperature triggering catastrophic damage, and the parameter period represents the length of each period in the model.

The fraction of reduced output due to climate damage to gross output is given by:

$${D}_{t}=1-L\left(\Delta {T}_{t}\right)\left[1-{I}_{TP}\left(1-{e}^{-T{P\_}_{damage}}~~\right)\right]$$

(5)

In this specification, ${I}_{TP}$ is an indicator variable, and ${I}_{TP}$ = 1 when the “tipping point” is hit; otherwise, ${I}_{TP}$ = 0. Next, ${e}^{-T{P\_}_{damage}}$ is the catastrophic damage function, and $T{P\_}_{damage}$ is drawn from a gamma distribution with parameters ${\alpha }_{2}$ and ${\beta }_{2}$.

The path from mitigation scenarios to climate damage is mapped via CRF, and damage is simulated for each state of nature for each period. Firstly, based on Eq. (5), a set of 100,000 Monte Carlo simulations is run to generate a damage distribution ${D}_{t}$ for each period, for each of the three concentration levels of 450, 650, and BAU. Secondly, according to Eq. (2), CRF is calculated for three concentrations. Thirdly, the damage distribution associated with a given level of CRF is interpolated or extrapolated relative to the damage distributions associated with the CRF estimated from three concentration levels. Fourthly, ${D}_{t}$ is ordered from largest to smallest, based on ${D}_{T}$, which is the damage in period T for each of the three concentration levels. States of nature are chosen with specified probabilities to represent different percentiles of the damage distribution. For example, if the first state of nature in period t represents the results for the worst 1%, the damage coefficient of the first state of nature in period t is the average damage for the worst 1% of values for ${D}_{t}$. Fifthly, the smooth damage function ${D}_{t}\left({CRF}_{t},{\theta }_{T}\right)$ is constructed. When BAU concentration exceeds 650 ppm, a linear interpolation of damages is assumed between 650 and BAU concentration and a quadratic interpolation between 450 and 650 ppm, including a smooth pasting condition at 650 ppm; below 450 ppm, it is assumed that climate damage decays exponentially toward zero. When BAU concentration ranges between 450 and 650, a quadratic interpolation is assumed between 450 and BAU concentration; below 450 ppm, it is assumed that climate damage decays exponentially toward zero. When BAU concentration is less than 450 ppm, it is assumed that climate damage decays exponentially toward zero.

According to Daniel et al. (2019), the damage function of period t in Eq. (1) is given by: ${D}_{t}\left({CRF}_{t},{\theta }_{t}\right)={\sum }_{{\theta }_{T}}P({\theta }_{T}|{\theta }_{t}){D}_{t}({CRF}_{t},{\theta }_{T})$, where $P\left({\theta }_{T}|{\theta }_{t}\right)$ is the probability that any one node in period t can reach all states of nature in period T, and ${D}_{t}\left({CRF}_{t},{\theta }_{T}\right)$ is the damage over all final states of nature in period T reachable from any one state of nature in period t.

Results and discussions

Parameter values

This section mainly introduces the parameter values of the EZ climate model in the base case. Global output is purchasing power parity (PPP) GDP as measured by the World Bank, at US $132.65 trillion (current US$) in 2020, which is converted to US $122.85 trillion, according to constant 2015 US$. The average global saving rate is predicted by the IMF (International Monetary Fund) from 2015 to 2025; this is used as the saving rate in the base case, at a value of 0.27. Based on the annual global carbon intensity from 2010 to 2018, the carbon intensity decline rate is about 2%. The carbon intensity in 2020 is calculated based on the carbon intensity in 2018 and the annual carbon intensity decline rate. The carbon intensity in 2018 is obtained from the International Energy Agency (IEA). According to the DICE-2016R2 model, CO₂ emissions from global land use changes were 2.6 GtCO₂ in 2015, and the reduction rate of carbon emissions from land use changes every 5 years was 11.5%. Therefore, CO₂ emissions from global land use changes in 2020 are 2.3 GtCO₂, and the carbon emission reduction rate of annual land use changes is 2.41%. Olivier and Peters (2020) pointed out that, if CO₂ emissions caused by land use changes are included, CO₂ emissions accounted for 74% of CO₂e emissions in 2019. Regardless of the impact of CO₂ emissions in CO₂e emissions over time, this paper assumes that CO₂ emissions account for 74% of CO₂e emissions. According to the EZ climate model, the parameters in the carbon sink equation are: ${a}_{0}$ = 0.47418, ${a}_{1}$ = 285.6268, ${a}_{2}$ = 0.88414, and ${a}_{3}$ = 0.741547. The parameters in the Epstein-Zin utility function are time preference rate, $(1-\beta )/\beta$ = 0.005; elasticity of intertemporal substitution, $1/(1-\rho )$ = 0.9; and relative risk aversion coefficient, $1-\alpha$ = 7.0. Therefore, we get $\beta$ = 0.995, $\rho$ = -0.111, $\alpha$= -6.0; $\gamma$ is an uncertainty parameter that connects non-catastrophic damage to economic loss. Hausfather and Peters (2020) concluded that the “most likely” temperature increase at the end of this century is 3 °C. For a 3 °C temperature increase, Pindyck (2012) noted that the 17%, 50%, and 83% confidence points of temperature increase distribution at 0.5%, 1.25%, and 2% of GDP loss, respectively. Thus, the $\gamma$ values of the 17%, 50%, and 83% confidence points of temperature increase distribution are ${\gamma }_{1}$ = 0.000037, $\bar{\gamma }$ = 0.000094, and ${\gamma }_{2}$ = 0.000151, respectively. Fitting a displacement gamma distribution based on these three $\gamma$ values yields ${\alpha }_{1}$ = 2.537, ${\beta }_{1}$ = 26,518, and ${\theta }_{1}$ =  − 0.000002, respectively. The parameters of gamma distribution of catastrophic damage function are ${\alpha }_{2}$ = 1 and ${\beta }_{2}$ = 18.

The gross output growth rate is calculated by adding the population growth rate (${r}_{{N}_{t}}$) to the per capita output growth rate (${r}_{{y}_{t}}$) (Gillingham et al. 2015). The United Nations Population Division of Economic and Social Affairs classified the world population growth into four trends, based on “women’s total fertility”: low fertility, medium fertility, high fertility, and constant fertility.⁴ According to the global predicted population in 2021–2100 under the low, medium, and high fertility growth trends from the World Population Prospects 2019 Report, the annual percentage population growth rate is calculated for each of three trends. The global population growth rate of medium fertility is used for the base case calibration.

Christensen et al. (2018) used normal distribution to fit global per capita GDP growth rates for 2010–2100, estimated from expert forecasts, with a mean of 2.06 and standard deviation of 1.12. A Monte Carlo simulation was performed, based on the mean and standard deviation of the normal distribution. Then, the per capita output growth rate is obtained at each of five quantiles: the 10th, 25th, 50th, 75th, and 90th. The 50th quantile value of per capita output growth rate distribution is used for base case calibration. Other parameters originate from DICE, the EZ climate model, or references. Table 3 summarizes the value of the main parameters.

Table 3 Calibration of the model

Based on the above parameter values, the atmospheric CO₂e concentration or BAU concentration of 2100 are calculated under various population growth rates and per capita output growth rates. Table 4 presents various BAU concentrations for 2100.

Table 4 Atmospheric CO₂e concentration in 2100 (ppm)

According to Wagner and Weitzman (2015), both the “median temperature increase” and “chance of > 6 °C” are calculated under various BAU concentrations. Based on the values in Table 4, gamma distribution is used to fit the temperature increase distribution. The parameters are shown in Table 5.

Table 5 Gamma distribution parameters

Model simulation results under optimal economic policy

Based on the framework of the EZ climate model, output growth uncertainty is introduced. Using the predicted global CO₂e emission data under growth uncertainty, carbon prices and average mitigation rates are simulated in each of the five emission reduction decision times, namely 2020, 2030, 2060, 2080, and 2095, in various states of nature, as shown in Fig. 3.

Fig. 3

Optimal price per ton of CO₂e across time and states (left, unit: $) and average mitigation rates up to a particular time and state (right) in the base-case calibration (optimal economic policy)

Figure 3 shows the carbon prices for the five listed emission reduction decision times for each state of nature and the average mitigation up to a particular time and state. The binomial tree structure contains 15 states of nature. Among them, only one state of nature exists in 2020, two in 2030, three in 2060, four in 2080, and five in 2095. All grouped nodes at a given time have the same degree of fragility and the same damage for a given amount of atmospheric CO₂e concentrations. We found that there are occasionally wildly different carbon prices at the same state. For example, the carbon prices are between $0.0 and $82.7/tCO₂e at the third state of nature in 2095, which shows that carbon prices are path dependent. The average emission reduction rate of the third state reached is 132% by the “uudd” path in 2095, while via the “dduu” path, the rate is 79%. The finding reveals the reason for the sometimes wildly different carbon prices at the same node.

The expected carbon price in each emission reduction decision time is the average value of the carbon prices for each state of each emission reduction decision time. Therefore, the expected carbon prices for 2020, 2030, 2060, 2080, and 2095 are calculated as $294.9/tCO₂e, $285.3/tCO₂e, $238.0/tCO₂e, $143.3/tCO₂e, and $15.4/tCO₂e, respectively. The corresponding average mitigation rates are calculated as 0%, 97%, 122%, 126%, and 116%, respectively. The expected carbon prices in future emission reduction decision times show a gradual decreasing trend. The main reason is that the marginal abatement cost decreases gradually, in line with emission reduction technological change.

Other researchers also have examined carbon pricing schedules. In most climate models, the optimal carbon prices have risen over time, i.e., Nordhaus (2014, 2017, 2018) and Gollier (2021). In these researches, frontloading the abatement effort is equivalent to an investment that has a cost and a benefit that are equal to the present and future MAC, i.e., the present and future carbon prices. Thus, the carbon price has risen over time. However, the optimal carbon price declines over time, as the “insurance” value of mitigation declines and technological change makes emissions cuts cheaper in our model. Although these articles share the objective of exploring the role of climate change in asset pricing, the channels of influence are radically different, leading to huge differences in conclusions.

Model simulation results under 1.5℃ temperature control policy

The predicted results in the EZ climate model are emulated under the optimal economic policy. By maximizing the discounted excepted utility, finding an emission reduction trajectory can balance the current abatement cost with the future climate damage caused by global warming. Allen et al. (2009) pointed out that global efforts to mitigate climate change are guided by predictions of future temperature changes. The Paris Agreement, signed in 2015, aims to control global temperature rise at the end of this century to within 2 °C, compared with the pre-industrial temperature and then making efforts to keep the increase below 1.5 °C. Therefore, this paper further studies the impacts of limiting the global temperature rise to within 1.5 °C in this century on the predicted results of the model and compares those results with the results under conditions of an optimal economic policy. This run is similar to the optimal case, except that the 1.5 °C temperature constraint is imposed on top of the economic damage estimates. The economic intuition of a 1.5 °C temperature rise limit is that the damage value turns up sharply and then causes catastrophic damage.

The left panel of Fig. 4 shows optimal CO₂e prices under the 1.5℃ temperature control policy across time and states. The expected carbon prices for 2020, 2030, 2060, 2080, and 2095 are calculated as $349.9/tCO₂e, $330.7/tCO₂e, $285.9/tCO₂e, $195.1/tCO₂e, and $4.0/tCO₂e, respectively. Compared with the values under the optimal economic policy, carbon prices are larger in any period, except in 2095. The right panel of Fig. 4 shows the average mitigation rate under the 1.5℃ temperature control policy across time and states. The expected average mitigation rates for 2020, 2030, 2060, 2080, and 2095 are calculated as 0%, 149%, 141%, 142%, and 131%, respectively. Compared with the values under the optimal economic policy, the expected average mitigation rates are larger in any period. As can be seen, under the 1.5℃ temperature control policy, the optimal carbon prices are higher, and the optimal average mitigation rates are greater. These results show that, in order to achieve the 1.5℃ temperature constraint climate policy goal, carbon prices should be raised in future periods, and stronger emission reduction measures should be adopted.

Fig. 4

Optimal price per ton of CO₂e across time and states (left, unit: $) and average mitigation rates up to a particular time and state (right) under the 1.5 ℃ temperature control policy

To achieve the 1.5℃ temperature control target, significant efforts should be made to increase the use of clean energy, especially zero-carbon emission energy, including energy sources such as hydropower, solar energy, wind energy, and nuclear energy. When zero-carbon emission energy reaches the production capacity constraint boundary, low-carbon emission energies, such as natural gas, are used to a greater extent. Finally, for industries that cannot achieve complete decarbonization, carbon removal equipment can be installed to reduce carbon emissions.

Sensitivity analysis

This section analyzes the impact of two output uncertainty parameters—population growth rate and per capita output growth rate—on future carbon prices under an optimal economic policy. To explore the impact of output uncertainty on the model’s results, carbon prices without output uncertainty are compared with the results under output uncertainty.

Impact of population growth on carbon prices

For the population growth rate, a sensitivity analysis was conducted, based on the global population growth rate derived from low fertility, medium fertility, and high fertility, according to the World Population Prospects 2019 report. The results are shown in Fig. 5 and Table 6.

Fig. 5

Impact of population growth on carbon prices (unit: $/tCO₂e)

Table 6 Carbon price and change rate under different population growth rates

According to the data shown in Fig. 5, when other parameters remain unchanged, the population growth rate is positively correlated with the carbon prices of 2030, 2060, and 2080. The faster the population grows, the higher is the carbon price needed to offset climate change, and vice versa. The underlying mechanism is that the carbon price depends on the optimal emission reduction rate, i.e., the ratio of the optimal emission reduction amount to uncontrolled carbon emissions. Compared with medium fertility, the high fertility scenario has higher uncontrolled carbon emission. When the increased ratio of optimal emission reductions exceeds the increased ratio of uncontrolled carbon emissions, the optimal emission reduction rate increases, and the carbon price thus increases. In parallel, under the low fertility scenario, when the decreased ratio of optimal emission reduction exceeds the decreased ratio of uncontrolled carbon emission, the optimal emission reduction rate decreases, and carbon price thus decreases.

Table 6 lists the carbon prices for different years and different population growth trends. Except for a few values, such as 21.00% and − 72.73%, the absolute values of the change rate under different population growth trends are less than 15%. Therefore, population growth rate has a relatively insignificant effect on carbon prices in the future.

Impact of per capita output growth rate on carbon prices

The 10th, 25th, 50th, 75th, and 90th percentile values of per capita output growth rate forecast distribution are used for sensitivity analysis. The results are shown in Fig. 6 and Table 7.

Fig. 6

Impact of per capita output growth rate on carbon prices (unit: $/tCO₂e)

Table 7 Carbon prices and change rates under different per capita output growth rates

According to Fig. 6, and if other parameters remain unchanged, the carbon prices of 2030, 2060, and 2080 are positively correlated with per capita output growth rate. The faster the per capita output grows, the higher is the carbon price needed to offset climate change, and vice versa. Compared with the 50th percentile scenario, the uncontrolled carbon emissions are higher in the 75th and 90th percentile scenarios. When the increased ratio of optimal emission reduction exceeds the increased ratio of uncontrolled carbon emission, the optimal emission reduction rate increases, and the carbon price thus increases. Similarly, in the 10th and 25th percentile scenarios, the uncontrolled carbon emissions are lower than in the 50th percentile scenario. When the decreased ratio of optimal emission reduction exceeds that of uncontrolled carbon emission, the optimal emission reduction rate decreases, and the carbon price thus decreases.

Table 7 lists the carbon prices for different years and different per capita output growth rates. For example, the carbon prices for the year 2080 range from $55.1/tCO₂e (gdprate-10) to $214.9/tCO₂e (gdprate-90), and the change rates range from − 61.55% (gdprate-10) to 49.97% (gdprate-90). Therefore, per capita output growth rate has a significant impact on the carbon prices given by MAC.

Impact of output uncertainty on carbon prices

To explore the impact of output uncertainty on the EZ climate model results, carbon prices without output uncertainty are compared with carbon prices that consider output uncertainty. Table 8 presents the key statistical values of carbon prices for each period. The 50th percentile values of the distribution of per capita output growth rate and the medium fertility values of population growth rate are used to calculate carbon prices without output uncertainty, i.e., the “baseline value.” Using the values of each of the three population growth scenarios (i.e., low fertility, medium fertility, and high fertility) and the values of each of the five listed per capita output growth scenarios (i.e., 10th, 25th, 50th, 75th, and 90th percentiles), 15 carbon prices are calculated. Then the average value of these 15 carbon prices is calculated as carbon prices with output uncertainty. The average value of the 15 carbon prices in each period is the “mean” value in Table 8. The median of the 15 carbon prices in each period is the “50th percentile” value in Table 8.

Table 8 Key statistics of carbon price (unit: $/tCO₂e)

Table 8 shows key carbon price statistics, including the three central value measurement indicators—mean, baseline value, and 50th percentile. Comparing the carbon prices of the second and third columns in Table 8, we find that the mean values are less than the baseline values except for 2095. This finding suggests that the baseline value scenario slightly overestimates carbon prices. The mean carbon price in 2030 is $273.6/tCO₂e, while the baseline value is $285.3/tCO₂e. Thus, the carbon price without output uncertainty is overestimated by 4.3%. Table 8 also shows two uncertainty measurements, namely standard deviation and coefficient of variation. The lowest coefficient of variation is 7.9% in 2020; the coefficient then increases gradually, reaching 48.9% by 2095. These results indicate that the uncertainty of carbon prices is relatively large, which is mainly caused by the high degree of output uncertainty.

Conclusions

The current study introduces output growth uncertainty into the EZ climate model, in which the predicted global carbon emissions under output growth uncertainty are used as weighted input. The objective of the present study is to calculate the future carbon prices represented by MAC, to maximize social welfare. Moreover, the sensitivity of the two parameters of output growth uncertainty, namely population growth rate and per capita output growth rate, is analyzed. Lastly, the significance and influence of output uncertainty for carbon price are also discussed. Taken together, the study concludes the following:

Firstly, there are wildly different carbon prices at the same node in the model tree structure. For example, the carbon prices are between $0.0/tCO₂e and $82.7/tCO₂e at the third state of nature in 2095. The finding shows that carbon prices are path dependent. The average emission reduction rate of the third state reached is 132% by the “uudd” path in 2095, while via the “dduu” path, the rate is 79%. This finding reveals the reason for the sometimes wildly different carbon prices at the same node. Therefore, due to different paths reaching the same node, the average mitigation rate up to that node is different, which in turn results in huge differences in carbon prices.

Secondly, the expected carbon prices under the optimal economic policy of the five emission reduction decision times of 2020, 2030, 2060, 2080, and 2095 are $294.9/tCO₂e, $285.3/tCO₂e, $238.0/tCO₂e, $143.3/tCO₂e, and $15.4/tCO₂e, respectively. In parallel, the average mitigation rates are calculated as 0%, 97%, 122%, 126%, and 116%, respectively. Compared with the 1.5℃ temperature control policy, the carbon prices and expected average mitigation rates, respectively, are both lower, except in 2095. This finding shows that both carbon prices and average emission reduction rates will rise in the future under 1.5℃ temperature policy constraints.

Thirdly, the influence of estimation of output uncertainty parameters is substantial, especially the per capita output growth rate (compared to the population growth rate). Population growth rate and per capita output growth rate both positively increased future carbon price in this study, which manifests the finding that the faster the population or per capita output grows, the higher will be the carbon price needed to offset climate change, and vice versa.

Fourthly, compared with output certainty, carbon prices are estimated to be lower with output uncertainty. For example, the carbon price in 2030 is $273.6/tCO₂e under output uncertainty, while the price is $285.3/tCO₂e under output certainty. Based on the coefficient of variation, carbon prices are found to be uncertain. The high uncertainty related to carbon price is primarily due to the high degree of output uncertainty.