Strain Rate Dependent Compressive Response of Open Cell Polyurethane Foam

Abstract

Polymeric foams are used for impact protection due to their ability to absorb large amounts of strain energy. In this work, the compressive response of an open cell polyurethane foam currently used as liner in the advanced combat helmet is examined across strain rates. A traditional load frame is used to investigate the quasi-static behavior, and two different modifications of a conventional Kolsky (split-Hopkinson) bar configuration are used to probe the dynamic response. A unique, independent method not relying on strain gage signals is presented that leverages high-speed full-field imaging to track the velocity on each side of the sample-bar interface and used to extract the dynamic stress-strain response; the results are compared against traditional strain gage measurements. X-ray tomography is used to examine the global morphological characteristics of the foam. The foam is found to be strongly rate dependent, where the characteristic properties vary logarithmically with strain rate. An analytical expression is presented to describe the rate dependency that collapses all stress-strain curves on a master curve. Full-field kinematic data from digital image correlation taken during loading is used to extract a nonlinear Poisson’s ratio as a function of strain, which is found to be strain rate insensitive. A tangent Poisson function is used to explore the foam’s auxetic behavior. These findings provide insight on physically-based constitutive modeling of foams, crucial to predictive brain injury simulations, as well as motivate the need to probe local heterogenous behavior across strain rates moving forward.

Introduction

The characteristic stress-strain response of cellular solids under compression makes them particularly suited for energy absorption applications [1]. Namely, this material class can convert large amounts of kinetic energy to strain energy during deformation and typicaly have three regimes of deformation under compressive load. Upon initial compression, a generally linear elastic region in the stress-strain response is exhibited, followed by a plateau region where a further increase in strain maintains a relatively constant, but potentially nonlinear stress response, and a densification regime where the stress rapidly increases with further incremental strain [2]. Cellular solids consist of two phases, a base solid material and fluid-filled cellular pore structures. The nonlinear response under compressive loading is dictated by the mesoscale morphological cellular structures. The base material of polymeric cellular solids, e.g. polyurethane foams, is viscoelastic, which manifests as strain rate dependent behavior [3, 4]. Identification of the rate dependent response of such materials can only be achieved through experiments. At the same time, knowledge of material viscoelastic response under a range of relevant loading rates is less studied, yet relevant to predictive computational capabilities [5,6,7,8]. Consequently, it is crucial to experimentally investigate the mechanical response of cellular solids under both quasi-static and high strain rate loading conditions, in order to appropriately guide constitutive models [2, 9,10,11]. In addition, probing cellular solids experimentally will elucidate physical mechanisms responsible for the rate dependent behavior of the material, leading towards physically-based, microstructurally-informed material models.

Well-controlled experiments on materials of such low density and stiffness are challenging to conduct at high rates for a number of reasons [12, 13]. It is difficult to meet the stringent assumptions that come with the traditional high-rate experimental procedures, such as the Kolsky (split-Hopkinson) pressure bar when examining low impedance materials. The analysis for the reduction of the raw data from a Kolsky experiment to useful stress-strain material response relies on two main assumptions. First, stress equilibrium must be achieved during the experiment, and second, constant strain rate should be maintained during the majority of the loading pulse. Kolsky recognized that it takes a finite amount of time for stress-state equilibrium to be reached, i.e. forces at both ends of the specimen are equal during loading. The equilibration duration is proportional to the thickness of the material and inversely proportional to its longitudinal wave speed [14]. The forces at the two specimen faces are not equal initially, and it takes a few wave transits within the sample before equilibrium is reached [15,16,17,18]. Another challenge arises due to the nature of wave reflection and transmission at an interface. A stress pulse traveling in one material and encountering an interface, i.e. a material with different properties, will partially reflect back and partially transmit through the interface. For low acoustic impedance specimens, most of the wave will be reflected back and only a small portion will transmit through the material making the quantification of the pulse from traditionally-employed strain gages difficult to achieve. Modifications of the Kolsky bar technique have been introduced which make probing the response of soft materials under high strain rates possible [12, 13, 17, 19,20,21,22,23,24,25].

A number of different studies on polymeric foam materials under high strain rate uniaxial compression have been performed. These studies include polymeric foams with different cell structures, densities, and chemical compositions [18, 21, 26,27,28,29,30,31,32,33,34,35,36,37]. The main findings of these studies share a common theme: the foams’ characteristic properties exhibit strong rate dependence. This is to be expected since the base materials of polymeric foams are viscoelastic and the rate dependency is attributed to the microstructure of the constituent material. More on the particular findings of previous literature will be discussed in the context of the results of this study in “Results & Discussion”.

Additional rate dependencies have been observed for non-polymeric foams, e.g. metallic foams [10], as well as polymeric foams beyond a certain strain rate threshold [34]. This additional rate dependency is attributed to the underlying mesoscale morphological structure of the foams [10]. One mechanism, coined “structural shock,” is due to a compaction wave creating a structural discontinuity propagating along the material [10]. This mechanism becomes active beyond a certain critical impact velocity [38]. Another mechanism for rate dependency that is specific to open cell foams is viscous dissipation as the pore fluid is forced out of the foam while the foam is compressed [2]. The viscous dissipation becomes important at high strain rates if the fluid is not highly viscous and the pores are of a larger characteristic size.

In this work, the compressive response of an open cell polyurethane foam used in defense applications is explored. The foam is manufactured by Team Wendy^®; and is currently being used as helmet liner in the US Army Advanced Combat Helmet (ACH). Its response is examined over seven orders of magnitude in strain rate. Quasi-static compression experiments using a standard load frame are compared with the dynamic compressive experiments implemented using two different Kolsky compression bar configurations; a modified aluminum bar and a polycarbonate bar setup. The foam global properties and the dependence of these properties on strain rate is quantified. in-situ full-field imaging is conducted for all compression experiments, mapping the kinematic response using digital image correlation (DIC). The value of the Poisson’s ratio is determined as a function of global axial strain, and its dependence on strain rate is explored.

Methods

An open cell polyurethane foams is explored. The foam has a commercial name Zorbium^®; and is fabricated by Team Wendy^®;. It is used to create the liners in the current ACH, a ballistic protection helmet shell. The liner consists of two foams of equal thickness and glued together when used inside the helmet. The comfort layer interfaces with the head, and the protective layer interfaces with the helmet shell and is referred to as the “hard foam”. In this study, the strain-rate dependent compressive response of the protective layer is explored. The density of the foam is 57.3 ± 0.7 kg/m³.

Microtomography

X-ray microtomography, also known as micro-CT, allows for imaging inside the volume of optically opaque materials. A 3D virtual volume, i.e. tomogram, is reconstructed digitally from hundreds of 2D image projections. For cellular materials in which two distinct phases exist, i.e. solid and gas, the morphological characteristics of the material can be qualitatively and (if further processed) quantitatively determined. The morphological structure of a material is known to influence its properties and behavior [1]. For this study, a Bruker SkyScan 1172 micro CT was used to visualize the interior structure of the foams. The source voltage was 59 kV and source current 167 μ A. A total of 1021 x-ray images were taken with a resolution of 2096 × 4000 px². The spatial resolution of the scans was 3 μ m/voxel. In recent years, there has been an ongoing effort to use 3D volumetric images to extract quantitative morphological properties of materials [39,40,41] and link them to observed material macroscopic behavior. In this case, an open source software iMorph(v3.2) [42] was used for image processing, segmentation, and analysis of the raw reconstructed image slices. The iMorph code was specifically designed for quantitative analysis of foams. In this work the quantification focused on global morphological characteristics of the foams using ct-scan imaging.

Quasi-static Compression

A Shimadzu 50 kN screw-driven load-frame (AG-IC 50 kN) was used to load the open cell polyurethane foam specimens under uniaxial compression. The foam specimens were cut by Team Wendy using steel rule die boards (much like a cookie-cutter) and a pneumatic press. The nominal dimension along the loading direction was 9 mm and the cross sectional area perpendicular to the loading direction was 30 × 30 mm². Such a low aspect ratio of the specimens was used for quasi-static experiments due to several compounding factors, such as a need to exclude any specimen size related differences between low and high strain-rate experiments, and practical issues related to sensor capabilities. The specimens were sandwiched between two stainless steel platens, as shown in Fig. 1. Molybdenum powder was applied to the platen-specimen interfaces to reduce friction. One of the platens was held fixed while the other platen moved with a constant velocity to obtain a constant nominal strain rate loading profile. The specimens were subjected to quasi-static strain rates of 2 × 10^− 4 s^− 1, 2 × 10^− 2 s^− 1, and 2 × 10^− 1 s^− 1. For an undeformed sample with nominal thickness of 9 mm, these strain rates correspond to cross-head displacement-controlled experiments under a constant velocity of 0.108 mm/min, 10.8 mm/min, and 108 mm/min, respectively. The displacement of the cross-head was tracked using a deflectometer (Epsilon 3540) and the specimens were subjected to a single compressive load up to 0.8 nominal compressive strain. The force was measured using a 50 kN load-cell, and converted to nominal stress by dividing the force magnitude with the initial undeformed specimen area, A₀, perpendicular to the loading direction. Both the load-cell and deflectometer signals were digitized and stored using a data acquisition unit (NI DAQ USB-6211) and the MatchID-Grabber software.

Fig. 1

Quasi-static loading of foam specimen using a traditional load frame. The bottom platen below the sample is fixed, while the top platen is moving at a constant predetermined velocity, v

Dynamic Compression

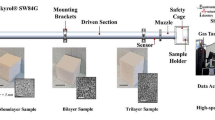
The Kolsky (split-Hopkinson) bar method was used to explore the compressive behavior of the hard foam under high strain rates, as shown schematically in Fig. 2.

Fig. 2

Schematic of a general compression Kolsky apparatus(left) Aluminum bar compression Kolsky apparatus. The foam specimen is sandwiched between two piezoelectric quartz crystals. Note that only the incident bar strain gage is used in this configuration. (right) Polycarbonate bar compression Kolsky apparatus. Both strain gages, one on each incident and transmitted bar, are utilized. Displacements of ROI 1 and 2 are measured using high-speed imaging and used to extract the stress-strain response of the specimen independently from the strain gage measurements

Principles of classic Kolsky compression bar

In a typical Kolsky compression experiment, a relatively short sample is placed between the two very long bars, the uprange incident bar and the downrange transmitted bar. A gas-gun typically fires a projectile between 5 to 30 m/s into the incident bar, sending a 1D elastic pulse down the length of the incident bar. The upper limit of the acceptable impact velocity is dictated by the yield point of the compression bars used. Upon reaching the sample, part of the wave is transmitted and part of the wave is reflected back towards the incident bar. After a few passes of the wave in the sample, it reaches a uniform loading state. With this condition met, signals of the incident, reflected and transmitted pulses measured from strain gages on the incident and transmitted bars can be used to infer the stress-strain response in the sample using 1D wave mechanics (more information can be found in [12]).

Modified Kolsky for soft materials

Polymeric foams have low acoustic impedance which makes high strain rate experiments using a conventional metallic Kolsky bar apparatus particularly challenging. The stress wave magnitude transmitted through the low acoustic impedance sample is extremely small, to the point that the signal-to-noise ratio of the strain gage instrumented on the transmitted bar is too small to be meaningfully utilized. Therefore, different modifications of the conventional Kolsky bar have been proposed in the literature to address this issue. These include a modified metallic (aluminum) Kolsky bar instrumented with quartz piezoelectric gages on each side of the sample which have three orders of magnitude higher sensitivity compared to resistive strain gages, and match the acoustic impedance of aluminum, for example [20,21,22, 43]. Another method involves a modified aluminum Kolsky bar in which the transmitted bar is hollow, which increases the transmitted signal by an order of magnitude [19]. Yet another method involves the use of lower modulus metallic bars made of magnesium [44, 45] or titanium [46] or even the use of polymeric bars with lower acoustic impedances and compliance compared to metallic bars that allow for a higher transmitted signal amplitude that can be probed using a conventional resistive strain gage. Yet polymeric bars run into potential viscoelastic stress-wave propagation effects [13]. Lastly, low impedance materials have been investigated using bars instrumented with embedded velocity gages to directly measure the velocity of the bar-specimen interface eliminating the need for viscoelastic wave propagation correction, but require specialized instrumentation to pursue [25]. In this work a new method for extracting the stress strain response of a specimen based on high-speed imaging, similar to the method introduced by Casem et al. [25] is proposed in “Novel Kolsky Data Reduction Method Using Particle Tracking” and implemented in “Stress-Strain Response: High strain rates”.

In addition to low amplitude transmitted signals, there is another challenge when performing high rate testing of foam materials. For a given bar material and geometry, there is a maximum observation time window before superposition of the incident and reflected wave at the strain gage location takes place, given by Δt = L/C, where Δt is the time duration, L is the length of the bar, and C is the longitudinal wave speed of the bar [23, 24]. Therefore, there is a limit on the maximum observable strain for a given experimental setup, $\epsilon _{max} = \dot {\epsilon } {\Delta } t$, given by the average strain rate multiplied by the maximum observation time during the experiment. For foams in particular, high compressive strains on the order of 60-80% are often necessary to explore, in order to study the transition from the plateau to the densification regime. Therefore, either the length of the bar needs to be increased or a bar material of lower wave speed needs to be used in order to increase the maximum observation time window, and consequently increase the maximum attainable strain of the Kolsky setup.

In this work two different Kolsky bar setups were utilized: a modified aluminum Kolsky bar setup with embedded quartz piezoelectric force sensors and a polycarbonate Kolsky bar setup, as shown in Fig. 2. The geometry of both Kolsky configurations used in this study were identical, each having a bar diameter of 12.7 mm, incident and transmitted bar length of 2.4 m, and a striker length 200 mm. The nominal specimen dimensions under dynamic loading conditions were 8 × 8 × 3 mm³. The thickness of the specimen along the loading direction was chosen in order to achieve stress equilibrium conditions. Specimen thickness is particularly important for achieving stress equilibrium, especially for specimens with low wave speeds [14, 17, 47]. Thinner specimens accelerate the equilibration process. In this work, specimen thickness could not be reduced below 3 mm in order to maintain a representative volume element of the cellular structure, which is at least 10 cells per characteristic thickness dimension. Moreover, pulse shapers were used for the same reason. For the aluminum bar experiments copper pulse shapers with 4 mm diameter and 0.27 mm thick were used. Whereas cardboard pulse shapers were used for the polycarbonate bar experiments that were 5 × 5 mm² and 1.2 mm thick.

Aluminum Kolsky bar

For the aluminum Kolsky bar, only the strain gage on the incident bar was used to quantify the incident and reflected strain pulses. The transmitted bar was not instrumented with a strain gage since the signal is too weak to utilize with these foams, as discussed previously. Two thin, 0.5 mm single crystal X-cut quartz discs were placed on each side of the specimen and used as a force gage. The charge produced by the two piezoelectric quartz gages was collected by copper electrodes, amplified through two charge amplifiers (Kistler 5010) that converted the signal to voltage, and read by a digital oscilloscope (LeCroy 4024). The conversion from charge to force is given by the piezoelectric constant of 2.3 pC/N. To ensure that the readings from the in-house piezoelectric force sensors are accurate the following procedure was followed for every experiment. Both sensors were checked for calibration before and after the experiment. If the sensors remained calibrated after the experiment, the experiment was deemed acceptable for further processing. If not, the experimental data were disregarded and the experiment was repeated. A typical force-time calibration curve is shown in Fig. 3 where a piezoelectric sensor is sandwiched between the incident and transmitted bar without a specimen. The force measured by the piezoelectric sensor should match the corresponding stress pulse measured by the incident and/or transmitted signal. This is a result stemming from 1D stress wave propagation considerations and given that the quartz crystal matches the impedance of the aluminum bars. The maximum observable strain with the available aluminum bar setup, 2.4 m incident and transmitted bar lengths, was 20%. Due to physical space constraints in the laboratory, the length of the aluminum Kolsky bar setup could not be further increased. Consequently, a polycarbonate Kolsky bar was utilized to explore higher strain levels of the hard foam under dynamic compression.

Fig. 3

Calibration of piezoelectric quartz sensor. Comparison between force signal measured from strain gage on the transmitted bar, F_1D, against signal from the quartz piezolectric sensor, F_quartz

Polycarbonate Kolsky bar

Polycarbonate has a lower longitudinal wave speed compared to aluminum. Therefore, by maintaining the identical bar length and only changing the bar material to polycarbonate, the maximum observable strain that can be probed increases to about 80%. This higher achievable strain allows for investigating the plateau and densification regime of the foam. Unlike aluminum bars, polymeric bars exhibit viscoelastic behavior which must be accounted for in the analysis [13]. One-dimensional waves propagating through viscoelastic media experience attenuation and dispersion. In this investigation, the method proposed by Bacon to experimentally determine the attenuation and dispersion coefficients of polymeric bars is utilized [48]. In particular, the viscoelastic propagation coefficient of the polycarbonate bars is derived experimentally, which is representative of the dispersion and attenuation of the stress pulse propagating in the bars. In order to determine this coefficient experimentally, free-end experiments on the incident and transmitted bars must be conducted separately. By using the free-end boundary condition, i.e. a traction free surface, and measuring the incident and reflected pulses at the strain gage location, the propagation coefficient γ = α + ik can be determined. This coefficient is a function of frequency. Its real part gives the attenuation coefficient, $\alpha = -\frac {ln{(r_{r}/r_{i})}}{2d}$, and its imaginary part the wavenumber, $k=-\frac {(\theta _{r} - \theta _{i})}{2d}$, where r_r and r_i are the amplitudes of the coefficients of the reflected and incident waves in the frequency domain and 𝜃_r and 𝜃_i the unwrapped phase angles of these waves. The distance that the stress wave travels during a free-end experiment is 2d, where d is the distance from the strain gage location to the free end. Once the dispersion and attenuation coefficients of the bars were determined, the incident 𝜖_i, transmitted 𝜖_t, and reflected 𝜖_r, pulses, measured at the strain gage location can be propagated correctly, i.e. accounting for the viscoelastic effects, to the specimen-bar interface at a distance d from the strain gage location, see Fig. 4. These propagated values are the ones used for the reduction of the raw signals to useful stress-strain responses. Force equilibrium can be calculated from the propagated signals using the 1- and 2-wave method[13] and shown in Fig. 4.

Fig. 4

Raw incident, reflected, and transmitted strain signals measured at the location of the strain gage, x = 0, for a characteristic experiment using the polycarbonate Kolsky bar setup (solid lines). The propagated strain signals are calculated using the experimentally determined propagation coefficient, γ, and are also shown at the bar-specimen interface, x = d₁, with dashed lines. From the propagated signals the force on the incident, F₁, and transmitted, F₂, bar interfaces are calculated and plotted

Novel Kolsky data reduction method using particle tracking

A separate, independent method for extracting the stress-strain response of the specimen using polycarbonate bars that does not utilize strain gages was also implemented. It is a unique method based on a similar method presented by Casem et al. [25], where electromagnetic velocity gages were embedded in the bars. For this study, instead of velocity gages, high-speed imaging and image processing advancements are leveraged to track the displacements of the incident and transmitted bar interfaces during loading, see Fig. 2. A global strain measure, and a global stress (for the first time to the best of the authors’ knowledge) measure can be extracted from the corresponding data by spatial and temporal differentiation of the displacement data. In particular, if u₁(t) and u₂(t) denote the incident and transmitted bar displacements as a function of time, see Fig. 2, the nominal global strain experienced by the foam specimen is given by:

$$ \epsilon(t) = \frac{u_{1}(t)-u_{2}(t)}{L_{0}}, $$

(1)

where L₀ is the initial thickness of the specimen along the loading direction, see Fig. 5a. Through temporal differentiation, denoted by an overdot in what follows, the velocity of the bar interfaces can be computed, Fig. 5d. The strain rate is then calculated by:

Fig. 5

Hard foam dynamic compression characteristic results from image tracking of the bar interfaces (5 μ s interframe time) (a) Global nominal strain, $\epsilon (t) = \frac {u_{1}(t)-u_{2}(t)}{L_{0}}$ (b) Incident bar displacement, u₁(t), and transmitted bar displacement, u₂(t) (c) Strain versus strain rate using the DIC method, $\dot {\epsilon }(t) = \frac {\dot {u_{1}}(t) - \dot {u_{2}}(t)}{L_{0}}$, compared with traditional strain gage reduction method using the reflected strain gage signal [12] (d) Incident bar velocity, $\dot {u_{1}}(t)$, and transmitted bar velocity, $\dot {u_{2}}(t)$

$$ \dot{\epsilon}(t) = \frac{\dot{u_{1}}(t) - \dot{u_{2}}(t)}{L_{0}} $$

(2)

and the stress on the transmitted bar interface can be calculated by employing the 1D conservation of momentum equation by:

$$ \sigma_{2}(t) = \rho_{b} C \frac{A_{b}}{A_{s}} \dot{u_{2}}(t) $$

(3)

where ρ_b and A_b is the density and area of the bars, A_s is the area of the specimen and $\dot {u_{2}}(t)$ is the specimen-transmitted bar interface velocity measured by image tracking, Fig. 5c and d. The advantage of this method is that there is no need to account for the attenuation and dispersion of the pulses propagating through the bars to the strain gage location, since the measurements are made directly at the bar-specimen interfaces. High-speed imaging was conducted using a Shimadzu (HPV-X1) high speed camera at 200,000 frames per second (fps). The bar interfaces were speckle-patterned and MatchID digital image correlation software was used to track the incident and transmitted bar displacements, shown in Fig. 2, as Region of Interest (ROI) 1 and 2. A characteristic example of displacement, strain, velocity and strain rate data extracted using the image tracking procedure are shown in Fig. 5. Stress is proportional to the velocity of the transmitted bar and can be extracted from the imaging data.

Full-Field Imaging and Digital Image Correlation

Imaging of the specimen surface during loading was conducted for all experiments. For the quasi-static investigations, images were captured in sync with the force and displacement data using the MatchID-Grabber software and an Allied Vision Stingray camera (2456 × 2056 px²) with a 105 mm Nikon lens. The specimen surface was lightly coated with white matte paint to enhance the contrast of the image and allow for 2D DIC analysis of the experiment. DIC is a non-contact full-field quantitative imaging method that allows the determination of both in-plane displacement components, i.e. the axial and lateral components of the displacement fields on the surface of the specimen, and consequently the surface strain fields experienced by the sample during loading [49]. The naturally occurring texture of the surface of the specimen, i.e. the cellular structure with contrasting white cellular walls and dark cellular pores, was used for correlation purposes. Details of the correlation settings using the Match-ID DIC software are shown in Table 1.

Table 1 DIC parameters

For large deformations, incremental DIC is often utilized to avoid decorrelation. For correlating purposes, the image of the previous displacement step, n − 1, is used as the reference image for correlating the positions of the speckles in the n^th displacement step. The total number of measurement points for the quasi-static full-field analysis was 52,416 using the Stingray camera. For the high strain rate experiments an 85 mm Otus Zeiss lens was mounted on a high-speed camera Shimadzu (HPV-X1) that captured images at 200,000 fps with a resolution of 400 × 250 px². Two high-power LEDs (GS-VITEC) pulsed in synchronization with the high-speed camera framing were used for illumination.

Poisson’s Ratio

Poisson’s ratio is the primary metric for quantifying the tendency of a material to distort, rather than change volume [50]. Poisson’s ratio has a precise definition for linear elastic solids, where it is assumed to be a material constant. Such a rigorous definition does not exist, in general, for non-linear materials such as hyperelastic foams [51, 52]. For nonlinear materials, the ratio of lateral deformation to axial deformation is not constant, but rather a function of the global axial strain. Therefore, a more appropriate definition for nonlinear materials is the Poisson’s function which is given by the tangent of the lateral-axial strain curve. This function gives the “instantaneous” value of the Poisson’s ratio as a function of global strain, as explained in [51]. It is analogous to the tangent modulus for nonlinear materials, in contrast to the secant modulus. The secant modulus would correspond to the original definition of the Poisson’s ratio. The axial nominal strain, i.e. the component along the loading direction-2, is e₂, and the lateral nominal strain component is e₁ (as shown in Fig. 1). Then the tangent Poisson’s function, ν_tan is defined as:

$$ \nu_{tan} = - \frac{de_{1}}{de_{2}} $$

(4)

whereas the secant Poisson’t ratio is:

$$ \nu_{sec} = - {\frac{e_{1}}{e_{2}}}\text{.} $$

(5)

Both definitions are used in this investigation, and results demonstrate which of the two is more appropriate, in that it captures the nonlinear behavior of the foam. In practice, the differentials of equation (4) will be approximated by finite differences since the strain values are sampled discretely in time with a specific sampling rate.

Results & Discussion

Morphological Characterization

Analysis of the reconstructed micro-CT slices are performed using iMorph open source software [42, 53, 54]. The two phases, solid and gas, are segmented using a thresholding algorithm. This binarization process provides a measure of the relative density of the foams, $\frac {\rho }{\rho _{s}}$, where ρ is the density of the foam and ρ_s is the density of the foam’s constituent material in its fully dense form. Traditionally surface measurements of these optically opaque foams are used to estimate their relative density. The advantage of obtaining this global quantitative measure through micro-CT imaging is that there is no need to rely on the limiting assumption of through-thickness homogeneity. The relative density is directly quantified by counting the number of voxels of the solid phase, i.e. total volume of the solid phase, and dividing by the total volume of the foam (Fig. 6). The relative density of the foam was found to be 4.2%. Relative density is known to be a key parameter in determining the compressive stress-strain response of the foams, as exemplified in the stress-strain maps and the corresponding contours separating the linear, plateau, and densification regimes of elastomeric foams with different initial relative densities found in [1, 2]. The average cell size is 112 ± 101μ m. Other morphological characteristics, such as individual cell sizes and orientations, can be determined but in this work the focus is on the macroscopic behavior of the foam.

Fig. 6

a Reconstructed volume of foam from micro-CT slices. Dark regions represent the gas phase, and lighter gray features represent the solid phase of the foam. Snapshot of plane-1, b and plane-2

Stress-Strain Response: Low strain rates

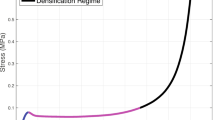
Figure 7 shows the nominal stress-strain response of the foam at different quasi-static strain rates spanning four orders of magnitude. The foam’s behavior at every quasi-static strain rate tested, exhibited the classic compressive response of elastomeric foams. Namely, the response can be segmented in three distinct regimes, an initial linear response up until a critical stress value is reached, followed by the plateau regime in which the strain continues to increase at an almost constant stress level, i.e. the critical stress level, and finally a densification regime due to impingement of the cell walls upon each other. It exhibits a strain rate dependent response at the quasi-static rates tested. This strain rate dependence of the foam at these rates exemplifies their strong viscoelastic character, which is manifested as a rate dependent behavior. It is worth noting that upon unloading, the foam recovered fully to its original dimensions after being allowed to recover for about 24 hours. Another mechanism through which strain rate dependence can arise is due to viscous gas flow through the open-cell structure of the foam as it is being compressed. In particular the initial slope during the linear regime and the critical stress value increase as a function of strain rate These metrics will be further quantified in “Strain Rate Dependence”, after the presentation of the response of the hard foam under high strain rates in “Stress-Strain Response: High strain rates”.

Fig. 7

Nominal stress-strain response of hard foam under quasi-static compression at different strain rates. The dependence of the compressive response of these foams to strain rate is evident. Characteristic properties such as the initial stiffness and the critical stress at the transition between the linear and plateau regimes are clearly strain rate dependent

Stress-Strain Response: High strain rates

The stress-strain response of the hard foam under compression was explored using a modified aluminum Kolsky bar setup. Experiments were conducted at a nominal strain rate of $\dot {\epsilon }=7\times 10^{2}$ s^− 1 as shown in Fig. 8b. A nominal specimen length of 3 mm was chosen as a representative volume since more than 10 cells are contained within that length. Equilibrium of the forces was checked using piezoelectric quartz force gages at either side of the specimen, interfacing with the incident and transmitted bar, respectively. The signal of the quartz force gage interfacing with the transmitted bar was used to measure the transmitted signal, since the signal amplitude of the transmitted stress wave is very low and cannot be picked up by conventional strain gages. The maximum observable strain with the current aluminum Kolsky setup is limited to 20% as can be seen in Fig. 8, given the geometry, i.e. length, and material of the incident bar. As discussed in “Dynamic Compression”, to extend the maximum observable strains to probe the plateau and densification regimes, longer bars should be used to avoid superposition of the incident and reflected waves. Due to this limitation, it is impossible to extract characteristic properties such as critical stress and specific strain energy of the hard foam at high strain rates with the aluminum bar configuration used in this investigation. However, the aluminum bars were utilized up until 20%, in order to have corroboration of results from a traditional elastic bar wave-guide with other, less traditional Kolsky configurations.

Fig. 8

Average compressive stress-strain response of 4 separate experiments on hard foam at high strain rates using a modified aluminum Kolsky bar setup

Polymeric bars were utilized to probe at higher strains. As explained in “Dynamic Compression”, polymer bars offer the advantage of extending the maximum allowable observable strains during Kolsky experiments due to their lower wave speeds. However, their viscoelastic nature causes additional challenges in the reduction of the raw signal data due to wave attenuation and dispersion. An experimental method, proposed by Bacon [48], was used to determine the propagation coefficient of the polymeric bars. In addition, a modified independent method based on similar work from Casem et al. [25] was utilized, the details of which are given in “Novel Kolsky Data Reduction Method Using Particle Tracking”. The displacement and velocity of the bar ends was tracked and used to analyze the stress-strain response of the specimen. This method has the advantage that there is no need to account for viscoelastic wave propagation in the bars, as discussed in [25]. Snapshots of a characteristic high strain rate experiment captured at 200,000 fps using a Shimadzu high-speed camera are shown in Fig. 9. From visual inspection of these images, as well as DIC full-field analysis, the specimen appears to be deforming uniformly. In particular, there is no compaction wave front propagating along the length of the specimen, thus suggesting any strain rate dependent behavior is not due to “structural shock” formation (at the rates investigated in this study). Stress-strain response of the hard foam at two strain rates is shown in Fig. 10. As can be seen, using the polymeric Kolsky bar setup allowed probing the plateau and densification regime at high rates of deformation. The strain rate dependency of the hard foam continues at these high rates. Specifically, the critical stress and specific strain energy continue to increase as a function of strain rate.

Fig. 9

A series of frames during a Kolsky test for the hard foam using the polycarbonate bar setup. Images taken with a high-speed camera at 200,000 fps with a resolution of 400 × 250 px². Incident bar is at the top and transmitted bar at the bottom

Fig. 10

Compressive stress-strain response of hard foam at high strain rates using a polymeric (polycarbonate) Kolsky bar setup

Strain Rate Dependence

The critical stress value, σ_cr, for the hard and soft foam is defined as the stress level at which the compressive behavior transitions from linear to the plateau regime. It is observed to be a function of the loading strain rate. Values of the critical stress are tabulated as a function of strain rate for the hard foam in Table 2. As the strain rate increases by two orders of magnitude, the critical stress increases by a factor of three. Semi-logarithmic plots, see Fig. 12a, show the strain rate dependence of this characteristic property of the foams. The stiffness, E, of the foams at the initial linear regime of the compressive stress-strain response is a function of the strain rate as well. Its dependence on strain rate follows the same dependence as critical stress with strain rate, i.e. logarithmic. Values of the initial stiffness are tabulated in Table 2. Specific strain energy is a measure of the ability of the material to absorb energy, e.g. kinetic energy of impact, through deformation. It can be calculated by integrating the stress-strain response of the specimen with the integration limits chosen somewhat arbitrarily. Since the most efficient energy storage for impact protection applications is thought to occur inside the plateau region at an almost constant stress, which allows for a constant and low magnitude acceleration [2, 55], the upper integration limit is chosen as 0.4 nominal strain, as shown schematically in Fig. 11a. That strain limit is below the onset of densification, in which the stress and the consequent acceleration level rises. Numerical integration of the stress-strain curve gives the specific strain energy as:

$$ \hat{u} = {\int}_{0}^{\epsilon_{f}=0.4}\sigma(\epsilon)d\epsilon. $$

(6)

The integration is performed using a trapezoidal method, and the results for the foam at the different low and high strain rates are shown in Fig. 11b. Strain energy absorption increases with increasing strain rate. This is to be expected since the critical stress increases as a function of strain rate, which leads to a larger area under the stress-strain curve. The values of the specific strain energy absorbed by foam are tabulated in Table 2 with the corresponding critical stress values at each strain rate. Note that for the experiments conducted with the aluminum bars, where the maximum attainable strain is 20%, only the critical stress is reported since the specific strain energy cannot be computed.

Table 2 Hard Foam: Critical stress, specific strain energy, and stiffness in the initial linear compressive stress-strain regime, as a function of strain rate

Fig. 11

The absorbed specific energy, in terms of strain energy, for the hard foam at different quasi-static and dynamic strain rates

The strain rate dependence of the foam in terms of the critical stress and specific strain energy metrics is summarized in Fig. 12. A useful analytical expression describing the rate-dependence of these characteristic properties of the foams, i.e. critical stress and strain energy, is given by the following equation:

$$ P(\dot{\epsilon}) = P(\dot{\epsilon_{0}}) \cdot \left[ m log_{10} \left( \frac{\dot{\epsilon}} {\dot{\epsilon_{0}}} \right) + 1 \right] \quad $$

(7)

in which P stands for any given property of interest, such as critical stress, σ_cr, or specific strain energy, $\hat {u}$, as a function of strain rate $\dot {\epsilon }$. The reference strain rate value is the lowest rate tested, $\dot {\epsilon _{0}} = 2 \times 10^{-4}$ s^− 1, and $P(\dot {\epsilon _{0}})$ is the value of the property at the reference strain rate. The factor, m, premultiplying the logarithmic term is m = 1.4. The value of both properties, i.e. critical stress and specific strain energy, are related to strain rate in a logarithmic fashion, i.e. for two orders of magnitude increase in the strain rate relative to the reference strain rate, there is a factor of three increase of any given property. Similarly, for three orders of magnitude increase of the strain rate there is a factor of four increase of that property, and so forth. This analytical expression was used for the analytical fit curves shown in Fig. 12 and demonstrates good agreement with the experimental data. The strain rate dependence is captured by this universal, albeit relatively simple expression. A similar analytical expression was used to describe the strain rate dependent properties of closed-cell polymeric foams by Daniel et al. [18] and by Song et al. [29]. Both of these studies used similar scaling factors, pre-multiplying the logarithmic term, to obtain a good fit between the experimental data and the analytical description. The analytical fit given by equation (7) works satisfactorily up to a strain rate of 3000 s^− 1.

Fig. 12

Characteristic properties, i.e. critical stress and specific strain energy, of the foam in terms of strain rate, shown with the analytical expression given by equation (7)

In-situ imaging using a high-speed camera at 200,000 fps verified that there is no discontinuous propagating compaction front that has been observed in similar materials under high rate compression, beyond a critical impact speed [10, 38, 56]. The incident bar loading velocity is of the order of 10 m/s, as can be seen in Fig. 5d. In addition to the viscoelastic nature of the base material of the foam, which can manifest as strain rate dependence, another mechanism exists for open cell foams; that of viscous dissipation of the pore fluid expelled as the foam is being compressed, see pg. 252-257 in [2]. The effect of gas flow and/or entrapment has been observed for closed-cell foams by Bouix et al. [33]. Although, for closed-cell foams it is thought that gas entrapment instead of gas-flow dissipation is causing the stiffening of the foam, Bouix et al. observed that under low and intermediate strain rates gas bubbles appeared at the faces of the foam as it was being compressed. This suggests, that the foam’s cell structure was not fully closed and that cell walls had partial aperture openings that allowed gas to escape. However, under high rates of deformation they observed that gas was not given enough time to escape the foam, thus effectively behaving as a closed-cell foam entrapping the gas. That was thought to increase the cell pressure and consequently the resistance of the foam to deformation as it was being compressed.

Both characteristic properties vary linearly with the logarithm of strain rate, and thus have the exact same functional form. As such, the results can be normalized by using equation (8), with the value of the characteristic property at the reference strain rate, $\dot {\epsilon }=2\times 10^{-4}s^{-1}$, and plotted in a master curve.

$$ P_{norm} = \frac{P(\dot{\epsilon})}{P(\dot{\epsilon_{0}})} = \left[m log_{10} \left( \frac{\dot{\epsilon}} {\dot{\epsilon_{0}}} \right) + 1 \right] \quad $$

(8)

The analytical expression of equation (8) suggests that a scaling of the stress-strain plot exists where the response of the foams at different strain rates would collapse to a single curve. By transforming the stress using the following scaling:

$$ \sigma^{\prime} = \frac{\sigma}{K} \quad $$

(9)

in which the factor K is equal to $\left [ m log_{10} \left (\frac {\dot {\epsilon }}{\dot {\epsilon _{0}}} \right ) + 1 \right ]$ and σ is the nominal stress, the stress-strain curves collapse on top of each other. This can be seen in the transformed master stress-strain curve plotted in Fig. 13 for the hard foam. The master curve exhibits that one only needs to know the compressive response of the foam at the reference strain rate. By using the scaling factor K, the stress-strain response at any other strain rate can be obtained via the stress scaling of equation (9). This would have particularly important implications when attempting to simulate blunt-impact traumatic brain injury scenarios which are thought to occur under intermediate strain rates. Using this simple scaling law the response of the foam at any intermediate strain rate can be extrapolated. However, as can be seen by the underprediction of the low strain rate properties in Fig. 12 it is crucial to develop valid experimental methodologies to probe the response of materials at intermediate rates. A similar analysis for a closed-cell polymeric foam was presented by Daniel et al. [18], although in that study a transformed strain was also used. Although this transformation mathematically simplifies the description of the response of the foams to one equation, it does not explain the physical mechanism of this strain rate dependency. However, it is still useful for a phenomenological model describing the compressive stress-strain response of the foam at different strain rates. Future work will try to address the physical mechanisms behind such a scaling law.

Fig. 13

Master stress-strain curve

Full-field Deformation Fields: Localization

From 2D DIC we obtain the in-plane displacement vector u at the measurement points, see Fig. 14a. The displacement data can be used to compute all 4 components of the deformation gradient tensor F at each measurement point, see Fig. 14b. Using indicial notation the deformation gradient in 2D can be written as $F_{ij} = \delta _{ij} + \frac {\partial u_{i}} {\partial X_{j}}$, where X denotes the position vector of each measurement point in the reference configuration of the foam, δ_ij is the Kronecker delta, and the range of the indices i,j = 1,2 in 2D space, see Fig. 1. Tensors of order two or less can be conveniently represented in matrix form, therefore F_ij in 2D can be written as:

$$ \mathbf{F} = \mathbf{I}+ \left[\begin{array}{ll} \frac{\partial u_{1}}{\partial X_{1}} & \frac{\partial u_{1}}{\partial X_{2}} \\ \frac{\partial u_{2}}{\partial X_{1}}& \frac{\partial u_{2}}{\partial X_{2}} \end{array}\right] \quad $$

(10)

where I is the identity matrix. The deformation gradient for every measurement point in the field of view and at each displacement step, is part of the output from the MatchID software. Here an analysis similar to Landauer et al. [57] is followed to extract the lateral and axial components of the deformation from the deformation gradient tensor F. In particular, the axial and lateral deformations of the foam under uniaxial compressive stress loading are of interest. In order to partition the rigid body rotations from the deformations, the polar decomposition of the deformation gradient, F_ij = R_ikU_kj, where R is the rotation tensor and U is the right-stretch tensor, a symmetric tensor that describes deformations is utilized. The summation convention is implied for repeated indices in a term over the range of the subscripts. In matrix form:

$$ \mathbf{F} = \mathbf{R} \mathbf{U} $$

(11)

In 2D obtaining the polar decomposition of F is straightforward and the right-stretch tensor U can be readily obtained. Since the right-stretch tensor is symmetric it can be diagonalized, i.e. spectrally decomposed, by transforming it to its principal basis given by the directions of its orthogonal eigenvectors. The diagonal values are the principle stretches λ₁ and λ₂. Through the polar decomposition of F it was determined that the loading direction-2 corresponds to one of the principal directions, e.g. the rotation angle is less than 2^∘, and the off-diagonal components of the deformation gradient tensor were close to zero. The lateral nominal strain can then be approximated by e₁ = λ₁ − 1 ≈ F₁₁ − 1 and the axial nominal strain e₂ = 1 − λ₂ ≈ 1 − F₂₂. Note that his definition keeps the nominal axial strain positive for compression, for ease of plotting.

Fig. 14

(Top row) horizontal component (Bottom row) vertical component, quasi-static compression of the hard foam at $\dot {\epsilon }=2 \times 10^{-4} s^{-1}$. From left to right, the global nominal compressive strain along the loading direction is 4%, 32%, 70%, respectively

Both in-plane components of the displacement appear to exhibit, at least qualitatively, non-linearly varying fields over the whole field of view, as can be seen in Fig. 14a. This is expected for uniaxial stress deformation of an inhomogeneous material since foam materials consist of two phases and cellular structures are heterogeneous with different distribution of sizes, orientations, and cell wall thicknesses throughout the material. This inhomogeneity of the material is more apparent in the deformation fields, e.g. the spatial derivative of the displacement fields, shown in Fig. 14b. The deformation fields are not homogeneous, or in other words the deformation gradient is not constant across the whole field at any given load step. Localization, or hot spots of deformation exist, that are appearing due to the location dependent stiffness of the sample. In the zoomed-in insets of Fig. 14b the cellular structures of the foam are overlayed on top of the DIC color maps. It can be seen that a band of cell structures have collapsed while some neighboring cells remain almost rigid. For example, for a global nominal compressive strain of 70%, there exist local areas with compressive strains as low as 52% and as high as 82%, as seen in the bottom right of Fig. 14b for the F₂₂ component. In order to take the non-homogenous effects into account, an approach similar to that introduced by Pierron in [52] is typically taken in which the incremental lateral components of the deformation were associated to the corresponding cumulative strain level along the loading direction. However, in this work we are interested in the global response of the foams and localization effects that are due to inhomogeneous mesoscale cellular structures will be explored in the future. Therefore, average values of lateral and axial strain are going to be used to extract a macroscopic Poisson’s function for the foam across strain rates.

Poisson Function

The average values of the lateral nominal strain e₁ ≈ F₁₁ − 1 and the axial nominal strain e₂ ≈ 1 − F₂₂ over the whole region of interest are plotted in Fig. 15a for the hard foam at a strain rate of $\dot {\epsilon }= 2 \times 10^{-4} \textit {s}^{-1}$. Initially the lateral strain increases as the foam is compressed up to a global axial compressive strain of 20%. In particular, there is a lateral expansion of about 2.5% for 20% nominal compressive axial strain. After the 0.2 axial strain mark, the lateral strain decreases, which indicates that the specimen contracts with further increase in compression. This demonstrates an auxetic behavior of the foam, i.e. the lateral dimensions of the foam contract as the foam is compressed beyond 20% strain. Figure 15b demonstrates that using the classical definition of Poisson’s ratio, i.e. the secant formulation described in “Poisson Function”, this auxetic behavior of the foam is missed. However, by using the tangent Poisson’s function formulation, which is the slope of the axial-lateral strain curve, the auxetic behavior is recovered, and it can be seen that the value of the tangent Poisson’s ratio is a function of the global strain and it decreases from an initial value of 0.5 to small negative numbers.

Fig. 15

a Axial versus lateral nominal strain for the hard foam. b Two different formulations of Poisson’s function at a compressive nominal strain rate of $\dot {\epsilon }=2 \times 10^{-4} s^{-1}$

Experiments using full-field imaging were conducted at different strain rates. There exists a slight dependency of the Poisson’s function on strain rate at quasi-static rates examined which can be seen in Fig. 16. Moreover, for the high strain rates the foam exhibits a similar to the quasi-static responses Poisson’s function. This suggests that the Poisson’s ratio is a function of the structure of the foam and is independent of the loading rate. Minimal strain rate dependency was recently reported by Sanborn et al. [58] for a hyperelastic silicone foam tested under quasi-static and dynamic compression. That foam exhibited a transition of the Poisson’s function from a value of 0.2 to a value of 0.4 around the densification initiation (50% nominal strain). Such a sharp transition of the value of the Poisson function at the densification initiation has not been observed in the current study. One major difference between the current study and that by Sanborn et al. [58] is the initial relative density. The foam in the Sanborn et al. study has an initial relative density of 50% which is a much more dense porous material compared to the material studied here that has an initial relative density of 5%. A transition like the one observed by Sanborn et al. [58] would be expected to occur for the foam studied here for a nominal compressive strain of ∼ 90 − 95%.

Fig. 16

Poisson’s function of hard and soft foam; tangent formulation. Results shown for two different quasi-static strain rates for both soft and hard foams, in addition to one high strain rate for the hard foam

Conclusion

The strain rate dependent uniaxial stress response under compressive loading for an open cell polyurethane foam currently used as military helmet liner was quantified. It exhibits characteristic properties that vary linearly with respect to the logarithm of strain rate. The variation of the foam’s characteristic properties, i.e. critical stress, specific strain energy, and stiffness, with respect to strain rate are described by a simple analytical expression in terms of the characteristic property value at the reference strain rate $\dot {\epsilon _{0}}$ given in equation (8). A master stress-strain curve collapses the responses of the hard foam to a single curve by introducing a transformation of the stress given in equation (9). This allows the stress-strain response of the foam to be inferred at any strain rate, only by knowing the response at a reference strain rate $\dot {\epsilon }_{0}$. This expression could prove valuable, especially for extrapolating the stress-strain response to the intermediate strain rate regime which is challenging to obtain experimentally, but is crucial for modeling blunt impact traumatic brain injury scenarios. Further, high-speed in-situ imaging verified that there was no compaction front propagating during the high-rate experiments in this study, which excludes strain rate dependencies associated with “structural shock” propagation in the foams [10, 38] (see Fig. 9).

Full-field imaging utilizing DIC allowed for the measurements of in-plane displacement components, and the corresponding strain maps. Global Poisson functions were mapped and demonstrate the foam’s highly nonlinear properties. The tangent Poisson function was shown to be a function of the applied global strain along the loading direction. Moreover, the Poisson value when using the tangent formulation, changed sign going from positive to negative denoting a regime where the foam behaves auxetically. Dependence of the Poisson function to strain rate was minimal indicating that the Poisson function depends only on the morphological structure of the material. Furthermore, looking at the mesoscale structural characteristics of the cells and the localizations occurring in the deformation fields due to these structures can aid towards an understanding of the transition from positive to negative values of the Poisson function [59].

The limitations of traditional experimental techniques, such as the Kolsky (split-Hopkinson) bar method, used for the determination of material properties at high strain rates are discussed. Intermediate strain rate regimes are relatively inaccessible with the bar methods. Alternative methods have been proposed in literature and show promise [23, 24, 60, 61]. Some of these methods not only allow for a relaxation of the stress equilibrium and constant strain rate assumptions imposed by the Kolsky analysis, but rather leverage deviations from these conditions and will be explored on these materials in the future.