Introduction

Vascular pathologies have a direct effect on the mechanical properties of the vessel wall, mainly located in the diseased area. The methods used to describe these properties and identify their parameters contribute to fundamental advances in the field of cardiovascular radiology and surgery. They allow clinicians and researchers to predict events such as aneurysm rupture [1] and the development of diseases such as atherosclerosis [2], to describe the vascular microstructure [3, 4], as well as to create biocompatible implants for vascular reconstruction [5] or synthetic replicas [6, 7], called “phantoms,” for clinicians’ preoperative training in usual or innovative surgical and radiological interventions [8].

However, the assessment of mechanical behavior is often challenging because it can only be characterized through indirect measurements. Experimentally, current techniques based on medical imaging, such as magnetic resonance imaging (MRI) [9], ultrasound (US) imaging [3, 1] and X-ray computed tomography (CT) [10] are used. These techniques contribute more or less accurate data on vascular wall motion according to their spatial and temporal resolution, with the result that the parameters identified can be affected by this resolution as well as by acquisition artifacts. Owing to these uncertainties, simplified linear constitutive equations are often considered based on in-vivo experiments, leading to parameters such as Young’s modulus [11], compliance [1] and distensibility [12, 9]. Nevertheless, studies from in vivo as well as ex vivo experiments have demonstrated that the actual vascular mechanical behavior is more complex. Indeed, in the case of the aorta tree, a nonlinear and reversible [3, 13, 14] behavior (hyperelasticity) with a phase shift between strain and stress, displaying a viscoelastic effect [15–18], has to be considered. The studies on the mechanical modeling of various vascular walls have used constitutive models that are able to predict either hyperelasticity or viscoelasticity, but the combination of both behaviors is seldom taken into account [16]. This can lead to a model inadequately describing the actual inflation and extension of the blood vessels. Indeed, longitudinal elongation is commonly overlooked in mechanical modeling [16, 3], but this approximation is not really justified, according to a recent study [19]. The identification of more realistic constitutive equations, and of the related material parameters, is a major challenge within the issues related to cardiovascular surgery.

Hence, the aim of the present study was to develop and validate a method based on medical imaging to identify the parameters of a hyper-viscoelastic model suitable for describing the mechanical behavior of vascular tissues, focusing on the aorta. This model comprises one hyperelastic element in parallel with one or more Maxwell elements. The proposed method to identify the hyper-viscoelastic model parameters was validated by applying the method to specific silicone materials and comparing the estimated parameters to reference values obtained by means of precise mechanical measurements such as uniaxial tensile and/or compression tests. This type of system has already been used in dynamic conditions to study flow [20–22] and to develop methods for disease prediction, but not for rigorous modeling of the hyper-viscoelastic behavior. The silicone samples, connected to this test bench, were subjected to various automatically controlled pressure cycles, in order to measure the induced elongation by means of ultrasound imaging.

This paper is organized as follows. The first section describes the materials used to validate the Inflation-Extension (I-E) test proposed. Then constitutive models are introduced in the second section, in which hyper-viscoelastic mechanical behavior is described. The third section deals with the experimental setup and also describes the experimental process and parameter identification procedures. Then the fourth section presents the numerical and experimental results of standard measurements and I-E test. Finally, these results are compared to validate the presented method and identify its limits.

Description of Materials

The validation method for the present work was based on the study of commercial silicone rubbers that were formulated from Bluestar Silicones (Lyon, France) products: Bluesil® RTV 3040 and Silbione® HC2/2011. The use of synthetic materials instead of real vascular tissues obtained post mortem avoided fast degradation of the latter, so that the comparison of different measurements obtained at different time-points remained relevant. Two materials were formulated: the first material was only composed of RTV 3040, and the second material was a 3040:HC2 mixture, with a 25:75 ratio, called 3040-HC2/75. These materials present different mechanical behaviors within a range typical for vascular walls [8] so that they can be used to produce patient-specific aorta phantoms. Specimens were prepared using the following procedure: (i) mixing the two liquid components, i.e., the uncured silicone and the curing agent, with a 10:1 and 1:1 ratio for RTV 3040 and HC2/2011 respectively, (ii) for 3040-HC2/75 material, mixing the RTV 3040 and HC2/2011 with a 25:75 ratio (iii) putting the uncured mixture into a syringe for centrifugation (5 min at 5000 rpm), in order to eliminate undesired trapped bubbles, (iv) injecting the liquid mixture into molds, plates for the tensile and compression test and in a specific tubular system for I-E tests, and (v) heating molds at 150 °C for 1 h to crosslink the silicone.

Constitutive Models

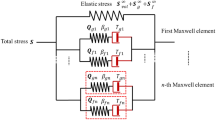
All the mechanical data are considered in isothermal conditions at ambient temperature. In the literature, several constitutive models have been used to describe vascular wall motion according to various assumptions (anisotropy, orthotropy, incompressibility). These assumptions can be based on the physical description of the vessels (form of collagen fibers, length of elastin) [3, 23, 24] but they generally result in very sophisticated models. More simply, some phenomenological models in use describe the overall mechanical behavior [25, 26]. In the present work, this type of constitutive equation was chosen to limit the number of adjustable parameters, while keeping the best possible description of the behavior. Therefore, a hyper-viscoelastic model, namely a generalized Maxwell solid model, was selected. In this model, the function ψ that describes the free-energy variation of a transformation in isochoric and isothermal conditions is given by [27]:

$$ \psi \left(\boldsymbol{C}\right)={\psi}_{iso}^{\infty}\left(\boldsymbol{C}\right)+{\displaystyle \sum_{\alpha =1}^m{\psi}_{\alpha}\left(\boldsymbol{C}\right),} $$
(1)

where ψ ∞ iso (C) is the strain-energy function characterizing the equilibrium state of the solid represented by the isolated spring, C the right Cauchy-Green strain tensor and m the number of relaxation times. The left-side term of equation (1) represents the hyperelastic behavior and can be experimentally assessed by a sufficiently slow deformation process. For this hyperelastic branch, a Yeoh equation [28] was used, representing an ideal elastic behavior with a nonlinear stress–strain relationship derived from a strain energy density function, which is expressed by:

$$ {\psi}_{iso}^{\infty}\left(\mathbf{C}\right) = {\displaystyle \sum_{i=1}^n}{C}_i{\left({I}_1-3\right)}^i, $$
(2)

with ψ ∞ iso being the hyperelastic potential, C i the hyperelastic parameters, I 1 the first invariant of C (I 1 = tr(C)), and n the order of the Yeoh model. This part of the model is able to accurately predict possible hardening encountered in the mechanical response of vascular walls [29, 26] or filled elastomers [27] as occurs in many silicones.

The right-hand term in equation (1), \( {\displaystyle \sum_{\alpha =1}^m}{\psi}_{\alpha}\left(\mathbf{C}\right) \), is the dissipative potential. It represents the viscoelastic contribution and is a function of C. It is straightforward to show that the PK2 (second Piola-Kirchhoff) stress tensor S is composed of the equilibrium isochoric part S ∞ iso and the non-equilibrium part Q α , α = 1,…, m:

$$ \mathbf{S}={\mathbf{S}}_{iso}^{\infty }+{\displaystyle \sum_{\alpha =1}^m}{\mathbf{Q}}_{\alpha }\ . $$
(3)

The strain free-energy function responsible for the relaxation with relaxation times τ α is expressed as ψ α (C) = β α ψ ∞ iso (C) and its corresponding stress tensor is expressed relative to the equilibrium isochoric part:

$$ {\mathbf{S}}_{iso,\alpha } = {\beta}_{\alpha }{\mathbf{S}}_{iso}^{\infty }, $$
(4)

where β α is a dimensionless factor.

Then, for each Maxwell element, a linear evolution equation can be considered:

$$ {\dot{\mathbf{Q}}}_{\alpha }+\frac{{\mathbf{Q}}_{\alpha }}{\tau_{\alpha }} = {\dot{\mathbf{S}}}_{iso,\alpha }\ . $$
(5)

Moreover, equation (5) can be turned into a convolution integral form giving:

$$ {\mathbf{Q}}_{\alpha } = {\displaystyle \underset{-\infty }{\overset{T}{\int }}}{e}^{-\left(\frac{T-t}{\tau_{\alpha }}\right)}{\dot{\mathbf{S}}}_{iso,\alpha }(t)dt\ . $$
(6)

In this equation, the entire strain history is taken into account via the time derivative of the stress tensor isochoric part \( {\dot{\mathbf{S}}}_{iso,\alpha } \).

Experimental Mechanical Setup

The number of material parameters (C i , τ α , β α ) to be determined for both the hyperelastic and viscoelastic components of the constitutive model can lead to ill-posed problems [30] if certain precautions are not taken. Therefore, to ensure the reliability of the parameters identified with the I-E test, it is relevant to corroborate their values from other experiments. For this purpose, it is helpful to separate the hyperelastic and viscoelastic behaviors using judiciously chosen tests: the uniaxial tensile test at a very low elongation rate and the dynamic compression test at a low strain value (by Dynamic Mechanical Analysis, DMA).

Tensile and Dynamic Compression Experiments

Tensile test

In order to analyze the hyperelastic behavior of the silicone materials, a CRITERION (MTS Systems, Créteil, France) tensile testing machine equipped with a 500-N load cell was used to perform uniaxial tensile tests. Dumbbell shaped samples approximately 1.5 mm thick were punched out of the previously prepared silicone plates. The initial useful length (l 0) of the samples was 20 mm for a width of 4 mm. The extension was applied up to λ = 1.5 (λ = l/l 0) with an extension rate \( \dot{\lambda} \) of 5 × 10−3 s−1. This very low extension rate was chosen to prevent any possible viscoelastic effect [31], no hysteresis was observed in these conditions. Moreover, two cyclic tensile tests were previously achieved at the same extension rate in order to detect and erase a possible Mullins effect [32]. The hyperelastic behavior was then analyzed on the third loading curve. Therefore, in the present study, this type of test and the deduced hyperelastic material parameters C i will be considered as a reference C ref i . For a uniaxial stress transformation, the right Cauchy-Green deformation tensor C is given by:

$$ \mathbf{C} = \left[\begin{array}{cc}\hfill {\lambda}_1^2\hfill & \hfill \begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \end{array}\hfill \\ {}\hfill \begin{array}{c}\hfill 0\hfill \\ {}\hfill 0\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \begin{array}{cc}\hfill {\lambda}_2^2\hfill & \hfill 0\hfill \end{array}\hfill \\ {}\hfill \begin{array}{cc}\hfill 0\hfill & \hfill {\lambda}_3^2\hfill \end{array}\hfill \end{array}\hfill \end{array}\right], $$
(7)

where λ 1 , λ 2 and λ 3 are the principal stretches (with the stretching direction corresponding to the subscript 3) such that, for an isotropic and incompressible material λ 1 = λ 2 and λ 1 λ 2 λ 3 = 1.

The Yeoh model applied for such a tensile test leads to the following expression of the corresponding component of the second Piola Kirchoff stress tensor S 33:

$$ {S}_{33}={\displaystyle \sum_{i=1}^n}\frac{i{C}_i}{\lambda_3^2}\left(2{\lambda}_3^2-\frac{2}{\lambda_3}\right){\left({\lambda}_3^2+\frac{2}{\lambda_3}-3\right)}^{i-1} $$
(8)

The identification procedure (9) consisted in minimizing the objective function f h obj that measures the gap between the measured stress and the computed one.

$$ \left\{{C}_i^{ref}\Big|i=1\dots n\right\}= \arg min{f}_{obj}^h\left({C}_i\Big|i=1\dots n\right), $$
(9)

with f h obj defined as:

$$ {f}_{obj}^h={\displaystyle \sum_j^N}{\left({S}_{33,\ j}-{S}_{33,j}^{mes}\right)}^2, $$
(10)

where S mes33,j  = σ mes33,j  × λ − 23 is the second Piola Kirchoff uniaxial stress obtained from the measured tensile true stress σ mes33,j and S 33,j is the one computed with hyperelastic parameters (Equation (8)), N is the number of measurements taken during the loading process. The optimization procedure was performed by using the optimization toolbox of Matlab software (The MathWorks, Natick, MA, USA) with the trust region reflective optimization algorithm [33].

Compression test

The viscoelastic behaviors of the silicone materials were characterized by frequency sweep experiments in dynamic mechanical analysis in compression mode. These experiments were conducted with a DMA Q800 device (TA Instruments, Guyancourt, France) using disk-shaped samples about 1.5 mm thick (diameter, 7 mm for RTV 3040 and 11 mm for 3040-HC2/75). Dynamic compression test was performed with an angular frequency ω range of 0.06 to 600 rad/s at a constant strain of 1.5 %, which is within the linear viscoelastic regime. For the dynamic compression tests, the silicone material underwent a periodical mechanical strain ε of very small amplitude ε 0 and of angular frequency ω:

$$ \varepsilon = {\varepsilon}_0 \sin \left(\upomega \mathrm{t}\right) $$
(11)

From the periodical stress measurement and its phase lag with regard to the strain, the material’s complex Young modulus E*(ω) was obtained as a function of the angular frequency ω. In the case of the generalized Maxwell model, the storage E '(ω) and loss E ' '(ω) parts of the complex modulus are expressed by equations (12) and (13):

$$ {E}^{\hbox{'}}\left(\omega \right)={E}_0\left[1 + {\displaystyle \sum_{\alpha =1}^m}\frac{\beta_{\alpha }{\omega}^2{\tau}_{\alpha}^2}{1 + {\omega}^2{\tau_{\alpha}}^2}\right], $$
(12)
$$ {E}^{\hbox{'}\hbox{'}}\left(\omega \right)={E}_0{\displaystyle \sum_{\alpha =1}^m}\frac{\beta_{\alpha}\omega {\tau}_{\alpha }}{1 + {\omega}^2{\tau_{\alpha}}^2}, $$
(13)

where E 0 is the Young modulus of the isolated spring. The relaxation times, τ α , and the dimensionless parameters β α stand for the contribution of each branch to the total stress. The relaxation time values were fixed regularly spaced between the reciprocals of the highest and the lowest frequencies of the experimental dynamic modulus. The chosen number of modes was sufficiently high to obtain accurate fitting, but not too large to avoid inconsistent results (e.g., negative values of β α ). Practically speaking, this led to five time constants (m =5), regularly spaced on a logarithmic scale between 3 × 10−3 s and 30 s. In the present study, this type of test and the deduced viscoelastic material parameters (E 0 , β α ) will be considered as a reference (E ref0  , β ref α ). Identification was achieved by solving the following minimization problem (with the same procedure as above):

$$ \left\{{E}_0^{ref},\ {\beta}_{\alpha}^{ref}\Big|\alpha =1,\dots, m\right\}= \arg min{f}_{obj}^v\ \left({E}_0,\ {\beta}_{\alpha}\Big|\alpha =1,\dots, m\right), $$
(14)

with f v obj defined as:

$$ {f}_{obj}^v = {\displaystyle \sum_{ij}^N}{\left({E}_j^{\hbox{'}}-{E}_{ij}^{\hbox{'}\ mes}\right)}^2, $$
(15)

where E ' mes j is the storage modulus obtained from the measured data and E ' j is that computed with viscoelastic parameters. As it will be shown in the results section, the Taylor series expansion of the Yeoh model shows that Young modulus E 0 should be six times C 1 [34].

Inflation-Extension Test

The I-E test was developed to simulate as faithfully as possible the deformation of a blood vessel when it is subjected to pulsating flow. Moreover, the device was designed to be coupled with stereovision or non-invasive medical imaging methods (MRI, CT or US) to assist in the calibration of these methods. In the present work, the deformation of the samples was followed using Antares US system (Siemens Healthcare, Saint-Denis, France), for reasons of its low cost and relatively high spatio-temporal resolution (15 μm, 26Hz). However, the use of other imaging methods will be discussed further on the basis of the results obtained.

The silicone tube-shaped sample (internal diameter = 20 mm, thickness = 1.5 mm and length = 100 mm) was positioned in a closed flow circuit (Fig. 1), in which a continuous or pulsed flow can be generated by a pump driven by a command device that can regulate the volume flow rate to simulate the diastole and systole times. This part constitutes the propulsive unit. The silicone tube under test was connected to a hydraulic connection with flexible rubber pipes in order to avoid circumferential and longitudinal prestreches. The sample was placed in an analysis unit filled with water in order to carry out US image-based measurements. These two units were connected together by a rigid PVC pipe and rapid connections presenting low regular and low singular pressure losses. Check valves were placed at the input and the output of the tube to avoid a flow back to the pump during the diastole time. The pressure loss coefficient K for these check valves was evaluated (K = 2.0 ± 0.2) [35]. In order to assess the stress components, an accurate determination of the internal pressure synchronized with the deformation measurements is required. The pressure was measured at a sampling frequency of 100 Hz using a 7-F micromanometer-tip catheter (Millar Instruments, Houston, TX, USA) positioned in the tube.

Fig. 1
figure 1

Inflation-Extension test: The silicone sample tube is placed in the analysis unit in series with the propulsive unit, which is filled with water. Hydraulic connections and rigid PVC pipe are used to ensure an impermeable flow circulation between the two units. Flexible rubber pipes are connected to the ends of the sample tube to avoid circumferential and longitudinal prestreches. The pressure in the sample is driven by a pulsated hydraulic circulation (closed circulation), which is controlled by a submersible pump and its control system. The pressure and elongation recording are measured by a micromanometer placed in the hydraulic circulation inside the tube (using the active valve) and by a US scanner, respectively. Check valves are positioned both upstream and downstream of the tube in order to subtract a possible fluid hammer

Full size image

With the objective of simultaneously following the circumferential λ θ (t) and longitudinal λ z (t) elongations, a linear 38 mm US probe operating at 5 MHz was placed lengthwise with regard to the tube. If this probe was placed in the tube width direction, the circumferential elongation would have been measured with higher accuracy but the longitudinal elongation could not have been determined. The images from the US scanner clearly depicted the inner and outer boundaries of the silicone tube due to the change of the wave speed between the silicone and water environments with a speed of sound close to 1000 and 1540 m.s−1, respectively. However, there is no natural contrasting marker that could be used for λ z tracking, neither along the tube wall nor in its thickness (Fig. 2(a)). In the absence of such markers, only the displacements perpendicular to the boundaries (and thus the circumferential elongations λ θ ) can be estimated, which is well known in image processing as the aperture problem. A first solution might be the incorporation of scatterers in the silicone formulation so as to create speckle similar to that observed in the images of tissues. However, the high density of such scatterers necessary to achieve this effect was likely to alter the mechanical behavior of material. Therefore, markers (strips approximately 2 mm thick) were stuck onto the tube surface in the circumferential direction (Fig. 2(b)) to make the longitudinal elongation measurement possible. These markers were sufficiently compliant to avoid any perturbation of the deformation.

Fig. 2
figure 2

Silicone tube visualization from US imaging: without (a) and with (b) longitudinal markers; blue lines define the first to third boundaries from top to bottom for each picture

Full size image

After acquisition, each picture of the kinematics data was interactively analyzed using the creaContoursFootnote 1 software, part of the CreaTools [36] platform to recover the elongation evolution as a function of time. To identify the model parameters, the thickness, the internal diameter and the distance between the two markers need to be quantified, with minimum effort on the part of the user. Furthermore, the low amplitude of the inflation movement justifies a simple assumption that interfaces can be considered rectilinear and parallel to each other. Consequently, it is sufficient to click on two points, a and b, simultaneously defining the first boundary and the distance between the markers, and two other points, c and d, located on the second and third boundaries, respectively (Fig. 3). Then the software builds the line x = (ab), its parallels x’ through c, and x” through d. The line y, perpendicular to x, x’ and x”, passes through d, so that x ∩ y = {b ’} and x ’ ∩ y ’ = {c ’}. Subsequently, the internal diameter \( D=\overline{c^{,}d} \), the tube wall thickness \( h = \overline{b^{,}{c}^{,}} \) and the length between the markers \( l=\overline{ab} \) are calculated. From these data, the circumferential and longitudinal elongations as a function of time were deduced. It is noteworthy that, in the case of a large number of image sequences acquired, automatic software called Carolab [37, 38], which has already been applied in clinical imaging, could be adapted to estimate these elongations.

Fig. 3
figure 3

Computation method for inflation-extension test

Full size image

In the present study, the I-E test was used in static and dynamic modes. The static mode consisted in applying a continuous flow at constant pressure for 30 s before recording the pressure and elongations. Hence, the measurement only contained the hyperelastic part of the behavior. Here, the imposed static pressure was chosen in a magnitude range (0 to 160 mmHg) consistent with that of a human aorta. For the material 3040-HC2/75, this range was reduced (0 to 75 mmHg) in order to stick to the circumferential elongation physiological range (λ θ <1.3). In the dynamic mode, a pulsed flow was imposed and, after 30 s, the pressure and elongations were recorded as a function of time. It must be added that, apart from the results presented in the present paper, the transient case was considered and it was verified that the stress pulsation calculated with the parameter sets obtained for the two materials was stabilized after six to eight cycles. Therefore, a delay of 30 s was ample to assume that the discontinuity at the beginning of the strain is sufficiently old so that it does not interfere in the stress evaluation. In these conditions, the steady state can then be used, which can be repeated to give an average over several cycles (we actually averaged five load–unload cycles) and thus increase the signal-to-noise ratio (Fig. 4) In this way, the calculation can be made using equation (6), as though the measured strain pulsation started from minus infinity. The amplitude of the imposed pressure pulsation was chosen in a large magnitude range bounded by the physiological limit values (P < 160 mmHg and λ θ <1.3). For the RTV 3040 material, the pressure range was P ∈ [2; 160] mmHg and for the 3040-HC2/75 material P ∈ [18; 48] mmHg. The pulsation rate was approximately 65 pulsations per minute.

Fig. 4
figure 4

Elongations (a) and pressure (b) tracking for 3040-HC2/75 material: Exp (experimental data); Av (Average). The Av curves have been obtained by: first, averaging the five cycles of measurements (Exp) represented in this figure, and then, repeatedly tracing the same average cycle

Full size image

However, it was not possible to fully ensure the accurate synchronization of the two signal acquisitions (pressure and US imaging), because of totally independent acquisition devices. Nevertheless, this synchronization must not be ignored because the phase lag between both periodical signals of deformation and stress is characteristic of the viscous behavior. Thus, the synchronization of the curves was performed simultaneously with the adjustment of the parameters to guarantee the consistency of the results. For that purpose, a trial-and-error method was applied. As a starting point, the time origins of the signals were set in such a way that the maxima of the deformation and the pressure coincided, as though the material was purely elastic. Then, a first parameter fitting was performed. If the value of the resulting viscosity was non-zero, a time lag was inevitably obtained between the maxima of the experimental stress and the stress calculated with this first parameter set. The time origin of the experimental stress was shifted to compensate this time lag, and the parameters were fitted for a second time. This led to a second time lag (smaller than the first one) and the origin of the time scale was again corrected accordingly. This procedure was repeated till the obtained time lag became insignificant, that is, smaller than the sampling time of the experimental signal. Hence, the signals were synchronized in that sense that the stress calculated with the fitted parameters exhibited a maximum at the same position as the experimental one.

Inflation-extension parameters

For the I-E test, cylindrical coordinates are much more appropriate to express the strain. For a tube dilation, the strain expression has been reviewed in detail by [14]. The right Cauchy-Green tensor is written:

$$ \boldsymbol{C} = \left[\begin{array}{ccc}\hfill {\lambda}_r^2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill {\lambda}_{\theta}^2\hfill & \hfill \gamma {\lambda}_{\theta }{\lambda}_z\hfill \\ {}\hfill 0\hfill & \hfill \gamma {\lambda}_{\theta }{\lambda}_z\hfill & \hfill {\lambda}_z^2\left(1+{\gamma}^2\right)\hfill \end{array}\right], $$
(16)

where λ r , λ θ and λ z are the radial, circumferential and longitudinal elongations, respectively. For an incompressible material, λ r λ θ λ z  = 1 so that λ r  = (λ θ λ z )− 1. The parameter γ is a term associated with the twist angle of the tube arising from the possible bending or torsion of the tube. In this study, for rectilinear parts, this can be ignored (γ = 0). To define the mechanical behavior of the sample, it is necessary to simultaneously record the circumferential (λ θ ) and longitudinal (λ z ) elongations and the internal pressure P(t) as a function of time. The circumferential elongation is obtained from the diameter measurement:

$$ {\lambda}_{\theta }=\frac{D(t)}{D\left(t=0\right)}, $$
(17)

where D(t = 0) and D(t) are the internal diameter at the reference and current states, respectively.

The longitudinal elongation is given by equation (18):

$$ {\lambda}_z = \frac{l(t)}{l\left(t=0\right)}, $$
(18)

where l(t = 0) and l(t) are the distances between the markers also at the reference and current states, respectively.

Moreover, as mentioned in the experimental part, the internal pressure is directly measured. For a thick wall, the circumferential stress σ θ induced by this internal pressure is expressed through equation (19):

$$ {\sigma}_{\theta }(t) = \frac{\left(D(t)+h\right)P}{2h}, $$
(19)

where h is the thickness of the tube wall.

The circumferential component of the PK2 stress tensor S ∞ iso,θ for the hyperelastic part on the constitutive model can be written:

$$ {S}_{iso,\theta}^{\infty } = \frac{1}{\lambda_{\theta }}\frac{\partial {\psi}_{iso}^{\infty }}{\partial {\lambda}_{\theta }}={\lambda}_{\theta}^{-2}{\sigma}_{iso,\theta}^{\infty }, $$
(20)

where σ ∞ iso,θ is the equilibrium Cauchy stress component. It must be noted that, because of the first invariant I 1 that appears in equation (2), the knowledge of both λ z and λ θ is required to determine σ ∞ iso,θ .

Then the expression of the total PK2 stress can be obtained from equations (3) and (6). Nevertheless, because of the integral equation including the time derivative of S ∞ iso,θ in equation (6), some numerical precautions must be taken for this calculation. Consequently, S ∞ iso,θ can be rewritten using equations (2) and (20) giving:

$$ {S}_{iso,\theta}^{\infty } = {\displaystyle \sum_{i=1}^n}{C}_i\frac{i}{\lambda_{\theta }}\frac{\partial {I}_1}{\partial {\lambda}_{\theta }}{\left({I}_1-3\right)}^{i-1}\ . $$
(21)

At this step, for the assessment of the integration in equation (6), it is judicious to expand the terms of equation (21) into Fourier series [17]. For instance, for a second-order Yeoh model, this leads to the series:

$$ \frac{1}{\lambda_{\theta }}\frac{\partial {I}_1}{\partial {\lambda}_{\theta }}={a}_0+{\displaystyle \sum_{k=0}^p}{a}_k \cos \left(k\omega t\right) + {b}_k \sin \left(k\omega t\right), $$
(22)
$$ \frac{2}{\lambda_{\theta }}\frac{\partial {I}_1}{\partial {\lambda}_{\theta }}\left({I}_1-3\right)={a^{\hbox{'}}}_0+{\displaystyle \sum_{k=0}^p}{a^{\hbox{'}}}_k \cos \left(k\omega t\right) + {b^{\hbox{'}}}_k \sin \left(k\omega t\right). $$
(23)

Thus, the time derivative of S ∞ iso,θ is given by:

$$ \begin{array}{cc}\hfill {\dot{S}}_{iso,\theta}^{\infty }={C}_1\left[{\displaystyle \sum_{k=0}^p}-k\omega {a}_k \sin \left(k\omega t\right)+k\omega {b}_k \cos \left(k\omega t\right)\right]\hfill & \hfill +{C}_2\left[{\displaystyle \sum_{k=0}^p}-k\omega {a^{\hbox{'}}}_k \sin \left(k\omega t\right)+k\omega {b^{\hbox{'}}}_k \cos \left(k\omega t\right)\right]\ .\hfill \end{array} $$
(24)

Consequently, equation (6) can present a closed-form expression because it is composed exclusively of products of exponential and sine or cosine functions, as shown in Fig. 5 for the 3040-HC2/75 material. This can be very helpful to avoid numerical integrations that may be blurred because of a relatively poor signal-to-noise ratio or time resolution.

Fig. 5
figure 5

Modeling results for equations (21 & 22) with third order Fourier series: Exp (experimental data); NR (numerical output data)

Full size image

From I-E test, the identification of hyper-viscoelastic material parameters (C IE i , β IE α ) was performed by solving the minimization problem (using the same procedure as above):

$$ \left\{{C}_i^{IE},\ {\beta}_{\alpha}^{IE}\Big|i=1,\dots,\ n;\ \alpha =1,\dots, m\right\}= \arg min{f}_{obj}^{IE}\ \left({C}_i,{\beta}_{\alpha}\Big|i=1,\dots,\ n;\ \alpha =1,\dots, m\right) $$
(25)

with f IE obj defined as:

$$ {f}_{obj}^{IE}\left({C}_i,{\beta}_{\alpha}\Big|i=1,\dots,\ n;\ \alpha =1,\dots, m\right) = {\displaystyle \sum_j^N}{\left({S}_{\theta, j}-{S}_{\theta, j}^{mes}\right)}^2, $$
(26)

where S mes θ,i is the second Piola Kirchoff measured circumferential stress and S θ,i is the one computed with hyper-viscoelastic parameters. Theoretically, from the pressure data, both circumferential (S θ ) and longitudinal (S z ) stresses can be expressed. Thus, it could be foreseen to use both of them in the minimization procedure. Besides, the calculation of these stresses requires both circumferential and longitudinal elongations (λ θ and λ z ). Nevertheless, the longitudinal stress is much more sensitive to λ z than the circumferential one and the accuracy of the longitudinal elongation measurement is most likely much poorer than this of the circumferential one (see Fig. 4(a)). Therefore, it appeared more convenient to use only the circumferential stress in the minimization procedure.

Results

Reference Parameter Identification from Standard Measurements

From uniaxial tensile and dynamic compression tests, the reference parameters were identified. First, for the two silicone materials studied, RTV 3040 and 3040-HC2/75, uniaxial tensile tests were performed, and the parameters of the Yeoh model were obtained from the stretching curves. As shown by the linear plots of the Cauchy stress versus \( \left({\lambda}^2-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.\right) \) in Fig. 6-a, a simple first-order Yeoh model, which is reduced to the Neo-Hookean model, is adequate to correctly describe the behavior for the two materials studied. Indeed, non-zero values were obtained for the parameters C ref1 (Table 1), whereas all the other C ref i ≥ 2 were negligible. The agreement between the calculated and experimental results is also shown in Fig. 6(a).

Fig. 6
figure 6

a Uniaxial tensile tests, b DMA compression tests: Exp (experimental data), Ref (numerical output data with reference parameters)

Full size image
Table 1 Hyperelastic and viscoelastic parameters identified from tensile and DMA tests
Full size table

Considering the viscoelastic behavior, the experimental storage moduli E '(ω) were fitted with equation (12). The contributions (β α ) and the modulus (E 0) were then adjusted. The agreement between the calculated and experimental storage modulus E '(ω) is shown in Fig. 6(b) and the results obtained are displayed in Table 1. However, each isolated relaxation time does not present a physical meaning when these are imposed. Thus, for the comparison of the two materials’ behaviors, it is worth showing an overall viscosity value (η 0) obtained by:

$$ {\eta}_0={\displaystyle \sum_{\alpha =0}^m}{E}_0{\beta}_{\alpha }{\tau}_{\alpha }\ . $$
(27)

In Table 1, the uncertainty of the parameters was obtained from two different experiments for each formulation. It can be mentioned that the obtained parameters for the present silicones compare very well with some values given in the literature for actual aortas. For example, Astrand et al. [3] obtained stiffness values (analogous to C 1) varying from 0.02 to 0.28 MPa according to the age. This confirms that the mechanical properties of the used silicone formulations are representative of the behaviors of actual aortas. Unfortunately, concerning the viscoelastic part, it is more difficult to find quantitative results of relaxation times in the literature to compare them with our results.

Identification of the Parameters from the I-E Test

Hyperelasticity

The results for the two materials, in static mode, are shown in Fig. 7 comparing the experimental points (Exp) and the curves calculated using the reference C ref1 parameters (Ref), and those identified from the I-E test (IE-S). We observe that the C IE − S1 parameters obtained, given in Table 2, are very close to the reference C ref1 (see the second column in Table 1) obtained from tensile tests. Here, the uncertainty of the parameters was calculated on the basis of the uncertainty of the elongation measured from the US images.

Fig. 7
figure 7

Inflation-extension test for hyperelastic modeling: experimental and computed true stress: Exp (experimental data); IE-S (numerical output data adjusted to the experimental data); Ref (numerical input data from uniaxial tensile test)

Full size image
Table 2 Hyperelastic parameters identified from I-E measurements (static mode)
Full size table

This also shows that, for the two materials tested, a simple first-order Yeoh model (i.e., Neo-Hookean) is adequate to describe the hyperelastic behavior, the other constants C ref i ≥ 2 being null. These preliminary results open the way to investigating the reliability of the I-E measurements in dynamic mode to extract the whole parameter set.

Hyper-viscoelasticity

In the second step, the hyper-viscoelastic behavior was analyzed on the basis of the I-E dynamic mode experiments (see Experimental Mechanical Setup section). Here the numerical input curves (Ref) are those calculated with the reference parameters resulting from the compression test, whereas the numerical output curves (IE-D) were calculated with the parameters identified from the dynamic I-E test data.

Figures 8 and 9 show the respective results for the RTV 3040 and 3040-HC2/75 materials. These stress curves are displayed together with the measured stress as a function of both time (to highlight the time shift) and strain (to highlight the dissipation hysteresis, while hiding the time notion). Taking into account the fact that the reference parameters were obtained from totally independent measurements, the agreement of the corresponding calculated and experimental curves is rather good. Moreover, after fitting, the simulated curves are very close to the experimental ones. This shows that, by nature, the used model is also able to account for the material behavior in the loading mode of the I-E test.

Fig. 8
figure 8

Inflation-extension test for hyper-viscoelastic modeling on RTV 3040: a stress versus time; b stress versus circumferential elongation: Exp (experimental data), IE-D (numerical output data), Ref (numerical input data with reference parameters)

Full size image
Fig. 9
figure 9

Inflation-extension test for hyper-viscoelastic modeling on 3040-HC2/75: a stress versus time; b stress versus circumferential elongation: Exp (experimental data), IE-D (numerical output data), Ref (numerical input data with reference parameters)

Full size image

For the two materials, the calculated parameters are displayed in Table 3. Here the uncertainty of the parameters was estimated from different sets of measurements on five cycles. The reverse calculation of the storage modulus curves, using the parameter sets deduced from the I-E measurements (IE-D) is shown in Fig. 10.

Table 3 Hyper-viscoelastic parameters identified from I-E measurements (dynamic mode)
Full size table
Fig. 10
figure 10

DMA compression experiments and curves calculated from I-E results: Exp (experimental data), Ref (numerical output data), IE-D (numerical input data from the I-E test)

Full size image

Discussion

The values obtained for C IE − S1 and C IE − D1 are very close to those obtained from uniaxial tensile test (C ref1 ), which confirms the consistency between all the evaluation methods. Concerning the values of the β α parameters, as was already mentioned, it is more judicious to compare the values of the overall viscosities (η 0) than each contribution one by one. We observe that only the viscosity of 3040-HC2/75 material was reasonably evaluated (0.675 MPa.s to be compared with 0.469 MPa.s).

For the RTV 3040 material, this overall viscosity is different compared to reference parameters (Table 1). Indeed, a zero value of the viscosity was calculated from the I-E test. Obviously, we meet the limit of I-E test to accurately identify the viscoelastic part of global mechanical behavior. This limit is partly related to the uncertainties of circumferential and longitudinal elongation measurements by US sonography (1 %), but mainly to the restricted frequency range reachable by the test. Indeed, the pulsation period imposed on the tube (0.92 s) corresponds to the lower bound of the angular frequency around 6 rad/s and the temporal resolution between two images (0.04 s) corresponds to the upper bound of the angular frequency, taking into account the Shannon’s theorem, around 80 rad/s. Additionally, the identification of the viscous component of the material becomes less accurate when the elastic modulus is large, since the (hyper)elastic component then tends to hide the viscous component. This observation can be illustrated on the storage modulus curve (Fig. 10) which exhibits a very low variation in the explored angular frequency range. In other words, if the storage modulus is nearly constant, it will be difficult to separate the viscoelastic and hyperelastic parts with the I-E test. Anyway, seeing the circumferential stress-stretch curve (Fig. 8(b)), where the hysteresis is not clearly observed, it would be unrealistic to expect an accurate identification of the viscosity in this case.

More generally, it must be mentioned that the global viscosity calculated is given just as an indicator but it is controversial to rely on this only value to estimate the quality of the results because it can be sensitive to the initial choice of the fixed relaxation times. A further development of the method would be to reconsider this choice regarding the frequency range accessible with the I-E test. The quality of the results is more easily appreciable in the comparison of the calculations in Figs. 8 to 10 where the calculated curves with the different parameters sets are relatively close of the experimental results.

The results of 3040-HC2/75 material are more encouraging: the experimental data show a significant hysteresis (Fig. 9(b)) and the elastic part is low, so it was possible here to identify a value of overall viscosity relatively close to the reference. The relaxation of this material appears clearly in a frequency range more compatible with the sampling time used in the I-E test.

From all these results, several conclusions can be drawn. First, despite the limitations previously noted, the presented I-E test was shown to be efficient in determining the behavior of the materials studied, which are representative of healthy or aneurysmal arterial tissues. Moreover, these results highlight that US imaging can provide relatively accurate information, opening the doors to the possible parameter identification of a blood vessel by in vivo measurements. Indeed, the hyper-viscoelastic behaviors of the silicone formulations tested are close to those of the aortic tissue (healthy and pathological). In this respect, it is worth recalling that the actual tissues behaviors can cover a very large range depending on the patient age and health and even on the location of the tissue along the aorta. The proposed method thus appears sufficiently accurate to distinguish these behaviors. This makes it possible to consider minimally invasive measurements and the modeling of hyper-viscoelastic behaviors that could be achieved directly from image acquisition using a US scanner or another imaging technique.

From a practical point of view, the method to identify the hyper-viscoelastic model parameters requires three conditions to be verified in clinical application: the temporal tracking of λ θ and λ z with sufficient time resolution, the measurement of the pressure in the region of interest in the aorta, and the synchronization of the two acquisitions.

Depending on the medical imaging modality used, the spatial and temporal resolutions are different. For the present work, the silicone tube motion was visualized by ultrasound imaging. However, in the absence of scatterers within the material, natural landmarks that could be used in λ z tracking are missing. This problem was solved by adding physical markers on the tube. It was then shown that both spatial and temporal resolutions of this imaging technique (15 μm and 26 Hz, respectively) are sufficient to identify the hyper-viscoelastic parameters. However, in the case of actual clinical tests, it is obviously impossible to use this type of marker. Fortunately, it has been shown by performing US imaging on blood vessels such as carotid arteries that some organic elements (elastin, collagen, extracellular matrix, etc.) in the arterial layers, act as scatterers. Hence, a “speckle” texture is generated, which can be advantageously used for λ z tracking. Nevertheless, for deep vessels like the aorta tree, it may be more difficult to use this technique because of a coarser spatial resolution achieved when the probe frequency is decreased to obtain a deeper penetration, and physical obstacles such as the ribs. The use of other imaging techniques, such as MRI or CT, might be considered. However, in CT, image acquisition is performed with a relatively low temporal resolution close to 4 Hz, which is not enough for the purposes of this study (only four measurements per cycle would be possible). Furthermore, this imaging technique involves X-ray radiation and might require an iodine contrast agent in the blood to observe the arterial lumen and it would be difficult to define longitudinal landmarks. Conversely, current sequences used in MRI give a higher temporal resolution close to 20Hz. Nevertheless, in dynamic physiological conditions, this technique demonstrates poor spatial resolution (about 1 mm).

Rigorously speaking, the simultaneous measurement of the blood pressure to assess stress is required to model hyper-viscoelastic behavior. At present, this only can be performed using a micromanometer placed within the region of interest in the aorta. As percutaneous introducing of a micromanometer is invasive, such a procedure would have to take advantage of the catheter used for coronarography in the cases where the latter is performed prior to surgery. Otherwise, blood pressure could be non-invasively measured in another part of the body, as a recent study [39] has obtained encouraging results in estimating local pressure variations via indirect measurements. Anyway, non-synchronization of the pressure and deformation measurements must be taken into account to evaluate the model parameters as long as integrated synchronizing solution is not implemented by scanner vendors. For this purpose, the procedure proposed in this work can be used.

Conclusion

The aim of this study was to validate an identification method using an inflation-extension measurement on a tube, in order to accurately predict the mechanical behavior of its wall in terms of both hyperelastic and viscoelastic components. Such a system can be used as a helpful tool for the development of aorta phantoms with a behavior as realistic as possible. The method was validated by showing that the hyper-viscoelastic behaviors of silicone materials, having properties similar to the aorta, were successfully identified and compared well with the standard measurements (tensile tests and DMA). Ultrasound imaging was able to track elongations throughout the dynamic solicitation of cylindrical samples. The use of the present method in the clinical environment for in vivo experiments using common imaging techniques can be foreseen provided precautions are taken in terms of spatio-temporal resolution and signal synchronization. Eventually, the methodology developed to identify the model parameters would be helpful to predict vascular pathologies from in vivo experiments considering the alteration of the tissue behavior due to the disease.