Introduction

Thermal field measurements are valuable tools for studying thermomechanical couplings which are often associated with deformation of materials. The intensity and spatiotemporal distribution of temperature variations depend on the material behavior (elasticity, plasticity, viscosity, damage, phase transformation, etc.) but also on the different characteristics of the thermal problem (geometry, thermal properties, boundary conditions, etc.). Previous work [1] highlighted the interest of studying local heat sources that cause temperature variations, e.g. when studying Lüders bands and necking in steels [1, 2], Portevin Le Châtelier bands in AlMg alloys [3], plasticity in Al oligocrystals [4] and stress-induced phase transformation in Nickel-Titanium (NiTi) shape memory alloys [5, 6]. In all of these studies, the thermal conductivity of the tested sample was assumed to be constant during deformation. However, this hypothesis no longer applies for some materials and/or types of loading.

The first objective of this paper is to present a methodology to obtain better heat source estimations when thermal conductivity is not constant. This method requires kinematic field measurements and spatiotemporal synchronization of thermal and kinematic full fields measured during a mechanical test.

The second objective is to apply the above methodology to the analysis of superelastic tensile tests in the case of nickel-titanium (NiTi) shape memory alloys (SMA). When superelastic deformation involves reversible stress-induced phase transformation, from austenitic phase (A) to martensitic phase (M), non-constant thermal conductivity occurs. NiTi SMAs have been extensively used in many engineering applications, especially in biomedical products (including stents and catheters) where the superelasticity of these alloys is required [7]. In spite of the ever-increasing interest in SMA modeling, there are still many unsolved problems with the predictability of the thermomechanical responses of this material [8]. One of the main limitations is the deformation localization that appears systematically during the stress plateau in tensile tests [9–16]. This localization may disappear for other mechanical loadings such as compression, shear or equibiaxial tension [16–18] or tension-torsion combined tests [19]. It may also be observed during the ferroelastic tensile deformation of polycrystalline NiTi SMAs [20]. This localization has been studied using qualitative optical observations [13, 15], multiple extensometers [14, 16], strain [6, 11, 18], temperature [6, 12, 15] full-field measurements and recently by in situ EBSD investigations [21]. Temperature measurements obtained by infrared thermography was previously used in [6] to estimate heat sources during the homogeneous stages of a tensile test on NiTi tubes. Such heat sources, linked to the local latent heat of the phase transformations involved in SMAs, brought new and precious information on deformation mechanisms in SMAs. When phase transformation is localized, the method to estimate localized heat sources is different; see [1] for thin sheets and [5] for thin tubes.

Thermophysical parameters, such as the specific heat C and the thermal conductivity k of the material, are necessary to estimate the heat sources. Few published studies have been attempted to monitor these thermophysical parameters in NiTi materials. For example, C and k were assumed to be constant in our previous studies carried out with polycrystaline NiTi SMAs [5, 6]. However, some experimental studies (e.g. see [22]) have shown substantial differences in C and k for austenite and martensite. The differences seem to be greater for the thermal conductivity. By working with a polycrystalline NiTi wire, Faulkner et al. [22] obtained a ratio of two between the thermal conductivity of austenitic k A and martensite phases k M , i.e. k A  = 28 W m−1 K−1 and k M  = 14 W m−1 K−1. Specific heat values given in the literature are also scattered, but in our study we decided to take a mean specific heat for the two phases for the sake of simplicity: C = 450 J kg−1 K−1. However, different k values (through different models) are proposed in order to take the possible variations in k with the volume fraction of martensite into account. Information on phase fraction changes during loading is thus obtained from local strain levels, measured via digital image correlation (DIC) applied to visible images recorded during the test.

Simultaneous strain field (from DIC applied to visible images) and thermal field measurements (obtained from infrared thermography) during mechanical testing were first reported in [23] and [24]. In the first work, kinematic fields were used to locally compute the true stress and to estimate the convective term in the heat diffusion equation. In the second paper, temperature, heat source and axial strain fields were qualitatively compared during a tensile test on an Al multicrystal. More recently, three other studies [25–27] proposed a major improvement in the synchronization of kinematics and thermal fields. They offer the possibility of computing the temperature field in the reference configuration, i.e. to monitor the temperature of material points, even in the case of in-plane displacements of these points. In [25], the two cameras each monitored one side of a thin plate steel sample. Heat sources were estimated from the thermal fields in the reference configuration. They were then integrated over time in order to achieve energy balances. An interesting optical set-up was proposed in [26] involving the use of a dichroic mirror, thus allowing two-cameras monitoring of the same surface of the sample. In these two latter research works, the temperature fields were projected in the reference configuration through displacement fields measured by DIC. A last study [27] proposed a motion compensation technique based on detection of reflective spots in visible and infrared images. In the present study, the same surface of the sample was simultaneously observed by a visible and an infrared camera. Thanks to a compatible coating, it was then possible to compute kinematics from DIC and temperature fields from radiations coming from the surface during a tensile test.

After a description of the experimental setup (Experimental Set-Up section), the adopted spatiotemporal synchronization of the thermal and displacement fields is presented (Spatiotemporal Synchronization of Kinematics and Thermal Fields section). This processing allows us time-course variations in temperature for each material point of the sheet sample to be determined. A method to estimate heat sources in the case of different thermal conductivities between the austenite and martensite phases is then presented (Heat Source Field Estimations section). Finally, typical results showing heat source and energy distributions during mechanical tests are given and compared with strain fields (Analysis of Localized Superelastic Tensile Tests of Niti Shape Memory Alloys section).

Experimental Set-Up

Heat source fields are estimated during the deformation of a specimen. Different types of loading can be studied. In many works, as here, quasi-static tensile tests are conducted on sheet samples at room temperature. As a complement to usual mechanical data (force F and cross-head displacement U), kinematic and thermal fields are measured by visible and infrared cameras. An example of such an experimental set-up is given in Fig. 1.

Fig. 1
figure 1

Experimental set-up. (a) Position of the infrared and visible cameras monitoring the same surface of the sheet sample. (b) Close-up of the DIC grid showing the resolution of the kinematic fields (grid step = 0.65 mm). (c) DIC grid (in green), position of the two extreme points A and B. The distances L 0 and l 0 are the gauge length and the distance between A and B, respectively

Full size image

In this study, a fast multidetector infrared camera (CEDIP Jade III MW, 14 bits, 320 × 240 pixels, thermal resolution 20 mK) was used to measure the temperature field T(M, t) in spatial points M of spatial position \( \vec{x} \) at current time t. The infrared frame rate was f IR   = 5 Hz. The spatial resolution (pixel size) of the thermal fields was estimated at 0.22 mm for the conducted test. The displacement field \( \vec{u}\left( {M,t} \right) \) at the sample surface was obtained using a digital visible camera (Hamamatsu, 12 bits, 1280 x 1024 pixels) and DIC processing software (7D software [28]). The frame rate for the visible images was f v   = 0.5 Hz. The grid size was 10 x 10 pixels and the spatial resolution (pixel size) was estimated to be 0.065 mm. The resolution of the kinematic fields (grid step) was then 0.65 mm (see [29] and Fig. 1(b)). The Green-Lagrange strain fields were estimated from the displacement field \( \vec{u} \) and can be represented in the referential (Lagrangian description) or deformed (Eulerian description) configurations.

The sample surface was coated (spray projection) with high emissivity black paint (commercial black paint spray) with a white texture on top of it, as shown in Fig. 1(a). As shown in [30], this coating is compatible with both the infrared and visible observations and its measured emissivity ε was 0.98, i.e. very close to black body emissivity (ε = 1). This difference was neglected and ε = 1 was used in the following. The optical axis of the visible camera was normal to this surface and the infrared camera was slightly oriented (at 15°) in the normal direction. Because the thermal radiation of a black body is not influenced by disorientation of the camera below 45°, our setup allows quantitative measurement of thermal fields [30].

As in [6], a mean nominal axial strain \( \varepsilon = \frac{{\Delta l}}{{{l_0}}} \) was measured from the displacement fields using the relative displacement Δl of two material points A and B located at the extremities of the gauge length (Fig. 1(b), (c)), with l 0   = 58 mm being the initial distance between these two points.

Spatiotemporal Synchronization of Kinematics and Thermal Fields

The method proposed in the present paper is the same type as that proposed in [25, 26]. The main characteristics of the methods used in these two references are recalled at the end of the Introduction section. However, our approach differed slightly from these studies since the two cameras directly monitored the same sample surface. First, the temporal synchronization necessary to get the signals at the same time is presented. Once this temporal synchronization is achieved, spatial synchronization is also done to obtain the temperature field at each material point. This synchronization will be presented in the second subsection.

Temporal Synchronization

During the experiments, mechanical data (including force, crosshead displacement), visible images together with infrared images were recorded. The three acquisitions have their own time base, defined by the initial time and frequency, as plotted schematically in Fig. 2. It is then often difficult to achieve, with good accuracy, temporal correspondence between the kinematic field, the temperature field and the usual mechanical data (including force). Moreover, such a situation is enhanced when the acquisition frequencies differ from each other and/or transient phenomena are observed.

Fig. 2
figure 2

Example of the different characteristics of the three used time bases

Full size image

The method used in this work manages, with a homemade software, the data recorded from the three different time bases. The mechanical data and times of the visible images (i.e. of the infrared ones, respectively) were projected onto the infrared time base (i.e. onto the visible time base, respectively) using linear interpolations between the temporal data.

Spatial Synchronization

The kinematic fields (displacements, strains) were obtained on the reference configuration (Lagrangian or material description) or in the current configuration (Eulerian or spatial description). During such measurements, the fixed infrared camera observes the temperatures of spatial positions whereas the material points can move towards the fixed observation area (see Fig. 5). The temperature fields are then given as function of spatial coordinates: T(x,y,t), where x and y are the spatial coordinates of the material point P (with P having integer pixel values) at time t.

Therefore, three coordinate systems CS (or virtual grids) are available:

  • CS-V: Visible image coordinate system, typically with a resolution of 1280 x 1024 pixels. In this coordinate system the initial and current positions of the material point are noted (X V ,Y V ) and (x V ,y V ), respectively.

  • CS-DIC: DIC coordinate system given by the DIC software. Using a virtual grid on the visible image, every n = 10 pixels, the resolution in both directions is divided by a factor n. The maximum resolution is then about 128 × 102 pixels. In this coordinate system the initial and current positions of the material point are noted (X DIC ,Y DIC ) and (x DIC ,y DIC ), respectively.

  • CS-IR: The infrared image coordinate system, with a maximum resolution of 320 × 240 pixels. In this coordinate system, the initial and current positions of the material point are noted (X IR ,Y IR ) and (x IR ,y IR ), respectively.

In the following, the subscripts ‘V, DIC or IR’ are omitted when the CS are indicated. The spatial synchronization can be achieved in any of the three coordinate systems. Due to the lower resolution of the kinematic grid compared to the infrared one, CS-DIC was chosen in this work. In that case, it enables the operator to know the temperature variation T(P,t) of a material point P, which is not possible with only one infrared camera. This is the same as having small thermocouples glued on the surface at the same position as the virtual DIC extensometers.

Spatial synchronization is useful if the sample is deformed (especially in case of large or localized deformations) or if it moves toward the camera (e.g. rigid body motion at the beginning of a mechanical test). Figure 3 shows the positions of selected material points A, B and P on a tensile sample prior to and after deformation (8% axial strain). The material point A was close to the lower grip. As this grip was fixed during the test, the vertical displacement of A was small. The point B was close to the moving grip. Its typical vertical displacement could go up to (u x ) maxi   = 23 pixels (in CS-IR), which was no longer negligible during 8% tensile strain. Moreover, at the beginning of loading, a rigid body motion of about u x   = 4 pixels and u y   = -3 pixels occurred.

Fig. 3
figure 3

Schematic view of the sample during a tensile test in an initial configuration (a) and in the current configuration (b). The initial and current coordinates of material points A, B, P are (X,Y) and (x,y), respectively. (c) Example of an experimental temporal variation pattern of horizontal (u y ) and vertical (u x ) displacements (in CS-IR) of points A and B. At the beginning, both points move together, due to rigid body motion

Full size image

With the proposed spatial synchronization, it was possible:

  1. (i)

    to calculate temperature variations of material points and not of spatial points. Without spatial synchronization, the temperature variation (noted θ 0) was estimated at each spatial point (pixel x IR ,y IR of the IR camera) in CS-IR using:

    $$ {\theta^0}\left( {{x_{{IR}}},{y_{{IR}}},t} \right) = T\left( {{x_{{IR}}},{y_{{IR}}},t} \right) - {T_0}\left( {{x_{{IR}}},{y_{{IR}}}} \right). $$
    (1)

    Initial measured temperature field on the sample may be heterogenous (T 0 (x IR ,y IR ) ≠ constant) either if a temperature gradient (often less than 0.5 K) is observed on the sample (due to the boundary conditions and the gripping system) or if the emissivity of the sample surface is not constant. So, if during the measurement there is displacement of the material points (rigid body motion or deformation), estimating the temperature variation using θ 0 can induce substantial errors. Instead, the temperature variation (noted θ) should be estimated for a material point P through:

    $$ \theta \left( {P,t} \right) = T\left( {P,t} \right) - T\left( {P,0} \right) = T\left( {{x_{{IR}}},{y_{{IR}}},t} \right) - {T_0}\left( {{X_{{IR}}},{Y_{{IR}}}} \right), $$
    (2)

    where X IR and Y IR are the initial coordinates of the material point P.

  2. (ii)

    to obtain heat sources at a material point and the corresponding energies (by integrating over time heat sources) in each material point (more details are given in Analysis of Localized Superelastic Tensile Tests of Niti Shape Memory Alloys section).

Spatial synchronization method

In order to allow spatial synchronization, both cameras need to be fixed during the measurement. The two coordinate systems CS-V and CS-IR, initially independent, were spatially linked by choosing reference points at the same initial time t 0   = 0, on the visible and infrared images.

The initial position (X V ,Y V ) on the visible image of any material point P can then be linked to its position (X IR ,Y IR ) on the infrared image using a rotation of angle α, a translation vector \( \vec{T} = \left( {{T_x},{T_y}} \right) \), and a homothetic transformation κ to change the length scale.

A transformation matrix \( \underline{\underline {v2ir}} \) is built to go from the visible to the infrared description with:

$$ \left( {\begin{array}{*{20}{c}} {{X_{{IR}}}} \hfill \\ {{Y_{{IR}}}} \hfill \\ 1 \hfill \\ \end{array} } \right) = \kappa \left( {\begin{array}{*{20}{c}} {\cos \left( \alpha \right)} \hfill & {\sin \left( \alpha \right)} \hfill & 0 \hfill \\ { - \sin \left( \alpha \right)} \hfill & {\cos \left( \alpha \right)} \hfill & 0 \hfill \\ \end{array} } \right)\left( {\begin{array}{*{20}{c}} {{X_V}} \hfill \\ {{Y_V}} \hfill \\ 1 \hfill \\ \end{array} } \right) + \left( {\begin{array}{*{20}{c}} {{T_x}} \hfill \\ {{T_y}} \hfill \\ 1 \hfill \\ \end{array} } \right) = \underline{\underline {v2ir}} \left( {\begin{array}{*{20}{c}} {{X_V}} \hfill \\ {{Y_V}} \hfill \\ 1 \hfill \\ \end{array} } \right), $$
(3)

and:

$$ \underline{\underline {v2ir}} = \left( {\begin{array}{*{20}{c}} {\kappa \cos \left( \alpha \right)} \hfill & {\kappa \sin \left( \alpha \right)} \hfill & {{T_x}} \hfill \\ { - \kappa \sin \left( \alpha \right)} \hfill & {\kappa \cos \left( \alpha \right)} \hfill & {{T_y}} \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right). $$
(4)

Conversely, the matrix \( \underline{\underline {ir2v}} \) enables one to obtain the position in the visible system from the infrared one: \( \underline{\underline {ir2v}} = {\underline{\underline {v2ir}}^{{ - 1}}} \). Note that the new coordinates after operation (3) are generally not integer values, but fractions of pixels. The four parameters of the transformation (α, κ,T x ,T y ) are identified from the initial positions of characteristic points selected in the initial visible and infrared images. A minimum of two characteristic points is necessary. However, the positions of such points are only known, in the two images, with one pixel accuracy. To reduce this uncertainty, the user can choose as many characteristic points as possible. Average values of the unknown parameters are then obtained from the set of selected points. An example is presented in Fig. 4, where three characteristic points were easily chosen in the two initial images (CS-V and CS-IR) via a steel ruler stuck on the sample surface.

Fig. 4
figure 4

Visible image (a) and infrared image (b) of a tube sample and a steel ruler prior the test. A grey colormap was used. Three characteristic points (A, B and C) were selected for each image on the ruler. The two images were rotated by 180° due to the position of the two cameras

Full size image

In order to obtain the temperature of a material point P, at current time t, the spatial coordinates (x IR ,y IR ,t) of this point P in the infrared coordinate system must be calculated. This is achieved through the following steps (Fig. 5):

Fig. 5
figure 5

Schematic view of the spatial synchronization. (a) Visible and (b) infrared image at initial time t 0   = 0. The initial positions of a material point P(0) in the two images are related by the transformation \( \underline{\underline {ir2v}} \) or \( \underline{\underline {v2ir}} \). (c) Visible image after deformation, at time t, corresponding to visible image 60. New current position of the material point P(t) obtained by DIC. (d) Infrared image 599 corresponding to time t and the material position of the particle P(t) using transformation \( \underline{\underline {v2ir}} \). The visible images are represented on CS-V (168 × 1260 pixels) and the infrared ones on CS-IR (40 × 311 pixels). The axial displacement in CS-IR of P between image 589 and initial image 99 was 9.5 pixels

Full size image
  1. 1.

    The position at time t 0 of the material point P, located in CS-IR (Fig. 5(b)), is computed in CS-DIC (Fig. 5(a)) using \( \underline{\underline {ir2v}} \) transformation.

  2. 2.

    At time t, the position of the material point P(t) is given by the DIC software, in CS-DIC (Fig. 5(c)).

  3. 3.

    The current position in CS-IR of P(t) is then obtained using \( \underline{\underline {v2ir}} \) transformation (Fig. 5(d)).

  4. 4.

    Finally, the temperature of P(t) is estimated with T(x IR ,y IR ,t) in CS-IR.

This procedure can be used: (i) to express, in the initial CS-IR, the temperature of a material point over the time, or (ii) to project the temperature field in the initial CS-DIC. Spatial interpolation, bilinear or bicubic (not detailed here) are necessary to obtain the temperature in sub-pixel positions. Figure 6 shows such a situation in a common case where the resolution in CS-DIC is lower than in CS-IR.

Fig. 6
figure 6

Scheme illustrating the spatial interpolation. The resolutions of the CS-DIC and CS-IR are indicated and show a higher resolution for the infrared grid. The initial and current grids, in CS-DIC, are projected in CS-IR using \( \underline{\underline {v2ir}} \) transformation. In the two cases, spatial interpolation (bi-linear or bi-cubic) was used to estimate the temperature of the initial or current position of the material points P described by the CS-DIC pixels

Full size image

Example of Synchronization

One example of spatiotemporal synchronization was chosen to illustrate the differences between the two expressions of the temperature variation (θ and θ 0) and also to show the capacity of the method to monitor the temperature of a material point. This example was built from a real quasi-static tensile test conducted on a NiTi tube in quasi-isothermal testing conditions [30] (see Fig. 7(a), (b)).

Fig. 7
figure 7

Illustration of spatiotemporal synchronization in the case of a real tensile test conducted on a NiTi tube sample in quasi isothermal conditions. Position of the tube (cross hatched) and of the processing area (red background color) at (a) initial (free) and (b) current (loading) time t. Material points A and B are also indicated in the two situations. (c) and (d) Green Lagrange axial strain field E xx and temperature variation field at current time t = 37 s, observed in CS-DIC, in Lagrangian description. (e) Temperature variation field at the same time, observed in CS-DIC, in Eulerian description. Time-course patterns of (f) the axial strain and (g) the temperature variation θ(X,Y,t) at the two material points A and B. (h) Time-course patterns of the temperature variation θ 0 (x,y,t) for the current position in pixel (x,y) of the two points A and B

Full size image

During this test, a deformation localization propagated from the left to the right side of the sample, associated with a phase transformation front. The instantaneous strain field E xx , plotted in Fig. 7(c) in Lagrangian description, shows two regions of very different strain values, with a boundary around material point B. The temperature variation fields (θ and θ 0) are plotted in Fig. 7(d) and e at the same time in CS-DIC, but not with the same description: Lagrangian for θ (i.e. on the initial configuration) and Eulerian for θ 0 (i.e. on the current configuration at time t). The thin thermal band, associated with the exothermic phase transformation, is well located at the material point B (Fig. 7(d)), at the same position as the strain jump (Fig. 7(c)). With the field θ 0 (x,y,t), obtained from equation (1) and presented in the Eulerian description (Fig. 7(e)), the position and intensity of the thermal band are modified. The intensity change is enhanced in this example because of the non-uniformity of the initial thermal image T 0 and the radial rigid displacement observed at the beginning of the loading.

The time course of strain (Fig. 7(f)) and temperature variations (Fig. 7(g) and (h)) at points A and B show the interest of monitoring the temperature of material points. The temperature variation peaks (Fig. 7(g)), associated with deformation localization phenomena, coincide with the strain jumps in the case of the Lagrangian description θ(X,Y,t). In contrast, a time lag (Fig. 7(h)) is observed in the Eulerian plot θ 0 (x,y,t), where x and y are the coordinates of the pixel coinciding with points A and B at the initial time. As noted before, a slight difference in amplitude, induced by the approximated evaluation (equation (1)) of the temperature variation, can also be observed in this figure.

Heat Source Field Estimations

Heat Diffusion Equation

The method to estimate heat source fields on the basis of thermal fields was extensively explained in [1]. At the current time t and at a spatial point of a domain Ω, located by its spatial position vector \( \vec{x} \), the heat diffusion equation model is:

$$ \rho C\left( {\frac{{\partial T}}{{\partial t}} + \overrightarrow v .\overrightarrow {\text{grad}} \;{\text{T}}} \right) + div\left( { - \underline{\underline k} \overrightarrow {\text{grad}} \;{\text{T}}} \right) = {s_e} + {s_i},\quad \forall \overrightarrow x, t \in \Omega \times \left[ {0,{t_f}} \right] $$
(5)

where T is the absolute temperature, \( \vec{v} \) the velocity vector, ρ the mass density, C the specific heat, \( \underline{\underline k} \) the heat conduction tensor, s e the heat source of external origin (e.g. radiation), s i the heat source of internal origin (e.g. thermoelastic effects, intrinsic dissipation, latent heat rate). The last term is dominant in the case of stress-induced transformation, as illustrated in Analysis of Localized Superelastic Tensile Tests of Niti Shape Memory Alloys section.

In the previous studies [1, 5], the following hypotheses were put forward: (i) the convective term \( \overrightarrow v .\overrightarrow {\text{grad}} \;{\text{T}} \) was considered as a negligible quantity, (ii) C was kept constant during deformation, (iii) \( \underline{\underline k} \) was considered as isotropic and constant, equal to k. Moreover, two other hypotheses were necessary to compute the heat sources: the sample was thin so that (iv) s i and (v) T were assumed to be homogeneous throughout its thickness.

Taking the previous hypotheses into account and integrating equation (5) in the thickness direction leads to the following bi-dimensional heat diffusion equation:

$$ \rho C\left( {\frac{{\partial \theta }}{{\partial t}} + \frac{\theta }{\tau }} \right) - k{\Delta_2}\theta = {s_i},\quad \forall \overrightarrow x, t \in {\Omega_{{2D}}} \times \left[ {0,{t_f}} \right] $$
(6)

where T 0 is the initial thermal equilibrium state, θ = T-T 0 is the temperature variation such that θ ≪ T 0 , ∆ 2 θ is the Laplacian calculated in the 2D mid-plane Ω 2D of the thin sample (sheets [1] or tube [5]), and where τ is a time constant modeling heat losses from the back and front surfaces of the thin sample. Finally note that assumption (i) can be validated depending on the testing material and conditions. In the example shown in Analysis of Localized Superelastic Tensile Tests of Niti Shape Memory Alloys section, we checked that it was relevant (see below).

Heat Source Estimations from Thermal Field Measurements

Taking the room temperature T 0 into account, the infrared camera gives the temperature variation fields θ at each spatial point (pixel) of the infrared image CS-IR. The default coordinate system for the thermal fields will be CS-IR. The coordinate system is indicated if this is not the case.

The internal heat sources s i (x,y,t) are obtained through an estimation of the left hand side of equation (6). The method, based on image processing, is explained and discussed in [1, 5]. In these previous works, all the material coefficients involved in equation (6) were assumed to be constant throughout the test, whatever the state of the material.

In the following, we consider a case in which the thermal conductivity is not constant. As illustrated in Part 5, this is the case during superelastic deformation of a shape memory alloy, which induces a phase transformation between austenite A and martensite M. The conduction term of equations (5) and (6) for a thin sample is then:

$$ \matrix{ {div\left( { - \underline{\underline k} \overrightarrow {grad} \,\theta } \right) = - div\left( {k\,\overrightarrow {grad} \,\theta } \right)} \\ { = - k\,{\Delta_2}\theta - {{\overrightarrow {grad} }_2}k.\overrightarrow {gra{d_2}} \theta } \\ } $$
(7)

where the thermal conductivity is still assumed to be isotropic. Four types of thermal conductivity models can then be proposed:

  1. Model 1:

    constant thermal conductivity throughout the test, independent of the position and the material state:

    $$ k = constant. $$
    (8)
  2. Model 2:

    spatially homogeneous thermal conductivity, but varying with time k = k(t). This is the case when the deforming material is a mixture of two phases A and M, with a martensite fraction f M evolving uniformly at the macro scale over the sample gauge length during its deformation. As a first rough approximation, the thermal conductivity of the two-phase material is written:

    $$ k = k(t) = k\left( {{f_M}(t)} \right) = {f_M}(t){k_M} + \left( {1 - {f_M}(t)} \right){k_A}. $$
    (9)

    Therefore, in equation (6), the term—kΔ 2 θ must be reconsidered as:

    $$ - {\hbox{k}}\left( {{{\hbox{f}}_{\rm{M}}}\left( {\hbox{t}} \right)} \right){\Delta_2}\theta \left( {{\hbox{P,t}}} \right) = - \left( {{{\hbox{f}}_{\rm{M}}}\left( {\hbox{t}} \right){{\hbox{k}}_{\rm{M}}} + \left( {1 - {{\hbox{f}}_{\rm{M}}}\left( {\hbox{t}} \right)} \right){{\hbox{k}}_{\rm{A}}}} \right){\Delta_2}\theta \left( {{\hbox{P,t}}} \right){.} $$
    (10)
  3. Model 3:

    spatially heterogeneous thermal conductivity, k = k(P,t), with values being either k A or k M . As presented in part 5, this is the case during the superelastic tensile test of an NiTi alloy for which localized deformation is associated with localized phase transformation. At each material point, in a first approach, two states are possible: either a low strain value associated with an almost fully austenitic A state or a high strain value associated with an almost fully martensitic M state:

    $$ \left\{ {\begin{array}{*{20}c} {{k = k_{A} \,if\,E_{{xx}} < E_{{AM}} }} \\ {{k = k_{M} \,if\,E_{{xx}} \geqslant E_{{AM}} }} \\ \end{array} ,} \right. $$
    (11)

    where E xx is the local axial component of the Green-Lagrange strain tensor measured by DIC and E AM is a fixed threshold indicating the A to M phase transition (see Analysis of Localized Superelastic Tensile Tests of Niti Shape Memory Alloys section). The value given by equation (11) will be used in equation (6) to locally compute the associated heat source.

  4. Model 4:

    heterogeneous thermal conductivity, k = k(f M (P,t)). The local value of the martensite fraction f M must be known to be able to evaluate k. As recalled in [6], this fraction can be computed from the specific phase transformation heat sources \( {\dot{q}_{{tr}}} = \frac{{{s_i}}}{\rho } \) according to:

    $$ {f_M}\left( {P,t} \right) = \int\limits_0^t {{{\dot{f}}_M}\left( {P,u} \right)du = \int\limits_0^t {\frac{{{{\dot{q}}_{{tr}}}(u)}}{{\Delta H_{{A - M}}^{{tensile}}}}} } \,du, $$
    (12)

    where \( \Delta H_{{A - M}}^{{tensile}} \) stands for the specific enthalpy for a complete martensitic transformation (f M  = 1). Equation (9), with space dependence of f M , and equation (7) are then used.

Analysis of Localized Superelastic Tensile Tests of Niti Shape Memory Alloys

The proposed heat source estimation method is now applied for analysis of the superelastic deformation of a NiTi shape memory alloy. In this paper, we decided to present only one tensile test, representative of several tests conducted on NiTi sheets. In the present work, only heat source estimations using Models 1 and 3 of Part 4 are presented. Model 2 was taken into account in [30] in the case of an homogeneous superelastic shear test. Experimental results using Models 2 and 4 will be presented in a forthcoming paper.

Material and Experimental Procedure

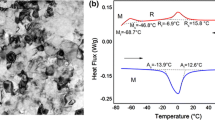
The used material was a commercial NiTi alloy produced in China by the PeierTech company with a composition of Ti-50.6 at.% Ni. The material was annealed for 1 h at 1023 K and then aged at 773 K for 30 min. A specimen for differential scanning calorimetry (DSC) analysis was cut from the sheet using a low-speed diamond cut-off wheel. DSC measurements are shown in Fig. 8 and exhibited standard A→M and M→A phase transformations upon cooling and heating, respectively. The transformation temperatures were determined to be M s   = 253 K, M f   = 230 K, A s   = 256 K and A f   = 272 K, and the enthalpies were ΔH A-M  = 13 J/g, ΔH M-A  = 15 J/g. The initial microstructure of the sample was thus fully austenitic at room temperature.

Fig. 8
figure 8

DSC measurements of the studied NiTi plate

Full size image

The presented tensile test was performed on one rectangular sheet sample of gauge length L 0  = 59 mm, 7.14 mm width and 0.5 mm thickness. It was conducted at room temperature (T 0   = 298 K) and at constant crosshead velocity \( \dot{U}/{L_0} = {4.9 10^{{ - 4}}}\,{s^{{ - 1}}} \). The experimental set-up was described in part 2.

Heat Source Estimation using Constant Thermal Conductivity (Model 1)

In order to analyze this tensile test, strain, temperature variation and heat source fields were synchronized using the method presented in Part 3. The synchronization was performed at the infrared frequency f IR on the CS-DIC (pixel size: 0.65 mm). The temperature variation fields used in equation (6) were computed with equation (2). The heat sources were calculated in the current CS-IR, then projected in the reference CS-DIC.

The nominal stress-strain curve is shown in Fig. 9(a). Figures 9(c) to f present the Green-Lagrange axial strain E xx , the temperature variations θ and the heat source s fields at four different times, as reported in Fig. 9(a). The area corresponding to the CS-DIC is indicated in a scheme in Fig. 9(b).

Fig. 9
figure 9

Comparison of axial strains E xx , temperature variations θ and heat sources fields s M at several times, plotted in reference CS-DIC. (a) Nominal stress strain curve and position of the selected times during loading. (b) Scheme of the area corresponding to CS-DIC. (c) Green Lagrange axial strain E xx (X,Y,t), temperature variation θ(X,Y,t) and heat source s M (X,Y,t) fields at the same time a, indicated in the first Figure. (d) to (f) same fields at times b, c, d

Full size image

Model 1 was first used to estimate heat source fields, with the arbitrary choice k = k M . In that case, the heat sources are noted s M . At this step, these first results will be considered as qualitative estimations of the heat sources.

The test started with an almost linear initial variation in the stress, where positive temperature variation was observed [6]. Then the stress-strain pattern was curving around time a. At this moment, the three fields plotted in Fig. 9(c) were almost homogeneous, despite the fact that weak thermal gradients were noted with the typical associated colorbar. A first deformation localization was then observed at the beginning of the plateau (time b) on E xx and s M fields. This localization took the shape of a thin band, noted B1 in Fig. 9(d). The band angle was about 59° to the tensile axis. At the same time, due to heat diffusion, weak thermal heterogeneities were observed in the thermal field θ. At the middle of the plateau (time c), localization was very important (Fig. 9(e)) and seems very clear considering heat source fields. Strain field monitoring revealed two regions, the first one with small strain values (dark red color) lower than 0.01 and the second one with high strain values (clear yellow color) higher than 0.06. The strain field did not give the current position of the transformation. This was not the case for the heat source field, which showed the zone where substantial phase transformation occurred. At the end of the loading (time d, Fig. 9(f)), the strain and heat sources were also localized. As shown by the strain fields, about 30% of the sample was not transformed and was still mostly in the austenitic phase. Temperature variations increased up to 11 K but, as noted before, were weakly localized. Conversely, the heat sources were strongly localized in thin-phase transformation bands with, qualitatively, the same characteristics (including width, amplitude).

In order to obtain a global view during loading, a spatiotemporal representation of these fields is plotted in Fig. 10. It represents temporal changes in an axial profile of the Green-Lagrange axial strain E xx , the temperature variation θ and the heat source s M . The grey dotted line and the superimposed black continuous line respectively represent the time-course pattern of the nominal stress and the nominal axial strain ε.

Fig. 10
figure 10

Spatiotemporal representations along the tensile axis (indicated by the green dotted line of the fixed Y0 coordinate in the left schemes) of: (a) the Green Lagrange axial strain E xx (X,Y 0 ,t), (b) the temperature variation θ(X,Y 0 ,t) and (c) the heat sources s M (X,Y 0 ,t). The two superimposed curves are the nominal stress σ and the local axial strain ε (refer to Fig. 9(a) to get their amplitude values)

Full size image

As can be seen on all the fields (in Fig. 10), localization phenomena started only around time b in the monitoring area. The first observed localization band (noted B1) occurred in the middle of the sample. At the same time, the temperature had also increased near the upper and lower grips. In fact, localization started before time b but was hidden by the grips. After time b, the middle band B1 became wider and the two bands B2 and B3 that initiated outside the observation area were also widening and therefore visible. Finally, three other bands (B4, B5 and B6) appeared in the middle of “cold areas” of the sample. The bands near the top grip B2, B4, B5 and the middle band B1 had the same orientation (≈59° to the loading axis). The bottom bands B3 and B6 were oriented in the opposite direction (≈−59°). Unlike NiTi tubes, where helical propagation was observed [5, 6, 30], the bands were stopped on the left and right edges of the sheet sample and could only grow wider along the vertical axis. As noted before, the strain fields were still strongly localized at the end of loading (time d) since the test was stopped before the end of the stress plateau. The unloading stress plateau was not observed in this test because the material was not superelastic at this temperature. A remaining strain of ε = 1.8% was noted at the end of the test.

Localization could easily be detected using the temperature field at the very beginning of localization (e.g. temperature field at time b in Fig. 10(b)). Soon after, due to conduction phenomena, temperature fields were difficult to analyze (see θ fields in Figs. 9(d), 10(b)). The spatiotemporal representation of the heat sources (Fig. 10(c)) is more contrasted, showing the continual propagation (spreading) of the active fronts of the bands, with about the same characteristics: width, amplitude and spreading velocity. The heat source bands were localized at the same positions as the strain jumps. When no strain jump was observed, the heat source was weak.

In order to show the influence of the value selected for thermal conductivity in Model 1 to estimate the heat source, heat sources s A and s M , respectively associated with k = k A and k = k M , were plotted for two material points A and B (Fig. 11). The heat sources s A , obtained with higher k values give upper bound values and s M are lower bound values of the actual heat sources. Material point A was chosen in the middle of the sample, where the first band appeared; whereas B was chosen in an area that remained outside of the localization bands (see position in Fig. 9(d)). Their strain patterns, E xx (A) and E xx (B), are plotted in Fig. 11(a) and (b) and the heat sources in Fig. 11(c) to (f).

Fig. 11
figure 11

Temporal variations in Green Lagrange axial strain E xx at (a) material point A and (b) material point B; see positions of points A and B in Fig. 9(d). (c to f) Temporal variations in heat sources s A and s M , computed with the thermal conductivity k A and k M

Full size image

For the two points, the strain pattern was the same before time a (Fig. 11(a, b)). Then, between times a and b, the strain increased quickly at point A, while it stayed almost constant at B. Just before time b, E xx (A) increased suddenly when the first deformation localization band appeared (Fig. 9(c)). After time b and until time d, strain E xx (A) increased in the localized transformation area but with a smaller strain rate, from E xx (A) = 0.055 to 0.07. At the same time, E xx (B) was still constant, about 0.01, in the outside region of the band.

The heat source variations for the two points, plotted in Fig. 11(c) and (d), confirm the previous strain observations. At point A, a sudden and intense peak appeared around time b, when the first transformation band appeared, then propagated in the direction of the mobile grip (see band B1 in Fig. 10(c)). A second smooth peak appeared at the same place just before time c. It corresponds to the widening of the band in the other direction. The heat sources at point B were positive but very weak, but an increase was observed at the end of loading when the transformation was close to point B.

The close-ups shown in Fig. 11(e) and (f) highlight the sensitivity of the heat source estimation with the thermal conductivity value. In areas where the heat sources were strongly localized (e.g. around point A at time b here) the laplacian term in equation (6) was important in the heat source estimation, compared to the other ones. Hence, the heat sources are strongly dependent on k, which explains the marked difference in amplitude between s A and s M (Fig. 11(e)). Some differences were also observed at the beginning of unloading at point A, where the material is supposed to be initially in the martensite phase (Fig. 11(f)). Heat sources s A appeared to be exothermic whereas they are almost zero and then negative when calculated (s M ) with k = k M .

Heat Source Estimation Using Non-Constant Thermal Conductivity (Model 3)

The two Fig. 11(a) and (b) have been merged into Fig. 12(a) in order to analyze the temporal pattern of E xx for material points A and B. This representation shows, for material point A, that the time interval (denoted D) between the less deformed and highly deformed states is very short. In this interval, the phase changed rapidly from almost fully austenitic to mostly martensitic. At the end of this short jump, the strain value (about 5.5%) indicates that the phase transformation was not complete. As reported by [13], complete phase transformation would lead to nearly 8% strain. Hence, the threshold E AM associated with Model 3 (equation (10)) was arbitrarily set at a mean value of 0.04. As a first approximation, the material was considered to be fully martensitic above E AM and k = k M was used to compute the heat sources within this strain range (now denoted s). The two regions E xx   < E AM and E xx   > E AM are indicated in Fig. 12(b) on a spatiotemporal representation along the vertical axis of the sample.

Fig. 12
figure 12

(a) Temporal variations in Green Lagrange axial strain E xx (A) and E xx (B), for material points A and B. The threshold E AM and the length D of the transformation in A are also indicated. (b) Background image showing the spatiotemporal pattern of E xx values plotted, in Lagrangian configuration, with a two-level colorbar defined by the E AM  = 0.04 threshold. The two superimposed curves are the nominal stress σ and the local axial strain ε (refer to Fig. 9(a) to get their amplitude values). The two horizontal dotted green lines indicate the spatial position of points A and B

Full size image

Figure 13(b) and (c) show the strain and heat source axial profiles at four selected times during loading. At time a, heat sources and strain fields were homogeneous and positive. When localization started at time b, heat source and strain peaks were observed in the same area. At times c and d, deformation localization bands were propagating by a widening mode. Heat source positions corresponded to the strain jump areas (see the dotted vertical lines in Fig. 13(b), (c) at time (d)), which are the current region of the A→M stress-induced transformation.

Fig. 13
figure 13

(a) Nominal stress-strain curve and position of selected times during loading. (b) Axial profiles, at the selected times, of the Green Lagrange axial strain E xx , plotted in Lagrangian configuration. (c) Axial profiles of heat sources s estimated with Model 3 of thermal conductivity, plotted in the same Lagrangian configuration. (d) Axial profiles of heat energy q, plotted in Lagrangian configuration and obtained by a time integration of s(X,Y,t). The heat energy, denoted q 0 , plotted in black dotted lines, was obtained by temporal integration of s(x,y,t)

Full size image

Energy Estimation (Application to the Case of Thermal Conductivity Model 3)

From s(P,t) it is possible, for each material point P(x,y,t) of initial coordinates (X,Y), to estimate the specific heat energies q(P,t) locally released during the tensile test by the following time integration:

$$ q\left( {X,Y,t} \right) = \frac{1}{\rho }\int\limits_0^t {s\left( {X,Y,u} \right)du} . $$

Such a local quantity can be considered as an in-situ local DSC of the material. The energy profiles, together with the axial strain and heat source profiles along the central column of the CS-DIC (see Fig. 10) are reported in Fig. 13 at the same time. At the end of loading, time d, the energy profiles reveal two typical levels, associated with the same localization area of the sample where high strains have also been measured. The upper energy values, about 27 J g−1, are associated with exothermic enthalpy of the martensite phase transformation \( \Delta H_{{A - M}}^{{tensile}} \). As noted before, when analyzing strain intensities, the transformation at time d was not complete. However, the intensity (27 J g−1) is still much higher than typical literature values for such alloys obtained by temperature induced transformation (ΔH tr  = 13 J g−1 in the DSC reported in Fig. 8). Such results were already obtained by [31, 32] but during free stress reverse transformation (M→A) consecutive to an initial mechanical loading.

To show the influence of spatial synchronization in the energy estimation, the energy q 0 obtained from spatial heat sources s(x,y,t) in equation (13) was plotted at time d in Fig. 13(d). This energy profile is noisier than q and the positions of the energy upper levels do not at all correspond to the upper strain levels.

From Figs. 10, 11 and 13, it is possible to quickly verify hypothesis (i) on the weakness of the convective term used in Heat Diffusion Equation section to establish equation (6). The strain jump in the band is about 0.045 in about 10 s (Fig. 11), so the mean axial strain rate in the band is about 0.0045 s−1. The bandwidth is close to 4 pixels (Fig. 13(b)), i.e. 2.6 mm. The axial velocity associated with the localized deformation in the band is then V = 0.0045*2.6 = 0,0117 mm s−1. The temperature increase in the band is about 2 K (Fig. 10(b)), such that \( \frac{{\partial T}}{{\partial t}} \approx 2/10 = 0.2 \) K s−1 and the projection of \( \overrightarrow {\hbox{grad}} \,{\hbox{T}} \) in the X direction is \( \overrightarrow {\hbox{grad}} \,{\hbox{T}} \approx {2/2}{.6} = {0}{.77}\,{\hbox{K}}\,{\hbox{m}}{{\hbox{m}}^{{ - {1}}}} \). The term \( \overrightarrow v .\overrightarrow {\text{grad}} \;{\text{T}} \), estimated through 0.00117*0.77 = 0.009 K s−1, is then about 20-fold lower than \( \frac{{\partial T}}{{\partial t}} \), which is in close agreement with hypothesis (i).

Finally, through a spatiotemporal representation, Fig. 14 gives a synthetic view of the axial strain field E xx and the local DSC heat q. These two experimental fields obtained by two independent set-ups (visible and infrared cameras) are very similar. The positions of the phase transformation given indirectly by E xx and q are located at the same place in these two types of representation. Due to the difficulty of taking the thermal conductivity coefficient into account, the results of the local DSC proposed in this work can be considered as a semi-quantitative result. However, the confrontation with the strain field is very encouraging and indirectly gives a kind of validation of the proposed method. Moreover, if the transformation strain Δε tr and the enthalpy \( \Delta H_{{tr}}^{{tensile}} \) for a complete transformation are known, these two fields can also give an estimation of the martensite phase fraction [6, 29, 30].

Fig. 14
figure 14

Spatiotemporal representation along the tensile axis, indicated by the green dotted line of the fixed Y 0 coordinate in the left schemes, of: (a) the Green Lagrange axial strain E xx ,(X,Y 0 ,t) and (b) of the heat energy q(X,Y,t). The two curves superimposed in these figures are the nominal stress σ and the local axial strain ε (refer to Fig. 9(a) to get their amplitude values)

Full size image

Heat Source and Energy Estimations: Comparison of Model 1/Model 3 Thermal Conductivities

The differences observed between models 1 and 3 in terms of heat source s and energy estimations q can be quantified from Fig. 15, in which the results at time d obtained with Model 3 for thermal conductivity are compared with those obtained with Model 1. The different plots confirm that s and q values, as estimated from Model 3 for k, are located between the lower and upper bounds obtained with Model 1 for k, i.e. respectively k = k M   = 8 Wm−1 K−1 and k = k A  = 18 Wm−1 K−1.

Fig. 15
figure 15

Comparison at time d (see Fig. 13(a)) of heat source (a) and energy (b) estimations from the two thermal conductivity models: Model 1 (with k = k M or k = k A ) and Model 3 (equation (11))

Full size image

There are substantial differences between the two models, indicating the key role played by the thermal conductivity values of the two phases, for heat source or energy estimations during localized phase transformations. At the end of loading (time d), the phase transformation energy varied from about 20 to about 30 J g−1, which are bounds for the mean value (27 J g−1) given in the previous section with Model 3. Finally, this study highlighted the necessity of increasing the accuracy on thermal conductivity data for this kind of material.

Conclusion

A methodology to obtain heat source estimations, when thermal conductivity is not constant, was proposed in this paper. It was applied to estimate heat sources during a localized superelastic tensile test of an NiTi shape memory alloy displaying both stress-induced phase transformation and localized deformation behavior.

The same side of an NiTi SMA sheet sample was observed with a visible and an infrared camera. A specific spatiotemporal method was first presented in order to obtain, at the same time and at the same material point, kinematic (displacement, strain) and thermal (temperature, heat sources) data. This synchronization: (i) allowed temperature monitoring at a material point which can move during deformation, (ii) improved the temperature variation measurement, and (iii) also improved the estimation of heat energy by temporal integration of the heat sources at each material point.

As the thermal conductivity of martensite (k = k A ) and austenite phases (k = k M ) can be different, four models of k have been proposed and discussed. Two of them were chosen and used in two methods to estimate, from the thermal fields, heat sources during the test. Coefficient k was supposed to be constant in the first method and depended locally on the phase type in the second one.

Kinematic, thermal and heat source fields have been compared during the stress plateau of a superelastic tensile test. As in [10–15], they showed substantial localization when considering the shape of the bands propagating along the sample. The axial strain fields had low (about 0.5%) and high (about 7%) values in areas where austenite and martensite phases were respectively predominant. The strain intensity indicates that martensitic transformation was not complete at the end of the loading. The temperature fields were very diffuse and hard to directly interpret. On the other hand, the heat sources clearly exhibited, at each current time, the area of the sample where the phase transformation occurred. These areas appeared to coincide with the transition area between low and high strain values.

Finally, heat sources were integrated at each material point over the time course in order to obtain a local estimation of heat energy associated with the phase transformation. Such measurement can be qualified as an in situ local DSC during a mechanical test. Due to the difficulty of modeling thermal conductivity, the result obtained can be considered as semi-quantitative. The scattering of specific heat values was not taken into account. The same kind of technique, taking the appropriate value for each phase, could be applied to process thermal data, as carried out for thermal conductivity. Studies are under way to measure this material property for the two phases of NiTi materials.

However, the spatiotemporal distribution of the energy fields was in close agreement with the strain field distribution. A forthcoming study will be carried out to improve the heat source estimation, in particular through better determination of the heat capacities and thermal conductivities, and to validate it, in the case of heterogeneous thermal conductivity.