Characterization of the Damping Behavior of a Nanoindentation Instrument for Carrying Out Dynamic Experiments

Abstract

A new displacement modulation based dynamic indentation method is demonstrated and shown to be effective for viscoelastic characterization of a glassy polymer. The analysis of dynamic experiments requires a complete understanding of the measuring system’s dynamic characteristics especially the damping. Accordingly, an improved method, based on the use of a wire spring, is developed for determining the damping characteristics. In general, damping in an indentation instrument is contributed by two elements: the eddy current damping from the electromagnetic loading coil and the squeeze film damping from the capacitive displacement transducer. Therefore, a method to determine the relative contribution from the different damping elements present in the system is demonstrated and the results are compared with the calibration obtained from the wire spring method. Finally, dynamic indentation tests are carried out on a glassy polymer to obtain the complex modulus; the values of which are compared with those obtained from bulk dynamic mechanical analysis (DMA) tests. Storage modulus values are found to be in good agreement with bulk data but some divergence in the case of loss modulus is observed. The calibration procedure of the measuring instrument is critically examined in view of these observations. Overall, displacement modulation based dynamic indentation is shown to be a promising method for viscoelastic characterization at the micron length scales.

Introduction

In recent years, instrumented indentation has become a popular technique for measuring the mechanical properties of solids at small length scales [1]. The methods for determining the elastic modulus and hardness have become fairly standard and rely on the fact that the displacements recovered during unloading are largely elastic, in which case the elastic punch theory can be used to determine the modulus from the unloading part of the load-displacement data. This method, when applied to polymers, leads to an overestimation of the elastic modulus [2]. Although some correction procedures have been suggested to obtain a better estimate [2, 3], the elastic modulus alone does not provide a complete representation of the time dependent rheological properties of polymers. Thus indentation analogues of creep, stress relaxation and dynamic mechanical analysis (DMA) have been actively pursued and applied to determine viscoelastic properties at the micro- and nano-length scales.

Dynamic nanoindentation, which is analogous to DMA, has received a lot of attention from researchers in the past few years [4–7]. The properties that can be obtained are frequency and temperature dependent storage and loss moduli, the loss tangent, tan δ, the glass transition temperature, T _g , the mechanical relaxation, and the activation energy for the relaxation process. Also, the application of time-temperature superposition is very easily accomplished on the frequency domain to extend the range of frequencies as demonstrated by Hayes et al. [8].

With dynamic nanoindentation, results can be obtained faster and over a wide range of frequencies and the variation of properties can also be obtained as a function of depth. Moreover, the loss tangent, which can also be obtained using this technique, has been considered by many as a measure of the degree of viscoelasticity of a material. It not only provides an estimate of damping and viscous energy losses in a material, but can give valuable information about the transition temperatures and the associated activation energies. Thus, dynamic nanoindentation can be very useful in characterizing the viscoelastic properties of polymers, polymer coatings and surface modified polymers. It can also be used to determine the variation of viscoelastic properties in heterogenous materials like polymer composites and biological tissues. Finally, in addition to determining viscoelastic properties, dynamic indentation can also find application in the characterization of dynamic contacts in MEMS and in contact processes like dry friction, abrasive and erosive wear.

The procedure for carrying out dynamic indentation testing involves the application of an oscillating force or displacement signal to the tip-sample contact and the measurement of the resultant output signal as well as the phase difference between the input and output signals. This information is used to obtain the contact stiffness and damping which are then analyzed to determine the viscoelastic properties of the material. The most common approach for carrying out dynamic indentation is a force modulation technique where an oscillating signal is superimposed on the quasi-static load and the output displacement and the phase difference are measured [7]. This approach is used by Triboindenter and Triboscope, NanoIndenter XP and Ultra-Micro Indentation System (UMIS; Commonwealth Scientific and Industrial Research Organisation).

An early description of the force modulation based dynamic nanoindentation technique using the MTS Nanoindenter II was presented by Loubet et al. [7] who measured the storage and loss modulus of rubber polyisoprene. Li and Bhushan [9] have also provided a description of the technique and its various applications, e.g., to determine the variation of contact stiffness with depth for elastic materials, to accurately determine the initial point of contact of the indenter with the sample and for testing uniform and multilayered hard structures. Several other researchers [6, 10–12] have used this technique and it has been shown to provide viscoelastic properties that are in reasonable agreement with bulk DMA measurements [6, 10, 11]. Most recently, White et al. [5] tested four polymers, a cured epoxy, polymethylmethacrylate (PMMA) and two polydimethylsiloxane (PDMS) samples with different crosslink densities using the MTS Nanoindenter. Good agreement was obtained between the nanoindentation and bulk rheological data for glassy polymers but more divergent results for the two PDMS samples. Most importantly, some significant issues involved in carrying out dynamic indentation measurements were discussed, including instrument calibration, high strains associated with sharp indenter tips and the validity of the working equations.

A brief review of the derivation of the working equations is provided here for the discussion of some critical issues in dynamic testing. Sneddon’s analysis [13] for a rigid flat punch leads to a simple relation between the indentation load, P, and the indentation depth, h, of the form,

$$P=\frac{4 \mu a}{1-\nu}h\;,$$

(1)

where a is the radius of the punch, μ is the shear modulus, and ν is the Poisson’s ratio. Noting that the area of the contact circle is A = πa ² and the shear modulus can be related to elastic modulus through E = 2 μ(1 + ν), differentiating P with respect to h leads to,

$$\frac{\mathrm{d} P}{\mathrm{d} h}=2\sqrt{\frac{A}{\pi}}\frac{E}{1-\nu^2}\;.$$

(2)

Using the method of functional equations proposed by Radok [14], which has been shown to be valid for the case of a non-decreasing contact area, we can obtain a solution for the complex modulus by replacing the elastic parameters with viscoelastic parameters to obtain the following expression,

$${\frac{\mathrm{d} P}{\mathrm{d} h}}^*=2\sqrt{\frac{A}{\pi}}\frac{{E}^*}{1-\nu^2}\;.$$

(3)

For a hold period, the complex stiffness, d P/d h ^*, can be written in terms of the superimposed oscillating force and displacement signals as,

$${\frac{\mathrm{d} P}{\mathrm{d} h}}^*=\frac{P_0 e^{i\delta}}{h_0}\;,$$

(4)

where the oscillating force and displacement signals are given as,

$$\Delta P=P_0 e^{i(\omega t+\delta)}\;, \qquad \Delta h= h_0 e^{i(\omega t)}\;.$$

(5)

Using equations 3 and 4, an expression for the complex modulus can be written as,

$$\frac{E^*}{1-{\nu}^2}=\frac{1}{2}\sqrt{\frac{\pi}{A}}~\frac{P_0 e^{i \delta}}{h_0}\;,$$

(6)

or in terms of the reduced complex modulus as,

$${E_r}^*=\frac{1}{2}\sqrt{\frac{\pi}{A}}~\frac{P_0 e^{i\delta}}{h_0}\;.$$

(7)

If the dynamic contact stiffness, S, and the dynamic contact damping, C, are known then the complex stiffness can be expanded as,

$$\frac{\mathrm{d} P^{*}}{\mathrm{d} h}=S+i C \omega\;,$$

(8)

and the reduced complex modulus can then be written as

$${E_r}^*=\frac{1}{2}\sqrt{\frac{\pi}{A}}(S+i C \omega)\;.$$

(9)

The above analysis, although strictly true only for a flat punch indenter, can be extended to sharp indenters. Pharr and Oliver [15] have shown that the relation in equation 2, which is the basis of the above derivation, is true even in the case of a punch of an arbitrary shape for the case of unloading. For a viscoelastic contact, during a hold period, the contact area gradually increases and the oscillations take place along the unloading curve. Moreover, the oscillation amplitude is significantly smaller than the indentation depth. Thus it is reasonable to assume that the analysis for a flat punch as shown above can be extended to a punch of an arbitrary shape for complex modulus measurements. Finally, the contact area A, required in equation 9, can be calculated from the contact depth, h _c , by assuming a shape function of the indenter, i.e.,

$$A=f(h_c)\;,\qquad h_c=h_{\max}-\epsilon\frac{P_{\max}}{\mathrm{d} P/\mathrm{d} h}\;.$$

(10)

The use of initial unloading slope as in equation 10, is known to give an overestimation of the contact area for a viscoelastic material. Alternative procedures for calculating the contact depth for viscoelastic contacts from the initial section of the unloading curve have been suggested by Tang et al. [3]. But for the purpose of this study on epoxy, it was found that the contact depth can be approximated to a good degree of accuracy by the actual depth of penetration of the indenter into the material.

The high strains associated with a Berkovich indenter are a problem during the loading of the indenter into the material, but the unloading part is free from such problems. Also, the unloading curve is known to provide good values of material properties for elastic materials. Moreover, a fast loading can be used to simulate a step loading condition to minimize viscoelastic effects during loading [16]. Thus it could be assumed that the linear viscoelastic properties can be extracted from the unloading curve. In this study, the hold period is used for dynamic measurements, and as discussed earlier, oscillations of the indenter on the material surface take place along the unloading curve.

This paper describes a new displacement modulation based dynamic nanoindentation method which is in contrast to the force modulation methods as it provides the excitation not through the force transducer but through controlled specimen oscillation. This allows the control of amplitude and frequency of excitation independently from the electromagnetic loading coil, potentially making available a wider range of amplitudes and frequencies of excitation that can be applied during indentation. This study is the first to develop and implement the displacement modulation based dynamic nanoindentation technique for viscoelastic characterization. A general description of the technique has also been presented earlier [17]. The tests are carried out on the NanoTest Platform (MicroMaterials Ltd., Wrexham, UK) which has a unique pendulum design and a special module for performing dynamic indentation.

Dynamic indentation offers several advantages over quasi-static testing for viscoelastic measurements, but the analysis of the experimental data from dynamic indentation requires the deconvolution of the material properties from the overall response of the system which includes the instrument response. Thus, it is of critical importance to determine the measuring instrument’s response, especially the system damping, as a function of the harmonic frequency. Asif et al. [18] have provided a description of the system damping calibration using a cantilevered calibration spring. A cantilever spring, as shown in Fig. 1(a), has also been used for the calibration of a displacement modulation based dynamic indentation instrument [17]. The use of a cantilever spring, however, can lead to bouncing or sliding of the indenter tip leading to inaccuracies in the measurements. This paper presents a wire spring based calibration procedure, as shown in Fig. 1(b), to alleviate these problems.

Fig. 1

Instrument calibration using the previously used cantilever spring [17] and the currently developed wire spring methods. (a) Cantilever spring setup. (b) Wire spring setup

System calibration using calibration springs is typically based on the use of spring–dashpot models that lump all the damping elements in the system into one damping parameter. While such procedures provide estimates of system damping that can be employed for analysis of dynamic indentation experiments, they don’t provide a physical basis for interpreting the system damping characteristics. Accordingly, in this study, a method to analyze the different damping elements present in the system is developed. First the calibration of the instrument for dynamic indentation tests is conducted. Subsequently, dynamic indentation tests are performed on epoxy and PMMA samples and the results are compared with data from bulk DMA measurements.

Experimental Setup

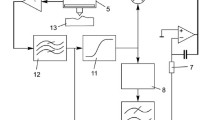
The nanoindentation setup shown in Fig. 2 has a unique pendulum design, with the pendulum pivoted at approximately midpoint. The load is applied through an electromagnetic transducer at the top of the pendulum and is transferred to the other end, which has the indenter in contact with the sample. Fixed to the bottom of the pendulum is an optically flat glass plate placed parallel to another glass plate mounted on the machine frame. The glass plate mounted on the frame is movable and can be used to adjust the gap between the two plates, allowing control over the damping of the system.

Fig. 2

A schematic of the NanoTest setup used for dynamic nanoindentation experiments

The specimen is mounted on a holder, which has a piezoelectric crystal that provides the oscillation. A lock-in amplifier signal generator provides the drive signal for sample oscillation. The sample is oscillated at a particular frequency, say 40 Hz, and the displacement signal obtained from a parallel plate capacitor mounted at the back of the indenter is detected at the same frequency. The capacitor is a part of a bridge circuit and the output from the bridge circuit is amplified, rectified and then fed back into the lock-in amplifier. The phase difference between the sample oscillation and the pendulum motion is then used to determine the elastic and damping properties of the contact.

Calibration of the NanoTest Instrument

Nanoindentation based techniques for measuring dynamic properties in general measure the damping and stiffness characteristics of the contact as a function of excitation frequency. The damping and stiffness of the contact has to be extracted from the overall response of the system which includes the response of the sample and the machine. Thus it is essential to obtain the measuring instrument’s response, the stiffness and damping, as a function of excitation frequency.

The issue of calibration for quasi-static testing has received a lot of attention. This effort in the calibration of indentation instruments for the case of quasi-static testing has contributed to the level of confidence in the determination of elastic and yield properties. A similar effort is required for the understanding of the system characteristics, especially the system damping, for carrying out dynamic experiments.

To date, most studies have assumed the system damping to be independent of the harmonic frequency [5, 6, 8, 18]. Moreover, in most studies, all the damping elements present in the system have been lumped into one damping parameter. Nonetheless, regardless of the form of the testing instrument, it has a capacitive transducer for measuring displacements and a loading coil for applying a load. These two elements contribute significantly to the system damping in the form of squeeze-film and eddy-current damping. These two types of damping are known to exhibit some sort of frequency dependence, either linear or quadratic. Therefore a frequency dependent calibration of the system is necessary, and should be ideally carried out by explicitly modeling the individual damping components. Experimental investigation of these phenomena is not only relevant for the calibration of the indentation instrument but also for other areas such as the analysis of squeeze-film damping in MEMS devices.

In this study, a lumped parameter model is first used to investigate the variation of net damping with frequency. This is followed by a more detailed model, considering different damping elements present in the system. Subsequently, these two approaches are compared to evaluate the validity of the lumped parameter approach.

Calibration Using a Lumped Parameter Model

Calibration of the system damping, in general requires a calibration spring of a known stiffness. A spring–dashpot model of the system with a calibration spring in place is shown in Fig. 3.

Fig. 3

Schematic of the lumped parameter model for damping calibration

The problem to be solved is analogous to a forced harmonic motion in which an oscillatory displacement is applied to the spring rather than the mass, and the equation of motion is given as,

$$m\frac{\mathrm{d}^2y}{\mathrm{d} t}+c_0\frac{\mathrm{d} y}{\mathrm{d} t}+k_0 y= 0\,,$$

(11)

where x is the oscillatory displacement applied directly to the sample holder and y is the oscillatory displacement response of the pendulum. Also, m is the system mass, c ₀ is the system damping, k ₀ is the stiffness of the pendulum springs, and k is the variable stiffness of the calibration spring. The input and output displacements are given as,

$$x=X_0 \cos (\omega t)\,, \qquad y=Y_0 \cos (\omega t + \phi)\,,$$

(12)

where, ω is the excitation frequency and ϕ is the phase difference between the input and output signals. Solving equations 11 and 12 gives the phase difference in terms of the frequency as,

$$\phi=\arctan\left[\frac{\omega c_0}{k_0+k-m \omega^2}\right]\,.$$

(13)

In addition, the system electronics introduce a phase offset, ϕ ₀, which results in a modification of equation 13 as,

$$\phi=\arctan\left[\frac{\omega c_0}{k_0+k-m \omega^2}\right]+\phi_0\,.$$

(14)

Calibration of the indentation instrument requires the determination of the three system parameters, viz., the electronics phase offset, ϕ ₀, the effective pendulum mass, m, and the effective system damping, c ₀.

The electronics time-delay induced system offset, ϕ ₀, was determined by measuring the phase difference between the input and output signals, as a function of frequency, with a hard contact between the oscillating sample holder and the pendulum. The hard contact was achieved by soldering a brass pin between the indenter holder and the sample holder. Phase offset measurements were carried out for two damping plate spacings of 140 and 360 μm corresponding to high and low damping, respectively. The results are shown in Fig. 4 and indicate that the system offset is independent of the excitation frequency, as expected.

Fig. 4

System damping as a function of harmonic frequency for two damping spacings

To obtain the remaining system parameters, m and c ₀, the best approach is to use a calibration spring between the indenter holder and the oscillating sample holder. In the past, a cantilevered leaf spring [17, 18] has been used, but this approach can lead to problems such as bouncing or sliding of the indenter on the spring. To overcome these problems, a wire calibration spring screwed between the indenter holder and the oscillating sample holder, as shown in Fig. 1(b), was used in this study.

The mass of the system, m, was determined by measuring the resonance frequency of the pendulum under forced oscillation. This provided an effective pendulum mass value of 0.209 kg. To determine the system damping, c ₀, oscillation data was acquired at different frequencies. For each frequency, the phase difference between the input and output signals was recorded by the lock-in amplifier and the spring stiffness was determined by carrying out load ramp tests. Since the system mass and system phase offset are already known using independent methods, damping being the only unknown can be calculated using equation 14.

The system damping values obtained using the above method for the frequencies of 10, 20, 30 and 40 Hz are shown in Fig. 5. It can be seen from the figure that the resonance of the system with the spring is close to 30 Hz and this resonance also affects the damping measurements. To obtain the system damping, an average of the values for all the frequencies except the ones affected by resonance was taken. This provided a damping value of 7.93±0.63Ns/m. This system damping value is used for the analysis of the dynamic indentation experiments on an epoxy sample as described in a subsequent section.

Fig. 5

Spring phase measurements and damping coefficient as a function of frequency

System Model with Separate Damping Elements

Currently, the calibration approaches for all types of dynamic indentation instruments (NanoTest, MTS, Hysitron, etc.) employ a lumped parameter model. There is no systematic verification of such an approach. Since three different damping elements are present in the NanoTest indentation system, it is of interest to determine the relative contribution from each of them towards the total system damping. This would not only provide a better understanding of the different damping mechanisms involved but also serve as a verification for the results obtained by assuming a lumped parameter model. A torsional model of the system with separate representations for the three different damping elements as shown in Fig. 6 was used for this purpose.

Fig. 6

An improved pendulum model of the nanotest setup

The governing equation of the system is given by,

$$I\ddot{\theta}+\left(\Sigma c_i {l_i}^2\right)\dot{\theta}+\left(Mgd+k{l_k}^2\right){\theta}=0,$$

(15)

where the constants c _i represent the damping coefficients c _e , c _c and c _d of the eddy current element, the capacitor plates and the glass damping plates respectively. The constants l _i are the distances of the corresponding damping elements from the pivot. Finally, θ is the angle of oscillation of the pendulum system and k is the stiffness of the calibration spring and this can be determined by carrying out load ramp tests.

The distances of the damping elements, l _i , and the mass of the pendulum, m, were obtained before it was assembled into the measuring instrument. The moment of inertia, I and the distance of the center of gravity, d can be obtained experimentally by measuring the natural frequency of the free oscillations of the pendulum system with and without the calibration spring. The expressions for the natural frequency of the system with and without the calibration spring are given by the equations 16 and 17 and these can then be used to determine the values of the unknown parameters d and I.

$$\omega=\sqrt{\frac{Mgd}{I}}$$

(16)

$$\omega_k=\sqrt{\frac{Mgd+k{l_k}^2}{I}},$$

(17)

With this, all the parameters in the equation 15 are known except the damping coefficients c _i . A method to determine these damping coefficients is described in the following paragraphs.

The solution of the governing equation 15 can be written as,

$$x=Ae^{-\xi \omega t}\cos \left(\sqrt{1-\xi^2}\omega t-\delta\right),$$

(18)

where x is the time dependent amplitude, A is the initial amplitude, ξ is the damping factor which is defined as the ratio of the damping coefficient and the critical damping coefficient, ω is the frequency of oscillation in radians per second and δ is offset angle defining the starting phase of the oscillation. Using oscillation experiments with a given spring, the damping factor, ξ, can be obtained by curvefit of the decrement data with the model in equation 18. The curvefit is shown in Fig. 7 for a spring of stiffness 4,575 N/m and a damping plate spacing of 460 μm.

Fig. 7

Amplitude decrement data for a spring of stiffness 4,575 N/m and a damping plate spacing of 460 μm

The damping factor, ξ, is a measure of the total damping of the system and can be written as,

$$\xi c_{cc}=\Sigma c_i {l_i}^2=c_e {l_e}^2+c_c {l_c}^2+c_d {l_d}^2,$$

(19)

in terms of the damping coefficients of the individual damping elements and their corresponding normal distances from the pivot. The critical damping coefficient, c _cc is given by

$$c_{cc}=2\sqrt{\left(Mgd+kl^2\right)I}.$$

(20)

The fact that the plate spacing of the glass damping plates at the bottom of the pendulum can be adjusted in a controlled manner is used to determine the variation of the corresponding damping coefficient, c _d . For a given frequency of oscillation, all the damping coefficients are constant and the equation 19 can be written as,

$$\xi c_{cc}=c_{eq}+c_d {l_d}^2,$$

(21)

where c _eq represents the equivalent damping of the eddy current and the capacitor plate damping elements. The squeeze film damping is known to vary as the inverse cube of damping plate spacing [19], h, as given by,

$$c=0.6 \frac{\mu L B^3}{h^3},$$

(22)

where 0.6 is a geometric factor, L and B are the length and breadth of the damping plates, μ is the viscosity of air and h is the damping plate spacing. Equation 22 can be rewritten as,

$$c_d=\frac{c_{d0}}{h^3}.$$

(23)

Theoretical calculations for the damping plate system provide a value of 0.46×10^− 11 Ns/m⁴ . Experimentally, c _d0 can be obtained by the modification of the equation 21 to

$$\xi c_{cc}=c_{eq}+\frac{c_{d0}}{h^3} {l_d}^2$$

(24)

using equation 23. Subsequently, damping factor, ξ, measurements can be carried out for different damping plate spacings to obtain the variation of the damping factor with the damping plate spacing, h. Curvefit of this data with the model in equation 24 provides the values of the constants c _eq and c _d0 for the given frequency. The experimental data for a spring of stiffness 4,575 N/m is shown in Fig. 8.

Fig. 8

Damping coefficient of damping plate obtained using a spring of stiffness 4,575 N/m along with the model curvefit

The above procedure is carried out with four different springs of stiffnesses 470, 800, 2,804 and 4,575 N/m corresponding to natural frequencies of 9.4, 17, 22, 34 Hz. A constant value of c _d0 of 1.17±0.053×10^− 11 Ns/m⁴ is obtained for all the frequencies demonstrating the independence of squeeze film damping from the frequency of oscillation. This value is in good agreement with the theoretical value obtained using equation 22. The values of c _eq are also obtained with each of the springs and a plot of c _eq is shown in Fig. 9 showing a linear variation with frequency. c _eq is the equivalent damping of the capacitor plates and the eddy current damping elements. Since the independence of the squeeze film damping from frequency has already been demonstrated, the y-intercept can be taken as the value of the squeeze film damping coefficient of the capacitor plates, c _c . The linear variation is attributed to the eddy current damping in the electromagnetic loading coil.

Fig. 9

Equivalent damping coefficient of the capacitor plates and the eddy current element

Comparison of the Two Calibration Techniques

With the individual damping coefficients of the different damping elements known from “System Model with Separate Damping Elements”, we can calculate the effective damping coefficient for the equivalent dashpot in a linear spring dashpot representation. This can be done by using the following equation,

$$c_0=\frac{\Sigma c_i l_i^2}{l_0^2},$$

(25)

where l ₀ is the normal distance of the indenter-sample interaction point from the pivot. The effective damping coefficient value obtained using the above equation (~20 Ns/m) is significantly higher than that obtained by the forced oscillation method (~8 Ns/m) where a lumped dashpot representation is used. The reason behind this observation could be the difference in the amplitudes of oscillation in the two methods. The forced oscillation method uses a piezoelectric transducer which has an amplitude of the order of nanometers and the free oscillations method has an amplitude of the order of microns. Since the plate spacing is in the range of microns, the amplitude of oscillation governs whether the damping is squeeze film or not. The calibration procedure using the forced oscillations is adopted because the tests on epoxy are also carried out using that process. The free oscillation method is useful for providing the relative contribution from the different damping elements. It is found that although the eddy current damping element provides a linear variation in damping, its contribution to the net damping is insignificant compared to the other two elements. This provides a justification for obtaining frequency independent damping results using the lumped parameter model. Finally, amplitude dependence of system damping has also been demonstrated, but this dependence can be ignored if the amplitude variation is of the order of nanometers.

Measurement of Complex Modulus

Model

A spring–dashpot model of the material-indenter interaction with a contact stiffness, k′, and a contact damping, c′, in parallel, was assumed. The schematic of the setup with the sample in place is shown in Fig. 10. The governing equation of the system with the sample in place is given by

$$m\frac{\mathrm{d}^2y}{\mathrm{d} t}+\left(c'+c_0\right)\frac{\mathrm{d} y}{\mathrm{d} t}+\left(k'+k_0\right) y= c\frac{\mathrm{d} x}{\mathrm{d} t}+kx\;.$$

(26)

The governing equation can be solved to obtain the phase difference between the input and output oscillations and is given by the following relation,

$$\phi=\arctan\left[\frac{\omega (c_0+c')}{k_0+k'-m \omega^2}\right]+\arctan\left[\frac{c'\omega}{k'}\right]+\phi_0 \;.$$

(27)

The second term in the above equation is very small in comparison with the first term for the case of glassy polymers, so is neglected in the present analysis. But it must be pointed out that this term can be significant in the case of soft polymers. Furthermore, both c′ and k′ are assumed to be frequency dependent. It is known that the contact stiffness k′ is proportional to the square root of the contact area, i.e., to x for a perfectly pyramidal indenter. The contact damping is also assumed to be proportional to depth, since this assumption leads to a loss modulus value that is independent of depth. Thus equation 27 can be written as,

$$\phi=\arctan\left[\frac{\omega (c_0+cx)}{k_0+kx-m \omega^2}\right]+\phi_0\;,$$

(28)

where x is the contact depth and c and k are constants.

Fig. 10

Spring dashpot model of the test setup with the sample in place

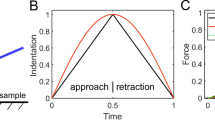
For the measurement of complex modulus, a set of load-partial unload indentations was produced as shown in Fig. 11, with the phase angle being measured during the dwell period. The contact depth is usually found from the unloading curve using the Oliver–Pharr analysis [4] assuming elastic deformation. But this procedure is known to give erroneous results for viscoelastic materials. Alternative procedures for calculating the contact depth for viscoelastic contacts from the initial section of the unloading curve have been suggested by Tang et al. [3]. But for the purpose of this study on epoxy, it was found that the actual depth of penetration of the indenter into the material provided a better approximation for the contact depth. This assumption is supported by the AFM imaging of an indentation on the material for a maximum load of 10 mN and a loading rate of 0.3 mN/s. The 3-D AFM image is shown in Fig. 12 and a scan of the profile is shown in Fig. 13. The significant pile up as seen in the figure leads to an increase in the actual contact area making the actual depth a better approximation for calculating the area.

Fig. 11

Cyclic load-hold-partial unload indentations on epoxy for measuring phase during hold period

Fig. 12

Three dimensional AFM scan of an indentation on epoxy

Fig. 13

Cross section of the indentation obtained using AFM showing pile-up

Finally, since m and c ₀ are known from the calibration procedure, fitting the phase versus depth data allows c and k to be determined. The storage modulus, E′, and the loss modulus, E′′, can then be calculated using [10],

$$E'=\frac{k}{2}\sqrt{\frac{\pi}{24.5}}\;,$$

(29)

$$E''=\frac{c\omega}{2}\sqrt{\frac{\pi}{24.5}}\;.$$

(30)

An ideal Berkovich geometry was assumed because it was found that for plastic depths beyond 400 nm, the diamond area function does not have a significant effect on the analysis.

Material and Experiments

Using the above method, complex modulus measurements were carried out on a thermosetting epoxy sample. The epoxy resin chosen for this study, EPON Resin 862 (Resolution Performance Products, Houston, Texas, USA), is a low-viscosity liquid epoxy resin manufactured from epichlorohydrin and bisphenol-F. It is a typical highly cross-linked thermosetting polymer that exhibits brittle behavior, and has the ideal structural formula as shown in Fig. 14. A moderately reactive, low viscosity aliphatic amine, EPIKURE 3274 (Resolution Performance Products, Houston, Texas, USA) was used as the curing agent. This curing agent provides a pot life of about 1 hour after mixing, which was required to remove the air bubbles trapped in the mixture before making the final cast. The mixed resin was cured at 25 °C for 24 h, followed by post-cure at 120 °C. for 6 h. Properties of neat EPON 862 resin cured with the EPIKURE 3234 curing agent are listed in Table 1.

Fig. 14

Structural formula of the epoxy resin used in this study

Table 1 Nominal bulk properties of the epoxy used in this study

The indentation samples were cut in the form of small tablets with nominal dimensions of 10 ×10 ×5 mm. The testing surface was polished on a metallographic polishing wheel using 0.05 μm colloidal alumina polishing suspension. Then the samples were mounted onto the sample holder using a cyanoacrylate based adhesive and dynamic indentation tests were carried out at the frequencies of 10, 20, 30 and 40 Hz. Figure 15 shows the variation of the experimental phase values, φ, as a function of the plastic depth, x. Curvefit of this data with the theoretical spring–dashpot model, as per equation 28, provides the contact stiffness and the contact damping. All curvefits were obtained with R ² values of better than 0.99. The model curvefits are also shown in Fig. 15 for each frequency.

Fig. 15

Experimental phase values and curvefits obtained using dynamic indentation tests on epoxy

The contact stiffness and damping values were then used to obtain the storage and loss moduli using equations 29 and 30 as described earlier. Figures 16 and 17 show the variation of the storage and loss moduli, determined using dynamic indentation, as a function of testing frequency, along with the storage modulus obtained using dynamic mechanical analysis (DMA) tests. The DMA tests were carried out in bending on a Tritec 2000 DMA machine (Triton Technology Ltd., Keyworth, UK) which provides data up to a maximum testing frequency of 20 Hz. Comparison of the two results shows that the storage modulus values obtained using dynamic indentation are in very good agreement with those from DMA. The loss modulus values obtained using DNI show a much better agreement than those obtained using the cantilever calibration spring approach.

Fig. 16

Storage modulus of epoxy obtained using DNI and DMA

Fig. 17

Loss modulus of epoxy obtained using DNI and DMA

With the success of the dynamic nanoindentation technique, further experiments were carried out on another polymer, PMMA. The results for storage and loss modulus are shown in Fig. 18 along with the DMA values.

Fig. 18

Storage and loss modulus of PMMA obtained using DNI and DMA

Reasonable agreement is seen between the results from two techniques.

Summary

With the increasing use of polymers and polymer composites in MEMS and in nanotechnology, the need for experimental methods to measure viscoelasticity at the micro and nanoscale is expanding. Instrumented indentation has been very successful for characterizing elastic properties at these length scales. But the testing of viscoelastic properties like creep and stress relaxation has proved a challenge although some progress has been made in recent years. Dynamic indentation offers several advantages over quasi-static indentation methods for viscoelastic characterization including faster testing times and easier analysis procedures.

A new displacement modulation based dynamic indentation method has been developed and demonstrated in this paper. In this technique, oscillation is provided through controlled sample oscillation rather than through the force transducer as is done in the case of force modulation methods. Extraction of the material properties requires the analysis of the overall response of the system, which includes the response of the machine as a function of frequency. Thus it is essential to obtain the measuring instrument’s response, especially damping, as a function of excitation frequency.

In our previous study, a simple spring–dashpot model has been used to obtain the system damping using a calibration spring and phase measurements [17]. This was based on the approach initially proposed by Asif et al. [18]. The calibration was carried out using a cantilevered spring that was loaded in contact with the indenter. This doesn’t rule out the possibility of slipping of the indenter on the spring during oscillation resulting in a scatter in the data. This scatter would affect the determination of system damping parameters. Furthermore, a spring–dashpot model was used and all the damping elements were lumped together into a single damping parameter. The system damping in the NanoTest is believed to be contributed by three elements: squeeze film damping between the damping plates, the squeeze film damping between the capacitor plates, and the eddy current damping in the loading coil. Thus, the use of a single damping parameter may not be an accurate representation of the system characteristics and would be a contributing factor for the discrepancies in loss modulus measurements.

In this paper, an improved method for carrying out the calibration of a nanoindentation instrument for carrying out dynamic indentation experiments is described. This method uses a wire calibration spring providing a better contact between the indenter holder and the oscillating sample holder. The results of calibration and sample testing show a marked improvement over the more commonly used cantilever calibration spring method. Furthermore, an attempt was made to understand the complete damping characteristics of the setup. A free oscillation method with the calibration spring was used to obtain the damping coefficients of the individual damping elements. The results were shown to be in agreement with the theoretical model for the squeeze film damping but were at variance with the results from the forced oscillation method. The reason behind this observation was the difference in amplitudes between the two methods. The higher amplitudes in case of free oscillations lead to squeeze film damping and thus the agreement with the theoretical model. Whereas in the forced oscillation method, the oscillation amplitude is an order of magnitude smaller than the damping plate spacing leading to a divergence from the squeeze film model. The eddy current damping element was shown to provide linear variation of damping with frequency but its magnitude is small compared to that of the damping plate element. Thus a better understanding of the relative contributions from the different damping elements is obtained. The system damping value obtained from the calibration procedure with the wire spring and forced oscillations is used to analyze the tests on epoxy and PMMA samples. The complex modulus values show good agreement with those obtained from conventional DMA tests.