A Flexible Dynamic Master–User Look-Up Table Approach for Evaluation of Trigonometric Values

Abstract

Systems which are computationally complex often include the calculation of sine/cosine values, which frequently uses its Taylor series expansion. For high accuracy the Taylor series expansion becomes computationally intensive. Therefore, the calculation of sine (or cosine) values may become the bottleneck of the system. In this paper, a novel concept is proposed that employs dynamic master–user look-up table (DMU-LUT) configuration for the calculation of trigonometric values with user defined precision. Initially, samples on a unit circle are evaluated at regular interval of $\Phi$, where $\Phi$ denotes the sampling angle. This results in $2\pi \Phi$ total number of samples for creation of master table. The values of sine/cosine are calculated at each sample and then stored in the master table. The application-specific user table is obtained by three proposed sampling scenarios (constant distance, section, and probabilistic sampling) of master table. The main advantage of this scheme is to provide flexibility to achieve the desired accuracy according to system requirements. For FPGA implementations of user table, $7{\times}$ delay improvement and 48% reduced components utilization has been observed while achieving better accuracy over high speed combinational CORDIC algorithm.

1 Introduction

TRIGONOMETRIC functions such as sine and cosine have found applications in various places such as navigation systems [1], digital signal processing [2], robot control [3], software radio [4], math processors [5], direct digital synthesis [6] and many more applications [7]. LUT based sine generators present several advantages such as simplicity, instantaneous frequency, and phase hopping [8]. The look-up table (LUT) approach involves storing values of sine and cosine at different angles. However, as the size of LUT decreases, the evaluation error increases. Conversely, a large memory is required for the LUT to achieve high accuracy. Moreover, the sine/cosine values can be computed using various other methods such as Taylor series method, and CORDIC algorithm [9] have limitations that include increased computational cost and error in the calculation of sine/cosine values. For instance, in the case of Taylor series expansion, we have to calculate the higher-order power values if we want high accuracy. While high speed requires the trade-off of accuracy, as higher power values are neglected.

Various applications require algorithms that involve the use of imaginary numbers (e.g., Fourier transform). The conversion from Euler’s form into the standard form is necessary to carry out further arithmetic operations on the imaginary numbers. Therefore, in this paper, a Dynamic LUT approach is presented to calculate sine/cosine values with high accuracy. The main theme of this method is twofold, first to determine sine/cosine values by a single division operation, allowing fast computation. Secondly, to provide a framework to allow flexibility on the precision of data and size of the table sampled for the specific application. This allows flexible computing as the bit precision and size of the LUT table can be changed in between different operations. Moreover, multiple users can sample the master table according to the application requirements.

2 Proposed Scheme

In the proposed method, all the possible sine/cosine values are pre-calculated and stored in a master table. The master table is then sampled as documented in Sect. 2.1 to create the user table. Required trigonometric values can be evaluated by using the index at which the sine/cosine value is stored, as explained at the end of Sect. 2.1.

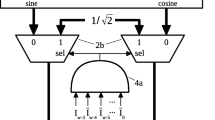
All the complex numbers lie on a unit circle with real axis as the abscissa and imaginary axis as the ordinate expressed in Euler’s form as Eq. (1).

$$\begin{aligned} re^{i\theta }=r(\cos \theta +i\sin \theta )=x+iy \end{aligned}$$

(1)

The graphical representation of Euler form is provided in Fig. 1a, where sine and cosine represent the imaginary and real part respectively. All possible values of $e^{i\theta }$, lie on the unit circle. In the proposed scheme, we sample the circle at an arbitrarily small least count ($\Phi$) as shown in Fig. 1b. Afterwards, we calculate $\sin (n\Phi )$ and $\cos (n\Phi )$ values, where n is a whole number such that $n\Phi \in [0,2\pi )$. These values are stored in the master table with the first, second, and third column as index (n), $\sin (n\Phi )$, and $\cos (n\Phi )$ values respectively, shown in Table 1. A master table shown in Table 1 represents approximately all the possible values of sine and cosine function. The analysis of the error involved in such a sampling operation is provided in Sect. 2.3. The master table stores the sine and cosine values to a certain precision, defined by the number of bits ($\beta$). It is important to note that precision is directly proportional to the number of bits used. This master table can be used to calculate any sine/cosine value by passing an angle (say $\omega$). The sine/cosine value is at the index value (n) calculated as given.

$$\begin{aligned} n=floor(\omega \Phi ) \end{aligned}$$

Table 1 Relation between index and corresponding sine/cosine values

Fig. 1

a Graphical representation of Euler form at an angle $\theta$, b concept of sampling used to create master table

Fig. 2

a Flowchart for the creation of master table for input parameters $\Phi$ and $\beta$, b flowchart for the creation of user table for input parameters $\phi$ and b

The master table is generated only once, flowchart shown in Fig. 2a, with highly accurate values to a bit precision of $\beta$ with arbitrarily small least count $\Phi$. We observe a trade-off between least count $\Phi$ and size of the master table. The overall size of the master table is represented as $(2\pi /\Phi )\times (2\beta )$ bits. Therefore, the size of the master table is dependent on parameters $\Phi$ and $\beta$. For instance, the size of the master table increases rapidly as we decrease the value of $\Phi$. It is worth noting that the table parameters $\Phi$ and $\beta$ varies according to the requirements of the particular application. The larger size of master table may limit the capabilities of a system. Therefore, it is advantageous to employ the DMU-LUT. This configuration involves the use of a universal master table and an application-specific user table. The requirements of different applications can be fulfilled by sampling the universal master table, as discussed in Sect. 2.1. The sampling of master table provides an application-specific user table. The advantage of such a system is that the application can request the master table for a user table of different parameters during run time without putting any computational load on the application itself. Moreover, multiple user tables can be obtained from the master table simultaneously. The sampling techniques for the master table are mentioned in the next subsection.

2.1 Sampling of Master Table to Create User Table

This subsection is devoted to the various proposed sampling scenarios such as constant distance sampling, section sampling, and probabilistic sampling used to sample the master table. We have assumed four parameters which define a user table i.e. least count ($\phi$), bit precision (b), starting point ($\gamma$), and ending point ($\delta$).

Constant distance sampling: In this sampling method, we sample the master table at regular interval of $N_{sample}$, where $N_{sample}=floor(\Phi \phi )$. The concept of creating user table is defined in flowchart as shown in Fig. 2b. The least count ($\phi$) and precision (b) are taken as input such that $\phi <\Phi$ and $b<\beta$. The starting ($\gamma$) and ending point ($\delta$) are set to 0 and $2\pi$ respectively. It should be noted that resultant sine and cosine values are sampled with greater accuracy on considering smaller value of $N_{sample}$. We first consider the integer multiples of $N_{sample}$ and inherit the sine/cosine values from master to user table. The value of integer multiples of $N_{sample}$ (represented as $k\times N_{sample}$) should not exceed $n_{max}$, where k denotes any whole number.

Section sampling method This method is executed similarly to the constant distance sampling method but the span of the user table is restricted by the parameters $\gamma$ and $\delta$ ($\delta -\gamma$ is termed as the section angle). This allows a smaller least count in the region specified, as shown in Fig. 3a, without an increase in table size. This method is restricted due to the absence of stored values at angles not between [$\gamma$, $\delta$] and hence must be used in cases where there is a higher number of sine/cosine values restricted to an angle or when sampling reoccurs for a different $\gamma$ and $\delta$. This method provides better accuracy with more samples in the selected region.

Probabilistic sampling This is another form of section sampling where instead of neglecting values outside $[\gamma ,\delta ]$, we have also assigned sine/cosine values to the outside region. Thus, this method defines two sampling rates for different regions. The region of consideration which is inside $[\gamma ,\delta ]$ should be assigned values at smaller intervals for better accuracy. In the example shown in Fig. 3b, we have taken the probability of 0.8 inside region $[\gamma ,\delta ]$. Hence 80% of our LUT will store the values inside region $[\gamma ,\delta ]$ while only 20% of LUT will store values outside the region. So, we can take more samples in the 80% region to increase accuracy. Also, the 20% region is not neglected in contrast to section sampling. It is worth noting that the least count inside region $[\gamma ,\delta ]$ can be increased or decreased according to the need of the application.

Fig. 3

a Section sampling used to obtain user table for different values of section angle $\delta -\gamma$, b concept of probabilistic sampling used to obtain user table, here $P_{r}$ denotes probability of occurrence os sine/cosine values between $\gamma$ and $\delta$

The user table is dynamic and thus, offers different configurations during run time. To evaluate any sine/cosine value at an angle, say $\theta$. We have to find the index in the user table at which the value is stored and return the sine/cosine value at that index. For a constant distance sampled user table, the index is simply given by $floor (\theta /\phi$). Similarly, in section sampling, the angle is checked first. If it lies in $[\gamma ,\ \delta ]$, then the index is simply $floor((\theta -\gamma )/\phi )$.

2.2 Size Reduction Methods for Master Table

LUT based approach for calculation of sine/cosine values provides accurate results but introduces the limitation of a larger LUT size. Therefore, to reduce the size of the master table this section explores the size reduction methods for the master table. Taking the symmetry of a circle into consideration, the two steps applied for reduction of size of the master table are as follows:

Step One A circle follows horizontal and vertical symmetry along the x and y axes. Due to this symmetry the sine/cosine values of the first quadrant can be used to calculate the sine/cosine values for quadrant II, III, and IV by assigning the correct sign. For example,

$$\begin{aligned} \cos (145^{\circ })=\cos (90^{\circ }+45^{\circ })=-\cos (45^{\circ }) \end{aligned}$$

(2)

Therefore, the size of LUT becomes (1/4)th of the original size.

Step Two The first quadrant is symmetric along the y = x line. By storing the values of the first quadrant before $\pi /4$ the other half of the first quadrant can be determined by the above-represented symmetry. This symmetry can be represented as:

$$\begin{aligned} \sin (45^{\circ }+\theta )&= \cos (45^{\circ }-\theta ) \end{aligned}$$

(3)

$$\begin{aligned} \cos (45^{\circ }+\theta )&= sin(45^{\circ }-\theta ) \end{aligned}$$

(4)

When “Step two” is used in conjunction with “Step one” it reduces the size of LUT to (1/8)th of the original size.

2.3 Impact of Least Count on User Table

This section first explores the relation between size (L) and least count ($\phi$) of user table. Further, the relation between $\phi$ and the maximum absolute error ($\xi _{([sine])}$, $\xi _{([cosine])}$) associated with the user table has also been derived. User table is defined by four parameters as mentioned in Sect. 2. These parameters have been used to find the size of user table (L) which can be expressed as:

$$\begin{aligned} L=b\left( \frac{\delta -\gamma }{\phi }\right) \end{aligned}$$

(5)

where, $\phi$, b, $\gamma$, and $\delta$ represents least count, bit precision, starting point and ending point respectively.

Absolute error ($\xi$) for the user table is expressed as:

$$\begin{aligned} \xi _{([sine])}&= \sin (\phi (k-1))-\sin (\phi (k)) \end{aligned}$$

(6)

$$\begin{aligned} \xi _{([cosine])}&= \cos (\phi (k-1))-\cos (\phi (k)) \end{aligned}$$

(7)

where k denotes the index where the correct value lies. As the maximum absolute error is directly dependent on the value of $\phi$. Therefore, by adjusting the user table parameters appropriately the mean error can be adjusted.

3 Simulation Setup and Experimental Results

To evaluate quality improvements, mean error and variance have been calculated using MATLAB simulation of CORDIC [9] and (proposed) DMU-LUT method. One million uniformly distributed random inputs in the range 0 to $2\pi$ were considered for evaluation of error metrics. It should be noted that for CORDIC algorithm, error decreases exponentially as we increase the number of iterations. This trend is emulated in Fig. 4a by the straight line obtained for base 10 logarithmic x axis. The (proposed) DMU-LUT method is implemented for a LUT containing 8192 addresses and 32-bit sine and cosine values. Moreover, the error metrics have been plotted for constant distance (general LUT) and section sampling scenarios of DMU-LUT.

It is observed from Fig. 4 that the proposed scheme with constant distance sampling (general LUT) demonstrates superior error metrics than CORDIC algorithm for a narrow range of iteration values ($<10$). However, using the proposed scheme with section sampling method, improvements over CORDIC algorithm are observed for a wide selection of section angles, as shown in Fig. 4. This demonstrates superior error metrics of the proposed work while maintaining a fixed LUT size.

Table 2 FPGA design metrics for different implementations

Design implemented metrics were obtained using Verilog with Xilinx ISE 14.7 tools for Artix7 family XC7A100TCSG324 FPGA. For comparison of design metrics, CORDIC algorithm is implemented as an efficient sine/cosine generator. It should also be noted that the hardware implementation of the proposed work is based on a general RAM with 13-bit addresses and 64-bit data values. The design metrics are summarized in Table 2. To aid in comparison BRAMs as well as DSP units, which are parts of the FPGA, were not utilized. Additionally, a 16-iteration combinational CORDIC implementation with 16-bit angles and 32-bit sine/cosine values have been considered. The proposed method has improved error metrics and outperforms CORDIC algorithm by $7{\times}$ in terms of delay performance, however it has been observed that the combinational CORDIC implementation occupies $2.48{\times}$ lesser components than the proposed work. Further improvements in component utilization can be obtained by employment of the proposed 1/8 compression technique, given in Sect. 2.2, which enables an average 48% improvement over the combinational CORDIC approach.

Fig. 4

Comparison of a mean error, b variance, for one million random inputs for CORDIC algorithm [9] and proposed method with constant distance and section sampling

4 Conclusion

So far in the existing literature, Taylor series expansion is used which is computation intensive. Traditional LUT is more efficient in the calculation of sine/cosine values. However, the large size of traditional LUT makes it infeasible for such general applications. This paper introduces the concept of a master–user table configuration for the calculation of sine/cosine values. The dynamic nature of the proposed scheme overcomes the limitation of traditional LUT by three sampling scenarios (constant distance, section, and probabilistic sampling) of the master table to create the user table with user-defined precision. The proposed technique offers the flexibility to achieve the desired accuracy according to system requirements while achieving 7${\times}$ and 48% improvement in delay and component costs respectively.