1 Introduction

OFDM is a multi-carrier modulation technique where transmission frequency band is partitioned into various narrower sub-bands. Each data symbol’s spectrum occupies one of these sub-bands. By making utilization of overlapping sub-bands, OFDM increases spectral efficiency. Since the sub-bands are orthogonal to each other in OFDM, interference is also avoided. The effect of frequency selective fading is combated by breaking the wide transmission band into narrower and multiple sub-bands.

OFDM based wireless systems provide very high speed transmission rates, high mobility, effective utilization of the spectrum and network resources. Some of the applications of OFDM include digital audio broadcasting (DAB), digital video broadcasting (DVB), European HIPERLAN/2, Japanese multimedia mobile access communications (MMAC), digital subscriber line (DSL), digital video broadcasting-handheld (DVB-H) and Media FLO. OFDM is also employed in physical layer of the worldwide interoperability for microwave access (Wi-MAX) and long term evolution (LTE) standards.

One of the major issues in the multi-carrier modulation systems is its high PAPR which is caused as the resultant of non-constant envelopes. Instantaneous power will be more than the average power when the independently modulated sub-carriers are added coherently. PAPR is defined as the ratio of the maximum instantaneous average power to the peak power. For the discrete time version x(n), PAPR is expressed as

$$PAPR\left( {x\left[ n \right]} \right) = \mathop {\hbox{max} }\limits_{0 \le n \le N - 1} \frac{{\left| {x\left( n \right)} \right|^{2} }}{{E\left[ {\left| {x\left( n \right)} \right|^{2} } \right]}}$$
(1)

where \(E\left[ . \right]\) refers to the expectation operator.

PAPR is used to quantify envelope fluctuations and is evaluated per OFDM symbol. Complementary Cumulative distribution function (CCDF) is one of the most informative metric used to evaluate the performance of PAPR reduction scheme. PAPR reduction capability is measured by the amount of CCDF reduction achieved. CCDF can be defined as the probability that the PAPR of the OFDM symbol with N sub-carriers is below a threshold δ.

Several PAPR reduction schemes were introduced to reduce PAPR in OFDM systems. PAPR reduction techniques can be classified into three broad categories such as Signal distortion, multiple signaling and probabilistic and coding techniques. SLM is a multiple signaling and probabilistic technique where multiple permutations of the OFDM signal are generated and one with the least PAPR is selected for transmission. [1].

In this paper, the performance of various phase sequences on Modified SLM scheme is analyzed. The rest of the paper is organized as follows. Section 2 presents the related works and Sect. 3 describes about the Conventional SLM scheme. Section 4 briefs about the Modified SLM scheme. Various Phase sequences and their influence on PAPR reduction are discussed in Sect. 5. Section 6 presents the Simulation results and discussion and concluding remarks are given in Sect. 7.

2 Related Works

SLM technique was initially introduced by Bauml et al. [2] in the year 1996 for reducing PAPR in multi-carrier modulation systems. Here {+ 1, − 1, + j, − j} were used as phase sequences. If the phase shifts are multiples of \(\frac{\pi }{2}\), no multiplications are required. The N frames are transformed into time domain and one with lowest PAPR is selected for transmission.

Jayalath et al. [3] presented Newman phase sequences for the reduction of PAPR in OFDM signal. Zhou et al. [4] proposed monomial phase sequences for SLM technique for reducing PAPR in OFDM systems. Monomial phase sequences offered significant reduction of computational complexity at the transmitter side. Irukulapati et al. [5] introduced a PAPR reduction scheme where the rows of normalized Riemann matrices were used as phase sequences for SLM for reducing PAPR in OFDM signals. This scheme gave lower PAPR value than Hadamard and Chaotic sequences. The mean and variance of this scheme was very much less when compared with other phase sequence sets.

A combination of M-ary Chaotic sequences and mapping scheme was introduced by Goel et al. [6] for reducing PAPR. The main advantage of this scheme is that it did not require side information (SI) as well as it provided SER performance with good PAPR reduction capability when compared with other existing SLM-OFDM methods. Namitha and Sameer [7] introduced Improved SLM with Gold/Hadamard code for reducing PAPR in OFDM systems. Pepin et al. [8] introduced the usage of SLM using Riemann sequences combined with DCT transform for reducing PAPR in OFDM communication systems. Saheed et al. [9] proposed Fibonacci-binary sequences for reducing PAPR in SLM based OFDM Communication systems. Pseudo-interferometry code was proposed by Wang et al. [10] as the phase sequence set for SLM to reduce PAPR in MC-CDMA systems. It was shown that pseudo-interferometry code was effective when compared with Walsh-Hadamard and Golay sequences.

Thitapha et al. [11] applied new phase sequence based on centering matrix to SLM for reducing PAPR in MIMO-OFDM systems. It was found that the centering matrix outperformed normalized Riemann matrix and Hadamard matrix in terms of PAPR reduction. Ning et al. [12] used a combination of exhaustive entropy, chaotic sequences and improved Lorenz sequences to evaluate randomness of phase sequences, reduce large side information and to enlarge sequence entropy respectively. Sharma et al. [13] proposed modified Chu sequences for reducing PAPR in OFDM systems. Haque et al. [14] proposed Hadamard matrix row factor as phase sequence for the reduction of PAPR. Abouty et al. [15] proposed an effective PAPR reduction scheme which combined DCT transform with SLM technique. A new phase sequence called Hanowa matrix was introduced which was found to perform better than Riemann and Hilbert matrices. The advantages of this scheme are randomness in phase sequence selection is avoided decoding is simpler at the receiver end. Other advantages include that this matrix can be generated at the receiver end to obtain original data signals and there is no need to transmit side information. Pyla et al. [16] introduced a new phase sequence which outperformed Riemann, Rudin-shapiro, Chaotic, Chu Pseudo-random and Hadamard sequences. Lehmer sequences were introduced and applied to SLM by Sudha et al. [17] for reducing PAPR without the need for side information.

3 Selective Mapping (SLM) Technique

SLM is a PAPR reduction technique which converts OFDM signal into several independent signals by multiplication with the phase sequence set and transmits the one with least PAPR. SLM is one of the distortion less PAPR reduction technique for OFDM systems. SLM needs the transmission of index of the selected signal along with the OFDM symbol. The amount of PAPR performance improvement depends on the number of candidates and type of phase sequences. The PAPR reduction is proportional to M but increase in M increases side information overload which is given in terms of \((log_{2} M)\) as side information. The selection of phase sequences plays an important role in reduction of PAPR. Figure 1 shows the block diagram of Selective mapping technique.

Fig. 1
figure 1

Block diagram of SLM technique [5]

Full size image

The algorithm of the SLM technique can be given as follows [5]

  • Step 1 The input data bits are mapped into constellation points of M-QAM or BPSK to provide sequence symbols \(X_{0} ,X_{1} ,X_{2}\).

  • Step 2 The symbol sequences are partitioned into blocks of length N, where N refers to the number of sub-carriers.

  • Step 3 Each block \(X = \left[ {X_{0} ,X_{1} ,X_{2} , \ldots ,X_{N - 1} } \right]\) is multiplied with U number of phase sequence vectors \(B^{(u)} = \left[ {B_{0}^{(u)} ,B_{1}^{(u)} , \ldots ,B_{2}^{(u)} } \right]^{T}\) where u refers to the row values of the corresponding matrices.

  • Step 4 A set of U different OFDM data blocks or candidate signals are generated as follows \(X^{(u)} = \left[ {X_{0}^{(u)} ,X_{1}^{(u)} , \ldots ,X_{N - 1}^{(u)} } \right]^{T}\), where \(X_{n}^{(u)} = X_{n} \cdot B_{n}^{(u)} ,n = 0,1,2, \ldots ,N - 1,u = 1,2, \ldots ,U\).

  • Step 5 Transform \(X^{(u)}\) into time domain to get \(x^{\left( u \right)} = IFFT\left\{ {X^{\left( u \right)} } \right\}\).

  • Step 6 Select the one from \(x^{\left( U \right)} ,u = 1,2, \ldots ,U\) which has the minimum PAPR and transmit.

4 Modified SLM

In modified SLM, random matrix is generated from the existing phase matrix of the classical SLM such that the new matrix has less number of rows than that of existing matrix. Reduction of the number of rows leads to reduction in computational complexity. Here, the original data block can be detected without sending any side information along with selected signal. PAPR of this technique is less than that of Classical SLM technique. The alternative phase vectors that are used in Classical SLM technique can be considered as \(U \times N\) matrix, where U refers to the total number of alternative signals and N is the number of sub-carriers. In the modified SLM, a new matrix \(B_{1}\) is generated having \(U /2\) number of rows according to the following steps. Each row of the new matrix is found by doing the following additions.

$$B_{1} \left( 1 \right) = B\left( 1 \right) + B\left( 2 \right)$$
(2)
$$B_{1} \left( 2 \right) = B\left( 3 \right) + B\left( 4 \right)$$
(3)
$$B_{1} \left( {{\raise0.7ex\hbox{$U$} \!\mathord{\left/ {\vphantom {U 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right) = B\left( {U - 1} \right) + B\left( U \right)$$
(4)

By applying the above steps, some elements of the matrix are zero. By applying the following condition, we get

$$B_{1} (u,n) = 0,\,{\text{then}}\,B_{1} (u) = 1\,({\text{or}})\,{\text{we}}\,{\text{can}}\,{\text{also}}\,{\text{put}}\,B_{1} (u,n) = - 1.$$

For the modified SLM technique, the number of complex additions is given by \({\raise0.7ex\hbox{$U$} \!\mathord{\left/ {\vphantom {U 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}Nlog_{2} N\) and the number of complex multiplications is given by \({\raise0.7ex\hbox{$U$} \!\mathord{\left/ {\vphantom {U 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}{\raise0.7ex\hbox{$N$} \!\mathord{\left/ {\vphantom {N 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}log_{2} N\). In this technique, 50% of the computational complexity is reduced as well as there is no requirement of sending side information along with the selected OFDM signal [17].

5 PAPR Reduction Using Different Phase Sequences

Selection of phase sequences plays an important role in the reduction of PAPR. Riemann and Centering are two matrices which when employed with SLM reduces PAPR to a great extent. These two matrices have the nature of reducing PAPR to a greater extent than any other phase sequences.

  1. (a)

    Riemann phase sequences

In this approach, the rows of normalized Riemann matrices are applied as phase sequences to the Modified SLM technique. A typical Riemann matrix is obtained by removing first row and first column of matrix R, where

$$R(i,j) = \left\{ {\begin{array}{*{20}l} {i - 1} \hfill & { if\, i\, divides\,j} \hfill \\ { - 1} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(5)

If Riemann matrix (R) is of size \(M \times M,\) the entries in the normalized Riemann matrix (B) is of size \(\left( {\frac{1}{M}} \right)R\) [5].

Riemann matrix (R) of order 8 can be represented as

$${\text{R}} = \left[ {\begin{array}{*{20}c} 1 & { - 1} & 1 & { - 1} & 1 & { - 1} & 1 & { - 1} \\ { - 1} & 2 & { - 1} & { - 1} & 2 & { - 1} & { - 1} & 2 \\ { - 1} & { - 1} & 3 & { - 1} & { - 1} & { - 1} & 3 & { - 1} \\ { - 1} & { - 1} & { - 1} & 4 & { - 1} & { - 1} & { - 1} & { - 1} \\ { - 1} & { - 1} & { - 1} & { - 1} & 5 & { - 1} & { - 1} & { - 1} \\ { - 1} & { - 1} & { - 1} & { - 1} & { - 1} & 6 & { - 1} & { - 1} \\ { - 1} & { - 1} & { - 1} & { - 1} & { - 1} & { - 1} & 7 & { - 1} \\ { - 1} & { - 1} & { - 1} & { - 1} & { - 1} & { - 1} & { - 1} & 8 \\ \end{array} } \right]$$
(6)

The elements in the uth row are of the values u or \(- 1\), \(1 \le u \le N\). The element values in the normalized Riemann matrix of value \(- 1\) results in phase change and the elements with value u results in change in amplitude of the modulated symbols. Additionally, the average power of the sub-carriers gets increased by a factor \(u^{2}\) which later results in lesser PAPR value.

  1. (b)

    Centering phase sequences

Centering matrix is a symmetric and idempotent matrix which when multiplied with a vector has the same effect as subtracting the mean components of the matrix. The centering matrix is obtained by modifying the elements of normalized Riemann matrix. The advantage of centering matrix is that it removes the mean of a single vector as well as that of multiple vectors stored in rows or columns of a matrix.

In MSC approach, the phase sequences given are the rows of the centering matrix. The Centering matrix is defined by \(n \times n\) matrix.

$$C_{n} = I_{n} - \frac{1}{n}O$$
(7)

where \(I_{n}\) is the identity matrix of size n and O is a n-by-n matrix of all 1’s.

\(I_{n }\) of size 8 is represented as

$$I = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(8)
$$O = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{array} } \right]$$
(9)
$$C_{8} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right] - \frac{1}{8}\left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{array} } \right]$$

Centering matrix (C) of order 8 can be represented as

$${\text{C}} = \left[ {\begin{array}{*{20}c} {0.875} & { - 0.125} & { - 0.125} & { - 0.125} & { - 0.125} & { - 0.125} & { - 0.125} & { - 0.125} \\ { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} \\ \end{array} } \right]$$
(10)
  1. (c)

    Centered-Riemann phase sequences

Modified Centered Riemann, the rows of Centered Riemann matrices are applied as phase sequences to the modified SLM technique. Centering of a data matrix can be done by multiplying a standard matrix with centering matrix. After the centering operation, values of the data matrix get closer to the mean value. Centered Riemann matrix is formed by the matrix multiplication between Riemann and Centering matrices which can be given as [18]

$$CR = C_{n} *R_{n}$$
(11)

where \(C_{n}\) is the centering matrix of size n-by-n.

\(R_{n}\) is the Riemann matrix of size n-by-n

$$C_{8} = \left[ {\begin{array}{*{20}c} {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} \\ \end{array} } \right]$$
$$R_{8} = \left[ {\begin{array}{*{20}c} 1 & { - \,1} & 1 & { - \,1} & 1 & { - \,1} & 1 & { - \,1} \\ { - \,1} & 2 & { - \,1} & { - \,1} & 2 & { - \,1} & { - \,1} & 2 \\ { - \,1} & { - \,1} & 3 & { - \,1} & { - \,1} & { - 1} & 3 & { - \,1} \\ { - \,1} & { - \,1} & { - \,1} & 4 & { - \,1} & { - \,1} & { - \,1} & { - \,1} \\ { - \,1} & { - \,1} & { - \,1} & { - \,1} & 5 & { - \,1} & { - \,1} & { - \,1} \\ { - \,1} & { - \,1} & { - \,1} & { - \,1} & { - \,1} & 6 & { - \,1} & { - \,1} \\ { - \,1} & { - \,1} & { - \,1} & { - \,1} & { - \,1} & { - \,1} & 7 & { - \,1} \\ { - \,1} & { - \,1} & { - \,1} & { - \,1} & { - \,1} & { - \,1} & { - \,1} & 8 \\ \end{array} } \right]$$

Centered Riemann matrix (CR) of order 8 can be represented as

$$CR = \left[ {\begin{array}{*{20}c} {1.75} & { - \,0.375} & {1.25} & { - \,0.625} & {0.625} & { - \,0.875} & {0.25} & { - \,1.50} \\ { - \,0.25} & {2.625} & { - \,0.75} & { - \,0.625} & {1.625} & { - \,0.875} & { - \,1.75} & {1.50} \\ { - \,0.25} & { - \,0.375} & {3.25} & { - \,0.625} & { - \,1.375} & { - \,0.875} & {2.25} & { - \,1.50} \\ { - \,0.25} & { - \,0.375} & { - \,0.75} & {4.375} & { - \,1.375} & { - \,0.875} & { - \,1.75} & { - \,1.50} \\ { - \,0.25} & { - \,0.375} & { - \,0.75} & { - \,0.625} & {4.625} & { - \,0.875} & { - \,1.75} & { - \,1.50} \\ { - \,0.25} & { - \,0.375} & { - \,0.75} & { - \,0.625} & { - \,1.375} & {6.125} & { - \,1.75} & { - \,1.50} \\ { - \,0.25} & { - \,0.375} & { - \,0.75} & { - \,0.625} & { - \,1.375} & { - \,0.875} & {6.25} & { - \,1.50} \\ { - \,0.25} & { - \,0.375} & { - \,0.75} & { - \,0.625} & { - \,1.375} & { - \,0.875} & { - \,1.75} & {7.5} \\ \end{array} } \right]$$
(12)
  1. (d)

    New-Centered phase sequences

New Centered matrix is formed by element-by-element multiplication between Centering and Riemann matrices. The elements of the new centered technique are given as phase sequences to the modified SLM technique. The new centered matrix can be generated using the expression given below [18].

$$NC = C_{n} .*R_{n}$$
(13)
$$\begin{aligned} NC = & \left[ {\begin{array}{*{20}c} {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} & { - \,0.125} \\ { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & { - \,0.125} & {0.875} \\ \end{array} } \right] \\ & \quad .*\left[ {\begin{array}{*{20}c} 1 & { - \,1} & 1 & { - \,1} & 1 & { - \,1} & 1 & { - \,1} \\ { - \,1} & 2 & { - \,1} & { - \,1} & 2 & { - \,1} & { - \,1} & 2 \\ { - \,1} & { - \,1} & 3 & { - \,1} & { - \,1} & { - \,1} & 3 & { - \,1} \\ { - \,1} & { - \,1} & { - \,1} & 4 & { - \,1} & { - \,1} & { - \,1} & { - \,1} \\ { - \,1} & { - \,1} & { - \,1} & { - \,1} & 5 & { - \,1} & { - \,1} & { - \,1} \\ { - \,1} & { - \,1} & { - \,1} & { - \,1} & { - \,1} & 6 & { - \,1} & { - \,1} \\ { - \,1} & { - \,1} & { - \,1} & { - \,1} & { - \,1} & { - \,1} & 7 & { - \,1} \\ { - \,1} & { - \,1} & { - \,1} & { - \,1} & { - \,1} & { - \,1} & { - \,1} & 8 \\ \end{array} } \right] \\ \end{aligned}$$

The New-Centered (NC) matrix of order 8 can be represented as

$${\text{NC}} = \left[ {\begin{array}{*{20}c} {0.875} & {0.125} & { - \,0.125} & {0.125} & { - \,0.125} & {0.125} & { - \,0.125} & {0.125} \\ {0.125} & {1.75} & {0.125} & {0.125} & { - \,0.25} & {0.125} & {0.125} & { - \,0.25} \\ {0.125} & {0.125} & {2.625} & {0.125} & {0.125} & {0.125} & { - \,0.375} & {0.125} \\ {0.125} & {0.125} & {0.125} & {3.5} & {0.125} & {0.125} & {0.125} & {0.125} \\ {0.125} & {0.125} & {0.125} & {0.125} & {4.375} & {0.125} & {0.125} & {0.125} \\ {0.125} & {0.125} & {0.125} & {0.125} & {0.125} & {5.25} & {0.125} & {0.125} \\ {0.125} & {0.125} & {0.125} & {0.125} & {0.125} & {0.125} & {6.125} & {0.125} \\ {0.125} & {0.125} & {0.125} & {0.125} & {0.125} & {0.125} & {0.125} & {7.0} \\ \end{array} } \right]$$
(14)

When comparing the variances of New-Centered and Centered Riemann matrices, it can be observed that the variance of phase sequences of New Centered scheme is lower than the Centered-Riemann scheme. Hence, there is a possibility of larger peak power in New Centered scheme which leads to reduced PAPR value.

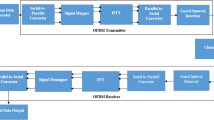
When comparing the elements of the Centered Riemann (8) and New Centered matrix (10), it can be seen that the diagonal element values of the new centered matrix are lesser than that of the Centered-Riemann matrix and all other elements in the new centered matrix tend to zero which leads to its better PAPR performance. The element-by-element wise multiplication also results in lesser number of computations than the Modified Centered Riemann technique which is another key feature of the new centered scheme. The matrix combination can be generated at the receiver end which results in reduction in side information (SI) as only the row index can be sent as SI. Figure 2 shows the block diagram of the modified SLM with new centered phase sequences.

Fig. 2
figure 2

Block diagram of the modified SLM with new centered phase sequences structure

Full size image

The algorithm methodology employed for the simulation is given below

  • Step 1 Initialization of number of message symbols to be transmitted, number of subcarriers, number of candidate sequences and phase factor values.

  • Step 2 Generation of random message and perform modulation on each symbol.

  • Step 3 Generation of different phase sequences such as Riemann, Centering, Centered-Riemann and New-Centered.

  • Step 4 Multiplication of the phase sequences with the modulated signals.

  • Step 5 Conversion of frequency domain signals to time domain modulated signals.

  • Step 6 PAPR is calculated for each signal and the one with lowest PAPR is selected for transmission.

6 Simulation Results and Discussion

Simulation results were carried out using MATLABR2016a software. The number of sub-carriers was considered to be 256 and 512. The number of transmitted message symbols is considered to be 103. The number of candidate sequences is considered to be 256 and 512. The phase weighting factors considered are \(\left\{ { \pm \,1, \pm \,j} \right\}.\) The simulation results were carried out for all the modulation schemes such as BPSK, QPSK, 16-QAM and 64-QAM. The CCDF at which the PAPR value is measured is 10−3. Modified SLM-Riemann (MSR), Modified SLM-Centering (MSC), Modified SLM- Centered Riemann (MCR) and Modified SLM- New Centered (MNC) techniques were compared with the performance of Conventional SLM scheme. The simulation parameters employed are tabulated in Table 1.

Table 1 Simulation parameters
Full size table

Figure 3 depicts the comparison of PAPR reduction of the various phase sequences on Modified SLM in BPSK modulation scheme. When N = 256, Modified SLM-Riemann sequence (MSR) and Modified SLM-Centering (MSC) schemes have a PAPR reduction of around 7.58 dB and 7.771 dB with respect to the Conventional OFDM and 2.813 and 3.004 dB reduction with respect to Conventional SLM. The modified centered Riemann (MCR) scheme had a PAPR reduction of around 7.653 dB with respect to Conventional OFDM and 2.886 dB reduction with respect to Conventional SLM. The Modified New Centered (MNC) scheme outperformed all the other schemes by providing a PAPR reduction of 8.181 dB with respect to Conventional OFDM and 3.414 dB with respect to Conventional SLM scheme.

Fig. 3
figure 3

PAPR reduction performance of MSR, MSC, MCR and MNC schemes for BPSK modulation when N = 256

Full size image

In Fig. 4 when number of sub-carriers were increased to N = 512, it can be seen that as MSR, MSC and MCR phase sequences have a PAPR reduction of 7.314 dB,7.431 dB and 7.353 dB over Conventional OFDM and 3.382 dB, 3.499 dB and 3.421 dB over Conventional SLM. The MNC scheme outperformed other phase sequences by providing a PAPR reduction of 7.761 dB and 3.414 dB with respect to Conventional OFDM and Conventional SLM respectively.

Fig. 4
figure 4

PAPR reduction performance of MSR, MSC, MCR and MNC schemes for BPSK modulation when N = 512

Full size image

Figure 5 shows the comparison of PAPR reduction of the various phase sequences when N = 256 for QPSK modulation scheme. MSR and MCR schemes have a PAPR reduction of 7.183 dB each and MSC scheme had a PAPR reduction of around 7.332 dB over Conventional OFDM. MSR and MCR schemes show a PAPR reduction of 2.76 dB over the Conventional SLM and MSC scheme has a PAPR reduction of 2.912 dB. The MNC scheme outperformed other schemes by proving a PAPR reduction of 7.81 dB and 3.835 dB over the Conventional OFDM and Conventional SLM respectively.

Fig. 5
figure 5

PAPR reduction performance of MSR, MSC, MCR and MNC schemes for QPSK modulation when N = 256

Full size image

Figure 6 shows the comparison of PAPR performance comparison of various phase sequences when N = 512 for QPSK modulation scheme. MSR, MSC and MCR schemes shows a PAPR reduction of 7.454 dB, 7.571 dB and 7.487 dB with respect to Conventional OFDM and 3.329 dB, 3.446 dB and 3.362 dB over the Conventional SLM scheme. The MNC scheme shows a comparatively better PAPR performance when compared with the other phase sequences by providing a PAPR reduction of around 7.96 dB and 3.835 dB over the Conventional OFDM and Conventional SLM respectively.

Fig. 6
figure 6

PAPR reduction performance of MSR, MSC, MCR and MNC schemes for QPSK modulation when N = 512

Full size image

Figure 7 shows the PAPR reduction comparison of various phase sequences versus Conventional OFDM and Conventional SLM for 16-QAM modulation scheme for N = 256. From the simulation results, it can be found that there is a reduction of around 7.57 dB, 8.051 dB and 7.554 dB for MSR, MSC and MCR phase sequences with respect to the Conventional OFDM. While considering Conventional SLM, there is a reduction of 3.116 dB, 3.588 dB and 3.091 dB for MSR, MSC and MCR phase sequences. The MNC scheme has a PAPR reduction of around 8.812 dB over Conventional OFDM and 4.349 dB in the case of Conventional SLM.

Fig. 7
figure 7

PAPR reduction performance of the proposed MSR, MSC, MCR and MNC schemes for 16-QAM modulation when N = 256

Full size image

Figure 8 shows the PAPR reduction performance of various phase sequences for 16-QAM modulation scheme when N = 512. It can be found that there is a reduction of 7.891 dB for MSR and MCR schemes and 8.143 dB reduction in the MNC scheme with respect to the Conventional OFDM. In the case of Conventional SLM, there is a reduction of 4.04 dB in the case of MSR and MCR schemes and a reduction of 4.292 dB in the case of MSC scheme. The MNC scheme outperforms other schemes by providing a PAPR reduction of around 8.691 dB and 4.84 dB in the case of Conventional OFDM and Conventional SLM respectively.

Fig. 8
figure 8

PAPR reduction performance of the proposed MSR, MSC, MCR and MNC schemes for 16-QAM modulation when N = 512

Full size image

Figure 9 shows the PAPR reduction of the proposed schemes for 64-QAM modulation scheme when N = 256. For MSR and MCR phase sequences, there is a PAPR reduction of around 7.598 dB and in the case of MSC scheme there is a PAPR reduction of 8.123 dB in the case of Conventional OFDM. When compared with Conventional SLM, the MSR and MCR phase sequences exhibit a PAPR reduction of 3.3 dB. The MSC scheme has a PAPR reduction of around 8.123 dB and 3.825 dB in the case of Conventional OFDM and Conventional SLM. MNC phase sequences perform better when compared with the other sequences by providing a PAPR reduction of around 9.265 dB and 4.9 dB in the case of Conventional OFDM and Conventional SLM.

Fig. 9
figure 9

PAPR reduction performance of MSR, MSC, MCR and MNC schemes for 64-QAM modulation when N = 256

Full size image

The simulation results of the proposed schemes for 64-QAM modulation scheme when N = 512 is depicted in Fig. 10. The MSR, MSC and MCR sequences provide a PAPR reduction of 7.739 dB, 8.447 dB and 7.94 dB respectively with respect to the Conventional OFDM and 4.087 dB, 4.795 dB and 4.288 dB reduction with respect to the Conventional SLM. The MNC scheme provides a PAPR reduction of 9.195 dB and 5.543 dB when compared with Conventional OFDM and Conventional SLM respectively.

Fig. 10
figure 10

PAPR reduction performance of the MSR, MSC, MCR and MNC schemes for 64-QAM modulation when N = 512

Full size image

In BPSK and QPSK modulation schemes, the modified SLM-New Centered phase sequences outperforms Modified SLM-Centered Riemann by 0.627 dB and 0.828 dB respectively when the number of sub-carriers(N) is 256. In 16-QAM and 64-QAM modulation schemes, Modified SLM New Centered phase sequence outperforms Modified SLM-Centered Riemann by 0.828 dB and 1.667 dB.

When the number of sub-carriers (N) is 512, the modified SLM-New Centered phase sequences outperform Modified SLM-Centered Riemann by 0.408 dB and 0.473 dB in BPSK and QPSK modulation schemes respectively. In 16-QAM and 64-QAM modulation schemes, Modified SLM-New Centered phase sequences outperform Modified SLM-Centered Riemann by 0.8 dB and 1.225 dB respectively.

Tables 2 and 3 gives a comparison of PAPR reduction performance of Modified SLM using Riemann, Modified SLM using Centering, Modified SLM-Centered Riemann and Modified SLM-New Centered phase sequences under various modulation schemes when N = 256 and N = 512 respectively.

Table 2 PAPR reduction comparison of various phase sequences for various modulation schemes when N = 256
Full size table
Table 3 PAPR reduction comparison of various phase sequences for various modulation schemes when N = 512
Full size table

7 Conclusion

In this paper, four types of phase sequences such as Riemann, Centering, Centered Riemann and New Centered are applied to Modified SLM and their performances on PAPR reduction are analyzed. Out of the four phase sequences, the new centered phase sequences when applied to modified SLM provides good PAPR reduction at the advantage of lower computational complexity. Modified SLM using New-Centered phase sequences provides a maximum PAPR reduction of around 87.32% when compared with the Conventional OFDM. When compared with the Conventional SLM, there is a PAPR reduction of around 80.59% in the Modified SLM using New Centered phase sequences. From the simulation results, it can also be inferred that the Modified SLM with new centered scheme achieves a significant PAPR reduction of the range 8.3–9.3 dB with respect to Conventional OFDM. When analyzed with Conventional SLM, there is a PAPR reduction of 3–5.5 dB in modified SLM using New centered phase sequences. Modified SLM using New Centered phase sequences can be used to reduce PAPR in OFDM systems more effectively.