The Performance of Systems Featuring Dynamic Decode-and-Forward and Network Coding

Abstract

We constructed a single-relay-station cooperative communications system, featuring integration between the dynamic decode-and-forward (DDF) protocol and network coding (NC) to examine the outage probabilities in the Rayleigh, Rician, and Nakagami fading channels. In addition, the diversity-multiplexing tradeoff of the system was analyzed to examine improvements for system performance through integrating these two technologies. Through simulations and analyses, we discovered that the systems featuring NC had lower outage probability and greater diversity gain, and consequently, greater system reliability compared to the ordinary system featuring only the DDF protocol. However, because we added a final phase for the transmission of network coded signals, the system showed lower multiplexing gain compared to the system featuring only the DDF. Users should adopt this system based on their needs. For example, in situations that have higher requirements for reliability and lower requirements for multiplexing gain, users can adopt a DDF-NC cooperative communications system.

1 Introduction

1.1 Preface

The recent gradual developments in cooperative communications systems and relay technologies have been critical to wireless communications. These technologies have been applied extensively. For example, Long Term Evolution-Advanced (LTE-Advanced) [11] and IEEE 802.16m [5] standards both support cooperative communications and relay technologies. The contributions of cooperative relay technologies have been substantial

The benefits of cooperative communications to wireless network have caused researchers to conduct continuous research on related topics [14]. Simulation results have shown that relay technologies effectively enhance communication service coverage and system throughput. In [7], the authors introduced a revision to the IEEE 802.16j and analyzed, from the perspective of system designers, the technical obstacles that must be overcome in applying relay technologies to wireless broadband networks. In [3], the authors used LTE-Advanced to explore the feasibility of decode-and-forward (DF) [6, 8, 9] and discovered that this technology enables satisfactory system performance gains.

1.2 Motivation and Objective

Cooperative communication is an important technology in wireless communications because it can reduce the negative effects of poor wireless channels. For example, it enables signals to be transmitted to farther locations while reducing the error rates of received signals. In an era in which everyone carries a mobile device, the quality of human communication can be enhanced if each mobile device can play the role of a relay station.

Network coding (NC) [1] is a recently developed technology and NC nodes integrate information from various sources and transmit this integrated information to other nodes. This effectively enhances system throughput and transmission efficiency.

Based on the results of [10], we discovered that the integration between DF and NC has development potential for enhancing system performance in the sense of outage probability and diversity-multiplexing tradeoff (DMT) [15]. Therefore, we propose building cooperative communications systems that feature DDF [2], which can be regarded as a modified protocol of DF. In addition, we propose adding NC to relay stations. Hence, the proposed system is called DDF-NC system. Subsequently, we examined the outage probability of the integration of these two technologies in frequently used wireless channels (i.e., Rayleigh, Rician, and Nakagami fading channels) and DMT in Rayleigh fading channel to analyze the system performance.

1.3 Paper Structure

The structure of this paper is as follows: Sect. 1 introduces the motivation and objective for this study and the foci of the various sections; Sect. 2 describes the model for the DDF-NC cooperative communications system; In Sect. 3, we derive the outage probability of DDF-NC system; Sect. 4 analyzes the DMT of DDF-NC system; Sect. 5 comprises the numerical results and discussions; Sect. 6 offers a conclusion and future research directions.

2 System Model

In this section, we introduce the construction of a simple system model that features the integration of the DDF protocol and NC.

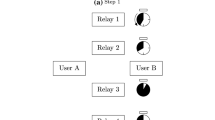
Please see Fig. 1. This model consisted of three nodes, that is, Nodes A, B, and C. When Node A acts as the signal source sender, Node B is the destination of the signal transmission. Similarly, when Node B acts as the signal source sender, Node A is the destination of the signal transmission. Node C is the relay station, which is responsible for receiving the signals from Nodes A and B and, subsequently, decoding and re-encoding the signals and forwarding them to their destinations.

Fig. 1

The DDF-NC system model

We divided the model into five phases to demonstrate the entire system flow. The first two phases were the DDF process, in which C (relay station) waits until it receives signals from A (signal source), decodes and re-encodes the signals, and forwards them to B (destination). Following this procedure, A constantly sends signals to B. During Phases 3 and 4, Node B is the signal sender, whereas C decodes and forwards the signals from B to Node A. The final phase is a transmission process for the network coded signals, where C performs NC on the signals it receives from A and B in the previous four phases and sends the network coded signals simultaneously to Nodes A and B. This is the complete transmission flow of the entire system.

2.1 System Assumptions

This study explores the performance of the DDF-NC system. The establishment of the system model was based on the following assumptions to simplify the problems we want to solve and for the convenience of the discussion and analyses.

• 1. In the beginning, Nodes A and B have information bit streams $a$ and $b$, respectively. We assume that the length of $a$ and $b$ are equal. Nodes A and B want to exchange their information through the help of Node C.

• 2. A code word that is sent from a signal source contains $l$ consecutive symbols.

• 3. The sender operates at a transmission rate of $R$ bps/Hz in all symbol intervals.

• 4. The $k$-th information symbols sent from Nodes A and B are represented with $x_{k,a}$ and $x_{k,b}$, respectively.

• 5. The channel gain remains constant during each phase; the channel gains in different phases were independent and identically distributed (i.i.d.) random variables.

• 6. The noise at the receiver was additive white Gaussian noise (AWGN).

• 7. The receiver used maximum ratio combining.

2.2 The Five Phases of the DDF-NC System

• Phase 1

Please Fig. 2. In Phase 1, A sends signals to B and C. Node C constantly waits for the signals sent from A; when C determines that a signal can be decoded, it decodes, re-encodes, and subsequently forwards the coded signal to B.

Fig. 2

Phase 1 of the DDF-NC system model

This phase requires $l'_a$ signal intervals. The formula of $l'_a$ is similar to the formula of $l'$ in the DDF protocol [2, (13)]:

$$\begin{aligned} l'_a = \min \left\{ l, \left\lceil \frac{l R}{\log _2(1 + |h_\mathrm{{AC}1}|^2 k_a \rho )} \right\rceil \right\} . \end{aligned}$$

(1)

In (1): $h_{XYi}$ is the channel gain of Channel $X$-$Y$ during Phase $i$, where $X, Y \in \{\mathrm{A}, \mathrm{B}, \mathrm{C}\}$, $X \ne Y$, $h_{XYi} = h_{YXi}$, and $1 \le i \le 5$; $k_a = \sigma _\mathrm{{B}}^2 / \sigma _\mathrm{{C}}^2$ is the noise variance ratio between B and C; $\rho$ represents the signal-to-noise ratio (SNR).

Within symbol intervals $1 \le k \le l'_a$, when A sends signal $x_{k,a}$ to B and C, the signals that B and C receive are, respectively, as follows:

$$\begin{aligned} y_{k,\mathrm {B}1}&= h_\mathrm{{AB}1} x_{k,a} + n_{k,\mathrm {B}1}, \quad 1 \le k \le l'_a;\end{aligned}$$

(2)

$$\begin{aligned} y_{k,\mathrm {C}1}&= h_\mathrm{{AC}1} x_{k,a} + n_{k,\mathrm {C}1}, \quad 1 \le k \le l'_a; \end{aligned}$$

(3)

where $n_{k,Xi}$ is the noise at Node $X$ during the $k$-th symbol interval of Phase $i$.

• Phase 2

The transmission of a complete code word requires $l$ signal intervals. However, in Phase 1, A sends $x_{k,a}$, which is a signal containing the first part of a code word, to B. This process requires only $l'_a$ signal intervals. Please see Fig. 3. In Phase 2, A continues to send the remainder of the code word, while C sends the re-encoded signal $x'_{k,a}$ to B. Therefore, we determined that Phase 2 requires $l-l'_a$ signal intervals.

Fig. 3

Phase 2 of the DDF-NC system model

The signals that B receives in this phase can be represented as follows:

$$\begin{aligned} y_{k,\mathrm {B}2} = h_\mathrm{{AB}2} x_{k,a} + h_\mathrm{{CB}2} x'_{k,a} + n_{k,\mathrm {B}2}, \quad l'_a < k \le l, \end{aligned}$$

(4)

where $x'_{k,a}$ is the signal that C receives from A and subsequently decodes, re-encodes and forwards to B.

• Phase 3

Please see Fig. 4. In Phase 3, Node B sends signals to Nodes A and C. Node C constantly waits for the signals sent from B. This phase requires $l'_b$ signal intervals, where

$$\begin{aligned} l'_b = \min \left\{ l, \left\lceil \frac{l R}{\log _2(1 + |h_\mathrm{{BC}3}|^2 k_b \rho )} \right\rceil \right\} . \end{aligned}$$

(5)

In (5): $l'_b$ is the number of signal intervals that C must wait for when B sends signal $x_{k,b}$; $k_b = \sigma _\mathrm{{A}}^2 / \sigma _\mathrm{{C}}^2$ is the noise variance ratio between A and C.

Fig. 4

Phase 3 of the DDF-NC system model

Within signal interval $1 \le k \le l'_b$, when B sends $x_{k,b}$ to A and C, the signals that A and C receive are, respectively, as follows:

$$\begin{aligned} y_{k,\mathrm {A}3}&= h_\mathrm{{BA}3} x_{k,b} + n_{k,\mathrm {A}3}, \quad 1 \le k \le l'_b;\end{aligned}$$

(6)

$$\begin{aligned} y_{k,\mathrm {C}3}&= h_\mathrm{{BC}3} x_{k,b} + n_{k,\mathrm {C}3}, \quad 1 \le k \le l'_b. \end{aligned}$$

(7)

• Phase 4

The transmission of a complete code word requires $l$ signal intervals. However, in Phase 3 when B sends $x_{k,b}$, which is a signal containing the first part of a code word, to A, the process requires only $l'_b$ signal intervals. Please see Fig. 5. In Phase 4, B continues to send the remainder of the code word, while C sends the re-encoded signal $x'_{k,b}$ to A. Therefore, we determined that Phase 4 requires $l-l'_b$ signal intervals.

Fig. 5

Phase 4 of the DDF-NC system model

The signals that A receives in this phase can be represented as follows:

$$\begin{aligned} y_{k,\mathrm {A}4} = h_\mathrm{{BA}4} x_{k,b} + h_\mathrm{{CA}4} x'_{k,b} + n_{k,\mathrm {A}4}, \quad l'_b < k \le l. \end{aligned}$$

(8)

• Phase 5

Please see Fig. 6. This phase requires $l$ signal intervals, during which time C forwards the network coded signals $x_{k,a \oplus b}$ to Nodes A and B. The operator $\oplus$ represents “Exclusive-OR” (XOR). The signals that these two nodes receive can be respectively represented as follows:

$$\begin{aligned} y_{k,\mathrm {A}5}&= h_\mathrm{{CA}5} x_{k,a \oplus b} + n_{k,\mathrm {A}5}, \quad 1 \le k \le l;\end{aligned}$$

(9)

$$\begin{aligned} y_{k,\mathrm {B}5}&= h_\mathrm{{CB}5} x_{k,a \oplus b} + n_{k,\mathrm {B}5}, \quad 1 \le k \le l. \end{aligned}$$

(10)

Fig. 6

Phase 5 of the DDF-NC system model

3 The Outage Probability of the System

3.1 Definition of Outage Probability

Assuming that, in a point-to-point wireless channel transmission, signals are sent at a rate of $R$ bps/Hz from $X$ (sender) to $Y$ (receiver), the mutual information between $X$ and $Y$ is $I$, which can be obtained using (11).

$$\begin{aligned} I_{XY} = c \log _2 (1 + \rho _{XY} |h_{XY}|^2) \end{aligned}$$

(11)

where $c$ is a coefficient related to the volume of transmitted signals and transmission time; $\rho _{XY}$ is the SNR at the receiver $Y$; $h_{XY}$ is the channel gain of Channel $X$-$Y$.

The outage event $O_{XY}$ occurs when the mutual information is smaller than the transmission rate $R$, i.e.,

$$\begin{aligned} O_{XY} = \{I_{XY} < R\}. \end{aligned}$$

(12)

The outage probability is then defined as $P(O_{XY})$, the probability of event $O_{XY}$. If there are multiple senders and one receiver $Y$, the outage event at $Y$ is defined as

$$\begin{aligned} O_Y = \bigcap _{X \in S} O_{XY}, \end{aligned}$$

(13)

where $S$ is the set containing all the senders.

3.2 A Derivation of the Outage Probabilities in DDF-NC System

According to the assumptions of this study that were introduced previously, channel gains were i.i.d. random variables. The channel gains of the same channel were independent of each other when the channel was used during different phases. We can consider this type of channel to be experiencing rapid channel change, which is similar to the fast fading phenomenon (Figs. 7, 8).

Fig. 7

Outages that occurred at Node A in the DDF-NC system model

Fig. 8

Outages that occurred at Node B in the DDF-NC system model

This system contains two receivers, that is, Nodes A and B; therefore, we first examined the outage probabilities of A and B. Thereafter, we combined the results and obtained the overall outage probability of the system.

• Outages that occur at Node A

The following factors determined whether outages occurred at Node A:

• 1. During Phase 4, Node C only performs DF when the mutual information between B and C is greater than the transmission rate. Under this condition, outage does not occur between B and C; therefore, we only considered whether outage occurs between C and A.

• 2. Whether outage has occurred at Node A during Phases 3 and 4.

• 3. Whether outage has occurred at Node A during Phase 5.

The following conditions must be satisfied simultaneously for outages to occur at Node A: (1) outages have occurred at A during Phases 3 and 4; and (2) outage has occurred at A during Phase 5. The outage event at A can be expressed using the following equation:

$$ \begin{aligned} O_\mathrm{{A}} = O_\mathrm{{A}3 \& 4} \cap O_\mathrm{{A}5} \end{aligned}$$

(14)

where $O_\mathrm{{A}3 \& 4}$ represents the outage that occurs at Node A during Phases 3 and 4:

$$ \begin{aligned} O_\mathrm{{A}3 \& 4} = \left\{ \frac{l'_b}{3l} \log _2 (1 + \rho |h_\mathrm{{BA}3}|^2) + \frac{(l - l'_b)}{3l} \log _2(1 + \rho (|h_\mathrm{{BA}4}|^2 + |h_\mathrm{{CA}4}|^2)) < R \right\} \qquad \end{aligned}$$

(15)

and $O_\mathrm{{A}5}$ represents the outage that occurs at Node A during Phase 5:

$$\begin{aligned} O_\mathrm{{A}5} = \left\{ \frac{2}{3} \log _2 (1 + \rho |h_\mathrm{{CA}5}|^2) < R \right\} . \end{aligned}$$

(16)

Since events $O_\mathrm{{A}3 \& 4}$ and $O_\mathrm{{A}5}$ are independent, the outage probability of Node A can be obtained through (17):

$$ \begin{aligned} P(O_\mathrm{A}) = P(O_\mathrm{{A}3 \& 4}) \cdot P(O_\mathrm{{A}5}). \end{aligned}$$

(17)

During Phases 3 and 4, signal transmission consists of two parts. In the first part, the signal source uses $\frac{l'_b}{3l}$ of the total signal intervals to send a signal to the receiver, and Phase 5 requires $\frac{(l - l'_b)}{3l}$ of the total signal intervals. During this period, the signal source sends a signal to the receiver, while, simultaneously, the relay station sends a signal to the receiver. Outages occur when the sum of mutual information of these two processes is smaller than the transmission rate $R$. During Phase 5, the relay station uses $\frac{1}{3}$ of the total signal intervals to send two information bit streams $a$ and $b$ to the receiver; outages occur when the mutual information in this phase is smaller than the transmission rate $R$.

In (15) and (16), the coefficient before the logarithm that represents the mutual information is determined by the transmission time and volume of the transmitted signals. For example, in $\frac{l'_b}{3l} \log _2 (1 + \rho |h_\mathrm{{BA}3}|^2)$, the coefficient before the logarithm of mutual information is $\frac{l'_b}{3l}$, indicating that the transmission of this signal consumes $l'_b$ signal intervals, whereas $3l$ represents the total amount of system time. The $\frac{2}{3}$ in $\frac{2}{3} \log _2 (1 + \rho |h_\mathrm{{CA}5}|^2)$ indicates that $\frac{l}{3l}$ of the total system time is used to send two signals.

• Outages that occur at Node B

The following factors determine whether outages occurred at Node B:

• 1. During Phase 2, Node C only performs DF when the mutual information between A and C is greater than the transmission rate. Under this condition, outage does not occur between A and C; therefore, we only consider whether outage occur between C and B.

• 2. Whether outages have occurred at Node B during Phases 1 and 2.

• 3. Whether outage has occurred at Node B during Phase 5.

The following conditions must be satisfied simultaneously for outages to occur at Node B: (1) outages have occurred at B during Phases 1 and 2; and (2) outages have occurred at B during Phase 5. Therefore, outage event at B can be expressed using the following equation:

$$ \begin{aligned} O_\mathrm{{B}} = O_\mathrm{{B}1 \& 2} \cap O_\mathrm{{B}5} \end{aligned}$$

(18)

where $O_\mathrm{{B}1 \& 2}$ represents the outage that occurs at Node B during Phases 1 and 2:

$$ \begin{aligned} O_\mathrm{{B}1 \& 2} = \left\{ \frac{l'_a}{3l} \log _2 (1 + \rho |h_\mathrm{{AB}1}|^2) + \frac{(l - l'_a)}{3l} \log _2 (1 + \rho (|h_\mathrm{{AB}2}|^2 + |h_\mathrm{{CB}2}|^2)) < R \right\} \qquad \end{aligned}$$

(19)

and $O_\mathrm{{B}5}$ represents the outage that occurs at Node B during Phase 5:

$$\begin{aligned} O_\mathrm{{B}5} = \left\{ \frac{2}{3} \log _2 (1 + \rho |h_\mathrm{{CB}5}|^2) < R \right\} . \end{aligned}$$

(20)

The outage probability of Node B can be obtained through (21).

$$ \begin{aligned} P(O_\mathrm{{B}}) = P(O_\mathrm{{B}1 \& 2}) \cdot P(O_\mathrm{{B}5}). \end{aligned}$$

(21)

The outage of the DDF-NC system is defined as the union of the outages that occur at Nodes A and B.

$$\begin{aligned} O_{\text {DDF-NC}} = O_\mathrm{{A}} \cup O_\mathrm{{B}}. \end{aligned}$$

(22)

Therefore, we obtained the outage probability of the entire DDF-NC system.

$$\begin{aligned}&P(O_{\text {DDF-NC}}) = P(O_\mathrm{A}) + P(O_\mathrm{B}) - P(O_\mathrm{A} \cap O_\mathrm{B}) \nonumber \\&\quad \mathop {=}\limits ^\mathrm{(a)} P(O_\mathrm{A}) + P(O_\mathrm{B}) - P(O_\mathrm{A}) \cdot P(O_\mathrm{B}), \end{aligned}$$

(23)

where (a) follows from the independency between outage events $O_\mathrm{A}$ and $O_\mathrm{B}$. By symmetry, we know $P(O_\mathrm{A}) = P(O_\mathrm{B})$. Hence,

$$\begin{aligned} P(O_\mathrm{{DDF-NC}}) = 2 P(O_\mathrm{A}) - [ P(O_\mathrm{A}) ]^2, \end{aligned}$$

(24)

where $P(O_\mathrm{A})$ can be obtained via (15), (16), and (17).

4 Analyses of the System Performance of the DMT

In this section, we derive the DMT of the system. The DMT of the system is

$$\begin{aligned} d(r)&= -\lim _{\rho \rightarrow \infty } \frac{\log _2 P(O_\mathrm{{DDF-NC}})}{\log _2 \rho } \nonumber \\&= -\lim _{\rho \rightarrow \infty } \frac{\log _2 P(O_\mathrm{A}) [2 - P(O_\mathrm{A})]}{\log _2 \rho } \nonumber \\&= -\lim _{\rho \rightarrow \infty } \frac{\log _2 P(O_\mathrm{A})}{\log _2 \rho } -\lim _{\rho \rightarrow \infty } \frac{\log _2 [2 - P(O_\mathrm{A})]}{\log _2 \rho }, \end{aligned}$$

(25)

where $d$ is the diversity gain and $r$ is the multiplexing gain [15]. Because $\lim _{\rho \rightarrow \infty } P(O_\mathrm{A}) = 0$, the second term is equal to zero. Substituting (17) into (25), we have

$$ \begin{aligned} d(r) = -\lim _{\rho \rightarrow \infty } \frac{\log _2 P(O_\mathrm{A3 \& 4})}{\log _2 \rho } -\lim _{\rho \rightarrow \infty } \frac{\log _2 P(O_\mathrm{A5})}{\log _2 \rho }. \end{aligned}$$

(26)

Let $v=|h_\mathrm{CA5}|^2$, which is an exponential random variable with unit mean. Then

$$\begin{aligned} P(O_\mathrm{A5})&= P\left[ \frac{2}{3} \log _2 (1+\rho v) < R\right] \nonumber \\&= P\left[ v < \frac{\rho ^{3r/2}-1}{\rho } \right] \nonumber \\&= 1 - \exp \left( -\frac{\rho ^{3r/2}-1}{\rho }\right) . \end{aligned}$$

(27)

Let $s = \rho ^{-1}$. Then

$$\begin{aligned}&-\lim _{\rho \rightarrow \infty } \frac{\log _2 P(O_\mathrm{A5})}{\log _2 \rho } = \lim _{s \rightarrow 0} \frac{\log _2 [1 - \exp (-s(s^{-3r/2} - 1))]}{\log _2 s} \nonumber \\&\quad \mathop {=}\limits ^\mathrm{(a)} 1-3r/2 \mathrm{\ for\ } 0 \le r \le 2/3. \end{aligned}$$

(28)

The equality (a) results from applying l’Hôpital’s rule two times.

Let

$$ \begin{aligned} d_1(r) = -\lim _{\rho \rightarrow \infty } \frac{\log _2 P(O_\mathrm{A3 \& 4})}{\log _2 \rho }, \end{aligned}$$

(29)

where

$$ \begin{aligned} P(O_\mathrm{A3 \& 4}) = P[(1 + \rho |h_\mathrm{BA3}|^2)^{l'_b} (1 + \rho (|h_\mathrm{BA4}|^2 + |h_\mathrm{CA4}|^2))^{l - l'_b} < \rho ^{3rl}]. \end{aligned}$$

(30)

When $\rho \rightarrow \infty$,

$$\begin{aligned} \lim _{\rho \rightarrow \infty } l'_b = \min \{l, 0\} = 0 \end{aligned}$$

(31)

and

$$ \begin{aligned} \lim _{\rho \rightarrow \infty } P(O_\mathrm{A3 \& 4})&= \lim _{\rho \rightarrow \infty } P[(\rho (|h_\mathrm{BA4}|^2 + |h_\mathrm{CA4}|^2))^l < \rho ^{3rl}] \nonumber \\&= \lim _{\rho \rightarrow \infty } P[\underbrace{|h_\mathrm{BA4}|^2 + |h_\mathrm{CA4}|^2}_x < \rho ^{3r-1}]. \end{aligned}$$

(32)

Since $|h_\mathrm{BA4}|^2$ and $|h_\mathrm{CA4}|^2$ are i.i.d. exponential random variables with unit mean, $x$ is an Erlang random variable with the shape parameter $k = 2$ [12]. The cumulative distribution function (CDF) of $x$ is

$$\begin{aligned} F(x) = 1 - (x + 1) e^{-x} \mathrm{\ for \ } x \ge 0. \end{aligned}$$

(33)

Then

$$ \begin{aligned} P(O_\mathrm{A3 \& 4})&= F(\rho ^{3r-1}) \nonumber \\&= 1 - (\rho ^{3r-1} + 1) \exp (-\rho ^{3r-1}). \end{aligned}$$

(34)

Apply l’Hôpital’s rule twice, we have

$$\begin{aligned} d_1(r) = 2-6r, \;\hbox {if}\;\quad 0 \le r \le 1/3. \end{aligned}$$

(35)

Substituting (28) and (35) in (26), we have

$$\begin{aligned} d(r) = {\left\{ \begin{array}{ll} 3-15r/2 , &{}\quad \hbox {if}\;\; 0 \le r \le 1/3 \\ 1-3r/2 , &{}\quad \hbox {if}\; \; 1/3 \le r \le 2/3. \end{array}\right. } \end{aligned}$$

(36)

5 Numerical Results and Discussions

Outage probability determines system reliability; therefore, it is a crucial indicator for analyzing the performance of wireless communications systems. Outage probability is related to the fading of wireless channels and signal transmission rates. In this section, we used the Rayleigh, Rician, and Nakagami fading channels to simulate and analyze the outage probability of the DDF-NC system. The number of consecutive symbols in a code word, l, is set to 10. We assume that $k_a = k_b = 1$, i.e., Nodes A, B, and C have equal noise variance. Based on the results of the DMT derivation, we used MATLAB to generate corresponding figures to analyze the system performance. At the end of this section, a comparison is conducted between the DDF-NC system and systems featuring other protocols.

5.1 A Simulation of the Outage Probabilities of the DDF-NC System Operating in Rayleigh Fading Channels at Various Transmission Rates

Figure 9 shows the outage probabilities for the Rayleigh fading channels at various transmission rates when $\sigma = 1$, where $\sigma$ is the parameter of the Rayleigh probability density function (PDF) [13].

Fig. 9

The outage probabilities of the DDF-NC system operating in the Rayleigh fading channels at various transmission rates

We have previously identified the relationship of outage probability, as shown by $P(O_{XY}) = P(c \log _2 (1 + \rho _{XY} |h_{XY}|^2) < R)$, where the greater $R$ is, the more likely it is for the mutual information (i.e., $c \log _2 (1 + \rho _{XY} |h_{XY}|^2)$) to be smaller than the transmission rate $R$, thereby creating a greater outage probability. Figure 9 shows that the greater $R$ becomes, the closer the outage probability is to 1, and when $R$ becomes smaller, the outage probability decreases, verifying this phenomenon.

5.2 A Simulation of the Outage Probabilities of the DDF-NC System Operating in the Rayleigh Fading Channels When $\sigma$ Differs

Figure 10 shows the outage probabilities in the Rayleigh fading channels when $R = 3$ bps/Hz and $\sigma$ differs.

Fig. 10

The outage probabilities of the DDF-NC cooperative communications system operating in the Rayleigh fading channels when $\sigma$ differs

As mentioned previously, greater $\sigma$ results in greater standard deviations and variances in the Rayleigh probability density function, and thus greater channel power. The results of $I(X; Y) = c \log (1 + \rho _{XY} |h_{XY}|^2)$ show that for the signals received through this type of channels, their mutual information increases as the channel power increases. The outage probability is obtained through $P(O_{XY}) = P( c \log (1 + \rho _{XY} |h_{XY}|^2) < R)$; therefore, as the mutual information increases, it is less likely for the mutual information to be smaller than the transmission rate $R$, and the outage probability decreases. Figure 10 shows that when $\sigma$ increases, the outage probability gradually declines.

5.3 A Simulation of the Outage Probabilities of the DDF-NC System Operating in the Rician Fading Channels at Various Transmission Rates

Figure 11 shows the outage probabilities of the system under the influence of various simulated transmission rates when the channel power $\varOmega = 1$ and the Rice factor $K = 1$.

Fig. 11

The outage probabilities of the DDF-NC cooperative communications system operating in the Rician fading channels at various transmission rates

Similar to the situation in Fig. 9, the greater the transmission rate of the system becomes, the greater the outage probability. Figure 11 shows that as $R$ increases, the outage probability approaches one, and when $R$ decreases, the outage probability declines, verifying the phenomenon. A smaller outage probability indicates greater system reliability. Outage probability is directly related to the diversity gain of the system, which is discussed in greater detail in the following section.

5.4 A Simulation of the Outage Probabilities of the DDF-NC System Operating in the Rician Fading Channels Under Various Rice Factors $K$

Figure 12 shows the outage probabilities of the system operating in Rician fading channels under the influence of various Rice factors $K$, when the transmission rate $R = 3$ bps/Hz and the channel power $\varOmega = 1$.

Fig. 12

The outage probabilities of the DDF-NC cooperative communications system operating in the Rician fading channels under various rice factors $K$

Figure 12 shows that when the Rice factor $K$ increases, the curve of the outage probability declines more steeply. This indicates that a greater Rice factor $K$ results in a lower outage probability of the system operating in a Rician fading channel.

The outage probability decreases as the Rice factor $K$ increases because the physical meaning of $K$ is the ratio of the signal power in the direct signal transmission paths (i.e., the line-of-sight (LOS) path) over the signal power in the paths with obstacle scattering and reflection. A greater $K$ indicates that the signal power of the direct transmission path occupies a larger proportion of the signal power of the overall transmission path. The SNR of the signals received through direct transmission paths are superior and have lower outage probabilities. Therefore, when this type of signal occupies a larger proportion in the overall system, the outage probability of the system is less.

5.5 A Simulation of the Outage Probabilities of the DDF-NC System Operating in the Nakagami Fading Channels at Various Transmission Rates

Figure 13 shows a comparison of the outage probabilities of the DDF-NC cooperative communications system when it operates in the Nakagami fading channels at various transmission rates and the shape factor of the channel is $m = 2$.

Fig. 13

The outage probabilities of the DDF-NC cooperative communications system operating in the Nakagami fading channels at various transmission rates

When the shape factor $m = 1$, the Nakagami distribution becomes a Rayleigh distribution. Therefore, we set $m = 2$ in the outage probability simulation to maintain the characteristics of Nakagami fading channels. Similar to the results of the previous simulation of the Rayleigh and Rician fading channels, when transmission rate $R$ was the only manipulated variable, a greater $R$ resulted in higher outage probabilities in the channels, and thereby a lower system reliability. Figure 13 shows that when $R = 1$ bps/Hz, the system has the minimum outage probability (i.e., $10^{-2}$) and the maximum reliability among the five curves when SNR $= 10$ dB. In contrast, the system outage probability becomes 1 and the system is the least reliable when SNR $= 10$ dB and $R = 5$ bps/Hz. This verifies that a greater $R$ results in higher outage probability and lower system reliability.

5.6 A Simulation of the Outage Probabilities of the DDF-NC System Operating in the Nakagami Fading Channels at Various Nakagami Fading Parameters $m$

Figure 14 shows a comparison of the outage probabilities of the system operating in the Nakagami fading channels when the transmission rate $R = 1$ bps/Hz and the Nakagami fading parameter $m$ varied.

Fig. 14

The outage probabilities of the DDF-NC cooperative communications system operating in the Nakagami fading channels at various Nakagami fading parameters $m$

We introduced the definition of the amount of fading (AF) [4] before analyzing the information in Fig. 14. First, we assumed that the channel gain was $h$ and the instantaneous fading amplitude was $r = |h|$. Subsequently, the AF was obtained, as shown in (37).

$$\begin{aligned} \hbox {AF} = \frac{\hbox {Var}[r^2]}{\hbox {E}^2[r^2]}. \end{aligned}$$

(37)

In the Nakagami fading channels, the following applies:

$$\begin{aligned} \hbox {AF} = \frac{1}{m}. \end{aligned}$$

(38)

For example, when $m = 1$, the Nakagami channels become Rayleigh channels. When we integrated $m = 1$ into (38), we obtained AF $= 1$, indicating that the AF of Rayleigh channels was 1. When $m \rightarrow \infty$, AF $= 0$, indicating that there was no AF.

According to (38), AF is inversely proportional to the Nakagami fading parameter $m$. Figure 14 shows that when $m$ increases, the system outage probability decreases. This is because AF decreases as $m$ increases, and a smaller AF results in lower outage probability and higher system reliability.

5.7 The System Outage Probabilities in the Rayleigh ($\sigma = 0.7$), Rician ($K = 0$), and Nakagami ($m = 1$) Fading Channels

Figure 15 shows a comparison of the simulated system outage probabilities in Rayleigh, Rician, and Nakagami fading channels when the transmission rate is set at $R = 3$ bps/Hz. We defined certain parameters and examined the simulation results to verify the relationships among the three channels under certain conditions. Rician fading channels become Rayleigh fading channels when the Rician factor $K = 0$ and the channel power $\varOmega = 1$; Nakagami fading channels become Rayleigh fading channels when the Nakagami fading parameter $m = 1$. We examined Fig. 15 and discovered that under the aforementioned conditions, the curves that represent the simulated system outage probabilities in Rician and Nakagami fading channels overlap with that representing the simulated system outage probabilities in Rayleigh channels when $\sigma = 0.7$. This verifies that Rayleigh fading channels are exceptions of Rician and Nakagami fading channels.

Fig. 15

The outage probabilities of the DDF-NC cooperative communications system operating in various channels (overlapped)

5.8 The System Outage Probabilities in Rayleigh ($\sigma = 1$), Rician ($K = 1$), and Nakagami ($m = 2$) Fading Channels

In Fig. 16, we set the transmission rate as $R = 3$ bps/Hz, the $\sigma$ of Rayleigh fading channels as 1, the $K$ of the Rician fading channels as 1, and the $m$ of the Nakagami fading channels as 2. Under these conditions, the Rician and Nakagami fading channels differed from the Rayleigh fading channels. After comparing the information in Figs. 15 and 16, we discovered that the system outage probabilities in the three types of channels all declined when the parameters increased. The outage probabilities in the Nakagami fading channels showed the most significant decreases, followed by those in the Rayleigh and Rician channels. The shape parameter of the Nakagami fading channels was ${\small m =\frac{\hbox {E}^2[r^2]}{\hbox {Var}[r^2]}}$. When $m$ increased, the variance $\hbox {Var}[r^2]$ decreased, resulting in a significantly narrower curve for the PDF. The mean channel power attenuation simultaneously controls increases in the extension parameter $\varOmega = \hbox {E}[r^2]$. Because $m$ is in a reciprocal relationship with AF, when $m$ increases by 100 %, AF decreases by 50 %, as shown in $\hbox {AF} = \frac{1}{m}$. This has significant influence on the degree of channel fading. The $\sigma$ of the Rayleigh channels are the root mean squares of the received signals. Therefore, when $\sigma$ increases, it directly causes the local average power to rise. The Rician factor $K$ is a ratio of the power of the direct transmission path over the power of the scattering path. When the total power remains constant, increases in $K$ have little influence because they affect only the power ratios of transmissions that use different path components. Increasing the system transmission power is more effective in lowering outage probabilities compared with increases in $K$.

Fig. 16

The outage probabilities of the DDF-NC cooperative communications system operating in various channels

5.9 A Comparison of the Outage Probabilities of the DDF Systems and the DDF-NC Systems

Figure 17 shows a comparison of the outage probabilities of the DDF cooperative communications system and the DDF-NC system when they both operated in Rayleigh channels at a transmission rate of $R = 1$ bps/Hz and $\sigma = 1$.

Fig. 17

A comparison of the outage probabilities of the DDF cooperative communications system and the DDF-NC cooperative communications system

Figure 17 shows that the outage probabilities of the DDF-NC system tended to be lower than those of the system featuring only DDF. This is because, although the NC process in the DDF-NC system consumed more time, it increased the diversity gain of the system, resulting in lower outage probabilities. This indicates that NC enables the achievement of higher system stability.

Figure 18 shows a comparison of the outage probabilities of the DF-NC cooperative communications system [10] and the DDF-NC cooperative communications system when the transmission rate is $R = 1$ bps/Hz.

Fig. 18

A comparison of the outage probabilities of the DF-NC cooperative communications system and the DDF-NC cooperative communications system

Figure 18 shows that although both cooperative communications systems feature NC integration, the outage probabilities of the DDF-NC system are significantly lower compared to those of the DF-NC system. Assuming the transmission of a complete code word requires $l$ signal intervals, DF is a simple procedure of decode-and-forward; the relay station must wait for $l$ signal intervals until the signal reception is complete before it forwards the signal to the next destination. In contrast, the criterion for the DDF system to identify a complete decode is that the mutual information is greater than the transmission rate. Therefore, the relay station consumes less time in decoding signals sent from the signal source; consequently, the relay station has more time to forward the recoded signals. Because Phase 1 (3) consumes only $l'_a$ ($l'_b$) signal intervals, the relay station can use $l-l'_a$ ($l-l'_b$) signal intervals to transmit signals. This extra transmission phase, compared with the DF system, results in lower outage probabilities and greater system reliability.

5.10 DMT of DDF-NC

Figure 19 is the figure for (36), showing the DMT of the system. The concept of diversity gain comprises transmitting the same signals through multiple independent channels to achieve lower outage probability and higher system reliability. In the system developed in this study, the destination B received three copies of information $a$, respectively, from Channel A-B (with a channel gain of $h_\mathrm{{AB}2}$), Channel C-B in Phase 2 (with a channel gain of $h_\mathrm{{CB}2}$), and Channel C-B in Phase 5 (with a channel gain of $h_\mathrm{{CB}5}$). The signal that was transmitted in Phase 5 as a recoded signal that had been network coded based on information $a$ and $b$. Because this NC signal contained information $a$, its diversity gain increased by 1 compared with that of the DDF protocol. Therefore, the maximum diversity gain was 3.

Fig. 19

The DMT of the DDF-NC system

The two senders in the system send signals to each other. Because NC was used, in Phase 5 the system used $l$ signal intervals to simultaneously transmit the signal that contained two signals. In addition, Phases 1–4 consumed $2l$ signal intervals. Therefore, the entire transmission process consumed $3l$ signal intervals. The system used three times the time of a regular transmission to transmit two different information $a$ and $b$, enabling the system multiplexing gain to reach an optimal value of $\frac{2}{3}$.

From the figure, we discovered that within the interval of $0 \le r \le \frac{1}{3}$, the DMT curve is in a trend of relatively steep decline until the diversity gain reaches 3. This is because the performance of the DDF protocol is determined by the amount of time consumed at the relay station for successful DF. When $r \le \frac{1}{3}$, the system has sufficient time remaining in the DDF phase to forward the recoded signals following successful decoding at the relay station. In addition, in the NC phase, the system forwards the network coded signals to the destination. These two transmissions cause the diversity gain to increase rapidly. When the multiplexing gain is zero, the diversity gain reaches its optimal value of 3 because the three independent transmission paths result in zero outage occurrences. When the multiplexing gain is $r = \frac{1}{3}$, the DMT has a turning point. This is because when $r > \frac{1}{3}$, as the transmission rate increases, the relay station can only decode and forward a small portion of the code word. This results in higher outage probability and lower system reliability and decreased diversity gains.

5.11 A Comparison of DMTs

Figure 20 shows a comparison of the DMTs of multiple protocols. We discovered that DDF-NC is significantly superior to DF. On the other hand, DDF-NC is superior to SDF when $0 \le r < \frac{2}{7}$ or $\frac{2}{5} < r < \frac{2}{3}$. The diversity gain of DDF-NC is inferior to the diversity gain of DF-NC in the interval of $\frac{2}{9} < r < \frac{2}{3}$. However, the diversity gain of DDF-NC is greater than that of DF-NC when the multiplexing gain is in the interval of $0 \le r < \frac{2}{9}$. Compared to the diversity gains of the $2 \times 1$ MISO and DDF, that of DDF-NC is superior when $0 \le r < \frac{2}{11}$ and inferior when $\frac{2}{11} < r < 1$.

Fig. 20

A comparison of the DMTs of multiple communications protocols

6 Conclusion and Future Directions

The primary purpose of this study was to explore improvements for system performance by integrating NC into relay stations that use DDF cooperative communications systems. We integrated NC to a relay station and added a phase subsequent to the DDF phase for the transmission of network coded signals. We examined the outage probability and DMT of this system to analyze the level of improvements for the signal reliability and transmission rates achieved by this system compared to traditional DDF systems.

The simulation results showed that because the DDF-NC cooperative communications system has an extra signal that is transmitted to the destination through an independent channel using NC, it has higher system reliability, lower outage probability compared to DDF systems, and enhanced diversity gain. However, because an extra phase is added to the transmission, the transmission time is extended, although the number of different information bit streams that are transmitted remain the same, which is equal to two. Therefore, the number of different information bit streams that are transmitted within a unit time decrease, resulting in a decline in the multiplexing gain.

DMT is a crucial indicator for measuring system performance. According to the information in Fig. 20, the DDF-NC system has advantages and disadvantages compared to other systems. Compared with DF-NC, the diversity gain of DDF-NC is superior when the multiplexing gains are smaller ($0 \le r < \frac{2}{9}$) and inferior when the multiplexing gains are greater ($\frac{2}{9} < r \le \frac{2}{3}$). This phenomenon is more evident when compared to traditional DDF systems: the diversity gain of DDF-NC is superior to that of DDF when multiplexing gains are $0 \le r < \frac{2}{11}$, whereas it is inferior when multiplexing gains are in the interval of $\frac{2}{11} < r < 1$.

The DDF-NC system can be applied to situations with low transmission rates and low requirements for multiplexing gain to achieve high diversity gain. In addition, this system demonstrates superior reliability compared to other systems when the transmission rates are low.