Game theoretic approach for multi-tier 5G heterogeneous network optimization based on joint power control and spectrum trading

Abstract

Multi-tier heterogeneous network (MHN) has recently emerged as a main technology in 5G network. Dense deployment of heterogeneous nodes in 5G MHN will have more density than single-tier networks. In 5G MHN, by increasing the number of small cells, network capacity, spectral efficiency, and data rate will increase. But reducing the dimension of the cell will cause inter/intra-tier interference in both uplink and downlink channels of MHN. High transmit power of Macro Base Station (MBS) downlink channel causes interference to Small cell User Equipment (SUE). Also, neighbor macrocell and small cell users suffer from interference created in both uplink and downlink channels of small cell. Thus interference management and mitigation is the important challenge for 5G MHN. In this paper, in order to mitigate both types of inter/intra-tier interferences, spectrum trading issue and power control are presented based on non-cooperative Stackelberg game under some sub-games through a pricing-based algorithm and convex optimization method. Finally, simulation results show that the performance of our system model such as average utility function of the small cell, SBS, energy efficiency and so on, will be improved through the proposed algorithm.

1 Introduction

The explosive growth of wireless data network and growing demands for various kind of services have trigged the investigation of 5G network. A heterogeneous network is one of the technologies for 5G network [1,2,3]. In recent years, the invention of the heterogeneous network that is known as HetNet has trended wireless network toward multi-tier network. A multi-tier network employs different classes of Base Station (BS) such as MBS providing general coverage and a large number of low power Small cell Base Stations (SBS). Deployment of HetNet has advantages such as higher spectral efficiency, higher data rate, higher energy efficiency, and development coverage area. However, due to small cell deployment is taking massively and dimension of small cell has been decreased, inter/intra-tier interference is one of the challenges this network. Inter tier interference between small cell and macrocell will be created when small cell network shares the same frequency bandwidth macrocell. Therefore, because of power level from Macrocell and small cell in the same frequency, small cell network may cause or suffer co-channel interference with overlay macrocell network. Another type of interference is intra-tier interference that arises between small cells. For instance, uplink interference will be caused by SUE to neighbor macrocell user and downlink interference will be created by SBS to other small cells. In [4] different kind of interference just classified. Then, using multiple antennas for SBS is explained to tackle the interference problem. Due to the importance of mitigation the inter/intra-tier interference, resource allocation problem plays the main role in 5G HetNet. Bandwidth allocation, power control, and joint frequency and power allocation are three approaches to solve the resource allocation problem. In [21] authors just focus on frequency allocation to improve the performance of the network, but they have not investigated power allocation to control interference. In [5], a fair Cell Range Expansion (CRE) with interference coordination scheme is exploited, also the interference that is caused by the MBS to SUE is mitigated using power control based on Foshini–Miljanic (FM) algorithm and frequency partitioning through Round Robin (RR) algorithm. In [6], to improve the performance of macrocell and small cells, a Stackelberg game is proposed for channel assignment, biasing and interference coordination. So that, to reduce interference, MBS(leader) decides an optimal set of channels being silent and power allocates to active channel, then SBS (follower) operates with biasing and allocate transmit power. In [7, 8], to solve the intra-tier interference problem, at first, small cells are clustered based on the graph coloring algorithm then power control is performed based on Differential Evolution (DE) algorithm. In [9], authors have proposed a coalition cooperative game to manage intra-tier interference and to achieve higher utility and throughput in their system model. In [10], non-cooperative game to power control is explained, so that each of femtocell users is considered as a player trying to maximize their utility function which is different with the utility function of SUE in this paper. In [11], authors have introduced distributed channel selection for interference mitigation in a small cell network. This problem is modeled as a potential game in which the Nash Equilibrium (NE) minimize the network interference. In [12], a game theory based on power control in Cognitive Radio (CR) is studied to investigate the performance of spectrum leasing. In [13], to avoid inter-tier interference in Orthogonal Frequency Division Multiplex (OFDM) femtocell network, resource allocation is introduced through self-organization strategy. In [14,15,16], to minimize the interference of femtocell to the macrocell and between femtocells, power control is considered based on game theory. Also, femtocell power control is modeled in the previous literature based on the learning algorithm and stochastic geometry. For example, In [17, 18], Q-learning algorithm is addressed to allocate power and mitigate the interference. The main contribution of this paper is to mitigate both types of inter/intra-tier interferences in downlink and uplink channel. Therefore, at first, to control strong inter-tier interference, some Macro User Equipment (MUE) attach to the small cell that is called CRE mechanism. Then, for allocation optimum bandwidth to SBS, SBS pays a price to MBS to purchase bandwidth then a certain portion of bandwidth is allocated to SUE and attached user.¹ So that, optimum bandwidth and allocated portion are calculated through the Stackelberg game. Then, received interference level from SBS, SUE and MBS and their transmit power in uplink and downlink channel is controlled via payment price scheme under constraint for the transmit power and interference tolerance level. For instance, by increasing interference tolerance for SUE and MUE in downlink, MBS and SBS can transmit with higher power then payment price will be decreased. Therefore, in this paper, unlike aforementioned papers, both types of inter/intra-tier interferences in uplink and downlink channel through joint spectrum trading to allocate bandwidth and power control are investigated based on non-cooperative Stackelberg game and convex optimization. This paper is organized as follows. In Sect. 2, the proposed system model is illustrated. Then spectrum trading is investigated in Sect. 3. After that, control power of SBS, SUE, and MBS is formulated in Sect. 4. Finally, simulation results are shown in Sect. 5.

2 System model

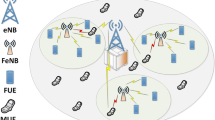
The proposed system model which consists of the macrocell and several small cells are shown in Fig. 1.

Fig. 1

system model

Let $i=\{1,\ldots ,I\}$ and $k_{s} =\{1,\ldots ,K\}$ denote the number of small cells and the number of small cell users consisting of users and attached-user in the small cell. Some abbreviations which are applied in the proposed model is shown in Table 1. The required parameter for the formulation is described in Table 2. Also, according to this table, the Signal to Interference plus Noise Ratio (SINR) of $i^{th}$ SBS and SUE can be written as:

$$\begin{aligned} SINR_{sbs(i)} &= \frac{{{P}_{sbs(i)}}\times \mathbf{h }_{s,s}{(i,{{k}_{s}})}}{{ \textit{I}}1+{I}2+{{P}_{noise}}},\nonumber \\ {\textit{I}}1 &= \sum _{\underset{j\ne i}{\mathop {j=1}}}^{I}{{{P}_{sbs(j)}}\times {{\mathbf{h }}_{s,s}}(j,{{k}_{s}})}, \nonumber \\ \textit{I}2 &= {{P}_{mbs}}\times {{\mathbf{h }}_{m,s}}(1,{{k}_{s}}). \end{aligned}$$

(1)

where I1 and I2 show the total interference is caused by neighbor small cell and macrocell in downlink channel, respectively and $P_{noise}$ is defined as noise power.

$$\begin{aligned} SINR_{sue({{k}_{s}})} &= \frac{{{P}_{sue({{k}_{s}})}}\times \mathbf{h }_{s,s}({{k}_{s}},i)}{\textit{I}2+\textit{I}3+{{P}_{noise}}}, \nonumber \\ \textit{I}3 &= \sum _{{j=1}}^{K}{{{P}_{sue(j)}}\times {{\mathbf{h }}_{s,s}}(j,{{k}_{s}})}. \end{aligned}$$

(2)

where I3 in denominator shows the total interference is caused by $j^{th}$ SUE in the neighbor small cell in uplink channel and I2 in denominator shows interference is caused by MBS in downlink channel. The achievable rate of SBS, SUE, and attached-user can be expressed as:

$$\begin{aligned}&{{R}_{sbs(i)}}={{W}_{i}}\times {{\log }}[1+SINR_{sbs(i)}]. \end{aligned}$$

(3)

$$\begin{aligned}&{{R}_{sue(k_{s})}}=(1-\lambda )\times {{W}_{i}}\times {{\log }}[1+SINR_{sue({{k}_{s}})}], \end{aligned}$$

(4)

$$\begin{aligned}&{{R}_{attached-user({{k}_{s}})}}=\lambda \times {{W}_{i}} \nonumber \\&\times {{\log }}\left[ 1+\frac{{{P}_{attached-user({{k}_{s}})}}\times {{\mathbf{h }}_{a,s}}({{k}_{s}},i)}{{{}{}}{{\textit{I}3}+\textit{I}2+{{P}_{noise}}}}\right] , \end{aligned}$$

(5)

where $W_{i}$ is the allocated bandwidth to SBS and $\lambda$ is defined as a parameter that shows what portion of bandwidth is used by users.

Table 1 List of notations in the proposed system model

Table 2 List of required parameter

3 Spectrum trading based on Stackelberg game

Spectrum trading [19] is a solution for bandwidth sharing with demand and pricing tradeoff. Based on Stackelberg game theory, in the proposed system model, MBS that plays as the leader imposes a price on SBS that plays as the follower for shared frequency bandwidth. By increasing bandwidth demand, SBS has to pay higher expenditure [20]. According to Stackelberg game, the leader moves first and then followers follow its movement. Therefore, competition between leader and follower is considered as two sub-games. Thus, sub-game(1) as a follower game is defined as:

$$\begin{aligned}&sub-game(1): \nonumber \\&\quad \quad \{\underset{{{W}_{i}}}{\mathop {Max}}\, {{U}_{sbs(i)}}\quad s.t. \quad 0\le W_{i}\le {{W}} \} \end{aligned}$$

(6)

where the utility function of SBS can be given by:

$$\begin{aligned} {{U}_{sbs(i)}}=D\times K\times ln\left( \frac{_{{{R}_{sbs(i)}}}}{{{R}_{ \min }}}\right) -(1- \lambda )\times {{W}_{i}}\times P. \end{aligned}$$

(7)

where $R_{min}$ is minimum data rate, P is a unit price of bandwidth, also W is total available bandwidth in MBS, $\lambda$ is defined as a parameter that shows what portion of bandwidth is used by users. D is distance between SBS and MBS, K is the number of SUE. Sub-game(2) as a leader game is defined as:

$$\begin{aligned}&sub-game(2): \nonumber \\&\quad \quad \{\underset{\lambda }{\mathop {Max}}\, {{U}_{mbs}} \quad s.t. \quad 0\le \lambda \le 1\} \end{aligned}$$

(8)

where the utility function of MBS can be obtained as:

$$\begin{aligned} {{U}_{mbs}} &= {{D}_{m}}\times {{K}_{m}}\times ln\left( \frac{{{R}_{mbs}}}{{{R}_{\min }}}\right) + \sum \limits _{i=1}^{I}{(1-\lambda )\times } \nonumber \\&\quad {{W}_{i}}\times P +K_{m}^{'}\times D_{m}^{'}\times Ln\left( \frac{{{R}_{attached-user}}}{{{R}_{\min }}}\right) , \nonumber \\&\quad {{R}_{mbs}}=(1-\lambda )\times W\times {{\log }}(1+SINR). \end{aligned}$$

(9)

where $D_{m}$ is distance between MUE and MBS, $D'_{m}$ is distance between attached-user and SBS, $K_{m}$ is the number of MUE, $K'_{m}$ is the number of user attached to SBS. Therefore, by solving sub-game(1), the best response of follower (SBS) is calculated according to appendix(1). Also (10) shows $W_{i}^{*}$ is depend on $\lambda$ that can be obtained by sub-game(2). For a given value of $\lambda$, by solving sub-game(1) the optimal value of $W_{i}$ is calculated as:

$$\begin{aligned} W_{i}^{*} &= \Bigg \{ \frac{K\times D}{(1-\lambda )\times P} \quad \forall \quad 0\le \lambda \le 1-\frac{K\times D}{W\times P}, \nonumber \\&\quad W \quad \forall \quad 1-\frac{K\times D}{W\times P}\le \lambda \le 1\Bigg \} \end{aligned}$$

(10)

Then by solving sub-game(2) according to appendix(1), the optimal value of $\lambda$ is calculated as:

$$\begin{aligned} {{\lambda }^{*}}=\frac{K_{m}^{'}\times D_{m}^{'}}{{{K}_{m}}\times {{D}_{m}}}. \end{aligned}$$

(11)

4 Power Control based on interference-pricing

The purpose of MBS is to protect its user from severe small cell interference in both uplink and downlink and maintain the Quality of Service (QoS) effective and SINR in desired level. Thus, due to inter-tier interference, MBS imposes a price on SBS and SUE, also due to intra-tier interference SBS that cannot transmit imposes a price on SBS transmitter. In this paper, imposed interference price on active SBS² by MBS and inactive SBS³ are assumed to be identical. Also, MBS causes interference for SUE. Therefore, SBS to protect its user imposes a price on MBS. These problems are investigated in 4.1 and 4.2, respectively. Also to maximize the utility function of MBS, SBS, and SUE, maximum interference tolerance is considered as a constraint [21].

4.1 Power control of SUE and SBS in uplink and downlink based on Stackelberg game

The purpose is to maximize the utility function of small cell via power control of SUE and SBS. Therefore, the utility function of small cell in Eq. (12) consists of SUE utility function in uplink channel and SBS utility function in downlink channel that is written as:

$$\begin{aligned} {{U}_{smallcell(i)}}= U_{sue({{k}_{s}})}^{ul}+U_{sbs(i)}^{dl} \end{aligned}$$

(12)

The utility function of $i^{th}$ active SBS in downlink channel is defined as:

$$\begin{aligned} U_{sbs(i)}^{dl} &= {{\log }}[ 1+ SINR_{sbs(i)}] \nonumber \\&\quad-[Price_{i}^{sbs}\times {{P}_{sbs(i)}}\times \sum \limits _{j=1}^{K}{{{\mathbf{h }}_{s,s}}\,(i,j)\,+}\nonumber \\&\quad Price_{i}^{mbs}\times {{P}_{sbs(i)}}\times \mathbf{h }{{\,}_{s,m}}\,(i,k)], \nonumber \\&\quad Price_{i}^{sbs}=Price_{i}^{mbs}=Price_{sbs(i)}. \end{aligned}$$

(13)

The utility function of ${k_{s}}^{th}$ SUE in uplink channel is determined as:

$$\begin{aligned} U_{sue({{k}_{s}})}^{ul} &= {{\log }}\,\,[1+ SINR_{sue({{k}_{s}})}]-\nonumber \\&\quad [Price_{sue({{k}_{s}})} \times {{P}_{sue({{k}_{s}})}}\times {{\mathbf{h }}_{s,m}}({{k}_{s}},k)]. \end{aligned}$$

(14)

Here, competition between leaders and followers to achieve an optimal value of transmit power and maximization of the utility function of small cell are considered in three sub-games. In these games, sub-game(1) is considered as a follower game to identify the optimum power of SBS and SUE, so that active SBS and SUE act as followers. Therefore, sub-game(1) is defined as:

$$\begin{aligned}&sub-game(1): \underset{{{P}_{sbs}},{{P}_{sue}}}{\mathop {Max}}\, {{U}_{small\ cell(i)}} \nonumber \\&\quad s.t. \quad 0\le {{P}_{sbs}}\le {P^{sbs}_{max}} \quad and \quad 0\le {{P}_{sue}}\le {P^{sue}_{max}}. \end{aligned}$$

(15)

Also, sub-game(2) and sub-game(3) are considered as a leaders game to calculation interference price that will be paid by active SBS and SUE. In sub-game(2) and sub-game(3) inactive SBS and MBS are assigned the leader role. Thus, these games are written as:

$$\begin{aligned}&sub-game(2): \underset{{{{price}}_{sbs(i)}}}{\mathop {Max}}\,{{U}_{sbs(j)}}\\&\quad s.t. \quad \sum \limits _{i=1}^{I}{\ P_{sbs(i)}^{*} \times \left[ \sum \limits _{j=1}^{K}{\mathbf{h }}_{s,s}(i,j)+{{\mathbf{h }}_{s,m}}(i,k)\right] \le \,\,{{I}_{\max }}}.\nonumber \end{aligned}$$

(16)

where the utility function of $j^{th}$ inactive SBS for revenue maximization is obtained as:

$$\begin{aligned} {{U}_{sbs(j)}} &= \sum \limits _{i=1}^{I}{{{{Price}}_{sbs(i)}}}\times \nonumber \\&\quad P_{sbs(i)}^{*}\times \left[ \sum \limits _{j=1}^{K}{{\mathbf{h }}_{s,s}(i,j)}+{{{{ \mathbf h }}_{s,m}}}{(i,k)}\right] . \end{aligned}$$

(17)

$$\begin{aligned}&sub-game(3): \nonumber \\&\quad \underset{{{{Price}}_{sue({{k}_{s}})}}}{\mathop {Max}}{{U}_{mbs}}= \nonumber \\&\quad \sum \limits _{{{k}_{s}}=1}^{K}{{{{Price}}_{sue({{k}_{s}})}}} \times P_{sue({{k}_{s}})}^{*}\times {{h}_{s,m}}({{k}_{s}},k), \nonumber \\&\quad s.t \quad \sum \limits _{{{k}_{s}}=1}^{K}{P_{sue({{k}_{s}})}^{*}\times {{h}_{s,m}}({{k}_{s}},k) \le {{I}_{\max }}}. \end{aligned}$$

(18)

For finding $P^{*}_{sbs(i)}$, it is required to solve sub-game(1). But, due to second derivation of $U_{sbs(i)}$ is less than zero(appendix(2.1)), $U_{sbs(i)}$ is a concave function and the maximization of concave function is a convex optimization problem [22]. Lagrangian method based on Karush–Kuhn–Tucker (KKT) condition can be used to solve the convex problem. Therefore, by solving sub-game(1) versus $P_{sbs(i)}$ according appendix(2.1), optimal value $P^{*}_{sbs(i)}$ can be obtained from the Lagrangian method based on KKT condition:

$$\begin{aligned} P_{sbs(i)}^{*} &= \left[ \frac{1}{ln2\ \times [{{{Price}}_{sbs(i)}}\times \textit{C}1{+{{\mu }}}} -\frac{{{I}_{sbs(i)}}}{{{{\mathbf{h }}}_{s,s}}(i,{{k}_{s}})}\right] _{0}^{max}, \nonumber \\ \textit{C}1 &= \sum \limits _{j=1}^{K}{{{\mathbf{h }}_{s,s}}(i,j)+{{\mathbf{h }}_{s,m}}(i,k)}. \end{aligned}$$

(19)

Also, $I_{sbs(i)}$ and $\mu$ as the total interference from neighbor SBS and MBS in downlink channel and the Lagrange multiplier respectively are written as:

$$\begin{aligned} {{I}_{sbs(i)}} &= \textit{I}4+{{P}_{noise}},\nonumber \\ \textit{I}4 &= \sum _{\underset{j\ne i}{\mathop {j=1}}\,}^{I}{{{P}_{sbs(j)}}\times {{\mathbf{h }}_{s,s}}(j,{{k}_{s}})+{{P}_{mbs}} \times {{\mathbf{h }}_{m,s}}(1,{{k}_{s}})}. \end{aligned}$$

(20)

$$\begin{aligned} {{\mu }} &= \frac{{{h}_{s,s}}(i,{{k}_{s}})}{ln2\times ({{I}_{sbs(i)}}+P_{\max }^{sbs}\times {{h}_{s,s}}(i,{{k}_{s}}))} \end{aligned}$$

(21)

According to (19), $P^{*}_{sbs(i)}$ is depend on $Price_{sbs(i)}$, therefore, it is calculated by sub-game(2). After replacing $P^{*}_{sbs(i)}$ in (16), it consists of two terms that is observed in appendix(2.1). Maximization of the convex function is difficult, so $Price^{*}_{sbs(i)}$ can be obtained by maximization of the first term or minimization of the second term of $U_{sbs(j)}$. Thus, to find the $Price^{*}_{sbs(i)}$, sub-game(2) is converted to the minimization problem according appendix (2.1). Therefore, $Price^{*}_{sbs(i)}$ can be written as:

$$\begin{aligned} Price^{*}_{sbs(i)} &= \frac{\sum_{i=1}^{I}{\sqrt{ \frac{ln2\times {{I}_{sbs(i)}} \times \textit{C}1}{{{\mathbf{h }}_{s,s}}(i,{{k}_{s}})}}}}{ln2\times \left[{{I}_{\max }}+\sum_{i=1}^{I}{\frac{{{I}_{sbs(i)}} \times \textit{C}1}{{{\mathbf{h }}_{s,s}}(i,{{k}_{s}})}}\right]}\nonumber \\&\times \left[\sqrt{ \frac{{{\mathbf{h }}_{s,s}}(i,{{k}_{s}})}{ln2\times {{I}_{sbs(i)}}\times \textit{C}1}} - \frac{{{\mu }} }{\textit{C}1}\right]. \end{aligned}$$

(22)

It is observed from (19) that the SBS cannot transmit if the $Price_{sbs(i)}$ is too high, so $Price^{*}_{sbs(i)}$ is optimum value if:

$$\begin{aligned} {{{Price}}_{sbs(i)}}\le \frac{{{\mathbf{h }}_{s,s}}(i,{{k}_{s}})}{ln2\times {{I}_{sbs(i)}} \times \textit{C}1} - \frac{{{\mu }}}{\textit{C}1}. \end{aligned}$$

(23)

To find $P^{*}_{sue({k}_{s})}$, it is required to solve sub-game(1). But, due to second derivation of $U_{sue({k}_{s})}$ is less than zero, $U_{sue({k}_{s})}$ is a concave function and maximization of the concave function is a convex optimization problem [22]. Therefore, by solving sub-game(1) versus $P_{sue({k}_{s})}$ according to appendix(2.2), the optimal value of $P_{sue({k}_{s})}^{*}$ can be obtained from the Lagrangian method based on KKT condition. Therefore, $P_{sue({k}_{s})}^{*}$ can be obtained as:

$$\begin{aligned} P_{sue({{k}_{s}})}^{*} &= \left[ \frac{1}{ln2\times [{{{Price}}_{sue({{k}_{s}})}} \times \mathbf{h }_{s,m}{{({{k}_{s}},k)}}+\beta ]} \right. \nonumber \\&\left. -\frac{{{I}_{sue({{k}_{s}})}}}{\mathbf{h }{{{s,s}_{({{k}_{s}},i)}}}}\right] ^{max}_{0}. \end{aligned}$$

(24)

Also ${{I}_{sue({{k}_{s}})}}$ and ${{\beta }}$ as the interference from $j^{th}$ SUE in the neighbor small cell in uplink channel and MBS in downlink channel and as the Lagrange multiplier respectively are written as:

$$\begin{aligned} {{I}_{sue({{k}_{s}})}} &= \textit{I}5+{{P}_{noise}}, \end{aligned}$$

(25)

$$\begin{aligned} \textit{I}5 &= \sum _{\underset{j\ne i}{\mathop {j=1}}\,}^{I}{{{P}_{sue(j)}}\times {{\mathbf{h }}_{s,s}}(j,{{k}_{s}})+{{P}_{mbs}} \times {{\mathbf{h }}_{m,s}}(1,{{k}_{s}})}. \nonumber \\ {{\beta }} &= \frac{{{\mathbf{h }}_{{s,s}}}({{k}_{s}},i)}{ln2 \times [{{I}_{sue({{k}_{s}})}}+ P_{\max }^{sue} \times {{\mathbf{h }}_{{s,s}}}({{k}_{s}},i)]}] \end{aligned}$$

(26)

According to (24), $P^{*}_{sue({k}_{s})}$ is depend on $Price_{sue({k}_{s})}$, therefore, it is calculated by sub-game(3). After replacing $P^{*}_{sue({k}_{s})}$ in (18), it consists of two terms that is observed in appendix(2.2). Maximization of the convex function is difficult, so $Price^{*}_{sue({k}_{s})}$ can be obtained by maximization of the first term or minimization of the second term of $U_{mbs}$. Thus, to find the $Price^{*}_{sue({k}_{s})}$, sub-game(3) is converted to the minimization problem according to appendix (2.2). Therefore, $Price^{*}_{sbs(i)}$ can be written as:

$$\begin{aligned}&{Price}_{sue({{k}_{s}})}^{*}= \frac{\sum \limits _{{{k}_{s}}=1}^{K}{ \sqrt{\ \frac{ln2 \times {{I}_{sue({{k}_{s}})}} \times \ {{\mathbf{h }}_{s,m}} ({{k}_{s}},k)}{{{\mathbf{h }}_{s,s}}({{k}_{s}},i)}}}}{ln2\times [{{I}_{\max }}+ \sum \limits _{{{k}_{s}}=1}^{K}{\frac{{{I}_{sue({{k}_{s}})}} \times {{\mathbf{h }}_{s,m}}({{k}_{s}},k)}{{{\mathbf{h }}_{s,s}}({{k}_{s}},i)}]} } \nonumber \\&\quad \times \left[ \sqrt{\frac{{{\mathbf{h }}_{s,s}}({{k}_{s}},i)}{ln2 \times {{I}_{sue({{k}_{s}})}}\ \times \ {{\mathbf{h }}_{{s,m}}}(k_{s},k)}}- \frac{{{\beta }}}{{{\mathbf{h }}_{s,m}}({{k}_{s}},k)}\right] . \end{aligned}$$

(27)

It is observed from (24), the SUE cannot transmit if the $Price^{*}_{sue({k}_{s})}$ is too high, so $Price^{*}_{sue({k}_{s})}$ is optimum value if:

$$\begin{aligned}&{{{Price}}_{sue({{k}_{s}})}} \le \frac{\ {{\mathbf{h }}_{s,s}}({{k}_{s}},i)}{ln2\,\times {{I}_{sue({{k}_{s}})}} \times {{\mathbf{h }}_{{s,m}}}({{k}_{s}},k)}- \nonumber \\&\quad \frac{{{\beta }}}{{{\mathbf{h }}_{{s,m}}}({{k}_{s}},k)}. \end{aligned}$$

(28)

4.2 Power control for MBS

SUE endures a severe interference from MBS, thus SBS to protect its users from interference imposes a price on MBS. In order to control power of MBS two sub-games are considered based on Stackelberg game. So that, sub-game(1) is assumed as a follower game to find the optimum power of ${{P}_{mbs}}$, so it is written as:

$$\begin{aligned}&sub-game(1): \nonumber \\&\quad \quad \{\underset{{{{\text {P}}}_{mbs(n)}}}{\mathop {Max}}\,{{U}_{mbs(n)}} \quad s.t. \quad {0} \le {P}_{mbs} \le {P^{mbs}_{max}}\}. \end{aligned}$$

(29)

where the utility function of $n^{th}$ MBS is obtained as:

$$\begin{aligned} {{U}_{mbs(n)}} &= \log \left[ 1 +\ \frac{{{P}_{mbs(n)}}\ \times \ \mathbf{h }_{m,m}{{(n,k)}}}{{{{\textit{I}6}_{}} +\textit{I}7 +{{P}_{noise}}}}\right] - \nonumber \\&\quad Price_{mbs(n)} \times P_{mbs(n)} \times \textit{C}2{}{{}}{{}}, \nonumber \\ I6 &= \sum _{\underset{j\ne i}{\mathop {j=1}}\,}^{n}{{{P}_{mbs(j)}}} \times \mathbf{h }_{m,m}{{(j,k)}}, \nonumber \\ \textit{I}7 &= \sum _{i=1}^{I}{{P}_{sbs(i)}}\times \mathbf{h }_{s,m}{{(i,k)}}, \nonumber \\ \textit{C}2 &= \sum \limits _{{{k}_{s}}=1}^{K}{}{ \mathbf h }_{m,s}{{(n,{{k}_{s}})}}+\mathbf{h }_{m,sd}{{(n,{{k}_{s}})}}. \end{aligned}$$

(30)

Sub-game(2) is assumed as a leader game to calculate the interference price that will be paid by MBS, so it is defined as:

$$\begin{aligned}&sub-game(2):\nonumber \\&\quad \quad \{\underset{{{{\text {price}}}_{mbs(n)}}}{\mathop {Max}}\,{{U}_{sbs}} \quad s.t. \quad {{P}_{mbs(n)}}\times \textit{C}2\le I_{max}\}. \end{aligned}$$

(31)

Also, the utility function of SBS for revenue maximization is obtained as:

$$\begin{aligned} {{U}_{sbs(i)}}={{{Price}}_{mbs(n)}}\times {{P}_{mbs(n)}}\times \textit{C}2. \end{aligned}$$

(32)

For finding ${{P}_{mbs(n)}^{*}}$, it is required to solve sub-game(1). But, due to second derivation of ${{U}_{mbs(n)}}$ in sub-game(1) is less than zero (appendix(3)), ${{U}_{mbs(n)}}$ is a concave function and maximization of the concave function is a convex problem [22]. Lagrangian method and KKT condition can be used to solve the convex problem according to appendix(3). By using Lagrange method and KKT condition the optimal value of ${{P}_{mbs(n)}^{*}}$ can be obtained as:

$$\begin{aligned} {P^{*}}_{mbs(n)} &= \left[ \frac{1}{ln2\times [{{{Price}}_{mbs(n)}} \times \textit{C}2+ \nu ]}-\right. \nonumber \\&\left. \quad \frac{{{I}_{mbs(n)}}}{\mathbf{h }_{m,m}{{(n,k)}}}\right] ^{max}_{0}. \end{aligned}$$

(33)

Also, ${{I}_{mbs(n)}}$ and $\nu$ as the total interference from neighbor MBS and SBS and as the Lagrange multiplier respectively are written as:

$$\begin{aligned} {{I}_{mbs(n)}} &= \textit{I}6+\textit{I}7+{{P}_{noise}}. \end{aligned}$$

(34)

$$\begin{aligned} \nu &= \frac{{{h}_{m,m}}(n,k)}{ln2\times ({{I}_{mbs(n)}}+P_{\max }^{mbs}\times {{h}_{m,m}}(n,k))} \end{aligned}$$

(35)

According to (33), $P^{*}_{mbs({n})}$ is depend on $Price_{mbs({n})}$, therefore, it is calculated by sub-game(2). After replacing $P^{*}_{mbs({n})}$ in (31), it consists of two terms that is observed in appendix(3). Maximization of the convex function is difficult, so $Price^{*}_{mbs({n})}$ can be obtained by maximization of the first term or minimization of the second term of $U_{sbs}$. Thus, to find the $Price^{*}_{mbs({n})}$, sub-game(2) is converted to the minimization problem according to appendix(3). Therefore, $Price^{*}_{mbs({n})}$ can be written as:

$$\begin{aligned} Price^{*}_{mbs(n)} &= \frac{\sqrt{\frac{ln2 \times {{{I}_{mbs(n)}} \times \textit{C}2}}{{\mathbf{h }_{m,m}{{(n,k)}}}}}}{ln2\times [{{I}_{\max }} + \frac{{I_{mbs(n)}} \times \textit{C}2}{\mathbf{h }_{m,m}{{(n,k)}}}]} \nonumber \\&\times \sqrt{\frac{\mathbf{h }_{m,m}{{(n,k)}}}{ln2 \times {{I}_{mbs(n)}} \times {\textit{C}}2}}- \frac{\nu }{{\textit{C}}2}, \end{aligned}$$

(36)

It is observed from (33), the MBS cannot transmit if the $Price^{*}_{mbs(n)}$ is too high, so $Price^{*}_{mbs(n)}$ is optimum value if:

$$\begin{aligned}&price_{mbs(n)}\le \ \nonumber \\&\quad \frac{\mathbf{h }_{m,m}{{(n,k)}}}{ln2 \times {{I}_{mbs(n)}} \times \textit{C}2+\mathbf{h }_{m,sd}{{(n,{{k}_{s}})}}} - \frac{\nu }{{\textit{C}2}{{}} {{}}}. \end{aligned}$$

(37)

4.3 Simulation result

According to algorithm that is described in Table 4, power control of each player in each sub-game is implemented in Matlab software. So, the performance evaluation of MHN can be presented by numerical results. The simulation parameters are given in Table 3.

Table 3 Simulation parameters

Table 4 Algorithm for joint optimum power control and spectrum trading

As it is shown in Fig. 2 by increasing the number of small cells, more bandwidth is shared between SBSs. Therefore, the bandwidth purchased will increase to serve more users.Also, the bandwidth purchased decreases by increasing spectrum price.

Fig. 2

Impact of increase small cell on bandwidth purchased

For higher distance between SBS and MBS, more bandwidth is required to achieve data rate demand and serve more users. So bandwidth purchased is increased by increment of number of users and distance between SBS and MBS that it is shown in Fig. 3.

Fig. 3

Impact of distance on bandwidth purchased

By increasing interference tolerance more SBS and SUE can transmit.Therefore, the utility function of active SBS according to (13) and the small cell utility functions according to (12) will increase and the interference price will decrease. Hence, all SBSs and SUEs can transmit with higher power. Figures 4 and 5 represent SBS and average small cell utility functions versus interference tolerance, respectively, for different values of interference and four small cells. By increasing interference tolerance, SBS utility function and average small cell utility function increase, also when interference is equal to zero, SBSs and small cells have more utility function.

Fig. 4

Utility of SBS versus maximum interference tolerance

Fig. 5

Average utility of small cell versus maximum interference tolerance

Figure 6 illustrates energy efficiency⁴ will increase with raising the number of small cells but by increasing interference tolerance, SBSs can transmit with more power. Thus energy efficiency will decrease that is shown in Fig. 7.

Fig. 6

Impact of increase small cell on energy efficiency

Fig. 7

Sum energy efficiency verses different number of small cell and interference tolerance

Figure 8 represents Cumulative Density Function (CDF) of SBS sum-utility that increase with increment of number of small cells.

Fig. 8

Empirical CDF of sum utility of SBS

Figure 9 illustrates MBSs can transmit with more power by increasing interference tolerance, thus, their sum-rate will increase.

Fig. 9

Sum rate of MBS versus interference tolerance

By increasing interference tolerance, interference price decreases, thus, SBS revenue according to (32) raises but due to SBS cannot increase its power more than determined maximum power, after a specific level (20 dB), SBS revenue level will be decreased, it is shown in Fig. 10.

Fig. 10

SBS revenue versus interference tolerance

5 Conclusion

In this paper, in order to mitigate both types of inter/intra-tier interferences, spectrum trading issue and power control is presented based on non-cooperative Stackelberg game and convex optimization method. Based on simulation results, the impact of dense deployment of small cells and optimal power allocation to MBS, SBS, SUE and optimal bandwidth allocation is shown on the performance of 5G MHN. Also, MBS traffic offloading is used by attaching some macro users with strong inter-tier interference to the small cells.

Appendix

1.1 Appendix(1)

According to Eq. (6), the second derivation of ${U}_{sbs(i)}$ on ${W_{i}}$ is computed:

$$\begin{aligned} \frac{{{\partial }^{2}}{{U}_{sbs(i)}}}{{{\partial }^{2}}{{W}_{i}}}=\frac{-D\times K}{W_{i}^{2}}\le 0\ \end{aligned}$$

(38)

As the second derivation is less than zero, it is concluded that ${U}_{sbs(i)}$ is a concave function. Therefore ${W_{i}}^{*}$ is obtained by:

$$\begin{aligned} \frac{\partial {{U}_{sbs(i)}}}{\partial ({{W}_{i}})}=\frac{D\times K}{{{W}_{i}}}-(1-\lambda )\times p=0 \end{aligned}$$

(39)

According to Eq. (8), the second derivation of ${U}_{mbs}$ on ${\lambda }$ is computed:

$$\begin{aligned} \frac{{{\partial }^{2}}{{U}_{mbs}}}{{{\partial }^{2}}\lambda } &= \frac{-{{D}_{m}}\times {{K}_{m}}}{{{(1-\lambda )}^{2}}}- \frac{D_{m}^{'}\times K_{m}^{'}}{{{\lambda }^{2}}} \nonumber \\&\quad -\frac{D_{m}^{'}\times K_{m}^{'}}{{{(1-\lambda )}^{2}}}\le 0 \end{aligned}$$

(40)

As the second derivation is less than zero, it is concluded that ${U}_{mbs}$ is a concave function. Therefore ${\lambda }^{*}$ is obtained by:

$$\begin{aligned} \frac{-{{D}_{m}}\times {{K}_{m}}}{1-\lambda }+\frac{{{{{D}'}}_{m}}\times {{{{K}'}}_{m}}}{\lambda }+\frac{{{{{D}'}}_{m}}\times {{{{K}'}}_{m}}}{1-\lambda }=0 \end{aligned}$$

(41)

1.2 Appendix(2)

1.3 Appendix(2-1)

${U}_{sbs(i)}$ is a concave function, due to the maximization of concave function is a convex problem so it can be solved by Lagrangian method as:

$$\begin{aligned}&L({{P}_{sbs(i)}},{{P}_{sue({{k}_{s}})}},\mu ,\beta )= {{U}_{smallcell(i)}}\nonumber \\&\quad +\mu (P_{\max }^{sbs}-{{P}_{sbs}})+\beta (P_{\max }^{sue}-{{P}_{sue}}) \end{aligned}$$

(42)

From (42) it can be written:

$$\begin{aligned}&\frac{\partial L({{P}_{sbs(i)}},{{P}_{sue({{k}_{s}})}},\mu ,\beta )}{\partial {{P}_{sbs(i)}}}= \nonumber \\&\quad \frac{1}{ln2}\times \left( \frac{A}{1+{{P}_{sbs(i)}}\times A}\right) -pric{{e}_{sbs(i)}}\times C1-{{\mu }}=0 \nonumber \\&\quad A=\frac{{{h}_{s,s}}(i,{{k}_{s}})}{{I}_{sbs(i)}} \end{aligned}$$

(43)

From above, ${{P}_{sbs(i)}^{*}}$ can be obtained according to Eq. (19). According to the Lagrangian method, we have:

$$\begin{aligned}&\frac{\partial L({{P}_{sbs(i)}},{{P}_{sue({{k}_{s}})}},\mu ,\beta )}{\partial \mu }=0 \Rightarrow P_{\max }^{sbs}={{P}_{sbs(i)}} \end{aligned}$$

(44)

Therefore, when SBS transmit at ${{P}_{max}^{sbs}}$, interference price will be minimum at this point so:

$$\begin{aligned} pric{{e}_{sbs(i)}}\approx 0 \end{aligned}$$

(45)

Then from (19) ${{\mu }}$ can be derived according to (21).

By solving sub-game(2), ${{Price}_{sbs(i)}^{*}}$ is calculated. Therefore, after replacing ${{P}_{sbs(i)}^{*}}$ in (16), sub-game(2) is written as:

$$\begin{aligned}&sub-game(2):\underset{Pric{{e}_{sbs(i)}}}{\mathop {Max}}\, \sum \limits _{i=1}^{I}Pric{{e}_{sbs(i)}}\nonumber \\&\times \left[ \left( \frac{1}{ln2\times [Pric{{e}_{sbs(i)}}+\frac{{{\mu }}}{C1}]}\right) - \frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}\right] _{0}^{\max } \nonumber \\&\quad s.t\sum \limits _{i=1}^{I}\left[ \left( \frac{1}{ln2\times [Pric{{e}_{sbs(i)}}+\frac{{{\mu }}}{C1}]}\right) -\frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}\right] _{0}^{\max }\nonumber \\&\quad \le {{I}_{\max }} \end{aligned}$$

(46)

But, due to the maximization of convex function is difficult [22], (46) is converted to the minimization problem as:

$$\begin{aligned}&sub-game(2): \nonumber \\&\quad \underset{Pric{{e}_{sbs(i)}}}{\mathop {Min}}\,\sum \limits _{i=1}^{I}{\frac{Pric{{e}_{sbs(i)}}\times {{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}} \nonumber \\&\quad s.t\sum \limits _{i=1}^{I}{(\frac{1}{ln2\times [Pric{{e}_{sbs(i)}}+\frac{{{\mu }}}{C1}]}})\nonumber \\&\quad \le {{I}_{\max }}+\sum \limits _{i=1}^{I}{\frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}} \end{aligned}$$

(47)

As problem (47) is a convex optimization, so ${{Price}_{sbs(i)}^{*}}$ can be obtained by the Lagrangian method as:

$$\begin{aligned} L(Pric{{e}_{sbs(i)}},\alpha ) &= \sum \limits _{i=1}^{I}{\frac{Pric{{e}_{sbs(i)}}\times {{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}}+ \nonumber \\&\quad \alpha \times \left[ \sum \limits _{i=1}^{I}\left( \frac{1}{ln2\times [Pric{{e}_{sbs(i)}}+\frac{{{\mu }}}{C1}]}\right) \right. \nonumber \\&\quad \left. -{{I}_{\max }}-\sum \limits _{i=1}^{I}{\frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}}\right] \end{aligned}$$

(48)

From (48) it can be written:

$$\begin{aligned} \frac{\partial L}{\partial Pric{{e}_{sbs(i)}}} &= \frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}\nonumber \\&-\frac{\alpha }{ln2\times {{[Pric{{e}_{sbs(i)}}+\frac{{{\mu }}}{C1}]}^{2}}}=0 \end{aligned}$$

(49)

From above, ${{Price}_{sbs(i)}^{*}}$ can be obtained as:

$$\begin{aligned} \left[ Price_{sbs(i)}^{*}=\sqrt{\frac{\alpha \times {{h}_{s,s}}(i,{{k}_{s}})}{ln2\times {{I}_{sbs(i)}}\times C1}}-\frac{{{\mu }}}{C1}\right] \end{aligned}$$

(50)

Due to, ${{Price}_{sbs(i)}^{*}}$ must be positive, we have:

$$\begin{aligned}&Pric{{e}_{sbs(i)}}\ge 0\Rightarrow \frac{1}{ln2\times [Pric{{e}_{sbs(i)}}+\frac{{{\mu }}}{C1}]}-{{I}_{\max }}\nonumber \\&\quad -\frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}=0 \end{aligned}$$

(51)

After replacing ${{Price}_{sbs(i)}^{*}}$ in (51), ${\alpha }$ can be calculated as:

$$\begin{aligned} \alpha =\left[ {{(\frac{\sum \limits _{i=1}^{I}{\sqrt{\frac{ln2\times {{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}}}}{ln2\times \left[ {{I}_{\max }}+\sum \limits _{i=1}^{I}\frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(iF,{{k}_{s}})}\right] })}}\right] ^{2} \end{aligned}$$

(52)

Also, (23) can be obtained by replacing ${{P}_{sbs(i)}^{*}}$ in (53):

$$\begin{aligned} P_{sbs(i)}^{*}\ge 0 \end{aligned}$$

(53)

1.4 Appendix(2-2)

${{U}_{sue({{k}_{s}})}}$ is a concave function, due to the maximization of concave function is a convex problem, so it can be solved by the Lagrangian method as:

$$\begin{aligned}&\frac{\partial L({{P}_{sbs(i)}},{{P}_{sue({{k}_{s}})}},\mu ,\beta )}{\partial {{P}_{sue({{k}_{s}})}}}= \frac{1}{ln2} \times \left( \frac{B}{1+{{P}_{sue({{k}_{s}})}}\times B}\right) \nonumber \\&\quad -price{_{sbs(i)}}\times {{h}_{s,s}}({{k}_{s}},k)-\beta =0 \nonumber \\&\quad B=\frac{{{h}_{s,s}}({{k}_{s}},i)}{{I}_{sue({k}_{s})}} \end{aligned}$$

(54)

From above, ${{P}_{sue({{k}_{s}})}^{*}}$ can be obtained according to Eq. (24).

According to the Lagrangian method, we have:

$$\begin{aligned} \frac{\partial L({{P}_{sbs(i)}},{{P}_{sue({{k}_{s}})}},\mu ,\beta )}{\partial \beta }=0 \Rightarrow P_{\max }^{sue}={{P}_{sue({{k}_{s}})}} \end{aligned}$$

(55)

Therefore, when SUE transmit at ${{P}_{max}^{sue}}$, interference price will be minimum at this point:

$$\begin{aligned} pric{{e}_{sue({k}_{s})}}\approx 0 \end{aligned}$$

(56)

Then from (24), ${\beta }$ can be driven according to (26). By solving sub-game(3), ${{Price}_{sue({k}_{s})}^{*}}$ is calculated. Therefore, after replacing ${{P}_{sue({k}_{s})}^{*}}$ in (18), sub-game(3) is written as:

$$\begin{aligned}&sub-game(3): \underset{Pric{{e}_{sue({{k}_{s}})}}}{\mathop {Max}}\,\nonumber \\&\sum \limits _{{{k}_{s}}=1}^{K}Pric{{e}_{sue({{k}_{s}})}}\times \left[ \left( \frac{1}{ln2\times [Pric{{e}_{sue({{k}_{s}})}}+\frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}]}\right) \right. \nonumber \\&\left. \quad \quad -\frac{{{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}\right] _{0}^{\max }\nonumber \\&\quad \quad s.t\sum \limits _{{{k}_{s}}=1}^{K}\left( \frac{1}{ln2\times [Pric{{e}_{sue({{k}_{s}})}}+\frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}]}\right) \le {{I}_{\max }}\nonumber \\&\quad \quad +\sum \limits _{{{k}_{s}}=1}^{K}{\frac{{{I}_{sue}}({{k}_{s}})\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}} \end{aligned}$$

(57)

But, due to the maximization of convex function is difficult [22], (57) is converted to the minimization problem as:

$$\begin{aligned}&sub-game(3): \nonumber \\&\quad \quad \underset{Pric{{e}_{sue({{k}_{s}})}}}{\mathop {Min}}\,\sum \limits _{{{k}_{s}}=1}^{K}{\frac{Pric{{e}_{sue({{k}_{s}})}}\times {{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}} \nonumber \\&\quad s.t\sum \limits _{{{k}_{s}}=1}^{K}\left( \frac{1}{ln2\times [Pric{{e}_{sue({{k}_{s}})}}+\frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}]}\right) \le {{I}_{\max }}+ \nonumber \\&\qquad \quad \quad \sum \limits _{{{k}_{s}}=1}^{K}{\frac{{{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}} \end{aligned}$$

(58)

As problem (58) is a convex optimization, so ${{Price}_{sue({k}_{s})}^{*}}$ can be obtained by the Lagrangian method as:

$$\begin{aligned}&\left[ L(Pric{{e}_{sue({{k}_{s}})}},{{\alpha }^{'}})= \right. \nonumber \\&\quad \quad \left. \sum \limits _{{{k}_{s}}=1}^{K}{\frac{Pric{{e}_{sue({{k}_{s}})}}\times {{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}}\right] + \nonumber \\&\quad \quad {{\alpha }^{'}}\times \left[ \sum \limits _{{{k}_{s}}=1}^{K}(\frac{1}{ln2\times [Pric{{e}_{sbs(i)}}+\frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}]}) \right. \nonumber \\&\left. \quad \quad -{{I}_{\max }}-\sum \limits _{{{k}_{s}}=1}^{K}{\frac{{{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}}\right] \end{aligned}$$

(59)

From (59) it can be written:

$$\begin{aligned}&\frac{\partial L}{\partial Pric{{e}_{sue({{k}_{s}})}}}=\frac{{{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)} \nonumber \\&\quad -\frac{{{\alpha }^{'}}}{ln2\times {{[Pric{{e}_{sbs(i)}}+\frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}]}^{2}}}=0 \end{aligned}$$

(60)

From above, ${{Price}_{sue({k}_{s})}^{*}}$ can be obtained according as:

$$\begin{aligned} Price_{sue({{k}_{s}})}^{*} &= \sqrt{\frac{{{\alpha }^{'}}\times {{h}_{s,s}}({{k}_{s}},i)}{ln2\times {{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}}- \nonumber \\&\quad \frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}] \end{aligned}$$

(61)

Due to, ${{Price}_{sue({k}_{s})}^{*}}$ must be positive, we have:

$$\begin{aligned}&Pric{{e}_{sue({{k}_{s}})}}\ge 0\Rightarrow \nonumber \\&\quad \sum \limits _{{{k}_{s}}=1}^{K}\left( \frac{1}{ln2\times [Pric{{e}_{sue({{k}_{s}})}}+\frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}]}\right) -{{I}_{\max }} \nonumber \\&\quad -\sum \limits _{{{k}_{s}}=1}^{K}{\frac{{{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}}=0 \end{aligned}$$

(62)

After replacing ${{Price}_{sue({k}_{s})}^{*}}$ in (62), ${{\alpha }^{'}}$ can be calculated as:

$$\begin{aligned} {{\alpha }^{'}}=\left[ {{(\frac{\sum \limits _{{{k}_{s}}=1}^{K}{\sqrt{\frac{ln2 \times {{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}} ({{k}_{s}},i)}}}}{ln2\times \left[ {{I}_{\max }}+\sum \limits _{{{k}_{s}}=1}^{K}{ \frac{{{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}} ({{k}_{s}},i)}}\right] })}}\right] ^{2} \end{aligned}$$

(63)

Also, (28) can be obtained by replacing ${{P}_{sue({k}_{s})}^{*}}$ in (64):

$$\begin{aligned} P_{sue({k}_{s})}^{*}\ge 0 \end{aligned}$$

(64)

1.5 Appendix(3)

${{U}_{mbs(n)}}$ is a concave function, due to the maximization of concave function is a convex problem, so it can be solved by the Lagrangian method as:

$$\begin{aligned}{}[L({{P}_{mbs(n)}},\nu )={{U}_{mbs(n)}}+\nu (P_{\max }^{mbs}-{{P}_{mbs}})] \end{aligned}$$

(65)

From (65) it can be written:

$$\begin{aligned} \frac{\partial L({{P}_{mbs(n)}},\nu )}{\partial {{P}_{mbs(n)}}} &= \frac{1}{ln2}\times \left( \frac{C}{1+{{P}_{mbs(n)}}\times C}\right) \nonumber \\ &\quad-pric{{e}_{mbs(n)}}\times C2-\nu =0 \nonumber \\&\quad C=\frac{{{h}_{m,m}}(n,k)}{{{I}_{mbs(n)}}} \end{aligned}$$

(66)

From above, ${{P}_{mbs(n)}^{*}}$ can be obtained to Eq. (33).

According to the Lagrangian method, we have:

$$\begin{aligned} \frac{\partial L({{P}_{mbs(n)}},\nu )}{\partial \nu }=0 \Rightarrow P_{\max }^{mbs}={{P}_{mbs(n)}} \end{aligned}$$

(67)

Therefore, when MBS transmit at ${{P}_{mbs(n)}^{*}}$, interference price will be minimum at this point so:

$$\begin{aligned} pric{{e}_{mbs(n)}}\approx 0 \end{aligned}$$

(68)

Then, from (33) ${\nu }$ can be derived according to (35).

By solving sub-game(2), ${{Price}_{mbs(n)}^{*}}$ is calculated. Therefore, after replacing ${{P}_{mbs(n)}^{*}}$ in (31), sub-game(2) is written as:

$$\begin{aligned}&sub-game(2): \underset{Pric{{e}_{mbs(n)}}}{\mathop {Max}}\,{{U}_{sbs}}= Pric{{e}_{mbs(n)}} \nonumber \\&\quad \times \left[ (\frac{1}{ln2\times [Pric{{e}_{mbs(n)}}+\frac{\nu }{C2}]}-\frac{{{I}_{mbs(i)}}\times C2}{{h}_{m,m}}(n,k)\right] _{0}^{\max } \nonumber \\&\quad s.t\sum \limits _{i=1}^{I}\left[ \left( \frac{1}{ln2\times [Pric{{e}_{mbs(n)}}+\frac{\nu }{C2}]}\right) - \right. \nonumber \\&\left. \quad \frac{{{I}_{mbs(n)}}\times C2}{{h}_{m,m}}(n,k)\right] _{0}^{\max } \le {{I}_{\max }} \end{aligned}$$

(69)

But, due to the maximization of convex function is difficult [22], (69) is converted to the minimization problem as:

$$\begin{aligned}&sub-game(2): \underset{Pric{{e}_{mbs(n)}}}{\mathop {Min}}\,\frac{Pric{{e}_{mbs(n)}}\times {{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)} \nonumber \\&\quad s.t\left( \frac{1}{ln2\times [Pric{{e}_{mbs(n)}}+\frac{\nu }{C2}]}\right) \le {{I}_{\max }}\nonumber \\&\quad +\frac{{{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)} \end{aligned}$$

(70)

As problem (70) is a convex optimization, so ${{Price}_{mbs(n)}^{*}}$ can be obtained by the Lagrangian method as:

$$\begin{aligned}&L(Pric{{e}_{mbs(n)}},\gamma )=\frac{Pric{{e}_{mbs(n)}}\times {{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)}+ \nonumber \\&\quad \gamma \times \left[ \frac{1}{ln2\times [Pric{{e}_{mbs(n)}}+\frac{\nu }{C2}]} -{{I}_{\max }}\right. \nonumber \\&\left. \quad -\frac{{{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)}\right] \end{aligned}$$

(71)

From (71) it can be written as:

$$\begin{aligned}&\frac{\partial L}{\partial Pric{{e}_{mbs(n)}}}= \nonumber \\&\quad \frac{{{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)}-\frac{\nu }{ln2\times {{[Pric{{e}_{mbs(n)}}+\frac{\nu }{C2}]}^{2}}}=0 \end{aligned}$$

(72)

From above, ${{Price}_{mbs(n)}^{*}}$ can be obtained as:

$$\begin{aligned} Price_{mbs(n)}^{*}=\sqrt{\frac{\gamma \times {{h}_{m,m}}(n,k)}{ln2\times {{I}_{mbs(n)}}\times C2}}-\frac{\nu }{C2} \end{aligned}$$

(73)

Due to, ${{Price}_{mbs(n)}^{*}}$ must be positive, we have:

$$\begin{aligned} Pric{{e}_{mbs(n)}} &\ge 0\Rightarrow \frac{1}{ln2\times [Pric{{e}_{mbs(n)}} +\frac{\nu }{C2}]} -{{I}_{\max }}\nonumber \\&\quad -\frac{{{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)}=0 \end{aligned}$$

(74)

After replacing ${{Price}_{mbs(n)}^{*}}$ in (74), ${\gamma }$ can be calculated as:

$$\begin{aligned} \gamma ={{(\frac{\sqrt{\frac{ln2\times {{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)}}}{ln2\times [{{I}_{\max }}+\frac{{{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)}]})^{2}}} \end{aligned}$$

(75)

Also, (37) can be obtained by replacing ${{P}_{mbs(n)}^{*}}$ in (76):

$$\begin{aligned} P_{mbs(n)}^{*}\ge 0 \end{aligned}$$

(76)