1 Introduction

Non-orthogonal multiple access (NOMA) has been proven as a promising technique for the fifth generation (5G) mobile networks due to its superior spectral efficiency [1]. Unlike orthogonal-multiple-access (OMA), NOMA allows multiple users to pair and share the same radio resources, either in time, frequency or in code. The key idea of NOMA is to explore power domain, where users are served at different power levels [2]. More importantly, NOMA has recently been recognized as a promising multiple access (MA) technique to significantly improve the spectral efficiency of mobile communication networks. It is also been envisioned as a key component in fifth generation (5G) mobile systems, it has also been applied to cooperative relay systems [3, 4]. In [3], the cooperative NOMA system with buffer-aided relaying was studied. Assuming that the relay node possesses a buffer, the authors proposed an adaptive transmission scheme in which the system adaptively chooses its working mode in each time slot. The authors in [4] proposed and investigated a dual-hop cooperative relaying scheme using NOMA, where two sources communicate with their corresponding destinations simultaneously over the same frequency band and via a common relay. After receiving symbols transmitted from both sources with different allocated powers, the relay forwards a superposition coded composite signal to the destinations by using NOMA technique.

On the other hand, despite of advantages of simultaneous wireless information and power transfer (SWIPT), the research on it is lack, especially studying of join of SWIPT and NOMA relay systems. There are several researches on NOMA systems combining radio frequency (RF) energy harvesting (EH) as follows. The general combination of NOMA and EH was investigated in [5,6,7]. SWIPT of NOMA networks where users are spatial randomly located, was also investigated [8]. The system in which the users closer to the source act as EH relays to help the users farther was analyzed. The outage performance of NOMA-EH relaying networks with antenna selection at the source and splitting power at the relay was discussed in [7]. To the best of our knowledge, the aforementioned work, the EH on the partial relay selection (PRS) combining with NOMA technique, has not been discussed. Therefore, we decide the main contributions of this paper are as follows:

  • We propose a NOMA system where the relay node harvests energy from the radio frequency by using time switching scheme to support the operation of forwarding information to both of users.

  • In order to evaluate the performance of partial selection relay scheme, we derive closed-form expressions of undecodable probability and ergodic capacity. Undecodable probability is defined as probability the desired information at the best relay node and/or the destination nodes can not be decoded successfully because of low signal to noise ratio (SNR).

  • The performance of NOMA-EH system under the imperfect SIC and perfect SIC is analyzed and compared with each other and with the orthogonal frequency division multiple access (OFDMA).

  • According to the channel gains, the detailed power allocation coefficient for is settled for fairness in performance of users

The rest of this paper is organized as follows Sect. 2 describes the system model of partial relay selection in NOMA system with RF EH. The mathematical analysis of the system is represented in Sect. 3. Numerical results are shown in Sect. 4 to examine the performance of our proposed system. Finally, the paper is concluded in Sect. 5.

2 System model

Fig. 1
figure 1

Partial relaying selection in NOMA downlink relay network with RF EH

Full size image

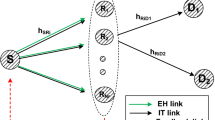
We consider a NOMA downlink system consisted of one source (\({\mathrm {S}}\)), two users ( \({\mathrm {D}}_{1}\) and \({\mathrm {D}}_{2}\)) as shown in Fig. 1. The source transmits the signal to the users via several relay nodes \({\mathrm{{R}}_{n}}\) with \(n \in \left\{ {1,\ldots,N} \right\}\) which are equipped one antenna and operate in a half-duplex mode. In this paper, we only consider the case of partial relay selection. Moreover, all relays have no fixed power supply and are powered by wireless energy transfer from the source. The channels from the \({\mathrm {S}}\) to \({\mathrm{{R}}_{n}}\) and from \({\mathrm{{R}}_{n}}\) to \({\mathrm{{D}}_{i}}\) with \(i \in \left\{ {1,2} \right\}\), exhibit frequency, flat Rayleigh block fading.

As shown in Fig. 1, \(h_{1,n}\sim {\mathcal {CN}}(0,\Omega _{1,n})\) is the complex channel coefficient between the \({\mathrm {S}}\) and \({\mathrm {R}}_n\). \({\mathrm {w}}_{\mathrm{{R}}}, ~{\mathrm {w}}_{\mathrm{D_i}}\sim {{\mathcal {C}}}{{\mathcal {N}}}\left( {0,1} \right)\) are the additive white Gaussian noise (AWGN) at \(R_n\) and \({\mathrm {D}}_{i}\), respectively. \({g_i} \sim {{\mathcal {C}}}{{\mathcal {N}}}(0,\Omega _{\mathrm{R_nD_i}})\) denotes the complex channel coefficient between \({\mathrm {R}}_n\) and \({\mathrm {D}}_{i}\). Since the path loss and shadowing effect of \({g_1}\) are more severe than \({g_2}\), we have \(\Omega _{\mathrm{R_nD_1}} < \Omega _{\mathrm{R_nD_2}}\) which is important for performing the successive interference cancellation (SIC) [10]. The relay and the user respectively receive the signal from the source and the best relay, hence the channel state information (CSI) between the source and the relay is available at the relay, the CSI between the best relay and the user is available at the user.

In this paper, we consider the PRS scheme where relay node is selected based only on the instantaneous knowledge of the channel pertaining to the first hop. The source terminal continuously monitors the quality of its connectivity with the relays via the transmission of local feedbacks. From this information, the source selects the best link \({\mathrm{{S}}} \rightarrow {\mathrm{{R}}_n}\) for data transmission. As multiple relay nodes form a group, one best relay \({\mathrm{R}}_b\) is selected before transmitting. This PRS strategy is expressed asFootnote 1

$$\begin{aligned} {\mathrm{b}} = \arg \,\,\max _{n = 1,\,2 \ldots ,N}|h_{1,n}|^2. \end{aligned}$$
(1)

We assume that the harvested power is consumed by the relays for forwarding signals to \({\mathrm {D}}_1\) and \({\mathrm {D}}_2\). The processing power required for the transmitting - receiving circuitry of relay is generally negligible compared to the power used for signal transmission. The time switching (TS) architecture for EH [11]Footnote 2 is applied. Specifically, the energy is harvested from the received information signal for a duration of \(\alpha T\) in each block, where \(\alpha\) is the fraction of the block time in which the relay harvests energy from the received information signal, and T is the block time in which a certain information is transmitted from the source to the users. Hence, the harvested energy is given by [12].

$$\begin{aligned} {E_h} = {{\alpha T\eta {P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2}}}, \end{aligned}$$
(2)

where\(\eta\)is the energy conversion efficiency, depends on the quality of energy harvesting electric circuitry,\(0 < \eta \le 1\), and \({P_{\mathrm{{S}}}}\)is transmission power of\({\mathrm{{S}}}\).

We assume that the duration time for relay to receive the signal from the source and to transmit the received signal to both of users is the same and equals \(( 1 - \alpha )T/2\). From (2), the transmission power of relay node is calculated as

$$\begin{aligned} {P_{\mathrm{{R}}}} = \frac{{{E_h}}}{{\left( {1 - \alpha } \right) T/2}} = \frac{{2\alpha \eta {P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2}}}{{1 - \alpha }}. \end{aligned}$$
(3)

The operation on the system is briefly described as follows. There are two time slots involving in each transmission block. All blocks are normalized to one unit. During the first time slot, the source node transmits the superimposed mixture, \({\sqrt{{a_1}} {x_1} + \sqrt{{a_2}} {x_2}}\), where \(x_i\) and \(a_i\) denote the signal and the power allocation coefficient of user i, respectively. It should be noted that \({a_1} + {a_2} = 1\), and without loss of generality, we assume that\({a_1} \ge {a_2}\) [13]. The baseband received signal at \({\mathrm{{R}}_n}\) is thus given by

$$\begin{aligned} y_{\mathrm{{R}}}^n = \sqrt{{P_\mathrm{{S}}}} {h_{1,n}}\left( {\sqrt{{a_1}} {x_1} + \sqrt{{a_2}} {x_2}} \right) + {\mathrm{{w}}_{\mathrm{{R}}}}. \end{aligned}$$
(4)

Since the key idea of NOMA technique is to use the power domain for multiple accesses, i.e. users are served at different power levels, and to adopt the superposition code at the transmitter. We use the SIC principle to decode signals at the receivers, such as the stronger signal is decoded and removed from the superposed signals, and then the weaker signal is decoded to obtain the desired information. Thus, in this paper, we only consider SIC process at the best relay node and the \({\mathrm {D}}_2\) because the \({\mathrm {D}}_1\), which is allocated higher transmit power, decodes the superimposed mixture signal and obtains its own signal while considering the other signal as noise.

When the SIC is employed at the \({\mathrm{{R}}_n}\), the best relay, \(R_b\), firstly decodes symbol \({x_1}\) by treating the symbol \({x_2}\) as noise. Then, it performs SIC to obtain symbol \({x_2}\). Thus, the received signal-to-interference-plus-noise ratio (SINR) for symbol \({x_1}\) and signal-to-noise ratio (SNR) for symbol \({x_2}\) at \(R_b\) are written as

$$\begin{aligned} {\gamma _{1u_1}}&= \frac{{{a_1}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2}}}{{{a_2}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2} + 1}}, \end{aligned}$$
(5)
$$\begin{aligned} {\gamma _{1u_2}}&= {a_2}{P_{\mathrm{{S}}}}{\left| {{h_{1,b}}} \right| ^2}. \end{aligned}$$
(6)

In the first time slot, \({\mathrm{{R}}_n}\) processes messages \({x_1}\), \({x_2}\) and in the second time slot, the selected relay sends the message \(\sqrt{{P_{\mathrm{{R}}}}} \left( {\sqrt{{a_1}} {x_1} + \sqrt{{a_2}} {x_2}} \right)\) to two users \({\mathrm{{D}}_1}\) and \({\mathrm{{D}}_2}\). Hence, the received signal at \({\mathrm{{D}}_i}\) is described as follows.

$$\begin{aligned} {y_{{\mathrm{{D}}_i}}} = \sqrt{{P_{\mathrm{{R}}}}} {g_i}\left( {\sqrt{{a_1}} {x_1} + \sqrt{{a_2}} {x_2}} \right) + {\mathrm{{w}}_{{\mathrm{{D}}_{\mathrm{{i}}}}}}, \end{aligned}$$
(7)

where \({g_i}\) denotes the channel gain between the selected relay and \({\mathrm{{D}}_i}\).

According to the SIC principle, the \({\mathrm{{D}}_1}\) decodes symbol \({x_1}\) while treating \({x_2}\) as noise. From (7), the signal-to-interference-plus-noise ratio (SINR) at \({\mathrm{{D}}_1}\) is given by

$$\begin{aligned} \gamma _{2u_1} = \frac{{{a_1}{P_{\mathrm{{R}}}}{{\left| {{g_1}} \right| }^2}}}{{{a_2}{P_{\mathrm{{R}}}}{{\left| {{g_1}} \right| }^2} + 1}}. \end{aligned}$$
(8)

It should be noticed that \({x_1}\) and \({x_2}\) coexist at \({\mathrm{{D}}_2}\). Therefore, the SIC is needed to decode own symbol \({x_2}\). To perform SIC, \({\mathrm{{D}}_2}\) decodes high-power symbol \({x_1}\) by treating the low-power symbol \({x_2}\) as noise, and cancels it using SIC to obtain symbol \({x_2}\). Thus, the received SINR for \({x_1}\) at \({\mathrm{{D}}_2}\) is given by

$$\begin{aligned} \gamma _{2u_1\rightarrow u_2} = \frac{a_1P_{\mathrm{R}}{|g_2|}^2}{a_2P_{\mathrm{R}}|g_2|^2 + 1}. \end{aligned}$$
(9)

After cencelling \({x_1}\), \({\mathrm{{D}}_2}\) decodes its own message, \({x_2}\), with the SNR as

$$\begin{aligned} \gamma _{2u_2} = {a_2}P_{\mathrm{{R}}}{\left| {{g_2}} \right| ^2}. \end{aligned}$$
(10)

3 Performance analysis

In this section, we discuss on undecodable probability and ergodic capacity of partial relay selection scheme NOMA system with RF EH. The undecodable probability can be refered as the probability that symbols \({x_1}\) and \({x_2}\) are not able to be decoded at \({\mathrm {D}}_1\) and \({\mathrm {D}}_2\). In additional, a symbol is not able to be decoded if the received SNR or SINR is lower than the threshold value, \(\gamma\).

3.1 Undecodable probability of \(x_1\)

We denote \({\mathrm{{P}}}_{x_1}^{\mathrm{error}}\) as the event that the best relay or \({\mathrm{{D}}_1}\) or \({\mathrm{{D}}_2}\) cannot decode \({x_1}\) successfully because the SINR/SNR is lower than the threshold value, \({\gamma _{\mathrm{{th1}}}}\). From (5), (8), and (9), we can write the expression of \({\mathrm{{P}}}_{x_1}^{\mathrm{error}}\) as in (11) [14],

$$\begin{aligned} {\mathrm{{P}}}_{{x_1}}^{\mathrm{{error}}}=\Pr \left\{ \begin{array}{c} \frac{{{a_1}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2}}}{{{a_2}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2} + 1}}< {\gamma _{\mathrm{{th1}}}},\\ {\mathrm{or}}~\frac{{{a_1}{P_{\mathrm{{R}}}}{{\left| {{g_1}} \right| }^2}}}{{{a_2}{P_{\mathrm{{R}}}}{{\left| {{g_1}} \right| }^2} + 1}}< {\gamma _{\mathrm{{th1}}}},\\ {\mathrm{or}}~\frac{{{a_1}{P_{\mathrm{{R}}}}{{\left| {{g_2}} \right| }^2}}}{{{a_2}{P_{\mathrm{{R}}}}{{\left| {{g_2}} \right| }^2} + 1}} < {\gamma _{\mathrm{{th1}}}} \end{array}\right\} =1 - \Pr \left\{ \begin{array}{c} \frac{{{a_1}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2}}}{{{a_2}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2} + 1}}> {\gamma _{\mathrm{{th1}}}},\\ \frac{{{a_1}{P_{\mathrm{{R}}}}{{\left| {{g_1}} \right| }^2}}}{{{a_2}{P_{\mathrm{{R}}}}{{\left| {{g_1}} \right| }^2} + 1}}> {\gamma _{\mathrm{{th1}}}},\\ \frac{{{a_1}{P_{\mathrm{{R}}}}{{\left| {{g_2}} \right| }^2}}}{{{a_2}{P_{\mathrm{{R}}}}{{\left| {{g_2}} \right| }^2} + 1}} > {\gamma _{\mathrm{{th1}}}} \end{array}\right\} , \end{aligned}$$
(11)

where \(\gamma _{\mathrm{th1}} = 2^{\frac{2r_1}{1-\alpha }} - 1\) and \(r_1\) is the target data rate of \(D_1\). Let \({\left| {{h_{1,b}}} \right| ^2} = {X}\), \({\left| {{g_1}} \right| ^2} = Y\), and \({\left| {{g_2}} \right| ^2} = Z\) be the channel gains from the source to the best relay and from the best relay to \({\mathrm{{D}}_1}\) and \({\mathrm{{D}}_2}\), respectively. In this paper, we assume that all channel coefficients are modeled as independent Rayleigh-distributed random variables (RVs). Therefore, RVs \(|h_{1,b}|^2\), \(|g_1|^2\), and \(|g_2|^2\) have exponential distributions, with

$$\begin{aligned} f_X(x)= & {} \sum \nolimits _{n = 1}^N ( - 1)^{n - 1}\left( {\begin{array}{c}N\\ n\end{array}}\right) \frac{n}{\Omega _1}\exp (-\frac{nx}{\Omega _1}),\\ f_Y(y)= & {} \frac{1}{\Omega _2}\exp (-\frac{y}{\Omega _2}), ~F_Y(y) =1-\exp (-\frac{y}{\Omega _2}),\\ f_Z(z)= & {} \frac{1}{\Omega _3}\exp (-\frac{z}{\Omega _3}). \end{aligned}$$

where f and Fare respectively the cumulative density function and probability density function,\(\Omega _1 = {\mathbb {E}}\{|h_{1,b}|^2\}, \Omega _2 = {\mathbb {E}}\{|g_1|^2\}\) and \(\Omega _3 = {\mathbb {E}}\{|g_2|^2\}\)are means of random variables. We can rewrite (11) to become (12)

$$\begin{aligned} {\mathrm{{P}}}_{{x_1}}^{\mathrm{{error}}} = 1 - \Pr \left\{ \begin{array}{c} X> \frac{{{\gamma _{\mathrm{{th1}}}}}}{{{P_{\mathrm{{S}}}}\left( {{a_1} - {a_2}{\gamma _{\mathrm{{th1}}}}} \right) }}\\ XY> \frac{{{\gamma _{\mathrm{{th1}}}}}}{{{P_{\mathrm{{S}}}}\phi \left( {{a_1} - {a_2}{\gamma _{\mathrm{{th1}}}}} \right) }}\\ XZ > \frac{{{\gamma _{\mathrm{{th1}}}}}}{{{P_{\mathrm{{S}}}}\phi \left( {{a_1} - {a_2}{\gamma _{\mathrm{{th1}}}}} \right) }} \end{array} \right\} , \end{aligned}$$
(12)

where \(\phi = \frac{{2\alpha \eta }}{{1 - \alpha }}\). As can be seen from (12), the outage always occurs if \({\gamma _{\mathrm{{th}}1}} > \frac{{{a_1}}}{{{a_2}}}\). Hence, we need to allocate more power for symbol \(x_1\) meaning \({a_1}> {a_2}\gamma _{\mathrm{th1}}\) is required. By using the conditional probability in [15], we can rewrite (12) as

$$\begin{aligned} {\mathrm{{P}}}_{{x_1}}^{\mathrm{{error}}}&= 1 - \int \limits _{{t_1}}^\infty {\Pr \left\{ {Y> \frac{{{t_2}}}{x},Z > \frac{{{t_2}}}{x}} \right\} } {f_X}\left( x \right) dx\nonumber \\&= 1 - \int \limits _{{t_1}}^\infty {\int \limits _{\frac{{{t_2}}}{x}}^\infty {\left[ {1 - {F_Y}\left( {\frac{{{t_2}}}{x}} \right) } \right] } } {f_Z}\left( z \right) {f_X}\left( x \right) dxdz, \end{aligned}$$
(13)

where

$$\begin{aligned} {t_1} = \frac{{{\gamma _{\mathrm{{th1}}}}}}{{{P_{\mathrm{{S}}}}\left( {{a_1} - {a_2}{\gamma _{\mathrm{{th1}}}}} \right) }}\,\,\, {\text {and}}\,\,\, {t_2} = \frac{{{\gamma _{\mathrm{{th1}}}}}}{{{P_{\mathrm{{S}}}}\phi \left( {{a_1} - {a_2}{\gamma _{\mathrm{{th1}}}}} \right) }}. \end{aligned}$$

From (13) and after some manipulation, we have

$$\begin{aligned} {\mathrm{{P}}}_{{x_1}}^{\mathrm{{error}}} = 1 - \sum \limits _{n = 1}^N(-1)^{n - 1}\left( {\begin{array}{c}N\\ n\end{array}}\right) \frac{n}{\Omega _1}{\underbrace{\int \limits _{t_1}^\infty \exp \left( { - \frac{\beta }{x} - \frac{{nx}}{{{\Omega _1}}}} \right) dx}_\psi }, \end{aligned}$$
(14)

where \(\beta =\frac{t_2}{\Omega _2} + \frac{t_2}{\Omega _3}\). Unfortunately, a closed-form expression for \(\psi\) in (14) is difficult to be derived, thus we employ the approximation method. By using expanded Taylor’s series, it follows that \(\exp \left( { - \frac{a}{x}} \right) = \sum \nolimits _{k = 0}^{{N_t}} {\frac{{{{\left( { - 1} \right) }^k}}}{{k!}}} {\left( {\frac{a}{x}} \right) ^k}\), where \({N_t} \in \left\{ {1, \ldots ,\infty } \right\}\). Then, we obtain

$$\begin{aligned} {\mathrm{{\psi }}}&= \sum \limits _{k = 0}^{N_t} {\frac{{{{\left( { - 1} \right) }^k}}}{{k!}}} \int \limits _{{t_1}}^\infty {{{\left( {\frac{\beta }{x}} \right) }^k}\exp \left( { - \frac{{nx}}{{{\Omega _1}}}} \right) } dx\nonumber \\&= \sum \limits _{k = 0}^{N_t}{\frac{{{{\left( { - 1} \right) }^k}{\beta ^k}}}{{k!}}} {\left( {\frac{1}{{{t_1}}}} \right) ^{k - 1}}{E_k}\left( {\frac{{n{t_1}}}{{{\Omega _1}}}} \right) , \end{aligned}$$
(15)

where \({E_k}\left( \cdot \right)\) is the exponential integral function [9]. Substituting (15) into (14), we get the expression of \({\mathrm{{P}}}_{{x_1}}^{\mathrm{{error}}}\) as

$$\begin{aligned} {\mathrm{{P}}}_{{x_1}}^{\mathrm{{error}}}\!\! =\!\! 1\!\!-\!\! \sum \limits _{n = 0}^N {\sum \limits _{k = 0}^{{N_t}} {\frac{{{{\left( { - 1} \right) }^{n }}{{\left( { - 1} \right) }^k}{\beta ^k}}}{{k!}}} {\left( {\begin{array}{c}N\\ n\end{array}}\right) }}\frac{n}{{{\Omega _1}}}{\left( {\frac{1}{{{t_1}}}} \right) ^{k - 1}}\!\!\!\!{E_k}\left( {\frac{{n{t_1}}}{{{\Omega _1}}}}\right) \!\!. \end{aligned}$$
(16)

As we can see from (14), if the transmit power lies in a high region, it leads to \({t_1} = \frac{{{\gamma _{\mathrm{{th1}}}}}}{{{P_{\mathrm{{S}}}}^{ \approx \infty }\left( {{a_1} - {a_2}{\gamma _{\mathrm{{th1}}}}} \right) }} \rightarrow 0\). Thus, we apply [9, (3.324.1)] to obtain the final expression of \({\mathrm{{P}}}_{{x_1}}^{\mathrm{{error}}}\) as

$$\begin{aligned} {\mathrm{{P}}}_{{x_1}}^{\mathrm{{error}}} \approx 1 - \sum \limits _{n = 1}^N {{{\left( { - 1} \right) }^{n - 1}}{\left( {\begin{array}{c}N\\ n\end{array}}\right) }}\sqrt{\frac{{4n\beta }}{{{\Omega _1}}}} {K_1}\left( {\sqrt{\frac{{4n\beta }}{{{\Omega _1}}}} } \right) , \end{aligned}$$
(17)

where \({K_1}\left( \cdot \right)\) is the first-order modified Bessel function of the second kind.

3.2 Undecodable probability of \(x_2\)

In this paper, we consider two scenarios, the first scenario is perfect SIC, and the second one is imperfect SIC at both\({\mathrm {R_n}}\)and\({\mathrm{{D}}_2}\).

3.2.1 In case of perfect SIC

In this NOMA system, the SIC technique is carried out at \({\mathrm{{D}}_2}\) to remove signal \({x_1}\) before detecting its own message. In case SIC is perfect at \({\mathrm{{D}}_2}\) and \({\mathrm{{P}}}_{{x_2}}^{\mathrm{{error}}}\) is denoted as the event that the best relay or \({\mathrm{{D}}_2}\) cannot correctly decode symbol \({x_2}\) because the SNR is lower than the threshold value, \({\gamma _{\mathrm{{th2}}}} = 2^{\frac{2r_2}{1-\alpha }} - 1\) where \(r_2\) is the target data rate of \({\mathrm {D}}_2\). Then, the expression of \({\mathrm{{P}}}_{{x_2}}^{\mathrm{{error}}}\) is given by

$$\begin{aligned} {\mathrm{{P}}}_{{x_2}}^{\mathrm{{error}}}&= \Pr \left( {\min \left( {{\gamma _{1u2}},{\gamma _{2u2}}} \right) \le {\gamma _{\mathrm{{th2}}}}} \right) \nonumber \\&= 1 - \Pr \left( {{a_2}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2}> {\gamma _{\mathrm{{th2}}}},{a_2}{P_{\mathrm{{R}}}}{{\left| {{g_2}} \right| }^2} > {\gamma _{\mathrm{{th2}}}}} \right) . \end{aligned}$$
(18)

Substituting \({P_{\mathrm{{R}}}}\) from (3) into (18), we can rewrite as

$$\begin{aligned} {\mathrm{{P}}}_{{x_2}}^{\mathrm{{error}}} = 1 - \Pr \left( {X> \frac{{{\gamma _{\mathrm{{th2}}}}}}{{{a_2}{P_{\mathrm{{S}}}}}},\,Z > \frac{{{\gamma _{\mathrm{{th2}}}}\left( {1 - \alpha } \right) }}{{X2{a_2}\alpha \eta {P_{\mathrm{{S}}}}}}} \right) . \end{aligned}$$
(19)

Based on the conditional probability [15], we can express (19) as

$$\begin{aligned} {\mathrm{{P}}}_{{x_2}}^{\mathrm{{error}}} = 1 - \int \limits _a^\infty {\left[ {1 - {F_Z}\left( {\frac{b}{x}} \right) } \right] } {f_X}\left( x \right) dx, \end{aligned}$$
(20)

where \(a = \frac{{{\gamma _{\mathrm{{th2}}}}}}{{{a_2}{P_{\mathrm{{S}}}}}}\) and \(b = \frac{{{\gamma _{\mathrm{{th2}}}}\left( {1 - \alpha } \right) }}{{2{a_2}\alpha \eta {P_{\mathrm{{S}}}}}}\). By substituting the cumulative distribution functions (CDF) and probability density function (PDF) of X and Y into (20) and then using expanded Taylor series, we obtain the expression of \({\mathrm{{P}}}_{{x_2}}^{\mathrm{{error}}}\) as in (21).

$$\begin{aligned} {\mathrm{{P}}}_{{x_2}}^{\mathrm{{error}}}&= 1 - \sum \limits _{n = 1}^N {{{\left( { - 1} \right) }^{n - 1}}{\left( {\begin{array}{c}N\\ n\end{array}}\right) }} \frac{n}{{{\Omega _1}}}\int \limits _a^\infty {\exp \left( { - \frac{b}{{{\Omega _3}x}}} \right) } \exp \left( { - \frac{{nx}}{{{\Omega _1}}}} \right) dx \nonumber \\&= 1 - \sum \limits _{n = 1}^N {{{\left( { - 1} \right) }^{n - 1}}{\left( {\begin{array}{c}N\\ n\end{array}}\right) }}\frac{n}{{{\Omega _1}}}\sum \limits _{k = 0}^{N_t} {\frac{{{{\left( { - 1} \right) }^k}}}{{k!}}} {\left( {\frac{b}{{{\Omega _3}}}} \right) ^k}{\left( {\frac{1}{a}} \right) ^{k - 1}}{E_k}\left( {\frac{{na}}{{{\Omega _1}}}} \right) . \end{aligned}$$
(21)

Similar to undecodable probability of \(x_1\), when the transmit power lies in a high region, it will lead to \(a = \frac{{{\gamma _{\mathrm{{th2}}}}}}{{{a_2}{P_{\mathrm{{S}}}}^{ \approx \infty }}} \rightarrow 0\). Hence, the approximate expression of \({\mathrm{{P}}}_{{x_2}}^{\mathrm{{error}}}\) is given by

$$\begin{aligned} {\mathrm{{P}}}_{{x_2}}^{\mathrm{{error}}}\, \approx 1 - \sum \limits _{n = 1}^N {{{\left( { - 1} \right) }^{n - 1}}{\left( {\begin{array}{c}N\\ n\end{array}}\right) }}\sqrt{\frac{{4bn}}{{{\Omega _1}{\Omega _3}}}} {K_1}\left( {\sqrt{\frac{{4bn}}{{{\Omega _1}{\Omega _3}}}} } \right) . \end{aligned}$$
(22)

3.2.2 In case of imperfect SIC

In this scenario, the symbol \({x_1}\) is incompletely removed and becomes the interference. The SINRs of symbol \(x_2\) at \({\mathrm {R_b}}\) and \({\mathrm{{D}}_2}\) are respectively given as

$$\begin{aligned} {\gamma _{1u_2}} = \frac{{{a_2}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2}}}{{{a_1}{\rho _1}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2} + 1}}, \end{aligned}$$
(23)
$$\begin{aligned} {\gamma _{2u_2}} = \frac{{{a_2}{P_{\mathrm{{R}}}}{{\left| {{g_2}} \right| }^2}}}{{{a_1}{\rho _2}{P_{\mathrm{{R}}}}{{\left| {{g_2}} \right| }^2} + 1}}, \end{aligned}$$
(24)

where \(0 \le {\rho _i} \le 1\) with \(i \in \left\{ {1,2} \right\}\) denotes the level of residual interference due to the imperfect SIC at \({\mathrm{{R_b}}}\) and \({{\mathrm{{D}}}_2}\). Especially, \({\rho _i} = 1\) and \({\rho _i} = 0\) refer to the cases of without SIC and perfect SIC, respectively. From (23) and (24), we have the undecodable probability of \(x_2\) for the case of imperfect SIC shown in (25).

$$\begin{aligned} {\mathrm{{P}}}_{{x_2}}^{\mathrm{ISIC}} = \Pr \left[ {\min \left( {\frac{{{a_2}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2}}}{{{a_1}{P_{\mathrm{{S}}}}{\rho _1}{{\left| {{h_{1,b}}} \right| }^2} + 1}},\frac{{{a_2}{P_{\mathrm{{R}}}}{{\left| {{g_2}} \right| }^2}}}{{{a_1}{P_{\mathrm{{R}}}}{\rho _2}{{\left| {{g_2}} \right| }^2} + 1}}} \right) \le {\gamma _{\mathrm{{th2}}}}} \right] . \end{aligned}$$
(25)

After solving (25), we get the result as

$$\begin{aligned} {\mathrm{{P}}}_{x_2}^{\mathrm{ISIC}} = 1 - \int \limits _c^\infty {\left[ {1 - {F_Z}\left( {\frac{d}{x}} \right) } \right] } {f_X}\left( x \right) dx, \end{aligned}$$
(26)

where

$$\begin{aligned}&c= \frac{{{\gamma _{\mathrm{{th2}}}}}}{{{P_S}\left( {{a_2} - {a_1}{\rho _1}{\gamma _{\mathrm{{th2}}}}} \right) }},\\&d= \frac{{{\gamma _{\mathrm{{th2}}}}}}{{\phi {P_S}\left( {{a_2} - {a_1}{\rho _2}{\gamma _{\mathrm{{th2}}}}} \right) }}. \end{aligned}$$

Then, with some further manipulations, we can rewrite (26) into (27).

$$\begin{aligned} {\mathrm{{P}}}_{{x_2}}^{\mathrm{ISIC}}&= 1 - \sum \limits _{n = 1}^N {{{\left( { - 1} \right) }^{n - 1}}{\left( {\begin{array}{c}N\\ n\end{array}}\right) }} \frac{n}{{{\Omega _1}}}\int \limits _c^\infty {\exp \left( { - \frac{d}{{{\Omega _3}x}}} \right) } \exp \left( { - \frac{{nx}}{{{\Omega _1}}}} \right) dx \nonumber \\&= 1 - \sum \limits _{n = 1}^N {{{\left( { - 1} \right) }^{n - 1}}{\left( {\begin{array}{c}N\\ n\end{array}}\right) }} \frac{n}{{{\Omega _1}}}{\sum \limits _{k = 0}^{N_t}{\frac{{{{\left( { - 1} \right) }^k}}}{{k!}}{{\left( {\frac{d}{{{\Omega _3}}}} \right) }^k}\left( {\frac{1}{c}} \right) } ^{k - 1}}{{{E}}_k}\left( {\frac{{nc}}{{{\Omega _1}}}} \right) . \end{aligned}$$
(27)

In high-power region, we have the approximate expression of \({\mathrm{{P}}}_{{x_2}}^{\mathrm{ISIC}}\) as

$$\begin{aligned} {\mathrm{{P}}}_{{x_2}}^{\mathrm{ISIC}} \approx 1 - \sum \limits _{n = 1}^N {{{\left( { - 1} \right) }^{n - 1}}{\left( {\begin{array}{c}N\\ n\end{array}}\right) }} \sqrt{\frac{{4nd}}{{{\Omega _1}{\Omega _3}}}} {K_1}\left( {\sqrt{\frac{{4nd}}{{{\Omega _1}{\Omega _3}}}} } \right) . \end{aligned}$$
(28)

3.3 Ergodic capacity

3.3.1 In case of perfect SIC

In this section, we investigate the ergodic capacity of the system, the achievable sum rate of the NOMA downlink is given as

$$\begin{aligned} {{\bar{\mathrm{C}}}_{sum}} = {{\bar{\mathrm{C}}}}_{D_1}^{x_1}+{{\bar{\mathrm{C}}}}_{D_2}^{x_2}. \end{aligned}$$
(29)

The achievable capacity at the \({\mathrm {D}}_1\) is given as

$$\begin{aligned} {\mathrm{C}}_{\mathrm{D_1}}^{x_1} =&\frac{{1 - \alpha }}{2}{\log _2}( {1 + \min \left\{ {{\gamma _{1u1}},{\gamma _{2{u_1}}}} \right\} })\nonumber \\ =&\frac{{1 - \alpha }}{2}{\log _2}\left( {1+\min \left\{ {\frac{{{a_1}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2}}}{{{a_2}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2} + 1}},\frac{{{a_1}{P_{\mathrm{{R}}}}{{\left| {{g_1}} \right| }^2}}}{{{a_2}{P_{\mathrm{{R}}}}{{\left| {{g_1}} \right| }^2} + 1}}} \right\} }\right) . \end{aligned}$$
(30)

In practice, the amount of harvested energy at the relay is always small, hence the transmit power of relay is much lower than that of the source, and then the assumption that SINR at the destinations is lower than the SINR at the relay is reasonable.

$$\begin{aligned} {\frac{{{a_1}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2}}}{{{a_2}{P_{\mathrm{{S}}}}{{\left| {{h_{1,b}}} \right| }^2} + 1}}>\frac{{{a_1}{P_{\mathrm{{R}}}}{{\left| {{g_1}} \right| }^2}}}{{{a_2}{P_{\mathrm{{R}}}}{{\left| {{g_1}} \right| }^2} +1}}}. \end{aligned}$$

Hence, from (30) we have

$$\begin{aligned} {\mathrm{C}}_{\mathrm{D_1}}^{x_1}&=\frac{{1 - \alpha }}{2}{\log _2}\left( {1 + \frac{{{P_{\mathrm{{R}}}}{{\left| {{g_1}} \right| }^2}{a_1}}}{{{P_{\mathrm{{R}}}}{{\left| {{g_1}} \right| }^2}{a_2} + 1}}} \right) \nonumber \\&= \frac{{1 - \alpha }}{2}{\log _2}\left( {\frac{{\phi {P_S}{{\left| {{h_{1,b}}} \right| }^2}{{\left| {{g_1}} \right| }^2} + 1}}{{\phi {P_S}{{\left| {{h_{1,b}}} \right| }^2}{{\left| {{g_1}} \right| }^2}{a_2} + 1}}} \right) . \end{aligned}$$
(31)

With the instantaneous capacity is derived in (31), we obtain the ergodic capacity of the \({\mathrm{D_1}}\) as

$$\begin{aligned} {{\bar{\mathrm{C}}}_{D_1}^{x_1}}&={\mathbb {E}}\left\{ {\frac{{1 - \alpha }}{2}{{\log }_2}\left( {1 + \phi {P_S}{{\left| {{h_{1,b}}} \right| }^2}{{\left| {{g_1}} \right| }^2}} \right) } \right\} \nonumber \\&\quad -{\mathbb {E}}\left\{ {\frac{{1 - \alpha }}{2}{{\log }_2}\left( {1 + {a_2}\phi {P_S}{{\left| {{h_{1,b}}} \right| }^2}{{\left| {{g_1}} \right| }^2}} \right) } \right\} \nonumber \\&=\underbrace{\frac{{1\! -\! \alpha }}{{2\ln 2}}\int \limits _0^\infty {\frac{{1 \!-\! {F_Q}\left( \xi \right) }}{{1 + \xi }}} d\xi }_{{I_1}} - \underbrace{\frac{{1 \!-\! \alpha }}{{2\ln 2}}\int \limits _0^\infty {\frac{{1 \!-\! {F_P}\left( \xi \right) }}{{1 + \xi }}} d\xi }_{{I_2}}, \end{aligned}$$
(32)

where \(Q = \phi {P_S}{\left| {{h_{1,b}}} \right| ^2}{\left| {{g_1}} \right| ^2}\) and \(P = {a_2}\phi {P_S}{\left| {{h_{1,b}}} \right| ^2}{\left| {{g_1}} \right| ^2}\). Based on the condition probability we have the CDFs of Q and P, respectively.

$$\begin{aligned}&{F_Q}(\xi ) = 1- \sum \limits _{n = 1}^N {{{(-1)}^{n - 1}}\left( {\begin{array}{c}N\\ n\end{array}}\right) } \sqrt{\frac{{4n\xi }}{{\phi {P_S}{\Omega _1}{\Omega _2}}}} {K_1}\left( {\sqrt{\frac{{4n\xi }}{{\phi {P_S}{\Omega _1}{\Omega _2}}}} } \right) . \end{aligned}$$
(33)
$$\begin{aligned}&{F_P}(\xi ) =1 -\sum \limits _{n = 1}^N {{{\left( { - 1} \right) }^{n - 1}}\left( {\begin{array}{c}N\\ n\end{array}}\right) }\sqrt{\frac{{4n\xi }}{{{a_2}\phi {P_S}{\Omega _1}{\Omega _2}}}} {K_1}\left( {\sqrt{\frac{{4n\xi }}{{{a_2}\phi {P_S}{\Omega _1}{\Omega _2}}}} } \right) . \end{aligned}$$
(34)

With the help of the [9, eq. (7.811.5), (9.34.3)] and after some manipulation we have.

$$\begin{aligned}&{I_1} = \frac{1 - \alpha }{2\ln 2}\sum \limits _{n = 1}^N {{{\left( { - 1} \right) }^{n - 1}}\left( {\begin{array}{c}N\\ n\end{array}}\right) } G_{13}^{31}\left( {\left. {\frac{n}{{\phi {P_S}{\Omega _1}{\Omega _2}}}}\right| _{0}^0}_{,\frac{3}{4},\, - \frac{1}{4}} \right) . \end{aligned}$$
(35)
$$\begin{aligned}&{I_2} = \frac{1 - \alpha }{{2\ln 2}}\sum \limits _{n = 1}^N {{{\left( { - 1} \right) }^{n - 1}}\left( {\begin{array}{c}N\\ n\end{array}}\right) } G_{13}^{31}\left( {\left. \frac{n}{{a_2}\phi {P_S}{\Omega _1\Omega _2}}\right| _{0,}^0}_{\frac{3}{4},\, - \frac{1}{4}} \right) . \end{aligned}$$
(36)

The achievable capacity at the \({\mathrm {D}}_2\) is given as

$$\begin{aligned} C_{\mathrm{D_2}}^{{x_2}} = \frac{1 - \alpha }{2}\log _2\left( 1 + \min \{\gamma _{1u_1},\gamma _{2u_2}\}\right) . \end{aligned}$$
(37)

Similarly, we get the ergodic capacity of the \({\mathrm {D}}_2\) is given as

$$\begin{aligned} {\mathrm{{{\bar{C}}}}}_{\mathrm{D_2}}^{x_2}\, = \frac{1 - \alpha }{2\ln 2}\sum \limits _{n = 1}^N {{(-1)}^{n - 1}\left( {\begin{array}{c}N\\ n\end{array}}\right) } G_{13}^{31}\left( {\left. \frac{nb}{\Omega _1\Omega _3}\right| _{0,\frac{3}{4},\, - \frac{1}{4}}^0} \right) . \end{aligned}$$
(38)

Combining Eqs. (35), (36) and (41) we have the sum ergodic capacity of the EH-NOMA downlink relay system.

3.3.2 In case of imperfect SIC

The ergodic capacity of imperfect SIC is similar to that of perfect SIC.

$$\begin{aligned} {{\bar{\mathrm{C}}}_{\mathrm {sum}}^{\mathrm{I-SIC}}} = {{\bar{\mathrm{C}}}_{D_1}^{x_1}}+{{\bar{\mathrm{C}}}_{D_2}^{x_2/{\mathrm {I-SIC}}}}. \end{aligned}$$
(39)

where the \({{\bar{\mathrm{C}}}_{D_1}^{x_1}}\) is derived by Eqs. (30)–(36) in the above section.

The \({{\bar{\mathrm{C}}}_{D_2}^{x_2/{\mathrm {I-SIC}}}}\) can be given as

$$\begin{aligned} C_{\mathrm{D_2}}^{{x_2/{\mathrm {I-SIC}}}} = \frac{1 - \alpha }{2}\log _2\left( 1 + \min \{\gamma _{1,u_2},\gamma _{2,u_2}\}\right) , \end{aligned}$$
(40)

From (23) and (24) we have

$$\begin{aligned} C_{\mathrm{D_2}}^{{x_2/{\mathrm {I-SIC}}}}&= \frac{1 - \alpha }{2}\log _2\left[ 1 + \min \left( {\frac{{{a_2}{P_{\mathrm{{S}}}}{{\left| {{h_{1,n}}} \right| }^2}}}{{{a_1}{P_{\mathrm{{S}}}}{\rho _1}{{\left| {{h_{1,n}}} \right| }^2} + 1}},\frac{{{a_2}{P_{\mathrm{{R}}}}{{\left| {{g_2}} \right| }^2}}}{{{a_1}{P_{\mathrm{{R}}}}{\rho _2}{{\left| {{g_2}} \right| }^2} + 1}}} \right) \right] \nonumber \\&= \frac{1 - \alpha }{2}\log _2\left[ 1 + \left( \frac{{{a_2}{P_{\mathrm{{R}}}}{{\left| {{g_2}} \right| }^2}}}{{{a_1}{P_{\mathrm{{R}}}}{\rho _2}{{\left| {{g_2}} \right| }^2} + 1}} \right) \right] . \end{aligned}$$
(41)

Hence, the ergodic capacity of the \(x_2\) in case of imperfect SIC can be rewritten as

$$\begin{aligned} {{\bar{C}}_{\mathrm{D_2}}^{x_2/{\mathrm{I-SIC}}}}&=\frac{1-\alpha }{2}{\mathbb {E}}\left[ \log _2\left( 1+P_{\mathrm{R}}|g_2|^2(a_1\rho _2+a_2)\right) \right] \nonumber \\&\quad - \frac{1-\alpha }{2}{\mathbb {E}}\left[ \log _2\left( 1+a_1\rho _2 P_{\mathrm{R}}|g_2|^2\right) \right] \end{aligned}$$
(42)
$$\begin{aligned} {{{\bar{C}}}}_{\mathrm{D}_2}^{x_2/{\mathrm{I}{\text{-}}{\rm SIC}}}&=\underbrace{\frac{{1 - \alpha }}{{2\ln 2}}\int \limits _0^\infty \frac{{1 - F_U(u)}}{{1 + u }} du}_{{J_1}} - \underbrace{\frac{{1 - \alpha }}{{2\ln 2}}\int \limits _0^\infty {\frac{{1 - {F_V}(v)}}{{1 +v }}} dv }_{J_2} \end{aligned}$$
(43)

where \(U=\phi P_{\mathrm{S}}|h_{1,n}|^2|g_2|^2\kappa\), and \(V=a_1\rho _2\phi P_{\mathrm{S}}|h_{1,n}|^2|g_2|^2\) with \(\kappa =a_1\rho _2+a_2\) , \(\phi =\frac{2\alpha }{1-\alpha }\).

Based on the condition probability, the CDFs of U and V is respectively represented as.

$$\begin{aligned} {F_U}(u)&=1- \sum \limits _{n = 1}^N {{{\!\!(-1)}^{n - 1}}\left( {\begin{array}{c}N\\ n\end{array}}\right) } \sqrt{\frac{{4nu }}{{(a_1\rho _2+a_2)\phi {P_S}{\Omega _1}{\Omega _3}}}} {K_1}\!\!\left( {\sqrt{\frac{{4nu}}{{(a_1\rho _2+a_2)\phi {P_S}{\Omega _1}{\Omega _3}}}} } \right) . \end{aligned}$$
(44)
$$\begin{aligned} {F_V}(v)&=1- \sum \limits _{n = 1}^N {{{\!\!(-1)}^{n - 1}}\left( {\begin{array}{c}N\\ n\end{array}}\right) } \sqrt{\frac{{4nv }}{{a_1\rho _2\phi {P_S}{\Omega _1}{\Omega _3}}}} {K_1}\!\!\left( {\sqrt{\frac{{4nu}}{{a_1\rho _2\phi {P_S}{\Omega _1}{\Omega _3}}}} } \right) . \end{aligned}$$
(45)

Replace (44) and (45) into (43) we have

$$\begin{aligned} {J_1}&= \frac{1 - \alpha }{2\ln 2}\sum \limits _{n = 1}^N {{{\left( { - 1} \right) }^{n - 1}}\left( {\begin{array}{c}N\\ n\end{array}}\right) } G_{13}^{31}\left( {\left. {\frac{n}{{(a_1\rho _2+a_2)\phi {P_S}{\Omega _1}{\Omega _3}}}}\right| _{0}^0}_{,\frac{3}{4},\, - \frac{1}{4}} \right). \end{aligned}$$
(46)
$$\begin{aligned} {J_2}&= \frac{1 - \alpha }{2\ln 2}\sum \limits _{n = 1}^N {{{\left( { - 1} \right) }^{n - 1}}\left( {\begin{array}{c}N\\ n\end{array}}\right) } G_{13}^{31}\left( {\left. {\frac{n}{{a_1\rho _2\phi {P_S}{\Omega _1}{\Omega _3}}}}\right| _{0}^0}_{,\frac{3}{4},\, - \frac{1}{4}} \right) . \end{aligned}$$
(47)

Finally, we have the ergodic capacity of the system in imperfect SIC as

$$\begin{aligned} {{\bar{\mathrm{C}}}_{sum}^{I-SIC}} = I_1-I_2+J_1-J2. \end{aligned}$$
(48)

where \(I_1, I_2\) is given in Eqs. (35) and (36), respectively.

3.3.3 Ergodic capacity of OFDMA

In order to compare with orthogonal frequency division multiple access (OFDMA), which is a well-known high-capacity orthogonal multiple access (OMA) technique, the ergodic capacity of OFDMA is described in this section and the calculation result is compared in the following section.

Let \(\beta\) and \((1-\beta )\) Hz denote the bandwidth assigned for \({\mathrm {D}}_1\) and the remaining bandwidth assigned for \({\mathrm {D}}_2\), respectively, where \((0\le \beta \le 1)Hz\). By using Equ. (7.4) of [13], the sum capacity of the OMA system is given by

$$\begin{aligned} {\mathrm{C}}_{OMA}&=\frac{1-\alpha }{2}\beta \log _2\left[ 1+\min \left( \frac{P_{\mathrm{S}}|h_1|^2}{\beta }, \frac{P_{\mathrm{R}}|g_1|^2}{\beta }\right) \right] \nonumber \\&\quad +\frac{(1-\alpha )(1-\beta )}{2}\log _2\left[ 1+\min \left( \frac{P_{\mathrm{S}}|h_1|^2}{1-\beta }, \frac{P_{\mathrm{R}}|g_2|^2}{1-\beta }\right) \right] . \end{aligned}$$
(49)

4 Simulation results

In this section, several representative numerical results are provided to evaluate the impact of the number of relays, the channel gain (distance or path loss), and the imperfect SIC on the performance of NOMA systems with RF EH. The system parameters are as follows. The target data rated \({r_1} = 0.5\,\,\,(bpcu)\) and \({r_2} = 1\,\,\,(bpcu)\), the energy harvesting fraction \(\alpha = 0.3\). The channel gains \({\Omega _{\mathrm{{S}}{\mathrm{{R}}_{\mathrm{{b}}}}}} = {\Omega _{{\mathrm{{R}}_{\mathrm{{b}}}}{\mathrm{{D}}_{\mathrm{{1}}}}}} = 1\) and \({\Omega _{{\mathrm{{R}}_{\mathrm{{b}}}}{\mathrm{{D}}_{\mathrm{{2}}}}}} = 2\), and the energy conversion efficiency \(\eta = 1\). The power allocation coefficient satisfies \(\frac{{\Omega _{{\mathrm{{R}}_{\mathrm{{b}}}}{\mathrm{{D}}_{\mathrm{{1}}}}}}}{{\Omega _{{\mathrm{{R}}_{\mathrm{{b}}}}{\mathrm{{D}}_\mathrm{{2}}}}}} = \frac{{{a_2}}}{{{a_1}}}\) which is used to keep the trade-off between system throughput and user fairness.

Fig. 2
figure 2

Undecodable probability of \(x_1\) for the perfect SIC and different number of the relay nodes, N

Full size image

Figures 2 and 3 plot the undecodable probability of symbols \(x_1\) and \(x_2\), respectively for the case of perfect SIC. The result calculated by Eqs. (16) and (21) is named as Analysis-Exact, whereas the result calculated by using closed-form, Eqs. (17)and (22),is named as Analysis-Approximation. In this scenario, we consider the PRS scheme in which the number of relays is varied. It is recognized from Figs. 2 and 3 that the performance gain is increased by increasing the number of relays from 1 to 3. The reason is the selected best relay provides the best channel from the source to the relay in order to achieve better decoding performance as well as higher RF EH from the source in the first phase. We can see that the simulations results are in excellent agreement with the analytical results in all cases.

Fig. 3
figure 3

Undecodable probability of \(x_2\) for the perfect SIC and different number of the relay nodes, N

Full size image
Fig. 4
figure 4

Comparison of undecodable probability of \(x_2\) for the perfect and imperfect SIC

Full size image

Figure 4 shows the comparison of the undecodable probability of \(x_2\) versus the average SNR for the cases of perfect and imperfect SIC with the levels of residual interference, \(\rho\), at the best relay and \({\mathrm {D}}_2\) are \(\rho _1 = 0.01\) and \(\rho _2 = 0.04\), respectively. We should be reminded that \({\mathrm {D}}_1\) should decode only symbol \(x_1\), while \({\mathrm {D}}_2\) has to correctly decode \(x_1\) first, and then use the SIC to obtain \(x_2\). The undecodable probability of symbol \(x_2\) is plotted according to the average SNR in dB. The round and square markers indicate the simulation results of the perfect and the imperfect SIC, respectively. From Fig. 4, we can know that the remaining coefficient SIC significantly impacts the performance of \({\mathrm {D}}_2\). It is noticed that the simulation results are again in excellent agreement with the analytical results in all cases, which validates our mathematical models.

Fig. 5
figure 5

Impact of fraction of block time, \(\alpha\), on the undecodable probability of symbol \(x_2\)

Full size image

We also investigate the impact of fraction of block time, \(\alpha\), on the undecodable probability of symbol \(x_2\) with different number of relay nodes, and depict the results in Fig. 5. In this scenario, we assume that the SIC is perfect and the transmit power from the source \(P_{\mathrm{{S}}}=20\) dB. As shown in Fig. 5, there is the optimal \(\alpha\) in the sense of minimal undecodable probability of symbol \(x_2\), and these minimal undecodable probabilities as well as the optimal \(\alpha\) depend on the number of relay nodes, N. When N increases, the minimal undecodable probability becomes smaller while the optimal \(\alpha\) becomes larger. The reason is, when N increases, the SINR of symbol \(x_2\), \(\gamma _{1u_2}\), also increases because of the application of PRS. Thus, the data rate between the source and the best relay increases, and then the transmission time from the source to the best relay becomes shorter meaning the duration time for EH, \(\alpha\), is extended. With the larger \(\alpha\), the transmission power of the best relay is higher, and then the SINR of symbol \(x_2\) at \(D_2\) also becomes better. Consequently, according to (18), the undecodable probability of symbol \(x_2\) decreases when the SINR of both the best relay and \({\mathrm {D}}_2\) increases.

Fig. 6
figure 6

Ergodic capacity versus SNR with number of relay nodes \(N=1\) and perfect SIC

Full size image

In Fig. 6, we plot the ergodic capacity of \({\mathrm {D}}_1\) and \({\mathrm {D}}_2\) versus \(E_b/N_0\). We can see that the analysis result of the ergodic capacity for \({\mathrm {D}}_1\) matches excellently with the simulation result at the high SNR. The reason is that, we changed the instantaneous capacity of the information symbol \(x_1\) from (30) into (31) under condition of the medium and high region power of the source. In addition, the upper bound curve of the ergodic capacity for \({\mathrm {D}}_2\) and sum of the ergodic capacity for all users are close to the simulation results due to approximation of the CDF of the information symbol \(x_2\) from (22).

Fig. 7
figure 7

Sum of ergodic capacity of two users with PRS scheme when the number of relays changes

Full size image

In Fig. 7, the impact of the number of relay nodes on SWIPT-NOMA is depicted through the sum of ergodic capacity of \({\mathrm {D}}_1\) and \({\mathrm {D}}_2\), for several number of relays, \(N = 1, 2, 3\). We can undestand that, the sum of ergodic capacity can be improved by setting up more number of relays. However, the sum of ergodic capacity is just slightly improved when the number of relay nodes is high.

Compared with perfect SIC, the ergodic sum capacity of imperfect SIC is lower, and the gap of them increases when the \(E_b/N_0\) increases. The reason is, while \(E_b/N_0\) increasing, the interference term due to imperfect SIC increases, therefore the SINR as well as the ergodic capacity slowly increase.

The ergodic capacity of OMA-EH is also depicted in Fig. 7. For OMA, the equal power and equal bandwidth are applied for each user. As shown in Fig. 7, in case of perfect SIC, NOMA outperforms OMA because the SNR of OMA is higher than that of NOMA, however the bandwidth is just a half of NOMA and the capacity is linear with bandwidth. In case of imperfect SIC, the OMA outperforms NOMA when\(\frac{E_b}{N_0}\)is high because of extremely decreasing of SINR of\(x_2\)

5 Conclusions

In this paper, we have analyzed the influence of EH technique in NOMA relay networks. The PRS scheme was applied to improve the system performance. The closed-form expression of the probability of unsuccessful decoding symbol \(x_1\), \(x_2\) and ergodic capacity were derived. The theoretical analysis was verified by the Monte Carlo simulation method. From the theoretical and simulation results, some important conclusions can be summarized as follows. (1) The represented simulation results verified the correctness of our mathematical analysis. (2) The undecodable probability and the ergodic capacity were improved by increasing the number of relay nodes, however the large number of relay nodes is unnecessary for significantly improving the system performance. (3) There is the optimal duration time of EH for the minimal undecodable probability and it is directly proportional to the number of relay nodes. (4) The proposed system was analyzed in both perfect and imperfect SIC, and compared with OFDMA system, the impact of residual interference was discussed.

As future works, we will apply NOMA into multiple-relay multiple-antenna EH relay networks and analyze the network performance over Nakagami-m fading channel or double Rayleigh fading channel. In addition, we will investigate the impact of imperfect CSI on the performance of relay selection method.