A novel scheme inspired by the compute-and-forward relaying strategy for the multiple access relay channel

Abstract

This paper proposes a novel scheme for the slow block fading Gaussian multiple access relay channel inspired by the compute-and-forward (CoF) relaying strategy. The CoF relaying strategy exploits interference to obtain significantly higher rates between users in a network by decoding linear functions of the transmitted messages. Unlike other approaches in the literature, our approach is valid for any number of transmitters and, most importantly, it only requires channel state information at the receiver side, while it still attains similar or higher rates than the other approaches found in the literature.

1 Introduction

It is well known that for point-to-point communications it is optimal to convert a noisy channel into a reliable channel by means of channel coding and to compress the information source into bits before using such reliable channel.

For that reason, when designing a communication network, the usual approach is to extend the classical strategy for point-to-point communications, i.e., route the messages through the network by establishing reliable channels between each pair of users. This approach has led to the successful deployment of the Internet and cellular telephone networks, among others.

Nevertheless, in a narrowband wireless network where all the users share the same chunk of spectrum, messages sent by a single transmitter are not only heard by the desired receiver, but also by all the other neighboring users. Likewise, the signal captured by a single receiver not only contains the signal sent by the intended transmitter, but a noisy linear combination of the signals sent by all other nearby transmitters.

One possible approach for extracting the desired signal from the received linear combination is to treat the unwanted signals as noise (interference). However, if the number of active nearby transmitters increases, so does the interference, and the data rate available to each transmitter decreases accordingly.

Another approach for designing narrowband wireless networks is to share the available time among all the transmitters and transmit by turns. Clearly, as the number of active transmitters increases the data rate available to each transmitter decreases.

This paper is based on an alternative approach: rather than trying to extract one message from the noisy combination of transmitted signals, the receiver attempts to reliably decode a function of the transmitted messages. Given that the receiver can decode sufficiently many independent functions, it can obtain the sent messages by solving the resulting equation system. This approach is known as computation coding, which was introduced in [1], and is essentially based on harnessing the interference caused by other users.

Typical use cases that can be modeled as wireless networks include, among others, the cellular telephone uplink network, wireless sensor networks, or wireless Multiple-Input Multiple-Output networks, where each user has more than one antenna.

In this context, we are going to design a novel scheme that follows the computation coding approach and will be applied to the Multiple Access Relay Channel (MARC). The MARC is an information-theoretic channel model that can be used to describe a wide variety of wireless communication scenarios.

Fig. 1

LTE with relays

The most significant use case in nowadays networks is the LTE Advanced mobile communication standard (see, e.g., [2]). This standard supports the use of relays and in particular, inband relays, where the link between the base station and the relay node is on the same carrier frequency as the link between the relay node and the users (see Fig. 1). The reasons for using relays in cellular telephony networks are threefold: increase network capacity, extend the network coverage, and provide easier methods of extending coverage during the early roll-out without the need of installing backhaul or large masts. In conclusion, the LTE Advanced standard can be modeled as a MARC when it uses relay nodes.

1.1 Context

The idea of harnessing the interference caused by other users fits particularly well in network coding techniques, where users send functions of messages that they receive. Although network coding techniques were initially introduced in [3] for wired networks, they have been extended successfully to wireless networks (see, e.g., [1, 4,5,6,7,8,9,10]).

The MARC has been extensively studied in the literature. In the MARC, several transmitters send data to a single common destination aided by an intermediate relay. The general setup of the MARC will be precisely stated in Sect. 2. In the past, different relaying strategies such as Decode-and-Forward (DF), Compress-and-Forward (CF), and Amplify-and-Forward (AF) have been applied to the MARC (see, e.g., [11, 12] and references therein). There are also a number of contributions dealing with practical coding schemes for the MARC considering the DF, CF, and AF relaying strategies (see, e.g., [13] and references therein).

Recently, El Soussi et al. [14] derived theoretical achievable data transmission rates for the MARC based on the compute-and-forward (CoF) relaying strategy (see [7]). This coding scheme can be seen as a particular case of the general CoF approach of Nazer and Gastpar in [7]. It is important to mention that both the coding schemes of [14] and [7] are based on an asymptotic sequence of lattices that are simultaneously good for covering, quantization and channel coding (see [15, Theorem 5]). There have also recently been contributions dealing with the design of practical codes for the CoF relaying strategy (see, e.g., [10, 16,17,18,19,20,21,22]). These codes would allow an implementation of the coding scheme proposed in [14] for the MARC.

1.2 Outline

The purpose of this paper is to propose a novel coding scheme for the slow block fading¹ Gaussian MARC. More precisely, in Sect. 3 we will present a scheme based on infinite dimensional lattices, only requiring Channel State Information (CSI) at the receiver sides (R-CSI), and which is valid for an arbitrary number of transmitters. We finally show in Sect. 5 that the data rates achieved by our approach are similar or even slightly improve the achievable data rates of different approaches found in the literature, but without requiring a full knowledge of the CSI.

2 Problem statement

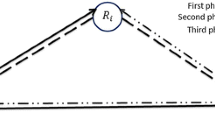
The general MARC studied in this paper is depicted in Fig. 2. Consider that M spatially separated sources want to transmit message vectors $\mathbf{w }_1, \mathbf{w }_2,\ldots ,\mathbf{w }_M$ of length nR to a destination aided by a single relay. Transmitter j is willing to convey a complex vector

$$\begin{aligned} \mathbf{w }_j\in \big \lbrace \{0,1,\ldots , L-1\}+i\{0,1,\ldots , L-1\}\big \rbrace ^{nR}\quad 1\le j\le M \end{aligned}$$

(1)

of $2nR \log _2 L$ information bits to the destination (symmetric-rate), where $L>1$ is a prime number. The spectral efficiency $\rho$ of the communication system is therefore $\rho = 2R \log _2 L$ bits per complex dimension or channel uses.

Fig. 2

MARC with M users and a single relay

The transmitted signals are bandlimited and the wireless channel considered in this paper is modeled as the well known slow block fading Gaussian channel (see, e.g., [24, pp. 99–100] or [25, p. 289]) with path loss attenuation ([24, Sect. 2.5]).

According to the CoF paradigm, the information of the M sources is sent simultaneously using n complex channel uses (see [7]), where n is small enough to consider slow block fading. Let $E_s$ be the average energy per transmitted complex dimension.

Each transmitter is provided with an encoder ${\mathcal {E}}_1, {\mathcal {E}}_2,\ldots ,{\mathcal {E}}_M$, so that the transmitted complex symbols are $\mathbf{x }_{j}={\mathcal {E}}_j(\mathbf{w }_j)\in {\mathbb {C}}^n$, $1\le j\le M$. The sets of sufficient statistics at the relay and at the destination to detect the information sent by the M sources are $\mathbf{y }_r,\;\mathbf{y }_d\in {\mathbb {C}}^{n}$ respectively, and their entries are given in terms of the transmitted complex symbols by

$$\begin{aligned} \mathbf{y }_{r}&= \left( \sum _{j=1}^M h_{j,r} \mathbf{x }_{j}\right) +\mathbf{z }_{r}, \end{aligned}$$

(2)

$$\begin{aligned} \mathbf{y }_{d}&= \left( \sum _{j=1}^M h_{j,d} \mathbf{x }_{j}\right) +\mathbf{z }_{d} \end{aligned}$$

(3)

where the real and imaginary parts of the transmitted symbols are considered independent.

The channel noise samples, which are the entries of $\mathbf{z }_{r}$ and $\mathbf{z }_{d}$, are modeled as independent and identically distributed (i.i.d.) circularly symmetric complex Gaussian random variables, with variance $N_0$ (zero mean).

In expressions (2) and (3), $h_{j,r}$ and $h_{j,d}$ denote the complex channel coefficient from user j to the relay or the destination respectively, and can be modeled as

$$\begin{aligned} h_{j,r} := \gamma \;d_{j,r}^{-\kappa /2}, \qquad h_{j,d} := \gamma \;d_{j,d}^{-\kappa /2} \qquad 1\le j\le M, \end{aligned}$$

(4)

where $\kappa$ is the path loss exponent, $d_{j,r}$ and $d_{j,d}$ are the distances between user j and the relay or the destination respectively, and $\gamma$ is a circularly symmetric complex Gaussian random variable with variance $2\beta ^2$ (zero mean), that is, the probability density function of the complex random variable $\gamma$ is

$$\begin{aligned} f_\gamma (x)=\frac{1}{\pi \beta ^2} e^{-\frac{|x|^2}{\beta ^2}}, \qquad x\in {\mathbb {C}}. \end{aligned}$$

(5)

Observe that the relay receives $\mathbf{y }_r$, which is given in (2). Since the relay is allowed to cooperate with the destination with another n complex channel uses, the vector $\mathbf{x }_r\in {\mathbb {C}}^n$ is sent to the destination. Consequently, the destination receives from the relay

$$\begin{aligned} \mathbf{y }_{r,d}= h_{r,d} \; \mathbf{x }_r+\mathbf z _{r,d}, \end{aligned}$$

(6)

where $\mathbf{z }_{r,d}$ is again a vector of noise realizations with complex entries given by independent and identically distributed (i.i.d.) circularly symmetric Gaussian random variables, with zero mean and variance $N_0$, and $h_{r,d} = \gamma \;d_{r,d}^{-\kappa /2}$ is the channel coefficient from the relay to the destination, being $\gamma$ the random variable with the probability density function given in (5) and $d_{r,d}$ the distance between the relay and the destination.

Finally, the destination is provided with a decoder so that it can obtain an estimate $\left( \widehat{\mathbf{w }}_1, \widehat{\mathbf{w }}_2,\ldots ,\widehat{\mathbf{w }}_M\right)$ of the transmitted messages $\left( \mathbf{w }_1, \mathbf{w }_2,\ldots ,\mathbf{w }_M\right)$ from $\mathbf{y }_d$ and $\mathbf{y }_{r,d}$.

In this paper, the decoder at the destination is designed to operate in two steps: (1) it decodes M independent linear combinations of the transmitted messages through $\mathbf{y }_d$ and $\mathbf{y }_{r,d}$. (2) it solves the resulting equation system in order to recover the sought transmitted messages. This decoding scheme will be further explained in Sect. 3.

In this scenario, we define the probability of error $P_e$ as

$$\begin{aligned} P_e := {\text {Pr}}\left\{ \left( \widehat{\mathbf{w }}_1, \widehat{\mathbf{w }}_2,\ldots ,\widehat{\mathbf{w }}_M\right) \ne \left( \mathbf{w }_1, \mathbf{w }_2,\ldots ,\mathbf{w }_M\right) \right\} , \end{aligned}$$

(7)

where ${\text {Pr}}\{\cdot \}$ denotes the probability measure.

3 Related work

We begin this Section by reviewing two main results related to achievable data transmission rates for the Gaussian Multiple Access Channel (MAC) using the CoF relaying strategy.

3.1 CoF on a MAC

The goal of the CoF relaying strategy is to recover a linear combination of the transmitted messages $\mathbf{w }_1, \mathbf{w }_2,\ldots ,\mathbf{w }_M$. The linear combination (real and imaginary parts) with coefficient vector ${{\varvec{\alpha }}}=(\alpha _1,\alpha _2,\ldots ,\alpha _M)^\top \in \{{\mathbb {Z}}+i{\mathbb {Z}}\}^M$ is given by

$$\begin{aligned} \mathbf{u }^{\text {Re}}({{\varvec{\alpha }}})&:=\left( \sum _{j=1}^M \left( {\text {Re}}(\alpha _j){\text {Re}}(\mathbf{w }_j)-{\text {Im}}(\alpha _j){\text {Im}}(\mathbf{w }_j)\right) \right) \mod L \end{aligned}$$

(8)

$$\begin{aligned} \mathbf{u }^{\text {Im}}({{\varvec{\alpha }}})&:=\left( \sum _{j=1}^M \left( {\text {Im}}(\alpha _j){\text {Re}}(\mathbf{w }_j)+{\text {Re}}(\alpha _j){\text {Im}}(\mathbf{w }_j)\right) \right) \mod L \end{aligned}$$

(9)

(1) Recovering a single linear combination From [7, Theorem 3–4] we get that for a complex valued M-user Gaussian MAC with channel coefficient vector $\mathbf{h }\in {\mathbb {C}}^M$, a linear combination with coefficient vector ${{\varvec{\alpha }}}\in \{{\mathbb {Z}}+i{\mathbb {Z}} \}^M$ can be recovered with arbitrarily low probability of error so long as the spectral efficiency of each transmitter does not exceed $\rho _{{\text {CoF}}}(\mathbf{h },{{\varvec{\alpha }}})$ bits per channel use, where

$$\begin{aligned} \rho _{{\text {CoF}}}(\mathbf{h },{{\varvec{\alpha }}}):= \log _2^+\left( \left( \Vert {{\varvec{\alpha }}}\Vert ^2-\frac{E_s |\mathbf{h }^*{{\varvec{\alpha }}}|^2}{N_0 + E_s\Vert \mathbf{h } \Vert ^2} \right) ^{-1}\right) , \end{aligned}$$

(10)

$\log _2^+(x):=\max \left\{ \log _2(x),0\right\}$ and $\Vert \cdot \Vert$ denotes euclidean norm.

(2) Recovering multiple linear combinations Similarly, from [26, Theorem 2], using the Successive CoF Cancellation, for a complex valued M-user Gaussian MAC with channel coefficient vector $\mathbf{h }\in {\mathbb {C}}^M$, two linear combinations with coefficient vectors ${{\varvec{\alpha }}}_1,{{\varvec{\alpha }}}_2\in \{{\mathbb {Z}}+i{\mathbb {Z}} \}^M$ can be recovered with arbitrarily low probability of error so long as the spectral efficiency of each transmitter does not exceed $\rho _{{\text {Opt}}}(\mathbf{h },{{\varvec{\alpha }}}_1,{{\varvec{\alpha }}}_2)$ bits per complex dimension, where

$$\begin{aligned} \rho _{{\text {Opt}}}(\mathbf{h },{{\varvec{\alpha }}}_1,{{\varvec{\alpha }}}_2):= \max \left\{ \rho _{1,2}(\mathbf{h },{{\varvec{\alpha }}}_1,{{\varvec{\alpha }}}_2),\rho _{2,1}(\mathbf{h },{{\varvec{\alpha }}}_1,{{\varvec{\alpha }}}_2)\right\} , \end{aligned}$$

(11)

and

$$\begin{aligned} \rho _{1,2}(\mathbf{h },{{\varvec{\alpha }}}_1,{{\varvec{\alpha }}}_2)&:=\min \left\{ \rho _{{\text {CoF}}}(\mathbf{h },{{\varvec{\alpha }}}_1) ,\rho _{\text {SCoF}}(\mathbf{h },{{\varvec{\alpha }}}_1,{{\varvec{\alpha }}}_2) \right\} , \end{aligned}$$

(12)

$$\begin{aligned} \rho _{2,1}(\mathbf{h },{{\varvec{\alpha }}}_1,{{\varvec{\alpha }}}_2)&:= \min \left\{ \rho _{{\text {CoF}}}(\mathbf{h },{{\varvec{\alpha }}}_2) ,\rho _{\text {SCoF}}(\mathbf{h },{{\varvec{\alpha }}}_2,{{\varvec{\alpha }}}_1) \right\} , \end{aligned}$$

(13)

with

$$\begin{aligned} \rho _{\text {SCoF}}(\mathbf{h },{{\varvec{\alpha }}}_1,{{\varvec{\alpha }}}_2):= \log _2^+\left( \left( \Vert {{\varvec{\alpha }}}_2\Vert ^2-\frac{({{\varvec{\alpha }}}_1^\top {{\varvec{\alpha }}}_2)^2}{\Vert {{\varvec{\alpha }}}_1\Vert ^2}-\frac{E_s \left| \left( \mathbf{h }-\frac{{{\varvec{\alpha }}}_1^\top \mathbf{h }}{\Vert {{\varvec{\alpha }}}_1\Vert ^2}{{\varvec{\alpha }}}_1\right) ^*{{\varvec{\alpha }}}_2\right| ^2}{N_0 + E_s\left( \Vert \mathbf{h }\Vert ^2-\frac{|{{\varvec{\alpha }}}_1^\top \mathbf{h }|^2}{\Vert {{\varvec{\alpha }}}_1 \Vert ^2}\right) } \right) ^{-1}\right) . \end{aligned}$$

(14)

Observe that the Successive CoF Cancellation technique is a generalization of the Successive Interference Cancellation strategy and therefore it can only lead to improvements in the rate for decoding multiple messages.

Finally, it is important to mention that these two results are asymptotic as $n\rightarrow \infty$, and based on using a sequence of lattices that are simultaneously good for covering, quantizing and channel coding over a Gaussian noise channel (see [15, Theorem 5]).

3.2 CoF on a MARC

Let us now focus on the MARC. First of all, as described in [11, 12] and references therein, one can verify that there are numerous contributions that provide different communication approaches for the MARC. These approaches are basically based on the DF, CF, and AF relaying strategies. Recently, El Soussi et al. [14] published a new approach for the same MARC scenario, but based on the CoF relaying strategy, and there they compare their performance with all the other cited contributions of the literature.

Although there are other recent contributions dealing with related multiaccess models using the CoF relaying strategy, these models do not consider the same communication scenario and therefore, they cannot be directly compared to our approach. For instance, in [27] they consider that the relay and the transmitters can send information simultaneously, in [28, 29] they send analog information and the destination tries to recover with the lowest possible distortion, and in [30] they consider that several relays are available and solve the problem of getting linearly dependent equations across the network.

The most similar model to our scenario is [14]. In such approach, both the relay and the destination choose jointly the linear combination coefficients that maximize the overall throughput. In particular, the relay chooses coefficient $\tilde{{{\varvec{\alpha }}}_r}$ and the destination chooses coefficient $\tilde{{{\varvec{\alpha }}}_d}$ such that

$$\begin{aligned} \tilde{{{\varvec{\alpha }}}_r},\tilde{{{\varvec{\alpha }}}_d} ={\mathop {{\mathop {{{\mathrm{arg\,max}}}}\limits _{{{\varvec{\alpha }}}_r,{{\varvec{\alpha }}}_d \in \{{\mathbb {Z}}+i{\mathbb {Z}} \}^2}}}\limits _{{{\varvec{\alpha }}}_r,{{\varvec{\alpha }}}_d{\text { lin.indep.}}}} \min \left\{ \rho _{{\text {CoF}}}(\mathbf{h }_r,{{\varvec{\alpha }}}_r), \rho _{{\text {CoF}}}(\mathbf{h }_d,{{\varvec{\alpha }}}_d), \log _2\left( 1+\frac{E_s}{N_0}|h_{r,d}|^2 \right) \right\} . \end{aligned}$$

(15)

With these coefficients, the destination correctly recovers the transmitted messages at a rate at most

$$\begin{aligned} \min \left\{ \rho _{{\text {CoF}}}(\mathbf{h }_r, \tilde{{{\varvec{\alpha }}}_r}),\rho _{{\text {CoF}}}(\mathbf{h }_d, \tilde{{{\varvec{\alpha }}}_d}), \log _2\left( 1+\frac{E_s}{N_0}|h_{r,d}|^2 \right) \right\} \end{aligned}$$

(16)

bits per complex dimension. This result is summarized in Proposition 1 (from [14]):

Proposition 1

For a complex valued 2-user Gaussian MARC with channel coefficient vector$\mathbf{h }_r:=(h_{1,r},h_{2,r})^\top$from the transmitters to the relay, channel coefficient vector$\mathbf{h }_d:=(h_{1,d},h_{2,d})^\top$from the transmitters to the destination, and channel coefficient$h_{r,d}$from the relay to the destination, the transmitted messages$\mathbf{w }_1$and$\mathbf{w }_2$can be reliably recovered so long as the spectralefficiency of each transmitter does not exceed²

$$\begin{aligned} {\mathop {\mathop {\max }\limits _{{{\varvec{\alpha }}}_r,{{\varvec{\alpha }}}_d \in \{{\mathbb {Z}}+i{\mathbb {Z}} \}^2}}\limits _{{{\varvec{\alpha }}}_r,{{\varvec{\alpha }}}_d{\text { lin.indep.}}}}\min \left\{ \rho _{{\text {CoF}}}(\mathbf{h }_r,{{\varvec{\alpha }}}_r),\rho _{{\text {CoF}}}(\mathbf{h }_d,{{\varvec{\alpha }}}_d), \log _2\left( 1+\frac{E_s}{N_0}|h_{r,d}|^2 \right) \right\} \end{aligned}$$

(17)

bits per channel use.

It is important to mention that, in order to solve (17), this approach requires that the relay and the destination have full CSI knowledge: this means that both the relay and the destination need to know $\mathbf{h }_r$, $\mathbf{h }_d$, and $h_{r,d}$, which is the major drawback of this approach. As we introduce next, the main contribution of this paper is to propose an approach that avoids this drawback.

4 Proposed approach

In this section, we propose a theoretical approach based on the CoF relaying strategy that only requires R-CSI and that is valid for an arbitrary number of transmitters M. Our approach is based on the theoretical results that have been introduced in Sect. 3. This section is devoted to explain and justify of our main result, which is later summarized in Proposition 2.

Our theoretical approach is as follows: M transmitters send their codewords simultaneously³. The relay computes the linear combination $\widehat{{{\varvec{\alpha }}}_r}\in \{{\mathbb {Z}}+i{\mathbb {Z}} \}^M$ that maximizes $\rho _{{\text {CoF}}}(\mathbf{h }_r,\widehat{{{\varvec{\alpha }}}_r})$, and forwards it to the destination in a second transmission period. The destination uses Successive CoF Cancellation to obtain the best M independent linear combinations through the first transmission period, and gets from the relay the additional $(M+1)$th linear combination (which of course will be linearly dependent). Finally, the destination chooses the best M linearly independent equations from the set of $M+1$ linear combinations, so that the linear combination coming from the relay might be chosen or might not.

Accordingly, observe that there are two different possibilities to recover the transmitted messages at the destination: (i) to use the help of the relay or (ii) disregard the information sent by the relay. Without loss of generality and for concision in the mathematical expressions, we explain those possibilities for the case where there are $M=2$ transmitters.

We next find the maximum achievable spectral efficiency of possibility (i):

• 1. The relay chooses the linear combination coefficient $\widehat{{{\varvec{\alpha }}}_r}$ that maximizes the achievable spectral efficiency of the transmitters with the CoF relaying strategy, that is,

  $$\begin{aligned} \widehat{{{\varvec{\alpha }}}_r}= {\mathop {{{\mathrm{arg\,max}}}}\limits _{{{{\varvec{\alpha }}}\in \{{\mathbb {Z}}+i{\mathbb {Z}} \}^2}}} \rho _{{\text {CoF}}}(\mathbf{h }_r,{{\varvec{\alpha }}}). \end{aligned}$$

  (18)

• 2. The relay sends to the destination the linear combination⁴$\mathbf{u }^{\text {Re}}(\widehat{{{\varvec{\alpha }}}_r})+i \mathbf{u }^{\text {Im}}(\widehat{{{\varvec{\alpha }}}_r})$. The destination will be able to correctly recover this linear combination as long as the spectral efficiency of the relay is at most

  $$\begin{aligned} \rho _r=\min \left\{ \rho _{{\text {CoF}}}(\mathbf{h }_r,\widehat{{{\varvec{\alpha }}}_r}),\;\; \log _2\left( 1+\frac{E_s}{N_0}|h_{r,d}|^2 \right) \right\} . \end{aligned}$$

  (19)

• 3. The destination chooses a linear combination coefficient $\widehat{{{\varvec{\alpha }}}_d}$ that is linearly independent to $\widehat{{{\varvec{\alpha }}}_r}$ and that maximizes the achievable spectral efficiency of the transmitters with the CoF relaying strategy, that is,

  $$\begin{aligned} \widehat{{{\varvec{\alpha }}}_d}= {\mathop {\mathop {{{\mathrm{arg\,max}}}}\limits _{{{\varvec{\alpha }}}\in \{{\mathbb {Z}}+i{\mathbb {Z}} \}^2}}\limits _ {{{\varvec{\alpha }}},\widehat{{{\varvec{\alpha }}}_r}{\text { lin.indep.}}}} \rho _{{\text {CoF}}}(\mathbf{h }_d,{{\varvec{\alpha }}}). \end{aligned}$$

  (20)

  Observe that the destination is able to correctly decode the linear combination $\mathbf{u }^{\text {Re}}(\widehat{{{\varvec{\alpha }}}_d})+i \mathbf{u }^{\text {Im}}(\widehat{{{\varvec{\alpha }}}_d})$ as long as the spectral efficiency of the transmitters is at most

  $$\begin{aligned} \rho _d= \rho _{{\text {CoF}}}(\mathbf{h }_d,\widehat{{{\varvec{\alpha }}}_d}). \end{aligned}$$

  (21)

• 4. With this strategy, the destination can correctly obtain the transmitted messages at a rate at most

  $$\begin{aligned} \rho _1=\min \left\{ \rho _r, \rho _d \right\} . \end{aligned}$$

  (22)

Similarly, we find the maximum achievable spectral efficiency of possibility (ii):

• 1. The destination chooses the best two linear combination coefficients $\widehat{{{\varvec{\alpha }}}_1}$ and $\widehat{{{\varvec{\alpha }}}_2}$ that maximize the achievable spectral efficiency of the transmitters, that is,

  $$\begin{aligned} \widehat{{{\varvec{\alpha }}}_1},\widehat{{{\varvec{\alpha }}}_2} ={\mathop {\mathop {{{\mathrm{arg\,max}}}}\limits _{{{\varvec{\alpha }}}_1, {{\varvec{\alpha }}}_2\in \{{\mathbb {Z}}+i{\mathbb {Z}} \}^2}}\limits _ {{{\varvec{\alpha }}}_1,{{\varvec{\alpha }}}_2{\text { lin.indep.}}}} \rho _{{\text {Opt}}}(\mathbf{h }_d,{{\varvec{\alpha }}}_1,{{\varvec{\alpha }}}_2). \end{aligned}$$

  (23)

  Observe that the destination can correctly decode the linear combinations $\mathbf{u }^{\text {Re}}(\widehat{{{\varvec{\alpha }}}_j})+i \mathbf{u }^{\text {Im}}(\widehat{{{\varvec{\alpha }}}_j})$, $j\in \{1,2\}$ as long as the spectral efficiency of the transmitters is at most

  $$\begin{aligned} \rho _2= \rho _{{\text {Opt}}}(\mathbf{h }_d,\widehat{{{\varvec{\alpha }}}_1}, \widehat{{{\varvec{\alpha }}}_2}). \end{aligned}$$

  (24)

Finally, the highest achievable spectral efficiency of our approach is given by the best of the two described possibilities, that is, $\max \{\rho _1,\rho _2\}$ bits per complex dimension. The achievable rate of our approach is summarized in the following proposition:

Proposition 2

For a complex valued 2-user Gaussian MARC with channel coefficient vector$\mathbf{h }_r:=(h_{1,r},h_{2,r})^\top$from the transmitters to the relay, channel coefficient vector$\mathbf{h }_d:=(h_{1,d},h_{2,d})^\top$from the transmitters to the destination, and channel coefficient$h_{r,d}$from the relay to the destination, the transmitted messages$\mathbf{w }_1$and$\mathbf{w }_2$can be reliably recovered so long as the spectral efficiency of each transmitter does not exceed

$$\begin{aligned} \max \{\rho _1,\rho _2\} \end{aligned}$$

(25)

bits per channel use.

Observe that our approach only requires that the relay knows $\mathbf{h }_r$, and the destination only needs to know $\mathbf{h }_d$ and $h_{r,d}$, that is, R-CSI.

5 Comparison and numerical results

In this section we show a comparison between our approach and the approaches found in the literature. To that end, we compare the spectral efficiency achieved by our approach (Proposition 2) with that achieved by the one proposed in [14] (see Proposition 1).

Note that since in [14] one can find the comparison of Proposition 1 with other approaches based on the DF, CF, and AF relaying strategies, our approach can also be compared with the latters through [14].

In Fig. 3 we show this comparison for different relative positions of the relay and the destination with respect to the transmitters. In this figure we show the average spectral efficiency (measured in bits per channel use or bps/Hz) for each approach. In order to obtain these plots, for each value of $E_s/N_0$, we have generated 10, 000 independent sets of channel coefficients ($\mathbf{h }_r=(h_{1,r},h_{2,r})^\top$, $\mathbf{h }_d=(h_{1,d},h_{2,d})^\top$, and $h_{r,d}$) according to the probability density function of a circularly symmetric complex Gaussian random variable (5). For each set of channel coefficients, we have computed (17)—Proposition 1, and (25)—Proposition 2, and finally we have averaged over all the 10, 000 sets of channel coefficients to obtain a point of the plot.

In the plots we can see that even if our approach only requires R-CSI, for most $E_s/N_0$ points it achieves on average similar or slightly higher rates than the approach in Proposition 1, which requires full CSI at the relay. For a clearer comparison, some numerical values are provided in Table 1.

Fig. 3

Comparison between the average spectral efficiency that is achievable with the approach proposed in [14] (Proposition 1) and our approach (Proposition 2) for different relative positions of the relay and the destination with respect to the transmitters. The considered parameters are $\kappa =3.52$ and $\beta =\sqrt{0.5}$, and a$d_{1,d}=d_{2,d}=d_{1,r}=d_{2,r}=d_{r,d}=1$, b$d_{1,d}=d_{2,d}=1,\;d_{1,r}=d_{2,r}=0.25,\;d_{r,d}=0.75$, c$d_{1,d}=d_{2,d}=1,\;d_{1,r}=d_{2,r}=0.5,\;d_{r,d}=0.5$, d$d_{1,d}=d_{2,d}=1,\;d_{1,r}=d_{2,r}=0.75,\;d_{r,d}=0.25$.

Table 1 Energy gain of our approach (Proposition 2) with respect to the approach proposed in [14] (Proposition 1) for the configurations described in Fig. 3 for average spectral efficiencies of 2, 4 and 6 bps/Hz or complex dimensions

In Fig. 3, we have considered $\beta =\sqrt{0.5}$ so that $\gamma$ has unit variance. Regarding the path loss exponent, we have considered $\kappa =3.52$. The reason is that this value is commonly accepted by the research community as an appropriate value (see, e.g., [34, p. 318], [35, p. 330], [36, p. 288], [37, pp. 129–131]).

Observe that, according to Table 1, in terms of data rates our approach is as good as, or even slightly outperforms [14]. The fact of obtaining gains in most scenarios can be explained because in [14], even if the best coefficients are jointly chosen for the linear combination of the relay and the destination, both linear combinations are decoded independently. For instance, consider the case in which the relay is in a deep fade while the destination has a better channel. In this situation, even if the best coefficients are chosen, the linear combination of the relay will be wrongly decoded with high probability and therefore the destination will not correctly solve the resulting equation system. Additionally, our approach lets the destination decide whether the linear combination coming from the relay can be beneficial or not, and whether such linear combination can help in decoding further linear combinations at the destination.

Finally, in order to be fair in the conclusions, although our approach does not require CSI except at the receivers, the major drawback of our approach is the computational complexity of the optimization involved in (23). The optimization involved in (19), (20) and (23) is non-linear and non-convex. Nevertheless, (19) and (20) are Mixed Integer Quadratic Programming (MIQP) problems and they can be transformed into an equivalent problem that can be efficiently solved using the branch-and-bound method (see e.g. [38, 39]). However, the optimization involved in (23) is not quadratic and there are no methods to solve it efficiently⁵. Instead, exhaustive search methods have to be used, which lead to a computational complexity that increases with the signal-to-noise ratio.

In fact, for the exhaustive search involved in (23), according to [7], the destination needs to search over all the non-zero complex integer vectors ${{\varvec{\alpha }}}_1$ and ${{\varvec{\alpha }}}_2$ in a sphere of radius $\sqrt{1+\frac{E_s}{N_0}\Vert \mathbf{h }_d\Vert ^2}$. Consequently, the complexity of (23) for the 2-user Gaussian MARC is at most ${\mathcal {O}}\left( \left( 1+\frac{E_s}{N_0}\Vert \mathbf{h }_d\Vert ^2\right) ^4 \right) ={\mathcal {O}}\left( \left( \frac{E_s}{N_0}\right) ^4\right)$.

On the contrary, the optimization problem from Proposition 1 can be solved using an algorithm provided in [14], and its complexity does not increase with the signal-to-noise ratio (${\mathcal {O}}(1)$), although such algorithm is iterative and exhaustive search is not.

6 Conclusion

In this paper we have proposed an approach for the block flat fading Gaussian MARC. After a thorough review of the literature, we found that the best approach so far was proposed by El Soussi et al in [14].

There main differences between our approach and [14] is that while [14] requires full CSI, ours only requires CSI at the receiver side and therefore, it is usable in practical communication system. We have shown that there is no rate loss if our approach is used. The counterpart is that our approach has a higher computational complexity for high signal-to-noise ratios, although the complexity is similar for lower signal-to-noise ratios.